Index Introduction Data and Methods Data Fitting growth models Finding equation Results Discussion References

Introduction

Predictions with better preciseness of adult stature are of great concern, not only for a pediatrician to decide the medical treatment especially for short children, but also for a coach of some sports to detect well-suited and/or -talented youths. To estimate adult stature, different methods have been reported (Bayley and Pinneau, 1952; Onat, 1975; Roche et al., 1975a, b; Wainer et al., 1978; Khamis, 1993; Khamis and Roche, 1994; Ali, 2000; Ali and Ohtsuki, 2001). Most of the above researchers predicted adult stature through skeletal age. It is possible to predict adult stature through asymptotic curve fitting only with longitudinal individual stature.

To estimate biological parameters, fitting parametric and non-parametric growth models have been attempted. Fitting curves to individual stature growth records permits the extraction of a maximum amount of information about child growth. When fitted growth-curve parameters are available for a large number of children, mean parameters and variation are a convenient way of summarizing a large amount of data for comparison of growth patterns between sexes or between populations (Thissen et al., 1976). Therefore, fitting curves provides a convenient means of characterizing individual or group differences in the pattern of growth.

To get greater precision with more accuracy, researchers are dealing with different models (e.g. Jenss and Bayley, 1937; Count, 1943; Bock et al., 1973; Preece and Baines, 1978; Berkey and Reed, 1987; Jolicoeur et al., 1988; Karlberg, 1989; Jolicoeur et al., 1992; Bock et al., 1994; Ledford and Cole, 1998; Ali, 2000). However, for a good prediction, it is necessary to select a good model. Jolicoeur et al. (1992) declared that, till then, the double phasic growth (JPA-2) model had the best fit compared with other structural growth models. Recently, Ali and Ohtsuki (2001) pointed out that the average root mean square error of the estimate for triphasic generalized logistic (BTT) model, on average, were smaller than that for the JPA-2 model; but that their proposed equations for predicting adult stature provides biased estimates for those individuals who do not have the mid-growth spurt, due to the problem of the triphasic model itself. Hence an improvement is necessary to remove that bias. The purpose of the present study is to derive some better equations than those of Ali and Ohtsuki (2001), to predict adult stature in the Japanese.

Data and Methods

Data

Longitudinal data of stature (body length in the case of infants) of 745 Japanese children and youths (483 males and 262 females), each between 0 and 20 years old and covering birth-years of 1967 to 1977, were taken from the data set of Ali and Ohtsuki (2001). The sample size is not consistent with that of Ali and Ohtsuki (2001) because the individuals’ data sets in which the information is incomplete (i.e., having missing observations in two or more successive age classes) were not considered. Also, data sets of some of the individuals were omitted when we intended to predict adult stature and to repeat the analyses based on the Mahalanobis and Cook’s distance (Cook, 1977; Cook and Weisberg, 1982) by discarding outliers and influential data points for the growth parameters. Thus, the data considered here are free from the problem of outliers and influential data points.

Fitting growth models

The JPA-2 model (Jolicoeur et al., 1992) was given as: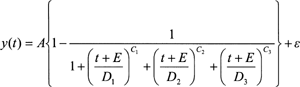

where t is the time (age) variable, y(t) is stature at age t, A is adult stature, E is a constant describing the average duration of pregnancy, D₁, D₂ and D₃ are positive age scale factors, C₁, C₂ and C₃ are positive dimensionless exponents, and ε is the error. To avoid ambiguity in the parameters, the {C, D} pairs are constrained so that D₁<D₂<D₃. Moreover, respecting the constraint that some parameters are non-negative, the initial section of growth models passing through the origin with respect to total age remains realistic even when there are few data points concerning young ages.

For the JPA-2 model, let

then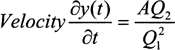

and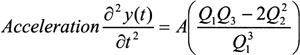

The Bock-Thissen-du Toit (BTT) model is the sum of three generalized logistic terms of the form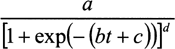

where t is the time (age) variable, a is the amount of growth contributed by the term, the quantity z=bt+c in the exponential function is the “logit,” b and c are its slope and intercept, respectively, and d is a fixed shape constant. Summing up three phases of growth, early, middle, and adolescent, the BTT model becomes

where the set of parameters (a₁, b₁, c₁), (a₂, b₂, c₂) and (a₃, b₃, c₃) refer to the parameters of early, middle, and adolescent phases of growth, respectively.

The velocity and acceleration of the BTT model can be written respectively as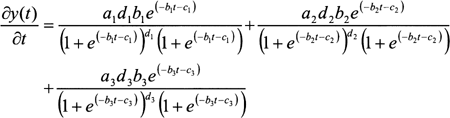

and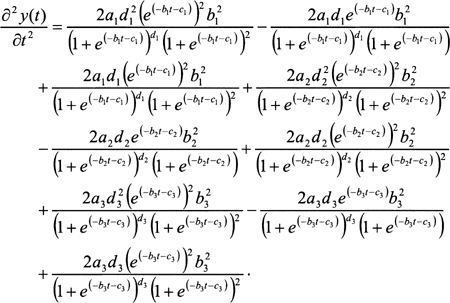

The JPA-2 model (Jolicoeur et al., 1992) and the BTT model (Bock et al., 1994) are continuous functions in time and have derivatives of all orders. They are strictly increasing functions of age and approach smoothly the horizontal asymptote that defines adult stature.

The JPA-2 model fits human stature data better than all other asymptotic models proposed till 1991 (Jolicoeur et al., 1992). However, Ali (2000) found that the BTT model fits the data better than the JPA-2 model when individual children have the mid-growth spurt. The JPA-2 model cannot show any mid-growth spurt, but the BTT model can. It is very true that fitting growth models is always data dependent. Therefore, before fitting any growth model to a data set, it is important to select an appropriate model first. The BTT model, through the AUXAL 2.01 software, is able to declare that the data have the mid-growth spurt or not on the basis of the raw data. Thus, this opportunity is used here to divide the whole data sets into two parts; one with the mid-growth spurt and the other without it. Individual data on which the BTT model was not convergent were considered as suitable for the JPA-2 model. For better precision, one would apply the BTT model on those data of individual children who have the mid-growth spurt, and the JPA-2 model on those of individual children who do not have this spurt.

The AUXAL 2.01 program arbitrarily hypothesizes that adult stature, as calculated from the model, is reached at 25 years of age. The zeroes in the acceleration curve imply maxima or minima of the growth velocity curve. The Bayes modal estimation method was used to estimate the parameters for fitting the growth model. The Bayes modal estimation process chooses from among a specified population of growth curves the one that is most probable given the data (see Bock et al. (1994) for a detailed description of the method of estimation). The AUXAL 2.01 program has default values for the population mean vector and covariance matrix in the prior distribution of the Bayes estimation for the parameters of the BTT model, and that of the JPA-2 model. These default values in AUXAL 2.01 were predicted based on data from the Fels Longitudinal Study (Bock et al., 1994). For the present study, it was necessary to substitute the mean vector and covariance matrix default values by those derived from the Japanese population. Since these were not available, they were estimated through the iteration process. For the mean vector and variance covariance matrix, for the JPA-2 model, the data of individuals without mid growth spurt, and for the BTT model, the data of individuals with mid growth spurt were used, respectively.

Growth parameters were extracted from distance, velocity and acceleration curves according to Ali (2000). These parameters from the BTT model were: age at early childhood minimum (AECM), stature at early childhood minimum (SECM), velocity at early childhood minimum (VECM), age at mid childhood maximum (AMC), stature at mid childhood maximum (SMC), velocity at mid childhood maximum (VMC), age at take-off (ATO), stature at take-off (STO), velocity at take-off (VTO), age at peak height velocity (APHV), stature at peak height velocity (SPHV), peak height velocity (PHV), and predicted adult stature (PAS). On the other hand, only the growth parameters age at take-off (ATO), stature at take-off (STO), velocity at take-off (VTO), age at peak height velocity (APHV), stature at peak height velocity (SPHV), peak height velocity (PHV), and predicted adult stature (PAS) were determined from the JPA-2 model.

Finding equation

Considering that we have to predict adult stature with respect to biological parameters, since the relationship between adult stature and biological parameters, e.g. SPHV, PHV, APHV, STO, etc. is linear (Ali and Ohtsuki, 2001), we can consider multiple linear regression of adult stature on the biological parameters. But the problem is how many variables are essential to explain the maximum percentage of variation (i.e., R²). To solve this problem, the method of forward stepwise regression with zero intercept was used (see Draper and Smith, 1966, pp. 169–171; Ali and Ohtsuki, 2001). Like Ali and Ohtsuki (2001), the problem of outliers and influential points were removed through the methods Mahalanobis distance (Stevens, 1996) and Cook’s distance (Cook, 1977; Cook and Weisberg, 1982).

Results

The JPA-2 and BTT models were run on the individual longitudinal data of stature (as described in the methodology) to find out the individual growth parameters extracted from each velocity and distance curve. Using forward stepwise regression, like Ali and Ohtsuki (2001), two parameter-variables are sufficient to explain the maximum percentage of variation by the regression equation (i.e., R²). That is, a three-variable linear regression (with zero intercept) model is found through forward stepwise method that is sufficient for predicting adult stature of the Japanese boys and girls. The model is

where β₁ and β₂ are the partial regression coefficients, and ε is the random error term assumed to be distributed normally with a mean of zero and variance of unity. A summary of the stepwise regression of the dependent variable PAS for different cases (Case 1, Case 2, and Case 3) is shown in Table 1. Case 1, 2, and 3 refer, respectively, to analysis based on the entire sample (where growth parameters are extracted from the JPA-2 and BTT models, accordingly), the sub-sample in which the mid-growth spurt exists (where growth parameters are extracted from the BTT model), and sub-sample in which the mid-growth spurt does not exist (where growth parameters are extracted from the JPA-2 model). Table 1 shows that the regression coefficients are highly significant (p<0.0000001) with small standard errors of the estimate. This table also shows that, for a three-variable regression equation, maximum R² is attained for all the cases.

Analyses of residuals for the individual cases were considered to understand the preciseness of the adult stature prediction. Average values of observed adult stature (extracted from the growth curve), predicted adult stature, and the residuals together with those (in parenthesis) of Ali and Ohtsuki (2001) are shown in Table 2. The residuals in all the cases were very small in both boys and girls. The predictions of adult stature, on average, were approximately unbiased in all the cases of boys. In the girls, a very negligible amount of bias, 0.01 cm in Cases 1 and 3 and 0.02 cm in Case 2, were found.

Discussion

In the present study, like Ali and Ohtsuki (2001), it was necessary to get STO and SPHV, which is possible after 12 years in girls and 14 years in boys, to predict adult stature. However, for clinical purpose, it would be better to predict adult stature near the onset of adolescent growth using the protocols reported by others using skeletal age (Bayley and Pinneau, 1952; Onat, 1975, 1983; Roche et al., 1975a, b; Wainer et al., 1978; Khamis and Guo, 1993). The present method does not require X-ray exposure to the subject, even though it is essential to estimate the skeletal age for clinical purposes or pediatric treatment for children of short stature. The present method is applicable not only for the purpose of sport talent detection and selection based on PAS, but also for giving advice for choosing a more suitable sport event and position from the viewpoint of PAS (Ali and Ohtsuki, 2001).

Standard errors of the estimated partial regression coefficients were very small, and smaller with those of Ali and Ohtsuki (2001) in all three cases of both boys and girls (Table 1). This implies that the present predicted equations are comparatively robust and stable. The sample sizes in Case 3 of both sexes were larger than those of Ali and Ohtsuki (2001) implying that, due to convergence and the over-parameterization problem, the BTT model is not applicable to those individual children who do not have the mid-growth spurt (Table 1). Conversely, the JPA-2 model fits well, rather than the BTT model, to those individuals who do not have the mid-growth spurt. Adult stature (both observed and predicted) for boys in Case 2 were greater than that in Case 3. However, an opposite picture was found in the girls. This may due to the characteristics of the individuals.

Predicted stature derived from the present proposed equations was closer to their corresponding observed stature (Table 2). The residuals were, on average, sufficiently smaller than those of others (Bayley and Pinneau, 1952; Roche et al., 1975a, b; Wainer et al., 1978; Khamis and Guo, 1993; Khamis and Roche, 1994; Ali and Ohtsuki, 2001). Also, standard deviations of the residuals in the present study imply that they were closer to their mean value compared with those of others (Bayley and Pinneau, 1952; Roche et al., 1975a, b; Wainer et al., 1978; Khamis and Guo, 1993; Khamis and Roche, 1994; Ali and Ohtsuki, 2001). Standard errors of PAS in the present study (Table 2) were smaller than those of some others (Onat, 1975, 1983; Ali and Ohtsuki, 2001). The 90% confidence bounds of the residuals of the present study (Table 2) indicate better prediction than those of some others (Roche et al., 1975a; Wainer et al., 1978; Khamis and Roche, 1994; Ali and Ohtsuki, 2001). The difference in the 90% confidence bounds of the present study and that Ali and Ohtsuki (2001) is remarkable. These are for boys Case 1: 0.149 cm versus 5.426 cm, Case 2: 0.201 cm versus 1.704 cm, Case 3: 1.009 cm versus 6.960 cm; and for girls Case 1: 0.328 cm versus 7.100 cm, Case 2: 0.615 cm versus 3.909, and Case 3: 0.315 cm versus 8.279 cm. The extent of the confidence bounds of the residuals in Ali and Ohtsuki (2001) is 36.4 times greater in Case 1, 8.5 times greater in Case 2, and 6.9 times greater in Case 3 for boys. In the girls these values were 21.6 in Case 1, 6.4 in Case 2, and 26.3 in Case 3. This extreme reduction of the 90% confidence bounds of the residuals in the present study indicates a better preciseness of the prediction equations.

The predicted errors of the proposed equations are thus comparatively more condensed around zero. This is interpreted to have happened due to 1) division of the data into two parts (having the mid-growth spurt and without the mid-growth spurt) as well as the omission of the over parameterization of the growth models, and 2) removing of the outliers and influential data points. Thus, from every point of view, the proposed equations for the prediction of the adult stature in the present study are better than those of Ali and Ohtsuki (2001). These equations are