| Collected Papers in Honor of Professor Emeritus Banri Endo: Commemoration of His Seventieth Birthday GEN SUWA, Corresponding author. e-mail: suwa@um.u-tokyo.ac.jp phone: +81-3-5841-2836; fax: +81-3-5841-8453 Published online 22 April 2005 in J-STAGE (www.jstage.jst.go.jp) DOI: 10.1537/ase.050118 |
In human and primate evolutionary studies, molar enamel thickness has been most extensively studied by sectioning the crown through the mesial cusps, and measuring thickness in that section (hereafter the MCS) (reviewed for example in Smith et al., 2003; Kono, 2004). Since the pioneering work of Martin (1983, 1985), a standard investigative approach has been to quantify the amount of enamel in the MCS by means of an ‘average’ thickness of enamel (e.g. Martin, 1985; Shellis et al., 1998; Martin et al., 2003; Smith et al., 2003). This is obtained by dividing enamel area by enamel dentine junction (EDJ) length in the MCS. The more appropriate 3-dimensionally based equivalent can now be derived from high-resolution data sets of whole crown enamel and dentine distributions (Kono, 2004), i.e. an ‘average’ thickness defined as enamel tissue volume divided by EDJ surface area. The significance of these parameters of ‘average’ thickness can be sought in their utility as a geometric summary of thickness, and as an estimate of average ameloblast secretory activity to the extent that ameloblast size could be considered comparable among individuals or taxa.
Other studies of human and primate molars have focussed on linear measures of enamel thickness in the MCS, and suggested that differential patterns within a molar contain functional and/or taxonomic information (e.g. Macho and Berner, 1993, 1994; Schwartz, 2000a). Regarding human molars, Macho and Berner (1993, 1994) reported the presence of a significant degree of serial difference in enamel thickness of the upper molars, although this was less apparent in subsequent studies of the lower molars (Schwartz, 2000b; Grine, 2002). Macho and Berner (1993) documented absolutely thicker enamel at the cusp tips and occlusal slopes in the MCS of the two posterior upper molars (upper M2 and M3) in comparison with the first upper molar (upper M1). They interpreted this and further details of buccal and lingual enamel thickness patterns to coincide with the hypothesized posterior increase of occlusal force and predisposition to a helicoidal wear pattern (Macho and Berner, 1993, 1994). Grine (2002, 2005) looked primarily at MCS enamel cross section area and relative enamel thickness, and suggested that it is only thickness relative to crown size that differs serially; he hypothesized that this effect is related to a posterior size reduction of the molar row and not to functional adaptation.
In the present study, by means of non-destructive micro-CT (computer tomography) based methodology and analysis, we investigate enamel thickness in the MCS of human molars on the largest sample (n = 167) yet reported. For each of six permanent molar positions, our sample sizes are between 19 and 37, i.e. approximately two to three times the size of each of the samples of the previous studies. Our aim is to provide baseline information, considerably better than currently available, on within-tooth, serial, and individual variation of linear enamel thickness in the MCS of human molars. We further aim to discuss the significance of the various measures of linear enamel thickness in the MCS, viewed from a whole crown 3-dimensional perspective (Kono et al., 2002; Kono, 2004). In doing so, we will make apparent some limitations inherent in traditional methodologies based on 2-dimensional sections. We then evaluate hypotheses (e.g. Macho and Berner, 1993, 1994; Schwartz, 2000b; Grine 2002, 2005) that relate to thickness dominance of the ‘functional’ (buccal in lowers and lingual in uppers) as opposed to the ‘non-functional’ (or ‘guiding’) side cusps, and the presence (or absence) of a positive serial gradient of thickness from M1 to M3. Additionally we intend to provide some realistic inferences on the magnitude of normal intraspecific (individual) variation in linear measures of enamel thickness, and investigate how controlled measures of linear enamel thickness relate to whole crown volumetric parameters. We are specifically interested in the latter because of the increasing interest in the enamel thickness of Mio–Pliocene fossil hominid taxa, hitherto based on few and ill-controlled linear observations of thicknesses (e.g. White et al., 1994; Senut et al., 2001; Brunet et al., 2002; Pickford and Senut, 2005; Semaw et al., 2005).
The human molar sample of the present study consists of archeologically derived, unworn, recent (mid 17th to mid 18th century, in the Edo period) and Holocene (ca. 2000–500 BC, in the Jomon period) Japanese permanent molars of the Kono (2004) series, and a larger series taken from jaws or associated dental sets of archeologically excavated individual burials from the Libben site, northern Ohio, USA, dating from 800–1100 AD (Lovejoy et al., 1977). The Libben sample of the present study consists of a total of 139 molars: 29 lower M1, 26 lower M2, 20 lower M3, 28 upper M1, 20 upper M2, and 16 upper M3. The Kono (2004) series, totaling 28 molars, includes eight lower M1, eight lower M2, three lower M3, and three each of upper M1, M2, and M3. The Kono (2004) series was also used to investigate the relationship between the MCS linear and 3-dimensionally based whole crown or cusp measures of thickness. Only teeth that are completely unworn, as determined from examination of the molar under a low-powered binocular microscope, were measured. Thus, the present sample includes only one molar from each upper or lower jaw of each individual, and is serially, effectively, a ‘cross-sectional’ sample (i.e. the serial positions are represented by different individuals).
Sex is unknown for most of the specimens since they were taken from juvenile individuals. Although this precludes analysis of potential sexual differences, absolute enamel thickness in molars have been reported not to differ significantly between sexes (e.g. Harris et al., 2001; Hlusko et al., 2004). Little is known concerning differences in molar enamel thickness among human populations, although a recent study based on conventional radiography reported a significant difference in deciduous molar enamel thickness between American ‘black’ and ‘white’ population samples (Harris et al., 2001). In the present study, specimens from three populations were combined because of the comparatively large individual variation within samples, and because the results of the basic statistics of only the Libben sample did not differ in any important way from the combined-sample analysis. We do note, however, that the potential presence of significant populational differences in enamel thickness is a largely unexplored matter, which merits attention in future studies.
Each molar was scanned at the micro-CT facility of the University Museum, the University of Tokyo (TX225-Actis, Tesco Corporation) with a tube voltage of 130 kV and current of 0.12 mA, using a 0.2 mm copper plate filter to lessen beam hardening effects. The scanning was performed at an SOD (source to object) to SID (source to detector) ratio of approximately 1:12, which enabled a pixel size of 28 microns in 512 by 512 matrix reconstructions. Size calibration was conducted to an accuracy of approximately 0.1% by scanning an aluminum rod of known diameter and empirically adjusting the SOD value. For each molar, a total of 231–378 horizontal cross section images were taken to obtain isotropic voxels that cover the entire molar crown. The entire volume data set of each molar crown was reduced to half resolution (56 micron voxels) for ease of measurement. Half maximum height linear measures were confirmed to be sufficiently accurate at either 28 or 56 micron voxel resolutions.
The acquired volume data set of each molar was standardized in orientation as follows. Each molar was initially placed in the scanner with the anatomical tooth axis set vertical, as visually assessed. Using the CT derived volume data set of the whole crown, we then redefined the horizontal plane of the tooth by a digitally based technique (Suwa and Kono, 1998; Kono, 2004). We empirically determined the orientation of each molar that maximizes the projected area of the occlusal surface (defined on the EDJ), and then rotated the entire volume data set to that orientation. This adjustment of orientation was usually within about 5–10° of tilt in mesiodistal and/or buccolingual directions from the initial visually determined orientation. We then rotated the volume data set around the new vertical axis so that the EDJ tips of the two mesial cusps lie in the same orthogonal plane of reference (Figure 1). The reformatted cross section image that runs through both protoconid and metaconid EDJ tips was designated the mesial cusp section (MCS). Linear enamel thicknesses were measured on the MCS. The half maximum height method was applied to derive thickness values at sub-pixel resolution, using tools developed by the authors as a part of the CT-Rugle software (Medic Engineering).
 View Details | Figure 1. Derivation of the mesial cusp section. (a) Left, original horizontal section at a level just below the dentine tips of the two mesial cusps; right, vertical section running through the protoconid but not through the metaconid EDJ tips. Line indicates the position of the vertical section. (b) Left, horizontal section after the entire volume data set of the molar crown was reoriented into a position that maximizes the projected occlusal surface area defined on the EDJ; right, vertical section running through the protoconid but not through the metaconid EDJ tips. (c) Left, horizontal section after the entire volume data set of (b) was rotated around a vertical axis so that protoconid and metaconid tips are aligned; right, vertical section running through both protoconid and metaconid EDJ tips, and an example of a thickness measure. |
Problem of section position
Previous studies that supposedly examined enamel thickness in the MCS of physically sectioned teeth suffer from the fact that it is not clear if the EDJ cusp tips were actually represented in the measured section. In contrast, the EDJ cusp tip position is resolved to within 28 microns in the present study, and this is the case, simultaneously, for both buccal and lingual cusps.
In past attempts to obtain the MCS, there appear to be two general methods of physical sectioning: (1) make a section through the cusp tips determined on the outer enamel crown surface (OES), and assume that the EDJ cusp tips occur within the thickness of the section, (2) make a section through or distal to the OES cusp tips, and lap the section face(s) to reveal the EDJ cusp tips.
With the former methodology, taken mostly in the earlier studies (e.g. Martin, 1983, 1985; Grine and Martin, 1988), the molar is cut through the two OES cusp tips, and enamel thickness is measured on either or both sides of the section (i.e. the remaining block faces). The stated assumption was that the actual EDJ cusp tip would lie within half the width of the lost thickness of the physical section. Section thicknesses were reported to be between 70 and 350 microns in the above-cited studies, depending on the cutting apparatus used. However, in reality, the EDJ cusp tips may occur outside such a zone of section determined from visual inspection of the OES. Because of this, Macho and Berner (1993) sectioned molars through the mesial OES cusp tips, and then lapped down the section faces as seemed necessary. In a more recent study (Martin et al., 2003), with a thinner initial cut of 50 micron thickness, a second section was made so that enamel thickness would be measured on two section faces separated by 200 microns. Either of the two section faces was assumed to approximate the ideal section running through the EDJ cusp tips.
Dean and Schrenck (2003) and Grine (2005) explicitly cut molars distal to the two mesial OES cusp tips. They then lapped down the mesial block face so that the actual EDJ cusp tip was seen on the physical section. This method appears to be potentially accurate for at least one EDJ cusp tip, but because lapping the section is done parallel to the initial arbitrarily formed plane of section, it would be unusual for both EDJ cusp tips to actually come to lie in the same plane of section. Thus, it is likely that one or the other of the EDJ cusp tips was off the plane by an unknown distance. Others made a thin section through the mesial cusps, and lapped this from either side to reveal the EDJ apices (e.g. Beynon et al., 1998; Reid et al., 1998). This method would be accurate so long as the EDJ cups tips occurred within the initial thin section.
Thus, despite the accuracy that is often claimed (e.g. “…ensuring that the section plane traversed both cusp tips and dentine horns…” Schwartz, 2000b), it is highly likely that in most cases, the measured sections did not correspond to the actual MCS. An instructive example was shown by Smith et al. (2003) who cut several sections in addition to the section that was initially measured as representing the MCS (Andrews and Martin, 1991). In that case of an Ouranopithecus molar, the mesial-most section of Smith et al. (2003), at an unstated distance from the initial section of Andrews and Martin (1991), exhibited a more salient EDJ cusp profile and a smaller enamel thickness value, indicating that the initially measured cross section was considerably off from the MCS. Similarly, we recently examined the measured block faces of an Australopithecus robustus molar sectioned by Grine and Martin (1988). In this case, both EDJ cusp tips occur internally within the remaining mesial tooth block, offset from the plane of physical section by over 0.6 mm (unpublished data).
Because of these problems inherent in physical sections, we believe that the present study is the first to actually document enamel thickness in a strictly defined MCS. Our prediction is that, in previous studies, measurement items such as cusp tip thickness that are affected by slight offsets from EDJ tips would be overestimated. This would be coupled with inflated variance from lack of consistency in section position relative to the actual MCS. In the present study, using a subset of ten Libben molars for each molar position of each jaw, we examined the effects of section position offsets on cuspal thickness measurements. This was done by comparing each measure of thickness in the MCS and in sections offset by approximately 0.15, 0.3, and 0.6 mm (3, 5, and 11 pixels) in both mesial and distal directions.
Problems in the definition of ‘radial’
Occlusal and lateral enamel thicknesses have been stated to be measured either perpendicular to the EDJ or ‘radially’. Martin (1983) illustrated his concept of ‘radial’ enamel thickness as a minimum measure of thickness running from a schematic cone-shaped EDJ and encasing OES surfaces. In such a simplified example, a measure perpendicular to the EDJ would indeed be both the minimum measure and ‘radial’ with regards to the cone. However, in reality, both EDJ and OES exhibit continuously curved surfaces, even with regards to the relatively simple lateral crown topography. Kono et al. (2002) discussed the actual complexity of defining ‘radial’ thicknesses between two continuously changing 3-dimensional surfaces, and proposed that ‘radial’ measures can be defined in reference to both OES and EDJ surfaces. Such two sets of measures would reflect slightly different information regarding enamel distribution and thickness patterns.
With regards to linear measures of thickness in the MCS, we consider occlusal thickness and ‘radial’ thickness of the lateral crown to be potentially affected by the definition of ‘radial’. Most authors defined occlusal enamel thickness to be taken perpendicular to EDJ (e.g. Grine and Martin, 1988; Macho and Berner, 1993; Schwartz, 2000a, b; Grine, 2005), although the same measurements were termed ‘radial’ by Martin (1983). Enamel thickness of the lateral crown has been defined as either perpendicular to the EDJ (e.g. Schwartz, 2000a; Grine, 2005) or as perpendicular as possible to both OES and EDJ (Macho and Berner, 1993). Both occlusal and maximum lateral thicknesses have been taken at designated distances from the EDJ apex (Schwartz, 2000a, b; Grine, 2005), or more flexibly as a maximum possible measure at EDJ positions at or away from such defined positions (Macho and Berner, 1993).
From our own 3-dimensional whole crown perspective (Kono et al., 2002; Kono, 2004), we note that a strict perpendicular definition at times results in trajectories oblique to the enamel layer under consideration, potentially yielding excessively large thickness values depending on the topography of EDJ and enamel distribution itself. The examples shown in Figure 2 suggest that a minimum distance from the EDJ (or OES) should be the preferred definition of a ‘radial’ measure in most locations of a molar. An exception to this is with the MCS occlusal enamel as discussed below.
 View Details | Figure 2. Examples of oblique trajectories of occlusal and lateral enamel thickness measures taken perpendicular to the EDJ (dotted lines), influenced by local undulations of the EDJ. The solid lines are the measures employed in this study. |
Linear measures of enamel thickness taken in the present study
From the foregoing methodological considerations, six linear measurements were taken on the MCS for the purpose of the present study. These were cuspal thickness, maximum occlusal thickness, and maximum ‘radial’ thickness of the lateral crown face taken for each of the two mesial cusps (Figure 3). ‘Radial’ is here defined as the minimum distance from a point on the EDJ to the OES. Some further comments regarding our choice of definitions are as follows.
 View Details | Figure 3. Enamel thickness measures taken in the mesial cusp section. 1, cusp tip thickness taken from the EDJ tip to the superiormost point on the OES cusp contour; 2, maximum occlusal thickness taken perpendicular to a line drawn from the EDJ cusp tip to the longitudinal groove of the EDJ occlusal basin; and 3, maximum lateral thickness, taken as the maximum ‘radial’ thickness measured from any point of the EDJ lateral crown face. |
In contrast to previous studies, we defined occlusal enamel thickness in relation to the overall orientation of the occlusal EDJ of each of the mesial cusps. We did so because we found ‘radial’ thicknesses from local EDJ positions of the occlusal EDJ to be influenced by both occlusal grooves and thin cuspal enamel (documented below). This sometimes results in underestimated maximum ‘radial’ thickness values and/or trajectories that follow an oblique path within the occlusal basin enamel. Lateral enamel thickness was measured as the maximum ‘radial’ thickness in the MCS, rather than being restricted to a defined distance from the EDJ tip (e.g. 0.5 mm or 1 mm). We made this choice because we were interested in documenting the magnitude of absolute enamel thickness of the lateral crown face, rather than investigating the effects of subtle distribution patterns within the lateral crown (which would be reflected in set position measures). Finally, we defined and measured mid-lateral crown thickness at the level of the lower-most point of the MCS EDJ contour in our digitally determined molar orientation (see above), but will report the results of this elsewhere (Kono and Suwa, in preparation). Our measure of mid-lateral crown thickness is not comparable to the equivalent measures of previous studies based on orientation by the OES cusp tips (Martin, 1983), the EDJ cusp tips (Grine and Martin, 1988; Grine, 2002, 2005), or the cervical line (e.g. Macho and Berner, 1993, 1994).
Relationship of the linear and 3-dimensional volumetric measures
Using the Kono (2004) dataset, the MCS linear measures were compared with 3-dimensionally based whole crown (and cusp) measures of thicknesses. This was done to examine the correspondence between linear measures and 3-dimensionally based, more comprehensive parameters of enamel thickness. In doing so, we hoped to evaluate the relative utility of the linear measures of thickness in representing regional and whole crown thicknesses.
One of our interests is to see which, if any, of the MCS linear measures actually track the 3-dimensionally based regional (cuspal) patterns of thickness documented by Kono (2004). For example, MCS occlusal thickness is expected to vary considerably according to the details of OES morphology (occlusal ridges and crenulation). We predict that linear occlusal thickness taken in the MCS has relatively high variance, and is likely to be an inadequate indicator of occlusal thickness of an entire cusp. Another focus of our interest is to see if any of the linear MCS measures of thicknesses would be reasonable estimators of whole crown thickness. We expect such information to be of use in interpreting fossil specimens, for which thickness measures are often available only in limited locations of the tooth.
 View Details | Figure 4. Enamel thickness at the mesial cusp section and at sections offset by approximately 0.15, 0.3, and 0.6 mm, plots of the lower M1 are shown as examples. Section position (x-axis) and thickness (y-axis) are given in mm. The mesial cusp section is depicted at section position 0, mesial sections are to the left, and distal sections are to the right. Box plots show the median, range of the central 50% values, range within the inner fence, and outliers (asterisks and circles). Variable names are as follows: BCTTIP and LCTTIP, buccal and lingual cusp tip thickness, respectively; BOCMAX and LOCMAX, buccal and lingual occlusal maximum thickness, respectively; BLATMAX and LLATMAX, buccal and lingual lateral maximum thickness, respectively. |
The magnitude of differences in measured enamel thickness with small changes in section position varies according to the measure of thickness. In particular, thickness values of the cusp tips were found to differ to a striking degree. Figure 4 shows some examples in which mean cusp tip thickness values of the lower M1 are seen to increase proportionally as the section departs from the MCS. In our test samples of 10 molars per jaw and serial position, with an offset of 0.6 mm, mean cusp tip thicknesses were overestimated by 0.3 to over 0.7 mm (20–90%), and by over 0.2 mm with an offset of about 0.3 mm. The central tendencies of the other measures of thickness were affected less.
Figure 5 depicts individual variation in the effects of a 0.6 mm offset. Cusp tip values were systematically overestimated, by up to over 1 mm in individual molars. Occlusal thickness values were also inaccurate by over 0.5 mm, with the added uncertainty that either underestimation or overestimation was the case depending on the specimen. Lateral enamel thickness was much less affected. Maximum lateral thickness values were generally accurate to within around 0.2 mm in individual molars, with mean values within 0.1 mm or 6% of the MCS value. The exception to this was lingual lateral enamel in the mesially offset sections, which exhibited a systematic bias wherein enamel thickness tended to be overestimated by up to 0.5 mm individually (mean overestimation 0.25 mm). The likely cause of this bias is the abbreviated mesiolingual crown contour in both upper and lower molars that makes a plane parallel to the MCS increasingly oblique mesially.
 View Details | Figure 5. Thickness difference between the mesial cusp section and sections offset by 0.6 mm. Thickness difference (y-axis) is given in mm; m, mesial offset; d, distal offset. Box plot formats and variable names are as in Figure 4. |
The basic statistics of the six linear MCS measurements of the modern human sample of the present study are given in Table 1 and their box plots are shown in Figure 6. The mean thickness values of the six linear measurements of the lower molars were 0.94–1.62 mm, 1.33–1.86 mm, and 1.25–1.78 mm in the M1, M2, and M3, respectively. The corresponding ranges in the upper molars were 0.85–1.76 mm, 1.35–1.95 mm, and 1.49–1.94 mm in the M1, M2, and M3, respectively. The large ranges shown by the mean values indicate the existence of considerable within-tooth thickness variation, and a closer look reveals some distinct patterning.
 View Details | Figure 6. Box plots of the six linear measures of enamel thickness of the mesial cusp section. Thickness (y-axis) is given in mm. Box plot formats and variable names are as in Figure 4. |
The buccal cusp tips had the thinnest enamel in the lower M1 and all three upper molars, while, in the lower M2 and M3, the thinnest enamel occurred at the lingual cusp tips. The thickest enamel in all three lower molars occurred at the buccal lateral crown face, while the lingual lateral enamel was thickest in all three upper molar positions. These results suggest the existence of a ‘non-functional’ to ‘functional’ side thickness gradient occurring in the cusp tip and lateral crown face enamel, with the exception of the characteristic thin enamel seen in both upper and lower M1 mesiobuccal cusps (Kono et al., 2002). Figure 7 summarizes this patterning between the corresponding buccal and lingual measures within each molar, where the ‘functional’ side cusp was shown to have thicker enamel at the cusp tips and lateral crown face, with the exception of the lower M1 protoconid cusp tip. However, occlusal MCS enamel did not show the same pattern. With maximum occlusal thickness, buccal or lingual dominance of enamel thickness was inconsistent across individuals.
 View Details | Figure 7. Buccolingual difference in enamel thickness. DIFCTTIP, DIFOCMAX, DIFLATMAX are the difference between the corresponding buccal and lingual thickness values (buccal minus lingual) of the cusp tip, maximum occlusal, and maximum lateral thicknesses, respectively. Thickness difference (y-axis) is given in mm. Box plot formats are as in Figure 4. |
Serial differences in thickness were found to be generally statistically significant between the M1 and the two posterior molars, but not between M2 and M3 (Table 2). However, the magnitude of such differences differed considerably among measures. The buccal cusp tips of both upper and lower molars showed the largest serial differences in thickness; the M1 buccal cusps had mean enamel thickness of only about 60% of the two posterior molars. However, the lingual cusp tips of both upper and lower molars and the other measures of thickness showed about a 10–15% magnitude of difference between the M1 and the two posterior molars in mean values. An exception to this was the occlusal and lateral enamel of the lingual lower molar crown, which were more comparable in thickness among serial positions.
We evaluated the magnitude of variation in the linear MCS measurements by means of the coefficient of variation (CV) (Table 3). Lateral enamel thickness tended to be the least variable (CVs of 7.2–9.3 in M1 and M2, and 9.1–13.3 in M3), approaching, but larger than, the CV values of traditional crown diameters (e.g. Kieser, 1990). The next least variable was occlusal thickness with CV values ranging generally between 10 and 15. Cusp tip measures were the most variable with CV values of mostly around 15–20.
Using the Kono (2004) data set, we investigated the relationship of the MCS linear measures with four of our 3-dimensionally based, more comprehensive measures of enamel thickness. One of these was the conventional 2-dimensional average enamel thickness (AET2D, the MCS cross section area of enamel divided by EDJ length), and another is the 3-dimensional average enamel thickness (AET3D) defined in Kono (2004) as enamel volume divided by EDJ surface area. In addition to these parameters, we calculated 3-dimensional average enamel thickness of the occlusal surface of the mesiobuccal and mesiolingual cusps (OAETMBC and OAETMLC, respectively).
Correlation between the linear measures and AET2D tended to be generally high, a finding that is not surprising in light of the fact that both were taken on the same MCS (Table 4). The linear measures also tended to exhibit relatively high correlations with whole crown enamel thickness as represented by AET3D, with the exception of the cusp tip measures which tended to show lower correlations. The MCS linear measures showed moderate to low correlations with the 3-dimensionally derived average enamel thickness of the occlusal surface of the two mesial cusps. Of note is that the corresponding linear measures of occlusal enamel thickness in the MCS appeared to be no better a predictor of overall occlusal thickness of the cusp (as represented by the average enamel thickness values) than the other linear measures of thickness.
Despite past reports and discussion of within-tooth and serial patterns of enamel thickness in human molar crowns (e.g. Macho and Berner, 1993, 1994; Schwartz, 2000b; Grine, 2005), we consider the present study to be the first unambiguous description of linear enamel thickness in the MCS. Sections that are offset from the true MCS, by definition, produce inaccurate thickness values. A likely example is the cusp tip mean thickness reported by Schwartz (2000b), the values of which are 0.5–1 mm greater than those of the present study. The Macho and Berner (1993) and Grine (2005) data sets are much closer to that of the present study, but their cusp tip mean values are nevertheless consistently 0.1–0.3 mm greater than those of this study. The implication is that especially the Schwartz (2000b) data set tended to be offset from the true MCS, which is also suggested from his inflated CV values, which range from 20 to 30 in both cusp tip and occlusal basin thicknesses (Table 3).
Previous discussions on the functional significance of enamel thickness depended on detailed assessments of MCS thickness values of the cusp tips and occlusal basins; some of these observations are not supported by the results of the present study. For example, the case for enamel thickness being part of an adaptation to helicoidal wear rested on the supposed change in direction of the buccolingual thickness gradient of the MCS occlusal enamel between the upper M1 and M2, and an increase of intensity of the same from M2 to M3 (Macho and Berner, 1994; Schwartz, 2000b). Such a pattern was not observed in the present study, a conclusion also reached by Grine (2005). Our controlled section data also caution that slight differences in section position could be a potential source of large deviations not only in the thickness values themselves but also in, for example, the direction of buccolingual thickness gradients.
The present study confirmed the presence of extremely thin enamel at the mesiobuccal cusp tips of both upper and lower M1s, which is not readily interpreted from a perspective of adaptation to masticatory function (Kono et al., 2002; Kono, 2004; Grine, 2005). With our own MCS data set, cusp tip thickness values were more variable than the other measures, but nevertheless showed an interpretable pattern regarding buccolingual thickness gradients. In both upper and lower M2s and M3s, the ‘functional’ side cusp tips (protoconid in lowers and protocone in uppers) had thicker enamel, but there was no significant difference in degree of buccolingual differences between the M2 and M3. In the M1, apparently because of the characteristically thin cusp tip enamel in both protoconid and paracone, the buccolingual gradient of thickness seen in the M2 and M3 was enhanced in the upper M1 and reversed in the lower M1.
Occlusal enamel thickness in the MCS was less variable than cusp tip thickness as assessed by CV values, but its within-tooth pattern was not readily interpretable. The buccolingual gradient in MCS occlusal thickness was variable and its direction inconsistent across individuals. This appears to be caused largely by variation in occurrence, placement, and development of occlusal ridges. In addition, because correlations between the linear MCS and whole cusp occlusal thickness measures were not high (Table 4), a more appropriate evaluation of buccolingual gradients in occlusal surface enamel would be to look at the 3-dimensionally based average thickness values of each cusp themselves. Although data available for such evaluations are still limited, we investigated this aspect using the 3-dimensional data set reported by Kono (2004). Our results show the probable existence of a pattern similar to that exhibited by cusp tip enamel (Figure 8). In both upper and lower M2s and M3s, occlusal enamel appears to be thicker on the ‘functional’ rather than the ‘non-functional’ side, while the thin M1 mesiobuccal cusp appears to enhance such a thickness gradient in the upper M1 and mask it in the lower M1.
 View Details | Figure 8. Buccolingual difference in average occlusal enamel thickness. Three-dimensionally based average enamel thickness of the occlusal surface was derived separately for each cusp by dividing occlusal enamel volume by occlusal surface EDJ area in each of the cusps. DIFOAET is the difference between the buccal and lingual values (buccal minus lingual). Thickness difference (y-axis) is given in mm. Box plot formats are as in Figure 4. |
Maximum lateral thickness in the MCS was least variable as assessed by the CV values. Buccolingual differences of MCS lateral enamel thickness exhibited a clear pattern of dominance of the ‘functional’ over the ‘non-functional’ side in all six molar positions. Among the three upper molars, there were no significant differences in the degree of lingual dominance. In the lower molars, M1 showed a significantly weaker degree of buccal dominance compared to the M2 and M3 conditions. We wonder if this subtle serial pattern seen in the mandibular molars is an artifact of methodology. For example, lingual lateral thickness may be systematically overestimated in the MCS, as evinced by the consistent pattern of overestimated thickness values in the mesially offset control sections (Figure 5). We wonder if this relates to the obliquity of the lingual MCS plane itself; lingual MCS plane obliquity increases mesially, possibly resulting in inflated thickness values.
In order to assess the likelihood of such a possibility, we recorded an additional lateral thickness measure taken on newly reformatted sections oblique to the MCS. We assessed OES and EDJ lateral contours in successive horizontal gray scale CT sections from the level of the EDJ tip downwards, and visually chose the direction in which a vertical section oblique to the MCS appeared to intersect the lingual (or buccal) crown EDJ and OES contours at overall a more ‘radial’ situation. We then rotated the entire volume data set, and measured maximum lateral enamel thickness in the newly reformatted section (hereafter the ‘radial’ section) (Table 1, Figure 9). This was done separately for both buccal and lingual cusps.
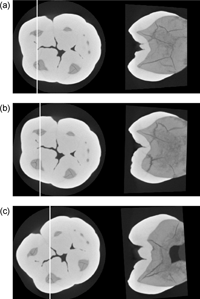 View Details | Figure 9. Derivation of the ‘radial’ section at each of the mesiobuccal cusps. (a) Right, the mesial cusp section; left, line indicating the position of the MCS. Note that the mesial cusp section appears to intersect the buccal and lingual crown contours somewhat obliquely. (b) Right, reformatted ‘radial’ section running through the protoconid tip; left, position of the ‘radial’ section. (c) Right, reformatted ‘radial’ section running through the metaconid tip; left, position of the ‘radial’ section. |
The results of this exercise were instructive in two ways. In the lower molar, we confirmed that lateral enamel thickness of the ‘radial’ section (lingual M1 and buccal side of all three molars) was significantly thinner than the corresponding MCS measure (paired t-test, 1% level), suggesting that the MCS may indeed not necessarily coincide with the ideal ‘radial’ section that gives the minimum thickness values. The upper molars showed a similar situation; in buccal M1 and lingual M2 and M3, lateral thickness of the ‘radial’ sections was significantly thinner than that of the MCS (paired t-test, 1% level). However, the magnitude of such differences between the MCS and ‘radial’ section thickness was small (mostly within ca. 0.04–0.05 mm in mean values). Furthermore, the general pattern of the resulting serial and buccolingual thickness gradients changed little.
To answer the question posed above concerning the degree of buccal dominance in lateral enamel thickness in the lower M1 relative to the M2 and M3 conditions, measurements taken in the reformatted ‘radial’ sections showed a pattern similar to that of the MCS analysis (Figure 10), with a statistically significant difference between the M1 and the two posterior molars (ANOVA). We interpret this to be yet another likely manifestation of the characteristically thin enamel at the mesiobuccal cusp tip of the M1, which apparently results in the weaker buccal dominance in lateral enamel thickness of the lower M1. That this is so is suggested by the reformatted ‘radial’ section thickness values of the upper molars. When the possible effects of MCS obliquity were removed, the lateral enamel thickness of the upper M1 was seen to possess a significantly greater degree of lingual dominance compared to the two posterior molars (ANOVA). This enhancement of buccolingual gradient in lateral enamel thickness of the upper M1 is likewise likely to be associated with the characteristically thin M1 mesiobuccal cusp tip enamel.
 View Details | Figure 10. Buccolingual difference of lateral enamel thickness taken in the ‘radial’ sections. DIFLATRAD is the difference between the corresponding buccal and lingual lateral thickness values (buccal minus lingual) of the ‘radial’ sections. Thickness difference (y-axis) is given in mm. Box plot formats are as in Figure 4. |
Serial variation in enamel thickness also featured prominently in past attempts at functional interpretations. While Macho and Berner (1993, 1994) suggested that absolutely thicker cuspal and occlusal enamel of the posterior molars reflect higher masticatory loads occurring in the posterior molars, Grine (2002, 2005) pointed out that MCS enamel cross section areas do not differ significantly across serial position, and suggested that it is rather an increase in relative enamel thickness that occurs posteriorly due to tooth crown size reduction. Kono (2004) showed in her 3-dimensional data set that volume-based measures of enamel thickness do not differ significantly between M1 and M2.
The results of the present study concerning serial differences in the linear measures of MCS enamel thickness are largely in accordance with previous reports (Macho and Berner, 1993, 1994; Grine, 2002, 2005). However, we emphasize that it is an M1 to posterior molar contrast as opposed to a general increase of thickness distally along the molar row; in our own data set none of the M2–M3 contrasts were significant. We found significant differences in thickness between the M1 and the two posterior molars in most of the linear measures, the exceptions being occlusal and lingual lateral thickness of the lower molars. We note here again that lingual lateral thickness may be affected by obliquity of the MCS section, and that occlusal MCS thickness is a potentially ‘unstable’ measure (see above). With maximum lateral thickness of the reformatted ‘radial’ sections, lingual enamel of both upper and lower M1 was found to be significantly thinner than that of the M2 (Table 2, Figure 11), but not of the M3. The situation with occlusal surface enamel is less clear, but when results of the Kono (2004) control data set are examined (Table 2, Figure 12), only the buccal cusps appear to exhibit an M1 to posterior molar gradient in occlusal thickness as represented by average enamel thickness. Whole cusp occlusal thickness of the lingual cusps appears to be more comparable among serial positions in both upper and lower molars. Thus, although the results of the present study do confirm that, relative to the M2 and M3, the human M1 tends to be characterized by thinner enamel, this was not so in all measured locations. In particular, the observed M1 to posterior molar differences in thickness, rather than being emphasized in the ‘functional’ side cusps, were more strongly expressed in the buccal cusps of both upper and lower molars (Table 2, Figure 6, Figure 11, Figure 12). This again suggests the influence of the thin mesiobuccal cusp enamel of the M1.
 View Details | Figure 11. Box plots of the lateral enamel thickness taken in the ‘radial’ sections. BLATRAD and LLATRAD refer to buccal and lingual lateral maximum thickness, respectively. Thickness (y-axis) is given in mm. Box plot formats are as in Figure 4. |
 View Details | Figure 12. Box plots of average enamel thickness of the mesiobuccal and mesiolingual cusp occlusal surfaces (OAETMBC and OAETMLC, respectively). Three-dimensionally based average enamel thickness was derived separately for each cusp by dividing occlusal surface enamel volume by occlusal surface EDJ area in each of the cusps. Thickness (y-axis) is given in mm. Box plot formats are as in Figure 4. |
The sum of the above evidence suggests that there is a consistent buccolingual gradient in enamel thickness that affects molars of all serial positions of both jaws, so that enamel of the ‘functional’ side cusps tend to be thicker than that of the ‘non-functional’ side in cusp tip, occlusal, and maximum lateral crown measures, with the exception of the effects of the characteristically thin enamel at and around the mesiobuccal cusp tips of both upper and lower M1. Evidence for a functionally based serial gradient in thickness between the M1 and the two posterior molars is more ambiguous, especially in light of comparable area (Grine, 2002, 2005) and volume (Kono, 2004) based measures of thickness. We reiterate here that the human M1, especially its mesial crown, is characterized by a particularly projecting EDJ cusp tip topography (Figure 13) (Macho and Berner, 1994; Kono et al., 2002; Kono, 2004), and that this appears to influence enamel distribution patterns within the molar crown. We interpret the above described serial and within-tooth patterning of enamel thickness in human molars to be a reflection of at least two superimposed factors of enamel thickness control mechanisms: (1) a factor responsive to selective pressures related to function, with the potential to differentially affect within-tooth regions, and (2) a developmental mechanism that limits thickness, and is most likely linked with steepness of EDJ topography at and around the cusp tips.
 View Details | Figure 13. Surface rendered images of the EDJ. Left, lower left M1; right, lower left M2. Mesial is to the left. |
From the above empirical evidence, we propose here a new hypothesis that concerns the regulation of ameloblast secretory activity duration. Because orientation of local EDJ surfaces is one factor that determines the direction of ameloblast movement during its secretory phase (Shellis, 1984; Risnes, 1998), as the 3-dimensionally aligned sheet of ameloblasts collectively move outwards during enamel matrix formation (Osborn, 1970; Shellis, 1984; Macho et al., 2003), distribution of cell–cell tension and/or compression within the ameloblast sheet is expected to be, in part, a function of initial EDJ topography. It is possible that, when compression and tension exceed certain threshold levels, ameloblasts terminate their secretory activity. This would explain how deep grooves are formed on occlusal surfaces where outward-migrating ameloblasts must eventually abut against each other and result in extreme cell–cell compression. Conversely, because prism orientation of lateral crown enamel at the EDJ is known to increase its horizontal component cervically (e.g. Dean, 1998), outward migrating ameloblasts must either increase in diameter (Risnes, 1998; Macho et al., 2003; but see Dean, 2004) or change their course to a more occlusally oriented one in order to prevent excessive cell–cell tension. It is of interest that prisms do actually change their course as suggested above (e.g. Osborn, 1968; Dean, 1998), and that the outermost enamel near the cusp tips has been reported to exhibit large prism diameters (Dean, 2004). We suggest that when the EDJ topography is especially steep, threshold levels of cell–cell tension are reached comparatively early (this would occur initially opposite the EDJ cusp tip, and then spread throughout the sheet of secretory phase ameloblasts), and among other factors, this contributes in forming thinner enamel, especially at the mesiobuccal cusps of both upper and lower M1s.
It has been stated by others (Macho and Berner, 1993; Schwartz, 2000a) that attempting to characterize and compare enamel thickness of hominid and hominoid taxa by overall measures of thickness, such as by Martin’s (1985) ‘average’ enamel thickness, has little validity given that substantial within-tooth and serial variation exists, for example as shown by Macho and Berner (1993, 1994) and above in human molars. In such an approach, one would need to compare homologous local thickness values across taxa, and moreover to do this by confining comparisons to single jaw and serial positions. Although such fine-tuned analysis might be conceptually ideal, it is nevertheless not without methodological problems. For example, the present paper reported on the problems of the various linear measures conventionally taken on the MCS of physically sectioned teeth. Aside from the difficulty of obtaining the correct section position, relying on the MCS includes the following potential problems. Cusp tip enamel is conspicuously thin and notoriously variable. The significance of occlusal enamel thickness of any defined section remains ambiguous as shown above. Regarding lateral enamel thickness, we have pointed out the possibility that the MCS does not necessarily provide a ‘radial’ section, although the effect of this factor appears to be of rather small magnitude (usually within circa 0.1 mm of difference in absolute thickness).
In actual taxonomic comparisons, there is the added difficulty that different taxa are likely to show divergent within-tooth patterns of enamel distribution (e.g. Kono, 2004), thereby potentially rendering comparisons based on any single measure of linear thickness to be of limited value. We here propose, then, that an overall whole crown parameter of thickness is actually useful for the simple reason that it is likely to be a valid estimator of overall durability of the tooth, given that enamel is more resistant to wear than dentine or cementum and will therefore function as a prime factor in prolonging the lifetime of the molar crown until all of the enamel is lost. That this is indeed the case for primate molars is seen, for example, in the crown structure of species with comparatively enhanced molar wear, wherein the ‘functional’ side of the tooth exhibits not only thicker enamel but also a lower cervical position (or higher crown) (e.g. Molnar and Gantt, 1977; Shimizu, 2002), thereby providing relatively more tooth material available for wear in the ‘functional’ side of the molar. However, an additional interest of ours is to evaluate fossil specimens and species, with which, more often than not, neither whole crown distributions of enamel nor extensive series of measurements at precisely defined locations of the tooth are possible.
We here focus on maximum lateral enamel thickness, which appears to provide reliable indications on aspects of within-tooth patterns of thickness and on the overall thickness of the whole crown. Our reasons for this choice of focus are as follows. Of all the linear measures investigated in the present and previous studies, maximum lateral enamel thickness appears to be the most ‘stable’ measure of thickness in the MCS, with CV values mostly under 10. ‘Stability’ here refers to the relative lack of idiosyncratic factors (such as the details of EDJ and OES topography) other than regional enamel thickness itself that potentially affect the measured thickness value. We consider the other linear measures of thickness with higher CV values, generally ranging from around 10 to 20, to be less ‘stable’ parameters of enamel thickness, and especially inadequate in evaluating individual specimens or small samples of fossil material.
With our precisely controlled MCS data set, in contradistinction to Macho and Berner (1993) and Grine (2005), M3 lateral thickness was the most variable, as expected from general morphological variability of the last molar. Despite the relatively low CV values of the M1 and M2 that we encountered, these are still higher than CV values of human and primate molar crown diameters (e.g. Gingerich and Schoeninger, 1979; Kieser, 1990). The comparatively higher variability seen in lateral enamel thickness may in part be related to the effects of the discrepancy of the MCS itself from a more appropriate ‘radial’ section of each cusp, as mentioned above. Indeed upper and lower M1 lateral thickness CVs of the reformatted ‘radial’ sections are lower (between 7.4 and 8.1) than the corresponding MCS values, but this was not the case in the M2. Alternatively, there are indications from non-human primate studies that lateral enamel thickness is characterized by higher variability than crown diameters, and with its significant genetic component hold substantial potential for adaptive morphological evolution (Hlusko et al., 2004).
Despite the above depiction of lateral enamel thickness as the most ‘stable’ and therefore the preferred measure of focus in comparisons intended for evaluation of overall enamel thickness, the normal range of within-human variation is nevertheless considerable. In MCS lateral enamel thickness, the combined range of variation of the three lower molars was 1.16–1.81 mm lingually and 1.38–2.23 mm buccally, indicating a range of about 60% even with the buccal and lingual sides segregated, and an almost two-fold range without such distinction. The corresponding figures for the three upper molars were 1.47–2.39 mm lingually and 1.15–1.98 mm buccally, again spanning a range of about 60–70%, and a two-fold range of variation without buccolingual distinction. When serial positions were taken into account, the observed ranges of variation did reduce somewhat, but were still substantial at 30–55% with buccal and lingual thicknesses segregated, and up to two-fold if buccolingual distinctions were not made (Figure 14). Such large degrees of normal individual variation in maximum lateral enamel thickness, the most ‘stable’ measure of linear enamel thickness, must be taken into account in any discussion of the taxonomic significance of enamel thickness—in particular, when dealing with fossil taxa comprised of small sample sizes.
 View Details | Figure 14. Range of variation of lateral enamel thickness. (a) Lower M1 buccal, 1.38 mm; (b) lower M2 buccal, 1.54 mm; (c) lower M1 buccal, 1.87 mm; (d) lower M2 buccal, 2.23 mm; (e) lower M1 lingual, 1.22 mm; (f) lower M2 lingual, 1.16 mm; (g) lower M1 lingual, 1.74 mm; (h) lower M2 lingual, 1.78 mm. Scale bar is 1 mm. |
In further considering lateral enamel thickness for the purposes of interspecific comparisons, attention must be paid to within-tooth and serial patterns, for example those observed in human molars as shown above and previously suggested by others (e.g. Macho and Berner, 1993). However, the results of the present study suggest that a serial segregation of M2 and M3 is much less crucial than a distinction between M1 and the two posterior molars. Furthermore, we have discussed above the indications that such serial differences appear to be in part related to EDJ topography. This provides us with a potentially useful morphogenetic guideline for how to consider enamel thickness in fossil samples. It is possible that taxa with comparable EDJ topography among serial positions may exhibit little serial differences in linear enamel thickness. Conversely, serial segregation may be more crucial when evaluating enamel thickness in taxa with significant serial differences in EDJ topography. However, this appears not to be the case, for example, in baboons (Hlusko, 2004), which suggests that other factors are also in play, perhaps related with tooth size and scaling, or timing of tooth formation.
Another characteristic of maximum lateral thickness, potentially useful for interspecific comparisons, is the ‘functional’ to ‘non-functional’ side gradient in thickness that was consistently expressed throughout both upper and lower human molars regardless of serial position. Our observations of modern great ape within-tooth thickness patterns (Kono, 2004; and unpublished data) suggest that such buccolingual thickness gradients are likely to be ubiquitous, at least within hominoids. This provides us with a means by which to estimate whole crown thickness from linear thickness values more accurately than otherwise possible. When buccal and lingual lateral thickness values are combined, correlations between linear and average enamel thickness (AET2D or AET3D) appear to increase (Table 4), although the small sample sizes of the currently available 3-dimensional control data set render this a preliminary observation. The same can be said of ‘radial’ section maximum lateral thickness, which appears to estimate whole crown thickness as accurately or better than the equivalent thickness measures made strictly within the MCS (Table 4, Figure 15). The above observations suggest that lateral enamel thickness measured opposite one or more of the major cusps can be usefully compared across taxa. We are currently in the process of more fully investigating this with mixed-species hominoid comparative samples.
 View Details | Figure 15. Regression analysis of maximum lateral thickness and 2-dimensional and 3-dimensional average enamel thickness of the lower molars. Thickness values in natural logarithms are plotted. The independent variable LATRAD is the summed buccal and lingual lateral thickness of the ‘radial’ sections. The least squares regression lines are ln(AET2D) = 1.274ln(LATRAD) − 1.277 (coefficient of determination, 0.835), and ln(AET3D) = 1.043ln(LATRAD) − 0.920 (coefficient of determination, 0.568). AET2D shows very weak positive allometry with a 95% confidence interval (1.274 ± 0.269) of the regression coefficient just above 1.0. The regression coefficient for AET3D includes isometry within its 95% confidence interval (1.043 ± 0.433). |
The purpose of the present study was to establish an accurate body of data regarding linear enamel thickness of human molars measured in the mesial cusp section (MCS), and to explore the significance of enamel thickness patterns in the MCS within a broader perspective of 3-dimensionally based whole crown enamel distribution patterns. We are interested in this because more comprehensive whole crown measures of thickness are not always available for examination, and because an accurate and detailed understanding of enamel thickness patterns in the MCS is an important step towards a fuller understanding of enamel distribution patterns of the entire molar crown, and of their functional and taxonomic significance. Nevertheless, previous studies of human and non-human primate enamel thickness relied on physical sections at and/or close to the mesial cusp tips, of unknown precision as to the actual traversing of internal EDJ cusp tips. That the claimed accuracy has not always been attained is seen in sectioned specimens that preserve the EDJ tips deeply within the remaining molar blocks.
In light of the substantial amount of MCS enamel thickness data that has been accumulated in the literature, we first systematically examined how slight deviations in section position might affect the various measures of linear enamel thickness, at and close to the MCS. We found that cusp tip and occlusal enamel thickness was unstable, with inaccuracies of up to 0.5 mm (occlusal) and 1 mm (cusp tips) with section offsets of 0.6 mm from the MCS. Maximum lateral enamel thickness was the most stable measure in planes at and close to the MCS, or in planes chosen as more ‘radial’ than the MCS itself. Such thickness values were found to be usually within ca. 0.1–0.2 mm of the corresponding MCS value.
By combining enamel thickness measurements taken in our precisely determined MCS with other selected measures of thickness, such as lateral thickness in the ‘radial’ section and 3-dimensionally based average enamel thickness of occlusal enamel, we were able to clarify aspects of within-tooth and serial variation in the enamel thickness of human molars. We found a consistent and functionally interpretable pattern of buccolingual gradient in thickness in the cusp tip, occlusal, and lateral enamel throughout the molar series, with the exception of the characteristically thin enamel in both upper and lower M1 mesiobuccal cusps. This thickness gradient consistently follows the expectancy that the ‘functional’ side cusps would be endowed with thicker enamel. The effects of the M1 mesiobuccal cusp were to enhance the ‘functional’ to ‘non-functional’ gradient in the upper M1, and to mask it in the lower M1, to varying degrees depending on the measure of thickness. Cusp tips would be affected the most, and lateral enamel thickness the least. The magnitude of ‘functional’ to ‘non-functional’ side gradient in thickness did not differ between M2 and M3.
In contradistinction to the functionally interpretable buccolingual gradient in thickness, serial differences in enamel thickness were varied in pattern and a functional interpretation was not readily justified. Our precise measures of enamel thickness did not reveal a general gradient of thickness that increases posteriorly along the molar row. Rather, the M1 was confirmed to have thinner enamel than the M2 and M3 in many but not all investigated measures of enamel thickness. Such differences were small in magnitude in some of the measures, but larger with regards to cusp tip thickness. Moreover, because the observed serial difference in thickness was not emphasized in the ‘functional’ side cusps, but was more strongly expressed in the buccal cusps of both upper and lower molars, we suspect a substantial influence of the thin M1 mesiobuccal cusp enamel on the M1 to posterior molar serial comparisons.
We interpret the above-described serial and within-tooth patterning of enamel thickness in human molars to be a reflection of two superimposed factors of enamel thickness control mechanisms: (1) a factor responsive to selective pressures related with function, with the potential to differentially affect within-tooth regions, and (2) a developmental mechanism that limits thickness, most likely linked with steepness of EDJ topography at and around the cusp tips.
Lateral enamel thickness was found to be not only methodologically the most stable measure of thickness, but also the least variable as evaluated by the CV (ranging between 7 and 10). Nevertheless, this includes substantial individual variation, which, together with serial and within-tooth variation, must be taken into account in interspecific evaluations of enamel thickness. This is especially the case when dealing with small samples of, for example, fossil hominid species. Given the above results of within-tooth and serial patterns of enamel thickness obtained in the present study, we suggest that further investigations should be made regarding the possibility that serial distinctions are more important in taxa that exhibit a significant degree of difference in EDJ topography among molar positions. We also suggest that a ‘functional’ to ‘non-functional’ side gradient of thickness is likely to be ubiquitous among hominoids, and that such buccolingual distinctions must routinely be made. Conversely, because of this consistent pattern, we propose that a combination of measures that span the gradient may function as a relatively simple but effective representation of whole-crown enamel thickness conditions.
We thank C.O. Lovejoy for kind access to the large Libben collection of unworn molars, and M. Serrat, P. Reno, and B. Rosenman for assistance in assembling the sample. We thank Y. Mizoguchi for access to some of the specimens included in the Kono (2004) series. The micro-CT scanning was done mostly by M. Chubachi, to whom we express our gratitude to her efficient scanning operation. We thank T. Abe and M. Ozawa for help in the complicated processing of the CT data, and T. Tanijiri for his long-term collaboration including the development of the customized routines of CT-Rugle on which our analyses are based, and for writing the software tool that enabled derivation of occlusal surface average enamel thickness of each individual cusp.
|