| * Correspondence to: Pete E. Lestrel, Sections of Orthodontics and Oral Biology, UCLA School of Dentistry, Los Angeles, CA 90025, USA. E-mail: plestrel@earthlink.net Published online 25 November 2010 in J-STAGE (www.jstage.jst.go.jp) DOI: 10.1537/ase.100630 |
All bisexual organisms reflect differences in morphology that can be attributed to sexual dimorphism. With respect to the non-human primates, substantial generic differences in sexual dimorphism, such as body mass and canine size, are seen in Macaca, Papio, Theropithecus, Mandrillus, Gorilla, Pongo, etc., while other genera such as Lemur, Tarsius, Hylobates, etc., reflect only slight sexual differences (Napier and Napier, 1967; Tobias, 1971; Crook, 1972; Oxnard, 1983; Watts, 1986; Plavcan, 2001). For the human species, these sexual differences, while moderate, manifest themselves in multiple ways such as size, shape, mass, and even in behavioral and cultural aspects (Worthman, 1995; Ruff, 2002). Primary sexual characteristics (dealing with reproduction) and secondary sexual traits (not related to reproduction and the focus here) are both largely under the control of the X-linked genes (Rice, 1984; Mays and Cox, 2000).
As females mature earlier and faster during growth, this also acts to differentiate the increasing dimorphic differences seen at puberty (Marshall, 1978). Conversely, poor nutrition acts to slow down fertility (Haas and Harrison, 1977) as well as growth (with its endocrine parameters) and with it the age of onset of pubertal spurt (Eveleth, 1979; Malcolm, 1979; Purifoy, 1981; Stinson, 1985).
Size differences between males and females have been the focus of interest for over 130 years (Giles and Elliot, 1963). Sex differences are involved at all levels of human anatomy, e.g. tissue components such as muscle and fat (Reynolds and Grote, 1948; Forbes, 1978; but see Davies, 1985), the corpus callosom (de Lacoste-Utamsing and Holloway, 1982; but see Ferrario et al., 1994, 1996a) and even the soft tissue profile of the human face (Ferrario et al., 1995). Sex differences in the human brain and the nervous system, affecting cognition and temperament, may also be involved (Harris, 1985; Waber, 1985; Wynn et al., 1996). Sex differences may also be implicated in the endocrine response to emotional stimuli (Purifoy, 1981).
Focusing on the skeletal system, sexual dimorphism seems to affect all bones, including the cranium, pelvis, long bones, and vertebral column. Some sexually dimorphic differences are present at birth, becoming more divergent during childhood and adolescence (Ubelaker, 1999). Presumably, the presence of increasingly obvious dimorphic differences at puberty is due to hormonal activity (Frayer and Wolpoff, 1985; Butenandt et al., 1985). Whether malnutrition has a significant effect on the size and shape of the adult craniofacial complex remains to be explored more fully, although some work suggests cranial size reduction with serious undernourishment (Israel, 1978). Whether this also has an effect on sexual dimorphism is currently unknown. The pelvic bones have received considerable attention over the years (Glanville, 1967; Coleman, 1969; Phenice, 1969; Day and Pitcher-Wilmott, 1975; Segebarth-Orban, 1980; Seidler, 1980). With respect to the vertebral column, a study has demonstrated sex differences in size for the thoracic and lumbar vertebrae resulting in a thinner lumbar spine in females compared to males (Taylor and Twomey, 1984). A recent study on metacarpals using the Spitafields collection at the Museum of Natural History, London, also displayed significant dimorphism (Sulzmann et al., 2008).
The assessment of sexual dimorphism remains an essential aspect of many disciplines, such as: (1) forensics, where the concern with skeletal identification includes sexing (Snow, 1982; İşcan, 1988); (2) archeology, where sexing of skeletal materials is essential to see if differences in sexual dimorphism exist between modern humans and ancestral populations (Frayer, 1980); (3) primatology, where sex differences are diverse and complex in character, and whether humans reflect any residual elements of primate sexual dimorphism; (4) paleoanthropology, the identification of sex can be critical in making taxonomic and phylogenetic decisions, often rendered uncertain because of sampling and the fragmentary nature of fossil materials (Armelagos and van Gerven, 1980; Brace and Ryan, 1980); (5) growth and development, to characterize differences before and after puberty, and to see how sex differences affect body build and performance; (6) orthodontics, where sex differences during growth may potentially influence treatment practices; (7) gerontology, with the search for underlying mechanisms that may lead to sexual differences in bone loss with aging (Borkan et al., 1982; Crews, 1993); (8) nutrition, to establish whether dimorphic differences are affected by diet and malnutrition (Garn, 1975; Robson, 1975); (9) medicine, to see whether response to disease is, in some cases, sex influenced and whether sex differences have an effect on medical treatment modalities (Robinow, 1982); etc.
While the best skeletal material for sexing is the pelvis (Phenice, 1969), the cranial bones are considered the second best source. It should be noted that the ability to correctly distinguish between the sexes using solely cranial materials, especially fragmentary ones, can lead to error (Weiss, 1972). Although males are, in general, larger than females, large females do arise that may mimic male attributes, and for non-Caucasian samples (e.g. Japanese) the more gracile males may be mistaken for females if the researcher’s experience is largely with Caucasian materials which contain specimens that are somewhat more robust in character. Thus, size, by itself, can lead to an erroneous assessment of sex for individual cases. The use of multivariate methods such as discriminant functions for sexual identification has been found useful in reducing misclassifications and represents a major improvement over the use of single variables. For example, Giles obtained an 85% correct classification (Giles, 1964; Kajanoja, 1966; Deshmukh and Devershi, 2006).
On the basis of the skull and mandible, correct identification of sex was found to be approximately 85% (Krogman, 1962; Ubelaker, 1999). A radiographic study using discriminant analysis based on both mandibular and cranial measurements yielded a correct classification rate of 89% (Hunter and Garn, 1972). Consequently, values derived from experienced investigators (ranging from 77% to 87%) are, in general, comparable to the more objective sexing using discriminant functions (Giles, 1967; Deshmukh and Devershi, 2006). It should be noted that sexing using pelvic materials has yielded a 96% correct rate (Phenice, 1969). However, a recent South African study, using 10 distances with stepwise discriminant analysis, achieved 95% correct sex discrimination (Franklin et al., 2006). An earlier study also on South Africans using eight distances with discriminant functions yielded 77–80% for cranial materials, suggesting that the cranium may be less dimorphic than the mandible (Franklin et al., 2005).
Of necessity, only a few selected studies will be reviewed here, as the literature on sexual dimorphism on the craniofacial complex is quite extensive. All aspects of the craniofacial complex reflect sexual dimorphism. For example, various measurements of the male craniofacial complex are about 4–10% larger than females (e.g. the mean cranial capacity of males is roughly 150–200 ml (or cc) larger).
An early study of South African Blacks found that of the 30 measures used (cranial capacity, weight of the cranium, weight of the mandible, 15 distances, 2 angles, 3 categorical variables, and 7 indices), 12 were presumed to be statistically significant; however, none of the indices were significant (Keen, 1950). A Danish study found statistically significant differences in size for a majority (18 out of 27) of linear distances in the craniofacial complex (including the mandible) (Ingerslev and Solow, 1975). In contrast, only 2 out of 29 angular measurements were found to be significant. The limitation of angular measurements as shape measures will be discussed subsequently. A study of sexual dimorphism in Modern Japanese crania using 16 linear dimensions correctly identified 84% using stepwise discriminant functions. They found that the variable, mastoid height, by itself, was able to discriminate 74% of the specimens correctly (İşcan et al., 1995). A longitudinal study (using materials from the Brush–Bolton study (n = 32) utilized 8 distance and 5 angle measurements (Ursi et al., 1993). Focusing on oldest cohort of 18 years, none of the angular measures were significant. They found that for two of the cranial base distances (sella–nasion and sella–basion) the males were significantly larger. For the maxilla, only one distance (condylion–point A) was significant, although technically this distance is not confined to the maxilla per se.
With respect to the mandible, a disproportionate sexual dimorphism was found: the ascending ramus height (articulare–gonion) was 14% larger in males, while the length (gonion–menton) was 9% (Hunter and Garn, 1972). A study of the mandible in 6–10 year old French-Canadian children documented the presence of significant sexual dimorphism (a prepubertal phenomenon) in mandibular length but not in ramus height (Buschang et al., 1986). However, others have found a sex difference for ramus height, so this issue may not be fully resolved (Coben, 1955; Maj and Luzi, 1964). The longitudinal study mentioned earlier found that only one mandibular distance (condylion–gnathion) to be statistically significant (Ursi et al., 1993).
A series of studies by Garn and his colleagues detail the sexually dimorphic features of the maxillary (MX) and mandibular (MD) dentitions. They have demonstrated that sex affects tooth size in both arches (Garn et al., 1967). These data also suggested the presence of considerable variability in canine sexual dimorphism across populations. This variability in MD canine breadth is also seen in the data amassed for three major categories: hunter-gatherers, horticulturalists/agriculturalists, and urban populations (Frayer and Wolpoff, 1985). Utilizing dental casts of the mesiodistal and buccolingual diameters in a stepwise discriminant study found that with data from just two teeth, the sex of about 83% could be correctly identified, with mesiodistal diameter again providing most of the discrimination (Garn et al., 1977a). The often-used ratio mesiodistal/buccolingual tended to produce the lowest discrimination (64%). A follow-up study using crown areas showed that although all male crown areas were larger, the discriminatory power for sexing was not as good (77%) when compared to the mesiodistal measure (Garn et al., 1977b). Finally, a study that utilized both crown diameters and root lengths showed the most potential for sexing with 87% based on solely mesiodistal teeth (Garn et al., 1979). These studies showed the usefulness of dentition for sexing, especially in a forensic or archeological context, especially if ratios are avoided.
The linear measurements used in all these studies showed that males were generally larger for most of the measurements, a fact now long accepted. The question of shape differences, if indeed present, cannot be easily inferred from these studies. Moreover, the existence of size differences tends to obscure the presence of most shape differences. Consequently, relatively few studies have focused on sexually dimorphic differences in shape in the craniofacial complex. This scarcity of craniofacial shape studies is based on at least three reasons: (1) the use of angles as measures of shape have produced equivocal results, e.g. the cranial base angle (Lestrel and Roche, 1986; Lestrel, 1989b); (2) angles do not describe the actual shape or contour in question; and (3) the need for more sophisticated approaches due to the challenges of measuring shape as visually perceived.
Differences in shape have been rarely considered because of difficulties in quantification. Shape is defined here as the contour or boundary of a form in 2-D (Lestrel, 1997b, 2000). However, the extension to 3-D (as a surface or solid), while theoretically perhaps straightforward, is fraught with difficulties. That is, its description in numerical terms increases exponentially in computational complexity and will not be considered further here. However, one simple 3-D application, the rabbit eye orbit as a curve in space, can be found in Lestrel (1997b).
The spate of newer methods, such as bi-orthogonal grids (Bookstein, 1978), median axes (Blum, 1973; Bookstein, 1979; Webber and Blum, 1979; Lee, 1982), thin plate splines (Cheverud and Richtsmeier, 1986; Bookstein, 1991), Euclidean distance matrix analysis (EDMA) (Lele, 1991; Lele and Richtsmeier, 1991), etc., represent important achievements that have advanced morphometrics (Lestrel, 1997a). While homologous landmarks have been, and continue to be, widely used for the numerical description of forms, they do not precisely express the shape as visually seen because of their dependency on (1) the comparatively few available homologous landmarks and (2) the exclusion of the boundary between landmarks (Read and Lestrel, 1986; Read, 1990). As Bookstein has explicitly stated, “Information about the curving form between landmarks, available from tracings of continuous biological outlines is excluded from discussion here” (Bookstein, 1984, p. 480). Moreover, such methods (e.g. thin plate splines) tend to display shape changes as deformations, making it difficult to readily compare the results with such methods as Fourier descriptors to be described in the next section. We hasten to add that that these observations are not intended as criticisms of those methods as they may be perfectly appropriate for particular research questions being asked and have produced valuable and interesting results.
The numerical description of form, if it is to be considered ‘sufficient’ in mathematical terms, must be viewed as a one-to-one mapping between the results of the computational procedure and the actual morphology. A test of this ‘sufficiency’ is the ability to precisely recreate the form from the measurements. Clearly, none of the methods cited above have been able to fully satisfy this requirement. If one is concerned with avoiding deformation methods because of their abstraction and is concerned with this mapping, then alternative methods must be sought. A boundary method that has been used with considerable success is Fourier descriptors (FDs) and one particular algorithm, elliptical Fourier functions (EFFs), is used here. The EFF equations were originally developed by Kuhl and Giardina (1982). Details and applications of EFFs can be found in Lestrel (1989a, b, 1997b, 2000).
Nevertheless, Fourier analytic methods, in concert with all methods, also share some disadvantages. It is important to appreciate that the use of frequency domain information (i.e. components such as amplitude and phase) does not provide information with respect to where in the spatial domain these frequency components occur. Thus, while Fourier coefficients or their amplitudes are useful for capturing the global aspects of a form, the localization or identification of local aspects is not readily possible. A method that has been recently developed to circumvent this constraint and will recognize any changes in curvature, are wavelets (see Lestrel et al., 2004a, 2005 for an extended discussion of these issues).
Few studies have focused solely on shape changes in the craniofacial complex. Studies that used FDs with cranial materials include a study of the ape and human orbits (Jacobshagen, 1986). Another study looked at the forehead shape of the skull, a clearly dimorphic feature (Inoue, 1990). Utilizing just the forehead and discriminant functions, Inoue was able to discriminate sexes at the 85% level. A study from an orthodontic perspective used FDs to fit seven cephalometric landmarks (Ferrario et al., 1996b, 1997). Data were standardized for size and orientation. While that study discerned differences due to growth, sex differences appeared to be negligible, possibly because not enough landmarks were utilized.
A study utilizing EFFs looked at the symphyseal shape of the great ape mandible (Daegling and Jungers, 2000). Significant symphyseal shape differences due to sex were found in Gorilla but not in either Pongo or Pan, which reflects the diversity of sexual dimorphism in the Great Apes and places limits on the use of the symphyseal aspect for solving taxonomic issues. This conclusion was reinforced in a more recent study using EFFs that looked at the mandibular shape in primates using the norma lateralis (Schmittbuhl et al., 2007). Another study of the mandible using EFFs looked at growth of the mandible and found systematic size and shape changes with age (Ferrario et al., 1996c). Unfortunately, no data regarding sex differences was provided. However, few studies using EFFs have focused on the human mandible from a sexually dimorphic perspective (Schmittbuhl et al., 2001). Schmittbuhl and colleagues were able to correctly discriminate the sexes at an average of 95%. Presumably the increase in discrimination is a consequence of more information (its outline) being assessed with EFFs in contrast to conventional measures.
This paper is a continuation of our studies of sexual dimorphism in the craniofacial complex. The purpose was to look at a number of structures of the craniofacial complex from a ‘shape only’ perspective. The justification for this approach is predicated on the following grounds: (1) measurement of the boundary of a form is the first start toward a precise numerical assessment that closely matches the visual depiction of the form (Lestrel, 1997b); (2) shape aspects such as the boundary are considered of greater import than size in the discrimination of form by the human visual system (Spoehr and Lehmkuhle, 1982); and (3) a procedure is needed that can estimate the variability of sexual dimorphism in the craniofacial complex.
Parts of this study are retrospective in the sense that some of the data used here were based on studies that have been published, while others have remained unpublished. The published studies often happen to contain data from both sexes, although sexual dimorphism was not the primary intent of some of those studies. Their inclusion here is justified on the grounds that: (1) the original purpose was designed to depict shape differences due to growth or treatment and not to sexual dimorphism at that time; and (2) the presence of both sexes provides data for the current study.
To attempt to document sexual dimorphism in the craniofacial complex, six datasets with multiple samples were utilized involving 1110 specimens. These included the human nasal bones, the cranial base of both M. nemestrina and humans, the human dental and mandibular arches, and the human cranial vault. The results of these studies, while indicative, do not even begin to exhaust the morphological structures that make up the craniofacial complex. Moreover, shape data expressively dealing with sexual dimorphism is not yet available for either the maxilla or the mandible in norma lateralis. This is especially regrettable in view of rather controversial literature regarding the presence of sexually dimorphic shape changes in the mandible (Koski, 1996; Loth and Henneberg, 1996, 1998; Indrayana et al., 1998; Hill, 2000). An attempt to rectify this situation has been initiated with a preliminary study of the human mandible in norma lateralis (Lestrel et al., 2010a). Each of the craniofacial samples used here will be described in turn.
The original purpose of this study was to produce normative standards based on shape against which departures seen in abnormalities such as Apert’s syndrome could be numerically described and visualized. A longitudinal study of the nasal bone was initiated using cephalometric radiographs in norma lateralis located at the Fels Research Institute, Yellow Springs, OH (Lestrel et al., 1990a, b, 1991a, b, c). That study documented, for the first time, the actual shape changes seen in the nasal bones from the first month of life to over 30 years of age. The data in the current study, extracted from that study, focused on sexually dimorphic shape changes and was limited to adults. The mean ages were: females 19.82 years and males 21.76 years (Table 1).
A longitudinal sample of the M. nemestrina cranial base was available from the Regional Primate Research Center, University of Washington. Cephalometric radiographs in norma lateralis were utilized. The original sample consisted of 14 females and 15 males, aged 1–8 years (Lestrel et al., 1993). Of a series of longitudinal and cross-sectional studies on the cranial base, this was the first non-human primate study. The procedures developed for that study where later extended to include human data. The M. nemestrina cranial base data reported in this study was restricted to adult specimens (n = 14 females and n = 9 males) aged 7 years (Table 1).
Results based on the M. nemestrina cranial base prompted further studies using human data to see if a similar pattern of sexual dimorphism could be discerned (Lestrel et al., 2004a, 2005). An early initial longitudinal study using conventional Fourier analysis hinted at cranial base shape differences due to sex, but these shape changes, while present, were not recognized or followed up at the time (Lestrel and Roche, 1986). The data used for the present study was based on a series of Japanese cranial base outlines traced from standardized headfilms available from the Nihon University School of Dentistry at Matsudo, Chiba Prefecture. This data was composed of four samples from Yayoi, Kamakura, Edo, and Modern (Table 1).
Numerous authors have attempted to quantify the form of the dental arch, especially with the orthodontic prediction in mind (Herren et al., 1973; Herren, 1976). Studies include the fitting of curves such as the catenary (Scott, 1957; McConnail and Scher, 1949), ellipse (Currier, 1969), parabolic (Jones and Richmond, 1989), polynomials (Lu, 1966), cubic spline (BeGole, 1979, 1980), beta function (Braun et al., 1996), conic sections (Sampson, 1981, 1983), etc. No studies to date have attempted to use FDs to describe the dental arch form. The possibility that systematic sexual dimorphic differences exist in the dental arch was an unexpected consequence of a sample from the Nihon University of Dentistry at Matsudo, Chiba that compared dental crowding with controls (Lestrel et al., 2004b). Only the controls, of healthy Japanese dental students, were used in the current study. Both MX and the MD arches were available. A sample of individuals (n = 119) with a mean age of 20.40 ± 1.68 years was utilized (Table 1).
Since the search for sexually dimorphic differences in the dental arch yielded positive results, it was decided to consider the whole mandibular arch to see if it also reflected sexually dimorphic differences in shape (Lestrel et al., 2006). This current study was based on Japanese materials and is detailed here for the first time. Samples were obtained from for four archeological periods: Okhotsk, Ainu, Edo, and Modern (Table 1).
Lastly, data was gathered on the cranial vault in norma lateralis specifically for the current study. Although the procedures were initially developed in another study comparing the cranial vault of H. erectus, H. neanderthalensis, and H. sapiens fossil specimens (Lestrel et al., 2010b; Lestrel et al., 2011), the same procedures were used here to look for sexually dimorphic differences. Four samples were analyzed, which were collected from Ainu, Edo, and modern Japanese populations. With respect to the Ainu, two separate samples were available, one from the Kyoto University Museum and other one from the Sapporo University Medical School collection (Table 1).
A number of the studies used here (dating from 1989 to 1998) were based on techniques current at that time (e.g. Lestrel et al., 1993). These included the use of radiographs or photographs of the specimens, followed by a tracing of the image outline, the superimposition of a grid (in polar or Cartesian coordinates) on the tracing to facilitate and ensure accurate placement of the points, and then the actual digitizing of these points using a digitizer.
In an effort to simplify, reduce errors, and speed up the data-gathering process, new Microsoft Windows™-based software, called MLmetrics (Available from the senior author a nominal cost), has been developed to expedite the data collection. Utilizing MLmetrics, the user no longer needs to trace the image outline; instead, the image can now be directly digitized, using the mouse, on the computer screen, obviating the need for the tracing step, which reduces one potential source of error.
Once digitized, all specimens were submitted as data to a set of earlier MS-DOS routines called EFF23 (Available from the senior author a nominal cost), which computed the EFFs. The process involved two steps: (1) each image was rotated (positional orientation) so that the major axis of the first ellipse was made horizontal to the x-axis; and (2) the bounded area was scaled up or down (size-standardization) so that it was equal to the square root of 10000 units. This area-standardization approach utilized here is different from the one advocated by Kuhl and Giardina (1982), which sets the length of the semi-major axis of the first ellipse to 1.0 as the size standardization (see Lestrel, 1989a, b for discussion of these normalizations).
Of the 16 samples utilized in this study, eight had been previously digitized. These eight samples were ready for analysis with EFFs. Thus, the procedures used for these earlier studies will only be briefly discussed as they have been published elsewhere. Only the four mandibular arch samples and the four cranial vault samples represented new data and required digital photography, pre-processing, digitizing, and computation of EFFs from scratch. These newer procedures will be described subsequently in some detail for the cranial vault data. All these procedures, with exception of the pre-processing step, apply to all the samples reviewed here.
The cephalometric headfilms were enlarged 2.74× prior to tracing the nasal bone outlines onto dimensionally stable acetate sheets (Lestrel et al., 1990b). Each nasal bone was traced in norma lateralis from nasion along the superior surface to rhinion (tip), along the inferior aspect until the nasofrontal suture and back to nasion to create a bounded outline. A set of 42 points was used to describe the outline. These points were then digitized using a Houston Instruments HIPAD digitizer and used to compute EFFs with 20 harmonics. The mean residual between the observed points and the expected values from the EFF curve fit was computed. This mean value (based on the 2.74× enlarged image) was 0.12 ± 0.03 mm (n = 141), indicating an acceptable fit.
Utilizing standardized radiographic films, the outline of the M. nemestrina cranial base was carefully traced onto matte acetate sheets and 54 points located (Lestrel et al., 1993). These 54 points were then digitized using a HIPAD digitizer and utilized to compute 20 harmonics. The mean residual between the observed points and the predicted values (using the total database of n = 275) was 0.13 ± 0.02 mm.
The human cranial base data was comprised of four Japanese samples. The standardized headfilms of the cranial base were traced onto matte acetate sheets and 54 points located (Lestrel et al., 2004a). Digitizing was carried out with a Calcomp DrawingBoard III. EFFs were then computed with 27 harmonics. The mean residual was found to be 0.095 ± 0.014 mm (n = 65).
This study was primarily intended as a comparison of a control sample with a crowding sample and sexual dimorphism was considered initially as secondary (Lestrel et al., 2004b). The control MX and MD dental study models were utilized here and photographed at a distance of 600 mm using a Nikon FM2 camera with a 105 mm Micro-Nikkor lens to minimize distortion. Standardized 1 : 1 prints were then made for digitizing. Twenty-four landmarks, describing the left and right tooth rows from the central incisor to the second molar, were carefully marked with a fine pen and then digitized using a Calcomp DrawingBoard III. Utilizing EFF23, an intermediate file was first generated, which created a ‘mirror-image’ of the dental cast about a horizontal line connecting the right and left distal cusps of the second molars. This ‘reflection’ about the x-axis resulted in a doubling of the points (from 24 to 48). This configuration has mathematical advantages in that: (1) a better EFF fit is obtained; and (2) the ‘odd’ or cosine trigonometric terms in the equation become zero and drop out of the equations (Lestrel, 1997b). EFFs with 24 harmonics were calculated for each dental cast. A mean residual of 0.24 ± 0.05 mm (n = 76) was computed.
The mandibular arch was photographed with the dentition facing down (inferior side up). A rubber wedge was placed between the central incisors and the table to raise the mandibular body (base) until it was parallel to the table surface. The mandible was slightly rotated, if necessary, to ensure that a line drawn tangential to the right and left inferior borders of the condyles was horizontal. Each JPEG image was then digitized directly using the ‘on-screen’ feature of MLmetrics. The origin for digitizing was found by dropping a vertical from the mental protuberance down to the horizontal line connecting the right and left condylar margins. Using a polar coordinate grid, a set of 90 points was digitized describing the mandibular arch outline. The digitized points were then used to generate EFFs with 45 harmonics. The mean residual (n = 81) was estimated as 1.76 ± 0.24 pixels or 0.32 ± 0.04 mm.
Both the mandibular arch and the human cranial vault samples represent new data and were prepared specifically with this paper in mind, and as the procedures dealing with the preparation of the images prior to digitizing as well as the actual digitizing of the specimens have substantially changed over time, so the procedures involved will be presented in some detail for the human cranial vault data.
Photographs of the cranial vault were taken in norma lateralis using a Fujifilm Z7000 digital camera attached to a copy stand. All images were shot at 6 MB resolution. To check for the presence of image distortion, focal lengths ranging from 130 to 300 mm were tested. The aspect ratio (image height to width) was found to differ from 1 to 2%, values that were considered acceptable. Images were then scanned into memory as TIFF files at 600 dpi using a Hewlett-Packard Scanjet 3970 and archived for further processing.
Using Photoshop (Adobe Systems Inc.), all TIFF images were pre-processed prior to digitization. The procedure consisted of loading each 600 dpi image and setting the resolution so that an image size of approximately 1000–1200 kb, which was appropriate for MLmetrics. A line was then constructed connecting nasion (Na) and porion (Po), and extended until it intersected the posterior outline of the occipital aspect. To ensure a common orientation, each image was rotated so that the Na–Po line was horizontal to the x-axis (positional orientation) and then saved as a JPEG file.
After pre-processing, the JPEG image was ready for on-screen digitizing. Each image was then loaded into MLmetrics. Since this study is based on size-standardized images, differences in size do not play a role in the analysis. Dimensions of 1800 pixels in width were found to be satisfactory and used for all images. Utilizing porion (Po) as a center, a computer-generated polar grid was superimposed on the image. This grid was divided into 72 equally spaced intervals. Utilizing the mouse, the on-screen digitizing progressed counterclockwise starting at nasion (point 1) and ending again at nasion (point 72), bounding the cranial vault outline (Figure 1).
 View Details | Figure 1. MLmetrics screen shot of a JPEG cranial vault image being digitized. The 72 points describing the cranial vault specimen displayed here are digitized on the screen using the mouse as the input device. |
MLmetrics was developed using sub-pixel technology (Western Vision Software) so precise positioning of the mouse for digitizing the outline of a form, at any magnification, can be maintained. The sub-pixel approach allows one to zoom into any location within a pixel. For example, starting with a good high-resolution image, zooming to 3× and using sub-pixel technology, the digitized points on the image are accurate to 1/3 of a pixel. Higher zooms may lead to greater accuracy but at an increase of the pixelation effect. Given a screen resolution of 1600 × 1200 pixels, an accuracy of 1/3 of a pixel yields 5760000 sub-pixels in the image. If the screen width is 12 inches, the accuracy of the digitized points would be 0.06 mm horizontally. The actual digitizing was carried out at 3× magnification. The points of the digitized image were saved into a Microsoft Access database as part of the MLmetrics program. The digitized points were then exported to the MS-DOS routine, EFF23, for computation of EFFs.
Utilizing the 72 digitized cranial vault points allowed for a maximum of 36 harmonics (Nyquist frequency constraint). The residual was computed for each point and then averaged over the whole cranial vault. The mean residual (X ± SD) based on a cranial vault test sample (n = 55) was 0.65 ± 0.09 pixels or 0.12 ± 0.02 mm. These 36 harmonics were considered adequate in terms of fit (Lestrel, 1997b). Size-standardization was accomplished by scaling all digitized outlines so that the area within the bounded region was equal to the square root of 10000 pixel units.
These EFF procedures (positional-orientation and size-standardization) discussed for the four cranial vault samples and the four mandibular arch samples were also applied to the other eight samples in this study. Once completed, the remaining step required the superimposition of the mean female outline onto the mean male outline for all samples. These generated outline plots were superimposed on the centroid to provide a visual assessment of the mean sexual dimorphic changes across the samples representing various morphologic aspects of the craniofacial complex.
Finally, a shape difference index (SDI) was developed as a simple measure for the comparison of superimposed images. This SDI provides an estimate of how close the superimposed outlines are to each other and is useful for studies such as sexual dimorphism by providing an objective measure for comparison. The positionally oriented and size-standardized EFFs depicting the mean male and female bounded outlines were superimposed on the centroid. The SDI was then computed by first finding the intersections (using a search algorithm) of the two superimposed outlines. These intersections determined the areas of interest, i.e. those not held in common. The area within each of these sections was then computed, the section areas were added and the mean area calculated. This averaged area value was further divided by a weighting factor based on the number of sections involved. This weighting factor was derived by using four sections as a basis (numerator) and forming a ratio with the actual number of sections found (denominator). This resulted in values such as: 1.3333 (4/3), 1 (4/4), 0.6667 (4/6), etc. This weighting factor was utilized so that the final SDI values reasonably reflected the visual evaluation of the superimposed images. SDI values ranged from roughly 0.3 to 5.0+. Values below 1.0 indicate a very close correspondence between superimposed images, while values of 3.0 or higher reflect the presence of considerable differences between the superimposed bounded outlines (Figure 2).
 View Details | Figure 2. An area shape difference index (SDI) was developed to compare the centroid-superimposed and area-standardized images. These cranial vault superimpositions are part of the data in Lestrel et al. (2010b). The figure on the left represents the area standardized superimposition of a H. erectus sample on a modern H. sapiens sample. The section areas not held in common are appreciable and the SDI of 3.811 reflects this. The figure on the right depicts the area-standardized superimposition of H. soloensis (Ngandong) specimens attributed to either H. erectus or H. neanderthalensis and superimposed on H. neanderthalensis. These two superimposed images are almost identical with very small sections that are not held in common yielding an SDI of 0.528, suggesting a close relationship. The plus (+) refers to the centroid. |
The size-standardized mean female and male nasal bone outlines were superimposed on the centroid and rotated so that the major axis of the first ellipse was parallel to the x-axis. After the doubling of the original 42 digitized points, the distance from point 1 (nasion) to point 30 (rhinion) or tip of the nasal bones was chosen to describe the major sexually dimorphic change. A t-test was computed using that mean distance which yielded a t = 2.32 value, which was significant at a P < 0.05 level. The superimposition displayed significant sexual dimorphic differences with the mean female nasal bone outline displaying a moderately narrower and longer shape that for the mean males (Figure 3).
 View Details | Figure 3. Superimposition on the centroid of the nasal bones. Mean plots have been oriented with the major axis of the first ellipse (first harmonic) of the EFF is parallel to the x-axis. Circles depict mean females (n = 22) and squares identify the mean males (n = 17). The original 42 digitized points have been doubled to 84 to generate smoother outlines. Point 1 depicts the location of nasion and point 30 is the tip of the nasal bones (rhinion). The plus (+) refers to the centroid. |
The area standardized mean female and male cranial base outlines were superimposed on the centroid and rotated so that the major axis of the first ellipse was parallel to the x-axis to ensure a common orientation. The original 54 digitized points were doubled. A t-test was computed using that distance from basion (Point 1) to the anterosuperior margin of the hypophyseal fossa (point 26), which yielded a t = 2.59 value, which was significant at the P < 0.05 level. These shape changes consisted of an anterior repositioning of the male hypophyseal or pituitary fossa (Figure 4).
 View Details | Figure 4. Superimposition on the centroid of the cranial base of M. nemestrina. Plots have been oriented with the major axis of the first ellipse of the EFF is parallel to the x-axis. Circles depict mean females (n = 14) and squares identify the mean males (n = 9). The original 54 digitized points were been doubled to 108 to generate smoother outlines. Point 1 refers to basion and point 26 refers to the anterosuperior margin of the hypophyseal fossa. The plus (+) refers to the centroid. |
Sexual dimorphism in the human cranial base was evident for all four samples investigated: the Yayoi, Kamakura, Edo, and the Modern group (Figure 5, Figure 6). The original 54 digitized points were again doubled. For all samples, the sexually dimorphic pattern was composed of the anterior repositioning of the dorsum sellae in males in a similar fashion to the M. nemestrina study (Lestrel et al., 1993). A two-way MANOVA (StatSoft 7.0) with two between-group (archeological age and sex) contrasts displayed statistically significant differences for both contrasts at the P < 0.001 level allowing for univariate F-tests. The interaction effect (Group age × Sex) was found to be statistically non-significant. Of the seven centroid-based distances chosen to characterize the cranial base, a distance of primary interest from the centroid to the superior aspect, or tip of the dorsum sellae (point 26), was found to be significant for the group contrast at P < 0.05, while the sex contrast was significant at the P < 0.005 level. Details of the measurements used can be found in Lestrel et al. (2004a).
 View Details | Figure 5. Superimposition on the centroid of the cranial base of (A) the Yayoi specimens and (B) the Kamakura specimens. Plots have been oriented so that the major axis of the first ellipse of the EFF is parallel to the horizontal axis. Circles depict mean females (Yayoi, n = 32; Kamakura, n = 17) and squares identify the mean males (Yayoi, n = 32; Kamakura, n = 10). The original 54 digitized points have been doubled to 108 to generate smoother outlines. Point 1 refers to basion and point 26 refers to the anterosuperior margin of the hypophyseal fossa. The plus (+) refers to the centroid. |
 View Details | Figure 6. Superimposition on the centroid of the cranial base of (A) the Edo specimens and (B) the Modern specimens. Plots have been oriented so that the major axis of the first ellipse of the EFF is parallel to the horizontal axis. Circles depict mean females (Edo, n = 31; Modern, n = 26) and squares identify the mean males (Edo, n = 33; Modern, n = 80). The original 54 digitized points have been doubled to 108 to generate smoother outlines. Point 1 refers to basion and point 26 refers to the anterosuperior margin of the hypophyseal fossa. The plus (+) refers to the centroid. |
The human dental arch also displayed sexually dimorphic differences. Both the MX and the MD reflected similar differences. Utilizing the size-standardized data, computer-generated plots have been superimposed on the centroid (Figure 7). Given that these are size-standardized images, and although the differences are quite moderate, the females displayed a relatively longer and narrower dental arch when compared to males. A set of 15 centroid-based distances and 5 individual distances to points identifying the teeth locations were initially utilized (see Figure 4 in Lestrel et al., 2004b for these distances). A correlation study was used reduced these 20 distances to 14 by removing those variables that were highly correlated (r > 0.80) and thereby redundant. A one-way MANOVA using the remaining 14 variables generated statistically significant differences for sex at the P < 0.001 level for both the MX and MD samples allowing individual F-tests. These were (P < 0.01) for the MX and (P < 0.05) for the MD data (see Lestrel et al., 2004b for details).
 View Details | Figure 7. Superimposition on the centroid of (A) the maxillary dental arch specimens and (B) the mandibular dental arch specimens. Plots have been ‘mirror imaged’ around a horizontal line connecting the distal cusps of the left and right second molars. Circles depict mean females (maxilla, n = 49; mandible, n = 50) and squares identify the mean males (maxilla and mandible, n = 69). The original 24 digitized points for each MX and MD were initially doubled to 48 to create the ‘mirror images’. They were then subsequently doubled again to 96 to generate smoother outlines. The details of this procedure can be found in Lestrel et al. (2004b). The plus (+) refers to the centroid. |
The sexually dimorphic differences in the mandibular arch were found in the length from the symphysis to the condyle (Figure 8, Figure 9). This distance was consistently longer in the females for all four groups (Lestrel et al., 2006). Note that while the initial superimposition was on the centroid, a subsequent superimposition was made on the superior margin of the symphyseal border (point 47) to display the dimorphic changes more clearly. This second superimposition is illustrated in Figure 8 and Figure 9. Nine initial distances were utilized. To measure the length from symphysis to the condyle, a distance was taken from point 47 (mental protuberance) to point 1 (most inferior point on the left condyle) and point 95 (most inferior point on the right condyle). Besides these two right and left distances from the symphysis to the condyle, the other seven distances consisted of the vertical thickness of the symphysis (points 47–137), the thickest part of the right and left mandibular bodies (points 33–148 and 61–127), the narrowest width of the right and left condyle necks (points 15–166 and 77–108), and finally the maximum width of the right and left condyle heads (points 8–175 and 85–100).
 View Details | Figure 8. Initial superimposition on the centroid, subsequent translation onto the symphyseal border (point 47) of (A) the Ainu and (B) the Okhotsk mandibular arch mean samples. Plots have been oriented so that most inferior aspect of the left and right condyles is tangential to a horizontal line. Circles depict mean females (Ainu, n = 31; Okhotsk, n = 7) and squares identify the mean males (Ainu, n = 50; Okhotsk, n = 10). The original 90 digitized points have been doubled to 180 to generate smoother outlines. Points 1 and 95 refer to the most inferior aspect of the condyles. The plus (+) refers to the centroid. |
 View Details | Figure 9. Initial superimposition on the centroid, subsequent translation onto symphyseal border (point 47) of (A) the Edo and (B) the Modern mandibular arch mean samples. Plots have been oriented so that most inferior aspect of the left and right condyles is tangent to a horizontal line. Circles depict mean females (Edo, n = 52; Modern, n = 17) and squares identify the mean males (Edo, n = 74; Modern, n = 36). The original 90 digitized points have been doubled to 180 to generate smoother outlines. Points 1 and 95 refer to the most inferior aspect of the condyles. The plus (+) refers to the centroid. |
Of the total of nine distances used, only the two distances from the mental protuberance (point 47) to the left and right condyles were found to be statistically significant. Consequently, these seven are not illustrated here (details of these seven distances are available from the senior author). Descriptive statistics of the two statistically significant distances are shown in Table 2. A two-way MANOVA (Group and Sex) showed that both Group and Sex were statistically significant at P < 0.001, while the interaction effect (Group × Sex) was not significant allowing for individual F-tests. Distance 1–47 was significant at a P < 0.001 level for both Group and Sex, while distance 47–95 was significant at P < 0.01 for Group and at P < 0.001 for Sex.
Specific differences were visually present in the cranial vault. Distances from the centroid to each of three regions were computed. These were: (1) glabella (mean centroid distance to point 12), (2) superior aspect (mean centroid distance to point 67), and (3) the occipital region (mean centroid distance to point 115). These distances to the three points, 12, 67, and 115, on the cranial vault outline represent mean distances over a local range. Specifically, the distance to point 12 is the mean of distances from point 4 to 20; distance to point 67 is the mean of points 55–80 and the distance to point 115 is the mean of points 100–130. This procedure was used to account for variability in these structures. Recalling that the digitized points were doubled during the creation of the EFFs, to generate smoother outlines, these point numbers here will therefore not match the specimen illustrated in Figure 1.
The means and standard deviations of these three centroid distances are shown in Table 3. Utilizing the three distances from the centroid to the mean point of each of these three regions, a two-way MANOVA (Group and Sex) showed that both Group and Sex were statistically significant (P < 0.001), while the interaction effect (Group × Sex) was not significant allowing for individual F-tests of the three centroid distances. Of the three distances from the centroid to the cranial vault boundary outline, only two, one to glabella (distance 12) and other to the occipital aspect (distance 115), respectively, were found to be significant (P < 0.001).
In sum, distinct differences in sexual dimorphism were present. The mean female outlines tend to be more globular with a greater height superiorly, while the males tend to be display a slightly more oblong aspect in the anteroposterior direction (Figure 10, Figure 11).
 View Details | Figure 10. Superimposition on the centroid of (A) the Ainu from Kyoto and (B) the Ainu from Sapporo mean cranial vault samples. Plots have been oriented so that a line drawn from nasion to superior aspect of the eam (external auditory meatus) was parallel to a horizontal line. Circles depict mean females (Ainu from Kyoto, n = 22; Ainu from Sapporo, n = 19) and squares identify the mean males (Ainu from Kyoto, n = 33; Ainu from Sapporo, n = 25). Point 12 refers to Glabella area, point 67 to the superior vault aspect, and point 112 to the occipital region. The plus (+) refers to the centroid. |
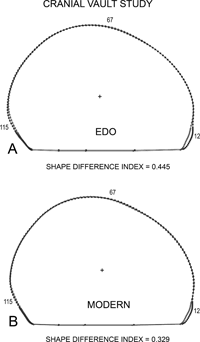 View Details | Figure 11. Superimposition on the centroid of (A) the Edo and (B) the Modern mean cranial vault samples. Plots have been oriented so that a line drawn from nasion to superior aspect of the external auditory meatus (EAM) was made parallel to the horizontal axis. Circles depict mean females (Edo, n = 52; Modern, n = 17) and squares identify the mean males (Edo, n = 74; Modern, n = 36). Point 12 refers to Glabella area, point 67 to the superior vault aspect, and point 112 to the occipital region. The plus (+) refers to the centroid. |
All 16 samples examined here displayed sexually dimorphic differences in varying degrees. The most dimorphic structure was found to be the nasal bones and the least dimorphic was the cranial vault followed by the dental arch. SDI values were found to be useful in partially answering the question of which of the craniofacial structures were more dimorphic (Table 4). Clearly, these SDI estimates are suggestive but preliminary. More studies are needed of these structures as well as others to ensure a relatively complete analysis of craniofacial sexual dimorphism. The results of each of the six studies will be briefly discussed in turn.
The nasal bone study displayed statistically significant dimorphic differences (Figure 3). The SDI values of 5.399 made this craniofacial structure the most variable with respect to sexual dimorphism. Turning next to the M. nemestrina cranial base study, the superimposition was again on the centroid and with the first principal axis of the EFF horizontal to the x-axis. The dimorphic differences consisted of an anterior repositioning of the male hypophyseal fossa (Figure 4).
The results from the M. nemestrina study suggested a study of the human cranial base. That study utilized four independent Japanese samples from four different age periods. The same procedure used with the M. nemestrina data was applied here. All of the samples displayed a similar dimorphic pattern with male outlines displaced anteriorly compared to the females (Figure 5, Figure 6). While the shape of the human cranial base is distinct from that of M. nemestrina, the pattern of sexual dimorphism seen in the human cranial base was similar to that of the earlier M. nemestrina study. This suggests that the pattern of sexual dimorphism, namely the anterior migration of the male hypophyseal fossa, is in excess of 30 million years old and represents an ancient primate bauplan. While the mean SDI value of 1.696 for the four human cranial base samples is less than the 2.435 value for M. nemestrina sample, it would be premature to suggest that the cranial base in non-human primates is more variable. More studies are needed to confirm this pattern.
The human dental arch study marked a departure from the earlier studies in that the data was ‘mirror-imaged’ about a horizontal line connecting the left and right distal cups on the second molars prior to being fitted with the EFF. Both the MX and the MD reflected similar differences in that the female arch was moderately narrower and longer than the male arch (Figure 7). This sexually dimorphic pattern is difficult to discern if the data has not been standardized for size since males are larger than females. The dimorphic difference is quite moderate as can be seen in the mean SDI value of 0.895. That the dimorphic pattern is the same in both MX and MD arches is not surprising since precise occlusion of the upper and lower dentitions is normally required.
The discovery of sexually dimorphic differences in the dental arch prompted a study of the total mandibular arch to see if it also reflected dimorphic differences. Again, the data from four Japanese samples were utilized (Figure 8, Figure 9). In each case, the size-standardized female mandibular arch was found to be significantly longer than that of the males. While variable across the four samples, the dimorphic differences between the sexes were consistently present. The mean SDI value was 2.680, making the mandibular arch the second most variable craniofacial structure after the nasal bones.
Finally, it should be noted that an ongoing study of the mandibular shape in norma lateralis (n = 158) showed that for the mean female data the ascending ramus was rotated posteriorly compared to the mean male data making the distance from the condyle head to menton relatively longer. This new study (Lestrel et al., 2010a) has now confirmed the above results presented here based on the inferior mandibular view.
With respect to the cranial vault, females exhibited a slightly more globular shape in contrast to males. This is apparent from the visual depiction (Figure 10, Figure 11). While these differences are numerically moderate as seen from the mean SDI of 0.458, they are nevertheless consistent across the four samples. While the more globular shape seen in females has been frequently noted in descriptive terms (Krogman, 1962), this is the first time that it has been visually and quantitatively characterized in global terms.
A study based on Japanese crania in norma lateralis merits mention (Yasui, 1986). This study did not use FDs but represents an independent approach, also size-standardized, using a series of closely spaced vectors from the centroid to the bounded outline of the cranium. The morphology chosen, however, also included the nasal bones and the maxilla. Consequently, this data was not comparable with the cranial vault data in the current study. The sexually dimorphic differences displayed in the Yasui paper (Figure 5) do not correspond with our results reported here, which is unfortunate. It is suggested that reasons for this discrepancy may be due to an undue influence of the nasal/maxillary region on the cranial vault or inadequate size standardization.
Another study (Rosas and Bastir, 2002) also reflects difficulties in comparison. In that study, thin-plate splines (TPSs) were used to characterize the craniofacial complex. The deformations shown in their paper (Figure 2) for sexual dimorphism are based on treating the cranium, maxilla, and mandible as a single unit. Moreover, their paper was based on landmarks and, therefore, cannot accurately depict the actual curvature in the craniofacial complex. Most importantly, it must be emphasized that TPS measures the differences between the male and female craniofacial complexes, which is displayed as a deformation. As a consequence, this makes it impossible to compare their results with those in this paper.
Nevertheless, the results presented here do not imply that all structures within the craniofacial complex will exhibit similar sexually dimorphic differences. An initial and very preliminary shape study of the anterior aspect of the central incisor, for example, demonstrated differences in size, a well-known effect, but did not display any sexually dimorphic differences in shape. This demonstrates that the craniofacial complex is not only a highly integrated structure that dynamically changes during growth, but also reflects immense complexity, which remains underestimated from a quantitative perspective. Clearly, growth processes are not only dynamic but are also quite variable. Within the craniofacial complex, maturation follows different growth trajectories for the different structures. This complicates matters and raises many questions with respect to the biological processes involved that ultimately determine sexual dimorphism.
What the biological process or processes are that determine these dimorphic differences in craniofacial shape are largely unknown at the moment. Few studies are available that have attempted to focus on the biological processes involved (Moss and Moss-Salentijn, 1977). Presumably, the initiation of hormonal activity at puberty is in some largely unknown way implicated, although it has been observed that some dimorphic differences already appear earlier than at adolescence. However, exactly what the mechanisms are that lead to these sexually dimorphic shape differences, or how activation in genetic activity is involved in shaping the phenotype, is simply not yet readily apparent.
The use of EFFs to model the shape of many of these structures in the craniofacial complex only represents the initial step in attaining these goals, namely the elucidation of the developmental biological process that underlies the adult shape. That is, the representation or measurement of the form (shape) is critically important as “Directly or indirectly, form is central to our understanding of biological and genetic processes” (Read, 1990, p. 417) and that “Ultimately, form must relate back to genetic information and developmental processes” (Read, 1990, p. 429). Clearly, the tasks facing the researcher are quite daunting and the answers to these challenging research questions lie in the future.
We are grateful for the assistance over the years of the following individuals and their respective institutions for allowing access to the various collections utilized in this research: Alex Roche, Fels Research Institute, Yellow Springs, OH; Daris Swindler, Department of Anthropology and the Burke Museum, University of Washington; Jan Huggare, Department of Orthodontics, School of Dentistry, Karolinska Institute, Huddinge, Sweden; Fumio Ohtsuki, Tokyo Metropolitan University, Department of Sports Medicine, Hachioji, Japan; Osamu Takahashi, Nihon University School of Dentistry at Matsudo, Chiba; Hisao Baba and Yuji Mizoguchi, National Science Museum, Shinjuku, Tokyo; Kazumichi Katayama, Kyoto University Museum; and Hirofumi Matsumura, Sapporo Medical University, Hokkaido.
|