Index INTRODUCTION METHOD AND RESULTS Model. Diffusion approximation. Properties for low migration. Numerical calculation and simulation. DISCUSSION References

INTRODUCTION

Various genetic factors, including natural selection and population structure, determine the pattern and amount of polymorphism in a natural population. The amount of polymorphism is often measured by nucleotide diversity (π), defined as the average number of pairwise nucleotide differences per site. Because of the simplicity, π is one of the most appealing measures to our intuition for the amount of polymorphism. Kimura (1969) showed that, assuming the infinite site model with free recombination between sites, under selective neutrality the expectation of the nucleotide diversity is given by E(π) = 4N_e υ, where N_e is the effective size of diploid population and υ is the mutation rate per site per generation. The result holds in the model without recombination between sites (Watterson 1975; Tajima 1983) or in any model for recombination. In a panmictic population with N_T diploids, E(π) = 4 N_T υ since N_e = N_T. Population structure generally increases E(π) in accord with N_e (e.g. see Nei and Takahata 1993 for the island model). In a panmictic population E(π) under selection is calculated by using formulae in Kimura (1969). Note that Kimura assumes free recombination between sites and the results of calculations for E(π) under selection are not the same as those in the model with linkage between sites. The calculations of E(π) under directional selection were shown in Table 1 of Nishino and Tajima (2004) or in Fig. 4 of Caballero and Hill (1992). Note that H in Nishino and Tajima and C[H] (in the case F = 0) in Caballero and Hill are the same quantity and E(π) is given by 2N_Tυ × H (or C[H]) as is described in MODEL. From the table or figure, we see that the negative selection decreases E(π). However, under positive selection the dominance of mutants has clearly different effect on E(π). When selection is strong, E(π) is raised at most about twice (8N_Tυ) in the semidominant (genic) selection as much as that under neutrality and at most about five times (20 N_Tυ) in the complete dominant selection. In the complete recessive selection, however, as the selection coefficient increases, E(π) decreases slowly and E(π) is always smaller than 4N_Tυ. Notably, under the directional selection E(π) is still of the same order as that under neutrality although the dominance has a clear effect on E(π). Furthermore, recently Nishino and Tajima (2004) have shown that in a subdivided population (the island model) the effect of dominance on E(π) becomes small as the migration rate decreases and that E(π) is raised by positive selection at most twice (8N_eυ) as much as that under neutrality irrespective of degree of dominance when the migration rate is very low.

View Details

Table 1. Accuracy of the diffusion approximation for E[π]

In contrast to the directional selection, the overdominant selection positively maintains polymorphism because of stability for allele frequency. There might be a clear example for overdominant selection in the mammalian histocompatibility complex genes (e.g., Hughes and Nei 1988, Takahata 1990). Those loci have many alleles probably by overdominant selection. Also in the plant gametophytic and sporophytic self-incompatibility, the similar mechanism is considered to work (e.g., Vekemans and Slatkin 1994, Schierup et.al 1998). At this moment it is not clear how many sites are under overdominance selection (e.g., Peters 2003; Fry 2004). Even if overdominant mutations are rare, it is important to investigate π under overdominant selection theoretically since each mutation can increase the amount of polymorphism substantially. In Fig. 1 the values of E(π) under symmetric overdominance in a panmictic population are shown as functions of N_Ts, where s is the selective advantage of heterozygotes. Those are calculated by using Kimura (1968) (in fact we use (8) of this paper as the concise form of Kimura’s expression). Fig. 1 shows that E(π) measured in units of 2N_Tυ increases exponentially with N_Ts. For example, if E(π) under neutrality is 0.1%, then E(π) under overdominant selection are about 0.2%, 1% and 6% in the case of N_Ts = 1, 3 and 5, respectively. In nature, however, a natural population is often divided into subpopulations and the consequence of subdivision is rather unclear. The purpose of this paper is to investigate the effect of subdivision on π under overdominant selection. In addition, the effect of subdivision on the fixation probability of an overdominant mutant is investigated. Although the fixation probability of an overdominant mutant has been considered in Cherry (2003), he did not show the case of symmetric overdominance and the case that mutatnt homozygote is disadvantageous. We also consider such cases. More importantly, using the fixation probability, we focus on the ratio of the amount of polymorphism to the evolutionary rate, which might be useful when we compare data between polymorphism and divergence between species.

View Details

Fig. 1. E[π] under symmetric overdominance in a panmictic population. E[π] is measured in units of 2NTυ and calculated by using (8).

METHOD AND RESULTS

Model.

The finite island model with L demes (subpopulations) is used. Each deme consists of N monoecious diploids. There are NL or N_T diploids in total. The migration rate (the fraction of genes in one deme that come from the other demes in the previous generation) is given by m. Consider the case where one mutant occurs in a site in a deme. Selection, migration and genetic drift influence the behavior of mutant until the mutant frequency is 1 (fixed) or 0 (extinct) in a total population. For symmetric overdominance model, the fitnesses of genotypes AA, Aa and aa are 1, 1+s and 1, respectively, where A is an ancestral type and a is a derived one. For more general model, which includes asymmetric overdominance, the fitnesses of genotypes AA, Aa and aa are assumed to be 1, 1+s₁ and 1+s₂, respectively. We refer this as the general selection model. It is also assumed that selection and random mating occur independently in each deme.

Here, define H as the expected sum of heterozygosity in a total population produced by one irreversible mutant, or the expectation of



Here, x(t) is the mutant frequency in generation t since the occurrence of mutation with x(0) = 1/(2N_T) and t_a is the absorption time (the time until fixation or extinction of a mutant in a population). Assuming the infinite site model (Kimura 1969), the expectation of π is given by E(π) = H × 2N_Tυ, since mutation occurs in a small rate 2N_Tυ per site per generation in the population. Thus, E(π) measured in units of 2N_Tυ is equal to H and we investigate H rather than E(π) in the following. Under neutrality H is given by H = 2N_e / N_T from E(π) = H × 2N_Tυ and E(π) = 4N_eυ. In a panmictic population H is 2. In a subdivided population, H is larger than 2 since N_e is larger than N_T. We are also interested in the evolutionary rate in the present model. The evolutionary rate per site per generation is given by u × 2N_Tυ, where u is the fixation probability of a mutant, whereas E(π) is given by H × 2N_Tυ. In this sense, H and u are analogous and the most basic quantities for within-species polymorphism and between-species divergence, respectively.

Diffusion approximation.

Recently, several authors used diffusion approximations to derive the fixation probability of a mutant with dominance in a subdivided population (Cherry 2003; Whitlock 2003; Roze and Rousset 2003; Nishino and Tajima 2004). In particular, Cherry related an island model of population structure to an approximately equivalent panmictic population with “the effective selection coefficient” and “the effective population size”. Cherry’s method helps us understand the effect of population subdivision intuitively. Thus we use Cherry’s method. First, consider symmetric overdominance model. According to Cherry (2003), assuming a large number of demes and weak selection, the effective population size, N_e, and the effective selection coefficient, s_e, are given by

respectively. Note that Cherry assumes N haploids or N/2 diploids in each deme, whereas we assume N diploids. Using N_e and s_e, defined in (1) and (2), respectively, we can regard an island model as a hypothetical panmictic population. Then the mean and variance of change in mutant frequency are given by M_δx = s_ex(1–x) (1–2x) and V_δx = x(1–x)/(2N_e). Substituting those M_δx and V_δx into the general formula for the fixation probability in Kimura (1962), the fixation probability, u(p), with the initial mutant frequency, p, is given by

The fixation probability of a newly arisen mutant is given by u = u(1/2N_T), which is reduced to

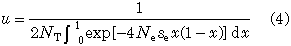
approximately, because p is very small (Kimura 1964). In order to see the effect of subdivision we consider the case where N_T is constant. Then u has only one independent parameter, i.e., N_es_e. From (1) and (2), we have

Thus, u in the island model is theoretically the same as that in a panmictic population with the effective selection coefficient s_e = 2Nms/(2Nm+1). The value of decreases and moves toward 0 as Nm decreases. This means that u monotonically decreases and approaches that of a neutral mutant as Nm decreases.

Next, consider H. Here, let us introduce the quantity, H’, defined by

Under neutrality, H is given by H = 2N_e / N_T as described above and H’ is always 2 irrespective of degree of subdivision. Thus, H’ can be a useful quantity for studying the effect of selection on H in a subdivided population. Under overdominant selection, the expected sum, H(p), of heterozygosity with the initial mutant frequency, p, is calculated numerically by using

where

This is obtained by substituting M_δx = s_ex(1–x) (1–2x), V_δx = x(1–x)/(2N_e) ν_m = 1 and into (11)–(14) of Kimura (1969). The expected sum of heterozygosity caused by a newly arisen mutant is given by H = H(1/(2N_T)), which is reduced to

approximately, because p is very small. From (8) H’ is given by

Assuming constant N_T, H is a function of N_es_e and N_e. As is the case with u, however, H’ has only one independent parameter, N_es_e, and H’ is a monotonically decreasing function of Nm. This is explained in a similar way to u. From (8) and (9), H’ in the island model is theoretically the same as H in a panmictic population with the effective selection coefficient s_e = 2Nms/(2Nm+1). This means that H’ monotonically decreases and approaches that of neutral mutant as Nm decreases. On the other hand, H is the product of H’ and the ratio of N_e to N_T, or H = N_e / N_T × H’. The ratio N_e / N_T increases as Nm decreases, so that the direction of change in H is determined by the two terms having opposite effects on H, i.e., H’ and N_e / N_T.

So far, we consider the symmetric overdominance. In the same way, H and u in the case of general selection model are described in Cherry (2003)’s expression. That is if we use N_e given by (1),

instead of N_T, s₁ and s₂, respectively, we can regard an island model as a hypothetical panmictic population. Then, the approximations of u, H, and H’ for general selection model, corresponding to (4), (8) and (9), are given by

and

As the migration rate decreases, the effect of s₁, N_es_1e, becomes small and approaches (1/2)N_Ts₂. The term N_es_2e, however, is constant over any degree of population subdivision. That is, the effect of fitness is moved toward additive as is pointed out by Cherry (2003).

Properties for low migration.

The diffusion approximations assume a large number of demes and weak selection. In this section, relaxing the assumptions, the properties of H and u in very low migration are given by “low migration approximation” (e.g., Lande 1979, Slatkin 1981, Takahata 1991). Note that our purpose of this section is only to see the points which the values of H and u approach as the migration is extremely restricted.

Under the assumptions of subdivided population and overdominant selection, mutants may stay within a deme for a long time in moderate frequency because of its stability. Consider the case where the migration becomes restricted. As the migration rate decreases, the staying time of the mutant within a deme in moderate frequency becomes relatively short compared with the staying time of the mutant in the total population. That is, even in the case of overdominant selection, the migration rate can be assumed to be so low that there are only two states in any deme, either “mutant” or “non-mutant”. In the following, we consider such a case. Slatkin (1981) investigated the fixation probability and the time to fixation under the assumption that the migration matrix is symmetric. Nishino and Tajima (2004) obtained the same result for the fixation probability as that of Slatkin (1981) in a more restricted model (the island model) but in a simpler manner, and extended the method to approximate the expected sum of heterozygosity. The results of Slatkin (1981) and Nishino and Tajima (2004) can be used in the case of overdominant mutant.

Let us consider the general selection model (refer to Model). In Nishino and Tajima (2004), the fitnesses of genotypes AA, Aa and aa are given by 1, 1+hs and 1+s, respectively. If we replace hs and s with s₁ and s₂, the same argument is possible for the low migration approximations as that of Nishino and Tajima (2004). The results are shown below.

The fixation probability of a mutant, u, is expressed as the product of the fixation probability to the initial deme in which the mutant occurs, f₀, and the fixation probability to the total population given that the initial deme is fixed, U₁. Then, the fixation probability u is given by

Here, f₀ is calculated as the fixation probability of a mutant in a panmictic population with N diploids using Kimura (1962). Note that in (14) U₁ is independent of s₁ and the same as the fixation probability of semi-dominant mutants with the initial frequency 1/L in a panmictic population with N_T diploids, but f₀ depends on s₁ (Slatkin 1981, Nishino and Tajima 2004). As a whole, u depends on s₁ because f₀ includes s₁. In the case of large L, however, u given by (14) is essentially independent of s₁. This is because Ns is small (Ns « 1) and f₀ is nearly equal to 1/(2N) when L is large. In this case, u in (14) becomes s₂/(1-exp[-2N_Ts₂]) approximately. This is consistent with u given by (11) for the case of low migration rate. From the limit of s₂ → 0 in (9), we have u = f₀ /L in the case of symmetric overdominance. In the case of large L, u becomes 1/(2N_T), which is consistent with u given by (14) for the case of low migration rate again.

Next, the expected sum of heterozygosity with the initial frequency of mutant 1/(2N_T), H(1/(2N_T)) or H, is approximately given by the product of the fixation probability to initial deme f₀ and the expected sum of heterozygosity given that the initial deme is fixed, denoted by H₁. H is given by

Interestingly, H is independent of s₁. Of course, f₀ depends on s₁ as described above. In addition, H₁ also depends on s₁. The product of f₀ and H₁ or H, however, does not depend on s₁. The fact that H is independent of s₁ is consistent with the low migration case for the diffusion approximation shown in (12). From (15) at the limit of s₂ → 0 (symmetric case), we have

This shows that H for symmetric overdominant mutant is identical with that for neutral mutant in the very low migration as is shown by the diffusion approximation in the previous section. The expression of (16) is obtained by substituting N_e = (4Na+1)/(4Na)N_T, where a = (L/(L-1))²m (Nei and Takahata 1993), into the relationship H = 2N_e / N_T and by assuming low migration. In fact, the expression of N_e is more exact than that given by (1) since the number of deme is considered. Next, if the genotype aa is more advantageous than AA such that 2Ns₂>>1, (15) is reduced to

since 1–e^–2ns ≈ 1 and U1 ≈ 1. In fact, this holds in weaker condition such that 2Ns₂ > 1 as is verified by comparison between (15) and (17). Formula (17) means that in the case of asymmetric overdominance H is at most twice as much as that of neutral mutant. This result is consistent with the diffusion approximation in the previous section, again.

Numerical calculation and simulation.

Fig. 2 shows the effect of population subdivision (the reduction of Nm) on π under symmetric overdominance. The expectation of π is measured in units of 2N_Tυ and calculated as H by using (8). For N_Ts = 0 (selectively neutral case), as Nm decreases, E(π) monotonically increases. E(π) is about 2 for Nm > 1 but effectively increases by subdivision for Nm < 1, and rapidly increases for Nm < 0.1. For N_Ts = 1, E(π) is almost constant (E(π) is around 4) over a wide range of migration rate, Nm > 0.5 (see also Table 1). For N_Ts = 3 and 5, E(π) is remarkably reduced as Nm decreases in a particular range of migration rate (Nm > 0.25 for N_Ts = 3 and Nm > 0.14 for N_Ts = 5). At such a migration rate, the reduction of H’ by subdivision overwhelms the increase of N_e by subdivision. In more restricted migration, E(π) increases by subdivision. As a result, for N_Ts = 3 and 5, E(π) is a U-shaped function of Nm. Roughly speaking, if N_Ts > 1 then E(π) is U-shaped. For any level of selection coefficient, E(π) approaches the value expected under neutrality along with the decreasing Nm, as is explained in the section for the diffusion approximation.

View Details

Fig. 2. E[π] under symmetric overdominance in an island model. E[π] for various selection intensity and neutrality are shown as a function of Nm. E[π] is measured in units of 2NTυ and calculated by using (8).

To test the accuracy of (8) for E(π) obtained by the diffusion approximation, computer simulations are conducted. The method of simulations was described in Model and we use the pseudosampling method (Kimura and Takahata 1983) to perform the random mating in each deme. Table 1 compared the theoretical values of E(π) measured in units of 2N_Tυ with the results of simulations in the cases of L = 10, 30 and 50. As a whole, the theoretical predictions are in agreement with the simulation results. The simulation results also confirm that E(π) for given N_Ts is almost only a function of Nm. In details, the theoretical prediction works better in the case of a large number of demes. More than 90% of predictions are within 5% of the simulation results for L = 50. This is because Cherry (2003) assumes a large number of demes and week selection within demes (Ns « 1) to approximate the distribution of within-deme mutant frequency as a β-distribution (Wright 1931). Thus, in the case for L = 50, for a given N_Ts the prediction is better not only by the large number of demes but also by small Ns. In fact, when N_Ts is 5, Ns is 0.5 or 0.1 for L = 10 or 50, respectively. When L is small (L < 10) and/or selection is not weak (Ns ?? 1), the diffusion approximation is not good. As the migration rate becomes small, however, E(π) approaches the value given by (16) assuming low migration. Table 2 shows E(π) obtained by simulations and (16) in the case where L is small (L = 2 and 5) and selection is strong (N_Ts = 5 and 10). When the migration rate is very low(Nm = 10^–3 or 10^–4), the predictions by (16) are in agreement with the simulation results.

View Details

Table 2. E[π] for a small number of demes

Theoretically (in the framework of Cherry’s diffusion method), the reduction of E(π) by population subdivision is attributed to the reduction of H’. In fact, in this framework, given the mutant frequency, x, in a population, the average of 2x_i(1- x_i) among all demes is determined, where x_i is the mutant frequency of the i-th deme. That is, given x, the average of 2x_i(1-x_i) among all demes is 2x(1-x)(1- F_ST) = 2x(1-x) 4Nm/(4Nm+1), where F_ST is the fixation index and equal to 1/(4Nm+1) calculated from a β-distribution (Wright 1931). Thus, H’ is theoretically equal to E(π_w) measured in units of 2N_Tυ, where π_w is nucleotide diversity within demes. Fig. 3 shows the predictions by (9) for E(π_w) measured in units of 2N_Tυ and the results of simulations with L = 50. In the simulations, E(π_w) in units of N_Tυ is the average of

over the replications of simu-

lation. Here, x_i(t) is the mutant frequency in the i-th deme in generation t since the occurrence of mutation, and t_a is the absorption time. From Fig. 3, the predictions agree with the results of simulations. The decrease of E(π_w) by subdivision is rapid and sensitive to Nm in the range of Nm < 10. For Nm = 0.01, E(π_w) is reduced to almost 2 in all cases of selection coefficient. In the case of L = 30 the predictions are slightly lower than the results of simulations and in the case of L = 10 the predictions clearly underestimate (data not shown). This is because in this case within-deme selection is not weak (Ns ?? 1) and the frequency of mutant tends to be near its deterministic equilibrium.

View Details

Fig. 3. E[πw] under symmetric overdominance in an island model. E[πw] measured in units of 2NTυ for various selection intensity and neutrality are shown as a function of Nm. The lines show the predictions by (9). The symbols show the simulation results for L = 50. The average values of sum of heterozygosity for 106 new mutations are used as E[πw].

Fig. 4 shows E(π) for asymmetric overdominance. Fig. 4 (A) is for the case where mutant homozygote is disadvantageous (s₂ < 0) and Fig. 4 (B) advantageous (s₂ > 0). The values of E(π) are calculated by (12). The results of symmetric overdominance and neutrality are also shown. From Fig. 4, as is the case for symmetric overdominance, population subdivision generally reduces E(π) in some range of migration rate. The effect of sign of s₂ on E(π) is interesting. In the case of random mating population (almost the same as the case of Nm = 100 in Fig. 4), E(π) tends to be large in the case of negative s₂, compared with the case of positive one. For example, in the case of N_Ts₁ = 5, E(π) are 114.41 and 55.76 for N_Ts₂ = –1.25 (negative s₂) and 1.25 (positive s₂), respectively. The reason may be that the deterministic equilibrium frequency of mutant is smaller and the mutant frequency tends to reach the equilibrium frequency in the case of negative s₂. The equilibrium frequency is given by s₁/(2 s₁– s₂) and in the case of N_Ts₁ = 5 the frequencies are 0.44 and 0.57 for N_Ts₂ = –1.25 (negative s₂) and 1.25 (positive s₂), respectively. The effect of sign of s₂ on E(π), however, gradually changes by subdivision along with decreasing Nm and the situation is reversed in the case of extreme subdivided population. For example, in the case of Nm = 0.01, E(π) are 34.56 and 75.54 for N_Ts₂ = –1.25 and 1.25, respectively. Whereas E(π) are 52 and 55 for neutrality (N_Ts₁ = N_Ts₂ = 0) and symmetric overdominance (N_Ts₁ = 5, N_Ts₂ = 0), respectively. That is, in the very low migration, E(π) for s₂ > 0 is larger than that for neutrality or symmetric overdominance. On the contrary, E(π) for s₂ < 0 is smaller. This is explained as follows. As the migration rate decreases, N_es_1e becomes small and approaches (1/2)N_Ts₂. That is, the effect of fitness is moved toward the additive directional selection. In the additive directional selection, as is explained in INTRODUCTION, E(π) is (at most twice) larger in the case of positive selection than that under neutral and smaller in the case of negative selection. This is consistent with the low migration approximation too. That is, E(π) for positive s₂, which is calculated by (15), is larger than E(π) for neutral mutation given by (16). Particularly when Ns₂ is large, E(π) is twice as that of neutral mutant as shown in (17). On the other hand, E(π) for negative s₂, which is calculated by (15), is smaller than that of neutral mutation.

View Details

Fig. 4. E[π] under asymmetric overdominance in an island model. E[π] is measured in units of 2NTυ and calculated by using (12). For comparison, E[π] for neutrality and symmetric overdominance are also shown. (A) The case in which mutant homozygote is disadvantageous (s2 < 0). (B) The case in which mutant homozygote is advantageous (s2 > 0).

The effect of subdivision on the fixation probability of an overdominant mutant, u, is shown in Fig. 5. The fixation probability for symmetric overdominance monotonically decreases with decreasing Nm as is explained in Diffusion approximation. This is also the case for an asymmetric overdominant mutant (Fig. 5). The extent of decrease, however, is small compared with the amount of polymorphism.

View Details

Fig. 5. Fixation probability of a overdominant mutant, u, in an island model. u is measured in units of 1/(2NT) and calculated by using (11).

The comparison between changes of E(π) and the evolutionary rate, 2N_Tυ u, by population subdivision is also of interest. For this comparison, in Fig. 6 the ratio of E(π)/( 2N_Tυ u) = H/u is shown as a function of Nm. The ratio is normalized by that under neutrality so that the ratio under neutrality is always one irrespective of the degree of subdivision, Nm. Then, the ratio was calculated as (H’/2)/(u/(2N_T)), where H’ and u were given by (13) and (11), respectively. In all cases for N_Ts₂, the ratio decreases as Nm decreases because the amount of polymorphism is largely reduced by subdivision, compared with the fixation probability. The ratio approaches an asymptotic constant in low migration. The constant is one in the case of s₂ = 0 (symmetric overdominance), more than one in the case of s₂ < 0 and less than one in the case of s₂ > 0. This is because the effect of fitness is moved toward additive directional selection by subdivision. The harmful mutations (s₂ < 0) are known to relatively contribute polymorphism compared with between-species variation (the fixation in a population). On the contrary, the advantageous mutations (s₂ > 0) are known to relatively contribute between-species variation (the fixation in a population) compared with polymorphism. As a result, for s₂ > 0, there is an interesting phenomenon. That is, the case exists that E(π)/( 2N_Tυ u) is more than one in a panmictic population or a population with high migration but less than one in a population with low migration. In Fig. 6, this case corresponds to N_Ts₂ = 1.25.

View Details

Fig. 6. The ratio of the amount of polymorphism to the evolutionary rate, E(π)/(2NTυ u). The ratio is normalized by that under neutrality.

DISCUSSION

In this paper we have investigated the effect of the population subdivision under the overdominant selection on the amount of polymorphism measured by π and the fixation probability of a mutant. The expectation of π is reduced by subdivision in some range of migration rate under overdominant selection when the expectation of π is large in a panmictic population. Particularly in the case of symmetric overdominance, the expectation of π is obviously reduced by subdivision when N_Ts > 1. Using simulations Schierup (2000) obtained the result related to the present study. That is, the number of alleles for gametophytic self-incompatibility or alleles under overdominant selection is reduced by subdivision. Muirhead (2001) derived the analytic result for this problem. The degree of reduction for polymorphism, however, is smaller than that in the present model (Fig. 2, 3 and 7 in Schierup 1998 and Fig. 1 in Muirhead 2001). Although the evolutionary rate under overdominant selection is also reduced by subdivision, the expectation of π is more affected by subdivision. And the ratio of the expectation of π to the evolutionary rate decreases as Nm decreases. Furthermore, there are the cases where the ratio measured by that under neutrality changes from more than one to less than one when the homozygote of mutant is advantageous. Recently, a Poisson random-field model of polymorphism and divergence that allows arbitrary dominance was developed in a random mating population (Williamson et al. 2004). On the other hand, Wakeley (2003) showed that estimates of the scaled selection coefficient N_Ts₀ using the Poisson random-field model, where s₀ is the genic selection coefficient, are remarkably robust to poplation subdivision when the sites for consideration are under genic selection. Our results suggest that if we apply the Poisson random-field model to the sites under overdominant selection in order to estimate the selection parameters, population subdivision much affects the estimated values unless the advantage of heterozygote is week. That is, the advantage of heterozygote is underestimated. Note that we have investigated π as a measure of polymorphism but Williamson et al. (2004) used the frequency spectrum of sequence polymorphisms. Still, the advantage of heterozygote should be underestimated.

We thank H. Tachida and two anonymous reviewers for their valuable suggestions and comments.