Index INTRODUCTION METHODS Estimating 4Nμ Model and Simulation Data analysis RESULTS Simulation Data analysis DISCUSSION References

INTRODUCTION

The pattern of DNA polymorphism in a population can give useful information about the evolutional history such as demographic change and natural selection. The pattern of DNA polymorphism can be expressed as the distribution of the number of nucleotide differences, namely mismatch distribution and the distribution of the number of segregating sites with allelic nucleotide frequency, namely allelic nucleotide frequency spectrum. In the study of mismatch distribution, Tajima (1983) showed the statistical properties of the average number of nucleotide differences. Slatkin and Hudson (1991) and Rogers and Harpending (1992) studied the effect of population growth on mismatch distribution. And several studies (Di Rienzo and Wilson, 1991; Sherry et al., 1994) including the above studies concluded that the data in human mitochondrial DNA (mtDNA) showed the signature of population expansion. On the other hand, in the study of allelic nucleotide frequency spectrum, Tajima (1989a) studied the relationship between the number of segregating sites and the average number of nucleotide differences, and developed the statistical method for testing the neutral mutation hypothesis. Furthermore, in that article, he obtained the expected allelic nucleotide frequency spectrum by using Ewens’s (1972) sampling theory. Fu and Li (1993) studied the statistical properties of the numbers of external and internal mutations, and developed the statistical method for testing the neutral mutation hypothesis. Therefore, Tajima’s D statistic and Fu and Li’s D statistic summarize the allelic nucleotide frequency spectrum. In observed data, the allelic nucleotide frequency spectrum in human mtDNA shows an excess of rare allelic nucleotides, so that Tajima’s D value in mtDNA is clearly negative (Excoffier, 1990; Merriwether et al., 1991). On the other hand, the allelic nucleotide frequency spectrum in human nuclear DNA does not always show an excess of rare allelic nucleotides, so that Tajima’s D value in nuclear DNA is not clearly negative (Wall and Przeworski, 2000). Fay and Wu (1999) examined the change of Tajima’s D value under some bottleneck models by the computer simulation, and showed that the difference of patterns of DNA polymorphism between mtDNA and nuclear DNA can be explained by population bottleneck.

In order to understand why the pattern of polymorphism in nuclear DNA is different from that of mtDNA, more detailed analyses in nuclear DNA are needed. To distinguish between demographic change and natural selection in nuclear DNA data, the analyses in multilocus data and SNP data might be necessary. The recent studies for world human populations by using SNP data and multilocus data (Marth et al., 2004; Voight et al., 2005) showed that the data in non-African populations such as European and Asian are compatible with the bottleneck models. For analyzing the allele frequency data in SNPs, Marth et al. (2004) developed three methods, i.e., a closed mathematical formulation for the allele frequency spectrum, correcting the ascertainment bias introduced by shallow SNP sampling, and dealing with variable sample sizes. In correcting the ascertainment bias, they developed a model consisting of k discovery samples and n genotyping samples, and showed that the allele frequency spectrum of constant size population is flat when k = 2. By examining the departure from the flat distribution of constant size population, they studied the allele frequency spectrum of world human populations.

In this study, for analyzing the allele frequency spectrum, we propose another simple method using a new statistic θ_i which estimates 4Nμ from the number of segregating sites whose allelic nucleotide frequency is i/n among n DNA sequences, where N is the effective population size and μ is the mutation rate per generation per nucleotide site. And we examine the effect of change in population size on distribution of θ_i by the coalescent simulation. Furthermore, we apply this method to the SNP data in the International HapMap Project (The International HapMap Consortium, 2005).

METHODS

Estimating 4Nμ

4Nμ can be estimated from the observed number of segregating sites per nucleotide site (S) in the samples by

(1)

(Watterson, 1975), where N is the effective population size, μ is the mutation rate per generation per nucleotide site and n is the sample size.

Considering the infinite site model (Kimura, 1969), two allelic nucleotides exist in a segregating site. One nucleotide exists with frequency i/n and another exists with frequency (n–i)/n, where n is the sample size and 1 ≤ i ≤ n–1. The expectation of the number of segregating sites per nucleotide site whose allelic nucleotide frequency is i/n in a sample of n DNA sequences (S_i) is given by

(2)

(Tajima, 1989a). Therefore, 4Nμ is also estimated by

(3)

Under the neutral mutation and constant population size model, the expectation of θ_i is equal to that of θ at any allelic nucleotide frequency, so that the distribution of θ_i is flat. Therefore, the departure of the distribution of θ_i from the horizontal line, which represents the value of θ, reflects change in population size and/or natural selection. Fu and Li (1993) indicated that, when mutations are selectively neutral, the number of segregating sites per site with low allelic nucleotide frequency (S_i) reflects the recent population size, because mutations with low allelic nucleotide frequency mainly occurred in the external branches of the genealogy, whereas the number of segregating sites per site with intermediate allelic nucleotide frequency (S_i) reflects the older population size, because mutations with intermediate allelic nucleotide frequency mainly occurred in the internal branches of the genealogy. On the other hand, when selective sweep occurred or purifying selection is operating, the number of segregating sites per site with low allelic nucleotide frequency (S_i) increases, compared to the neutral mutation model, since the proportion of the lengths of external branches in the genealogy increases. When balancing selection is operating, the number of segregating sites per site with intermediate allelic nucleotide frequency (S_i) increases, compared to the neutral mutation model, since the proportion of the lengths of internal branches in the genealogy increases.

Model and Simulation

We consider nuclear autosomal DNA sequences of a human population whose effective population size is N. Mutations are assumed to be neutral. We have simulated the coalescent process of the nuclear DNA sequences under several demographic models and examined the average number of nucleotide differences per site (π), the number of segregating sites per site (S) and the number of segregating sites per site with each allelic nucleotide frequency (S_i). In the increase model, we assumed that the constant population size (N = 5,000) suddenly increased to another constant size (N = 50,000) 10,000 generations ago. In the decrease model, we assumed that the constant population size (N = 50,000) suddenly decreased to another constant size (N = 5,000) 10,000 generations ago. The bottleneck models are shown in Fig. 1. The parameters are as follows: t is the backward time in generation; N₀ (= 50,000) and N₁ are the current and bottleneck population sizes, respectively; and T₀ and T₁ are the time to the bottleneck and the duration of the bottleneck in generation, respectively. Table 1 shows the values of parameters in the bottleneck models.

View Details

Fig. 1 The bottleneck model. t represents backward time in generation.

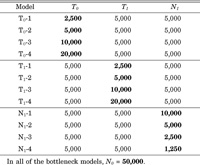View Details

Table 1 Parameters of the bottleneck models

We consider the infinite site model (Kimura, 1969). The parameters are assumed as follows: the mutation rate per site per generation in nuclear DNA is μ = 1 × 10^–8; the length of DNA sequences sampled is 1 kb, so that mutation rate per sequence per generation in nuclear DNA is v = 1 × 10^–5.

In simulating the coalescent process, we applied Hudson’s (1990) method with some modifications. The coalescent simulation where the sample size is 40 (n = 40) was conducted backward in time. The procedure of the coalescent simulation is described as follows.

1. To determine the topology of the genealogy and the coalescent time (T_j) when j DNA sequences coalesce into j–1 ones, where 2 ≤ j ≤ 40, the coalescent simulation is conducted as follows. First, 40 DNA sequences are tried to coalesce into 39 DNA sequences. Continually, 39 DNA sequences are tried to coalesce into 38 DNA sequences. This procedure continues until 40 DNA sequences coalesce into one DNA sequence (MRCA). The coalescent probability that j DNA sequences coalesce into j–1 DNA

sequences is



This probability changes, depending on the population size (N).

2. Mutations are generated on each branch of the genealogy under the Poisson distribution with the mean of vT_j, where v is the mutation rate per sequence per generation.

3. To examine the number of segregating sites, the number of mutations in all branches of the genealogy is counted. To examine the number of segregating sites with each allelic nucleotide frequency and the average number of nucleotide differences, the number of mutations in each branch of the genealogy is counted depending on the number of descendent DNA sequences. A mutation in the branch that has i descendent DNA sequences represents the case where one nucleotide exists with frequency i/40 and another nucleotide exists with frequency (40–i) /40. And a mutation in this branch is counted i × (40–i) times, when every pairwise nucleotide differences among 40 DNA sequences are examined.

Data analysis

The SNP data were downloaded from the website of the International HapMap Project (The International HapMap Consortium, 2005). We analyzed the allele frequency data (http://www.hapmap.org/downloads/frequencies/latest_ncbi_build36/rs_strand/non-redundant) in the autosomal chromosomes. These data were observed in the samples of the four populations, i.e., Yoruba in Ibadan, Nigeria (abbreviation: YRI), CEPH (Utah residents with ancestry from northern and western Europe) (abbreviation: CEU), Han Chinese in Beijing, China (abbreviation: CHB) and Japanese in Tokyo, Japan (abbreviation: JPT). In YRI and CEU populations, 60 individuals were sampled, respectively. In CHB and JPT populations, 45 individuals were sampled, respectively. These SNP data, however, includes many non-typing data. So we used the SNP data where more than 115 nucleotides were genotyped in the samples of 120 in YRI and CEU. In CHB and JPT, the SNP data were used, where more than 85 nucleotides were genotyped in the samples of 90.

In order to use the SNP data including non-typing allelic nucleotides, we have adjusted the sample size in the SNP data by using the Marth et al.’s (2004) procedure of equivalence sample size reduction with some modifications. Here, we consider the reduction of sample size from n to m and denote the number of segregating sites whose allelic nucleotide frequency is j/m after adjustment of sample size by S_m(j). Marth et al. (2004) adjusted the sample size after counting the all segregating sites, where the sample size is m or more, with each allele frequency. On the other hand, we count the segregating sites, where the sample size is more than m, in proportion to the probability for adjustment. In the reduction of sample size, there are some events of how many major allelic nucleotides or minor allelic nucleotides are reduced. The probability that each event occurs can be calculated. Therefore, the number of segregating sites whose allelic nucleotide frequency is i/n before adjustment of sample size (S_n(i)) can be divided into S_m(j) in proportion to the probability of

when i – j = 0, the probability of

when 0 < i – j < n – m, and the probability of

Fig. 2 illustrates the method for adjustment of sample size, considering the case where the number of major allelic nucleotides is 115 and the number of minor allelic nucleotides is 5. There are five events when the number of sample size in this SNP site is reduced from 120 to 116. The probability in each event is shown in Fig. 2. The number of segregating sites with each allelic nucleotide frequency is counted in proportion to this probability.

View Details

Fig. 2 The method for adjustment of sample size. The sample size represents the number of nucleotides which are genotyped in the SNP site. We consider the case where the number of major allelic nucleotides is 115 and the number of minor allelic nucleotides is 5. There are five events when the number of sample size in this SNP site is reduced from 120 to 116. The probability in each event is shown. The number of segregating sites with each allelic nucleotide frequency is counted in proportion to this probability.

RESULTS

Simulation

The coalescent simulation was repeated 1 × 10⁶ times for each set of parameter values. Fig. 3 shows the distributions of θ_i in nuclear DNA under the increase and decrease models. Usually, in allelic nucleotide frequency spectrum, the number of minor allelic nucleotides is shown. In this study, however, both the number of minor allelic nucleotides and that of major allelic nucleotides are shown in order to characterize the distribution of θ_i. In the increase model, Tajima’s D is negative and the distribution of θ_i is U-shaped. On the other hand, in the decrease model, Tajima’s D is positive and the distribution of θ_i is upside-down U-shaped.

View Details

Fig. 3 The distributions of θi of nuclear DNA in the increase model where the constant population size (N = 5,000) suddenly increased to another constant size (N = 50,000) 10,000 generations ago and the decrease model where the constant population size (N = 50,000) suddenly decreased to another constant size (N = 5,000) 10,000 generations ago. In the increase model, D = –0.965. In the decrease model, D = 0.645.

Table 2 shows π, θ and Tajima’s D in nuclear DNA obtained under the bottleneck models. The longer the time to the bottleneck is, the larger π and θ in nuclear DNA are. The longer the duration of the bottleneck is, the smaller π and θ in nuclear DNA are. And the smaller the population size of the bottleneck is, the smaller π and θ in nuclear DNA are. Tajima’s D in nuclear DNA is positive under some bottleneck models, but negative under the other bottleneck models.

View Details

Table 2 π, θ and Tajima’s D in nuclear DNA observed under the bottleneck models

The time to the bottleneck, the duration of the bottleneck and the population size of the bottleneck influence the distribution of θ_i (Fig. 4). The distribution of θ_i in nuclear DNA is W-shaped in some bottleneck models. Fig. 4A shows the effect of the time to the bottleneck on the distributions of θ_i in nuclear DNA. In the recent bottleneck model (T₀-1), the distribution of θ_i is nearly upside-down U-shaped. As the time to the bottleneck becomes longer, θ_i increases at low allelic nucleotide frequency, but θ_i decreases at intermediate allelic nucleotide frequency. Therefore the distribution of θ_i becomes W-shaped. Fig. 4B shows the effect of the duration of the bottleneck on the distributions of θ_i in nuclear DNA. In the long duration bottleneck model (T₁-4), the distribution of θ_i is nearly U-shaped. As the duration of the bottleneck becomes shorter, θ_i increases more at intermediate allelic nucleotide frequency than at low allelic nucleotide frequency. Therefore, the distribution of θ_i becomes W-shaped. Fig. 4C shows the effect of the population size of the bottleneck on the distributions of θ_i in nuclear DNA. In the bottleneck model (N₁-4) with the small population size, the distribution of θ_i is nearly U-shaped. As the population size of the bottleneck becomes larger, θ_i increases more at intermediate allelic nucleotide frequency than at low allelic nucleotide frequency. Therefore, the distribution of θ_i becomes W-shaped.

View Details

Fig. 4 The effect of (A) the time to the bottleneck, (B) the duration of the bottleneck and (C) the population size of the bottleneck on the distributions of θi in nuclear DNA.

Data analysis

We have analyzed the allele frequency data in the autosomal chromosomes in the International HapMap Project. Table 3 shows the number of SNPs and the number of segregating sites found in the data. For example, in YRI population, 3,676,729 SNPs were found. We used 3,135,774 SNPs where more than 115 nucleotides were genotyped in the samples of 120. The number of segregating sites is 2,416,048, because many monomorphic sites are included in the SNP data.

View Details

Table 3 The number of SNPs and the number of segregating sites found in the data

Fig. 5 shows the distributions of θ_iL in the autosomal chromosomes in the four populations, i.e., YRI, CEU, CHB and JPT. Here, L represents the length of DNA sequences used for finding SNP sites. Since L is unknown in this genome-wide SNP data, the observed number of segregating sites whose allelic nucleotide frequency is i/n in a sample of n DNA sequences cannot be divided by L. Therefore, θ_iL is shown as the relative value. In YRI population, the distribution of θ_iL is flat, except for low allelic nucleotide frequencies which are 0–25% or 75–100%. We ignored θ_iL in low allelic nucleotide frequencies, because we could not depend on these values because of ascertainment bias. This pattern of the distribution is similar to that of the case where the population size is constant. In CEU, CHB and JPT populations, the distributions of θ_iL are upside-down U-shaped. This pattern of the distribution is similar to that of the decrease model in the simulation.

View Details

Fig. 5 The distributions of θiL in the autosomal chromosomes in the four populations, i.e., YRI, CEU, CHB and JPT. L represents the length of DNA sequences used for finding SNP sites. Since L is unknown in this genome-wide SNP data, the observed number of segregating sites whose allelic nucleotide frequency is i/n in a sample of n DNA sequences cannot be divided by L. Therefore, θiL represents a relative value.

DISCUSSION

In this study, we have developed a simple method using a new statistic θ_i. This method has two merits. The first is that allelic nucleotide frequency spectrum can be analyzed in detail. Although allelic nucleotide frequency spectrum is often summarized by Tajima’s (1989a) D statistic and Fu and Li’s (1993) D statistic, these statistics show a deviation in the two directions, namely, too many rare allelic nucleotides or too many intermediate allelic nucleotides. On the other hand, our method can directly analyze allelic nucleotide frequency spectrum at any allelic nucleotide frequency. The W-shaped distribution of θ_i reflects three population sizes, which are the size before the bottleneck at intermediate allelic nucleotide frequency, the size after the bottleneck at low allelic nucleotide frequency and the size during the bottleneck at between low and intermediate allelic nucleotide frequency. In other words, the population bottleneck consists of the reduction and the following recovery of the population size. Tajima (1989b) studied the effect of the bottleneck on the amount of DNA polymorphism. By the numerical computation, he showed that M, which is equal to 4Nv estimated from the number of segregating sites, is smaller than the average number of nucleotide differences (k) during the reduction of the bottleneck and that M is larger than k during the recovery of the bottleneck. This relationship between M and k in the bottleneck suggests the W-shaped distribution of θ_i.

The demerit of our method is that many observed data are needed to estimate 4Nμ at intermediate allelic nucleotide frequency, because the observed number of segregating sites with intermediate allelic nucleotide frequency is much less than that with low allelic nucleotide frequency. Indeed, the distribution of θ_i obtained from the ENCODE data (ENCODE Project Consortium, 2004) fluctuates at intermediate allelic nucleotide frequency, because the number of segregating sites is about 10,000 which is 1/200 of that in the genome-wide data (data not shown). So the pattern of the distribution of θ_i in the ENCODE data is not clear. Today, we can obtain enormous allelic nucleotide frequency data from human genome-wide SNP data. SNP data, however, have ascertainment bias and include many non-typing data. So the second merit of our method is that, in analyzing SNP data, the data in low allelic nucleotide frequency influenced by ascertainment bias do not conceal the data in intermediate allelic nucleotide frequency, because our method can directly analyze allelic nucleotide frequency spectrum at any allelic nucleotide frequency. Our method can correctly evaluate the allelic nucleotide frequency spectrum except for low allelic nucleotide frequency in SNP data and can use the SNP data including non-typing allelic nucleotides by adjusting the sample size. The results of data analyses show that the distributions of θ_i in the CEU (European), CHB and JPT (Asian) populations are different from the distribution in the YRI population (African) and that the CEU, CHB and JPT populations experienced the population size reduction in the far past. Since we cannot use the distribution of θ_i in low allelic nucleotide frequency because of ascertainment bias, we cannot know the recent change of population size. In recent change of population size, however, the data in human mtDNA shows the signature of population expansion (Rogers and Harpending, 1992). Therefore, we infer that CEU, CHB and JPT populations experienced the bottleneck.

Fig. 6 shows the distributions of θ_i in nuclear DNA and mtDNA in the results of coalescent simulation under the bottleneck model T₀-2, where the difference of the pattern of polymorphism between nuclear DNA and mtDNA is the clearest in our models. In this simulation, the effective population size of mtDNA sequence is assumed to be one quarter that of nuclear DNA sequence, because mitochondrial genome is haploid and maternally inherited. The mutation rate per site per generation in mtDNA is assumed to be μ = 1 × 10^–7 which is one order larger than that of nuclear DNA. Although the mutation rates in mtDNA and nuclear DNA are not known exactly, similar results were obtained even when different mutation rates were used in the simulation (data not shown). In the results of this simulation, Tajima’s D in mtDNA is negative, but D in nuclear DNA is positive. And the distribution of θ_i in mtDNA is U-shaped, but the distribution of θ_i in nuclear DNA is W-shaped. The W-shaped distribution in nuclear DNA reflects both the recent population expansion and the older population reduction in the bottleneck model, whereas the U-shaped distribution of mtDNA reflects only the recent population expansion in the bottleneck model. In the analyses of the data of human nuclear DNA, if the number of segregating sites with low allelic nucleotide frequency such as singleton can be obtained without ascertainment bias, the distributions of θ_i in non-African populations might be W-shaped distributions which are similar to that of nuclear DNA in this bottleneck model.

View Details

Fig. 6 The distribution of θi of nuclear DNA and mitochondrial DNA (mtDNA) in the results of coalescent simulation under the bottleneck model T0-2. In nuclear DNA, D = 0.195. In mtDNA, D = –0.903.