Effect of Substitutional Element Addition on Hall-Petch Relationship in Interstitial Free Ferritic Steels

Abstract

The effects of individual substitutional element addition (Si, Al, Mn, Cu, Ni and Cr) on Hall-Petch relationship in interstitial free ferritic steels were systematically investigated by employing experimental examinations, the pie-up models and grain boundary segregation theory. Chemistry-dependent Hall-Petch coefficients were observed, which was principally interpreted based on the established correlations between the critical grain boundary shear stress and the grain boundary segregation depending on the kind of elements. Exceeded grain boundary segregation levels were found to be the predominant contributions of enhanced grain refinement strengthening abilities.

1. Introduction

Grain refinement strengthening is one of the most attractive methods to increase the strength of polycrystalline materials. The yield strength (σ_y) measured by tensile tests is usually expressed by the well-known Hall-Petch relationship as a function of average grain size (d), as shown below:^1,2,3)   

$${\sigma }_{\mathrm{y}}={\sigma }_0+k_{\mathrm{y}}{d}^{-1/2}$$(1)

where σ₀ is the friction stress within metal matrix, k_y is the parameter presenting the efficiency of grain refinement strengthening, i.e. Hall-Petch coefficient. In the dislocation pile-up models,^1,2) Hall-Petch coefficient (k_y) can be expressed as a function of the critical grain boundary (GB) shear stress (τ*) as follows:^1,2,3,4)   

$$k_{\mathrm{y}}=M\sqrt{\frac{2Gb\tau *}{\pi k}}$$(2)

where M is Taylor factor, G is shear modulus, b is the Burgers vector, and k is a constant depending on the character of dislocation (edge/screw). Recently, the key parameter k_y was indicated to be strongly influenced by the addition of interstitial elements (i.e., C and N) in ferritic steels.^3,5,6,7)

On the other hand, the effects of substitutional element additions on k_y have not been widely studied and well understood yet, though there are a few reports on the effects of Ni, Cr and P.^{8,9,10,11,12)} In this work, the effects of individual addition of substitutional elements (Si, Al, Mn, Ni and Cr) on Hall-Petch relationship were investigated in IF ferritic steel to evaluate their effects systematically by combining experimental examinations, the dislocation pile-up model and the GB segregation theory by McLean.¹³⁾ The quantitative correlation between critical GB shear stress (τ*) and GB segregation magnitude was then established to interpret the mechanisms of k_y increment due to alloying elements.

2. Experimental Procedure

The nominal chemical compositions of employed IF steel specimens with various substitutional element additions (Si, Al and Mn) are summarized in Table 1. The preparation processes of above specimens for determining the Hall-Petch relationship were given in previous works.^8,9) The results on the effects of Ni and Cr could be found in previous works.^8,9) Small amounts of C and N (<0.002 wt.%) were designed to be fixed as Ti(C,N) by sufficient Ti addition.^8,9) Tensile tests were carried out on standard specimens according to JIS13B with strain rate of 1.0×10⁻³ s⁻¹. The microstructure was observed by optical microscopy and electron backscatter diffraction (EBSD) to quantify (nominal) average grain size. Detailed instructions on X-ray diffraction (XRD) and Young’s modulus measurement experiments were given in the recent publication.¹⁴⁾

Table 1. Nominal chemical compositions (wt.%) of the present steels. “–”: Not examined. The atom percent (at.%) of predominant substitutional element (X_i) is also given in the last column.

Specimens	Si	Al	Mn	Ni	Cu	C	N	S+P	Ti	Xi, (at.%)
1% Si steel	0.93	0.051	0.001	0.002	0.001	0.0012	0.0005	<0.0005	0.028	1.84
2% Si steel	1.97	0.053	0.002	0.002	0.002	0.0012	0.0003	<0.0005	0.025	3.86
3% Si steel	3.14	0.066	0.002	0.003	0.005	0.001	0.0005	<0.0005	0.028	6.09
1% Al steel	0.027	1.080	0.001	–	0.001	0.001	0.0005	<0.0005	0.021	2.05
4% Al steel	0.022	3.97	0.0049	–	0.002	0.0008	0.0006	<0.0005	0.019	7.95
0.5% Mn steel	0.020	0.050	0.520	0.002	0.002	0.0012	0.0004	<0.0005	0.025	0.53
1% Mn steel	0.016	0.053	1.07	0.003	0.003	0.001	0.0009	<0.005	0.0278	1.09
2% Mn steel	0.011	0.066	2.090	0.002	0.003	0.0008	0.0006	<0.0005	0.025	2.13

3. Experimental Results and Discussions

Figures 1(a)–1(c) show the Hall-Petch plots of IF ferritic steels with various Si, Al and Mn contents. It is observed that the addition of alloying elements significantly varies both the intercept with vertical axis (σ₀) and the slope of the lines (k_y). In Fig. 1(d), EBSD micrographs of selected samples with different substitutional element additions indicate full recrystallization grains and little difference on texture. Figures 2(a) and 2(b) summarize the plots of σ₀ and k_y values with various Si, Al, Mn, Ni⁸⁾ and Cr⁹⁾ contents (at.%). The obtained values of σ₀ are the combined contributions of friction stress of pure iron and solid solution strengthening of each element, in which the GB strengthening function is not included.⁸⁾ Hence, the solid solution strengthening ability of various substitutional elements exhibits the following sequence: Si > Al ≈ Ni > Mn > Cr. The present results generally coincide with previous works in IF steels.^{12,15,16,17,18)} The slight differences could be the included GB strengthening in some works,^9,15,18) the presences of different impurities,¹⁷⁾ few interstitial elements¹²⁾ and experimental factors.^8,9,17) As shown in Fig. 2(b), complicated effects of various substitutional elements on the values of k_y are observed. Mn, Si and Ni additions significantly increase k_y, while 4% Al steel gives a slight increase of k_y. In addition, Cr has little influence on k_y.

Fig. 1.

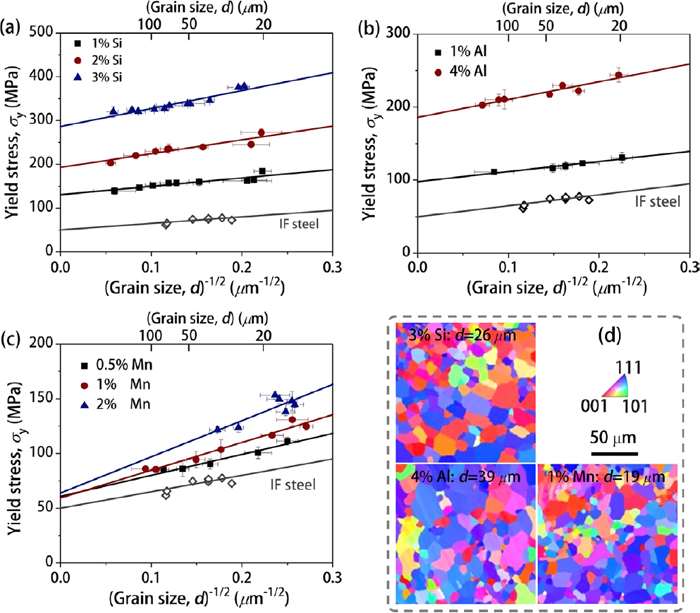
The Hall-Petch plots of IF ferritic steels with various substitutional element additions: (a) Si, (b) Al and (c) Mn. The plot of IF steel³⁾ is presented as reference. (d) Selected EBSD micrographs showing the recrystallized grains of various steels. (Online version in color.)

Fig. 2.

Summarized plots of (a) σ₀ and (b) k_y values with various Si, Al, Mn, Ni⁸⁾ and Cr⁹⁾ contents. The results from other references on the effect of various alloy elements on σ₀^{12,15,16,17,18)} and (b) k_y¹²⁾ are also compared. Experimental results of the effect of substitutional element additions on (c) lattice parameter (a) and (d) Young’s modulus (E). (Online version in color.)

By utilizing the Nelson-Riley refinement from XRD results,¹⁹⁾ the estimated lattice parameter, a, of the present steels are summarized in Fig. 2(c). Si is found to decrease lattice parameter while other substitutional elements increase it. The change of lattice parameter with Al additions is the most remarkable. In Fig. 2(d), the measured Young’s modulus (E) values of the present steels are exhibited. Si and Al additions significantly decrease Young’s modulus, while the additions of Ni, Mn and Cr display little effect on it. The obtained values of a and E will also be used to calculate τ* (Eq. (2)) subsequently.

According to Langmuir-McLean approach,^13,20) equilibrium GB segregation level ($X_i^{\mathrm{G}\mathrm{B}}$) in Fe-i binary alloy can be given by:   

$$\frac{X_i^{\mathrm{G}\mathrm{B}}}{X_i^{\mathrm{G}\mathrm{B}*}-X_i^{\mathrm{G}\mathrm{B}}}=\frac{X_i}{1-X_i}exp\left(-\frac{\mathrm{\Delta }{G}_{i,T}}{RT}\right)$$(3)

where $X_i^{\mathrm{G}\mathrm{B}*}$ is the GB interface saturation, X_i is the atomic fraction of solute i in host matrix, ΔG_i,T is the Gibbs energy of segregation of solute i at GB, R is the universal gas constant and T is the given temperature. This equation is generally believed to be well accorcadance with the GB segregation levels in sufficiently annealed steels since the validity has been experimentally demonstrated.^20,21,22) However, Eq. (3) solely gives the equilibrium concentration of solute i at GB, and thus, the kinetics of the experimental segregation process is not included.^13,20) In practical annealing situations, the alloy atoms rarely have sufficient time to reach full equilibrium GB segregation level (i.e., unsaturated state), because of the limited diffusion rate of solute i. To consider the transport of solute i by volume diffusion from the neighbored grain volume toward the GB, McLean¹³⁾ proposed the following equation to describe the GB segregation kinetics:   

$$\frac{X_{i, t}^{\mathrm{G}\mathrm{B}}-X_{i, t=0}^{\mathrm{G}\mathrm{B}}}{X_{i, t=\infty }^{\mathrm{G}\mathrm{B}}-X_{i, t=0}^{\mathrm{G}\mathrm{B}}}=1-exp\left(-\frac{D_{i}t}{{\beta }_i^2{\delta }^2}\right)erfc\left(\frac{\sqrt{D_{i}t}}{{\beta }_i\delta }\right)$$(4)

where $X_{i, t=\infty }^{\mathrm{G}\mathrm{B}}$ is the equilibrium GB segregation level at given annealing temperature (T), $X_{i, t}^{\mathrm{G}\mathrm{B}}$ is the actual GB segregation magnitude under annealing time (t). $X_{i, t=0}^{\mathrm{G}\mathrm{B}}$ is the initial GB segregation magnitude before annealing, β_i is the enrichment coefficient, δ is the width of the grain boundary and D_i is the volume diffusion coefficient of the solute i. It is found from Eqs. (3) and (4) that the practical segregation level at given annealing conditions (T and t) is dominated by the potential GB segregation level ($X_i^{\mathrm{G}\mathrm{B}}$) and diffusion coefficient (D_i).^13,20)

To calculate the practical GB segregation magnitude, the following assumptions were made first: (a) There is little effect from impurities and the present specimens were treated as Fe-i binary alloys; (b) Little segregation during recrystallization treatment is formed (i.e., $X_{i, t=0}^{\mathrm{G}\mathrm{B}}$ ≅ X_i); (c) Little non-equilibrium GB segregation is resulted during quenching owing to lower D_i of current substitutional elements.^20,21) The values of the parameters for calculating practical GB segregation magnitudes are summarized in Table 2. In order to demonstrate the validity of this calculation, the GB segregation level estimated by utilizing Eq. (4) was compared with the experimentally measured values^8,23) for representative alloys. The red and black curves of Fig. 3(a) show the calculated GB segregation levels in 3% Ni steel and 1.5% Si steel with increased annealing time (t), respectively. Simultaneously, the experimentally measured values are plotted in Fig. 3(a). This figure reveals calculated results and experimental ones coincide very well, which demonstrates the reliability of current calculations. In Fig. 3(b), increased Si contents are observed to increase equilibrium GB segregation levels and accelerate segregation processes.

Table 2. Summarized values of the parameters for calculating practical GB segregation magnitudes in the present work. ΔG₀ is the estimated Gibbs energy of segregation at particular experimental conditions in which the equilibrium GB segregation was examined experimentally.²⁰⁾ D_i is estimated by the equation $D_i=D_{0}exp\left(-\frac{Q}{RT}\right)$.^25,26,27)

	β	δ (nm)	ΔG0 (kJ/mol)	ΔGi,T (kJ/mol)	D0 (cm2/s)	Q (kJ/mol)
Si	3×104	1	−9	ΔG0+0.012ΔT	1.47	233
Al	3×104	1	−12	ΔG0+0.008ΔT	5.31	196.5
Mn	3×104	1	−11	ΔG0+0.025ΔT	1.49	233.6
Ni	3×104	1	−14.4	ΔG0+0.016ΔT	1.4	245.8
Cr	3×104	1	−4.9	ΔG0+0.009ΔT	0.44	253.3

Fig. 3.

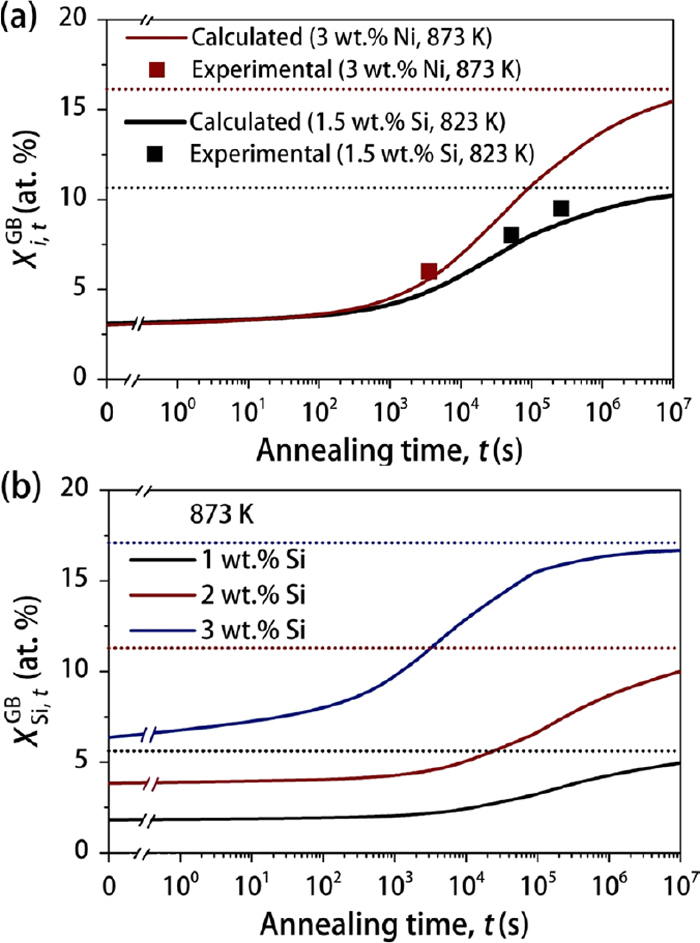
(a) A comparison of calculated GB segregation kinetics and experimental measurements^8,23) on GB segregation levels to demonstrate the reliability of current calculations; (b) Influences of Si contents on GB segregation kinetics at 873 K. The dashed lines indicate equilibrium GB segregation level. The parameters for the present calculations are listed in Table 2. (Online version in color.)

Figure 4(a) summarizes the calculated GB segregation levels under the experimental conditions in which Hall-Petch relationship is determined (Fig. 1). The deviations from the initial alloy contents ($X_{i, t=0}^{\mathrm{G}\mathrm{B}}$, dashed line) reflect the magnitudes of GB segregation. It is indicated that Si, Mn and Ni additions show clear GB segregation, which also enlarge the values of k_y (Fig. 2(b)). While Al and Cr additions have little effects on both GB segregation (Fig. 4(a)) and k_y (Fig. 2(b)). It should be noted that experimental examinations^20,21,22,23) have demonstrated the remarkable and complex effects of GB misorientation/types on GB segregation of solutes. Therefore, the calculated GB segregation levels reflect the (nominal) average magnitude of all GBs.^{13,20,21,22,23)} In Fig. 4(b), the values of τ*, estimated from the Eq. (2) with the experimental results of k_y (Fig. 2(b), lattice parameter (Fig. 2(c)) and Young’s modulus (Fig. 2(d)), is now plotted as a function of the exceeded levels of GB segregation ($\mathrm{\Delta }X=X_{i, t}^{\mathrm{G}\mathrm{B}}-X_i$). Here, the value of k in Eq. (2) was estimated to be 0.945 based on the experimental evaluation of edge and screw dislocation fraction obtained by XRD line profile analysis.^3,24) The τ* values are found to be increased gradually with increased ΔX. It is revealed that the all plots are almost on the single line, which indicates that substitutional alloying elements have a similar effect on the GB strength though they might have different tendency to segregate to GB. Although the physical meaning of this phenomenon is unclear so far, we need more experimental plots and additional simulations to confirm this result and clarify the mechanism of atomic-scale yielding phenomenon at GB in the future. Such outcomes are of vital importance for modern GB segregation engineering, e.g., interfaces design, alloys and processing developments.^28,29,30)

Fig. 4.

(a) Summarized results on the calculated GB segregation levels corresponding to the experimental conditions in which Hall-Petch relationship is determined (Fig. 1). The experimental examination on Ni added steel is also presented.⁸⁾ (b) Quantitative correlations between τ* values and exceeded levels of GB segregation (ΔX). (Online version in color.)

4. Conclusions

To sum up, on the basis of experimental examinations, the dislocation pile-up models and GB segregation theory, the influences of substitutional element additions (i.e., Si, Al, Mn, Ni and Cr) on Hall-Petch relationship were systematically studied in IF ferritic steel. The substitutional elements had particular effects on the values of σ₀ and k_y. Exceeded GB segregation levels (ΔX) were found to dominate the critical grain boundary shear stress (τ*), and this leads to the enhanced grain refinement strengthening abilities resulted from the increment of k_y.

Acknowledgments

This work was supported by JSPS KAKENHI Grant Number JP15H05768.

References

• 1)   E. O.  Hall: Proc. Phys. Soc. Lond. B, 64 (1951), 747.
• 2)   N. J.  Petch: J. Iron Steel Inst., 174 (1953), 25.
• 3)   S.  Takaki,  D.  Akama,  N.  Nakada and  T.  Tsuchiyama: Mater. Trans., 55 (2014), 28.
• 4)   W. J.  Morris, Jr.: ISIJ Int., 48 (2008), 1063.
• 5)   D. V.  Wilson: Acta Metall., 16 (1968), 743.
• 6)   S.  Araki,  K.  Fujii,  D.  Akama,  T.  Tsuchiyama,  S.  Takaki,  T.  Ohmura and  J.  Takahashi: Tetsu-to-Hagané, 103 (2017), 491 (in Japanese).
• 7)   J.  Takahashi,  K.  Kawakami,  K.  Ushioda,  S.  Takaki,  N.  Nakata and  T.  Tsuchiyama: Scr. Mater., 66 (2012), 207.
• 8)   D.  Akama,  N.  Nakada,  T.  Tsuchiyama,  S.  Takaki and  A.  Hironaka: Scr. Mater., 82 (2014), 13.
• 9)   A.  Hironaka,  N.  Nakada,  T.  Tsuchiyama and  S.  Takaki: Mater. Sci. Forum, 706 (2012), 2130.
• 10)   S.  Gao,  M.  Chen,  S.  Chen,  N.  Kamikawa,  A.  Shibata and  N.  Tsuji: Mater. Trans., 55 (2014), 73.
• 11)   N.  Nakada,  M.  Fujihara,  T.  Tsuchiyama and  S.  Takaki: ISIJ Int., 51 (2011), 1169.
• 12)   W. B.  Morrison and  W. C.  Leslie: Metall. Trans., 4 (1973), 379.
• 13)   D.  McLean: Grain Boundaries in Metals, Clarendon Press, Oxford, (1957), 296.
• 14)   F.  Jiang,  T.  Masumura,  K.  Hirata,  T.  Tsuchiyama and  S.  Takaki: Int. J. Plast., 112 (2019), 89.
• 15)   A.  Uenishi and  C.  Teodosiu: Acta Mater., 51 (2003), 4437.
• 16)   S.  Takeuchi: J. Phys. Soc. Jpn., 27 (1969), 929.
• 17)   K. D.  Sibley and  N. N.  Breyer: Metall. Mater. Trans. A, 7 (1976), 1602.
• 18)   W. C.  Leslie: Metall. Trans., 3 (1972), 5.
• 19)   B. D.  Cullity and  S. R.  Stock: Elements of X-Ray Diffraction, 3rd ed., Pearson, London, (2001), 271.
• 20)   P.  Lejček,  M.  Šob and  V.  Paidar: Prog. Mater. Sci., 87 (2017), 83.
• 21)   P.  Sutton and  R. W.  Balluffi: Interfaces in Crystalline Materials, Clarendon Press, Oxford, (1995), 16.
• 22)   B. W.  Kempshall,  B. I.  Prenitzer and  L. A.  Giannuzzi: Scr. Mater., 47 (2002), 447.
• 23)   B. W.  Krakauer and  D. N.  Seidman: Acta Mater., 46 (1998), 6145.
• 24)   E.  Schafler,  M.  Zehetbauer and  T.  Ungár: Mater. Sci. Eng. A, 319 (2001), 220.
• 25)   R. J.  Borg and  D. Y. F.  Lai: J. Appl. Phys., 41 (1970), 5193.
• 26)   J.  Kučera and  K.  Stránský: Mater. Sci. Eng., 52 (1982), 1.
• 27)   M.  Gemmaz,  M.  Afyouni and  A.  Mosser: Surf. Sci., 227 (1990), L109.
• 28)   D.  Raabe,  M.  Herbig,  S.  Sandlöbes,  Y.  Li,  D.  Tytko,  M.  Kuzmina,  D.  Ponge and  P. P.  Choi: Curr. Opin. Solid State Mater. Sci., 18 (2014), 253.
• 29)   W.  Xing,  A. R.  Kalidindi,  D.  Amram and  C. A.  Schuh: Acta Mater., 161 (2018), 285.
• 30)   J.  Hu,  Y. N.  Shi,  X.  Sauvage,  G.  Sha and  K.  Lu: Science, 355 (2017), 1292.