Elecronic Structure Calculation of Time-Dependent Quantum Wave Packet in Meshless Particle Method with Bohmian

Abstract

In order to describe the time evolution of the electronic state, we have developed a new method, using the particle method with the Bohmian, to solve the time-dependent Schrödinger equation. The method has been applied to the time-dependent coherent state for a harmonic potential, whose analytical solutions are well-known. To evaluate this method, the ground state is evolved to estimate the excited state, and we follow the dynamic dipole moment as the linear responses of the system under externally applied perturbations in real time. From the polarizability obtained as the Fourier transform of the dipole moment, we calculate the optical strength function. As a result, a single peak is observed, which was exactly expected from the analytical solution. We recognize that the method is quite valid for the time dependent electronic structure calculation.

1 はじめに

粒子法はメッシュを用いない計算手法であるため粒子(計算点)を自由に配置することができる．粒子法を電子状態計算に用いる場合，高精度な計算が必要な領域へ集中的に計算点を配置することで効率的な計算を行う．粒子法の中でも比較的精度の高いSymmetric Smoothed Particle Hydrodynamics (SSPH)を用いている [1, 2]．粒子法では粒子の配置は任意であるという特徴がある．これを用いて固有状態を算出することも可能である [3, 4]．一方，動的な時間依存の電子状態を解析するためには，計算点である粒子を電子状態の変化とともに動かす必要がある．この課題は波動関数をBohm形式で記述することで解決することが報告されている [5]．

今回，この手法を用いて3次元の調和ポテンシャル上でコヒーレント状態の解であるGaussian波束を振動させ，その時間発展から振動子強度分布を算出することができた．この結果について報告する．

2 計算手法

電子状態計算にSPHを用いて解析するとき波動関数は積分形式で表現される．有限数のサンプリング点を用いて表現するため粒子法と呼ばれる．波動関数は次のような恒等式で表される．   

$\psi \left(r^{\prime }\right)=\underset{\text{Ω}}{\overset{}{\int }}\psi \left(r\right)\delta \left(r-r^{\prime }\right)dr\cong \underset{\text{Ω}}{\overset{}{\int }}\psi \left(r\right)W\left(r-r^{\prime }, h\right)dr$(1)

ここではδ(r)をKernel関数 W(r,h) = W(|r|,h)として近似している．ここでhはsmoothing lengthでありWの広がりを表す指標である．Kernel関数としては，δ 関数的な性質があれば何でもよい．我々はWendland関数を採用している [6]．局所的に値を持つ関数であり数値計算上の負荷が少ない．

我々が用いているSSPHでは，式(1)とその k-次のモーメントについてψ(r)をr_iのまわりでTaylor展開を行うと式(2)となる．   

$\begin{array}{c}\underset{\text{Ω}}{\overset{}{\int }}{\left(r-r_i\right)}^k\psi \left(r\right)W\left(r-r_i, h\right)dr\\ \cong \sum _{l=0}^m\left(\underset{\Omega }{\overset{}{\int }}{\left(r-r_i\right)}^{k+l}Wdr\right) \left(\frac{1}{l!}{\frac{{\partial }^l\psi }{\partial r^l}|}_{r_i}\right)\\ \left(k=0,1, \dots , m\right)\end{array}$(2)

(2)式の次に左辺がk-次モーメントについてのベクトルP, 右辺はk-次モーメントとl-次展開による行列Mと, l-次の微係数を成分としたベクトルDの積になり，MD = P の形で表される1次連立方程式となる [2]．最終的に電子状態計算で必要になる ψ, ∇ψ, ∇²ψなどの項はMD = Pを解きDを求めればよい．もちろんSPHだけを用いて電子状態を計算することができるが，粒子を動かすことはできないため，適用範囲が静的な解析に限定されてしまう．    波動関数に合わせ粒子を動的に配置する場合，時間依存のSchrödinger方程式は

$\psi \left(r,t\right)=R\left(r,t\right)\exp \left[iS\left(r,t\right)\right]$

のBohm形式で表すと，次のようなHamilton–Jacobiの運動方程式と連続の式となる [7]．この連続の式により粒子についてLagrange描像での解析が可能になる．   

$-\frac{\partial S\left(r,t\right)}{\partial t}=\frac{1}{2}{\left(\nabla S\right)}^2+V\left(r,t\right)+Q\left(r,t\right)$(3)

  

$\frac{\partial \rho \left(r,t\right)}{\partial t}+\nabla \cdot \left(\rho \nabla S\right)=0$(4)

ここで Q は量子ポテンシャルであり次式で表され   

$Q=-\frac{1}{2}\frac{{\nabla }^{2}R\left(r,t\right)}{R\left(r,t\right)}$(5)

量子効果を与えるものである．なおR(r,t) ≅ 0となる付近では数値計算上はゼロ割に注意する必要がある．その手法が幾つか提案されているが [8]，我々はR(r,t)を解析解に接続することで Q の算出を安定化させている．

一般に実空間・実時間での電子状態計算の振動子強度分布を求めるためには，時間依存の波動方程式の初期に$\tilde{\psi }\left(r,0\right)={\text{e}}^{ikz}\psi \left(r,0\right)$によるδ 関数的な刺激を与え，波動関数の時間発展の様子を解析する．ここでkはz方向の外部摂動による微少な波数である．この線形応答として分極率α(ω)は，双極子モーメントμ(t)のフーリエ変換として求められる．また式(7)に示すように振動子強度分布S(ω)は分極率の虚部から算出する．   

$\alpha \left(t\right)=\frac{1}{k}\int dt\exp \left[i\omega t\right]\mu \left(t\right)$(6)

  

$S\left(\omega \right)=\frac{2\omega }{\pi }\text{Im} \alpha \left(\omega \right)$(7)

3 結果と考察

我々の開発した手法の検証を行うため，解が良く知られている調和ポテンシャルにて波束が運動する解析を行った．調和振動子に対するコヒーレント状態はGaussianの形が崩れず古典力学と同様に振動をする [9]．また遷移はΔn = ±1のみ起こることが知られているため，この手法の検証のためには最適である．

調和ポテンシャルV = (x² + y² + z²) / 2上に基底状態のGaussian波束$\psi =\exp \left[-\left(x^2+y^2+z^2\right)/2\right]$を置き，その動的な解析を行ったものである．Figure 1はランダムに計算点を配置した場合の波動関数(左)と3次元での調和ポテンシャル(右)を表している．各点は実際の計算点を表し，電子密度に従って色分けされている．3544個の粒子を3次元空間上に波動関数の広がりに合わせ格子状またはランダムに配置した．この波動関数の外側に電子状態を計算する粒子(計算点)はない．いずれの場合もラグランジュ描像であるので粒子は波動関数とともに移動する．これは粒子配置に制約がないという粒子法の特徴によるものである．

Figure 1.

 The particle arrangement for the Gaussian wave packet, whose density is expressed by color dots (left), and the half of the 3D contour of the harmonic potential (right).

この波動関数の初期状態に，δ関数的な刺激を与え動的な双極子モーメントの計算を行った．Figure 2は，それぞれこの計算から求めた動的な双極子モーメントと振動子強度分布を示したものである．いずれの粒子配置でも同様な結果が得られた．Gaussian波束が変形することなく十分な時間にわたり時間発展を行なった．波束の移動に従って粒子が移動していくので，計算上の精度にも問題が生じない．また，基底状態の動的変化から算出される励起状態は，上述のように解析的に一つだけであることが知られている．我々の計算結果からも一つのピークが得られた．我々の手法は，時間依存の電子状態を解析に有効である．

Figure 2.

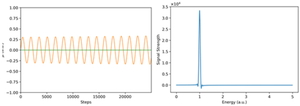
 The dipole moment (left) and the optical strength function (right) of the Gaussian wave packet for the harmonic potential.

4 まとめ

実空間・実時間での電子状態計算の空間離散化手法としてSSPHを用い，更に波動関数をBohm形式で記述することで時間発展を行った．これにより波動関数の動的変化を粒子の動きとして記述できることを確認した．また解析解の存在する調和ポテンシャル上で動的双極子モーメントから，振動子強度分布の算出を行った．解析的な結果と一致する結果が得られ，我々の開発した手法が動的な時間依存の電子状態を解析するために有効であることが確認できた．

謝辞

なお，この研究はJSPS科研費16K05047の助成支援を受けたものである．

参考文献

• [1]   R. C. Batra, G. M. Zhang, Comput. Mech., 41, 527 (2007). doi:10.1007/s00466-007-0209-3
• [2]   S. Sugimoto, Y. Zempo, J. Phys. Conf. Ser., 510, 012037 (2014). doi:10.1088/1742-6596/510/1/012037
• [3]   S. Sugimoto, Y. Zempo, J. Comput. Chem. Jpn., 13, 187 (2014). doi:10.2477/jccj.2014-0027
• [4]   K. Kitayama, M. Toogoshi, Y. Zempo, J. Phys. Conf. Ser., 905, 012011 (2017). doi:10.1088/1742-6596/905/1/012011
• [5]   F. Hirono, M. Iwasawa, S. S. Kano, Y. Zempo, J. Comput. Chem. Jpn., 18, 159 (2019). doi:10.2477/jccj.2019-0015
• [6]   H. Wendland, Adv. Comput. Math., 4, 389 (1995). doi:10.1007/BF02123482
• [7]   C. L. Lopreore, R. E. Wyatt, Phys. Rev. Lett., 82, 5190 (1999). doi:10.1103/PhysRevLett.82.5190
• [8]   R. E. Wyatte, " Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics", Springer (2005)
• [9]   e.g., L. I. Schiff, 3rd ed., " Quantum Mechanics", McGraw Hill (1968)