大規模分子動力学計算と新規動的モンテカルロ法による大規模不均一系の物質輸送に関する研究

概要

複雑な構造を持つ「不均一系」の内部で分子拡散により生じる物質輸送は，様々な材料や環境で生じる普遍的な現象であり，ミクロ機構の解明が色々な場面で求められている．しかしながら，全原子分子動力学シミュレーションにより直接現象を追跡することは，不均一系で生じる物質輸送の時定数が長いため困難である．そこで，全原子動力学計算と動的モンテカルロ法を組み合わせることにより新たな研究手法を開発し，不均一系で生じる物質輸送の研究を行ってきた．特に，高分子電解質膜におけるガス透過の経路などを明らかにしてきた．本稿では，開発した手法と高分子電解質膜への応用研究について概説する．最近では，より大規模な系に手法を応用するために，機械学習モデル展開の応用を提案している．この概要についても簡単に触れたい．

1　 はじめに

複雑な構造を持つ「不均一系」で生じる分子拡散による物質輸送は，様々な材料や環境で生じる普遍的な現象である．そのため，不均一系での物質輸送の研究は，広い応用範囲を持つ重要な基礎科学である．不均一系の例には，高分子と溶液が3–10 nm程度のスケールでミクロ相分離している燃料電池の高分子電解質膜がある．また，同デバイスの電極に利用される多孔質炭素の内部に閉じ込められた電解液も不均一系の例である．このような不均一系における活物質の輸送の理解と制御は，脱炭素社会達成の重要な技術である燃料電池の改良にも重要であり，現代の社会問題の解決にも欠かせない．

しかしながら，不均一系における物質輸送の時定数は，全原子分子動力学（Molecular Dynamics: MD）シミュレーションで到達できる典型的な時定数より長く，全原子MDシミュレーションによる追跡は困難である．この問題を解決するために，微視的な解像度を持つ全原子MDシミュレーションにメソ・マクロスケールの解像度を持つ動的モンテカルロ法を接続するマルチスケールな計算手法を展開してきた（図1参照）［1］．本手法により，全原子MDシミュレーションだけでは到達できない10 ms程度の時定数で生じるμmオーダーの大域的な拡散現象をシミュレーションできるようになり，不均一系で生じる物質輸送をシミュレーションできるようになった．本稿では，この手法について概説し，高分子電解質膜中のガス輸送への応用について述べる．

図1  不均一系における物質輸送を解明するために提案している計算手法の概要．MD計算により自由エネルギー地形$F\left(\mathit{r}\right)$と位置に依存した拡散係数$D\left(\mathit{r}\right)$を求め，これらを入力として動的モンテカルロ法によるシミュレーションを実行する．大量の軌跡を粒子描像で得ることができ，任意の解析を実行できる．

2　 手法論について

2.1　 動的モンテカルロ法を使った大規模不均一系における物資輸送機構解明の手法の骨子

この提案手法では，輸送される分子に働く駆動力の尺度である自由エネルギー地形F(r)と易動度の尺度である位置に依存した拡散係数D(r)を全原子MDシミュレーションにより0.4 nm程度の分解能で求め，拡散方程式を満足する動的モンテカルロ法［2,3］を実行することで，ガス分子に対する粗視化ダイナミクスを評価する．この動的モンテカルロ法で生成される軌跡は，位置に依存した自由エネルギー地形と位置に依存した拡散係数を持つ拡散方程式

  

$$\frac{\partial \rho (\mathit{r},t)}{\partial t}=\frac{\partial }{\partial \mathit{r}}·(D\left(\mathit{r}\right)\frac{\partial }{\partial \mathit{r}}+\beta D\left(\mathit{r}\right)\frac{\partial F\left(\mathit{r}\right)}{\partial \mathit{r}})\rho (\mathit{r},t)$$(1)

を統計的に満足し，分子拡散のシミュレーションを実行できる．ただし，ここで，ρ(r, t)は密度分布でβは逆温度である．動的モンテカルロ法により得られる大量の軌跡から任意の解析が実行できる．

以下では，自由エネルギー地形の計算法について述べ，次に，位置に依存拡散係数の評価手法について述べる．我々が開発した位置に依存した拡散係数の評価方法［4］は，水素分子などの軽い分子を計算する際に従来法よりも精度がよい．その後，動的モンテカルロ法の詳細を述べる．

2.2　 自由エネルギー地形の計算方法

本研究では，位置依存の溶媒和自由エネルギーを粒子挿入法［5］やオーバーラッピングディストリビューション法［6］により評価することで，自由エネルギー地形を求めた［7］．具体的には，

  

$$\begin{array}{l}\mathrm{\Delta }F\left(\mathit{r}\right)\\ =-k_{\mathrm{\text{B}}}T\mathrm{\text{ln}}\frac{{\int }_V^{}\mathrm{\text{exp}}\left(-\beta U(\mathit{x},\mathit{X})\right)\mathrm{\delta }(\mathit{r}-\mathit{r}\left(\mathit{x}\right))\mathrm{\text{exp}}\left[-\beta E_0\left(\mathit{X}\right)\right]d\mathit{x}d\mathit{X}}{{\int }_V^{}\mathrm{\delta }(\mathit{r}-\mathit{r}\left(\mathit{x}\right))\mathrm{\text{exp}}\left[-\beta E_0\left(\mathit{X}\right)\right]d\mathit{x}d\mathit{X}}\end{array}$$(2)

を計算した．ただし，$\mathit{r}\mathrm{(}\mathit{x}\mathrm{)}$はガス分子（溶質）の重心である．また，$\mathit{x}$はガス分子内の原子の座標を表しており回転の自由度が含まれている．大文字の$\mathit{X}$は，溶媒の座標を表している．系の全ポテンシャルエネルギーは，$E(\mathit{x},\mathit{X})=E_0\left(\mathit{X}\right)+U(\mathit{x},\mathit{X})$であり，$E_0\left(\mathit{x}\right)$は溶媒間の相互作用を，$U(\mathit{x},\mathit{X})$は溶媒–溶質間の相互作用を示している．本研究では，ガス分子に剛体モデルを利用したため，溶質の分子内相互作用は省略した．系の体積，温度，ボルツマン定数をそれぞれV, T, $k_{\mathrm{\text{B}}}$で示した．

2.3　 位置に依存した拡散係数のMDによる計算方法

我々は，フラットボトムポテンシャルを用いた位置に依存した拡散係数の評価手法［4］を開発し利用した［8］．手法の手順を図2に示す．提案手法の核は，図2に示した（Step 1）から（Step 3）までの3つの計算であり，順に説明する．

図2  提案手法の手順．（Step 1）では平均力を求める．（Step 2）では平均力を相殺しつつフラットボトムポテンシャルを課した分子動力学計算から局所的な平均二乗変位${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$を求める．ここで，$g$はフラットボトムポテンシャルの位置を表す．(Step 3)では，${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$を形状因子FFで補正することで，拡散係数を得る．

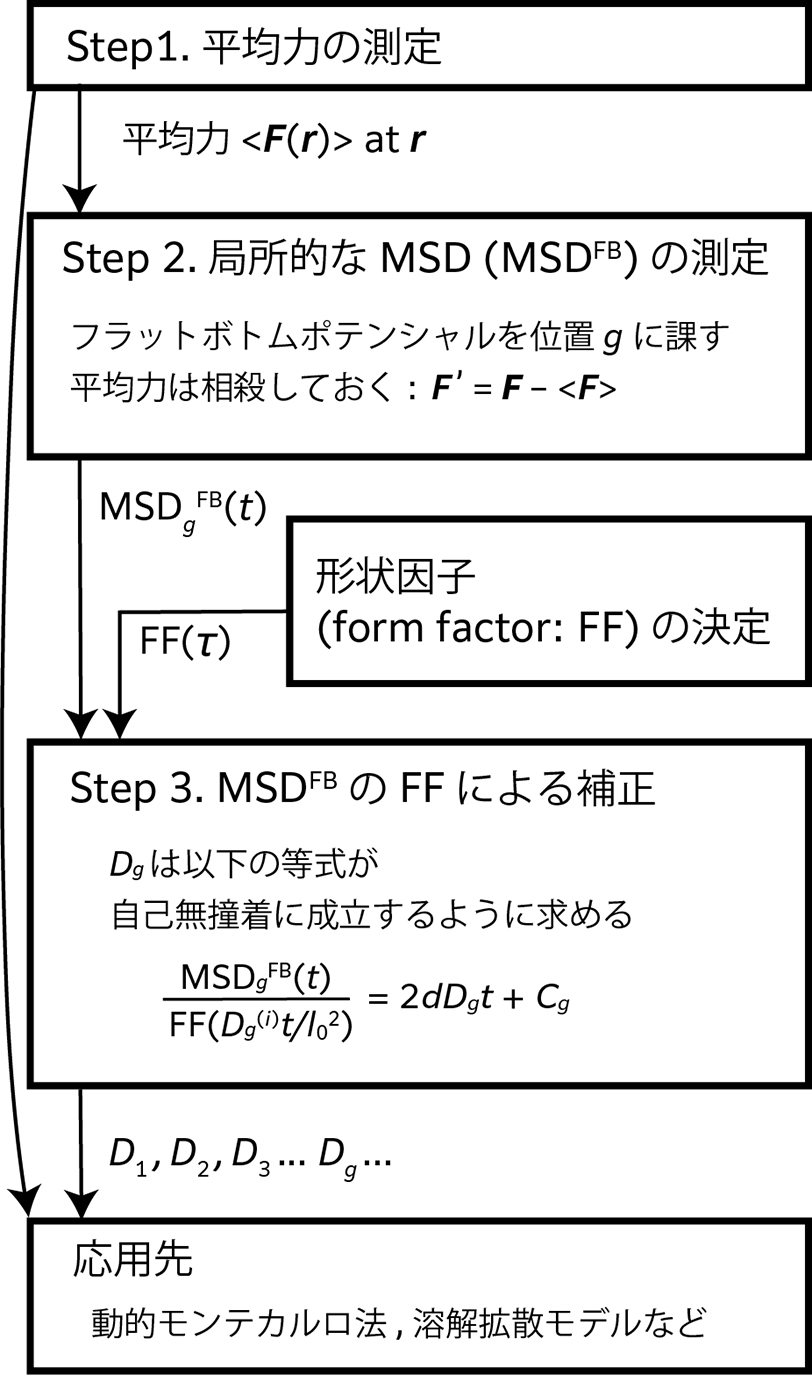
（Step 1）では平均力$\mathcal{⟨}\mathit{F}\left(\mathit{r}\right)\mathcal{⟩}$の計算を行う．平均力を直接計算してもよいが，自由エネルギーの計算結果を数値微分して求めることもできる．

（Step 2）では，位置$g$について局所的な平均二乗変位${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$の計算を行う．この計算のために行うMD計算では，（Step 1）で得た平均力を相殺しておく．理由は，平均力ポテンシャルの影響を取り除きランダム力にのみ由来する溶質の運動を観測するためである．また，位置$g$での測定値を得るために，位置$g$を中心とするフラットボトムポテンシャルにより溶質の位置を拘束しておく．計算する${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$は，フラットボトムポテンシャルが平らな部分を運動している軌跡の断片を利用して計算される平均二乗変位である．具体的な定義は原著論文［4］を参照頂きたい．興味のある空間範囲を覆うためには，フラットボトムポテンシャルの位置$g$を変えて複数の分子動力学計算を行う必要がある．

ここで，${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$の性質ついてもう少し述べたい．${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$は，フラットボトムポテンシャルの底が平らな部分における溶質の運動を解析することで得られている．そのため，外力の影響がない溶質が本来もつ運動を反映した測定値である．けれども，測定範囲の影響は受けてしまう．つまり，測定範囲を限定せずに同じ運動を観察して得られる平均二乗変位${\mathrm{MSD}}_g^{\mathrm{true}}\left(t\right)$は直線領域を持つ一方で，${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$は直線領域をもたない上に凸な曲線となる．${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$から拡散係数を得るためには，次に述べる（Step 3）で，形状因子（form factor: FF）による補正を行う．

（Step 3）では，${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$の形状因子による補正を行うことで，拡散係数を求める．明確な線形領域のない${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$を形状因子により補正し，線形領域の存在する測定範囲を限定しない${\mathrm{MSD}}_g^{\mathrm{true}}\left(t\right)$に変換することで拡散係数を計測する．

補正方法の前提となるMSDの性質について述べる．MSDは，

  

$${\mathrm{MSD}}^{\mathrm{true}}\left(t\right)=6Dt$$

と与えられるが，適当な長さ$l_0$を導入しMSDを無次元化することで，

  

$${\overline{\mathrm{MSD}}}^{\mathrm{true}}\left(\tau \right)\equiv \frac{{\mathrm{MSD}}^{\mathrm{true}}(t=\left(\frac{l_0^2}{D}\right)\tau )}{l_0^2}=6\tau$$(3)

というマスターカーブに乗ることが分かる．同様に，${\mathrm{MSD}}^{\mathrm{FB}}\left(t\right)$も同じ変換をすることでマスターカーブを得ることができる．これは，

  

$${\overline{\mathrm{MSD}}}^{\mathrm{FB}}\left(\tau \right)\equiv \frac{{\mathrm{MSD}}^{\mathrm{FB}}(t=\left(\frac{l_0^2}{D}\right)\tau )}{l_0^2}$$(4)

と与えられ，拡散係数に依存しない．但し，${\overline{\mathrm{MSD}}}^{\mathrm{FB}}\left(\tau \right)$は測定範囲の大きさにパラメトリックに依存する．

形状因子はこれらの2つの量の比

  

$$\mathrm{FF}\left(\tau \right)\equiv \frac{{\overline{\mathrm{MSD}}}^{\mathrm{FB}}\left(\tau \right)}{{\overline{\mathrm{MSD}}}^{\mathrm{true}}\left(\tau \right)}$$(5)

として定義され，拡散係数に依存しないマスターカーブである．この形状因子$\mathrm{FF}\left(\tau \right)$は拡散方程式や分子動力学シミュレーションから求めることができる．

このマスターカーブを利用することで補正方法を構築できる．${\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)$を$\mathrm{FF}\left(\tau \right)$で除したものは，${\mathrm{MSD}}_g^{\mathrm{true}}\left(t\right)$であり，傾き$6D_g$の直線でなければならない．したがって，

  

$$\frac{{\mathrm{MSD}}_g^{\mathrm{FB}}\left(t\right)}{\mathrm{FF}(\tau =\frac{D_{g}t}{l_0^2})}=6D_{g}t+C_g$$(6)

が成立する．未知数である拡散係数$D_g$が両辺にあるので，この等式を自己無撞着に解くことにより$D_g$を求められる．

2.4　 動的モンテカルロ法

拡散する分子に対する自由エネルギー地形と位置に依存した拡散係数が与えられた際に，拡散係数が位置に依存する拡散方程式［式(1)］を満足する粒子の軌跡を生成するシミュレーションが実行できれば，粒子の軌跡に基づき拡散経路などを議論できる．そこで拡散係数が位置に依存する拡散方程式を満足する粒子の軌跡を生成するシミュレーションを動的モンテカルロ法により実行するための方法を開発した［2］．

以下，簡単のために離散化された1次元系で記載するが，連続座標や多次元への拡張は，拡散が等方的であれば容易である．

動的モンテカルロ法を実行するためには，遷移確率を決める必要がある．ここで空間座標は$\mathrm{\Delta }x$ごとに離散化されているものとする．遷移確率を

  

$$p_{x\to x+\mathrm{\Delta }x}=\frac{1}{M_s}d(x,x+\mathrm{\Delta }x){p\prime }_{x\to x+\mathrm{\Delta }x}$$(7)

の形式で表したときに，以下の条件を満たせば，式(2)の遷移確率で生成された軌跡が式(1)の拡散方程式を満足することを我々は示した．ここで，$M_s$は移動可能なサイトの数である．1次元の格子系では$M_s=2$である．${p^{\prime }}_{x\to x+\mathrm{\Delta }x}$に関する条件は，

  

$$\pi \left(x\right)\propto exp\left[-\beta F\left(x\right)\right]$$(8A)

  

$$\pi \left(x\right){p^{\prime }}_{x\to x+\mathrm{\Delta }x}=\pi (x+\mathrm{\Delta }x){p^{\prime }}_{x+\mathrm{\Delta }x\to x}$$(8B)

  

$$\underset{\mathrm{\Delta }x\to 0}{lim}{p^{\prime }}_{x\to x+\mathrm{\Delta }x}=1$$(8C)

である．また，$d(x,x+\mathrm{\Delta }x)$についての条件は，

  

$$d(x,x+\mathrm{\Delta }x)=d(x+\mathrm{\Delta }x,x)$$(9A)

  

$$\underset{\mathrm{\Delta }x\to 0}{lim}d(x,x+\mathrm{\Delta }x)=𝔇\left(x\right)$$(9B)

  

$$𝔇\left(x\right)=\frac{D\left(x\right)}{D_{max}}$$(9C)

である．ただし，$D_{max}=maxD\left(x\right)$とした．また，一次元格子系では，シミュレーション1ステップあたりの時間間隔は

  

$$\mathrm{\Delta }t=\frac{\mathrm{\Delta }{x}^2}{2D_{max}}$$(10)

と定まる．ここで，$\mathrm{\Delta }x$は格子サイズである．

定式化の方法の概要は次の通りである．まず，ボルツマン分布と詳細釣合い$\pi \left(x\right)p_{x\to x+\mathrm{\Delta }x}=\pi (x+\mathrm{\Delta }x)p_{x+\mathrm{\Delta }x\to x}$の十分条件として，(8A)，(8B)および(9A)が導かれる．さらに，式(7)を元に各格子上の粒子の存在確率$\rho (x,t)$に対してマスター方程式を立て$\mathrm{\Delta }{x}^2/\mathrm{\Delta }t=\text{(定数)}$の条件下で$\mathrm{\Delta }t\to 0$の極限を取る際に，立式したマスター方程式が式(1)と一致するための十分条件は，式(8C)，(9B)，(9C)および(10)であることが示せる．なお，連続座標についてもほぼ同様の定式化が可能である．詳細は，原著論文［2］を参照頂きたい．

上述の条件を満たす遷移確率には複数の方法が考えられる．例えば，${p^{\prime }}_{x\to x+\mathrm{\Delta }x}$にメトロポリス判定［9］を利用し，$d(x,x+\mathrm{\Delta }x)$に$𝔇\left(x\right)$と$𝔇(x+\mathrm{\Delta }x)$の算術平均を用いると，

  

$$p_{x\to x+\mathrm{\Delta }x}=\frac{1}{M_s}\left[\frac{𝔇\left(x\right)+𝔇(x+\mathrm{\Delta }x)}{2}\right]min[1,e^{-\beta \mathrm{\Delta }F}]$$(11)

となる．ただし，$\mathrm{\Delta }F=F(x+\mathrm{\Delta }x)-F\left(x\right)$である．この形式は実装が容易で効率も良い．

3　 高分子電解質膜への応用研究

Nafion^®膜は，代表的な高分子電解質膜であり，水相と高分子相にミクロ相分離した不均一な構造を持つ（図3を参照）．水素を燃料とする燃料電池に利用されており，その性能向上のためには，高いプロトン伝導度だけでなく，酸素や水素の移動が遮断されていることも重要な性質である．しかしながら，ガス分子の透過に関する分子論的な機構はよく分かっておらず，ガスがミクロ相分離して生じる高分子相と水相あるいはその間の境界相のどの部分を透過しているのかは長年の謎であった．我々は，開発した手法をNafion^®膜における水素ガスの輸送問題に応用し，ガス輸送が主に高分子相と境界相で生じていることを見いだした．

図3  $\lambda =6$の時の分子構造．水分子は青い球により表され，高分子は赤い棒で示されている．水分子が局所的に集合し，水相を形成している．

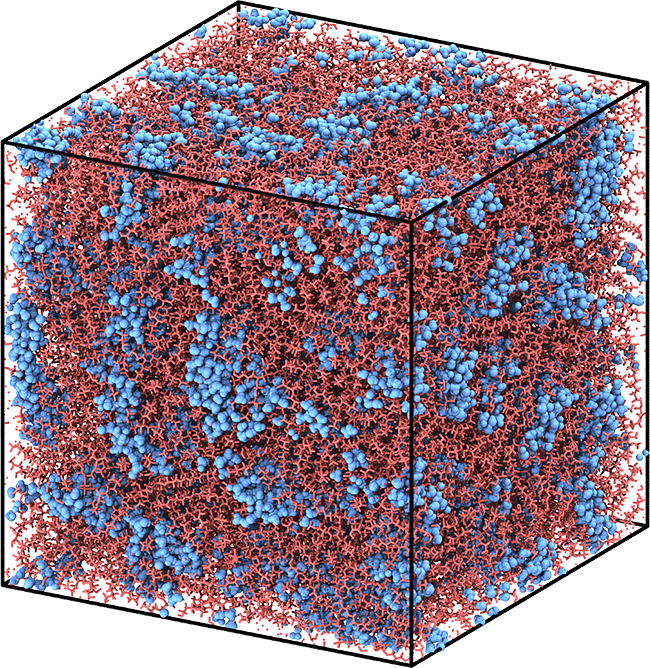
本稿では，高分子電解質のガス透過解明に関する我々の研究［7,8］を概観したい．

3.1　 ガスの自由エネルギー地形

図4には，粒子挿入法により計算した水素ガスの三次元の自由エネルギー地形の断面図を示す．自由エネルギー地形に対応する位置の分子構造を同時に示している．分子構造と自由エネルギー地形の高低を照らし合わせると，以下のことが分かる．高分子相は自由エネルギーの高い場所と低い場所があり，起伏に富んだ自由エネルギー地形をしている．水相の自由エネルギー地形は平らであるが，値は高く，水相にはガスが来にくいことが分かる．そのため自由エネルギーの低い経路は，主に高分子相に存在している．また，0.4 nmの領域で定義された局所的な密度と自由エネルギーは相関していた．

図4  (a)では自由エネルギー地形の断面図に対応する分子構造の断片を重ねて表示している．データは$\lambda =6$のものである．黒枠で印を付けた領域は(b)から(g)で拡大表示されている．酸素原子，水素原子，フッ素原子，炭素原子がそれぞれ，赤，白，桃色，シアンで示されている．Reproduced from J. Chem. Phys. 156, 044507 (2022), with the permission of AIP Publishing.

3.2　 ガスの位置に依存した拡散係数

図5には，位置に依存した拡散係数の地形を示している．拡散係数の大きい場所は，高含水率で生じる大きな水相の中心であることがわかる．このことは，拡散係数が直近の構造だけでなく，数nm離れた構造にも影響されていることを示唆している．

図5  (a), (b), (c)はそれぞれ含水率（スルホ基あたりの水分子の数）λ = 6，10，14における位置に依存した拡散係数と分子構造の対応を示す．赤，白，黄，シアン，桃色は，それぞれ，酸素，水素，硫黄，炭素，フッ素の原子を表す．背後のマップの赤い部分で拡散係数が大きくなっているが，このような場所は主に大きな水相の中心部である．Reproduced from J. Chem. Phys. 157, 054502 (2022), with the permission of AIP Publishing.

3.3　 ガス分子に対する粗視化ダイナミクス

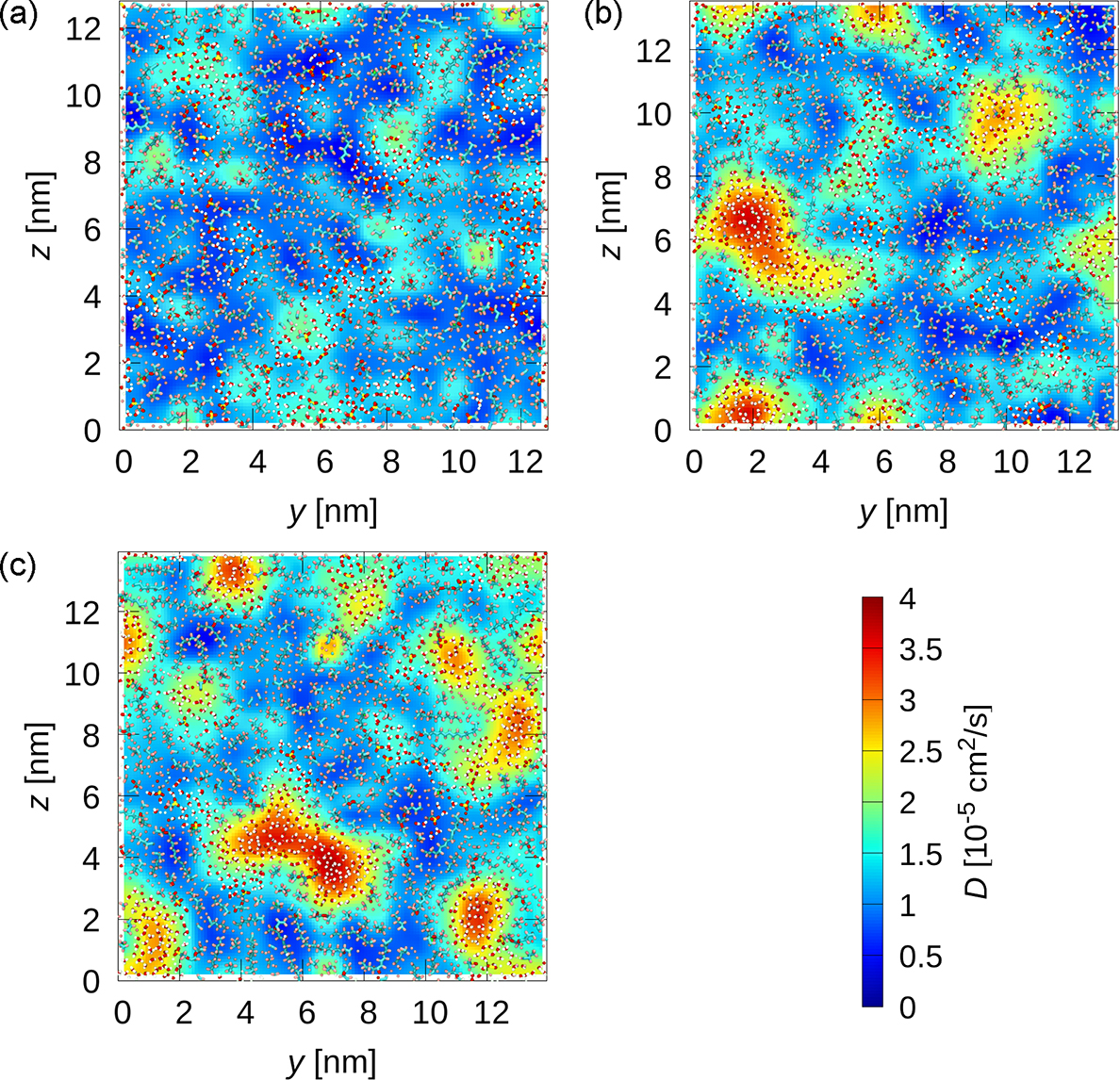
MD計算により得られたNafion^®膜中の水素ガスに対する自由エネルギー地形と位置に依存拡散係数を利用して，動的モンテカルロ法による粗視化ダイナミクスを評価した．動的モンテカルロ法を利用することにより粒子描像で水素ガスの拡散の軌跡を得ることができる．そのため，様々な解析が可能であるが，ここでは，平均二乗変位を評価した（図6）．動的モンテカルロ法の計算は非常に高速であり，マイクロ秒オーダーの平均二乗変位を精度よく評価でき，長時間ダイナミクスで得られた平均二乗変位の傾きから長時間挙動における大域的な拡散係数を求めることができる．得られた大域的な拡散係数と自由エネルギーから溶解拡散モデルにより透過係数を求めたところ，実験値をよく再現しており（図7），本研究手法の妥当性が示された．

図6  動的モンテカルロ法により得られた平均二乗変位を時間の関数として示す．赤，緑，青の線はそれぞれ，含水率λ = 6，10，14を示す．Reproduced from J. Chem. Phys. 157, 054502 (2022), with the permission of AIP Publishing.

図7  透過係数Pの相対湿度依存性を示す．本研究で得られた計算値であり黒丸は，実験値を表す橙のバツや青の四角と整合しており，実験をよく再現している．Reproduced from J. Chem. Phys. 157, 054502 (2022), with the permission of AIP Publishing.

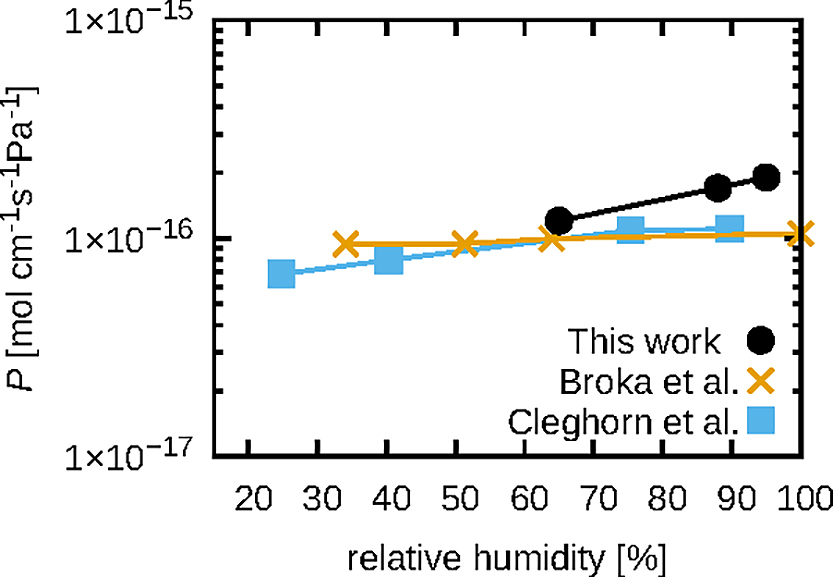
自由エネルギー地形や動的モンテカルロ法により得られた軌跡を利用して水素ガスの透過経路について検討したところ，主な経路は高分子相と境界相にあることを見いだし，ガスの透過経路を解明することができた．

4　 最近の展開

さて，開発した手法論の中で計算コストのかかる場所は自由エネルギー地形F(r)の計算と位置に依存した拡散係数D(r)の計算である．特に大規模な系においてこれらの物理量を直接求めるのは非常に負荷の重い計算である．

この負荷を軽減する方法として機械学習モデルの利用を検討している．調べたい大規模系と似た小さなモデル系に対するF(r)やD(r)を学習データとして利用し，局所構造からF(r)やD(r)を予測する機械学習モデルを作成すれば，F(r)やD(r)の直接計算が難しい大規模系に対しても，F(r)やD(r)を求めることができる．

現在は，高分子電解質膜バルクの系を利用して，局所構造からF(r)やD(r)を予測する機械学習モデルが作成できることを検証している．具体的には，smooth overlap of atomic positions（SOAP）カーネルを利用したsupport vector regression（SVR）モデルにより局所分子構造から自由エネルギーや位置に依存拡散係数を求めるモデルを作成し，ハイパーパラメータを調整したところ，R²値で0.8以上の精度を持つ機械学習モデルが作成可能であった．また，得られた値を入力として粗視化ダイナミクスの計算を行うと，大域的な拡散係数も4 %程度の誤差で得ることができ，実用に十分耐えることが分かった．

そのため，適切なモデル系から作成した機械学習モデルを大規模系に対して適用することで，大規模系に対しても自由エネルギー地形F(r)と位置に依存した拡散係数D(r)を求め，動的モンテカルロ法を応用できると期待できる．

また，局所分子構造として記述子に含めるべき構造の範囲は，拡散係数では長く，自由エネルギー地形では短いことが分かった．このことは，自由エネルギー地形の値は局所的な密度とよく相関する一方，位置に依存した拡散係数は大きな水相の中央で大きく，より広い範囲の環境によって拡散係数が決まっているというこれまでの結果とも整合するものであった．

5　 おわりに

本稿では，近年著者らが開発してきた長時間の拡散ダイナミクスを評価できる新規研究手法について概要を記した．この計算手法では，全原子分子動力学計算により自由エネルギー地形と位置に依存した拡散係数を求め，これらを入力として動的モンテカルロ法による粗視化ダイナミクスを評価することで，全原子MDシミュレーションだけでは到達できない10 ms程度の時定数で生じるμmオーダーの大域的な現象をシミュレーションできる．そのため，空間的に複雑な物質分布をもつ不均一な媒体で生じる物質輸送の分子論的な研究が可能となった．

提案手法で計算負荷の大きい自由エネルギー地形と位置に依存する拡散係数の計算についても，機械学習の応用により軽減する筋道を立てることができた．

現在は，富岳成果加速プログラム「燃料電池触媒層の物質輸送機構解明に向けた，マルチスケール計算技術構築とその活用」の一環として，これまで開発してきた手法を燃料電池カソード触媒層における物質輸送に応用している．これらの詳細については，分子シミュレーション討論会やアンサンブルなどで報告できれば幸いである．

 謝辞

一連の研究を行うにあたり，物質・材料研究機構に所属する安藤嘉倫氏には，MODYLASの利用に関して大変お世話になりました．この場を借りて深く感謝します．本研究は，文部科学省「富岳」成果創出加速プログラム「燃料電池触媒層の物質輸送機構解明に向けた，マルチスケール計算技術構築とその活用」（JPMXP1020230318）の助成，福岡大学の研究助成（課題番号GW2404, 215008）を受け実施しました．研究の一部には，スーパーコンピュータ「富岳」（課題番号：hp230200, hp240208），国立共同研究機構計算科学研究センター（課題番号：23-IMS-C136, 24-IMS-C065, 23-IMS-C504, and 24-IMS-C502）を利用しました．

参考文献

• [1]   永井  哲郎， 岡崎  進，アンサンブル，24, 160–166 (2022).
• [2]   T.  Nagai,  A.  Yoshimori, and  S.  Okazaki, J. Chem. Phys., 156, 154506 (2022).
• [3]   S.  Okazaki, J. Chem. Phys., 160, 174111 (2024).
• [4]   T.  Nagai,  S.  Tsurumaki,  R.  Urano,  K.  Fujimoto,  W.  Shinoda and  S.  Okazaki, J. Chem. Theory and Comput., 16, 7239 (2020).
• [5]   B.  Widom, J. Chem. Phys., 39, 2808 (1963).
• [6]   C. H.  Bennett, J. Comput. Phys., 22, 245 (1976).
• [7]   T.  Nagai,  K.  Fujimoto and  S.  Okazaki, J. Chem. Phys., 156, 044507 (2022).
• [8]   T.  Nagai and  S.  Okazaki, J. Chem. Phys., 157, 054502 (2022).
• [9]   N.  Metropolis,  A. W.  Rosenbluth,  M. N.  Rosenbluth,  A. H.  Teller and  E.  Teller, J. Chem. Phys., 21, 1087 (1953).

著者紹介

永井 哲郎（博士（理学））

〔経歴〕2013年名古屋大学理学研究科博士課程修了，2022年4月から現所属．〔専門〕分子シミュレーション．〔趣味〕音楽鑑賞・読書．

吉川 信明（博士（理学））

〔経歴〕2016年東北大学大学院理学研究科化学専攻博士課程修了，同年株式会社豊田中央研究所に入社，現所属．〔専門〕分子動力学，古典統計力学，バンディット問題．〔趣味〕お酒，プログラミング，スキー，育児？

陣内 亮典（博士（工学））

〔経歴〕2003年東京工業大学大学院理工学研究科機械制御システム専攻博士課程修了，同年株式会社豊田中央研究所に入社，現所属．〔専門〕第一原理計算，機械学習ポテンシャル，電気化学，触媒科学，燃料電池．〔趣味〕ピアノ．

木村 将之（博士（工学））

〔経歴〕2021年京都大学大学院工学研究科材料工学専攻博士課程修了，2016年トヨタ自動車株式会社に入社，現所属．〔専門〕第一原理計算，電気化学，燃料電池．〔趣味〕スキー，車，バイク．

岡崎 進（工学博士）

〔経歴〕1982年京都大学大学院工学研究科博士課程修了，名古屋大学名誉教授，分子科学研究所名誉教授，2024年から現職．〔専門〕分子シミュレーション．〔趣味〕畑，山歩き，古典文学．