2011 Volume 1 Issue 1 Pages 11-22
各クラスターに分類される個体の数，つまり，クラスターのサイズを所与の定数に固定して，個体× 変数の多変量データ行列の個体をクラスタリングする方法を提案する．このサイズ固定クラスタリングでは，各クラスターの重心ベクトルと，そのクラスターに分類される個体の変数ベクトルとの平方距離が最小になるように，データ行列の行（個体）の置換が行われ，重心ベクトルと置換行列を交互に推定する交互最小二乗法のアルゴリズムが使われる．ここで，置換行列を求めるステップは最小二乗置換と呼べるもので，新たなアプローチである．シミュレーションと実データへの適用によって，アルゴリズムの挙動が確認される．なお，提案するサイズ固定クラスタリングは，サイズ固定の制約を課したK平均法と見なすこともできる．
個体× 変数の多変量データ行列から，互いに類似した個体どうしが同一のクラスターに属し，似ていない個体が別々のクラスターに属するように個体を分類する統計手法は，クラスタリング（クラスター分析）と総称され，階層的方法と非階層的方法に大別される（例えば，足立, 2006, 齋藤・宿久, 2006）．
本研究で提案する手法は非階層的クラスタリングに属するが，例えば，100 個体を，個体数がそれぞれ30 個体，30 個体，および，40 個体からなる3 つのクラスターに分類するというように，クラスター数に加えて，各クラスターに分類される個体の数，すなわち，クラスターのサイズを事前に決めた定数に固定して，個体の分類を行うものであり，これをサイズ固定クラスタリングと呼ぶことにする．現在までに数多くの非階層的方法が開発されているが(Gan, Ma, & Wu, 2007;佐藤, 2009)，本研究で提案するようなサイズ固定のクラスター分析法は，見られない．
通常の非階層的クラスタリングでは，クラスター数を固定した上で分析を行い，各クラスターのサイズは分析前に定められない．従って，提案するサイズ固定クラスタリングは，例えば，100個体をサイズが50 の均等な2 クラスターに折半したい，あるいは，20，30，および50 といった3 クラスターに個体を分割したいといったニーズに答えるものであり，現実場面を考えると，全個体を等質的な個体からなる集団に分けて，各集団を特定スペースに配置したいが，スペースのサイズが制限されるケースに役立つ．例えば，ブランドを配置する3 つのスペースが2:3:4 の比率であり，各スペースに類似ブランドを配置したいケースには，ブランドの総数が90 であれば，3クラスターのサイズを20，30，40 と固定したクラスタリングが役立つ．また，学力テストデータに基づいて，学力特性の似たものどうしの学生からなるクラス（つまりクラスター）を作りたいが，各クラスの人数を均等にしたいケースにも，サイズ固定クラスタリングが使える．同様のケースの例は，その他にも数多いと考えられる．
非階層的クラスタリングの中でも最も基本的なK平均法は，クラスターを特徴づける重心ベクトルと，そのクラスターに分類される個体の変数ベクトルができるだけ近くなる個体の分類を目指すが(MacQueen, 1967)，提案手法もこれと同じ分類を目指す．この目的をクラスターのサイズを固定しながら達成するために，提案手法では，置換行列の推定が主要な役割を果たす．ここで，置換行列とは，それが前（後）から乗じられる行列の行（列）を置換する，すなわち，並び替える作用をする行列である．これまで，データ解析において，置換行列は前面に出ることは少なかったが，提案手法では重要な役割を果たす．2 節で置換行列の推定法とそれに基づくサイズ固定クラスタリングのアルゴリズムを詳述した後，その挙動を評価する数値実験を3 節で報告する．なお，クラスター数が多い場合には一般に正しい分類が容易でないことが予想され，サイズ固定という新たな制約を導入する本研究では，クラスター数が4 以下と少数のケースだけを考慮する．
2.1 節では，K平均法を概説した後，それとの違いからサイズ固定クラスタリングの目的関数を導入する．その最適化において重要な役割を果たす置換行列の選択原理を2.2 節で記し，2.3 節で提案手法のアルゴリズムを記す．
2.1. 目的関数n個体×m 変数のデータ行列X = [x′1, · · · , x′n]′ の行に並ぶ個体を，K個のクラスターに分類するために，K平均法（K-means Clustering; KMC）では，目的関数
を最小にする行列G とY を求める(MacQueen, 1967; Hartigan & Wong, 1979)．ここで，G = (gik) は個体のクラスターへのメンバーシップを表すn 個体× K クラスターの2 値行列であり，個体i が配属されるクラスターをc(i) と表せば，gi,c(i) = 1，第i 行のgi,c(i) 以外の要素は全て0 である．また，Y = [y′1, · · · , y′K]′ はK クラスター× m 変数の行列であり，第k 行y′kはクラスターk の重心ベクトルと呼ばれ，その要素はクラスターk を特徴づけるm 変数の値を表す．目的関数(1) 
と書き換えられ，K平均法は，個体iの変数ベクトルxi とそれが配属されるクラスターの重心ベクトルyc(i) との平方距離の総和が最小になるようなy′1, · · · , y′K，および，{c(i); i = 1, · · · , n} つまりメンバーシップ行列G を求める方法であるといえる．
さて，クラスターk に配属される個体の数，すなわち，k のサイズをnk と表そう．ここで，
である．K平均法ではnk の値は分析結果として出力されるのに対して，本研究で提案するサイズ固定クラスタリングでは，例えば「nk = 10」のようにnk を一定の値に固定する．この制約のもとに，K平均法と同様に，個体i の変数ベクトルxi とそれが配属されるクラスターの重心ベクトルyc(i) との平方距離の総和が最小になるような分類を目指す．この分類を達成するために最小化される目的関数を，次に定義する．
まず，n 個体× K クラスターの行列G を，推定対象とするのではなく，
と固定する．ここで，1nk は要素が全て1 のnk ×1 のベクトルを，右辺の行列内の空欄は対応部の要素が0 であることを表し，この空欄による要素0 の表示は以下でも同様である．そして，目的関数
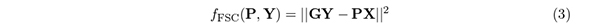
を最小にするK クラスター× m 変数の重心ベクトルの行列Y と，n 個体× n 個体の置換行列P = (pij) を求める．これが，提案するサイズ固定クラスタリング（Fixed Size Clustering; FSC）である．ここで，置換行列とは，要素が1 か0 だけの正規直交行列と定義される(Harville, 1997,pp.86–88)．例えば，n = 3 とすると，P は，
のいずれかであり，
として左から
に乗じると
となることで例示されるように，pij = 1 であれば，X の第j 行がPX の第i 行となる．
目的関数(3) を最小化することの意味を把握するために，(3) をK平均法の目的関数(1) と比較する．(1) では，メンバーシップ行列Gを推定するのに対して，nk が既知であるサイズ固定クラスタリングでは，G を(2) のように固定することができる．こうした固定のもとで，個体のクラスターへのメンバーシップを決めるのは，G ではなく，X の行（個体）を並び替えてPX とする置換行列P である．すなわち，X の行を置換したPX の行が，GY の行を近似するようにさせる役割を，置換行列P が担うわけである．さらに，n × n の単位行列をIn と表すと，
より，サイズ固定クラスタリングの目的関数(3) は，fFSC(P,Y) = ||P′GY − P′PX||2 =||P′GY − X||2 と書き換えられるので，
が個体× クラスターのメンバーシップ行列となる．なお，K平均法の目的関数(1) も，(3) と同じ形で書ける．ただし，K平均法では，クラスターのサイズnk は未知であるので，||GY−PX||2を最小にするP,Y, nk (k = 1, . . . , K) を求める方法としてK平均法を定式化できる．従って，サイズ固定クラスタリングは，nk を定数に等しいと制約したK平均法と位置づけることができる．
サイズ固定クラスタリングの解は，[A] P を固定して(3) を減少させるYを求めるステップと，[B] Y を固定して(3) を減少させるP を求めるステップを，収束するまで交互に反復することによって得られる．2.3 節に記すように[A] は容易であるが，[B] は独自の反復解法を要するので，それを次節に詳述する．
2.2. 最小二乗置換Y を固定した目的関数(3) の最小化は，Z = GY と表すと，所与のn × p の行列X とZ について，
を最小にするn × n の置換行列Pを求める問題，言い換えれば，X の行を置換したPX によるターゲット行列Z の近似を最良にするP を求める問題と定式化される．最小二乗基準(7) の置換行列P による最小化を，最小二乗置換（Least Squares Permutation; LSP）と呼ぶことにする．その解は解析的には得られないが，n×n の置換行列は計n! 種であるため，例えばn が3 のようにごく少数であれば，(4) に示すようにn! = 6 に限られ，n! 種のP の中で(7) を最小にするPを解とすればよい．しかし，n の増加に伴ってn! は爆発的に増大し，たかだかn = 20 でもn! は20!≅3.04 × 1063 と莫大な数にのぼり，n! 種すべてのP を(7) に代入するには，膨大な時間を要する．そこで，最小二乗置換のための簡便な反復解法を提案する．
提案する解法は，t 回目の反復で得られる置換行列をP[t] と表すと，適当な初期行列P[0] から始めて
による置換行列の更新を反復するものである．ここで，Q[t] も置換行列であり，次の段落で解説するように，P[t]X の行i とj を置換するQij の中で，目的関数(7) を最もよく減少させるQijが，Q[t] として選ばれる．このQij は，(i, j) 要素，(j, i) 要素，および，(i, i) 要素と(j, j) 要素を除く対角要素が1，それ以外の要素は全て0 であるn × n の行列であり，ei を要素i だけが1で他はすべて0 のn × 1 のベクトルとすると，
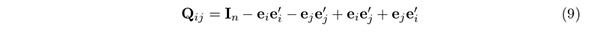
と定義される．例えば，n = 4のとき，
である．Qij = Qji を考慮し，置換を行わないことに対応するQii = In を除けば，考えうるQij の集合は，{Qij : 1 ≤ i < n,i < j ≤ n}と表せ，その要素数は，N(n) = n(n − 1)/2 となる．例えば，N(20) = 190，N(100) = 4950，N(200) = 19900 のように，(9) の種類は，n! のように膨大な数にはならない．すなわち，多くの計算回数を必要とせず，かつ，次段に記すように，簡便な演算によって選定されるQ[t] によって，反復のたびに目的関数の単調減少を達成できる点で，現実的なものである．なお，置換行列どうしの積も置換行列であることが，(8) の更新式の基礎にある．
Qij の集合の中から更新(8) に使うQ[t]を選択するために，まず，P[t]X の行i と行j の置換に伴う最小二乗基準(7) の減少量
に着目する．ここで，
は，更新前のZ の第i, j 行とP[t]X の第i, j 行の要素の誤差平方和
を表し，
は，Qij による置換後の対応部の誤差平方和
である．そして，Δ[t](Qij) を正とするQij の集合Θ = {Qij : 1 ≤ i < n,i < j ≤ n,Δ[t](Qij) >0} の中で，Δ[t](Qij) を最大にするQij を，Q[t]とする．しかし，Θ が空集合のときもあり，その時は置換をしない．従って，Q[t]の選択法は
と表せる．(13) のQ[t]を用いた更新(8) によって，明らかに最小二乗基準(7) の単調減少fLSP(P[t]) ≥ fLSP(P[t+1]) は保障される．
以上より，提案する最小二乗置換の解法は，適当なP の初期行列から始めて，(13) のQ[t]を用いたP の更新(8) を，収束するまで反復するものである．なお，3.1 節のシミュレーションでは，更新前後の基準(7) の変化量を行列サイズnm で除した値が，0.17 以下になることをもって，収束したものと判定する．
2.3. アルゴリズムサイズ固定クラスタリングでは，[A] P を固定して最適なY を求めることと，[B] Z = GY を固定して最小二乗置換によってP を求めることを反復する．ここで，[A] のY は，
で与えられ，P を固定すると，(14) によって目的関数(3) は最小化される．一方，同じクラスターに属する個体どうしを置換しても(3) は減少しないので，[B] の最小二乗置換で使われる(13) 式の集合は，Θ = {Qij : 1 ≤ i < n,i < j ≤ n,Δ[t](Qij) > 0, δij = 1} のように限定される．ここで，(13) 式の適用時に，個体i とj が互いに異なるクラスターに属しているときはδij = 1，同じクラスターに属しているときはδij = 0 である．さらに，[A] と[B] の反復によって(3) を単調減少させるためには，[B] の最小二乗置換おけるP の更新(8) を収束するまで反復する必要はなく，たった1 回のP の更新だけでも，(3) の単調減少fFSC(P[t],Y) ≥ fFSC(P[t+1],Y) は保障される．そこで，所与のX，Z = GY，および，P の初期行列POLD に対して，上記のΘ に基づく(13) および(8) による更新をT 回繰り返して，新たなP を出力する関数を，LSP(POLD,X,Z, T)と表す．以上より，サイズ固定クラスタリングのアルゴリズムは，次のように表せる．
[1] nk を決めて(2) のようにG を定め，P を初期化し，POLD とする．
[2] (14) によって，Y を求める
[3] P = LSP(POLD, X, GY, T) とする．
[4] 収束していれば終了し，その他のときは，POLD = P として[2] に戻る．
ここで，本稿の3.2 節と4 節では，T = 1とし，P の初期行列はランダムに選択する．さらに，[4]の収束判定については，目的関数(3) のステップ間変化量を行列のサイズnm で除した値が0.17以下になることをもって，収束したもの見なす．
なお，K平均法のG と同様に，サイズ固定クラスタリングのP も二値行列であり，このようにパラメータが離散的である場合には，局所解の発生は避けがたい．そこで，より良い解を得るために，アルゴリズム[1]～[4] を複数のランダムなP の初期行列からスタートさせて，得られた複数組の解の中で，目的関数(3) の値を最小にするP とY を最適解とする．
サイズ固定クラスタリングによる個体の分類の精度と局所解の発生頻度を評価することが，数値実験の最終目的であるが，その前に，クラスタリングの主要ステップをなす最小二乗置換も新たなアプローチであるため，3.1 節では，最小二乗置換だけに関わるシミュレーションについて報告する．そして，3.2 節と3.3 節で，シミュレーションおよび実データによるサイズ固定クラスタリングの挙動評価を報告する．
3.1. 最小二乗置換のシミュレーション最小二乗置換による真の置換行列P の再現精度と局所解の発生頻度を評価するために，次の手続きで100 × 10 のX とZ を生成した．すなわち，100 × 100 の真のP をランダムに生成し，Zの要素を区間[−1, 1] の一様分布から抽出した上で，モデル
を満たすX を生成した．ここで，E はその要素が標準正規分布に従う誤差行列であり，
は誤差水準を表す．この(16) 式はρ = ||Z||2/(||Z||2 + σ(ρ)2||E||2) と書き換えられ，誤差水準σ(ρ) の引数ρ は，Z によるPX の分散説明率を近似する．すなわち，Z とE がほぼ独立でZ′E≅ Om ならば，近似的な平方和の分割||PX||2 ≅ ||Z||2 +σ(ρ)2||E||2 が成り立ち，分散説明率は||Z||2/||PX||2 ≅ ||Z||2/(||Z||2 + σ(ρ)2||E||2) となって，この右辺は上記のρ と一致する．以下では，値域が明確でないσ(ρ) よりも，0 以上1 以下の比率のために値の大きさを把握しやすいρ を，誤差の小ささを表す指標として参照する．分散説明率ρ を1.0, 0.85, および，0.7 と設定して，上記の手続きを反復し，100 組のP, X, Z を得た．なお，(5) を使えば，モデル(15) を満たすX は，X = P′{Z + ε(ρ)E} で与えられる．
計300 組（= 3種のρ×100 組）のX, Z の各組について，P のランダム初期行列を変えながら，2.2 節に記す最小二乗置換を100 回行った．第s 回目のP の解をPs と表すと，1 組のデータに対して，100 個の解P1, · · · ,P100 が得られることになるが，それらの中で目的関数(7) の値が最小である解を
と表し，最適解と見なした．
0 以上1 以下の値をとるように標準化された最適解と真のP の二乗誤差
を，P の再現精度(の悪さ) の指標とした．また，各組のデータについて，100 個の解の中で最適解と異なる解，つまり，
となるPs を局所解と見なして，その発生回数を数えた．各ρ の100 個のデータに対する再現精度指標と局所解発生回数のパーセンタイルを，それぞれ，表1(A) と(B) に示す．まず，(A) をみると，ρ = 1つまり誤差なしのデータすべてについて，真のP は完全に再現され，ρ = 0.7 と誤差水準が高い場合でも二乗誤差は0に比較的近く，P の再現精度は良好であるといえる．一方，(B) をみると，誤差水準が高いほど局所解は頻発し，特に，ρ = 0.7 のデータの過半数について，100 個の解のうち99 個が最適解と異なる，つまり，全ての解が異なっていることがわかる．このような局所解の頻発にもかかわらず，P の再現精度は良好であった事実から，最適解は有用なものとして受け入れられると結論づけられる．
サイズ固定クラスタリングによる個体の正分類率と局所解の発生頻度を評価するため，各クラスターは独自の平均ベクトルをもつ多変量正規母集団であるが，クラスター間および変数間で分散は等しいという想定のもとにデータを生成した．すなわち，クラスターk のl 番目の個体の変数ベクトルxl(k) を，平均ベクトルμk，共分散行列v(θ)Im のm 変量正規分布Nm(μk, v(θ)Im)から発生させる．ここで，各変数の分散v(θ) は，クラスター間分離度（相関比）を表すθ の関数であり，全平均
群間平方和を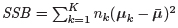
と表すと，
と定義される．群内平方和を
と表すと，クラスター間分離度がθ = SSB/(SSB + SSW = SSB/{SSB + nv(θ)} と表せ，この式から(17) が導かれている．
クラスター数K = 2, 3, 4，および，クラスター間分離度θ = 0.9, 0.75, 0.6 を組み合わせた計9条件のそれぞれについて，クラスター・サイズnk を区間[30, 70] の整数の一様分布から，クラスターの平均ベクトルμk の要素を区間[−10, 10] の実数の一様分布から抽出し，m は10 と固定した上で，Nm(μk, v(θ)Im) に従って抽出されたx′l(k) (k = 1, · · · ,K; l(k) = 1, · · · , nk) をランダムにX の行に並べた．以上の手続きを100 回行って，計900 個（= 9 条件× 100 組）のデータ行列X を得た．なお，X の行数は
となる．
各Xについて，K とn1, · · · , nK を真の値に設定した上で，Pのランダム初期行列を変えながら2.3 節のアルゴリズムを30 回実行した．s 回目の実行で達成された目的関数(3) の値を
そして，
と表す．最小値
を与えた解から，メンバーシップ行列(6) によって各個体が配属されたクラスターを求め，付録Aに記す手続きによって，正分類率，すなわち，個体の配属クラスターが真のクラスターと一致する個体の比率を求めた．また，
となる解を局所解と定義して，各Xについて，30 回のアルゴリズム実行のうちに局所解が発生する回数を求めた．表2 に，各条件の100 個のX についての，正分類率と局所解発生回数のパーセンタイルを示す．正分類率は，クラスター数K が少なく，クラスター間分離度θ が高い場合には高率であり，特にK = 2でθ = 0.9 のときは全てのパーセンタイルが100%に達したが，K の増加と分離度θ の低下に伴って，正分類率は低下することが見出せる．しかし，K = 4 でθ = 0.6のケースでも正分類率25 パーセンタイルが，偶然確率の1/4 = 0.25 を十分に上回っている．一方，局所解の発生回数は，K = 2 でθ = 0.9 のときでも多く，さらに，K の増加と分離度θ の低下に従って増大することが窺え，特に，クラスター数K が4 のときは，全てのパーセンタイルが，30 個の解のうち29 個が最適解と異なる，つまり，全てが異なる解であることを示す値となっている．このような局所解の頻発にもかかわらず，上述のように正分類率は十分に高かったことから，クラスター数K が4 以下の場合には，サイズ固定クラスタリングによる分類結果が有用なもとして受け入れられると結論づけられる．
サイズ固定クラスタリングを，150 個体× 4 変数のあやめ科植物のデータ行列(Fisher, 1936)に適用した．ここで，個体は，セトーサ，ヴェルシコール，ヴィルジニカのそれぞれに属する50個体の植物である．つまり，150 個体はそれぞれサイズ50 の3 クラスターに分類されることが既知である．一方，4 つの変数は，がくの長さと幅，花弁の長さと幅であり，それぞれの変数のクラスター間分離度つまり全体平方和に対する群間平方和の比は，0.62，0.40，0.94，0.92 である．さらに，全変数をまとめたクラスター間分離度，すなわち，変数を通した全体平方和の合計に対する群間平方和の合計の比は0.87 である．
上記のデータに，K = 3，n1 = n2 = n3 = 50 として，P のランダム初期行列を変えながら2.3 節のアルゴリズムを30 回実行した．サイズ固定クラスタリングを適用して，正分類率と局所解の発生回数を求めた．その結果，局所解は発生せずに，正分類率は92%と高かった．
以上は，クラスター・サイズを真の値（n1 = n2 = n3 = 50）に設定した上での結果であるが，実際場面では最適なサイズは未知である．そこで，[n1, n2, n3] を[40, 50, 60] や[30, 30, 90] のように逸脱させて，それ以外はここまでと同じ手続きで分析を行った結果を，クラスター・サイズが真値のケースとともに，表3 に示す．まず先に局所解の発生回数をみると，真値のケースの0回は稀なことであり，他のケースでは局所解が頻発している．次に，表の最下行に掲げた正分類率の上限を見る．その求め方は付録B に記すが，例えば，[n1, n2, n3] = [30, 40, 80] のときには，サイズを真値50 以上の80 と設定されたクラスターに配属される個体のうち，80−50 = 30 個体は必然的に誤分類となることから，上限が100%に達しないことは直感的にも理解できよう．表3 の正分類率の行と最下行の上限を比較すると，[n1, n2, n3] が真値と異なるケースでも，上限に近い正分類率が達成されたことがわかり，この結果は，サイズ固定クラスタリングの挙動の良さの証左となろう．
本研究では，クラスターのサイズを定数に固定した上で，各クラスターの重心ベクトルと，そのクラスターに配属される個体の変数ベクトルとの平方距離が，できるだけ小さくなるように，個体をクラスタリングする手法を考案した．このサイズ固定クラスタリングのためのアルゴリズムは，重心ベクトルを推定するステップと，データ行列の行つまり個体を置換するステップを交互に繰り返すものである．ここで，後者のステップは，単独の分析法として，最小二乗置換と呼べるものであるが，この最小二乗置換のために提案した反復解法が，しばしば局所解を与えるものの，高い精度で真の置換行列を再現することを，シミュレーションによって確認した．そして，サイズ固定クラスタリングの挙動を，シミュレーション，および，クラスターが既知のデータへの適用によって評価した結果．局所解が頻発するものの，高い比率で個体を正しいクラスターに分類できることが確認された．
サイズ固定クラスタリングの主要ステップをなす最小二乗置換は，データ行列の前から置換行列を乗じて得られる行列が，ターゲット行列にできるだけ合致するような置換行列を求める方法である．置換行列が正規直交行列に含まれることから，ターゲット行列に近似するように，別の行列を直交回転させる直交プロクラステス回転(Gower & Dijksterhuis, 2004) の特殊ケースとして，最小二乗置換を位置づけることができる．しかし，直交プロクラステス回転の正規直交行列は，特異値分解によって解析的に求められるが，2 値である最小二乗置換の置換行列は解析的に求められず，データ行列の任意の二つの行の置換の中で，最小二乗基準を最も低下させる置換を選ぶという解法をとった．しかし，これが唯一無二の解法ではなく，より洗練された最小二乗置換の解法の開発は，課題の一つとして残る．例えば，本論文の査読者は，3 つ以上の行を同時置換することの考慮を示唆したが，そうしたアプローチによって，より精度の高いアルゴリズムを構成できるかもしれない．また，直交プロクラステス回転における特異値分解に相当するような行列の分解を，最小二乗置換においても見出せるかどうかを検討することも興味深い課題かもしれない．
局所解の多さへの対応も，今後の検討を要する課題であろう．数値実験の結果が，サイズ固定クラスタリングによる十分な正分類率の達成を示したことから，局所解の発生は，離散値をパラメータとする分析では避けられないこととして放置することもできるが，ランダム初期行列を変えながらのアルゴリズムの複数実行の回数を，3.2 節と3.3 節で採用した30 回よりも増やせば，よりよい解が得られ，より高い正分類率を達成できると考えられる．しかし，実行回数を増やせば，もちろん分析の時間も延長する．そこで，どの程度のアルゴリズムの実行回数が合理的であるかを検討することは，今後の検討課題の一つである．また，実行回数を事前に決めるのではなく，アルゴリズム実行の繰り返しの途上で，何らかの基準をもって繰り返しを打ち切る手続きを想定した上で，打ち切り基準を考えるのも一つの方向性であろう．
真のクラスターに対する個体のメンバーシップを表すn 個体×K クラスターの二値行列をGTと表そう．一方，分析結果の解として出力されるメンバーシップ行列は，(6) のGP で与えられる．従って，K クラスター×K クラスターの正方分割表F = G′TGP の対角(k, k) 要素fkk が，真の第k クラスターに属して，解の第k クラスターに配属された個体数を表す．ここで，真および解の第k クラスターが，必ずしも同じクラスターに対応しないことに注意しなければならない．例えば，F の第1, 2, および3 行のクラスターが，それぞれ，第2, 3 および1 列のクラスターに対応するかもしれない．こうした不一致が生じる理由は，目的関数(3) からわかるように，分析中に，X の行を自由に置換したPX がGY にマッチングされ，クラスター× 変数の行列Y の第k行が，真の第k クラスターに対応するように固定されてはいないからである．この不一致を解決して正分類率を求めるためには，F = G′TGP の対応する行と列が同じクラスターを表すように，GP の列を並び替えなければならない．そのためには，重心ベクトルの行列に着目すればよい．
真のクラスターの重心ベクトルの行列をYT と表そう．ここで，YT = (G′T GT)−1G′TX である．YT の第k 行に最も近似するY の行（解の重心ベクトル）が，真のクラスターk に対応すると考えられる．そこで，K ×K の置換行列R でY の行を置換したRY の各行ベクトルと，対応するYT の各行ベクトルとの平方距離をできるだけ小さくするR を
と表せば，
の各行がYT と同じく真のクラスターに対応することになる．このは，次の手順で求められる．任意のRに基づくRY の第j 行ベクトルと，YTの第i 行ベクトルの平方距離を(i, j) 要素とするK（真のクラスター）×K（解のクラスター）の行列を，R の関数としてD(R) と表せば，全てのK ×Kの置換行列の中でtrD(R) を最小にするR が，となる．なお，クラスター数がK = 4であっても全ての置換行列は計4! = 24 種に限られ，ˆR は容易に求められる．この置換に伴って，解のメンバーシップ行列は
のように列置換され，その結果得られる正方分割表
の行と列は同じ真のクラスターに対応するため，正分類率の百分率は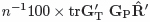
によって与えられる．
カードが全くなくなるまでインタビューを続けなければいけない」という訳ではない．
分析に使うクラスターk のサイズnk に対して，k の真のサイズをNk と表そう．付録A より，正方分割表
の第k 行および第k 列の周辺頻度は，それぞれ，Nk およびnk となる．ここで，正しく分類された個体の数を表す対角要素は，対応する行と列の周辺頻度よりも大きい値をとりえないので，その上限はmin(Nk , nk) である．従って，全クラスターを込みにした正分類率の百分率の上限は，
となる．
貴重なご指摘をいただいた査読者の先生方に感謝いたします．
