2012 Volume 2 Issue 1 Pages 33-51
本研究では，クラスタリングの1 手法である，K-平均法と，バイプロットのアルゴリズムを組み合わせることにより，個体と変数の分類と，分類後のクラスターのプロットを同時に行う方法を提案する．一般に，多くの個体・変数から成るデータ行列のバイプロットは，個体に対応する点，変数に対応するベクトルの数が非常に多くなり，煩雑なプロットとなるため，その解釈は困難である．提案手法は，個体・変数を少数のクラスターに分類し，そのクラスターを2 次元平面上にプロットするものであるため，データ行列の規模が大きい場合であっても，単純で解釈のしやすいバイプロットを得ることが可能である．提案手法の有用性は，数値シミュレーションと，実データ解析により，実証的に検証される．
バイプロット(Gabriel, 1971; Gower & Hand, 1996; Gower, Lubbe & Roux, 2011) は，行に個体，列に変数が並ぶデータ行列の，各行を点，各列をベクトルとして，2 次元空間上に同時にプロットした図を指す．一般に，データ行列XのサイズがI × J，すなわち，データ行列がI個体とJ 変数から成る場合，Xのバイプロットは，以下のように得られる．まず，最小二乗基準
を，制約条件．
のもとで最小化する，行列F(I × r)，G(J × r) を求める．続いて，Fの各行を個体に対応する点として，Gの各行を変数に対応するベクトルとして，r次元空間上にプロットする．ここで，行列Fの各行は，個体に対応する点の座標を表し，行列Gの各行は，変数に対応するベクトルを表す．また，rは，点とベクトルをプロットする空間の次元数を表す定数であり，通常は2 に設定される．行列Xの階数をt ≤ min(I, J) とすれば，(1) の基準を最小化するF，Gは，Xの特異値分解
を用いて
とすれば得られる．ここで，K(I × t)，および，L(J × t) は，K′K = L′L = It を満たす，特異ベクトルを並べた行列であり，Λ は特異値が降順対角に並ぶ t × t の対角行列である．また，Kr(I × r)，Lr(J × r) はK，L のそれぞれ上位r列からなる行列，ΛrはXの上位r 個の特異値が降順対角に並ぶr 次対角行列である．(4) のF，Gは，Xの主成分スコア，主成分負荷量とそれぞれ等しいため，以上の方法に基づくバイプロットは，Xの主成分分析とその結果のプロットと同等のものであるといえよう．
(1) の最小二乗基準からも推察されるように，バイプロットとは，(3) の特異値分解によって，データ行列Xを，行列F，Gに分解し，それらの各行をr 次元空間上にプロットしたものである．また，Fの第i 行ベクトルをf(i)(i = 1, . . . , I)，G の第j行ベクトルをg(j)(j = 1, . . . , J) とすれば，(1) の基準は，||X−FG′ ||2 = Σi,j(xij − f(i)g′(j))2 と表すこともできる．従って，バイプロットとは，データ行列の各要素を，その内積により最もよく近似するようなベクトルf(i)，g(j)をすべてのi, j について求め，それらを2 次元平面上にプロットしたもの，とも解せられよう．また，(3)，(4) より
が成り立つことから，上の方法で求められるバイプロットでは，Xが列中心化されているとき，以下の2 つの性質が成り立つ．まず，Xの第j変数の標準偏差I−1||xj || が，||g(j)||，すなわち第j変数に対応するベクトルの長さによって近似されている．さらに，第m変数と第n変数(m ≠ n) の相関係数(x′mxn)/(||xm|| × ||xn||) が，それぞれに対応するベクトルがなす角の余弦(g′(m)g(n))/(||g(m)|| × ||g(n))||) を近似している．
バイプロットにおいて，変数を表すベクトルの長さは任意であり，そのことを利用して様々な情報を視覚的に付加する試みがなされている．例えば，前川(1997) はその長さを各変数の分散説明率に比例させることにより，その変数のモデルへの当てはまりの良さを表現出来ることを示した．しかし，本研究では，単純性を考慮して，ベクトルの長さの2 乗が，元の変数の分散に比例するように，(4) の形で変数ベクトルを定義した．
図1(a) は，15 人の受験者の，5 教科からなる，試験の成績データ（仮想数値例）のバイプロットを，前述の方法で求めたものである．図中のΔは各個体（受験者）に，ベクトルは各変数（国語・英語・数学・理科・社会）に，それぞれ対応する．また，本論文におけるバイプロットでは，左軸と下軸が個体（点）のスケールを，右軸と上軸が変数（ベクトル）のスケールを表す．前述のように，上の方法で得られたバイプロットにおいて，2 つのベクトルのなす角度の余弦は，対応する変数の相関係数を近似し，一方ベクトルの長さは，対応する変数の標準偏差を近似する．また，この数値例においては，それぞれの教科が0 ∼ 100 点の同一尺度上に位置づけられると考えられることから，データを標準化せず，列中心化のみを行なっている．これらのことから，図1(a) からは，例えば次のような解釈が可能であろう．まず，国語・英語・社会を表すベクトルが，理科・数学に対応するベクトルと直交していることから，この試験においては，文系科目と理系科目がほぼ独立であること，加えて，ベクトルの長さから，英語と理科が，他の3 科目と比べ，得点の分散が小さいことが推察される．さらに，各受験者について，文系・理系のどちらかを得意とする受験者や，そのどちらも得意でない受験者が存在することも，点とベクトルの相対的な位置関係から，直感的に把握できよう．このように，多変量データ行列のバイプロットによって，個体と変数の関係性や相関の構造を，視覚的に捉えることが可能である．
しかしながら，データが多くの個体・変数から成る場合には，そのバイプロットの解釈は困難となる．その1 例として，500 人，200 項目からなる，試験の成績データ（仮想数値例）のバイプロットを，図1(a) と同様の方法で求め，図1(b) に示した．データ行列は500 個体の，200 変数分のデータからなるため，図1(a) と比べて，プロット中の点・ベクトルの数が非常に多くなり，はっきりとした解釈がしづらくなっていることが見て取れよう．このように，データ行列が多くの個体・変数から構成される場合，すなわち，データの規模が大きな場合には，バイプロットは煩雑となり，その解釈は非常に困難となる．
そこで，本研究では，2 相2 元データに対する分類の手法として代表的なK-平均法(MacQueen,1967) と，バイプロットのアルゴリズムを組み合わせることにより，個体・変数の分類と，各クラスターのプロットを同時に行う方法を提案する．従来のバイプロットでは，データの個体・変数と同数の点，ベクトルがプロットされるが，提案手法では，個体・変数は少数のクラスターに分類された上で，そのクラスターがプロットされる．従って，大規模なデータであっても，解釈のしやすいバイプロットを得ることが可能となる．提案手法は，いわば，大規模データのバイプロットを「要約」するための方法であるといえよう．
本稿の構成は以下のとおりである．まず，3 節で，提案手法と解の推定アルゴリズムを詳細に論じる．4 節では，アルゴリズムの挙動を確かめるために行った，数値シミュレーションの結果を報告し，続く5 節では，実データ解析により，提案手法の有用性を実証的に検証する．最後の5 節では，得られた結果を踏まえた，総合的な考察を行う．
本節では，まず，K-平均法の概要とそのアルゴリズムに関して述べる．続いて，クラスタリングを伴うバイプロットの方法と，そのアルゴリズムを提案する．
2.1. K-平均法クラスタリング，あるいは，クラスター分析とは，多変量データで表される個体を，その特徴に従って，少数のクラスターに分類する手法であり，これまで様々な方法が開発されている(Gan,Ma & Wu, 2007; 齋藤・宿久，2006; 足立，2011)．クラスタリングは，その方法論的特徴から，階層的クラスタリングと，非階層的クラスタリングに大別されるが，後者の非階層的クラスタリングの代表的方法として，K-平均法が挙げられる．
ここで，サイズがI（個体）× J（変数）のデータ行列をY = (y′(1), . . . , y′(I))′として，I個体をK (≤ J) 個のクラスターに分類することを考えよう．前述のK-平均法は，最小二乗基準
を最小化する，メンバーシップ行列Mと，セントロイド行列Cを求める手法として定式化されている(MacQueen, 1967; Hartigan & Wong, 1979)．本研究では，クラスターの重心，すなわち，任意のクラスターに属する個体の平均座標値を，セントロイドと呼ぶ．ここで，I × Kの行列M = (mnk) は，各個体のクラスターへの所属を0 か1 で表すメンバーシップ行列であり，第i個体がクラスターk に所属すれば，mik = 1，そうでなければmik = 0 である．さらに，Mの各行の総和は1，すなわち，各行のK個の要素のうち1 つだけが1，それ以外はすべて0 である．このことは，それぞれの個体が単一のクラスターに，必ず所属することを意味する．また，K × Jの行列C = (c′(1), . . . , c′(K))′は，クラスターのセントロイドが，各行に並ぶ行列である．セントロイドとは，その定義から，それぞれが対応するクラスターを代表する点であるので，各クラスターを最も特徴づけるJ個の変数の値として，セントロイドを解釈することもできよう．
(5) の目的関数を最小化するMとCは，以下に述べる，繰り返しアルゴリズムにより得ることができる．
[1] クラスター数を与え，各個体を，ランダムにクラスターに所属させる．
[2] 所与のメンバーシップ行列Mから，Cの第k行c(k) を，クラスターkに所属する個体の重心
により更新する．ここでNk は，クラスターk に所属する個体の総数を表す．すなわちNk =Σimik である．
[3] [2] で求めたセントロイド行列Cから，各個体が，最も近いセントロイドのクラスターに所属するよう，Mを更新する．
[4] (6) の目的関数の変化が小さくなれば計算を終了し，そうでなければ，[2] に戻る．
以上がK-平均法の概要である．
2.2. 提案手法本節では，個体・変数のクラスタリングと，個体クラスター・変数クラスターのバイプロットを同時に行う方法を提案する．
まず，従来のバイプロットにおいて推定対象となるパラメータF, Gを，メンバーシップ行列U(I × K)，V(J × L) と，それぞれのクラスターに対応するr次元空間上の座標が行に並ぶ，クラスター座標行列P(K × r)，Q(L × r) の積に，それぞれ分割，すなわち，F = UP，G = VQとすることを考えよう．ここでU，Vは，各要素の値が0 か1，かつ，行和が1 であるような，(5) のMと同様のメンバーシップ行列であり，Uは，I個体のK (≤ I) 個の個体クラスターへの所属を，Vは，J変数のL (≤ J) 個の変数クラスターへの所属を，それぞれ表す．また，Pの各行には，個体クラスターに対応する座標値が，Qの各行には，変数クラスターに対応するベクトル，つまり，個体・変数クラスターのセントロイドが，それぞれ並ぶ．従って，目的関数
を，(2) にもとづく制約条件
のもとで最小化する，P，Q，U，Vを求め，Pの各行を点として，Qの各行をベクトルとして，r次元空間上にそれぞれプロットすれば，個体・変数の分類と，クラスターのプロットを同時に行うことができる．つまり，提案手法は，従来手法のように「個体」×「変数」のデータ行列のバイプロットを得るのではなく，「個体クラスターのセントロイド」×「変数クラスターのセントロイド」のバイプロットを，後述するtandem analysis とは異なり，直接得る方法である．その結果として，少数の点とベクトルから構成される，単純なバイプロットが得られ，大規模なデータのバイプロットよりも，その解釈が容易になることが期待される．ここで，r は，解の次元数を表し，従来のバイプロットと同様に，通常2 に設定される．さらに，個体クラスターの数Kと，変数クラスターの数Lは，K-平均法と同様に，分析前に設定される．通常のバイプロットにおいて，個体は点として，変数はベクトルとして表現されるが，提案手法により得られるバイプロットでは，点・ベクトルが個体クラスター・変数クラスターにそれぞれ対応する．その意味で，提案手法によるバイプロットは，従来手法により得られるバイプロットを「要約」したものであるものとも言えるだろう．以上が本研究で提案する手法の骨子である．
提案手法を用いずに，まず，従来のバイプロットを行い，点・ベクトルの座標値を求め，それらのクラスタリングを行った後に，クラスター中心のプロットを行なうことで，提案手法と同様のバイプロット，メンバーシップ行列を得ることも可能であろう．このように，ある分析手法の結果に対して，別の分析手法を適用する手法は，tandem analysis と呼ばれている．既に述べたように，バイプロットはデータ行列の主成分分析を行い，解の第1・第2 次元のみをプロットしたものであるが，個体と変数のクラスター構造を決定する要因が，解の第3 次元以降に存在する場合も十分に考えられる．この場合，tandem analysis，すなわち，得られたバイプロットに対してクラスタリングを適用しても，適切な個体・変数のクラスター構造を発見できるとは考えづらい．このように，tandem analysis は，真のクラスター構造を抽出できない，あるいは，推定誤差が累積的に増加してしまうなどの問題点を持つことが，これまで指摘されている(Arabie & Hubert, 1994)．しかしながら，提案手法は，クラスタリングとバイプロットを，1 つの目的関数に組み込み，メンバーシップ行列U,V と，クラスター座標行列P,Q を同時に推定するものであるため，前述のtandem analysis と異なり，より正確なクラスター構造の把握が可能となることが予想される．
2.3. パラメータ推定とそのアルゴリズムまず，P，Q，V を固定して，(7) の目的関数fCB(P,Q,U,V) を，制約条件(8) のもとで最小化するU を求めることを考えよう．このとき，目的関数は
と書き換えることができ，この関数は，メンバーシップ行列をU，セントロイド行列をPQ′V′とした，(6) のK-平均法の目的関数とみなすことができる．したがって，(9) を最小化するUは，前述のK-平均法のアルゴリズムにおいて，セントロイド行列PQ′V′からメンバーシップ行列を推定するステップ，すなわち，2.1 節で述べた，Xに対するK-平均法のアルゴリズムのうち，[3]のステップのみを実行すれば得ることができる．
続いて，P,Q,U を固定し，同じ制約条件のもとでfCB(P,Q,U,V) を最小化するV を求める．(7) の目的関数は，(9) と同様にして
と書き換えられるから，(10) の目的関数を最小にするVは，前述のUに関する最小化と同様に，X′に対するK-平均法のアルゴリズムのうち，セントロイド行列QP′U′から，メンバーシップ行列を推定するステップを実行すれば，得ることができる．
さらに，所与のU,Vのもとで，fCB(P,Q,U,V)を最小化するP，Qを求めることを考えよう．ここで，目的関数は，H = (U′U)−1/2U′XV(V′V)−1/2 を用いて
と書き換えられる(ten Berge, 1993)．(11) の第2，3 項は，パラメータP,Qに関連しない部分であるので，同式の第1 項g(P,Q|U,V) = ||H−(U′U)1/2PQ′ (V′V)1/2||2 を，同じ制約条件のもとで最小化するP，Qを求めれば良い．そのようなP，Qは，特異値分解
を用いて
とすれば得られる(ten Berge, 1983)．ここで，rank(H) = h (≤ min(K,L)) とすれば，K#(K × h)，および，L#(L × h) は，K#′K# = L#′L# = Ih を満たす，特異ベクトルを並べた行列であり，Λ# は特異値が降順対角に並ぶh×h の対角行列である．また，
はK#，L# のそれぞれ上位r 列からなる行列，
はHの上位r個の特異値が降順対角に並ぶr次対角行列である．T(r×r) は，任意の正規直交行列を表す．U′U，V′Vは，各クラスターに所属する個体・変数の総数が対角要素に並ぶ，対角行列であるため，第k個体クラスターに所属する個体の総数をMk = Σi uik，第ℓ 変数クラスターに所属する変数の総数をNℓ = Σj vjℓとすれば，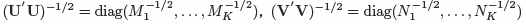
である．従って，いかなる個体・変数も所属しない，空の個体クラスター，変数クラスターが発生しない限り，(U′U)−1/2，(V′V)−1/2 は必ず存在する．なお，本研究では，特別に断らない限り，T = Ir としている．
以上の結果から，以下の交互最小二乗法のアルゴリズムにより，(7) の目的関数を最小化するP，Q，U，V を推定することができる．なお，目的関数の値は常に正，かつ下限は0 であり，さらに，ステップごとに目的関数の値は必ず減少することから，以下のアルゴリズムにより，目的関数の値は必ず収束することが保証される．
[1] P，Q，V に適当な初期値を与える．
[2] X に対するK-平均法において，セントロイドPQ′V′から求められるメンバーシップ行列により，Uを更新する．
[3] X′へのK-平均法において，セントロイドQP′U′から求められるメンバーシップ行列により，V を更新する．
[4] (13) によりP，Q を更新する．
[5] 目的関数fCB(P,Q,U,V) の値の変化が十分小さくなれば，計算を終了し，そうでなければ[2] に戻る．
通常のK-平均法に関しても，たびたび指摘されているように，これまで述べたアルゴリズムは，多くの場合局所解に陥ることが予想される．この問題を回避するためには，複数の初期値から，上記のアルゴリズムを実行し，得られた解の組のうちで，最も目的関数の値を小さくするようなパラメータの組を，最終的な解として採用することが有効であろう．
上のアルゴリズムで用いたK-平均法は，一般に多変量のデータから個体の分類を行うものであるが，その拡張として，個体の分類と変数の分類を同時におこなうクラスタリングの方法が，これまでいくつか提案されている(Hartigan, 1972; van Mechelen, Bock & De Boeck, 2004; )．van Rosmalen et al. (2005) はこれらの諸手法におけるアルゴリズムを概観した上で，局所解の多さを指摘し，手法の比較および，局所解を避けるための方法・アルゴリズムの提案を行なっている．これらの方法は，個体・変数の同時分類を行うという点で，本研究で提案する手法と類似したものであるが，本研究では，バイプロットを要約するという目的で，セントロイド行列の低ランク近似を行なっていること，さらに，クラスタリングとバイプロットを単一の目的関数に統合している点で，他の研究で提案されている手法とは異なることに注意しよう．著者の知る限りでは，提案手法のように，バイプロットと個体・変数のクラスタリングを一つの枠組みで実行するための方法は，これまで提案されていない．
2.4. 提案手法の性質1 節で述べたように，既存手法によるバイプロットでは，変数同士の相関係数が，対応するベクトルのなす角度の余弦によって，さらに，変数の分散がベクトルの長さによって，それぞれ近似されている．一方，提案手法においては，(13) および，(8) の制約条件によって，次式が成り立つ．
行列の積VQ は，各変数が所属する変数クラスターに対応するQ の行，すなわちクラスターの座標値が，行に並んだものである．ここで，データ行列X が列中心化されていることを仮定する．このとき，第j 変数が第ℓ(j) 変数クラスターに所属し，Q の第ℓ 行ベクトルをq(ℓ) と表すものとすれば，上式より，[1] 第j 変数の分散が，所属するクラスターの座標値の平方和，つまり，||qℓ(j)||2 によって近似されていること，[2] 第m, n (m ≠ n) 変数の共分散が，内積qℓ(m)q′ℓ(n) によって近似されていることがわかる．さらに，[1] より，同一クラスターに所属する変数の標準偏差が，そのクラスターに対応するベクトルの長さによって近似されていること，続いて，[2] より，変数同士の相関係数は，それぞれが所属するクラスターに対応するベクトルがなす角度の余弦によって近似されているといえる．なぜならば，(14) より，第j変数が所属する，第ℓ(j) 変数クラスターに対応するベクトルの長さの||qℓ(j)|| について
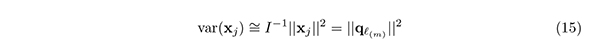
が成り立ち，さらに，第ℓ(m)，第ℓ(n) 変数クラスターベクトルがなす角度の余弦(qℓ(m)q′ℓ(n))/(||qℓ(m)|| × ||qℓ(n)||) について，(14)，(15) より
成り立つからである．これらの性質は，既存手法によるバイプロットと共通するものであり，本論文で提案する手法は，既存手法の延長線上に位置づけられる手法であると理解できよう．
本節では，アルゴリズムの挙動を確認し，提案手法の有用性を検証するために行った，数値シミュレーションの結果に関して報告する．
3.1. シミュレーションのデザイン提案手法による解の再現度と，局所解の発生頻度について評価するために，個体数I を300，変数数J を100，個体クラスターの数K, 変数クラスターの数L を共に4 と定め，以下の流れで人工データを生成した．まず，300 個体，100 変数を，それぞれ4 つのクラスターへランダムに所属させ，メンバーシップ行列U，V の真値，UT ，VT を定めた．続いて，次の行列PT ，QT
を，クラスター座標行列P，Q の真値として定めた．PT の第k 行ベクトル
は，第k 個体クラスターのセントロイドを，QT の第ℓ 行ベクトル
は，第ℓ 変数クラスターのセントロイドを，それぞれ表す．また，第i 個体の所属する個体クラスターを第OC(i) クラスター，第j 変数の所属する変数クラスターを第VC(j) クラスターと表す．さらに，i = 1, . . . , I について，第i 個体の所属するクラスターに対応するセントロイド，つまり，PT の第OC(i) 行ベクトル
を平均とした，2 変量正規分布
から，2 次元ベクトルfi を発生させた．同様に，j = 1, . . . , J について，第j 変数の所属するクラスターに対応するセントロイド
を平均とした，
から，2 次元ベクトルgj を発生させた．ここで，σ2 はクラスター内でのばらつきを表す定数である．以上の手続きの後，
として，これらの各行を2 次元平面上にプロットすれば，300 個体，100 変数が，PT ，QT の各行を中心として，それぞれ分散σ2 でばらつくようなバイプロットを得ることができる．さらに，各要素が標準正規分布に従う誤差行列E(300 × 100) をランダムに発生させた上で
として，誤差を加えた人工データ行列X を生成した．ここで，θ(ρ) は
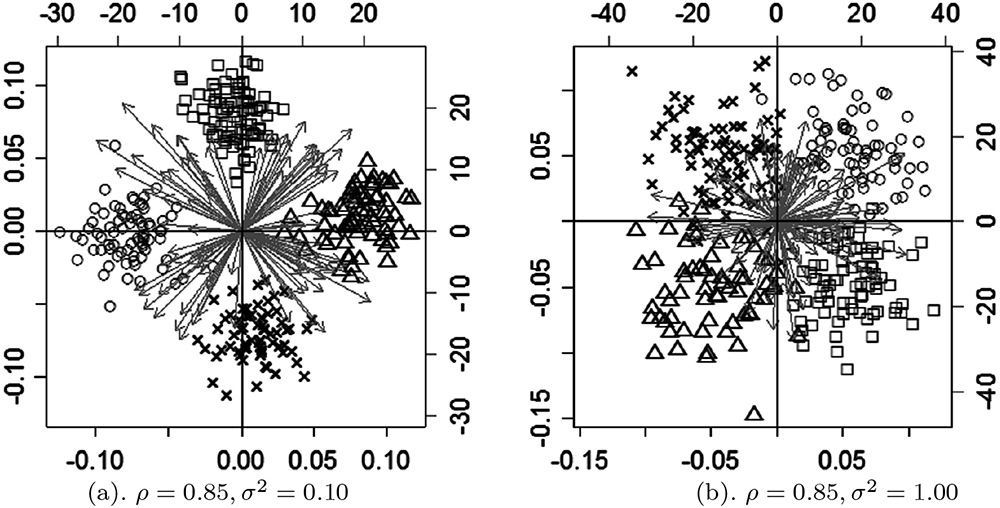
を表し，誤差の水準を意味する(Adachi，2009)．ρ は0 ∼ 1 までの値を取り，1 ならばデータの分散が完全にモデルUTPTQ′TV′T の分散に等しいことを，0 ならばデータの分散が誤差の分散に等しいことを表すため，ρ の値により，データに含まれる誤差の相対的な大きさを調整することが可能である．図2 には，人工データのバイプロットの例を示した．なお，図2 中では，個体に関して，それぞれの個体が所属する真のクラスター毎に点のシンボルを変えて表示している．
クラスター内分散σ2 = 0.01, 0.10, 1.00，および，分散説明率ρ; = 1.00, 0.85, 0.70 を組み合わせた，3 × 3 = 9 通りの各条件において，これまで述べた手続きにより，X を100 個ずつ発生させ，それぞれに提案手法，および，2.2 節で述べたtandem analysis をそれぞれ適用した．提案手法に関しては，1 つのX に対して，2.3 節で述べたアルゴリズムを，P, Q,U, V の初期値を変えながら10 回実行し，10 組の解 S1 = {P1,Q1,U1,V1}, . . . , S10 = {P10,Q10,U10,V10} を得た．これらの解のうち，(5) の目的関数を最も小さくする解の組を，最終的な解として採用した．さらに，採用された解の組をSs = {Ps,Qs,Us,Vs} とすれば，fCB(Ss) < fCB(Si) を満たす解の組Si を，局所解とみなして，その発生回数を数え上げた．
さらに，次の手続きにより，それぞれの解の再現度を評価した．まず，メンバーシップ行列U，V に関する解の再現度の指標として，付録A に示す手順により，正分類率を求めた．ここで用
いた正分類率は0 から100 までの値を取り，値が高ければ分類の精度が高いことを表す指標である．また，次式で表される，任意のm×n 行列WT ，Wの類似度を評価する関数，StandardizedSimilarity (Adachi, 2011)
を用いて，SS(PT ,P)，SS(QT ,Q) により，クラスター座標行列P,Q の再現度を評価した．ここで，
であり，SS(WT ,W) は，0 ∼ 1 までの値を取る．また，上の関数は，WT = Wのとき，上限1 を達成する．ただし，(13) に示すように，P とQには，正規直交行列T による回転の不定性が残るため，P とQ の再現度を適切に評価するためには，何らかの基準でT を決定した上で，SS(PT ,P)，SS(QT ,Q) を評価しなければならない．そこで，本研究では，付録B に示す方法によりT を推定し，解の再現度の評価を行った．
提案手法とtandem analysis に関して，各条件で得られた100 組の解についての，正分類率の25，50，75 パーセンタイルを表1 に，P 再現度(SS(PT ,P))，Q 再現度(SS(QT ,Q)) の25，50，75 パーセンタイルと局所解発生数の平均値を表2 に，それぞれ示す．
表1，2 を見ると，ρ の値が大きい時，すなわち誤差が小さい場合に，非常に高い精度での分類，解の再現が達成されていることがわかる．σ2 の値が増大，つまり，クラスター内の個体・変数のばらつきが大きくなるに従って，正分類率は若干低下するが，最もσ2 が大きい水準でさえも，6 ∼ 7 割程度の高い分類精度が観測された．このことから，クラスター内のばらつきが大きい，いいかえれば，データのクラスター構造がはっきりしない場合であっても，高精度な個体・変数の分類が可能であることが推察される．一方，P，Q の再現度は，ρ の減少に伴って減少し，
その減少の程度は，σ2 が大きくなればなるほど，大きくなることが見て取れる．σ2 が最も大きく，ρ が最も小さい水準であっても，P，Q の再現度は0.7 程度であり，解の再現性は良好であるといえよう．
特筆すべきは，局所解の平均発生数が，σ2 = 0.1，すなわち，クラスター内のばらつきが中程度の場合に最も小さくなり，それ以外の水準ではほぼ同等であることである．つまり，クラスター内の分散が小さいと，かえって局所解が頻発する．このことは，一見不自然な結果のように思われるが，以下のように説明することができる．K-平均法では，各個体をクラスターにランダムに所属させ，そのメンバーシップ行列を初期値として，アルゴリズムをスタートする．従って，K-平均法の計算結果は，当然この初期値に大きく依存する．もしも，真のクラスター内のばらつきがあまりにも小さく，かつ，メンバーシップ行列の初期値が真値と異なれば，初期値から計算されるセントロイドが真のセントロイドから大きくずれ，結果として局所解に陥りやすくなるであろう．ランダムに生成されるメンバーシップ行列の初期値が，真値と一致することはほぼ無いため，σ2 の値が最も小さい時に，局所解が多く発生したと考えられる．しかしながら，たとえ局所解が多くても，分類率，解の再現度は，上で述べたように，クラスター内分散σ2 が大きく，分散説明率ρ が小さい場合でも，ある程度良好であることから，提案手法によって得られた最適解は有用なものであるといえよう．
一方，tandem analysis の結果に関しては，ほぼすべての条件において，提案手法の結果を下回る正分類率，P およびQ の再現度が観測された．表1 に示す正分類率は，多くの条件において提案手法と同等あるいは若干下回る程度の分類精度であったが，表2 に示す，解の再現度に関しては，すべての条件において，再現精度が提案手法と比べ大きく劣っていることが見て取れる．この結果から，tandem analysis は，個体と変数の分類については提案手法に若干劣るだけの性能を有するものの，個体・変数クラスターの付置の推定精度は非常に劣ること，すなわち，バイプロットの要約という側面から評価すれば，提案手法はtandem analysis の性能を大きく上回るものであると結論付けることができる．
以上の数値シミュレーションとその結果の考察から，提案手法の有用性とアルゴリズムの挙動の性質，さらに，提案手法がtandem analysis を上回る性能を有することが，実証的に検証された．
本節では，提案手法の有用性を実証的に検証するために行った，提案手法による実データ解析の結果を報告する．
解析にはUCI Machine Learning Repository (Frank & Asuncion, 2010) に収蔵される，ワイン評定データを用いた．このデータは，ワインA・B・C の3 種のワインのうちいずれかからサンプリングされた，178 個のサンプルに対して13 の化学的特性を測定したものであり，データは178（サンプル）×13（変数）の行列となる．図3(a) には，1 節で述べた方法により，データ行列をそのままバイプロットした図を示す．ここで，図3(a) において各個体は×として表現されている．なお，個体と変数の同時布置を得る方法として，多次元展開法(Coombs, 1950) を用いることもできるが，計算の過程で非線形計算を含み，特に大規模データに対しては高い計算負荷が予想されること，さらに，モデルの数学的簡素さを重視し，バイプロットによって布置を得ることが適切であろうと判断した．このデータの個体数・変数数はそれほど多いものではなく，図3(a)に示すバイプロットをそのまま解釈しても，大きな問題はないと思われるが，提案手法の適用によって，バイプロットと，個体と変数のメンバーシップを組み合わせた，従来手法では行えない解釈ができることを，以下の解析例で例証する．
分析に先立って，個体クラスターと変数クラスターの個数を指定する必要があるが，178 個のサンプルが，3 種類のワインのうちいずれかからサンプリングされたものであることとに注目して，個体のクラスター数を3 に設定した．データには，それぞれのサンプルがどのワインからサンプリングされたかを示す変数が，あらかじめ含まれているため，分析後の個体メンバーシップU と，サンプリング元を表す変数を照合することによって，個体分類の正しさを検討することが可能である．また，図3(a) から見て取れるように，各変数を表すベクトルが，大きく分けて3 つのグループに分けられることから，変数クラスターの個数を3 に設定した．
上記の事実から，個体・変数クラスターの個数をそれぞれ3 個に設定し，上で述べたデータに対して提案手法を適用した結果を，図3(b) に示す．図3(b) においてOC は個体クラスターを，VC は変数クラスターをそれぞれ表す．図3(b) を見ると，個体・変数がそれぞれ3 つのクラスターに分類されてプロットされているため，図3(a) よりも個体と変数の関係性が直感的に把握しやすくいバイプロットが得られていることがわかる．
ここで，変数のメンバーシップ行列V から，それぞれの変数クラスターを構成する変数は，第1 変数クラスターは，リンゴ酸・ソーダ灰のアルカリ度・非フラボノイド石灰酸の3 変数，第2 変数クラスターは，アルコール濃度・ソーダ灰・マグネシウム・色の強さ・プロリンの5 変数，第3変数クラスターは，石灰酸の総量・フラボノイド・プロアントシアニジン・色調・DNA 濃度の5変数であった．この結果は，図3(a) において視認できる変数クラスター構造・変数メンバーシップと大きく矛盾しない．．
変数は次の通り：アルコール濃度(Alc)，リンゴ酸(MAc)，ソーダ灰(Ash)，ソーダ灰のアルカリ度(AA)，マグネシウム(Mg)，石灰酸の総量(Phe)，フラボノイド(Flv)，非フラボノイド石灰酸(NP)，プロアントシアニジン(ProA)，色の強さ(Col int)，色調(Hue)，DNA 濃度(DNA)，プロリン(Pro)．
また，各サンプルのサンプリング元と個体のメンバーシップを照合し，各個体クラスターに分類されたサンプルを，そのサンプリング元に従って集計した結果を表3 に示す．表3 から，ワインA が第3 個体クラスターに，ワインB が第2 個体クラスターに，ワインC が第1 個体クラスターにそれぞれ対応し，各サンプルの分類が非常に高い精度で達成されていることが見て取れる．
以上の事実を考慮して，個体クラスターと変数クラスターの関係性を，2.4 節で述べた提案手法の性質を踏まえた上で，図3(b) に示されるそれらの付置から考察すれば，以下のような解釈が可能である．まず，第1 個体クラスターと第3 個体クラスターにそれぞれ対応する，ワインC とワインA は，正反対の化学的特性を有するワインであることが推察される．なぜなら，図3(b)にプロットされる第1・第3 クラスターの中心(OC1・OC3) は，第2 変数クラスターに対応するベクトル(VC2) を挟んで対極に位置し，かつ，OC1 側には第1 変数クラスターのベクトル(VC1) が，OC3 側には第3 変数クラスターのベクトル(VC3) が，ほぼ正反対の方向に位置しているためである．また，VC2 はVC1，VC3 とほぼ直交していることから，第2 変数クラスターは，その他の変数とは無関係な化学的特性を反映する変数によって構成されていることが推察される．このことから，ワインB は，ワインA とC とは全く異なる化学的特性を持ち，第2変数クラスターに所属する変数の「値の小ささ」によって特徴付けられるワインであると推測できる．一方，ワインA とC は，第2 変数クラスターに所属する変数に対して一定の値を示しつつも，その他の変数に関しては正反対の値を示すワインであるともいえるだろう．以上のような解釈は，提案手法の適用によって，単純で解釈のしやすいバイプロットのもとでしか行うことのできないものである．このことから，提案手法によってバイプロットの効果的な要約が確かに行えることと，その有用性が例証された．ここでは比較的小さなデータセットを用いた適用例を紹介したが，大規模なデータに対して提案手法を適用すれば，その有用性はより顕著になるであろう．
本研究では，個体・変数が多いデータのバイプロットを要約して表示する手法として，個体・変数のクラスタリングと，クラスターのバイプロットを同時に行う方法を提案した．数値シミュレーションの結果，提案手法は，多くの状況において，高精度な分類，良好な解の再現が可能であることが実証された．また，実データの解析例から，多くの個体・変数からなるデータのバイプロットを，提案手法によって，効果的に要約できることが例証された．
本研究では，バイプロットとして，(4) で表されるバイプロットを採用しているが，一般に(3)の特異値分解が与えられたとき，t を任意の定数として
とすることで，F ならびにG をΛr によって様々にスケーリングしたバイプロットを得ることも可能であり，(21) においてt = 0 としたものが(4) である．この場合に限り，ベクトルの長さが変数の標準偏差に，2 つのベクトルがなす角度の余弦が変数同士の相関係数に対応する．また，t = 1 とすれば
となり，この場合，X の各行における分散が各点から原点までの距離に，各行の相関が各点と原点を結ぶ直線がなす角の余弦に対応する．本研究では，主成分分析との関連と，変数の相関構造の把握を重視して，t = 0 としたバイプロットを採用しているが，分析者が，変数の相関構造の把握を主眼に置いて分析を行う場合には，t = 0 と定めたバイプロットを得るのが適切であるし，むしろ個体どうしの相関に関心がある場合には，t = 1 と定めた(22) のバイプロットを得るのが適当である．このようにt の値の選択は，分析者がデータの何に主眼を置くかに依存する．また，提案手法に関しても，制約条件を適切に変更した上で，(13) において
として，分析者の関心に応じた，様々な性質を持つバイプロットを得ることも可能である．提案手法に関して，
によるスケーリングを様々に変えた種々のバイプロットの性質を検討することも，今後の重要な課題である．
D = PQ′とすれば，(6) はfCB(U,D,V) = ||X − UDV′ ||2 であり，この最小二乗基準は，データ行列X(I × J) を，メンバーシップ行列U(I × K),V(J × L) と，階数r の行列D(K × L)の積によって近似するための基準であるとも見なせる．したがって，提案手法によって得られた解を用いれば，fCB(U,D,V) を最小化するという意味において最適な，X ≅UDV′という行列の近似を行うことができる．この行列近似，あるいは分解が，X の特異値分解X = KΛL′と異なる点として，[1] U，V がメンバーシップ行列であること，[2] （K ≠ Lのとき）Dは一般に対角行列ではなく，階数がr の行列であること，[3] X の近似精度を決める値が，特異値分解ではK の列数（あるいはΛ の階数，L の列数）のみであるのに対し，提案手法では，K,L, r の3 つ存在すること，の3 点があげられる．このような行列の近似の方法は，これまで提案されておらず，その性質を詳細に検討することも興味深いテーマのひとつである．
4 節の実データ解析において，個体クラスターと変数クラスターの個数を設定する際に，個体・変数に関する付加的な情報を用いてクラスター数を定めたが，そのような情報が利用できない場合も多いであろう．そういった場合には，まずクラスター数を多めに設定し，各クラスターに所属する個体あるいは変数の数に，大きなばらつきが出なくなるまでクラスター数を減らして，最適なクラスター数を探索する方法をとることも考えられる．ただし，どのクラスター数から出発して探索を行うか，あるいは，クラスターサイズのばらつきがどの程度小さくなれば探索を終了するかなどに関しては，分析者の主観に依存する部分が多く，この方法の妥当性には疑問が残る．クラスター数とは，データに対しての分析者の仮説を反映するものであるため，その決定には何らかの客観的判断が必要不可欠である．従って，今後の課題として，クラスター数K，L をも同時に推定する新たなアルゴリズムや，クラスター数決定のための指標を開発することが有効であろう．クラスター数をいかにして定めるかという問題は，本研究で提案する手法にとどまらず，非階層的クラスター分析に関わる様々な手法に共通する問題であるため，この問題を解決するためのさらなる研究が今後望まれる．
また，3 節の数値シミュレーションの結果からも明らかなように，提案するアルゴリズムの特性の1 つとして，多くの場合，局所解に陥る可能性が高いことが挙げられる．この点に対応するために，2 節では，多くの初期値から出発し，得られた複数組の解のうちから最も目的関数の値を小さくするものを，最終的な解として採用する方法を提案した．数値シミュレーションにおいては，この方法を用いて，10 個の初期値からアルゴリズムをそれぞれスタートさせ，その結果として，真値の高い再現性が確認されている．この事実から，複数個の初期値から計算を開始する方法が，局所解を避けるために十分有効である事が推察される．もしも初期値の個数を10 個からさらに増やせば，より高い解の再現率が観測されるであろうが，それに伴う計算コストの増大が懸念される．また，反対に初期値が少なすぎれば，計算コストは減少しても，かえって局所解に陥る可能性が高くなる．そのため，少なすぎず多すぎない，合理的な初期値の個数を設定する必要性が生まれるが，この点に関しては，これまでのところ，経験的な視点から判断をせざるを得ない．そこで，多くの初期値から出発する事に加えて，局所解を避けるK-平均法のアルゴリズム(Rose, Gurewitz & Fox, 1990; Krishna & Murty, 1999) を採用した新たなアルゴリズムを開発することや，通常のバイプロットの結果にクラスタリングを適用して得られる，tandem analysisの解を初期値として，計算をはじめることなどが有効であると考えられる．局所解を避けるための一連の方法を開発するにあたっては，van Rosmalen et al. (2005) による各種アルゴリズムの比較検討が大きな示唆を与えるであろう．
本研究では，個体と変数を分類する方法としてK-平均法を用いたが，その拡張として，ファジィK-平均法(Zadeh, 1965; Bedzek, 1981) を用いて，個体・変数のファジィなメンバーシップを得る方法を開発することが，今後の拡張として考えられる．K-平均法が，非所属を意味する0 と所属を意味する1 の二値変数によって，クラスターへの所属を表現するのに対し，ファジィK-平均法では，0 ∼ 1 までの連続量によって所属を表現する．つまり，メンバーシップ行列に対して「各要素は0 か1 の二値変数」と制約を課したものが，K-平均法であり，その制約を緩め，「メンバーシップ行列の要素が0 ∼ 1 の値を取り，かつ行和が1」としたものがファジィK-平均法である．従って，ファジィK-平均法とは，K-平均法の一般化であり，ファジィK-平均法による提案手法の拡張は，提案手法の一般化として位置づけることが可能である．ただし，ファジィK-平均法の目的関数は，一般に，（5）のような行列表記によって書き表すことができないため，2.3 節で述べたパラメータ推定のアルゴリズムをそのまま用いることはできない．従って，ファジィなメンバーシップを得るためには，3 節で述べたアルゴリズムではなく，その一般化であるような，新たなアルゴリズムを開発することが必要である．ただし，たとえそのような拡張的方法が開発されたとしても，得られたファジィなメンバーシップ行列を，すべての個体・変数について解釈することは難しいため，この拡張が実際に適用可能な状況は，限定的であろう．
ここでは，3 節の数値シミュレーションにおいて用いた，足立(2011) による正分類率の算出方法に関して説明する．
I（個体）×J（変数）のデータ行列X の各個体を，個体数I よりも少ない数のK クラスターに分類する状況を考える．I × K のメンバーシップ行列の推定値をM，その真値をMT で表せば，trM′TMは，正しく分類された個体数の合計を表す．しかし，解の第k クラスターと真値の第kクラスターが，必ずしも一致するとは限らない．例えば，K = 2 のとき，Mの第1 列がMT の第2 列に，Mの第2 列がMT の第1 列に，それぞれ対応する可能性もあるだろう．一般に，クラスタリングにおいて，それぞれのクラスターに所属する個体さえ変わらなければ，クラスターのラベルを入れ替えたとしても，解の意味は変わらない．特にK-平均法に関して，各行に1 つだけ1 が並び，それ以外の要素はすべて0 である，K× K の置換行列R (例えば，Harville, 1997)を用いれば，(6) に示すK-平均法の目的関数を次のように書き換えることができる．
ここで，M∗ = MR，C∗ = R′C である．すなわち，K-平均法には，メンバーシップ行列Mに関する列置換の不定性が存在する．したがって，正分類率を適切に算出するためには，MとMTではなく，Mの各列を適切に入れ替えて，M，MT の各列が同じクラスターを表すようにMの各列を適当に入れ替えた，MRとMT を比較する必要がある．
Mの列置換を行うRは，次の手続きで求めることができる．まず，真のクラスターのセントロイド行列を，CT (K× J) で表す．つまり，CT = (M′TMT )−1M′TXである．同様に，解のクラスターのセントロイド行列をC (K× J) とすれば，C = (M′M)−1M′Xである．ここで，Mの列置換に伴い，解のセントロイド行列は，(R′M′MR)−1R′M′X= R′ (M′M)−1RR′M′X= R′Cと変化するが，このR′C がCT を最もよく近似するとき，すなわち，解のクラスターのセントロイドと，真のクラスターのセントロイドが最も近くなるときに，MT の各列に対応するように，正しくMの列置換が行われていると考えられる．したがって，すべてのK × K 置換行列の中で，||CT − R′C||2 を最も小さくするようなRによって，Mの列置換を行えばよい．クラスター数が4 の時，すべての4 × 4 置換行列は，高々4! = 24 通りであるので，そのすべての置換行列をそれぞれ考慮することにより，R は簡単に求めることができる．
以上のようにRを求め，RによってMの列置換を行ったMRとMT を比較することによって，次のように正分類率CC(M,MT ) を算出する．
つまり，正しく分類された個体数trM′TMRを，全個体数I で除したうえで，百分率に変換した値が，正分類率である．ただし，この値は0 ∼ 100 までの値を取り，MR = MT ，つまり，完全に正しい分類が行われたとき，上限100 を達成する．
B. (13) のTの推定方法(13) に示されるように，提案手法で推定されるP とQ には，r × r 正規直交行列T による回転の不定性が存在する．そのため，3 節の数値シミュレーションにおいては，P，Q とそれらの真値PT ，QT を比較する際に，T を適切に推定したうえで，両者の比較を行わなければならない．そこで，本研究では，次の目的関数
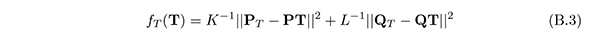
を最小にするように，すなわち，真値PT ，QT と推定値P，Q とを最も近づけるように，T を定めた．
(B.3) の基準は，次のように書き換えることができる．
ここで，const とは，T に関係のない項をまとめたものを表す．従って，fT (T) の最小化は，gT (T) = tr(K−1P′TP + L−1Q′TQ)T の最大化と同等である．K−1P′TP + L−1Q′TQ の特異値分解を
と定義すれば，ten Berge (1983) より，gT (T) を最大化する，つまり，fT (T) を最小化するT は次式で与えられる．
ここで，K∗，L∗ は，左特異ベクトル，右特異ベクトルがそれぞれ並ぶ行列であり，Λ∗ は，降順に特異値が並ぶ，対角行列である．3 節においては，まず，提案手法によりP とQ を求めた上で，(B.6) によってT を推定し，P とQ の右側からT をかけた，PT とQT を，それぞれの真値と比較することにより，解の再現度を算出した．
