2016 Volume 5 Issue 1 Pages 27-47
本研究は，多重対応分析（MCA）の解を，斜交回転した負荷行列を生み出す主成分分析（PCA）の結果として解釈可能な形に変換するための一方法を提案する．MCAの各変数に対応する個別数量化得点を正規直交化することにより，MCAの定式化がPCAのそれに変換される．さらに，カテゴリーに付与される重みの不定性を利用して，正規直交多項式による数量化を行い，得られた変量に回転をともなうPCAを適用する．以上の手続きは，MCAに対して許容される変換の範囲にあることが示される．実データの分析を通じて，Likert尺度の通常の用法について一定の正当性が示されるとともに，評定尺度に関する新たな情報を引き出す可能性が示される．
We proposed a method for transforming solutions provided by multiple correspondence analysis (MCA) to the form of principal component analysis (PCA) to justify the exploratory factor analysis of Likert-type items, and to extend it. We began by reformulating MCA as the maximization of the sum of variances of quantified variables, defined as the sum of quantified scores for each categorical variable. Next, we obtained a PCA formulation that yielded the same quantified scores as did the MCA through orthonormalizations of quantified scores by singular value decomposition of each block of a matrix of quantification weights. Owing to entire indeterminacies under orthonormal transformations of quantified scores for each variable, we proposed a way of providing metrics to ordered categories by orthonormal polynomials. We also proposed a method for computing a component pattern matrix after rotating a matrix of weights for PCA. The method can be viewed as Harris-Kaiser's independent cluster rotation. Finally, we demonstrated the application of the proposed procedures and interpreted the output using a real data set consisting of university student responses to Likert-type items asking experiences of positive and negative emotions in academic situations.
順序のあるカテゴリーという択一型の選択肢をもつ複数の質問項目への反応から，比較的少数の個人差測定尺度を，カテゴリーコード（整数）の単純和によって求める方法は，その創始者にちなんでLikert 尺度と呼ばれる( Likert, 1932)．特に，（広義の）探索的因子分析（exploratory factoranalysis; EFA）によって質問項目を分類し，複数の尺度を定義する手続きは，その簡便さと有用性から，主に心理学研究において広く用いられてきた．
他方，「Likert 尺度は，数値として扱うべきでない評定尺度を，量的変数として扱っている」という趣旨の批判が常にあった（たとえば， 西里, 2010）．その問題に対応する方法の1 つが多重対応分析（multiple correspondence analysis; MCA）である．しかしながら，EFA とMCA の結果は，見かけ上著しく異なっており，研究目的から考えるとき，後者は前者の代用にはなりえないという理解が，経験的に共有されてきた．その一因として，MCA では結果のグラフィカルな表示が重視される結果，2 次元を超える解を求めたり解釈したりすることが必ずしも容易でないことがあげられる．また，馬蹄現象（たとえば， Gifi, 1990）に代表される余剰次元の出現も問題になる．
以上のような背景のもとに，Likert 尺度の新しい分析方法を開発し，それを実データに適用して一定の実用性を確認するとともに，上記の問題点を克服した上で，従来の方法によっては得られなかった情報を得る可能性を検討することが，本研究の目的である．
その目的を達成するために，正規直交多項式主成分分析（orthonormal polynomial principalcomponent analysis; OPPCA）と呼ぶ方法を開発した．開発の手順は以下の通りである．
① 開発の準備として，順序制約条件を課さない通常のMCA を再定式化する．
② MCA の解法の中核となる基準化Burt 行列の固有値分解に，自明解の存在と，それにともなう重み行列の項目ごとの中心化という性質があることを確認する．
③ MCA の重み行列を項目ごとに，カテゴリーの数量と数量化得点算出のための重みに分解する．カテゴリーの数量を用いて得られる相関行列は，基準化Burt 行列と同じ固有値をもち，MCA は主成分分析（principal component analysis; PCA）の手続きに還元できることが示される．実際，PCA による主成分得点は数量化得点と一致する．
④ その際，カテゴリーの数量は中心化され相互に直交している限り，全く任意であることが導かれる．解を一意に定め，解釈を容易にするために，カテゴリーコードを数値として扱う正規直交多項式によって重みを定める．
⑤ 重み行列を単純構造に向けて回転する．回転された重み行列を用いて得られる主成分得点とその間の相関行列，およびパターン行列ならびに関連する統計測度を求める．
以上の提案の多くは，先行研究の延長線上にある．MCA をPCA の発展として定式化する試みには，たとえば， 足立・村上(2011) の成分負荷基準があるが，ここでは，それとは異なる定式化を用いる．MCA の解をPCA に変換した際の，カテゴリーの数量の任意性については，著者の知る限りそれを指摘した文献はない．ただしこの手続きを，後述する正準相関分析の一般化と見れば，自明の事実であるとも言える．MCA への直交多項式の適用については， Lombardo & Meulman (2010)， Lombardo & Beh (2010) がある．しかし，彼らの手続きでは，MCA の最適解としての性質は失われている．他方，量的変数を多項式変換してPCA を行うことは古くから行われており，これらは近年のKernel 主成分分析などにも引き継がれている（たとえば， Izenman,2008）が，いずれもMCA との関連を論じるものではない． ⑤で採用される回転方法は，直交回転による斜交回転（ Harris & Kaiser, 1964），あるいは，独立クラスター回転（ Kiers & Ten Berge,1994）として知られている．
本研究は，あくまでもMCA の解に対して許容される範囲の変換によって，PCA としての扱いと解釈を可能にするものである．すなわち，OPPCA は，MCA の固有値や数量化得点を不変に保ったまま，EFA としての特徴をもたせた手続きである 2 ．
次の節ではまず，実データにもとづいて，MCA とEFA の解が一致しないとはどのようなことかを例示する．
大学生に対するつぎのような質問項目への回答を考える（ 鈴木，2009）．「あなたは，過去3 ヶ月の間に，以下の感情を学業の場面でどのくらい経験しましたか？ それぞれ最もあてはまると思う数字を，○印で囲んでください．」という教示の後に，(1) うれしい気持ち，(2) 満足な気持ち，(3) ∗ いらいらした気持ち，(4) 楽しい気持ち，(5) ∗ 心配な気持ち，(6) 面白い気持ち．(7) ∗ 悲しい気持ち，(8) 充実した気持ち，(9) ∗ 憂うつな気持ち，(10) 安心した気持ち，(11) ∗ 満たされない気持ち，(12) ∗ 腹立たしい気持ち，の12 項目をならべる（番号に*印のついたものはネガティブ感情，印のないものはポジティブ感情である）．各項目に，「5. とてもよく感じた」，「4. かなり感じた」，「3. 少し感じた」，「2. あまり感じなかった」，「1. 全く感じなかった」の5 件法で回答を求める．
これを490 名の大学生に実施し，欠損値のない459 名のデータをMCA によって分析した結果が図 1 である．数量化行列の要素（重み）も数量化得点も，ともに横向きの2 次関数状を呈している．数量化重みについては，項目ごとに，5 件法の評定値を線でつないでいる．☆はポジティブ項目，□はネガティブ項目である．第1 軸（横軸）の高得点側には1 と5 という極端な反応が，低得点側には，4，3，2 といった中間的な評定値が集まっている．第2 軸は上方にポジティブな反応（ポジティブ項目への5，ネガティブ項目への1），下方にネガティブな反応（ポジティブ項目への1，ネガティブ項目への5）が布置している．あえて解釈すれば，第1 軸は，反応が極端か控えめかという対象者の（質問内容とは無関係な）反応の構え(Cronbach, 1946) を，第2 軸は，ポジティブ感情の多さとネガティブ感情の少なさを1 つの次元であらわしている．こうした2 次関数状の布置が，馬蹄現象と呼ばれるものである．
次に，5 つの反応選択肢につけられた，5，4，3，2，1 というカテゴリーコードをそのまま数値とみなしてPCA を行い，さらに直交回転（Varimax 回転）を行った結果を図 2 に示す．左は，負荷量，右は対応する主成分得点である．第1 主成分（横軸）はポジティブ感情，第2 主成分（縦軸）はネガティブ感情の諸項目が高く負荷しており，負荷行列は，ほぼ完全な単純構造を示している．主成分得点には，馬蹄現象は見られず，2 変量正規分布とみなしても大過ない結果である．
図 2 のような分析は，名義尺度，あるいは，順序尺度にすぎないものを間隔尺度として扱っているとして，MCA 等，非計量的方法の提唱者・支持者から非難されることが多い．しかし，図 2 左のような単純構造を実現した負荷行列から，項目をポジティブ感情測定項目とネガティブ感情測定項目という2 つの群に分け，そこから（多くの場合，カテゴリーコードの単純和による）得点を作った上でさらに他の変数との関連を分析するといった手続きによって，心理学的個人差研究は多くの成果をあげてきたのも事実である．その点では，「正しい」方法としてのMCA によって図 1 のような結果を得て，大いに失望した心理学研究者は多いと思われる．同一のデータを分析していながら，このような差異が生じる理由を解明することが，以下の議論の1 つのモチベーションとなっている．
n 人の対象者に p 個の項目からなるLikert 型評定尺度の選択肢を付した質問をすることによって得られた反応を考える．すべての質問に共通の反応カテゴリー数を c (≥ k 番目の質問項目への全回答者の回答を要素とするカテゴリカル変数を x k と書き，それを横に並べてできる n × p の行列を
と書く．各カテゴリーには，連続する自然数（カテゴリーコード），1, 2, . . . , c を与えるが，当面これらの数値は，選択肢を区別するための単なる記号であり，これらの間では，演算はもとより，大小関係の判断も行えないものとする（名義尺度）．すべてのカテゴリー数の総和は pc である．また，すべてのカテゴリーに最低1 人の反応はあるものとする．
各カテゴリカル変数 x k について， n × c のダミー変数行列 G k を定義する．この i 行 j 列要素 g ijk は，以下のように定義される．
行列 G k から次を定義する．
ここで，1
n
はすべての要素が1 であるような
n
次元ベクトルであり，したがって，
d
k
の要素はk番目の質問項目の各カテゴリーへの反応数である．なお，
でもある．また，
G
k
,
D
k
,
d
k
については，以下の性質も随時利用される．
各ダミー変数に対して c × r の数量化行列 V k を定義し，
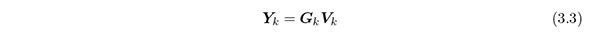
によってカテゴリカル変数 x k を r 次元の量的変数に変換する．本論文では， Y k を（項目ごとの）個別数量化得点行列と呼ぶ．ここで， r は数量化の次元である．これらをすべての項目にわたって合計して得られる n × r の行列，
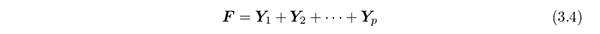
を，全体数量化得点行列と呼ぶ．伝統的なMCA の定式化（たとえば，
Greenacre, 1984）では，これを
で割ったものが用いられるが，ここでは，後に変換の結果得られるPCA による得点とスケールを一致させるため(3.4) の定義を採用する．
とすると，
となる．なお，
とする．ここで，次の性質も後に利用される．
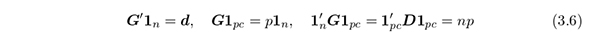
G k1 c = 1 n という性質から， G のランクは高々 p ( c − 1) + 1 であるが，簡単のため， n は pc と比較して十分大きく， G のランクは p ( c − 1) + 1 を下回らないものとする．
次に，MCA の最適化基準と制約条件について確認する．制約条件は，項目ごとの数量化得点
Y
k
に対して設定される．第1 の制約条件は，各列の和を0 とする（中心化）．つまり，
であるが，
だから，
である．第2 の制約条件は，全項目を通しての平均積和行列（制約条件(3.7) が成り立てば共分散行列）について，対角要素（分散）が1 で直交するというものである．
であることから，第2 の制約条件は，次のようになる．
また，最適化基準は，全体数量化得点行列 F の各列の分散の総和，すなわち(3.5) から，
の最大化である．ここで，右辺にあらわれる G′ = B という行列は，創始者の名前にちなんでBurt 行列と呼ばれている．こうして最大化基準は次のようになる．
式(3.8) の下で(3.9) を最大化する解は，一般化された固有方程式
から得られるが，
D
−1/2
が正定値行列なので，これは基準化されたBurt 行列と呼ばれる非負定値行列
D
−1/2BD
−1/2
の固有値分解に帰着する（たとえば，
Gower & Hand, 1996
）．
ここでは，行列 D −1/2BD −1/2 には，自明解と呼ばれる特別な固有値と対応する固有ベクトルが存在するので，それを取り除いて考える必要があること，および，それと関係するが，同じ行列の固有ベクトルに特殊な性質があることを述べた上で，MCA の解法を示す．
まず，次のような c 次元の列ベクトルを考える．
これは，項目k の各カテゴリーへの反応数の平方根からなるベクトルである．これを，全項目についてならべた pc 次元ベクトル，
を行列 D −1/2BD −1/2 に掛け，(3.6) を用いて変形すると，
となる．すなわち， s は行列 D −1/2BD −1/2 の固有ベクトルの1 つであり，対応する固有値は p であることがわかる．これから求められる数量化重みベクトルは，後に見る(3.14) を適用すると，すべての個体の全体数量化得点が一定値p となるという無意味なものであり，自明解と呼ばれる（たとえば， Greenacre, 1984）．さらに， p は D −1/2BD −1/2 の最大固有値であることが証明される( Gower & Hand, 1996)．そこで，基準化されたBurt 行列の第1 残差行列 S は，(3.10)から s′ = np であり s に対応する固有値が p であることから，
となる．以後はこの p ( c − 1) × p ( c − 1) の非負定符号行列 S の固有値分解，
を考えていく．ここで，Λ S のすべての非ゼロ（正）の固有値を降順に並べた対角行列， K は対応する固有ベクトルを要素とする行列である．
前述のように，ダミー変数行列 G のランクは p ( c − 1)+1 であり，その結果， D −1/2BD −1/2 のランクも同じである．したがって，その第1 残差行列 S のランクは p ( c − 1) であるから，Λ p ( c − 1)， K の大きさは pc × p ( c − 1) である．なお，簡単のため，固有値はすべて相互に異なるものとする．すなわち，
である．
D −1/2BD −1/2 は対称行列であるから，すべての相異なる固有値に対応する固有ベクトルは相互に直交する．すなわち， K′ = I p ( c - 1) であるだけでなく， K のすべての列は s と直交する．
さらに，この直交性はダミー変数のブロック単位でも成り立つ．次に，そのことを示す．固有方程式 SK = KΛ の，上から k 番目のブロックを次のように記す．
この左から
を掛け，左辺を(3.2)，(3.6) を用いて変形することにより，
が得られる．そこで0′ s′ kK k ΛΛ
自明解の存在については，よく知られているが，(3.13) について指摘されることは少ないように思われる（たとえば， Gower & Hand, 1996, p.60）．
次元の数を r とするとき，MCA の重み行列 V は固有ベクトルの最初の r 列を K ( r ) と記すことにすると，次によって得られる（たとえば， Ten Berge, 1993）．
これは，制約条件(3.8) を満たし，さらに，(3.13) から， p 個のダミー変数ブロックごとにもう1 つの制約条件(3.7) も満たすことになる．全体数量化得点は(3.5) によって求められ，(3.9) で定義される最大化基準は次のようになる．
MCA によって得られた数量化得点をPCA 的に解析することについては，各項目の数量化得点 Y k の同一の列の要素だけを集めて（列を項目ごとに標準化した上で）PCA を行うことなどが提案されている（たとえば， Nishisato, 2007）．その際，各次元の個別数量化得点と全体数量化得点の相関係数の2 乗和が，対応する固有値と一致することは知られている( Tenenhaus & Young,1985)．しかしながら，項目ごとの数量化得点行列の全体，
をPCA にかけても，そこで説明される分散の大きさは，これらの解を生み出したMCA のそれとは一致しない． Y の各列の分散は異なっており，PCA は相関行列にするために各列を基準化してしまうからである．基準化しないで共分散行列の固有値分解を行うことによってもMCA とは異なる解が得られる．根本的な問題は，個別主成分得点 Y k の列数 r が c −1 を超えるとき， Y k の列が1 次独立でないことである．
そこで， S の固有ベクトルを要素とする行列 K の第 k ブロックである c × p ( c − 1) の行列 K k の性質について考える．式(3.13) により，この行列の各列は，すべて s k と直交するから，1 次独立な列の数は，高々 c − 1 である．先に G k のランクを c と仮定したから， K k のランクが c − 1を下回ることはない．そこで， K k を（特異値分解等により），
と分解する．ただし，
P
k
は
c
× (
c
− 1) の正規直交行列
とする．そこで，
とすると，
である．ここで， K′ = I p ( c −1)， P′ = I p ( c −1) から，
でもあることがわかる．そこで，ダミー変数行列 G k に適用される重みを，
と定義すると，(4.1) から，
である（
L
k
のランクは
c
− 1 を下回らない）が，これは，(3.13) から
を意味し，さらに(3.10) を用いて，(4.4) から，
が得られる．また．
であることから，
も得られる．そこで，新たな量的変数の行列を次のように定義する．
すると，(4.6)，(4.7) によって，
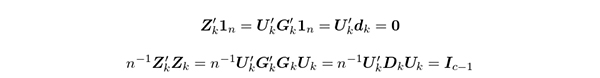
となる．すなわち， Z k の要素は，中心化，正規直交化されていることがわかる．そこで，
は， p ( c − 1) × p ( c − 1) の相関行列となる．
ここで，
として，(3.11)，(4.4)，(4.5) を用いると，
である．そこで，これと(4.2)，(4.3)，を用い，最後に(3.12) から，
すなわち， S と R は同じ固有値をもつことが示された．
4.2. MCAのPCA への変換そこで， W を p ( c − 1) × r の正規直交行列，すなわち，
を満たすものとし，主成分得点を
と定義した上で，この分散の和，
を最大化基準とする手続きを考える．すなわち，(4.10) を制約条件として，
の最大化を目指す．これは， Z のPCA である．この解は，(3.15) のΛ ( r ) に対応する固有ベクトルからなる行列を L ( r ) として，
となる． S と R の固有値が等しいことから， Ψ ( W ) = Φ ( V ) であり，かつ，
であることも用いると，
が得られる．したがって，
である．すなわち，(4.11) で定義されるPCA の主成分得点は，MCA の数量化得点と一致することが示された．そこで以下においては，主成分得点を F (= ZW ) と記す．
4.3. カテゴリーに与えられる数量の不定性
上記の定式化には直交回転に関する不定性がある．実際，
を
c
− 1 次の任意の直交行列とすると，(4.13) を用いて，
だから，これらの直交回転を施しても F = GV の値は不変である．
ここで，行列
U
k
のサイズは
c
× (
c
− 1) であり，(4.6) が成り立っている．すなわち，
U
k
の
c
−1 本の列ベクトルは
d
k
の直交補空間である
c
−1 次元空間にあり，これを
c
−1 次の直交行列
によって回転するわけであるから，
c
−1 本のベクトルは，(4.7) の制約条件を満たしている限り，
c
− 1 次元空間内での向きが全く定まらない．換言すれば，(4.6) と(4.7) という2 つの制約条件を満たす限りにおいて，
U
k
は完全に任意の値をとりうるということになる．どんな数量（たとえば乱数）を用いたとしても(4.14) により，MCA の数量化ウェイト
V
は不変である．すなわち，(4.10) の制約の下で(4.12) を最大化するPCA は，MCA の固有値と数量化得点を完全に維持した変換の範囲内にあるが，その値は数量としては不定である．
ただし，2 値変数，すなわち， c = 2 の場合については，(4.6)，(4.7) が，
を意味するから，これらの制約条件だけで，2 次元ベクトル u k は定まる．従来，繰り返し確認されてきた，2 値データのMCA の結果がPCA のそれと一致するという事実( De Leeuw, 1973) が確認される．2 値データには，数量化を行う余地がない．
4.4. カテゴリーへの直交多項式のあてはめ前項の結果により，たとえば一様乱数によって各カテゴリーに割り当てる数値を定め，それを変数ごとに(4.6)，(4.7) を満たすように変換してPCA にかければ，MCA と同じ固有値と得点をもつ結果を生み出すことはできる．しかし，生成される乱数に依存して変動する結果から，意味のある解釈を引き出すことは不可能であろう．結果を一意に定めるためには，なんらかの条件を追加する必要がある．それにはたとえば，4.5 節で導入する F の回転まで含めて， W k を左右から回転する方法（ 足立・村上, 2011）を適用することもあり得る．しかし，ここでは，本研究で適用の対象と考えているLikert 型項目の特徴を考慮し，かつ，より頑健な結果を得ることが期待できる直交多項式の適用を提案する．
順序のあるカテゴリカル変数のMCA から，2 次関数の形状を呈する数量化得点が出現することがあることは，図 1 において見た通りであるが，さらに次元の数を増やしていくとカテゴリーコードに対して3 次関数，4 次関数の形をとる数量があらわれることは，経験的に知られていた（たとえば， Beh & Rombardo, 2014）．ここでは，その性質を項目ごとにメトリックな数量として定義しようとする．
まず， c 個のカテゴリーに等間隔のメトリック（カテゴリーコードそのまま），に対して，次のように0 から c − 1 次のベキ乗を定義する．
この上で，つぎのようにして，正規直交多項式（orthonormal polynomials）の列を得る
上記の手続きは，古典的なGram-Schmidt の直交化法を，制約条件に合わせて修正したものである．これらを配列した次の U k は，(4.6)，(4.7) を満たしている．
これを用いて(4.8) によって得られる Z k がPCA の対象となる．
こうした直交多項式をカテゴリーの数量として埋め込むことが可能であることは，非計量的な方法が計量的な構造と完全に両立すると解釈することもできるであろう．
4.5. PCA 重み行列の回転とパターン行列の算出しかしながら，ここまでの議論は，MCA とPCA との数理的関係を明らかにする理論上の興味はあるとしても，実用上は，単にMCA と同一の数量化得点を生み出すに過ぎず，ここからは特に結果の解釈上のメリットは生じてこない．
また，多項式の当てはめは，PCA の対象となる変数の数を一挙に c − 1 倍に増加させるものであるから，通常の分析よりも多くの次元を扱わなければならなくなる．MCA の結果は，図 1 のようなグラフィカルな表示から解釈されることが多かったが，印刷したグラフで考える限り，3 次元以上の表示は難しく，4 次元を超えればいかなる表現方法を用いても，それらを直観的に把握することは困難であろう（たとえば， Rovan, 1994）．
多次元の結果を把握するには，できる限り個別の次元を残りの空間から分離し，軸単位で解釈ができるようにするのが便利である．その目的を達成するための1 つの方法が，（広義の）EFA における解の，単純構造に向けた解の回転である．単純構造の基準とは，ほぼ，(1) 回転の対象となる行列の各行の要素が，1 つを除きゼロに近いこと，(2) 異なる行のゼロでない要素はできるだけ多くの列に散らばること，と言える（たとえば， 芝, 1979）．単純構造によって，変量は（可能な限り）重複しないクラスターに分類され，算出される主成分得点は，対応するクラスターに含まれる項目内容によって命名・解釈できる．
本研究におけるPCAの制約条件は(4.10)，最大化基準は(4.12) であるが， T を r 次の直交行列とし，これによって W を WT と変換するとき，前者は， T′′ = T′ = I r ，後者は， tr T′′ = tr W′′ = tr W′ だから，最適解という性質を維持したまま，重み行列 W を直交回転することができる．このように，本研究では，PCA の（負荷行列ではなく），重み行列 W を右から回転して単純構造を得ようとする．その結果として主成分得点 F の列間には相関が生じることになる．なぜなら，回転前の共分散行列 n −1F′ は対角行列であるが，直交行列 T によって回転された後の n −1T′′ の非対角要素は0 とは限らないからである．これは，この方法が直交回転による斜交回転( Harris & Kaiser, 1964) と呼ばれる理由である．
この際， W′ = I r という性質により，単純構造への回転方法として高い頻度で用いられてきたOrthomax 回転（たとえば， 芝, 1979）の族はすべて，最も単純なQuartimax 回転に帰着する．これは， W の要素の4 乗和が最大になるような直交回転を意味する．
回転された主成分得点への個別変数の標準偏回帰係数の行列がパターン行列と呼ばれるものであるが，この方法の場合，その第 k ブロックは次のようになる．
なお，dg は，行列の対角要素を取り出して新たな対角行列を作る関数である（たとえば， Abadir & Magnus, 2005）．ここで， F = ZW，RW = WΛ ( r )， n −1F′ = Λ ( r )により，
という簡単な形になる．この回転法の1 つの長所は，PCA 重み行列 W k とパターン行列 A k が列ごとに比例することである( Kiers & Ten Berge, 1994)．さらに， A′ = dg T ′ Λ ( r ) T なので， A の各列は相互に直交していることも意味している．これは，他の斜交回転の方法にはない貴重な性質である．さらに， tr T′ Λ ( r ) T = trΛ ( r )だから，その合計（ tr A′ ）は最大化基準の値でもある．
主成分間相関行列は，主成分間共分散行列が T′ Λ ( r ) T なので，次のようになる．
これを用いて，それぞれの変数の主成分への回帰の重相関係数（因子分析の用語では共通性）は，
であることから，
によって算出される．ただし， a jk , w jk は，項目 k の j 次重みに対応する負荷行列と重み行列の行ベクトルを転置したものである．これは直交解のように，負荷行列の行平方和としては算出できない．
W はMCA の全体数量化得点と同じ得点を算出する回転前の主成分重み行列， WT は回転後のPCA の主成分得点を生み出す重み行列であることから，回転行列 T = W′ ( WT ) 要素はMCAとPCA の解のそれぞれの次元間の関係を表していると解される．したがって回転行列の要素を検討することによって，本研究の目的の1 つであるMCA とPCA の解がどのように異なるのかを検討できる可能性がある．
4.6. 説明力の指標と主成分の数の決定最後に，分析の成功度を評価する指標について述べる．これは，主成分の数（数量化の次元数）rの決定とも関わってくる問題である．まず分析の成功度については，主成分によって説明される，（直交多項式によって定義された）量的変数の分散の大きさ，すなわち最大化基準でもある trΛ ( r )を変数の総数 p ( c −1) で除した数値（EFA でいう因子によって説明される分散の大きさ）が考えられる．本研究ではデータ全体の説明力はこれに限定する．ただし，前項で述べた負荷行列の各列の要素の2 乗和（因子分析でいう因子寄与）の値は参考になるであろう．直交多項式を導入した結果として考えられるのは，(4.19) で定義された行ごとの重相関係数の2 乗を，数量の次数ごとに総和した次の指標である．
主成分数の決定に関しては，固有値の推移に関するscreeplot の視察や，結果の解釈可能性といった実用的観点からの判断以上に，現時点で述べられることはない．しかし，使用経験の蓄積によって，より適切な判断基準を見出しうる可能性はある．
まず，ここで提案したOPPCA のフローを示しておこう．主成分の数 r は，あらかじめ定めておくものとする．そのため，OPPCA の実行に先立って，通常のMCA とカテゴリーコードによるPCA を実行することが勧められる．特に，MCA の固有値によって得られるscree plot は r を定めるのに役立つ．
1) 欠損値をリストワイズに除去した上で，入力 X をダミー変数行列 G に変換する．
2) Burt 行列 B = G′ とその対角要素によって，カテゴリーへの反応数 d を求める．3
3) 式(4.15)，(4.16) により，直交多項式による重み行列 U を求める．
4) R = n −1UBU によって相関行列を求める．
5) R の全固有値と対応する固有ベクトルの行列（ Λ ）を求める．
6) PCA 重み行列 W = K ( r )をQuartimax 回転して WT とする．
7) 式(4.17)，(4.18)，(4.19) により，負荷行列，主成分間相関行列，重相関係数の2 乗などを算出する．
8) F = GUWT によって主成分得点を求め，ヒストグラム，散布図などを描く．
このように，4) 以降は（やや特殊な回転方法を含んでいるものの），完全にメトリックなPCAのアルゴリズムである．
ここでは，2 節で説明した感情体験に関する12 の5 段階評定の項目について，各カテゴリーに1 次～4 次の正規直交多項式による重みを用いて分析した例を示す．固有値は降順に，5.17，4.32，2.98，2.77，2.05，1.98，1.78，1.32，1.21，1.18，…であり，7 番目と8 番目の間に大きな差が見られる．図 3のscree plot からも主成分数は7 としてよいように思われる．7 番目までの固有値の合計は21.64，説明力は約0.438 である．
次に，(4.15)，(4.16) により，全項目の5 つのカテゴリーに当てはめられた正規直交多項式を図 4に示した．左から U k の第1～4 列の要素である．以下，それぞれを，1 次重み，2 次重み等と呼ぶ．1 次重みは完全な直線となるが，2 次以降の重みは，後に表 2に示すような各カテゴリーへの反応率の違いによって，通常の直交多項式表の値とは，少しずつ違った形態を示している．式(4.6)，(4.7) を満たさなければならないからである．
次に，これらの正規直交多項式を用い，(4.8) によって量的変数
Z
k
を求めた．これらを1～4次変量と呼ぼう．12×4 = 48 の変量を対象に
r
= 7のPCA を行い，行列
W
をquartimax 回転した上で，(4.17) によって計算したパターン行列
A
k
，(4.18) による主成分間相関Φ
，さらに，回転後の主成分得点の分散（パターン行列の列平方和）を表
1 に示した．式(4.20) の次数ごとの説明力の合計
ρ
j
は，1 次から順に，7.30（0.609），5.95（0.496），4.63（0.386），3.16（0.263）で，高次変量ほど小さくなっている．なお，( ) 内は，それぞれの値を項目の数12 で除した説明力である．
パターン行列では，絶対値が0.3 を超える負荷量を，「目立つ値」としてゴシックで示している．ポジティブ項目，(1)，(2)，(4)，(6)，(8)，(10) については，主成分Ⅰ，Ⅱ，Ⅲ にそれぞれの1次，2 次，3 次変量，ネガティブ項目，(3)，(5)，(7)，(9)，(11)，(12) については，主成分Ⅳ，Ⅴ，Ⅵ に同様に対応した負荷が見られる．4 次変量のみ，項目内容にかかわりなく，主成分Ⅶに負荷している．以下においては，主成分Ⅰ とⅣ を1 次主成分，Ⅱ とⅤ を2 次主成分，Ⅲ とⅥ を3 次主成分，Ⅶ を4 次主成分と呼ぶ．
表 2 に各項目への反応数（ d k ）とともに，図 2 左に示したメトリックなPCA の結果と，表 1 から抜き出した1 次変量の1 次主成分への負荷量をならべて示した．また，主成分間相関行列も表示した．これによると，主成分Ⅰ とⅣ の負荷行列（右端の2 列）は，メトリックなPCA による負荷行列（中央）と，ほとんど違いがない．対応する主成分得点もほぼ完全に相関している．すなわち，（少なくともこのデータでは）7 次元のMCA の解の中には，メトリックなPCA の結果が，ほぼ含まれていたことになる．
次に，1 次主成分と2 次主成分の関係を示したのが図 5 である．ここでは，それぞれを定義した重みの形状を反映して，放物線状の布置が得られている．すなわち，ポジティブ感情とネガティブ感情にそれぞれ対応する1 次主成分の両極に位置する回答者は，2 次重みの大きいカテゴリー1 とカテゴリー5 という評定尺度の両極に反応することが多いことを意味している．他方，放物線の内部の，それも比較的上方に位置する回答者が，特に右側の主成分Ⅳ と主成分Ⅴ の間の散布図で目立つ．これは彼らが必ずしも一貫しない反応をしていることを意味している．
また，2 つの2 次主成分（主成分Ⅱ と主成分Ⅴ）の間に，表 1 に示したように0.44 という比較的高い相関が認められる．Likert タイプの評定尺度上で，質問内容とは無関係に極端な反応をする程度に関して個人差があることは，回答者の反応の構えの1 種である極端反応傾向として古くから知られている( Cronbach, 1946)．したがって，2 次主成分の少なくとも一部はこの極端反応傾向を反映するものと見ることができる．
それと関連して，図 6 に示した1 次主成分と3 次主成分の関係が興味深い．それぞれの図の逆N 字状の分布の2 つの屈曲点の間の右上がりの線分の両端付近には，極端反応傾向が低く，カテゴリー2 と4 のような控えめな反応をしながら，一貫したポジティブ感情（図左），あるいはネガティブ感情（図右）の経験の有無を表明している対象者がいることを示している．これらの対象者は，通常のLikert 尺度をメトリックに扱う分析においては，構造にあまり影響を与えない．また，主成分得点においても，今回の分析の主成分Ⅰ とⅣ（図 5 の横軸）において中庸の位置を占めるにすぎない．したがって，反応の単純和で評価する通常のLikert 尺度をassessment やscreeningの目的で用いるなら，これらの回答者は注意の対象にならない．しかしながら，2，3 次変量を含めた分析を行い，1 次主成分3 次主成分との関係をある程度注意深く見るなら，これらの回答者の問題を見過ごす可能性は低くなるであろう．
4.5 節の最後に述べたように，回転行列をみることで，MCA とPCA の解の関係はより明らかになる．表 3 は，行列 W を単純構造化するために使われた回転行列 T の要素である．行側がMCA の解，列側が回転後のPCA の解に対応する．MCA の次元の順番は，固有値の大小順，回転後の解は表 1 の通りである．小数点以下の桁数は1 とした．
ここからは，MCA の第2 次元がPCA の主成分Ⅰ と主成分Ⅳ に分かれたのは，MCA の第3次元があったからであることがわかる．MCA の第2 と第3 次元の全体数量化得点を図示すると，図 2 右の散布図がやや傾いた形，すなわち回転前のPCA の主成分得点に近いものが現れる．表 3 の2 行，3 行，Ⅰ列，Ⅳ 列でできる[0.9 − 0.4; 0.4 0.8] という2 × 2 の行列が，近似的にその回転行列と見ることができる．同様に，MCA の第1 次元が，PCA において主成分Ⅱ と主成分Ⅴ に分かれたのは，MCA の第7 次元の存在によることが読み取れる．3 次変量と4 次変量が負荷するPCA の主成分Ⅲ，Ⅵ，Ⅶ は，MCA の第4，5，6 次元から出現していることがわかる．結論的に，表 1 のような解釈しやすい構造に到達するために回転が必要であることも明らかになったと思われる．
本論文では，（スケールを除き）古典的な方法で定義したMCA を，主成分の分散（の和）の最大化という，同じく古典的な定式化によるPCA に変換する方法について提案した．さらに，解に含まれる直交変換に関する不定性から，MCA の（全体）数量化得点を変えないままカテゴリーに任意の数量を与えることが可能であることを示した．その上で，カテゴリーコードを正規直交多項式によって変換して得られる変量にPCA を適用し，さらに，PCA の重み行列を単純構造に向けて回転するという一連の手続きであるOPPCA を提案した．これにより，従来MCA で主に行われてきた空間中心の解釈に代えて，軸にもとづく解釈が可能になる．
4.3 節で示された，カテゴリーに与えられる数量が全く任意であるという事実は，数量化理論の考え方からは少々意外に感じられるが，（一般化）正準相関分析（ Horst, 1961; Generalized canonicalanalysis; GCA）のことを考えれば特に不思議はない．すなわち，対角ブロックが単位行列となるという(4.9) の R の形からすれば，OPPCA は，個々の Z k を変数集合とするGCA とみることもできる．GCA においては，対角ブロックを単位行列化する変換がどのようなものであるかによって，正規直交化された変量は直交変換の範囲で異なるものとなり得るが，最終結果には影響がない．このことは，(4.14) において数量化重み V が変量に与えられる重み U k の回転に関係なく一定であることと同じである．
実データの分析においては，Likert 型尺度のカテゴリーコードをそのままEFA にかけるというしばしば用いられている手法の適切性が示されるとともに，2 次以上の変量からも内容とは独立した回答者の反応の構えのような無視し得ない現象も見出された．従来，図 5 に見られるような馬蹄現象は，全項目反応の1 つの次元への寄与が圧倒的に大きい場合に出現するとされ（たとえば， Gifi, 1990），解釈にあたっては余剰次元として捨て去るべきものとされることが多かった（たとえば， Bekker & De Leeuw, 1988）．むしろ，Likert 尺度が順序のついたカテゴリー反応であるという面が強調され，順序制約を課した分析に傾いていたと思われる．本研究は，それに反して，Likert 尺度を名義尺度として扱うことから，従来の分析では得られなかった情報が得られることを示唆した．同じ形式の質問項目を用いた他の調査データの分析からも，ほぼ同様の結論が得られている．
しかしながら，2 次以上の主成分が単なるアーチファクトにもとづく余剰次元ではないかという懸念は残る．それについては，ここで分析した実データと同じ相関行列をもつ多変量正規乱数を，やはり実データと同じ度数分布をもつようなカテゴリカルデータに変換したシミュレーションの結果が参考になる．まず，3～7 番目の固有値は図 3 に見られるものよりはるかに小さくなる．また，確かに2 つの2 次主成分は現れるがその間の相関は低く，かつ，値が5 を超えるような外れ値が現れる．多変量正規分布では，極端なカテゴリー反応が同一個体に同時に現れる確率は低いからである．やはりLikert 型項目への反応には内容と独立な反応傾向は存在し，本研究で提案した手続きはそれを明らかにしていると考えられる．ただし，このような事実が，主観的評定尺度以外の順序のついたカテゴリカルデータにおいても現れるとは限らない．
5 節で見た(4.20) で定義される ρ j の値に見られるように，高次成分ほどEFA によって説明できるような規則性をもつ成分が少なくなるとすれば， U k の次元を c − 1 より小さくすることで，より節約的な表現が可能になると考えられるかもしれない．ただしその場合，次元数を主成分数と一致させない限り，解はMCA とは異なったものとなり，何らかの反復計算を要するだけでなく，本研究で見出したような解の不定性は消失する．こうした方法は確かに可能である．実際，次元数を1 に制約するのが非計量主成分分析（nonmetric princilal component analysis; NCA; たとえば， De Leeuw, 2006）であるが，そうした方法は本研究の射程外である．
本研究で提案したOPPCA は，あくまでもMCA に許容される変換を行ったものである．このことの重要性は過小評価されるべきではない．アルゴリズムの頑健性だけでなく，MCA に関して蓄積された膨大な理論的，経験的成果が利用できるからである．
