2013 Volume 53 Issue 5 Pages 774-781
2013 Volume 53 Issue 5 Pages 774-781
The formation mechanisms of the complex Ca-rich ferrite iron ore sinter bonding phases SFCA and SFCA-I, during heating of a synthetic sinter mixture in the range 298–1623 K and at pO2 = 0.21, 5 × 10–3 and 1 × 10–4 atm, were determined using in situ X-ray diffraction. SFCA and, in particular, SFCA-I are desirable bonding phases in iron ore sinter, and improved understanding of the effect of parameters such as pO2 on their formation may lead to improved ability to maximise their formation in industrial sintering processes. SFCA-I and SFCA were both observed to form at pO2 = 0.21 and 5 × 10–3 atm, with the formation of SFCA-I preceding SFCA formation in each case, but via distinctly different mechanisms at each pO2. No SFCA-I was observed at pO2 = 1 × 10–4 atm; instead, a Ca-rich phase designated CFAlSi, formed at 1420 K. By 1456 K, CFAlSi had decomposed to form melt and a small amount of SFCA. Such a low pO2 during heating of industrial sinter mixtures is, therefore, undesirable, since it would not result in the formation of an abundance of SFCA and SFCA-I bonding phases. In addition, CFA phase, which was determined by Webster et al. (Metall. Mater. Trans. B, 43(2012), 1344) to be a key precursor phase in the formation of SFCA at pO2 = 5 × 10–3 atm, was also observed to form at pO2 = 0.21 and 1 × 10–4 atm, with the amount decreasing with increasing pO2.
Iron ore < 6.3 mm in size is too fine for direct use in a blast furnace and must first be agglomerated into iron ore sinter. Sinter is often the major component of blast furnace burden, and the production of high quality sinter is important for efficient blast furnace operation. During the iron ore sintering process, these iron ore fines are mixed with fluxes (e.g. limestone) and coke breeze and rapidly heated in 2–4 min to temperatures of ~1573 K, followed by slower cooling in air.1) This results in partial melting of the mixture and converts the loose raw materials into a porous but physically strong composite material in which the iron-bearing minerals (40–70 vol% hematite, Fe2O3, and magnetite, Fe3O4) are bonded together by a matrix containing complex Ca-rich ferrite phases (20–50 vol%), glasses (quenched melt) and calcium silicates (each up to 10 vol%).2) Oxygen partial pressure (pO2) values range from reducing during the initial stages of sintering as the coke breeze is consumed to oxidising during cooling.3,4)
The complex Ca-rich ferrite bonding phases typically also contain some silica and alumina and are known collectively by the acronym ‘SFCA’, which stands for Silico-Ferrite of Calcium and Aluminium.5) Other ferrite phases observed in industrial sinters include monocalcium ferrite, CaO.Fe2O3 (abbreviated to CF), dicalcium ferrite, 2CaO.Fe2O3 (C2F), hemicalcium ferrite, CaO.2Fe2O3 (CF2) and brownmillerite (2CaO.(Al2O3).(Fe2O3), C2AF, i.e. A = Al2O3).6) SFCA phases are believed to be the most desirable bonding phases in iron ore sinter because of their high reducibility,7) high mechanical strength and low reduction degradation,8,9) all of which are significant factors in determining the productivity and efficiency of the blast furnace.
The SFCA produced in iron ore sinter has, in the past, been divided on the basis of composition, structure and morphology into two main types. One is a high-Fe, low-Si form called SFCA-I, which has been described as having a platy morphology but also as being acicular. Mumme et al.10) reported that an SFCA-I found in plant sinter contained 84 mass% Fe2O3, 13 mass% CaO, 1 mass% SiO2 and 2 mass% Al2O3, and also synthesised material with the SFCA-I structure which had composition 83.15 mass% Fe2O3, 12.61 mass% CaO and 4.24 mass% Al2O3. The second ‘SFCA’ type is a low-Fe form that is simply referred to as SFCA and which exhibits a prismatic or columnar morphology in polished sections. SFCA found in industrial, plant sinters typically contains 60–76 mass% Fe2O3, 13–16 mass% CaO, 3–10 mass% SiO2, 4–10 mass% Al2O3 and 0.7–1.5 mass% MgO.11,12) Patrick and Pownceby13) systematically resolved the equilibrium solid solution range and thermal stability of SFCA within the quaternary system Fe2O3–CaO–SiO2–Al2O3 in air at 1513–1663 K. More recently a third SFCA with composition 67.3 mass% Fe2O3, 12.3 mass% CaO and 20.4 mass% Al2O3 and designated SFCA-II was reported by Mumme.14) It has been reported to be present in plant sinters from South Africa.15,16)
McAndrew and Clout17) suggested that the texture of intersecting microplates of SFCA-I imparts superior strength and easier reducibility, and sinters containing significant amounts of this phase are of high quality. By comparison, sinters containing high amounts of prismatic SFCA, which is usually associated with glass, are typically weaker, have lower reducibility and are generally of lower quality. The effect of SFCA-II on strength and reducibility of iron ore sinter is unknown.
A large number of investigations2,3,18,19,20,21,22,23,24,25) have aimed to determine the formation mechanisms of complex Ca-rich ferrite phases. Increased understanding of the mechanisms has the potential to improve the efficiency of the sintering process by a) being able to predict the optimal sintering conditions (temperature, pO2) to produce high quality product based on the chemical and physical composition of the iron ore fines, and b) being able predict the chemical and physical modifications of a particular iron ore fines mixture required to produce high quality product. Both are becoming increasingly important as the total iron content in many iron ores is decreasing and the concentration of alumina and silica-containing gangue minerals is increasing.
In the most recent of these mechanistic investigations, Webster et al.25) implemented in situ X-ray diffraction (XRD) in order to determine the SFCA and SFCA-I formation mechanisms in synthetic iron ore sinter mixtures, containing 1, 5 and 10 mass% Al2O3, in the range 298–1623 K and at an oxygen partial pressure of 5 × 10–3 atm. The selection of the pO2 was based on work of Hsieh and Whiteman,2) where it was shown that this oxygen partial pressure maximised the formation of Ca-rich ferrite phases, whilst producing mineral assemblages similar to those found in industrial sinters. Webster et al.25) showed that during heating, SFCA-I formation was associated with reaction between Fe2O3, SiO2 and Al2O3-substituted C2F [i.e. C2(F1–xAx)]. In contrast, SFCA formation was associated with reaction between CF, SiO2 and a phase designated CFA which had average composition 71.7 mass% Fe2O3, 12.9 mass% CaO, 0.3 mass% SiO2 and 15.1 mass% Al2O3. The initial formation of SFCA at ~1433 K was independent of SFCA-I, however at higher temperature (T > 1473 K) SFCA-I was consumed in the formation of SFCA. Eqs. (1) and (2) (unbalanced) summarise the reactions involved in the formation of SFCA-I and SFCA determined by Webster et al.25) (the ‘±’ in Eq. (2) represents the initial formation of SFCA being independent of SFCA-I).
| (1) |
| (2) |
The formation of CFA during heating had not been described in a previous in situ XRD investigation of reaction sequences in the formation of SFCA phases, which was performed under vacuum in the range 298–1533 K by Scarlett et al.23,24) Eqs. (3) and (4) summarise the reactions involved in the formation of SFCA-I and SFCA determined by Scarlett et al.:
| (3) |
| (4) |
The nominal concentration of the synthetic starting sinter mixture for the in situ XRD experiments, in terms of mass% of oxides, was 77.36, 14.08, 3.56 and 5.00 mass% Fe2O3, CaO, SiO2 and Al2O3, respectively. This mixture was equivalent to mixture SM4/5 previously investigated by Webster et al.25) and was designed to maximise the formation of the SFCA phase.13) It was prepared from fine grained (< 20 μm) synthetic Fe2O3 (Acros Organics, 99.999%), calcite, CaCO3 (Thermo Fisher, 99.95%), quartz, SiO2 (Sigma Aldrich, 99.995), and gibbsite, Al(OH)3 (Alcan OP25 Super White, 99.9%); these were mixed under acetone in a mortar and pestle. In terms of its relevance to a typical industrial iron ore sinter mixture of fines, flux and coke, this composition is indicative of the reactive ultra-fine coating component of the mixture (< ~1 mm), rather than the bulk composition which also includes larger ‘nuclei’ ore particles.
2.2. In Situ XRDIn situ XRD experiments were performed using an INEL diffractometer, which incorporates a CPS120 position-sensitive detector allowing for simultaneous collection of up to 120° 2θ of diffraction data. The Co tube was operated at 40 kV and 35 mA. An Anton Paar model HTK 10 high temperature chamber, employing a platinum resistance strip heater inside it, was positioned on the instrument (Fig. 1). A slurry of the sinter sample mixture and ethanol was prepared and placed into a sample well, measuring approximately 20 × 7 × 0.2 mm, on the platinum heater.

The high temperature chamber fitted to the laboratory INEL X-ray diffractometer.
The experimental pO2 values of 0.21, 5 × 10–3 and 1 × 10–4 atm were obtained by flowing compressed air, and special gas mixtures containing 0.5 and 0.01% O2 in N2 (BOC Gases), respectively, into the Anton Paar chamber. Before each experiment the chamber was purged for 10 min by a flow (~ 1 L min–1) of the designated gas mixture, after which the sample was heated under a continuous flow of the gas.
A heating rate of 20 K min–1 was used from 298 to 873 K (approaching the decomposition temperature of CaCO3), then a slower rate of 10 K min–1 to 1623 K was used during the period of SFCA-I and SFCA phase formation and melting. The temperature was measured by a Pt/PtRh10% thermocouple connected to the underside of the platinum strip. In situ XRD data were collected throughout heating, with individual datasets collected for 0.5 min. Data were collected in asymmetrical diffraction geometry with an incident beam angle of 10º, over the range 10º ≤ 2θ ≤ 112º. The temperatures of phase formation/transformation given throughout the manuscript are those at the start, which is when the temperatures were automatically recorded, of the relevant dataset. The uncertainty in these temperature values, therefore, was the difference between the temperatures at the start of successive datasets, and the magnitude of the uncertainty depended on the heating rate (i.e. 10 and 5 K for the 20 and 10 K min–1 heating regimes, respectively).
For the purposes of visualisation of the decomposition and formation of phases as the experiment progressed, the datasets were stacked to produce a plot of accumulated data with temperature plotted vs 2θ, viewed down the intensity axis (Figs. 2(a), 2(b) and 2(c)). Rietveld refinement was performed using TOPAS,26) with the crystal structure information provided in Blake et al., Maslen et al., Saalfeld and Wedde, Lager et al., Oftedal, Bersetegui et al., Decker and Kasper, and Hamilton used for Fe2O3, CaCO3, Al(OH)3, SiO2, CaO, C2(F1–xAx), CF and Fe3O4, respectively.27,28,29,30,31,32,33,34) Single peak fitting to extract reflection intensities was also performed using TOPAS, with reflections modelled using a pseudo-Voigt profile function. The background was modelled using a Chebychev polynomial function.

In situ XRD data collected at a) pO2 = 5 × 10–3 atm, b) 0.21 atm and c) 1 × 10–4 atm. Annotated on the plots are: the major reflections for materials in the starting mixture; the low-temperature (< 923 K) phase transformation (α → β-SiO2) and decomposition (e.g. CaCO3 → CaO) events; the formation events of C2(F1–xAx), CF, SFCA-I, SFCA, the Fe3O4 + melt phase assemblage (for a and c), and the Fe2O3 + melt phase assemblage (for b); and the major reflections for CFA. X denotes the reflections for the unknown phase (for c).
Laboratory heat/quench experiments were performed in order to investigate key phases revealed by the in situ XRD experiments in more detail. For these experiments, 0.5 g of the starting sinter mixture was pelletised and heated in a platinum crucible in a vertical tube furnace under the required pO2 condition, followed by water quenching. The temperature adjacent to the crucible was measured using a Pt/PtRh13% thermocouple connected to an ice-point cell, and the temperature is considered accurate to ± 10 K.
Scanning electron microscopy (SEM) was performed using a FEI Quanta 400 Field Emission Environmental SEM operated at an accelerating voltage of 10 kV and a working distance of 10 mm. Energy dispersive spectroscopy (EDS) was performed on this instrument using a Bruker X-Flash 5010 Si-drift EDS detector. Electron probe microanalysis (EPMA) was performed using a JEOL JXA-8900F Superprobe. Fe2O3, wollastonite (CaSiO3, CS) and “Magalox” (a synthetic spinel, composition MgAl2O4) were used as standards for the microprobe analyses which were conducted in wavelength dispersive mode using an accelerating voltage of 10 kV, a beam diameter of < 1 μm and counting times of 15 sec.
2.4. Synthesis and Characterisation of SFCA and SFCA-I MaterialsSynthesis of SFCA and SFCA-I materials, in order to investigate their structures in more detail, was carried out by heating pellets of the desired mixtures in a vertical tube furnace in air at 1533 K for 24 hr. This was followed by air quenching, grinding, re-pelletising, and reheating for a further 24 hr followed by air quenching. This process was repeated to produce the final materials with a total heating time of 72 hr. EPMA data were collected using the procedure in Section 2.3.
Synchrotron XRD (S-XRD) data were collected for these materials, at room temperature on the powder diffraction beamline at the Australian Synchrotron35) over the range 2º ≤ 2θ ≤ 82.5º. Samples were contained within 0.3 mm glass capillaries which were continuously rotated during data collection to improve particle statistics and to reduce the effects of preferred orientation. The X-ray wavelength was 0.7279 Å, calibrated using LaB6 (NIST 660b line position and profile standard) contained in a 0.3 mm ID capillary. Pawley refinements36) of the S-XRD data were performed using TOPAS. The triclinic (P
For determination of Fe2+ content, the materials were dissolved with hydrofluoric and hydrochloric acids. The resulting solutions were then titrated to the electrochemical equivalence point against a standard dichromate solution using a 798 Metrohm MPT Titrino autotitrator. The Fe2+ content was calculated from the titre volumes.
Figure 2(a) shows the plot of accumulated in situ XRD data for the pO2 = 5 × 10–3 atm experiment. The results, in terms of the phases observed and the temperature range of their stability, are in excellent agreement with those reported previously by Webster et al.25) for the corresponding experiment for this sinter mixture composition performed at the Australian Synchrotron and for which the reaction mechanisms presented in Eqs. (1) and (2) applied. More specifically, Al(OH)3 decomposition to an amorphous Al-oxide was complete by 562 K, transformation of the α-form of SiO2 to β-SiO2 was complete by 845 K (in excellent agreement with the 846 K reported by Kihara,37) which gives a high level of confidence in the accuracy of the thermocouple), and decomposition of CaCO3 to CaO was complete by 883 K. The first Ca-rich ferrite to form was C2(F1–xAx) at 1037 K, followed by CF and CFA at 1243 K, SFCA-I at 1377 K, and SFCA at 1441 K. Melting of both SFCA-I and SFCA was complete by 1532 K, after which the Fe3O4 + melt phase assemblage had formed. Fe3O4 formed as a result of incongruent melting of SFCA, since Fe2O3 was fully consumed in the reactions to form the ‘SFCA’ phases by 1472 K, which is before the predicted Fe2O3 → Fe3O4 transformation temperature of 1513 K.38) Table 1 summarises the formation temperatures of these phases and phase assemblages.
| pO2 (atm) | Temperature (K) | |||||
|---|---|---|---|---|---|---|
| C2(F1–xAx) | CF/CFA | SFCA-I | X (i.e. CFAlSi) | SFCA | Fe3O4 + melt/ Fe2O3 + melt | |
| 0.21 | 1027 | 1223 | 1416 | – | 1446 | 1594 |
| 5 × 10–3 | 1037 | 1243 | 1377 | – | 1441 | 1532 |
| 1 × 10–4 | 1027 | 1230 | – | 1420 | 1438 | 1479 |
Figures 2(b) and 2(c) show the plots of accumulated in situ XRD data for the experiments conducted at pO2 = 0.21 and 1 × 10–4 atm, respectively. The low temperature (< 923 K) phase decomposition and transformation events are very similar to those in Fig. 2(a). Oxygen partial pressure, therefore, does not have a significant effect on these events. In addition, pO2 does not have a significant effect on the initial formation temperature of C2(F1–xAx) and CF (Table 1).
In contrast, however, pO2 did have an effect on the stability of Fe2O3. At pO2 = 1 × 10–4 atm, Fe3O4 formed through the Fe2O3 → Fe3O4 reduction reaction which was complete by 1367 K, in good agreement with the theoretical value of 1371 K.38) In the 0.21 atm experiment Fe3O4 did not form, with Fe2O3 remaining stable up to 1623 K. In air the Fe2O3 → Fe3O4 reduction reaction is predicted to occur within the range 1623–1682 K; the presence of labile Ca2+ in the system will likely displace the reaction to lower temperature than the theoretical value of 1682 K.38,39)
3.1. CFA FormationSimilarly to the experiment at pO2 = 5 × 10–3 atm, characteristic CFA reflections were observed at pO2 = 0.21 and 1 × 10–4 atm, occurring at 34.5 and 39.9° 2θ (d = 3.02 and 2.62 Å, respectively, annotated in Figs. 2(b) and 2(c)). The reflections in the experiment at pO2 = 0.21 atm appeared to be of lower relative intensity to those in the other experiments, suggesting less CFA was formed under the more oxidising conditions. In the absence of previously published structural information for CFA necessary to perform Rietveld refinement-based quantitative phase analysis (QPA) of this phase, and also the absence of single-phase CFA material necessary to perform QPA using the PONKCS method,40) an alternative method was required in order to confirm that the amount of CFA formed at pO2 = 0.21 atm was less than at the other pO2 values. In the alternative approach, the intensity (ICFA) of the major CFA-phase reflection with d = 2.62 Å was normalised by the intensity of the major Fe2O3 reflection (IHem) at 38.8° 2θ in the dataset collected at room temperature. Figure 3 shows ICFA/IHem as a function of temperature for each pO2.
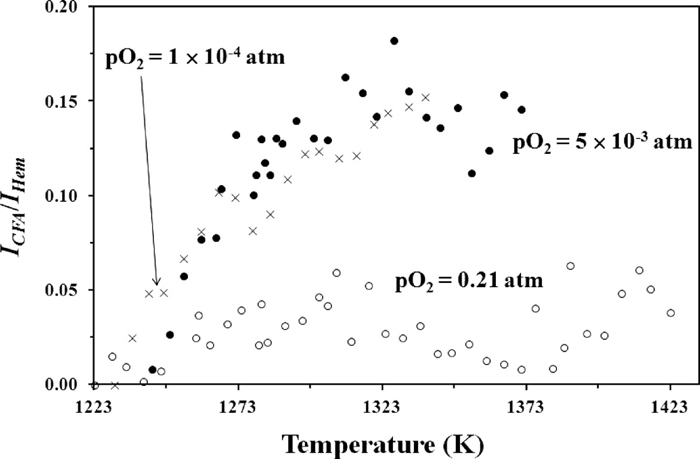
The variation in normalised intensity, ICFA/IHem, of the characteristic CFA reflection (d = 2.62 Å) as a function of temperature and pO2.
For the experiment at pO2 = 5 × 10–3 atm ICFA/IHem is plotted from 1223 to 1371 K (i.e. just before the initial formation temperature of SFCA-I) due to significant overlap between the CFA and SFCA-I reflections. For the same reason ICFA/IHem is plotted up to 1412 K for the pO2 = 0.21 atm experiment, while for the pO2 = 1 × 10–4 atm experiment it is plotted to 1338 K (i.e. just before the initial formation temperature of Fe3O4), due to overlap between the CFA and Fe3O4 reflections. Figure 3 confirms that the amount of CFA that formed at pO2 = 0.21 atm was less than at the more reduced pO2 values, and that the amount of CFA formed at pO2 = 5 × 10–3 and pO2 = 1 × 10–4 atm was similar.
3.2. SFCA and SFCA-I Phase Formation and MeltingSimilar to the experiment at pO2 = 5 × 10–3 atm, SFCA-I and SFCA were observed to form at pO2 = 0.21 atm, at 1416 and 1446 K, respectively. Melting of both SFCA phases was complete by 1594 K, producing the Fe2O3 + melt phase assemblage. For the pO2 = 1 × 10–4 atm experiment, very weak reflections for SFCA were observed; SFCA initially formed at 1438 K and was present until melting was complete by 1479 K producing the Fe3O4 + melt phase assemblage. The decrease in melting point with decreasing pO2 is in agreement with previous work.39) Characteristic reflections for SFCA-I were not observed for the pO2 = 1 × 10–4 atm experiment. Instead, reflections from an unknown phase (annotated with ‘X’ in Fig. 2(c)) were first observed at 1420 K and were present until decomposition of this phase was complete at 1456 K. No suitable match could be made between this phase and any phase within the Database of the International Centre for Diffraction Data (ICDD). However, based on the d-spacings of its reflections in Fig. 2(c) (5.66, 3.77 and 2.83 Å at 1431 K), it appears likely to have a simple cubic crystal structure. Further work is required to determine the details of its crystal structure.
Based on a comparison of the three experiments the effect of decreasing pO2 was to significantly decrease the thermal stability range of SFCA which was 1446–1594, 1441–1532 and 1438–1479 K at pO2 = 0.21, 5 × 10–3 and 1 × 10–4 atm, respectively (see Table 1). In contrast, the effect of decreasing oxygen partial pressure from 0.21 to 5 × 10–3 atm was to stabilise the formation of SFCA-I at a lower temperature, and it is hypothesised that SFCA-I may accommodate more Fe2+ into its structure than SFCA.
Following on from the latter observation it is noted that in SFCA and SFCA-I materials synthesised in air in the range 1473–1573 K by Mumme et al.,10) the SFCA-I contained a higher amount of Fe2+ in its structure compared with SFCA. However, the assignment of the amount of Fe2+ was based purely on charge balance considerations, and a more rigorous analytical approach was required to determine whether this is indeed the case. Here, SFCA and SFCA-I materials were synthesised in air at 1533 K. Table 2 shows the EPMA-determined compositions for each. Figure 4 shows the output of Pawley refinements to the high resolution S-XRD data collected for SFCA (Fig. 4(a)) and SFCA-I (Fig. 4(b)). The quality of the fit shown in Fig. 4(a) indicated that the SFCA was single phase; conversely the fit to the data collected for SFCA-I indicated the presence of a minor impurity phase, which was subsequently identified as Fe2O3 (ICDD No. 33-0664).
| Sample | Composition (mass%) | ||||
|---|---|---|---|---|---|
| Fe2O3 | CaO | SiO2 | Al2O3 | Total | |
| SFCA | 80.0 (1.2) | 13.5 (0.3) | 3.0 (0.2) | 4.7 (0.1) | 101.2 (1.2) |
| SFCA-I | 83.5 (2.0) | 12.9 (0.1) | 0.0 (0.1) | 5.0 (0.8) | 101.5 (1.7) |
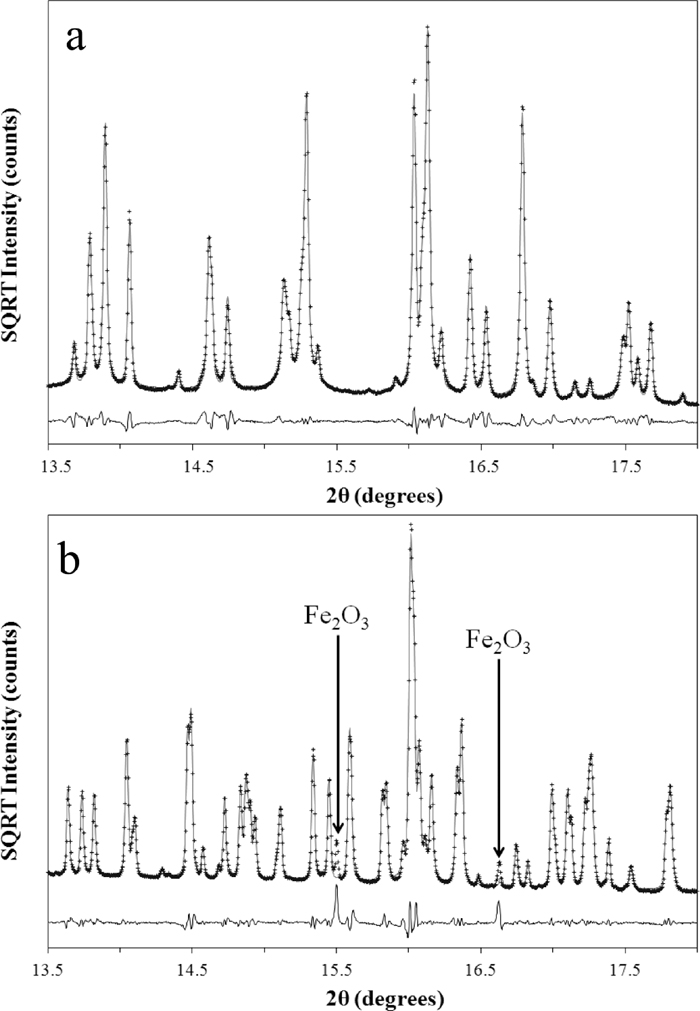
Output of Pawley refinements to S-XRD data collected for a) SFCA; and b) SFCA-I synthesised at pO2 = 0.21 atm at 1533 K for 72 hr. The data are shown only at low 2θ values over a narrow angular range of the complete datasets. Experimental data are shown as plus signs, the calculated patterns are solid lines, and the difference patterns are the solid lines below. Fe2O3 reflections are annotated on the SFCA-I plot.
Subsequent Fe2+ determination via titration showed that the bulk SFCA and SFCA-I materials contained 0.46(0.01) and 1.38(0.01) mass% Fe2+, respectively. If it is assumed that Fe2O3 contains Fe3+ only, then these results are in agreement with the hypothesis that SFCA-I can accommodate more Fe2+ than SFCA. Future work will aim to further test this hypothesis, by investigating the effect of oxygen partial pressure in the range pO2 = 0.21 – 1 × 10–4 atm, on the equilibrium phase assemblages produced from these SFCA and SFCA-I starting mixtures at a number of temperatures in the range 1423–1573 K.
3.3. Characterisation of the Unknown Phase, pO2 = 1 × 10–4 atmThe ‘X’ phase appears to be a short-lived transient phase, and attempts to quench-in this phase by heating pellets of the starting sinter mixture in a platinum crucible in a vertical tube furnace were unsuccessful. In order to quench-in X phase for ex situ examination using SEM, EDS and EPMA, a repeat in situ XRD experiment was performed, under the same conditions except that the sample was cooled at 200 K min–1 to 298 K once the temperature had reached 1433 K (the temperature at which X phase reflections were most intense). Diffraction data were also collected during cooling, and the reflections for X phase, as well as Fe3O4 and SFCA, persisted down to 298 K. The product was then removed from the Pt strip heater and prepared for microscopic and compositional examination.
Figure 5 shows backscattered electron micrographs of the product of this experiment; Fig. 5(a) shows a grain containing Fe3O4 and X phase, and Fig. 5(b) shows a grain containing X phase and a dark-contrast phase which EDS suggested was likely to be quenched melt. Table 3 shows the composition of each of these phases, determined using EMPA, assuming all Fe was present as Fe3+. The results show that the Fe and Ca totals for X phase are similar to that for CF (i.e. 74 and 26 mass% Fe2O3 and CaO, respectively), and too Ca-rich and Fe-poor to be closely related to SFCA-I (see Section 1). X phase is renamed CFAlSi throughout the remainder of the manuscript, which reflects its compositional similarity with CF and its low Al and Si content.

Backscattered electron micrographs of the product of the in situ XRD experiment designed to quench in the unknown X phase. a) Shows regions of Fe3O4 and X phase, and b) shows regions of X phase and melt. The black areas are pores.
| Phase | Composition (mass%) | ||||
|---|---|---|---|---|---|
| Fe2O3 | CaO | SiO2 | Al2O3 | Total | |
| Fe3O4 | 96.5 (2.2) | 2.5 (1.3) | 0.1 (0.1) | 1.5 (0.1) | 100.5 (1.0) |
| X (i.e. CFAlSi) | 71.6 (1.0) | 24.1 (0.3) | 0.3 (0.1) | 2.4 (0.3) | 98.5 (0.9) |
| Melt | 19.2 (1.6) | 37.4 (0.4) | 18.9 (0.4) | 21.6 (1.7) | 97.1 (0.9) |
Figure 6 shows the in situ XRD data collected over the range 1401–1456 K at pO2 = 1 × 10–4 atm. The appearance and subsequent increase in intensity of the reflections for CFAlSi at 1420–1431 K coincided with a decrease in intensity (and ultimately the disappearance) of the C2(F1–xAx), CF and SiO2 reflections. Figures 6 and 2(c) showed that melting of CFAlSi at temperatures above 1438 K coincided with the appearance of the minor SFCA reflections, and an increase in the background which is consistent with the formation of melt.

In situ XRD data collected at pO2 = 1 × 10–4 atm over the range 1401–1456 K. The datasets have been offset in the intensity axis to avoid overlap and improve clarity.
Whilst not evident in Fig. 6, the formation of CFAlSi did correspond with the consumption of some Fe3O4 and it is considered likely, therefore, that CFAlSi contains a significant amount of Fe2+. Figure 7 shows the results of Rietveld-refinement based QPA, in the temperature range 1073–1456 K, performed for the pO2 = 1 × 10–4 atm experiment. The values for phase concentration are absolute, rather than relative, values which were determined using the relationship shown in Eq. (5) (after Madsen and Scarlett41)),
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
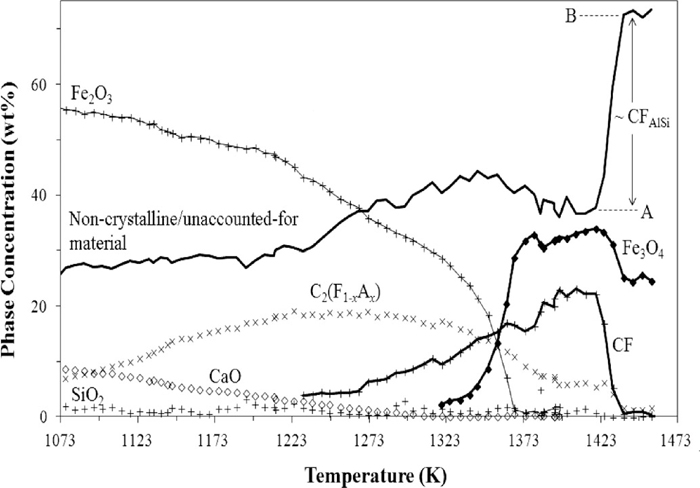
Results of the Rietveld refinement-based quantitative phase analysis for the in situ XRD experiment performed at pO2 = 1 × 10–4 atm. Shown are the absolute concentrations of the phases in the system as a function of temperature, which were calculated using the relationships shown in Eqs. (5) and (9).
One of the key differences between the results of this experiment, and the results at pO2 = 5 × 10–3 atm described by Webster et al.25) and here in Eqs. (1) and (2), is that C2(F1–xAx), instead of being directly involved in the reaction to form SFCA-I, was fully consumed in its reaction with Fe2O3 to form CF and CFA before the formation of SFCA-I. Figure 8 shows the in situ XRD data collected over the range 1423–1575 K at pO2 = 0.21 atm. The typical C2(F1–xAx) reflections at 26.4 and 37.2° 2θ (d = 3.92 and 2.80 Å, respectively) are not present at 1423 K which is before SFCA-I was first evident. A second difference from the results at pO2 = 5 × 10–3 atm is that instead of the amount of CF increasing during the early stages of SFCA-I formation, CF was directly involved in the formation of SFCA-I, with the intensities of the CF reflections in Fig. 8 decreasing with the appearance, and subsequent increase in intensity, of the SFCA-I reflections. Both of these results correlate with those obtained by Scarlett et al.,23,24) which is evidence that their experiments which yielded the SFCA-I and SFCA formation mechanisms shown in Eqs. (3) and (4) were conducted towards the high pO2 end of the range pO2 = 0.21 – 5 × 10–3 atm. The formation of SFCA-I was also associated with a decrease in intensity of the Fe2O3 and SiO2 reflections. Further formation of SFCA-I, and the initial formation of SFCA, resulted in a further decrease in intensity of the Fe2O3 reflections and the disappearance of the SiO2 reflections.
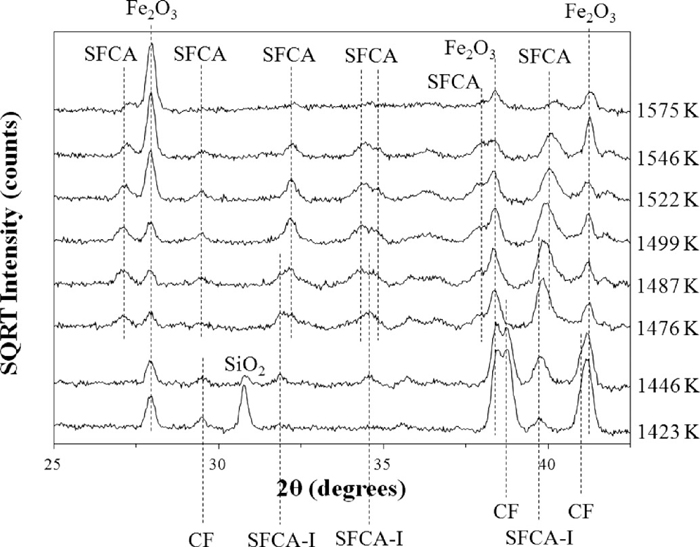
In situ XRD data collected at pO2 = 0.21 atm over the range 1423–1575 K. The datasets have been offset in the intensity axis to avoid overlap and improve clarity.
Given the low intensity of the CFA reflections, and the overlap of the major CFA reflection at 39.9° 2θ with a major SFCA-I reflection, it is difficult to determine from these in situ data whether, like CF, CFA was involved in the reaction to form SFCA-I or, as was the case at pO2 = 5 × 10–3 atm, it was only involved in the reaction to form SFCA. Given that C2(F1–xAx) was not directly involved in the reaction to form SFCA-I, and CF and Fe2O3 do not incorporate significant amounts of Al3+,25) it is considered likely that CFA did react to provide the Al3+ content required to form SFCA-I. Figure 9 shows a backscattered electron micrograph of the product of the heat/quench experiment performed at pO2 = 0.21 atm and 1323 K for 24 h, with unreacted amorphous Al-oxide encased by CFA, meaning that CFA reacts before the Al-oxide itself is available. EDS analysis confirmed that CF contained a very low concentration of Al3+ similar to that which was determined by Webster et al.25) Eqs. (10) and (11) summarise the reactions involved in the formation of SFCA-I and SFCA at pO2 = 0.21 atm:
| (10) |
| (11) |
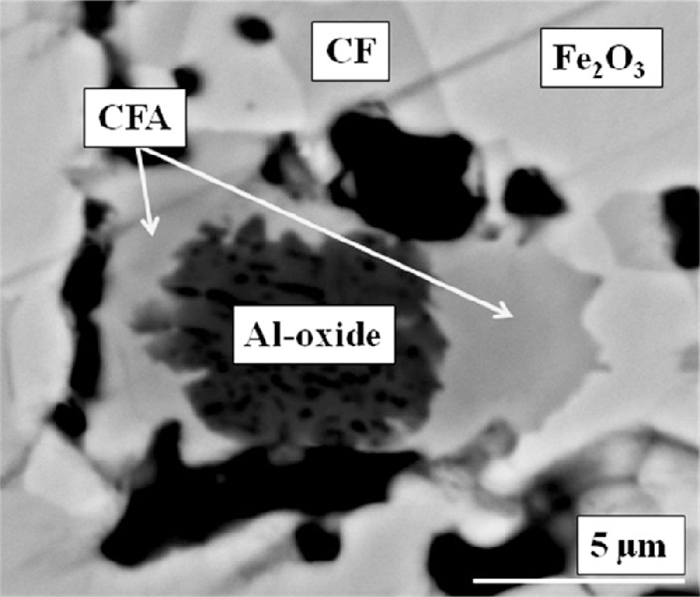
Backscattered electron micrograph of the product of the heat/quench experiment performed at 1323 K for 24 h at pO2 = 0.21 atm, showing CFA, Fe2O3, CF and unreacted Al-oxide. The black areas are pores.
The formation mechanisms of SFCA and SFCA-I iron ore sinter phases during heating of a synthetic iron ore sinter mixture in the range 298–1623 K and at pO2 = 0.21, 5 × 10–3 and 1 × 10–4 atm were determined using in situ XRD. Oxygen partial pressure has a significant effect on the formation of SFCA-I and SFCA. Importantly, if the oxygen partial pressure is too low, then desirable SFCA-I will not form. Rather, a Ca-rich ferrite phase designated CFAlSi, will form through reaction between C2(F1–xAx), CF, SiO2 and Fe3O4. On the other hand, if the pO2 is too high, the thermal stability range of SFCA-I before the formation of SFCA will be reduced. In addition, CFA, which had previously been determined to be a key precursor phase in the formation of SFCA at pO2 = 5 × 10–3 atm, was also observed to form at pO2 = 0.21 and 1 × 10–4 atm with the amount decreasing with increasing pO2. Future work will investigate the effect of pO2 on the equilibrium phase assemblages produced from a number of different starting mixtures at a number of temperatures in the range 1423–1573 K. It will also implement in situ XRD to investigate the phase formation mechanisms, during heating in the range 298–1623 K, in sinter mixtures with compositions designed to form SFCA-I instead of SFCA, and will be the first in situ XRD-based study to do so.
ANSTO are acknowledged for providing financial support for this research. This research was performed, in part, on the powder diffraction beamline (10BM1) at the Australian Synchrotron, Victoria, Australia, under beamtime award AS113/PD4160. The authors wish to thank: Caroline Johnson (CSIRO Process Science and Engineering) for assistance with synchrotron data collection; Matthew Glenn (CPSE) for assistance with scanning electron microscopy; Nick Wilson (CPSE) for assistance with EPMA analyses; and Lisa -Famularo (CPSE) for conducting Fe2+ determination.