Solid/liquid Mass Transfer Correlated to Mixing Pattern in a Mechanically-stirred Vessel

Abstract

Cold model experiment on ion-exchange reaction between pearlite particles and HCl aq. was carried out in order to understand the effect of particles dispersion and operating factors on solid/liquid mass transfer rate in a mechanically-stirred vessel. Inner diameter of vessel was varied in conjunction with both bath depth as 400 (base) and 300 mm. Rotation speed and volume ratio of particles to liquid were changed between 0–240 rpm, 0.02–0.24 (–), respectively.

When rotating speed increased, solid/liquid mass transfer rate increased moderately both in the regions I and III, whereas it increased in the region II. When impeller depth decreased, it was kept almost constant in the region I, increased in the region II and increased moderately in the region III. Solid/liquid mass transfer rate changed less than liquid/liquid one in the region II when rotation speed and impeller height were changed, whereas both of solid/liquid and liquid/liquid mass transfer rates were kept almost constant in the region I. The dimensionless equation on solid/liquid mass transfer rate of each region was given as a function of Sherwood number, Reynolds number, volume ratio of particles to liquid and bath depth normalized by vessel diameter. Dispersion ratio in the region II was ranged by solid/liquid mass transfer coefficient and rotation speed or impeller height of the transitions I–II and II–III. Solid/liquid mass transfer rate of mechanical stirring was larger than that of gas injection practice for the same supplied rate of energy into bath.

1. Introduction

Hot metal desulfurization by mechanical stirring has been re-evaluated¹⁾ for high reaction efficiency and stable operation, and approach to accelerate desulfurization has been proposed in a variety of methods.^{2,3,4,5,6,7,8)}

On the other hand, authors carried out the cold model experiment on solid/liquid mixing pattern,⁹⁾ which was clarified into three types as well as liquid/liquid one.¹⁰⁾ Figure 1 shows the categorized three types of solid/liquid mixing pattern. I: region where solid/liquid interface does not reach at upper part of impeller and has no dispersion, II: region where solid arrives at upper part of impeller and dispersion of particles starts into liquid phase, III: region where gas/liquid interface arrives at upper part of impeller and solid and gas dispersion occurs hard into liquid. Solid/liquid mixing pattern transits from I to II, and from II to III as impeller depth, H, decreased and rotation speed, N, increased. And some of authors¹¹⁾ revealed that liquid/liquid mass transfer rate showed characteristic trend depending on liquid/liquid mixing pattern. It was kept nearly constant at lower level in the region I, monotonically increased in the region II except near the region III and its increasing rate decreased in the region II near the region III. However, there is few cold model investigation on the effect of solid/liquid mixing pattern on solid/liquid mass transfer rate with particles lighter than liquid, with the exception that Nakai et al.¹²⁾ studied a relation between solid/liquid mixing pattern by cold model experiment and desulfurization rate by hot model experiment.

Fig. 1.

Schematic view of solid/liquid mixing pattern.

Thus, in order to understand the effect of particles dispersion and operating factors on solid/liquid mass transfer rate, cold model experiment on ion-exchange reaction between pearlite particles and HCl aq. was carried out in a mechanically-stirred vessel. Additionally, solid/liquid mass transfer rate of mechanical stirring was compared with that of gas stirring under the same supplied rate of energy, and with liquid/liquid one.

2. Experimental

2.1. Solid/liquid Mass Transfer

Figure 2 shows a schematic view of experimental apparatus. Perlite particles and 2.35×10^–4 M of HCl aq. were put into an acrylic vessel of inner diameter, D (mm) and height, L (mm) so as to be static bath depth, H₀ (mm). Pearlite (density, ρ_d=100 kg/m³, Mitsui Mining & Smelting Co., Ltd.) was arranged in the almost equal size, immersed into 2×10^–3 M of NaOH aq. for 6 hours and dried in the room for 12 hours. Four blades of impeller was used as shown schematically in Fig. 3. The impeller whose diameter was expressed as d_i mm, thickness as b_i mm and width as w_i mm was set in the central axis of the vessel.

Fig. 2.

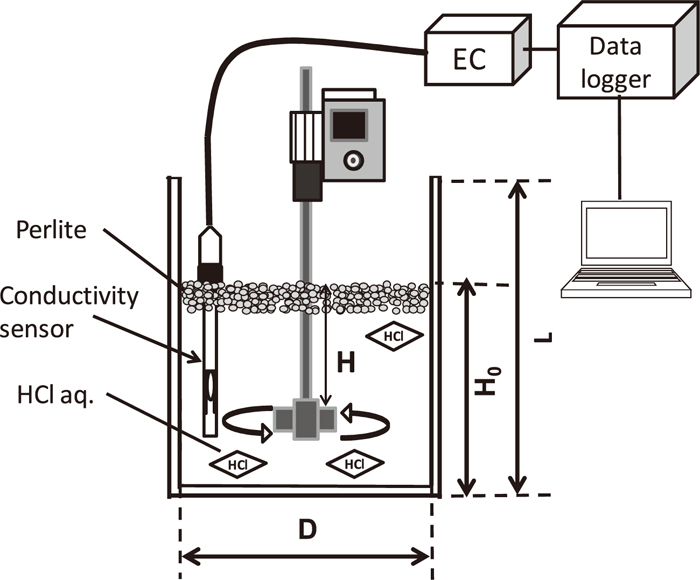
Schematic view of experimental apparatus of mechanical stirring.

Fig. 3.

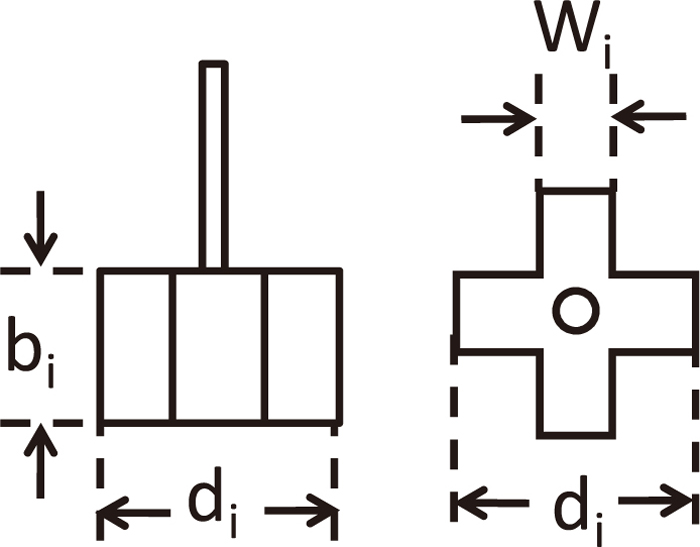
Schematic view of impeller.

H⁺ in HCl aq. reacts with Na⁺ on pearlite surface according to mechanical stirring. H⁺ was measured by electrical conductivity meter (Automatic system research, mk-250EC) shown as EC in Fig. 2 and mass transfer rate was calculated from its temporal change. Experimental condition is shown in Table 1. The operating factors such as rotating speed, N (rpm), impeller depth, H (mm), volumetric ratio of solid to liquid, V_S/V_L were changed on the basis of D=H₀=300 mm, (d_i, b_i, w_i)=(116 mm, 67 mm, 31 mm) and d_p=2.3 mm.

Table 1. Experimental condition of mechanical stirring.

Variables
Vessel inner diameter, D (mm)	300, 400
Bath depth, H0 (mm)	300, 400
Impeller diameter, di (mm)	116, 156
Impeller thickness, bi (mm)	67, 85
Impeller width, wi (mm)	31, 42
Rotating speed, N (rpm)	0–335
Impeller depth, H (mm)	0–300
Solid-liquid ratio, VS/VL (–)	0.02, 0.06, 0.12, 0.24
Dispersion phase	Perlite
Mean diameter of perlite, dp (mm)	1.3, 2.3, 3.1

Gas injection practice was carried out for comparison with mechanical stirring. The nozzle with four holes at regular intervals was set in the central axis of the vessel. Gas was injected horizontally into liquid. Experimental condition is shown in Table 2. Gas flow rate, Q (L/min) and nozzle depth, H (mm) were changed under D=H₀=300 mm, hole diameter, d=3 mm and V_S/V_L=0.12.

Table 2. Experimental condition of gas stirring.

Variables
Inner diameter, D(mm)	300
Bath depth, H0 (mm)	300
Gas flow rate, Q (L/min)	5, 20, 40
Nozzle depth, H (mm)	100, 150, 200, 250
Solid-liquid ratio, VS/VL (–)	0.12
Hole diameter, d (mm)	3
Number of hole	4

2.2. Conversion Principle of Conductivity to Concentration of Hydrochloric Acid

As hydrochloric acid is strong acid, it is ionized perfectly by Eq. (1) in water.   

$$\text{HCl}\to {\text{H}}^{+}+{\text{Cl}}^{-}$$(1)

Mole electric conductivity, λ, of strong electrolyte defined by electric conductivity, κ (S/cm), per electrolyte concentration, C (mol/L) was expressed as Eq. (2).   

$$\lambda \equiv {10}^3\kappa /C={\lambda }_{({\text{H}}^{+})}+{\lambda }_{{\text{(Cl}}^{-})}={\lambda }^{\infty }$$(2)

where λ^∞: infinitely-diluted mole electric conductivity (Scm²mol^–1), λ_(H+) = 349.8 (Scm²mol^–1), λ_(Cl–) = 76.4 (Scm²mol^–1).¹³⁾ Thus, Eq. (2) became   

$$\lambda ={10}^3\kappa /C={\lambda }^{\infty }=349.8+76.4=426.2$$(3)

  

$$\kappa =426.2\text{C}$$(4)

Equation (4) was verified by the experiment where a given amount of hydrochloric acid was dissolved in ion-exchanged water of 100 mL and electric conductivity was measured. Relation between electric conductivity and concentration of hydrochloric acid is shown in Fig. 4(a). “Theoretical” in Fig. 4(a) means Eq. (4). Theoretical electric conductivity values agreed well with measured ones. Figure 4(b) shows relation between measured and theoretical electric conductivity. It was found that concentration of hydrochloric acid is obtained from Eq. (4) by measuring electric conductivity from these two figures.

Fig. 4.

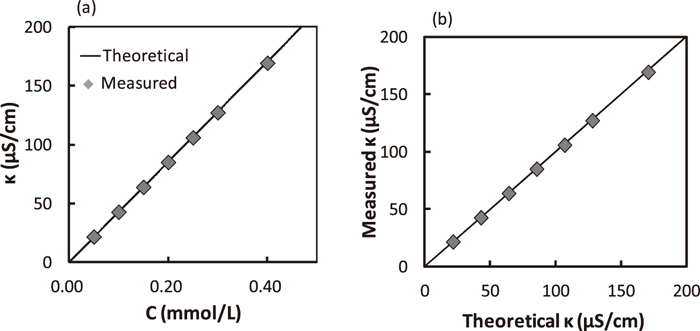
Relation between electric conductivity and concentration of hydrochloric acid.

3. Results and Discussion

3.1. Effect of Solid/liquid Mixing Pattern on Mass Transfer

3.1.1. Calculation of Solid/liquid Mass Transfer Coefficient

Ion-exchanged reaction of pearlite is expressed by Eq. (5).   

$$\text{R}-{\text{Na}}^{+}+\text{HCl}\to \text{R}-{\text{H}}^{+}+\text{NaCl}$$(5)

Ion-exchanged reaction rate is determined by diffusion in the fluid film, chemical reaction on the solid/liquid interface or diffusion in the solid phase. As the rate is normally controlled by the diffusion in the fluid film¹⁴⁾ at the early stage, solid/liquid mass transfer rate is given by Eq. (6).   

$$-\text{VdC}/\text{dt}={\text{k}}_{\text{S}-\text{L}}{\text{a}}_{\text{S}-\text{L}}\left(\text{C}-{\text{C}}_{\text{i}}\right)$$(6)

where, k_S-L: solid/liquid mass transfer coefficient (m/s), a_S-L: total surface area of pearlite particles (m²), C: HCl concentration (kgmol/m³), C_i: HCl concentration on pearlite (kgmol/m³), V: volume of HCl aq. (m³). On the assumption that C_i equals to be 0,^15,16) integration of Eq. (6) gives Eq. (7) , where C₀: initial HCl concentration (kgmol/m³).   

$$\text{Vln}\left({\text{C}}_0/\text{C}\right)={\text{k}}_{\text{S}-\text{L}}{\text{a}}_{\text{S}-\text{L}}\mathrm{\hspace{0.17em} }\text{t}$$(7)

Some examples of temporal change in C₀/C are shown in Fig. 5. As logarithmic C₀/C increased almost linearly with time, the slope enabled us to achieve k_S-L. The a_S-L was obtained from the average diameter regarding as sphere. As perlite particles moved quickly on HCl aq. even at the minimum rotation speed, N=40 rpm in the experimental condition, total surface area of pealite particles was used for Eq. (7).

Fig. 5.

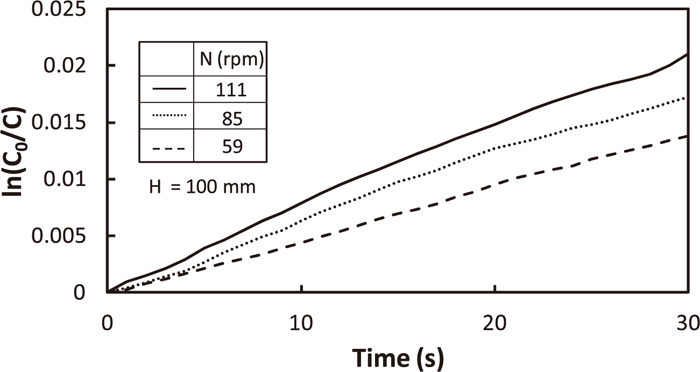
Typical examples of temporal change in hydrochloric acid concentration.

3.1.2. Effect of Rotation Speed on Solid/liquid Mass Transfer Rate

Relation between k_S-L and rotating speed is shown in Fig. 6. V_S/V_L is fixed to 0.12 and H is varied between 50 and 200 mm. Each plot is differentiated by solid/liquid mixing pattern⁹⁾ describer in chapter 1. The k_S-L value was near 0 for N=0 rpm, which meant that solid/liquid mass transfer rate depended on mechanical stirring. k_S-L increased with the increase in N due to the stirring energy in bath. k_S-L increased moderately with the increase in N in the region I, the increasing rate of k_S-L against N became larger in the region II, and it returned to the moderate increase in the region III. The reason of the behavior in the region II is why solid particles are partly dispersed in continuous liquid phase where solid/liquid stirring is seemed to be more severe than the floated solid particles/liquid. The additional discussion will be made in section 3.4. On the other hand, both in the region I where no solid particles disperse and in the region III where almost all of solid particles exist in liquid, the increase in k_S-L depends only on the stirring energy by impeller rotation.

Fig. 6.

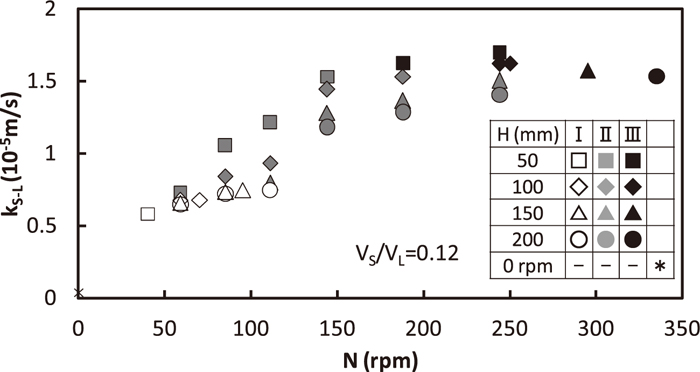
Relation between solid/liquid mass transfer coefficient and rotating speed.

3.1.3. Effect of Impeller Height on Solid/liquid Mass Transfer Rate

Relation between k_S-L and depth, H, from gas/solid interface to upper part of impeller is shown in Fig. 7. V_S/V_L is fixed to be 0.12 and N is varied between 59 and 244 rpm. k_S-L increased with the decrease in H because of the increasing ratio of dispersed particles in the region II. However, k_S-L was kept to be almost constant in the region I shown in N=59 rpm, because the change in H gave no change in stirring energy nor dispersion.

Fig. 7.

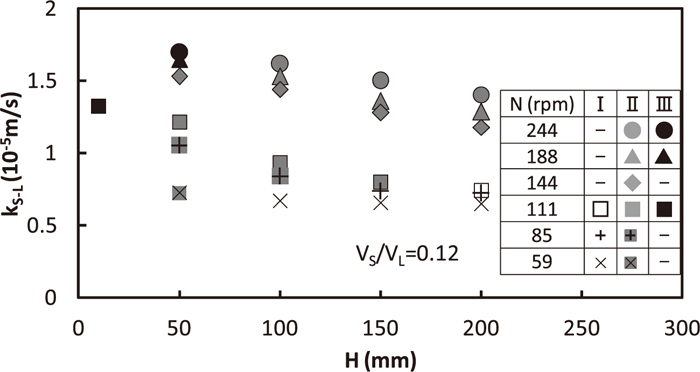
Relation between solid/liquid mass transfer coefficient and impeller position.

3.1.4. Effect of Ratio of Solid/liquid on Solid/liquid Mass Transfer Rate

Effect of V_S/V_L on k_S-L for N=111 rpm is shown in Fig. 8. Both in the regions of II and III, k_S-L had no change in V_S/V_L. However, k_S-L in the region I increased with the decrease in V_S/V_L for the equal H because dispersed solid particles contacted with liquid more sufficiently.

Fig. 8.

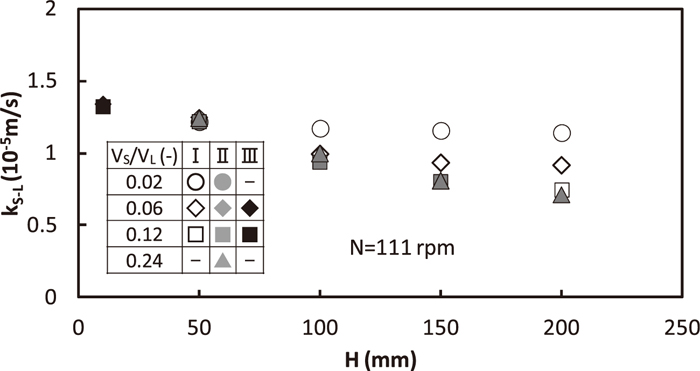
Effect of V_S/V_L on solid/liquid mass transfer coefficient.

3.1.5. Effect of Impeller Diameter on Solid/liquid Mass Transfer Rate

Relation between k_S-L and H in the region II is shown in Fig. 9. Here, both impeller diameter and rotation speed changed so as to supplied rate, ε, of energy into bath and V_S/V_L was fixed to be 1.86×10^–2 w/kg, 0.12 (–), respectively. ε was calculated from the method in section 3.2. Solid/liquid mass transfer rate has no change for the same ε.

Fig. 9.

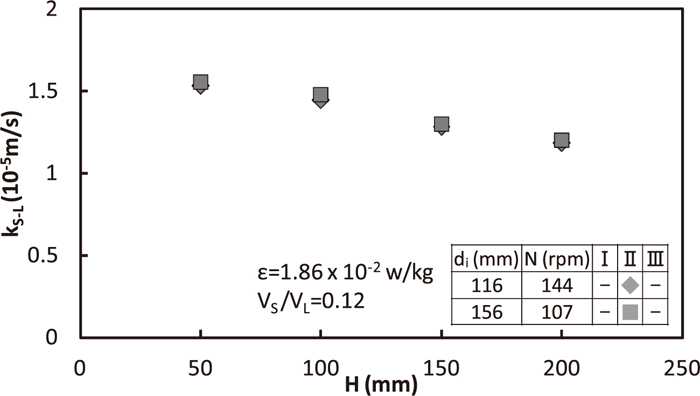
Effect of impeller diameter on solid/liquid mass transfer coefficient for the equal energy supplied rate into bath.

3.1.6. Effect of Vessel Diameter on Solid/liquid Mass Transfer Rate

Relation between k_S-L and H in the region II is shown in Fig. 10. Here, both impeller diameter and rotation speed changed and V_S/V_L, d_i was fixed to be 0.12 (–), 116 mm, respectively. ε equaled to 1.86×10^–2 w/kg for (D,N) = (300 mm, 144 rpm) as well as (400 mm, 178 rpm). Both of larger vessel diameter and rotation speed increased k_S-L, for the same ε value.

Fig. 10.

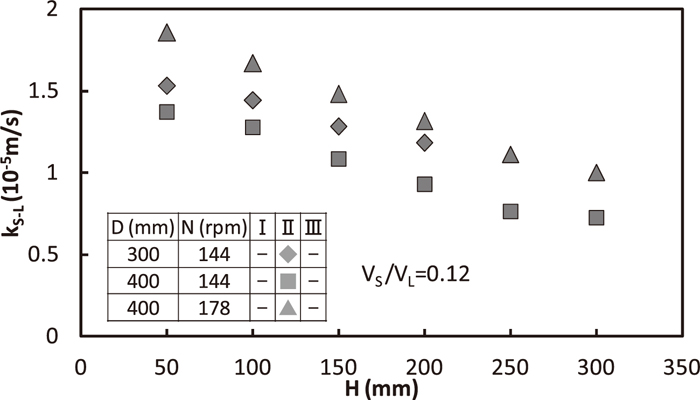
Effect of vessel diameter on solid/liquid mass transfer coefficient.

3.1.7. Effect of Pearlite Diameter on Solid/liquid Mass Transfer Rate

Relation between k_S-L and H is shown in Fig. 11. Pearlite diameter, d_p was changed from 1.3 mm to 3.1 mm, although V_S/V_L, N and D are fixed to be 0.12 (–), 144 rpm, 300 mm, respectively. k_S-L did not depend on pearlite diameter.

Fig. 11.

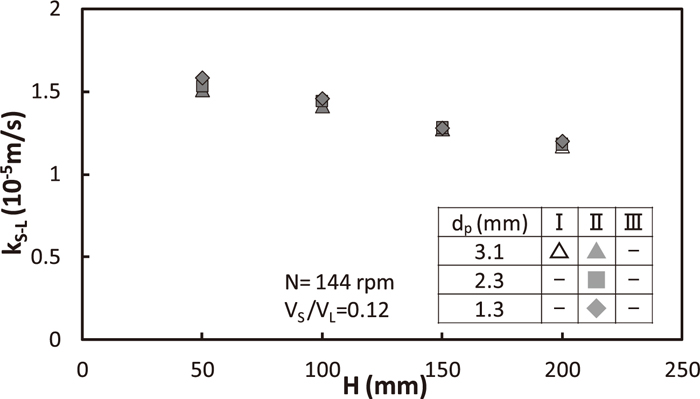
Effect of particle diameter on solid/liquid mass transfer coefficient.

3.2. Comparison between Solid/liquid and Liquid/liquid Mass Transfer Rates

Relations between k_S-L and H, and liquid/liquid capacity coefficient, k_L-La_L-L (m³/s) and H¹¹⁾ are shown in Fig. 12. Although both of solid/liquid and liquid/liquid mass transfer rates increased with the decrease in H in the region II, the increasing ratio of the liquid/liquid is more remarkable than that of the solid/liquid. It is due to the fact that the decrease in H causes the increase in liquid/liquid interfacial area, a_L-L as the dispersed phase increases, whereas it is not expected for the solid/liquid. Both of liquid/liquid and solid liquid mass transfer rates were almost constant in the region I.

Fig. 12.

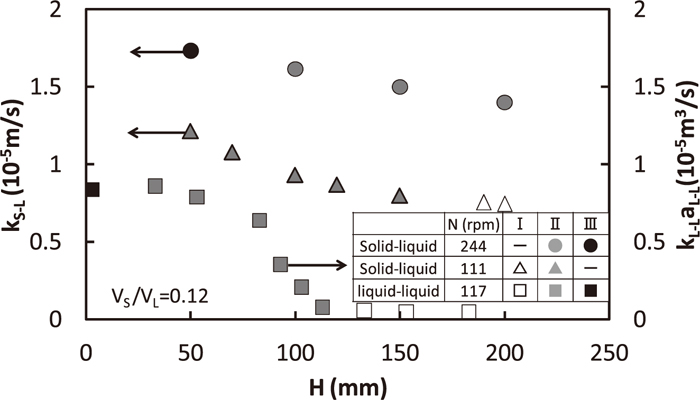
Comparison between solid/liquid and liquid/liquid mass transfer capacity coefficients.

3.3. Dimensionless Equation of Solid/liquid Mass Transfer Rate

Assuming that a single particle moves into liquid at a terminal velocity, Froessling formula¹⁷⁾ on solid/liquid mass transfer rate was introduced as Eq. (8). Semi-empirical equations¹⁸⁾ for particles/liquid mass transfer rate in a mechanically-stirred vessel were proposed as Eq. (9), based on Eq. (8).   

$$\text{Sh}=2+0.6{\text{Re}}_{\mathrm{p}}^{1/2}{\text{Sc}}^{1/3}$$(8)

  

$$\text{Sh}=\text{A}+{\text{BRe}}_{\text{p}}^{\text{n}}{\text{Sc}}^{\text{m}}$$(9)

where Sh: Sherwood number (=k_S-Ld_p/D_HCl), Re_p: particle Reynolds number (=ρNd_pd_i/μ), Sc: Schmidt number (=μ/ρD_HCl), D_HCl: diffusivity coefficient of HCl (m²/s), ρ: density of HCl aq. (kg/m³), μ: viscosity coefficient of HCl (Pa·s). A, B, n and m in Eq. (9) are factors determined by the experiment.

The k_S-L values were affected on V_S/V_L in addition to N in the region I as seen in Fig. 8, and on H in the regions II and III like Figs. 6, 7, 8, 9, 10, 11, 12. Thus, the dimensionless Eq. (9) for region I and II was modified as Eqs. (10) and (11), respectively.

The region I;   

$$\text{Sh}=2+{\text{BRe}}_{\text{p}}^{\text{n}}{\text{Sc}}^{1/3}{\left({\text{V}}_{\text{S}}/{\text{V}}_{\text{L}}\right)}^{\text{P}}$$(10)

The region II and III;   

$$\text{Sh}=2+{\text{BRe}}_{\text{p}}^{\text{n}}{\text{Sc}}^{1/3}{\left(\text{H}/\text{D}\right)}^{\text{q}}$$(11)

where p and q are factors obtained from regression analysis.

The dimensionless equation of each region is obtained as shown in Fig. 13. Data in the region II dispersed more widely than those in the regions I or III due to partly dispersed two reaction zones. Factors (B, n, p) in the region I were (0.071, 0.65, –0.24) obtained from the data of N ≧ 40 rpm (Re_P ≧ 4.0) in this experimental condition, whereas (B, n, q) in the regions II and III are (0.063, 0.87, –0.38), (0.28, 0.46, –0.09), respectively. Power of Re_p in the region II was larger than any other regions and that of (H/D) in the region II was smaller than that in the region III. It result from the change in dispersion behavior of particles which generates only in the region II. From the point of dispersion ratio of particles, the change in k_S-L is described in the following section 3.4.

Fig. 13.

Dimensionless equation on solid/liquid mass transfer coefficient corresponding to mixing pattern.

The dimensionless equation of all data in the regions I to III is obtained from Fig. 14. As power of (V_S/V_L) was negligible small, (B, n, q) became (0.079, 0.74, –0.24).

Fig. 14.

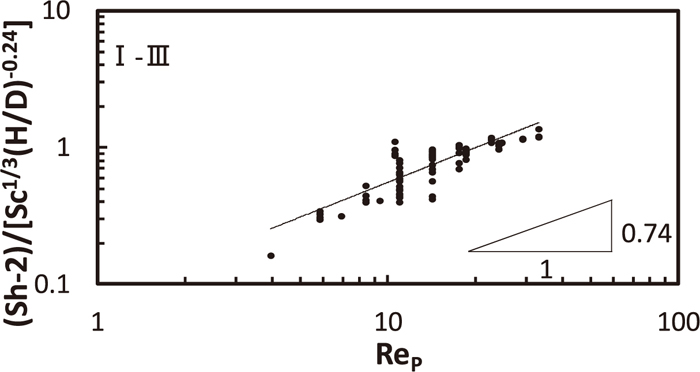
Dimensionless equation on solid/liquid mass transfer coefficient for the region I–III.

3.4. Dispersion Ratio in the Region II

All particles exists on liquid in the region I and most particles disperse into liquid in the region III. On the other hand, in the region II dispersion of particles increases with the increase in rotation speed and the decrease in distance between free surface and impeller position. Defining k_S-L between floating particles and liquid as k_I, and that between dispersed particles and liquid as k_III, k_S-L of the region II, k_II is expressed by the dispersed particles ratio, α, as follows.   

$${\text{k}}_{\text{II}}=(1-\alpha ){\text{k}}_{\text{I}}+\alpha {\text{k}}_{\text{III}}$$(12)

Rearranging Eq. (12),   

$$\alpha =({\text{k}}_{\text{II}}-{\text{k}}_{\text{I}})/({\text{k}}_{\text{III}}-{\text{k}}_{\text{I}})$$(13)

Here, α is expressed using the k_S-L value of the region I near the transition I–II as k_I and the k_S-L value of the region III near the transition II–III as k_III.

When H is changed under constant N, H of the transition I–II and II–III are defined as H_I,t, H_III,t, respectively. Relation between α and (H_II–H_I,t)/(H_III,t–H_I,t) is shown in Fig. 15. H_II means H in the region II. Dispersion ratio in the region II was ranged by normalized H. Change rate of α was shelving in the center of the region II and sharp near the regions I and III.

Fig. 15.

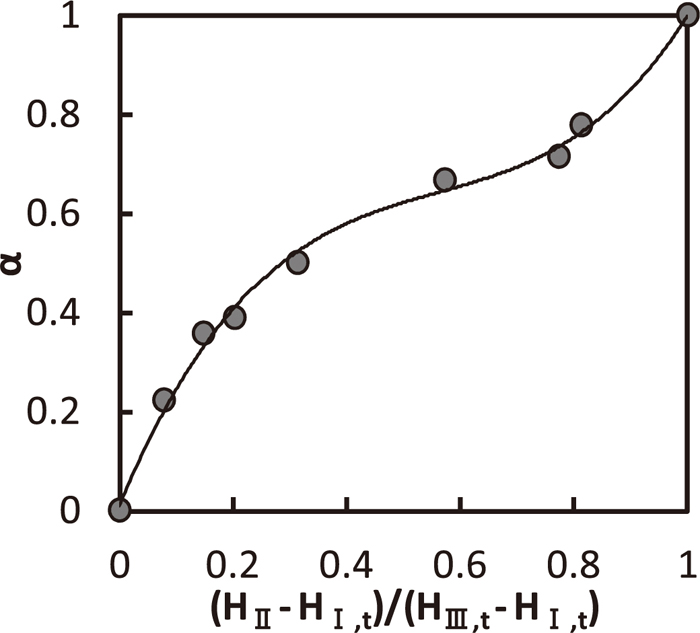
Relation between particles dispersion ratio and impeller position in the region II.

When N is changed under constant H, N of the transition I–II and II–III are defined as N_I,t, N_III,t, respectively. Relation between α and (N_II–N_I,t)/ (N_III,t–N_I,t) is shown in Fig. 16. N_II means N in the region II. As well as Fig. 15, k_S-L values of the region I near the transition I–II and of the region III near the transition II–III were used as constant k_I, k_III, respectively. However, as k_I and k_III in the region II change normally with N because of change in supplied rate of energy into bath, k_I is underestimated, whereas k_III overestimated in Fig. 16. Thus, it was lead to larger α value than the actual one in Eq. (13). From Fig. 16, dispersion ratio in the region II was roughly ranged by normalized N in spite of an overestimate of α curve.

Fig. 16.

Relation between particles dispersion ratio and rotating speed in the region II.

3.5. Comparison of Solid/liquid Mass Transfer Rate between Mechanical Stirring and Gas Injection

3.5.1. Solid/liquid Mass Transfer Rate of Gas Injection Practice

Relation between k_S-L and the distance between gas/solid surface and hole position of the immersed nozzle, H, for the various gas flow rate, Q, is shown in Fig. 17. k_S-L increased with the increase in H and Q, because supplied rate of energy into bath increased.

Fig. 17.

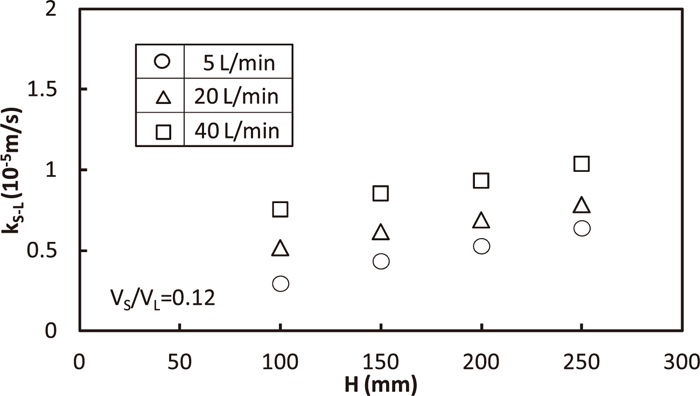
Effect of gas flow rate and gas-injected position on solid/liquid mass transfer coefficient.

3.5.2. Comparison of Solid/liquid Mass Transfer Rate between Mechanical and Gas Stirrings

Here, solid/liquid mass transfer rate was compared between mechanical and gas stirring in the case of the same supplied rate of energy into bath. Supply rate of energy by gas stirring expressed as ε_g (W/kg) is given by Eq. (14).¹⁹⁾   

$${\epsilon }_g=0.0143\text{QT}/{\text{W}}_{\text{w}}\text{log}\left(1+\text{H}/10.3\right)$$(14)

where Q: gas flow rate (NL/min), T: bath temperature (K), W_w: mass of water (kg), H: depth from free surface to the position of gas injection (m).

On the other hand, supplied rate of energy by mechanical stirring expressed as ε_i (W/kg) is given by Eq. (15).²⁰⁾   

$${\epsilon }_{\text{i}}={\text{N}}_{\text{P}}{\rho }_{\text{w}}{\text{N}}^3{\text{d}}_{\text{i}}^5/{\text{W}}_{\text{w}}$$(15)

where N_P: power number (–), ρ_w: liquid density (kg/m³), N: rotation speed (rps), d_i: impeller diameter (m). N_P is calculated from Nagata’s formula.²⁰⁾

Both of ε_g for Q=5, 10 and 20 L/min were calculated from Eq. (14) for D=H₀=0.3 m, H=0.1 m and T=298 K. Rotation speed for mechanical stirring was obtained by substituting ε_i values corresponding to the above calculated ε_g ones and N_p given by Horiuchi et al.¹¹⁾ into Eq. (15). As shown in Table 3, the rotation speeds, N=111, 146 and 189 rpm correspond to gas flow rates, Q=5, 10 and 20 L/min, respectively.

Table 3. Gas flow rate and rotating speed for the same supplied rate of stirring energy.

Q (L/min)	N (rpm)	ε×103 (W/kg)
5	111	9.4
20	188	37.5
40	244	74.9

Comparison of k_S-L between mechanical and gas stirring for the same supplied rate of energy into bath is shown in Fig. 18. k_S-L values of mechanical stirring were distinguished by the mixing pattern. No region I occurred at ε_i = 37.5 × 10^–3 and 74.9 × 10^–3 w/kg, even if the impeller was just set on the vessel bottom. Solid/liquid mass transfer rate of mechanical stirring was faster than that of gas stirring in this experimental condition regardless of the mixing pattern. On the other hand, liquid/liquid mass transfer rate of mechanical stirring in the region I and up to a point of the region II is smaller than those of gas stirring, whereas they were larger than above the point of the region II and the region III.¹¹⁾ As known by the visual observation, it is due to the fact that solid/liquid mixing during gas injection practice is limited to the gas passing part and a lot of particles floated on liquid steadily.

Fig. 18.

Comparison of solid/liquid mass transfer coefficient between mechanical stirring and gas injection for the equal energy supplied rate into bath.

4. Conclusions

Cold model experiment on ion-exchange reaction between pearlite particles and HCl aq. was carried out, and the effect of particles dispersion and operating factors on solid/liquid mass transfer rate was made in a mechanically-stirred vessel. Additionally, solid/liquid mass transfer rate of mechanical stirring was compared with that of gas stirring under the same supplied rate of energy, and with liquid/liquid one.

(1) Solid/liquid mass transfer rate depends on solid/liquid mixing pattern. When rotating speed increased, it increased moderately both in the regions I and III, whereas it increased in the region II. When impeller depth decreased, it was kept almost constant in the region I, increased in the region II and increased moderately in the region III.

(2) Solid/liquid mass transfer rate increased with the increase in rotation speed, the decrease in impeller height and volumetric ratio of solid to liquid in the region I, although it was not influenced by particles diameter. Solid/liquid mass transfer rate did not depend on impeller diameter, but it increased with the increase in vessel diameter for the same supplied rate of energy into bath.

(3) Solid/liquid mass transfer rate changed less than liquid/liquid one in the region II when rotation speed and impeller height ware changed, whereas both of solid/liquid and liquid/liquid mass transfer rates were kept almost constant in the region I.

(4) The dimensionless equation of each region was obtained as follows:

region I; Sh=2+0.071Re_p^0.65Sc^1/3(V_S/V_L)^–0.24

region II; Sh=2+0.063Re_p^0.87Sc^1/3(H/D)^–0.38

region III; Sh=2+0.28Re_p^0.46Sc^1/3(H/D)^–0.09

(5) Dispersion ratio in the region II was ranged by solid/liquid mass transfer coefficient and rotation speed or impeller height of the transitions I–II and II–III.

(6) Solid/liquid mass transfer rate of mechanical stirring was larger than that of gas injection practice for the same supplied rate of energy into bath.

Acknowledgements

This work was performed under the Cooperative Research Program of “Network Joint Center for Materials and Devices”.

References

• 1)   N.  Kikuchi,  S.  Nabeshima,  S.  Takeuchi,  T.  Yamauchi,  Y.  Kitano and  S.  Ogura: Tetsu-to-Hagané, 90 (2004), 322.
• 2)   T.  Nomura and  M.  Iguchi: Tetsu-to-Hagané, 88 (2002), 1.
• 3)   S.  Sato,  T.  Ohmi and  M.  Iguchi: Tetsu-to-Hagané, 92 (2006), 469.
• 4)   S.  Sato,  T.  Ohmi and  M.  Iguchi: Tetsu-to-Hagané, 95 (2009), 837.
• 5)   T.  Sukawa and  M.  Iguchi: ISIJ Int., 45 (2005), 1145.
• 6)   S.  Kuroyanagi,  N.  Yamamoto,  J.  Matoba,  H.  Horii,  K.  Ito and  N.  Kikuchi: Tetsu-to-Hagané, 90 (2004), 329.
• 7)   K.  Ito,  N.  Yamamoto and  S.  Kuronaga: ISIJ Int., 46 (2006), 1791.
• 8)   A.  Matsui,  Y.  Nakai,  N.  Kikuchi,  Y.  Miki,  S.  Sato,  R.  Kawabata and  A.  Ichikawa: Tetsu-to-Hagané, 99 (2013), 458.
• 9)   R.  Shiba, Md. A. Uddin, Y. Kato and Y. Uchida: Private Communication, (2014).
• 10)   S.  Horiuchi, Md. A.Uddin, Y. Kato and N. Kikuchi: ISIJ Int., 54 (2014), 82.
• 11)   S.  Horiuchi, Md. A. Uddin, Y. Kato, Y. Takahashi and Y. Uchida: ISIJ Int., 54 (2014), 87.
• 12)   Y.  Nakai,  I.  Sumi,  H.  Matsuno,  N.  Kikuchi and  Y.  Kishimoto: ISIJ Int., 50 (2010), 403.
• 13)  Chemical Society of Japan: Handbook of Chemistry, Basic Edition, Rev. 2nd ed., Maruzen, Tokyo, (1975), 1191.
• 14)   H.  Yamamoto: Seisan Kenkyu, 12 (1960), No. 2, 31.
• 15)   A. G.  Livingston and  J. B.  Noble: Chem. Eng. Sci., 48 (1993), 1174.
• 16)   R.  Hausmann,  C.  Hoffmann,  M.  Franzerb and  W. H.  Holl: Chem. Eng. Sci., 55 (2000), 1477.
• 17)  Society of Chemical Enginees, Japan: Handbook of Chemical Engineering, Rev. 7th ed., Maruzen, Tokyo, (2011), 355.
• 18)  Satake Chemical Equipment Mfg Ltd.: Kakuhan Gijyutsu (Mixing Technology), Satake Chemical Equipment Mfg Ltd., Osaka, (1992), 318.
• 19)   K.  Nakanishi,  Y.  Kato,  T.  Nozaki and  T.  Emi: Tetsu-to-Hagané, 66 (1980), 1307.
• 20)  Society of Chemical Enginees, Japan: Handbook of Chemical Engineering, Rev. 7th ed., Maruzen, Tokyo, (2011), 339.