Direct Measurement of Agglomeration Force Exerted between Alumina Particles in Molten Steel

Abstract

As a fundamental study to clarify the agglomeration and coalescence of alumina inclusions in molten steel from the viewpoint of interfacial chemical interactions, it has been experimentally verified for the first time that significant agglomeration force is exerted between alumina particles in aluminum deoxidized molten steel by using a newly established experimental method. In this method, the agglomeration force exerted between alumina particles in molten steel is directly measured separately from the effect of molten steel flow. In addition, it has been quantitatively demonstrated that the contact angles measured between aluminum deoxidized molten steel and an alumina plate are larger than those between the molten iron-oxygen alloy and the alumina plate, which have already been measured by other researchers. Moreover, it has also been indicated by analyzing the actual measurement values of agglomeration force with an interaction model taking contact angles and interfacial properties into consideration that the agglomeration force between the alumina particles in aluminum deoxidized molten steel derives not from the van der Waals force but from the cavity bridge force occurring due to molten steel, which is unlikely to wet the alumina particles. Meanwhile, it has been assumed that the agglomeration force on spherical alumina inclusions in aluminum deoxidized molten steel calculated on the basis of the interaction model according to the cavity bridge force is greater than the buoyant force and drag force, and the alumina inclusions once coming into contact are therefore not prone to be simply dissociated even under molten steel flow. Thus, they maintain the agglomeration state and are subsequently sintered and form comparatively solidly bonded alumina clusters.

1. Introduction

Refined molten steel is usually deoxidized with relatively inexpensive aluminum having high deoxidizing ability. Generated alumina inclusions having approximately few microns in size form alumina clusters through collision, agglomeration, and coalescence, with some of them remaining in the continuously cast slabs, thus becoming the cause of surface and internal defects. In steelmaking processes, alumina inclusions, as coarse inclusions favorable for flotation, must be removed from the inside of molten steel by facilitating the agglomeration and coalescence of alumina inclusions by stirring or flow control of molten steel. In order to meet this need, it is extremely important to scientifically elucidate the agglomeration mechanism of alumina inclusions in molten steel.

In early studies on the inclusion behavior in molten steel, the kinetic elucidation was energetically performed on the deoxidation of molten steel based on the oxygen concentration variation in molten steel and particle size distribution of deoxidation products in rapidly quenched samples, which indicated that the deoxidation rates are controlled by the agglomeration and separation step of deoxidation products. Taniguchi et al. have recently given a detailed explanation of fluid dynamic actions such as Brownian agglomeration, agglomeration by laminar shear flow, turbulent agglomeration, and agglomeration by Stokes collision regarding the agglomeration and coalescence of inclusions.¹⁾ They conducted water model experiments²⁾ and molten aluminum model experiments³⁾ using quasi-inclusion particles and evaluated the behavior of turbulent agglomeration according to the agglomeration coefficient taking the van der Waals force into consideration as interparticle interaction. In addition, through in-situ observation on the behavior of inclusions drifting on the molten steel surface using a confocal scanning laser microscope combined with an infrared image furnace, Yin et al.⁴⁾ indicated that powerful agglomeration force attributable to the capillary force is exerted especially between alumina inclusions. Moreover, Nakajima et al.⁵⁾ indicated that the agglomeration force is intensively affected by the phase condition (solid phase, liquid phase, or solid-liquid phase) of an inclusion and its contact angle, by quantitatively analyzing the agglomeration force based on the capillary force as the interparticle interaction on the molten steel surface in consideration of size, shape, composition, and interfacial properties of inclusions. Thus, in addition to fluid dynamic actions, the importance of interfacial chemical interactions between particles has been pointed out regarding the agglomeration and coalescence of inclusions in molten steel. Nevertheless, the agglomeration mechanism of alumina inclusions in molten steel has not yet been adequately elucidated because it is difficult to independently extract only interfacial chemical interactions between inclusions in molten steel and to investigate them in detail based only on the size distribution evaluation of inclusions in a rapidly quenched sample, water model experiments and molten aluminum model experiments using quasi-inclusion particles, or a direct observation of inclusions on the molten steel surface.

In this paper, as a fundamental study to clarify the agglomeration mechanism of alumina inclusions in molten steel from the viewpoint of interfacial chemical interactions, the contact angle between aluminum deoxidized molten steel and an alumina plate was actually measured, its quantitative validity was verified, and the agglomeration force exerted between the alumina particles in molten steel was directly measured separately from the effect of molten steel flow. The origin of agglomeration force exerted between alumina particles in molten steel was identified by analyzing the actually measured agglomeration force using an interaction model, allowing for interfacial properties between molten steel and alumina particles. In addition, the mechanism where alumina inclusions maintain the agglomeration state under molten steel flow was also discussed by comparing the agglomeration force calculated from the interaction model with the buoyant force and drag force for the spherical alumina inclusions.

2. Experimental Methods

2.1. Experiment for Contact Angle Measurement

Steel samples for contact angle measurement were fabricated by cutting into cubes of 3 mm from solidified steel ingots, which were obtained from electrolytic iron (carbon concentration = 0.001 mass%, sulfur concentration = 0.0001 mass%, and oxygen concentration = 0.005 mass%) that was melted by high-frequency induction melting furnace under an Ar gas atmosphere, and deoxidized by adding a designated amount of Al at a molten steel temperature of 1600°C. The steel samples had an Al concentration in the range of 0.006–0.057 mass%. Al₂O₃ plates with a smoothly ground surface and a thickness of 7 mm were prepared by manufacturing the cylindrical tablets of 10 mm in diameter from an alumina reagent with a high purity of 99.9 mass% by one-axis compression formation under a pressure of 196 MPa and sintering for 90 min under an Ar gas atmosphere at a temperature of 1600°C.

A schematic view of the experimental apparatus used in the contact angle measurement is shown in Fig. 1. A resistance heating furnace with heating elements of graphite cylinders, heated by high-frequency induction coils, was used for the contact angle measurement experiment. An alumina tube of 12 mm inside diameter and 25 mm height with an Al₂O₃ plate arranged at the bottom was placed in an alumina crucible of 21 mm inside diameter and 45 mm height and then fixed with gaps at the bottom and the side filled with an alumina reagent. This complete alumina crucible was put into a graphite crucible of 52 mm inside diameter and 160 mm height, which was placed in the melting furnace. The steel sample of 3 mm cube with a designated Al concentration was loaded onto the Al₂O₃ plate and the temperature of the resistance heating furnace was raised to 1600°C under an Ar gas atmosphere. A drop of molten steel was brought into contact with the Al₂O₃ plate for 30 min before the power source of the melting furnace was disconnected, and this was solidified into the shape at the time of melting and then cooled to room temperature without any change. Photographs were taken of the front shape of the solidified specimens having a drop shape, which were taken out and placed on a flat table after the experiment. The average value of contact angles on the right and left, which were directly estimated from these photographs, was assumed to be the contact angle between molten steel and Al₂O₃ plate.

Fig. 1.

Schematic view of the experimental apparatus for contact angle measurement.

2.2. Experiment for Agglomeration Force Measurement

An experimental apparatus for measuring the agglomeration force between Al₂O₃ particles in molten steel is shown in Fig. 2. A resistance heating furnace with heating elements of graphite cylinders (graphite heater), heated by high-frequency induction coils, and a graphite crucible were used in the agglomeration force measurement experiment for the purpose of restraining the molten steel flow as much as possible. For the agglomeration force measurement, Al₂O₃ cylinders of a designated diameter were fastened vertically on the inner wall of an alumina crucible having an inner diameter of 40 mm and a height of 150 mm. On the other hand, Al₂O₃ cylinders with the same diameter and a length of 30 mm for the agglomeration force measurement were fastened to the lower end of an alumina protective tube of 8 mm in outer diameter and 380–440 mm in length. The upper end of this tube was connected to an aluminum rod on the melting furnace such that the Al₂O₃ cylinders could be arranged to be brought into contact with each other in parallel inside molten steel within the crucible. The alumina protective tube had such a structure that it could smoothly revolve around the rotation axle positioned 40 mm below the upper end of the aluminum rod. A force gauge was set on a moving stage on guide rails and linked to a driving motor via a wire. The force gauge was horizontally connected by a hook to a position 30 mm above the rotation axle of the aluminum rod, where when the aluminum rod was pulled by the driving motor, the traction force generated against the agglomeration force between the Al₂O₃ cylinders in molten steel was outputted on a chart recorder from the force gauge.

Fig. 2.

Schematic view of the experimental apparatus for agglomeration force measurement.

Six hundred grams of electrolytic iron having the same composition as that in the contact angle measurement experiment was melted in the alumina crucible with the Al₂O₃ cylinders fastened on the inner wall under an Ar gas atmosphere. After maintaining the temperature of molten steel at 1600°C, the molten steel was deoxidized by adding a specified amount of Al. The Al₂O₃ cylinders attached to the lower end of the alumina protective tube were immersed in molten steel and brought into contact with the Al₂O₃ cylinders on the inner wall of the crucible in parallel at a position 10 mm above the bottom of the crucible. As an experimental condition, the diameter of Al₂O₃ cylinders for the agglomeration force measurement was varied in a range of 6–10 mm. The moving stage was moved in the direction away from the aluminum rod at a velocity of 0.16 mm·s^–1 by the driving motor, the traction force outputted from the force gauge was recorded on a chart recorder, and based on a change in the traction force, the agglomeration force was evaluated using a later-described method. All Al₂O₃ cylinders between which the agglomeration force was measured were made of Al₂O₃ with a high purity of 99.6 mass%. In order to grasp precisely the molten steel composition during the experiments, the molten steel was sampled using a transparent quartz tube of 6 mm in inner diameter before and after the agglomeration force measurement, and these samples were used for the analysis of Al concentration in molten steel. Al concentration in molten steel during the experiments ranged from 0.005 to 0.073 mass% as the average values of the analytical results before and after the agglomeration force measurement.

3. Experimental Results

3.1. Contact Angles between Al Deoxidized Molten Steel and Al₂O₃ Plates

When a molten steel drop has a radius sufficiently small relative to the capillary length λ_CL (m) calculated from Eq. (1), the shape of the molten steel drop is dominated by surface tension rather than by gravity and can thus be considered to be a partial sphere.   

$${\lambda }_{\mathrm{C}\mathrm{L}}={({\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot {\rho }_{\mathrm{F}\mathrm{e}}{ }^{-1}\cdot \mathrm{g}{ }^{-1})}^{1/2}$$(1)

Here, σ_Fe is the surface tension of molten steel (N·m^–1), ρ_Fe is the density of molten steel (7000 kg·m^–3), and g is the acceleration of gravity (m·s^–2). In this case, the relation between the drop shape and contact angle ${\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ (°) is expressed in Eq. (2).   

$$\mathrm{t}\mathrm{a}\mathrm{n}({\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}/2)=2{\mathrm{h}}_{\mathrm{D}}/{\mathrm{d}}_{\mathrm{C}}$$(2)

Here, h_D is the height of the molten steel drop (m) and d_C is the diameter of the contact face between the molten steel drop and plate (m). When seeking the oxygen concentration in equilibrium with the molten steel drop with an Al concentration of 0.006–0.057 mass% at the experimental temperature of 1600°C by using the thermodynamic reevaluation value⁶⁾ of Al deoxidation equilibrium by Itoh et al., it resulted in the range of 0.0005–0.0020 mass%. At the oxygen concentration within this range, when a surface tension of 1.784–1.939 N·m^–1 calculated from the Table 2 mentioned later was applied to Eq. (1), a capillary length of 5.10–5.32 mm was obtained. Meanwhile, the molten steel with a comparatively low oxygen concentration as in this experiment is unlikely to wet the Al₂O₃ plate (contact angle higher than 90°). Accordingly, assuming that the shape of molten steel drops varies from a perfect sphere (equivalent to a contact angle of 180°) to a hemisphere (equivalent to a contact angle of 90°), the radius of the molten steel drop formed by a steel sample of 3 mm cube was calculated to be 1.94–2.44 mm. If the radius of molten steel drops lies within this range, it is sufficiently small compared with the previously obtained capillary length. Therefore, the shape of molten steel drops in this experiment can be assumed to be a partial sphere, and the contact angle can be evaluated approximately by applying Eq. (2) as the result.

Table 2. Effects of oxygen concentration in molten steel on the surface tension of molten Fe–O alloy.

σFe=1.91–0.358·ln(1+210·aO) (N·m–1) at 1873 K, Ogino et al.11)

σFe=1.97–0.318·ln(1+200·aO) (N·m–1) at 1823 K, Takiuchi et al.8)

σFe=1.90–0.327·ln(1+96·aO) (N·m–1) at 1873 K, Takiuchi et al.9)

σFe=1.97–0.288·ln(1+280·aO) (N·m–1) at 1873 K, Nakashima et al.7)

As an example of the results of this contact angle measurement experiment, a photograph of a solidified drop specimen at an Al concentration [Al] of 0.057 mass%, which was shot from the front, is shown in Fig. 3. As expected from the calculation of capillary length, the solidified drop specimen represents a relatively uniform spherical shape. Accordingly, the comparison between directly measured contact angles and indirectly calculated contact angles by using Eq. (2) from the drop shape h_D/d_C read out from the photographs of solidified drop specimens is shown in Table 1. Both contact angles correspond approximately, and more precisely, the directly measured contact angles are slightly larger. Strictly, the drop shape becomes slightly flat due to gravity; thereby, the actual contact angles are marginally larger than the calculated values according to Eq. (2), where it is assumed that the drop shape is a sphere. Hence, it is judged that the directly measured contact angles are reasonable values, and high-precision evaluation can thus successfully be conducted.

Fig. 3.

Photograph of a solidified drop specimen obtained in the contact angle measurement experiment ([Al] = 0.057 mass%, ${\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ = 150°).

Table 1. Comparison between directly measured contact angles by an angle gauge and indirectly calculated contact angles from 2h_D/d_C by assuming a spherical drop shape.

[Al]	Measured ${\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ by an angle gauge (°)	Calculated ${\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ from 2hD/dC by assuming a spherical drop shape (°)
0.006	138.5	138.2
0.021	155.3	154.9
0.057	150.0	148.1

The effect of Al concentration in molten steel on the directly measured contact angle between molten steel and Al₂O₃ plate is shown in Fig. 4. Although the contact angle increases with Al concentration in molten steel, an approximately constant contact angle is exhibited when the Al concentration reaches 0.02 mass% or higher. This reason is presumed as follows. In the region where the Al concentration in the molten steel is less than 0.02 mass%, the oxygen concentration being an interfacial active element decreases as Al concentration increases, so that the contact angle increases. In contrast, in the region where the Al concentration is 0.02 mass% or more, the molten steel is sufficiently deoxidized and the effect of oxygen is negligible, so that the contact angle becomes constant. In this study, contact angles of 155.3° and 150.0° obtained in the sufficiently deoxidized molten steel at an Al concentration of 0.02 mass% or more were considered to be the contact angles between Al deoxidized molten steel and Al₂O₃ plate.

Fig. 4.

Effect of Al concentration in molten steel on the contact angle between molten steel and Al₂O₃ plate.

3.2. Agglomeration Force between Al₂O₃ Cylinders in Al Deoxidized Molten Steel

Regarding the two cases of Al concentration in molten steel, 0.005 mass% and 0.063 mass%, the changes in the traction force F_T (N) outputted from the force gauge in the agglomeration force measurement experiment are shown in Fig. 5. Here d_CY is the diameter of an Al₂O₃ cylinder (mm), L_D is the distance from the rotation axle to the lower end of the Al₂O₃ cylinder (mm), L_U is the distance from the rotation axle to the attachment position of the force gauge (mm), and L is the length of the Al₂O₃ cylinder (mm). In the experimental apparatus in Fig. 2, when the moving stage is moved to the side of the driving motor, force is applied in the direction separating the Al₂O₃ cylinders in molten steel away from each other, and thus the traction force measured by the force gauge gradually increases with time. Once the traction force separating the Al₂O₃ cylinders away from each other surpasses the agglomeration force between the Al₂O₃ cylinders, the two Al₂O₃ cylinders are instantly divided and the traction force sharply decreases. Even if the Al concentration in molten steel is varied, the behavior of the measured traction forces is the same and only the absolute value varies according to the molten steel compositions. Therefore, it is considered that the maximum traction force F_T,Max (N) at the moment when the Al₂O₃ cylinders are separated from each other is equivalent to the agglomeration force between the Al₂O₃ cylinders in molten steel at the corresponding Al concentration. Accordingly, it can be seen that the agglomeration force between the Al₂O₃ cylinders in molten steel can be directly measured by using this experimental method according to the compositions of molten steel.

Fig. 5.

Changes in the traction force outputted from the force gauge in the agglomeration force measurement experiment.

The true agglomeration force F_A (N·m^–1) exerted between the Al₂O₃ cylinders is derived through applying the principle of leverage from the maximum traction force measured by the force gauge as shown in Eq. (3).   

$${\mathrm{F}}_{\mathrm{A}}={\mathrm{L}}_{\mathrm{U}}/\{({\mathrm{L}}_{\mathrm{D}}-\mathrm{L}/2)\cdot \mathrm{L}\}\cdot {\mathrm{F}}_{\mathrm{T},\hspace{0.17em}\mathrm{M}\mathrm{a}\mathrm{x}}$$(3)

Figure 6 shows the effect of Al concentration in molten steel on the agglomeration force between the Al₂O₃ cylinders in molten steel. The agglomeration force between the Al₂O₃ cylinders increases with the Al concentration in molten steel, and the former settles at a constant of 14.86 N·m^–1 as the latter reaches 0.02 mass% or more. It is assumed that the reason that the agglomeration force becomes smaller in the region of an Al concentration lower than 0.02 mass% is due to the effects of oxygen in molten steel, which is an interfacial active element, as in the experiment for the contact angle measurement; however, these details remain to be clarified. In this study, a certain agglomeration force obtained at an Al concentration in molten steel of 0.02 mass% or more is considered to be the agglomeration force between the Al₂O₃ cylinders in Al deoxidized molten steel. Figure 7 shows the relation between the agglomeration forces between the Al₂O₃ cylinders in Al deoxidized molten steel and the diameter of Al₂O₃ cylinders. As the diameter of Al₂O₃ cylinders increases, the agglomeration force acting between the Al₂O₃ cylinders in molten steel also increases.

Fig. 6.

Effect of Al concentration in molten steel on the agglomeration force between Al₂O₃ cylinders in molten steel.

Fig. 7.

Relation between the agglomeration forces between Al₂O₃ cylinders in Al deoxidized molten steel and the diameter of Al₂O₃ cylinders.

Figure 8 shows a cross-sectional photograph of Al₂O₃ cylinders in a solidified steel ingot, which were brought into contact with each other in the molten steel at an Al concentration of 0.064 mass% and then rapidly cooled by turning off the power source of the melting furnace. It can be seen that cavity bridges are formed at the contact area between the Al₂O₃ cylinders in Al deoxidized molten steel.

Fig. 8.

Cross-sectional photograph of Al₂O₃ cylinders in a solidified steel ingot ([Al] = 0.064 mass%, d_CY = 8 mm).

4. Discussion

4.1. Effect of Al Deoxidation on Contact Angle between Molten Steel and Al₂O₃

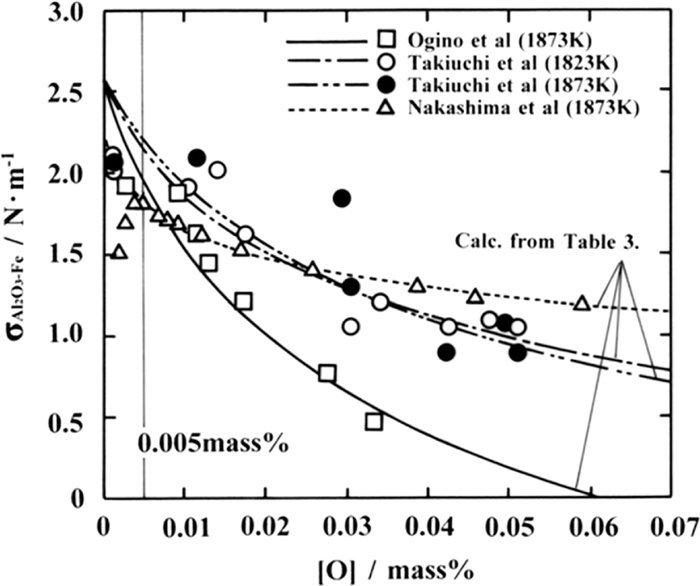
Figure 9 shows the effect of oxygen concentration [O] (mass%) in molten steel on the contact angle between molten steel and an Al₂O₃ plate. Furthermore, as previously mentioned, the oxygen concentration in molten steel in this experiment are equilibrium oxygen concentrations at 1600°C calculated from Al concentrations in molten steel by using the thermodynamic reevaluation value⁶⁾ of the Al deoxidation equilibrium by Itoh et al., and those by Nakashima et al.,⁷⁾ Takiuchi et al.,^8,9) and Ogino et al.¹⁰⁾ are oxygen analytical values of the Fe–O alloy that are not deoxidized with Al. According to their reports,^7,8,9,10) the contact angle between molten steel and Al₂O₃ plate falls to approximately 115–135° as the oxygen concentration in molten steel decreases in the region where the oxygen concentration is not higher than 0.005 mass%. Nevertheless, a large contact angle in the range of 150.0–155.3° was obtained according to the measurement by the author. It has been reported^7,8,9) that the decrease in the measured contact angle between the molten Fe–O alloy and Al₂O₃ plate in the region of low oxygen concentration results from the dissociation of Al₂O₃ plate. It is presumed that since the target of the measurement results by the author is the Al deoxidized molten steel with a dissolved Al of 0.02 mass% or more, there is no dissociation of the Al₂O₃ plate so that the contact angle becomes lager. However, this detail will be quantitatively discussed below.

Fig. 9.

Effect of oxygen concentration in molten steel on the contact angle between molten steel and Al₂O₃ plate.

The contact angle between molten steel and Al₂O₃ is expressed by the following Young’s equation:   

$$\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}=({\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3}-{\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}})/{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}$$(4)

Here, ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3}$ is the surface tension of Al₂O₃ (N·m^–1), and ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ is the interfacial tension between molten steel and Al₂O₃ (N·m^–1). According to the report by Ogino et al.,¹⁰⁾ the surface tension of Al₂O₃ at 1600°C takes a constant value of 0.75 N·m^–1, and thereby, it is found that the contact angle between molten steel and Al₂O₃ depends on the balance between the surface tension of molten steel and the interfacial tension with Al₂O₃. Therefore, the contact angle between molten Fe–Al–O alloy and Al₂O₃ can be quantitatively estimated by applying the surface tension of molten Fe–Al–O alloy and the interfacial tension of molten Fe–Al–O alloy with Al₂O₃, which are formulated from the surface tension of molten Fe–O alloy and the contact angle of molten Fe–O alloy with the Al₂O₃ measured by other researchers,^7,8,9,10,11) to Eq. (4).

4.1.1. Formulation of Surface Tension in Molten Fe–Al–O Alloy

Ogino et al.,^10,11) Takiuchi et al.,^8,9) and Nakashima et al.⁷⁾ investigated the effect of oxygen concentration in molten steel on the surface tension of molten Fe–O alloy, and arranged those measurement results based on Szyszkowski’s equation¹²⁾ capable of allowing for a reduction in the surface tension due to oxygen absorption as shown in Table 2. a_O denotes the activity of oxygen in molten steel. Additionally, the experimental equation by Nakashima et al. in Table 2 was formulated by the author based on their measurement results⁷⁾ according to the later-mentioned procedure as in the case of interfacial tension. Keene¹³⁾ reported dσ_Fe/d[Al]= –0.037 N·m^–1·mass%^–1 as the effect of Al concentration on the surface tension of molten Fe–Al alloy. Even if the Al concentration in molten steel increases to approximately 0.1 mass%, the reduction in the surface tension is no more than 0.0037 N·m^–1, and is thus extremely small compared with a surface tension of 1.90–1.97 N·m^–1 in molten pure iron. Accordingly, the effect is negligible in the Al concentration range of this study, and the experimental equation of Table 2 regarding molten Fe–O alloy thus allows the appropriate evaluation of the surface tension of molten Fe–Al–O alloy.

4.1.2. Formulation of Interfacial Tension between Molten Fe–Al–O Alloy and Al₂O₃ Plates

The Szyszkowski’s equation¹²⁾ of Eq. (5), in which oxygen in molten steel is considered to be an interfacial active element, is also applied to the interfacial tension between molten steel and Al₂O₃, as in the case of surface tension.   

$${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}={\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}{ }^{\mathrm{P}}-\mathrm{R}\cdot \mathrm{T}\cdot {\mathrm{\Gamma }}_{\mathrm{O},\hspace{0.17em}\mathrm{I}}{ }^{\mathrm{S}}\cdot \mathrm{l}\mathrm{n}(1+{\mathrm{K}}_{\mathrm{O},\hspace{0.17em}\mathrm{I}}\cdot {\mathrm{a}}_{\mathrm{O}})$$(5)

Here, ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}{ }^{\mathrm{P}}$ is the interfacial tension between molten pure iron and Al₂O₃ (N·m^–1), R is the gas constant (N·m·K^–1·mol^–1), T is the absolute temperature (K), Γ_O,I^S is the saturated excess of oxygen on the interface between molten steel and Al₂O₃ (mol·m^–2), and K_O,I is the absorption coefficient of oxygen on the interface between molten steel and Al₂O₃. In addition, in the case where oxygen in molten steel is absorbed to the interface between molten steel and Al₂O₃, the interfacial excess of oxygen, Γ_O,I (mol·m^–2), is presented by Gibbs’s isothermal absorption equation of Eq. (6).   

$${\mathrm{\Gamma }}_{\mathrm{O},\hspace{0.17em}\mathrm{I}}=-1/(\mathrm{R}\cdot \mathrm{T})\cdot \mathrm{d}{\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}/\mathrm{d}(\mathrm{l}\mathrm{n}\mathrm{\hspace{0.17em} }{\mathrm{a}}_{\mathrm{O}})$$(6)

The effect of oxygen concentration in molten steel on the interfacial tension between molten steel and Al₂O₃ plate is shown in Fig. 10. The data in Fig. 10 are the interfacial tension between molten Fe–O alloy and Al₂O₃ sought from Eq. (4) by using the surface tensions in Table 2, contact angles in Fig. 9, and Al₂O₃ surface tension of 0.75 N·m^–1. As in the case of contact angles in Fig. 9, when oxygen concentration in molten steel is lowered to 0.005 mass% or less, the reduction in interfacial tension due to the dissociation of Al₂O₃ occurs. However, no dissociation of Al₂O₃ occurs in molten Fe–Al–O alloy. Hence, no decrease but an increase in interfacial tension is expected along with Eq. (5) concomitantly with the reduction in oxygen concentration, even when the oxygen concentration decreases to 0.005 mass% or below. On the other hand, it was reported by Ogino et al.,¹⁴⁾ Takiuchi et al.,⁸⁾ and Nakashima et al.⁷⁾ that FeO·Al₂O₃ (hercynite) is created on the interface between molten steel of high oxygen concentration and Al₂O₃ plates. According to McLean et al.,¹⁵⁾ the oxygen concentration at which Al₂O₃ and FeO·Al₂O₃ coexist is 0058 mass% at 1600°C; therefore, specifically, the data at this oxygen concentration or higher could be affected by FeO·Al₂O₃ existing on the interface. Accordingly, the interfacial tension between molten Fe–Al–O alloy and Al₂O₃ can be formulated by Eq. (5) satisfying the data in Fig. 10 at an oxygen concentration of 0.005–0.058 mass% in molten steel without Al₂O₃ dissociation or FeO–Al₂O₃ formation. Respective ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}{ }^{\mathrm{P}}$ and Γ_O,I^S were sought by extrapolation of data in Fig. 10 to an oxygen concentration of 0 mass% and according to the saturation value of Γ_O,I obtained by applying Eq. (6) to the relation between ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ and ln a_O. In addition, the values of K_O,I were determined by trial and error so that the data ranging from 0.005 to 0.058 mass% of oxygen concentration in Fig. 10 can be best represented by Eq. (5), substituted by ${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}{ }^{\mathrm{P}}$ and Γ_O,I^S obtained above. Moreover, it was regarded to be a_O ≒ [O] because molten Fe–O alloy were used in the measurement by Ogino et al.,^10,11) Takiuchi et al.,^8,9) and Nakashima et al.,⁷⁾ as well as because the oxygen concentration of analysis object lies in the region of 0.058 mass% or below, and the activity coefficient of oxygen estimated using the equilibrium values¹⁶⁾ recommended by the Japan Society for the Promotion of Science also falls within approximately 1–0.98. The experimental equations thus obtained regarding the interfacial tension between molten Fe–Al–O alloy and Al₂O₃ are collectively shown in Table 3, and the calculated values according to these are shown in Fig. 10 for each researcher. These calculated values approximately correspond to the data of the interfacial tension between molten Fe–O alloy and Al₂O₃ in the range of an oxygen concentration of 0.005–0.058 mass% according to each researcher, and also increase concomitantly with a reduction in the oxygen concentration in the region of low oxygen concentration equal to 0.005 mass% or below; therefore, it is conceivable that the experimental equations in Table 3 broadly reproduce the interfacial tension between molten Fe–Al–O alloy and Al₂O₃.

Fig. 10.

Effect of oxygen concentration in molten steel on the interfacial tension between molten steel and Al₂O₃ plate.

Table 3. Effects of oxygen concentration in molten steel on the interfacial tension between molten Fe–Al–O alloy and Al₂O₃.

${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ =2.60–1.049·ln(1+176·aO) (N·m–1) at 1873 K, Ogino et al.

${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ =2.60–0.660·ln(1+208·aO) (N·m–1) at 1823 K, Takiuchi et al.

${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ =2.60–0.834·ln(1+121·aO) (N·m–1) at 1873 K, Takiuchi et al.

${\mathrm{\sigma }}_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}$ =2.20–0.275·ln(1+635·aO) (N·m–1) at 1873 K, Nakashima et al.

4.1.3. Verification of Validity concerning Contact Angle between Al Deoxidized Molten Steel and Al₂O₃

The contact angle between molten Fe–Al–O alloy and Al₂O₃ calculated by substituting the surface tensions in Table 2 and interfacial tension in Table 3, formulated with respect to molten Fe–Al–O alloy for Eq. (4), is shown in Fig. 9 for respective researchers. Considering the variation in actual measurement values, the calculated contact angle comparatively agrees with the corresponding actual measurement value by each researcher under the condition without either Al₂O₃ dissociation or FeO–Al₂O₃ formation on the interface, i.e., at an oxygen concentration range of 0.005–0.058 mass%. Consequently, it is considered that the calculated contact angle also correctly reflects the contact angle between molten Fe–Al–O alloy and Al₂O₃ in the region of low oxygen concentration of 0.005 mass% or below.

Accordingly, the validity of the measured contact angles between Al deoxidized molten steel and Al₂O₃ in this experiment will be verified below by comparing them with the calculated results. Since both the contact angle in Fig. 4 and agglomeration force in Fig. 6 indicate a steady value at an Al concentration of 0.02 mass% or higher, an equilibrium oxygen concentration of 0.0009 mass% is obtained⁶⁾ by assuming the representative Al concentration of Al deoxidized molten steel to be 0.02 mass%. As can be seen from Fig. 9, the estimated contact angles between Al deoxidized molten steel and Al₂O₃ at this oxygen concentration are 156.4° (by Ogino et al. at 1600°C), 154.8° and 160.2° (by Takiuchi et al. at 1550°C and 1600°C, respectively), and 134.0° (by Nakashima et al. at 1600°C), with an average of 151.3°. The actually measured contact angles between Al deoxidized molten steel and Al₂O₃, 150.0° and 155.3°, lie within the range of contact angles calculated by each researcher (a range of 134.0–160.2° between the dotted line and two-dot chain line), and the average of these contact angles, 152.6°, indicates a good correspondence with the average value of previously calculated contact angles. Therefore, it is judged that the average contact angle of 152.6° sought from the actually measured values is an appropriate value as the contact angle between Al deoxidized molten steel and Al₂O₃.

4.2. Origin of Agglomeration Force Exerted between Al₂O₃ Cylinders in Molten Steel

The agglomeration forces exerted between the Al₂O₃ cylinders in molten steel are considered to include: (a) liquid bridge force due to molten oxide that is prone to wet Al₂O₃, (b) van der Waals force, and (c) cavity bridge force attributed to the fact that molten steel is unlikely to wet Al₂O₃.^17,18,19)

Regarding (a), the authors have reported that molten FeO produced by significant reoxidation of molten steel or molten TiO₂–CaO–Al₂O₃ produced with Ca treatment forms a liquid bridge between Al₂O₃ inclusions, which agglomerate with each other in molten steel.^17,18,19) However, because of the fact that molten steel was sufficiently deoxidized with Al in the present experiments as in ordinary Al deoxidized molten steel so that no molten oxides such as FeO existed in molten steel and that no molten oxides were observed between Al₂O₃ cylinders, it is inconceivable that the agglomeration force between Al₂O₃ cylinders is caused by the liquid bridge force (a).

Consequently, whether the agglomeration force exerted between the Al₂O₃ cylinders in molten steel arises from the van der Waals force (b) or the cavity bridge force (c) will be quantitatively analyzed below by using the interaction model for each.

4.2.1. Agglomeration Force Due to van der Waals Force

In general, an interaction that is exerted when solid particles mutually approach in liquid principally includes the repulsion force owing to the overlapping of diffuse electric double layers and the dispersion force (van der Waals force). Since it is not necessary to consider the diffuse electric double layer in the Al₂O₃ particles in molten steel,¹⁾ the agglomeration force alone due to van der Waals force, F_A,V (N·m^–1), approximately represented by Eq. (7) acts on the two isodiametric Al₂O₃ cylinders in the present experiments.²⁰⁾   

$${\mathrm{F}}_{\mathrm{A},\mathrm{V}}=\mathrm{H}\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}{ }^{0.5}/(16{\mathrm{a}}^{2.5})$$(7)

Here, H is the Hamaker constant (J), r_CY is the radius of an Al₂O₃ cylinder (m), and a is the surface distance between the Al₂O₃ cylinders (m) and satisfies the condition of a≪r_CY. The Al₂O₃ cylinders used for the experiments affect not a perfect circular but an uneven surface. Assuming that the roughness (height difference between concavity and convexity) of an Al₂O₃ cylinder is b (m) and the average shape of an Al₂O₃ cylinder is a perfect circle having the surface at the intermediate position of roughness, it may be approximately considered that the surface distance between Al₂O₃ cylinders is distanced away from a to a+b. Therefore, the agglomeration force according to the van der Waals force between two isodiametric Al₂O₃ cylinders considering the surface roughness is represented by Eq. (8) and results in reduction to {a/(a+b)}^2.5 times that without surface roughness.   

$$\begin{array}{l}{\mathrm{F}}_{\mathrm{A},\mathrm{V}}=\mathrm{H}\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}{ }^{0.5}/\left\{16{(\mathrm{a}+\mathrm{b})}^{2.5}\right\}\\ \hspace{1em}\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }={\{\mathrm{a}/(\mathrm{a}+\mathrm{b})\}}^{2.5}\cdot \mathrm{H}\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}{ }^{0.5}/(16{\mathrm{a}}^{2.5})\end{array}$$(8)

The Hamaker constant between Al₂O₃ particles through the medium of molten steel is reported to be 2.3×10^–20 J by Taniguchi et al.²⁾ As can be seen from Eq. (8), the van der Waals force is intensified as two objects approach each other; therefore, the closest surface distance for the purpose of estimating the maximum agglomeration force was regarded to be 4×10^–10 m.²¹⁾ The evaluation by taking the cross-sectional photographs of Al₂O₃ cylinders used in the experiments provided an average height difference of 4.6×10^–6 m between concavity and convexity as the surface roughness. The agglomeration force due to the van der Waals force between two isodiametric Al₂O₃ cylinders with a diameter of 6–10 mm calculated by substituting the above values for Eq. (8) ranged from 1.78×10^–9 to 2.30×10^–9 N·m^–1. Since these agglomeration forces are much lower than those shown in Fig. 7, it is considered that agglomeration forces exerted between two isodiametric Al₂O₃ cylinders in molten steel does not originate from the van der Waals force.

4.2.2. Agglomeration Force Due to Cavity Bridge Force

When the Al₂O₃ cylinders having poor wettability with molten steel come into contact with each other, a cavity bridge is formed between them, as shown in Fig. 8. In this case, the agglomeration force F_A,S (N·m^–1) created between two isodiametric Al₂O₃ cylinders is expressed as the sum of the pressure difference ∆P_Fe (Pa) between cavity bridge and molten steel, and the surface tension of molten steel, which is given by Eq. (9).   

$${\mathrm{F}}_{\mathrm{A},\mathrm{S}}=2{\mathrm{X}}_4\cdot \mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}+2{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}$$(9)

where X₄ is the half-width of the neck of the cavity bridge (m). The relation obtained from the geometrical condition is expressed by Eq. (10).   

$${\mathrm{X}}_4{ }^2+2{\mathrm{R}}_3\cdot {\mathrm{X}}_4+2{\mathrm{R}}_3\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}=0$$(10)

where R₃ is the radius of curvature of the cavity bridge (m). The Laplace relation allows Eq. (11) to hold true.   

$$\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}={\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}/{\mathrm{R}}_3$$(11)

Equation (12) can be obtained in terms of X₄ by eliminating R₃ from Eqs. (10) and (11) and rearranging them.   

$$\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{X}}_4{ }^2+2{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{X}}_4+2{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}=0$$(12)

Equation (13) is obtained when X₄ is sought from Eq. (12).   

$${\mathrm{X}}_4=\{-{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}+{({\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}{ }^2-2{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot \mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{r}}_{\mathrm{C}\mathrm{Y}}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}})}^{0.5}\}/\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}$$(13)

Consequently, the agglomeration force between two isodiametric Al₂O₃ cylinders due to cavity bridge force may be calculated by substituting this value of X₄ sought by using Eq. (13) for Eq. (9).^18,19)

An average value of 1.884 N·m^–1 on the calculated surface tensions at the equilibrium oxygen concentration of Al deoxidized molten steel of 0.0009 mass%, according to the respective equations in Table 2, was considered to be the surface tension of Al deoxidized molten steel. In addition, the contact angle between Al deoxidized molten steel and Al₂O₃ was 152.6°. By using these values and the expected values of ∆P_Fe, the agglomeration force per unit length between two isodiametric Al₂O₃ cylinders, calculated according to Eqs. (9) and (13), is shown in Fig. 7. Although not precisely known, the pressure in the cavity bridge may be considered to be 8.2 Pa corresponding to the vapor pressure of Fe (at 1600°C) or higher, and simultaneously, lower than the addition of the static pressure of molten steel and atmospheric pressure 1.05×10⁵ Pa. When the pressure within the cavity bridge is equal to the vapor pressure of Fe, i.e., when it is assumed that ∆P_Fe is 1.05×10⁵ Pa, the calculation value of the agglomeration force, indicated by the dotted line in Fig. 7, results in being approximately five times higher than the corresponding experimental value. However, both values are broadly equivalent with respect to the order of magnitude, and the diameter dependency of Al₂O₃ cylinders on the agglomeration force is analogous in both. Moreover, assuming that the pressure within the cavity bridge is 1.01×10⁵ Pa, ∆P_Fe becomes 3.86×10³ Pa, and the calculated agglomeration force indicated by the solid line thus successfully agrees with the experimental value. Furthermore, when ∆P_Fe is 3.86×10³ Pa, X₄ obtained from Eq. (13) is found to be 1.44 mm, which approximately corresponds to 1.35 mm of the half-width of the neck of the cavity bridge in Fig. 8.

From the above mentioned results, the agglomeration force exerted between Al₂O₃ particles in molten steel is presumed to originate in the cavity bridge force between Al₂O₃ particles, which is unlikely to be wet with Al deoxidized molten steel.

4.3. Mechanism for Agglomeration Maintenance of Al₂O₃ Inclusions in Molten Steel

Based on these experimental results, the agglomeration force exerted on spherical Al₂O₃ inclusions in Al deoxidized molten steel is estimated below. As shown in Fig. 8, when a cavity bridge between two isospherical Al₂O₃ inclusions is formed, the agglomeration force F_A,S (N) is expressed by Eq. (14).   

$${\mathrm{F}}_{\mathrm{A},\mathrm{S}}=\pi \cdot {\mathrm{R}}_4{ }^2\cdot \mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}+2\pi \cdot {\mathrm{R}}_4\cdot {\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}$$(14)

Here, R₄ is the radius of the neck of the cavity bridge (m). Even if Al₂O₃ inclusions are spherical, the geometrical conditions in Eq. (15) hold true as in the case of Eq. (10) for the cylindrical forms.   

$${\mathrm{R}}_4{ }^2+2{\mathrm{R}}_3\cdot {\mathrm{R}}_4+2{\mathrm{R}}_3\cdot \mathrm{r}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}=0$$(15)

Here, r is the radius of a spherical Al₂O₃ inclusion (m). Equation (16) holds true according to the Laplace relation.   

$$\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}={\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot (1/{\mathrm{R}}_3-1/{\mathrm{R}}_4)$$(16)

Equation (17) can be obtained by eliminating R₃ and rearranging in terms of R₄ based on Eqs. (15) and (16).   

$$\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{R}}_4{ }^2+3{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{R}}_4+2{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot \mathrm{r}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}}=0$$(17)

Equation (18) is obtained when R₄ is solved from Eq. (17).   

$${\mathrm{R}}_4=\{-3{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}+{(9{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}{ }^2-8{\mathrm{\sigma }}_{\mathrm{F}\mathrm{e}}\cdot \mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}}\cdot \mathrm{r}\cdot \mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3-\mathrm{F}\mathrm{e}})}^{0.5}\}/(2\mathrm{\Delta }{\mathrm{P}}_{\mathrm{F}\mathrm{e}})$$(18)

Accordingly, the agglomeration force between two isospherical Al₂O₃ inclusions due to cavity bridge force can be calculated by substituting R₄ solved from Eq. (18) for Eq. (14).^18,19) Assuming that the surface tension of Al deoxidized molten steel, contact angle between Al deoxidized molten steel and Al₂O₃ inclusions, and ∆P_Fe are 1.884 N·m^–1, 152.6°, and 3.86×10³ Pa, respectively, the relation between the agglomeration force between two isospherical Al₂O₃ inclusions due to cavity bridge force and particle diameter d (μm) of the Al₂O₃ inclusions is calculated and indicated by the solid line in Fig. 11. Individual Al₂O₃ inclusions constituting alumina clusters in molten steel have a particle diameter of approximately 1–10 μm; therefore, it can be seen that the agglomeration force exerted between the Al₂O₃ inclusions in Al deoxidized molten steel ranges from 3.50×10^–6 to 3.51×10^–5 N.

Fig. 11.

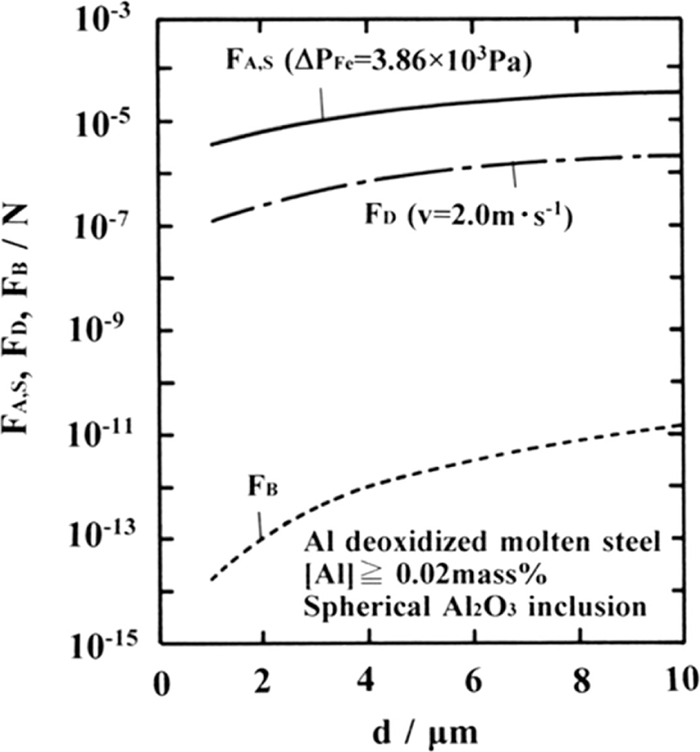
Relation between the agglomeration force between two isospherical Al₂O₃ inclusions due to cavity bridge force and the diameter of Al₂O₃ inclusions.

The buoyant force F_B (N) exerted on Al₂O₃ inclusions in molten steel can be evaluated using Eq. (19).   

$${\mathrm{F}}_{\mathrm{B}}=4\pi \cdot {\mathrm{r}}^3\cdot ({\rho }_{\mathrm{F}\mathrm{e}}-{\rho }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3})\cdot \mathrm{g}/3$$(19)

where ${\rho }_{\mathrm{A}{\mathrm{l}}_2{\mathrm{O}}_3}$ is the density of Al₂O₃ inclusions given as 3970 kg·m^–3. The relation between the buoyant force exerted on spherical Al₂O₃ inclusions and their particle diameter calculated by Eq. (19) is indicated in Fig. 11 by the dotted line. The buoyant force exerted on the spherical Al₂O₃ inclusions with a particle diameter of 1–10 μm is 1.56×10^–14–1.56×10^–11 N. In addition, the drag force F_D (N) that acts on the Al₂O₃ inclusions due to a relative movement to molten steel is presented in Eq. (20).   

$${\mathrm{F}}_{\mathrm{D}}={\mathrm{C}}_{\mathrm{D}}\cdot {\rho }_{\mathrm{F}\mathrm{e}}\cdot {\mathrm{v}}^2\cdot \mathrm{S}/2$$(20)

where C_D is the drag coefficient; v is the flow velocity of molten steel (m·s^–1); and S is the projected area of an inclusion particle toward the flow direction (m²) and is given by π·r² for spherical inclusions. The drag coefficient can be estimated by using Eq. (21),²¹⁾ which gives a favorable value corresponding to the experimental values when a particle’s Reynolds number, Re_P (=2r·v/ν), is 1000 or below.   

$${\mathrm{C}}_{\mathrm{D}}=24(1+0.158\mathrm{R}{\mathrm{e}}_{\mathrm{P}}{ }^{2/3})/\mathrm{R}{\mathrm{e}}_{\mathrm{P}}$$(21)

The kinematic viscosity coefficient ν of molten steel was 7.14×10^–7 m²·s^–1. The relation between the drag force exerted on a spherical Al₂O₃ inclusion and its particle diameter is calculated by using Eq. (20) and indicated by the chain line in Fig. 11. Here the flow velocity of molten steel was assumed to be 2 m·s^–1, corresponding to that inside an immersion nozzle regarded to be the fastest one in the continuous casting process. The drag force exerted on spherical Al₂O₃ inclusions with a particle diameter of 1–10 μm ranges from 1.24×10^–7 to 2.32×10^–6 N. It is presumed that the agglomeration force between two isospherical Al₂O₃ inclusions according to the cavity bridge force in Fig. 11 is large relative to the buoyant force and the drag force exerted on Al₂O₃ inclusions; therefore, once Al₂O₃ inclusions come into contact with each other and cavity bridges are formed, they are unlikely to be separated and agglomerated state is thus maintained, and they are subsequently sintered to form comparatively solidly bonded alumina clusters.

5. Conclusions

As a fundamental study for revealing the agglomeration and coalescence of Al₂O₃ inclusions in molten steel in view of the interfacial chemical interaction, direct measurement of the agglomeration force exerted between Al₂O₃ particles in molten steel was performed separately from the effects of molten steel flow, and the contact angle between Al deoxidized molten steel and Al₂O₃ plates was actually measured, where it was quantitatively verified that these values are valid. In addition, based on these results and an interaction model considering interfacial properties, the origin of the agglomeration force exerted between Al₂O₃ particles in molten steel and mechanism by which Al₂O₃ inclusions maintain their agglomeration state under molten steel flow were analyzed. The conclusions obtained are as follows:

(1) The contact angle between Al deoxidized molten steel (Al concentration≧0.02 mass%) and Al₂O₃ plates is 152.6°, and indicates a larger value than those between the molten Fe–O alloy and Al₂O₃ plates already measured by other researchers. This is explained by the fact that the dissociation of Al₂O₃ plates occurs in the molten Fe–O alloy, whereas it does not occur in Al deoxidized molten steel under the influence of dissolved Al.

(2) The surface tension of the molten Fe–Al–O alloy as well as its interfacial tension of molten Fe–Al–O alloy with Al₂O₃ plates was formulated according to the surface tension of molten Fe–O alloy and the contact angle of molten Fe–O alloy with Al₂O₃ plates measured by Nakashima et al., Takiuchi et al., and Ogino et al., and the contact angle between molten Fe–Al–O alloy and Al₂O₃ plates was quantitatively estimated by applying these formulated functions to Young’s equation. The values were validated by comparing the contact angles between Al deoxidized molten steel and Al₂O₃ plates obtained in this study with these estimated values.

(3) A new experimental method for direct measurement of the agglomeration force exerted between the Al₂O₃ particles in molten steel separately from the effect of molten steel flow was established, and by using this method, it was practically verified for the first time that a large agglomeration force is exerted between Al₂O₃ particles in Al deoxidized molten steel.

(4) The agglomeration force between Al₂O₃ particles in Al deoxidized molten steel is caused not by the van der Waals force but by the cavity bridge force created due to Al₂O₃ particles, which is unlikely to be wet with molten steel.

(5) The agglomeration force between Al₂O₃ inclusions due to the cavity bridge force in Al deoxidized molten steel is large compared with the buoyant force and drag force exerted on Al₂O₃ inclusions; therefore, once the Al₂O₃ inclusions come into contact with each other, they maintain their agglomeration state without being easily separated even under a flow of molten steel and are subsequently sintered and form relatively firmly bonded alumina clusters.

References

• 1)   S.  Taniguchi and  A.  Kikuchi: Tetsu-to-Hagané, 78 (1992), 527.
• 2)   S.  Taniguchi,  A.  Kikuchi,  T.  Ise and  N.  Shoji: ISIJ Int., 36 (1996), S117.
• 3)   S.  Taniguchi,  T.  Nakaoka and  K.  Matsumoto: Proc. Japan-Korea Workshop on Science and Technology in Iron making and Steelmaking, ISIJ, Tokyo, (2003), 61.
• 4)   H.  Yin,  H.  Shibata,  T.  Emi and  M.  Suzuki: ISIJ Int., 37 (1997), 936.
• 5)   K.  Nakajima and  S.  Mizoguchi: Metall. Mater. Trans. B, 32B (2001), 629.
• 6)   H.  Itoh,  M.  Hino and  S.  Ban-ya: Tetsu-to-Hagané, 83 (1997), 773.
• 7)   K.  Nakashima,  K.  Takihira,  K.  Mori and  N.  Shinozaki: J. Jpn. Inst. Met., 55 (1991), 1199.
• 8)   N.  Takiuchi,  T.  Taniguchi,  N.  Shinozaki and  K.  Mukai: J. Jpn. Inst. Met., 55 (1991), 44.
• 9)   N.  Takiuchi,  T.  Taniguchi,  Y.  Tanaka,  N.  Shinozaki and  K.  Mukai: J. Jpn. Inst. Met., 55 (1991), 180.
• 10)   K.  Ogino,  K.  Nogi and  Y.  Koshida: Tetsu-to-Hagané, 59 (1973), 1380.
• 11)   K.  Ogino,  K.  Nogi and  C.  Hosoi: Tetsu-to-Hagané, 69 (1983), 1989.
• 12)   B.  von Szyszkowski: Z. Phys. Chem., 64 (1908), 385.
• 13)   B. J.  Keene: Int. Mater. Rev., 33 (1988), 1.
• 14)   K.  Ogino,  K.  Nogi and  O.  Yamase: Tetsu-to-Hagané, 66 (1980), 179.
• 15)   A.  McLean and  R. G.  Ward: J. Iron Steel Inst., 204 (1966), 8.
• 16)   Steelmaking Data  Sourcebook,  Revised  Edition, The 19th Committee on the Steelmaking, The Japan Society for the Promotion of Science, Tokyo, (1984).
• 17)   K.  Sasai and  Y.  Mizukami: Taikabutsu, 53 (2001), 56.
• 18)   K.  Sasai and  Y.  Mizukami: ISIJ Int., 41 (2001), 1331.
• 19)   K.  Sasai and  Y.  Mizukami: Taikabutsu, 54 (2002), 504.
• 20)   J. N.  Israelachvili: Intermolecular and Surface Forces, 2nd ed., translated by T. Kondo and H. Oshima, Asakura Publishing, Tokyo, (1996), 173.
• 21)  Fundamentals of Powder Engineering, Editorial Committee on Fundamentals of Powder Engineering, Nikkan Kogyo Shimbun, Tokyo, (1992), 119, 206.