2014 Volume 54 Issue 4 Pages 774-780
2014 Volume 54 Issue 4 Pages 774-780
An arc driven by an alternating magnetic field was investigated theoretically and experimentally in swirling plasma gas flow. The governing equation to ascertain the arc motion was assumed to include not only an electromagnetic force term but also a Magnus force one. The electromagnetic force term derives from interaction between the arc current and the imposed magnetic field. The Magnus force is produced when the rotating gas travels in the surrounding gas. The obtained equation was solved numerically using commercial software (Mathematica). Numerical calculation revealed that the movement of the magnetically driven arc is twisted by the Magnus force. The twist direction depends on that of the swirling motion of the plasma gas. Clockwise-swirling plasma gas produces clockwise twisted arc movement. The amplitude of the oscillatory arc motion decreases concomitantly with increasing swirling strength.
The experiment was performed to examine the theoretical predictions. Results from experimental observations showed that the theoretical modeling was reasonable.
Because of their intense energy concentration to a small arc root, transferred arcs have been used widely in various industrial processes such as the cutting and welding of metals. In steel industry, many applications other than welding are utilized such as tundish plasma heating in steelmaking process. However, conventional arcs have remained inconvenient for heating and melting over a wide area. Several trials to expand the heating area of the transferred arc have been conducted.1,2,3) The authors succeeded in expanding the arc area by imposing an alternating magnetic field perpendicularly to the arc current. The arc was driven by electromagnetic force resulted from the interaction between the imposed magnetic field and the arc current, as presented in Fig. 1. Such a magnetically driven arc opens the new applications to a wide area thermal treatment of materials.4,5,6,7) In previous studies, theoretical consideration was restricted to the plasma gas flow without swirling motion. Nowadays, swirling gas flows are often used for plasma arc cutting and plasma spraying to improve the thermal efficiency.8,9) However, little work has been done on the effect of the swirling gas flow upon the magnetically driven arc.

Plasma arcs in various magnetic fields: no magnetic field (a), DC magnetic field (b), and AC magnetic field (c).
When a ball with a rotating motion travels in the air, its trajectory curve is well known to differ from a straight path because the rotating material experiences a force designated as the “Magnus force”.10) The present work investigated the movement of the magnetically driven arc under the swirling motion of the plasma gas flow. Considering the Magnus effect, the theoretical model for the arc motion is constructed. Then numerical calculations are conducted. Experiments are reported to examine the theoretical predictions.
A schematic illustration showing modeling is presented in Fig. 2. As depicted therein, the following coordinate system (x, y, z) is used for this study. The origin 0 (0, 0, 0) is located at the center of the arc torch exit. A metal plate serving as an anode expands in the x–y plane. A magnetic field is imposed parallel to the x axis. The magnetic flux density is uniform in space, but its value varies over time. A transferred arc is generated between an anode and a cathode in the arc torch. Argon gas is fed to the arc torch at the mass flow rate of Q0. Tangential movement of the gas flow is produced inside the arc torch. The gas is ionized near the cathode region. It is then ejected from the torch as a plasma gas with swirling motion. For plasma gas without swirling motion, precise investigations have been done of arc motion under an alternating magnetic field.4) Different from the previous work, swirling motion of the plasma gas should be considered. The plasma gas column presented in Fig. 2(b) is assumed to be in the form of a vorticity tube. The authors consider an elementary tube of the vorticity of length ds resting on a circle of radius r0 perpendicular to a vector of vorticity ω. Hereinafter, the elementary tube of vorticity is referred to as “a disk”, as presented in Fig. 2(b). It is expected that the Magnus force acts on the disk that moves in a static atmosphere.10) Considering the electromagnetic force and the Magnus force, we follow the disk of plasma gas as it moves according to a Lagrangian manner. The trajectory of the disk is determined by solving the momentum equation under similar assumptions to those used in a previous study.4)
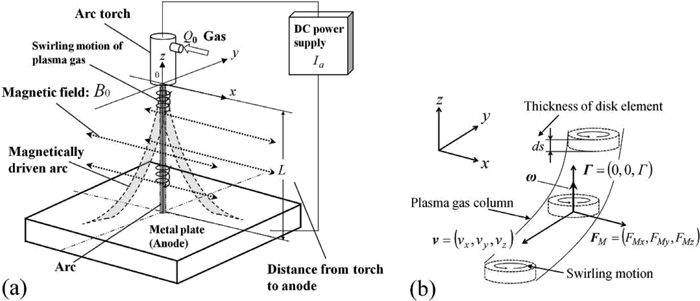
Schematic illustration used to simulate a plasma gas motion under the magnetic field (a) and the disk of the plasma gas column with circulation Γ (b).
The disk movement is governed by the following momentum equation.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
In this consideration, the alternating magnetic field is imposed along the x direction uniformly in space. If the flight time of the disk from the torch to the anode is much smaller than the period of the alternating field (τo), then the disk can be assumed to travel under a constant magnetic flux density. Such a condition is satisfied under the relation of τo >> L/v, where v is the plasma gas velocity and L is the distance between arc torch and anode. According to the model arrangement shown in Fig. 2, a magnetic field and a circulation are expressed respectively as
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Differentiating Eq. (12) with respect to t and substituting Eqs. (11) and (13), following Eq. (16) is obtained.
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
The conservation of kinetic energy for the disk is induced from Eq. (8). Scalar products of vector v to both sides of Eq. (8) result in
| (30) |
| (31) |
| (32) |
| (33) |
From inspection of Eq. (28), it is readily apparent that the main parameters which affect the trajectory of the disk are λ, γ and v0. Using the relations presented above, then λ can be described with parameters of Ia, B0 and Q0, which are measurable in experiments.
| (34) |
As for the determination of γ, its magnitude is difficult to estimate. The swirling motion generated in the arc torch does not remain constant because the physical properties of the plasma gas change drastically there. However, the direction of γ can be ascertained. As described in the experiment, the swirling motion direction depends on the type of the screw nut. Clockwise motion is obtained if a screw nut with clockwise grooves is used, and vice versa. If a nut with straight grooves is used, then the plasma gas flow with no swirling motion is obtained.
Numerical calculations were conducted. Commercial software (Mathematica)11) was used to solve the set of differential equations presented by Eq. (28) under the set of initial conditions of Eq. (29). The disk starts at a time t = 0 from the torch orifice and travels to the anode located at z = –L. It reaches there at a time t = tL. The location of the disk at time t is given as the set of x(t), y(t) and z(t). The disk trajectory is described by the variation of (x, y, z) with time (0 ≤ t ≤ tL). Parameter λ is given by the arc current Ia, the imposed magnetic flux density B0, and the mass flow rate of the plasma gas Q0, as expressed in Eq. (34). Experimental parameters Ia and Q0 are always positive, but B0 varies from negative to positive depending on the direction of the magnetic field vector. Parameter γ also varies from negative to positive depending to the direction of the vorticity vector. Various trajectories of the disk are obtainable under arbitrary combinations of λ and γ.
In Fig. 3, arc profiles in an alternating magnetic field are shown under the condition of plasma gas flow without swirling motion. Numerical parameters used for the calculation are presented in Table 1. The magnetic flux density changes between +B0 and –B0. For the initial velocity of the plasma gas, v0 = –80 [m/s] is adopted. This value was measured as a typical velocity in the previous experiment.4) As depicted in Fig. 3, the anode root of the arc oscillates along the y-axis.
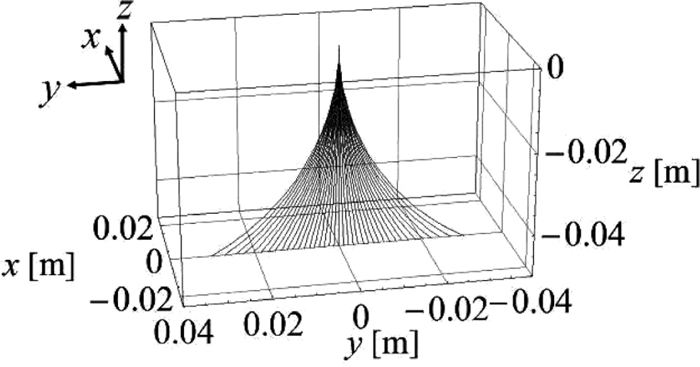
Arc profiles in the alternating magnetic field at γ = 0 [s–1].
| Parameters | Symbol | Value |
|---|---|---|
| Magnetic flux density [T] | B0 | 9.5 × 10–3 |
| Arc current [A] | Ia | 80 |
| Standoff distance between torch and anode [m] | L | 50 × 10–3 |
| Mass flow rate of Ar gas [kg/s] | Q0 | 5.3 × 10–4 |
| Initial velocity of plasma gas [m/s] | v0 | –80 |
Trajectories of the disk with swirling motion are typically portrayed in Figs. 4 and 5. Parameters used for the numerical calculations are the same as those in Table 2, except γ. For γ = –3000[s–1], the arc profile variation with magnetic flux density is presented in Fig. 4(a). Different from the results under γ = 0, the anode root does not move along the y-axis. Movement of the anode root on the x-y plane at z = –0.05 [m] is portrayed in Fig. 4(b). As this figure shows, movement of the anode root is twisted counterclockwise when γ is negative. The trajectory of the anode root is not straight. Strictly speaking, it is curved slightly. To simplify the discussion, the trajectory is assumed straight as shown by a dotted line in Fig. 4(b). If the twist angle ψ is defined as the shift from the y-axis, then ψ is equal to –42 [deg] at γ = –3000 [s–1].
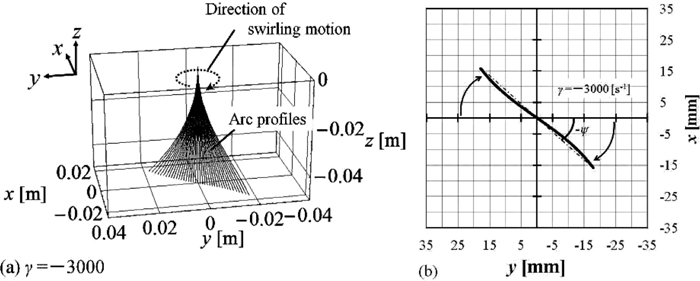
Arc profiles (a) and movement of arc roots on anode (b) at γ = –3000 [s–1].
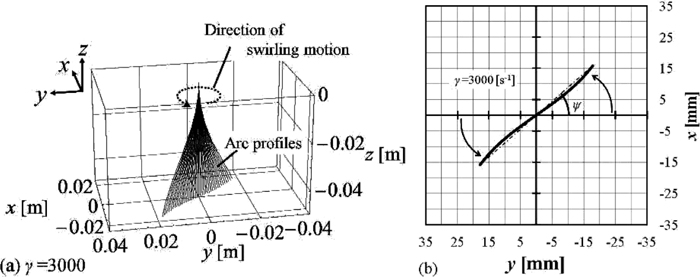
Arc profiles (a) and movement of arc roots on anode (b) at γ = 3000 [s–1].
| Parameters | Symbol | Value |
|---|---|---|
| Magnetic flux density [T] | B0 | 9.5 × 10–3 |
| Frequency of the alternating magnetic field [Hz] | f | 50 |
| Arc current [A] | Ia | 80 |
| Standoff distance between arc torch and anode [m] | L | 50 × 10–3 |
| Mass flow rate of Ar gas [kg/s] | Q0 | 5.3 × 10–4 |
Arc profiles obtained under the condition of γ = 3000 [s–1] are presented in Fig. 5(a). The movement of the anode root is twisted clockwise as presented in Fig. 5(b), where ψ is equal to 42 [deg]. Numerical analyses reveal that the twist angle |ψ| increases with increased |γ|.
Experiments were conducted to assess the theoretical results. Experimental arrangements are presented schematically in Fig. 6. A transferred arc was generated between an arc torch and a water cooled copper plate. A tungsten cathode and a water cooled copper plate were connected respectively to a negative pole and a positive one of the DC power supply. Argon gas was fed into the arc torch at Q0 = 5.3 × 10–4 [kg/s]. Inside the torch, the gas was introduced to a screw nut. By changing the screw nut type, various patterns of gas flows such as a straight flow or a swirling one were produced. In the present work, screw nuts of three different types were used; as portrayed in Fig. 7, they were a screw nut with straight grooves (a), one with counterclockwise grooves (b) and one with clockwise grooves (c). Main dimensions for these screw nuts are shown in Fig. 8. For all types of the screw nuts, the width of a groove was designed to be 3 × 10–3 [m] and its depth was 1 × 10–3 [m]. The magnetic field was produced by an electromagnet. Alternating electric current was supplied to the magnetic field coil. The arc was driven alternatingly by the electromagnetic force. The origin (0, 0, 0) of the coordinate system was located at the arc torch exit, and a magnetic field was applied along the x-axis and the arc torch was installed along the z-axis.
Experimental arrangement.

Screw nuts: Type A with straight grooves (a), Type B with counterclockwise grooves (b), and Type C with clockwise grooves (c).

Schematic illustration of the screw nut.
The twist angle ψ and amplitude of the oscillatory movements W were determined as depicted in Fig. 9. Experimental results were compared with theoretical predictions.

Twist angle ψ and amplitude of the oscillatory movement W.
Experimental conditions are presented in Table 2. The frequency of the alternating magnetic field was 50 Hz (τo = 20 [ms]). Its magnitude varied in a sinusoidal form. Its amplitude B0 is 9.5 × 10–3 [T]. Because |v0| = 80 [m/s] and L = 5 × 10–2 [m], the necessary condition for quasi-static magnetic field, τo >> L/|v0|, was satisfied in this experiment.
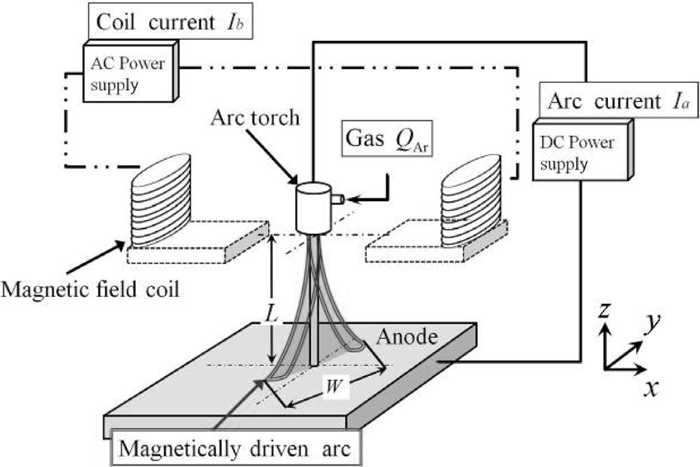
4.2. Experimental ResultsFigure 10 presents the track of the anode root obtained using the screw nut with straight grooves (screw nut of Type A). When the Type A nut is used, the plasma gas flow has no swirling motion. It was known that the anode root moved along the y-axis, as expected in Fig. 3.
Track on the anode root obtained using a Type A nut.
If the screw nut with counterclockwise grooves (screw nut of Type B) is used, then a counterclockwise swirling motion is produced in the plasma gas flow. The track of the root on the anode plate is shown in Fig. 11. The Result shows that the twisted angle ψ was negative under the counterclockwise swirling motion of the plasma gas, as predicted from the theoretical calculation.

Track on the anode root obtained using a Type B nut.
If the screw nut with clockwise grooves (screw nut of Type C) is used, then the clockwise swirling motion is produced in the plasma gas flow. As presented in Fig. 12, the twist angle ψ was positive in this experiment, in contrast to the result from Fig. 11.

Track on the anode root obtained using a Type C nut.
The variation of twist angle ψ with γ is presented in Fig. 13, where the solid curve represents the theoretical relation. The twist angle varies almost linearly with γ. It is zero at γ = 0. As described in theoretical considerations, it was difficult to ascertain the numerical value of γ. By fitting the experimental values of the twist angle to the theoretical curve, we were able to estimate the values of γ for the screw nuts of Type A, Type B, and Type C.
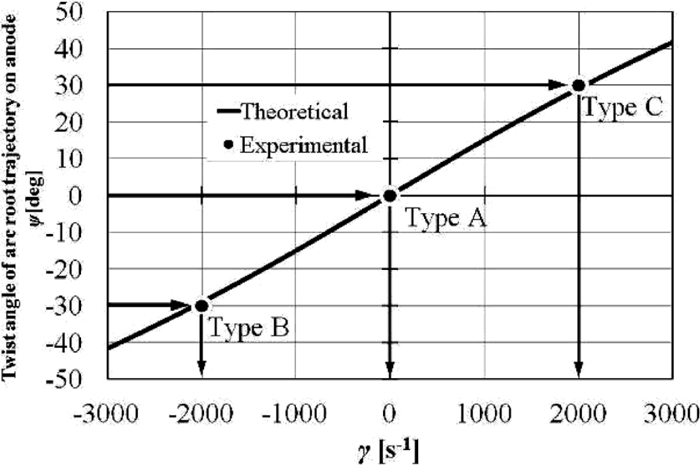
Twist-angle ψ with γ.
When the nut of Type A was used, ψ obtained from experiment was zero. When the nut of Type B was used, ψ = –30 [deg] was obtained. Furthermore, when the nut of Type C was used, ψ = 30 [deg] was obtained. After the fitting, the following values were obtained: γ = 0 [s–1] for the nut of Type A, γ = –2000 [s–1] for the nut of Type B, and γ = 2000 [s–1] for the nut of Type C.
5.2. Amplitude of the Magnetically Driven ArcThe anode root movements of the magnetically driven arc were calculated for various values of γ. In Fig. 14, the positions of the anode root at B0 = ±9.5 × 10–3 [T] are presented for various values of γ between –3000 ≤ γ ≤ 3000 [s–1]. Without swirling motion, the trace locates at the position of (x = 0 [m], y = –0.030 [m]) for B0 = 9.5 × 10–3 [T], and at the position of (x = 0 [m] and y = 0.030 [m]) for B0 = –9.5 × 10–3 [T]. With swirling motion of γ = 3000 [s–1], for example, the traces for B0 = 9.5 × 10–3 [T] and for B0 = –9.5 × 10–3 [T] locate respectively at (x = 0.013 [m], y = –0.020 [m]) and at (x = –0.013 [m], y = 0.020 [m]).
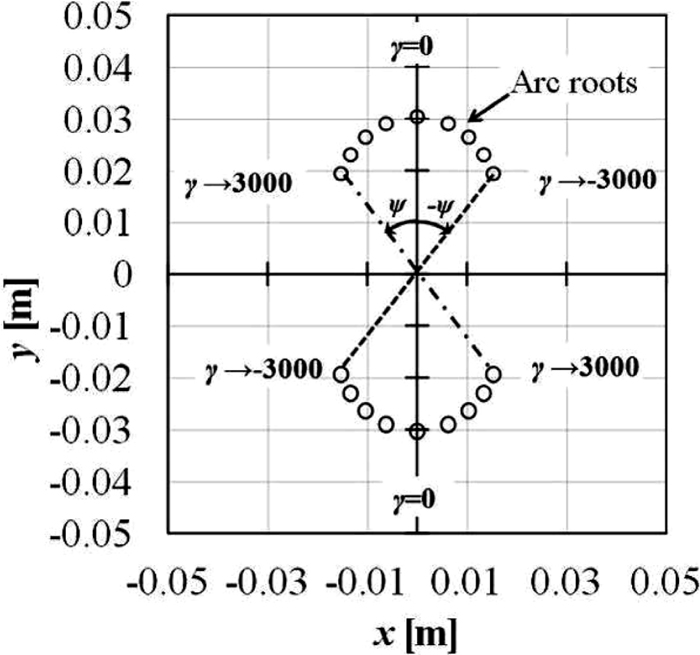
Traces of arc roots on the anode.
In Fig. 15, the amplitude variation of the anode root movement was presented as a function of γ. As shown in this figure, the variation of the amplitude W is normalized with W0 at γ = 0. As presented in Fig. 15, the amplitude is reduced with increased |γ|.
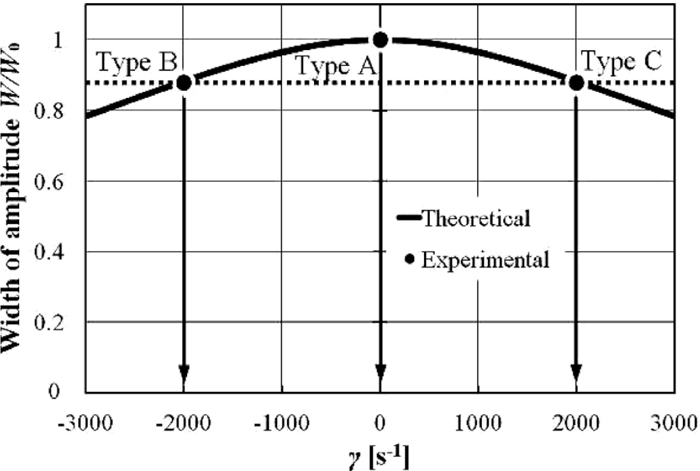
Variation of width of amplitude with γ.
In experiments using screw nuts of three different types Type A, Type B, and Type C, the amplitudes of the anode root movement were observed. These amplitudes were normalized by W0 obtained for Type A. The normalized amplitude for Type B was measured to 0.83 and that for Type C was also 0.83. By fitting these experimentally obtained results to the theoretical curve, we can also estimate the values of γ for Type A, Type B, and Type C. Those are γ = 0 [s–1] for the nut of Type A, γ = –2000 [s–1] for the nut of Type B and γ = 2000 [s–1] for the nut of Type C.
To estimate the experimental values of γ, two approaches were used. One was from the measurement of the twist angle and the other was from that of the oscillation amplitude. Agreement between the values obtained from the two approaches suggests good validity of the present theoretical model.
The movement of the magnetically driven arc in the swirling plasma gas was investigated theoretically. A theoretical model was constructed on the idea that the arc movement would be controlled not only by the electromagnetic force but also by the Magnus force. Electromagnetic force is produced by interaction of the arc current with the imposed magnetic field. The swirling motion of the plasma gas results in the Magnus force. Numerical calculations were conducted using commercial software (Mathematica). Theoretical predictions obtained from the numerical analyses were examined by experimentation. Results of that experimental examination confirmed the validity of the theoretical model. The main results are presented below.
(1) The governing equation used to determine the arc motion is the momentum equation including electromagnetic force and Magnus force.
(2) The plasma gas trajectory is determined by solving a set of three third-order linear ordinary differential equations.
(3) Numerical analyses and the experimental observations reveal that the arc movement is twisted by the influence of the Magnus force.
(4) The twist direction depends on the direction of the swirling motion of the plasma gas. If the direction of the swirling motion is clockwise, then that of the twist is clockwise, and vice versa.
(5) The swirling motion reduces the arc motion amplitude.
Vector quantities are shown in bold.
B: Magnetic flux density B = (B0,0,0), |B| = B0, T
f: External force (Electromagnetic force and Magnus force) per unit length, N/m
FE: Electromagnetic force per unit length, N/m
FM: Magnus force per unit length, N/m
Ia: Arc current Ia = (Iax,Iay,Iaz), |Ia| = Ia, A
L: Distance between arc torch and anode, m
m: Mass of plasma gas column per unit length, kg/m
Q0: Mass flow rate of Ar gas, kg/s
r0: Radius of plasma gas column, m
v: Velocity of plasma gas fraction v = (vx,vy,vz), |v| = v, m/s
v0: Initial velocity of the disk, m/s
W: Amplitude of the magnetically driven arc motion, m
W0: Amplitude of the magnetically driven arc motion at γ = 0 [s–1], m
α: α = –Ia/v = Ia/v, A s/m
Γ: Circulation of the column Γ = (0,0,Γ), |Γ| = Γ, m2/s
γ: γ = ρΓ/m, s–1
θ: Angle of the screw nut groove, deg
λ: λ = αB0/m, s–1
ρ: Mass density of ambient fluid, kg/m3
ψ: Twist angle of the arc roots track, deg
ω: Vorticity of the disk ω = (0,0,ω), |ω| = ω, s–1