2014 Volume 54 Issue 4 Pages 836-844
2014 Volume 54 Issue 4 Pages 836-844
In oxygen steelmaking, splashing from the injection of oxygen plays an important role in the kinetics of the process. Though waves inside the cavity and formation of various modes (i.e. dimpling, splashing, and penetrating) have been investigated in the past, it is not clearly understood how these wave behaviour affects splashing. Therefore, in the present work, a cold model experimental study has been carried to establish if it was possible to quantitatively identify various modes of cavity. Fast Fourier Transform (FFT) on cavity depth oscillation showed that amplitude and frequency of cavity oscillation is highest in penetrating mode. Important aspects of the droplet generation process were identified from high speed imaging. Formation of sheet structure was identified and the height of these structures above the bath surface were found to decline as the cavity mode changed from splashing to penetrating. Existence of the splash sheets emphasizes that the sampling position can be a crucial issue in interpreting plant studies.
In oxygen steelmaking, the metal droplets are generated due to impact of supersonic jets. The supersonic jet strikes the metal surface and is deflected upwards. Then, with the shearing action of the gas, metal droplets are torn from the cavity surface.1) This phenomenon is generally referred to as “spitting” or “splashing”.2) In top blown oxygen steelmaking, there is significant evidence to show that many of the key reactions occur in the emulsion, which in turn is directly related to the quantity of splash generated from the injection and subsequent behaviour of the droplets in the emulsion. Previous studies3,4) have identified the formation of waves inside the cavity. But it is not yet clearly understood how waves inside the cavity affect splashing. The oscillation frequency of the cavity has been studied.4,5) Alam et al.6) showed experimentally how the modes of cavity direct the trajectory of splash droplets into emulsion which can thereby affects decarburization process. Molloy7) identified three cavity conditions namely dimpling mode, splashing mode and penetrating mode (as shown in Fig. 1). Dimpling is termed as the cavity condition when there is a slight depression but no droplet formation. In splashing, there is a shallow depression as well as large outwardly directed splash. In case of penetrating mode, there is decrease in outward splash with much deeper cavity. Molloy7) termed the three modes depending on the general appearance of cavity, change in sound of the bath and reduction of splash. The impact velocity above which the cavity entered into splashing mode from dimple mode was found to be 15.24 m/s whereas impact velocity of 76.2 m/s indicated that the cavity was in penetrating mode. Lee et al.4) investigated cavity modes at various lance heights, lance angles and gas flow rates. They4,8) predicted that cavity modes can be distinguished depending upon the frequency of oscillation of cavity, rather than visual observation. Hwang et al.9) studied different cavity modes with a wall jet configuration at a water model study using Fast Fourier Transform (FFT) and power spectral density (PSD) analysis. Their work showed that the impact velocity on the bath surface was 13 m/s at transition from “dimpling to splashing” mode and 28 m/s at transition from splashing to penetrating mode. Both velocities were different than that of Molloy’s study.7) Standish and He10) described the two mechanisms of droplet generation observing from high speed films namely “dropping” (which indicates single droplet ejecting from the edge of the cavity) and “swarming” (indicating single droplets as well as large tears of liquid producing from the edge of the crater). Standish and He10) also stated that splashing and penetrating modes are different from “dropping” and “swarming” mechanisms of the drop generation.

Different cavity modes.7)

Schematic of the experimental set up.
It can be concluded from the literature review that understanding of different cavity modes is limited and has not been incorporated into providing useful predictions of droplet generation in oxygen steelmaking. The aim of the present work is to investigate droplet generation and measure the oscillation of the cavity and identify if it is possible to differentiate among various cavity modes quantitatively. Cold modelling techniques have been shown to be useful in studying high temperature processes due to the ease in controlling different variables such as gas flow rate, lance height and lance angle. Water-air models have been used to simulate steelmaking process over the years as water at 25°C has the similar kinematic viscosity to molten steel at 1600°C.4) The work of Sharma et al.11) showed that the motion in the liquid bath is influenced by impact force of the jet, not by the presence of the slag and carbon content of the liquid steel. Subagyo et al.12) showed that droplet generation rate per volumetric flow of blown gas in different Blowing numbers followed same relationship in water models as well as the case of oxygen injected on the surface of molten liquid iron. Therefore, in the present work, water-air system has been used to represent the case of oxygen injected on the surface of molten iron.
The present model is a 1/10th scaled model of an actual BOF steelmaking converter stated in the work of Luomala et al.13) Compressed air was passed through a top straight nozzle. Water was used to simulate liquid iron. The slag phase was not included in this first phase of study assuming that the high speed jet pushed the slag layer away when it hit the bath.10) A transparent cylindrical rig, made of Perspex sheet, was taken as the vessel for the cold model. The bottom surface of the rig was flat which is dissimilar from the actual steelmaking practice and therefore, it may have affected the fluid dynamics of the bath to some extent. A laser level set was used to ensure the nozzle was kept at 90° during the experiments. A flow meter (range: 10 L/min to 100 L/min, accuracy ±3% of full scale) was used to control the flow rate of compressed air.
He and Standish14) simulated droplets formation with both water and mercy bath and found that in both cases, the patterns of droplet generation were similar. Therefore, they proposed “nominal weber number”, which is a ratio of inertia force to the surface tension force, as similarity criteria of droplet generation between real furnace and a model. Subagyo et al.12) further developed the model and proposed a dimensionless number called ‘Blowing number’ incorporating the Kelvin-Helmholtz instability criteria into droplet generation condition. Therefore, The Blowing number similarity criteria has been given preference over other dynamic similarity criteria. The Blowing number is as follows
| Dimensions | BOF | 1/10th model |
|---|---|---|
| Nozzle diameter, d (m) | 0.029 | 0.003 |
| Vessel diameter, D (m) | 4.30 | 0.420 |
| Vessel height, l (m) | 7.20 | 0.50 |
| Bath height, H (m) | 1.50 | 0.15, 0.20 |
| Lance height, L (m) | 1.50–2.00 | 0.05,0.08,0.10,0.12,0.15,0.16,0.17 |
| Number of nozzles, N | 5 | 1 |
| Nozzle angle, θ (°) | 15 | 0 |
| Dimensionless number | Numerical definition | Industrial | Present model |
|---|---|---|---|
| Geometrical Similarity | |||
| Distribution number | Nd2/D2 | 0.0002 | 0.00005 |
| Bath Aspect ratio | H/D | 0.35 | 0.36, 0.48 |
| Dimensionless lance distance | L/d | 52 to 69 | 16.67 to 56.67 |
| Dynamic Similarity | |||
| Modified Froude number |
| 0.11 to 0.20 | 0.14 to 3.20 |
| Blowing Number |
| 4.61 to 6.11 | 0.64 to 5.99 |
| Momentum number |
| (1.5 to 3.6)*10–3 | 3.12*10–3 to 8.42*10–2 to |
Table 3 represents the various operating conditions of the experimental work and also states the cavity modes at each condition. A high speed camera named MotionPro Y (model Y4L) was used to take photos of the cavity and the splashing of droplets. The camera has the resolution of 1024 H × 1024 V and maximum frame rate of 4000 frames/second. Photos were taken at a rate of 30 frames/ second for time duration of 4 minutes. In addition, a video of 2 second was taken at 2000 frames/second rate in order to observe the droplet generation process. The recorded images were transferred from the high speed camera to a Laptop by Motion Studio software.
| Lance height (m) | Compressed air flow rates (L/min) | Bath height (m) | Cavity modes |
|---|---|---|---|
| 0.17 | 50 | 0.20 | Dimpling |
| 60, 70, 80 | 0.20 | Splashing | |
| 0.16 | 50, 60, 70, 80 | 0.20 | Splashing |
| 0.15 | 40 | 0.15, 0.20 | Dimpling |
| 50, 60, 70 | 0.15, 0.20 | Splashing | |
| 0.12 | 30 | 0.15, 0.20 | Dimpling |
| 40, 50, 60, 70 | 0.15, 0.20 | Penetrating | |
| 0.10 | 30 | 0.20 | Dimpling |
| 40, 50, 60, 70 | 0.20 | Penetrating | |
| 0.08 | 20 | 0.20 | Dimpling |
| 30, 40, 50, 60 | 0.20 | Penetrating | |
| 0.05 | 20, 30, 40 | 0.20 | Penetrating |
The images, taken at different operating conditions, were analyzed by ImageJ 1.45 s.15) At each operating condition, 30 images of the cavity and its splashing were acquired in 1 second. The images sequences of 1 second were imported from the saved files. The frame number was displayed at each image. The process of measuring the cavity depth, cavity width and splash sheet height are described below.
3.1. Measuring Cavity DepthUsing grids, the imported images were divided into different zones. Grids were selected in such a way that one horizontal grid could be put along the water surface which was used as a reference line for all the images. The pixels were converted into measurable values using scale selection. The edges of cavity were sharpened to give out a clear outline of the cavity so that the depth of the cavity could be measured easily. At each image, the depth of the cavity was measured by drawing a vertical line from the water surface to the deepest part of the cavity (as shown in Fig. 3). The measured data was showed in separate window. After all the measurements have been done, the data was saved in a excel spread with frame numbers. It was easy to check if all frames were measured or not. Thus, the error of measuring data from the same image was eliminated.

Measuring of the cavity depth with ImageJ.
Measuring width of the cavity was particularly challenging. As flow rate was increased, number of waves formed inside the cavity (as shown in Figs. 6(a) and 6(b)) grew. Also, there was a creation of secondary cavity beside the main one. Both of these two factors made it difficult to define the width of the cavity from image study. Although, there were limitations, width of the cavity was measured in the same way as the cavity depth.

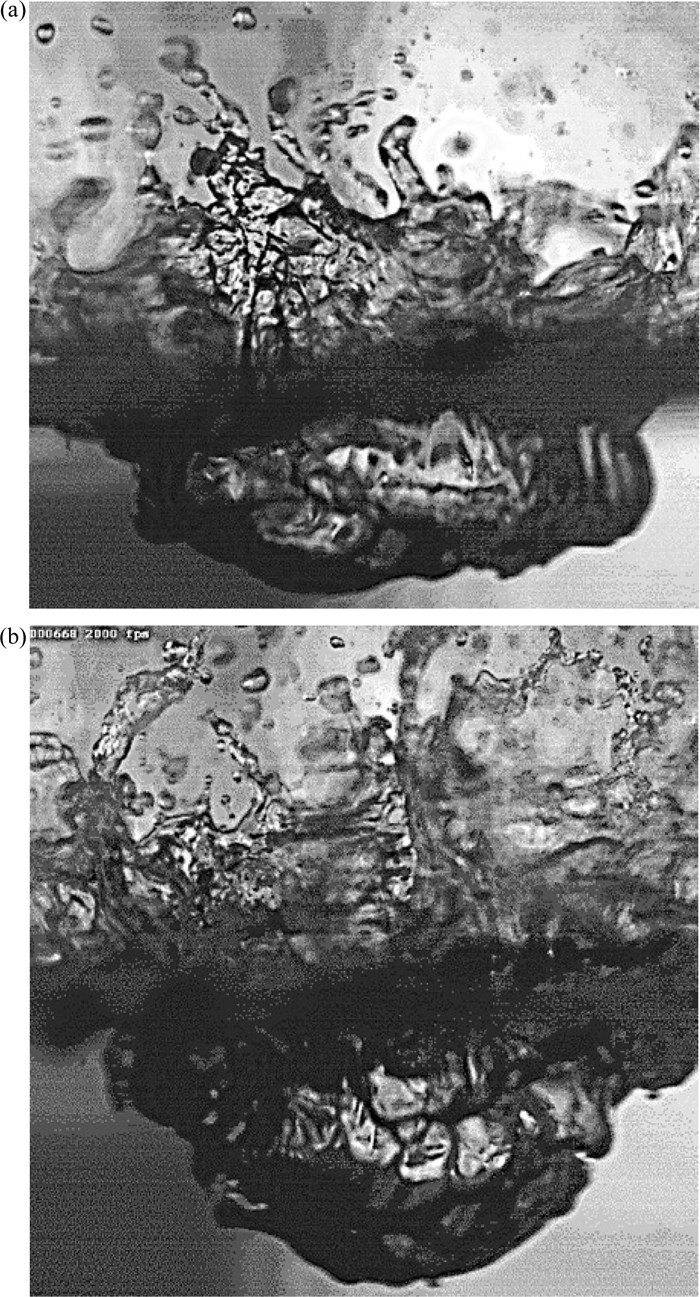
(a) Droplet generation at lance height 0.120 m and flow rate 50 L/min (b) Droplet generation at lance height 0.120 m and flow rate 70 L/min.
As air pushed the liquid surface to generate the cavity, waves were formed inside the cavity. These waves grew and formed sheets at the rim of the cavity. These sheets rose up to a certain height, until instability developed in the sheets, fingers were formed which ultimately broke into droplets. These sheets will be termed as “splash sheet” in this paper (as shown in Fig. 4(b)). At each frame, many splash sheets could be observed at the edge of the cavity. Among them, the highest splash sheet (as shown in Fig. 4(b)) was measured from each frame the same way as depth of the cavity was measured. Then, average height of the sheets from 30 images was calculated and was taken as the splash sheet height at that operating condition.

(a) Peregrine sheet;16) (b) sheet formation at flow rate 50 L/min, lance height 0.150 m.
Errors of the experiments were estimated. Error occurred during the measurement process were of two types: (a) sampling error (b) image analysis error. The sampling error for measuring cavity depth, splash sheet height and cavity width was 0.0011 m, 0.0030 m and 0.0032 m respectively. The image analysis error was 1.82% (details are provided in Appendix B).
The high speed camera video footage (2000 frames/second) was used to observe air-water interaction and droplet generation. Observation of high speed photograph showed greater insight into the droplet formation process which is described below.
As air jet hit the water surface, it created a cavity in bath. Waves were formed inside the cavity. These waves were pushed towards the edge of the cavity by high speed flow of air. At the edge of the cavity, these waves formed sheet structure which grew into certain critical amplitude. They have similarity in shape with “peregrine sheet” found in general splashing literature.16) These sheets are termed “crown” by Cullinan et al.17) and “sheets” by Liow et al.18) Figures 4(a) and 4(b) shows peregrine sheet in general splashing literature and sheets observed in the cold modeling experiment respectively.
From the high speed video, droplet formation was observed and three stages could be identified.
1. Amplitude of the waves (which will be called “splash sheets” from now on) increased at the edge of the cavity.
2. At the rim of the sheets, instability grew and fingers were formed.
3. Fingers broke up into one or number of droplets.
Figures 5(a) to 5(c) shows the gradual formation of a droplet from one particular sheet (collected from 2000 frames/second video). Depending upon lance height and flow rate, stage 1 or stage 1 and 2 or all three stages 1, 2, 3 were found. For example, at lance height 0.15 m and flow rate of 40 L/min, only sheets were formed with no droplet formation. Keeping the lance height constant, as the flow rate was increased to 50 L/min, all three stages of droplet formation were observed.

(a) At lance height 0.170 m, flow rate 60 L/min, formation of sheet; (b) Growth of fingers; (c) Droplet generation from breaking of fingers.
Observation from video suggested at constant lance height but increasing gas flow rate, the fingers were detaching quickly from the sheets before they could break into droplets. At higher flow rates, more droplets were found in irregular forms rather than circular shape. Figure 6(a) shows shapes of the droplets at flow rate 50 L/min and Fig. 6(b) shows droplets at flow rate 70 L/min. Droplet generation by two mechanisms such as “dropping” and “swarming”10) were also observed from the high speed video image. In case of the “dropping” mechanism, the frequency of droplet formation was quite low and droplets were formed from the edge of the cavity (as shown in Fig. 5(c)). As impact velocity on the bath was increased, droplets began to form by the “swarming” mechanism and the frequency of droplet formation was greatly increased (as shown in Fig. 6(b)).
5.2. Variation in Depth of the CavityThe cavity depth was found to be dependent on both gas flow rate and lance height. As gas flow rate was increased and lance was placed closer to the bath, the depth of the cavity increased. The height of the water bath was kept at 0.20 m and 0.15 m during the experiments. No significant variation was found on the depth of the cavity with the change in water bath height.
Applying image analysis on the saved images (recorded at 30 frames/second), change of the cavity depth in 1 second was produced. Figure 7 shows a time series of the depth of cavity at lance height 0.12 m with various flow rates. At low flow rates (i.e. 30 and 40 L/min), the change of the cavity was following a regular wave pattern, whereas at higher flow rates (i.e. 50 L/min and above), the wave pattern became irregular.

Time series of cavity depth at lance height 0.120 m, bath height 0.15 m.
The time series of the width of cavity was generated at different operating conditions. In contrast to cavity depth time series (as shown in Fig. 7), the pattern of change in Fig. 8 didn’t show any clear trend.

Time series of cavity width at lance height 0.120 m, bath height 0.15 m.
Molloy’s description7) of penetrating mode contained deep cavity, reduction in splashing as well as change in the sound of the bath. In the present work, investigations on cavity modes were taken on two aspects which were - (a) the overall appearance of the cavity and (b) quantity of droplets produced. The appearance of a deep cavity is a qualitative issue and therefore, it can not be used for identifying cavity modes. Also, the “deep” appearance didn’t necessarily associate with the reduction of splashing. Figure 9 shows the appearance of the cavity at flow rate 70 L/min and 80 L/min at lance height 0.16 m. Though the cavity generated at 80 L/min was much deeper in appearance and measurement compared to that of 70 L/min, both of them was actually in splashing mode. Therefore, study of splashing was taken to identify various modes. Experiments were done in different operating conditions (as given in Table 3) and generated droplets were measured by sampling above the bath.19) Then droplets collected were compared for different lance heights and gas flow rates. Due to the limited scope of this paper, the detailed splashing study will be explained elsewhere. It was found that when the lance got closer to the bath, cavity mode changed from splashing to penetrating mode. Splashing per unit volume of blown gas was found much higher at lance height 0.17 m, 0.16 m and 0.15 m whereas there was drastic reduction of splashing for the lance heights 0.12 m, 0.10 m, 0.08 m and 0.05 m. So, the cavity modes at lance height 0.15, 0.16, 0.17 were termed as splashing modes. The modes of the cavity for the rest were termed as penetrating modes.
(a) Cavity at lance height 0.16 m and flow rate 70 L/min (b) Cavity at lance height 0.16 m and flow rate 80 L/min.
The Fast Fourier Transform (FFT)20) technique was used to analyse the measured time series of cavity depth for all operating conditions (showed in Table 3) in order to find amplitude and frequency of cavity oscillation. Origin Pro 8.521) software was used to carry out this task. At each condition, frequency and amplitude of change in the cavity depth was measured using FFT. FFT results showed a number of frequencies at each operating condition. The total range of the frequencies was between 3 to 9 Hz. In previous studies, the range is reported as being4,5) between 5 to 16 Hz. Therefore, FFT results from the present work were compatible with the reported frequencies. At a particular operating condition, no “one” dominant frequency with highest amplitude was found in the FFT result. Rather, there were several dominant frequencies. For example, FFT results of lance height 0.12 m and gas flow rate of 40 L/min showed that 5 Hz and 6 Hz were dominant frequencies (as shown in Fig. 10). In order to get an overall idea of frequency at a particular condition, three frequencies which had the highest amplitudes were taken and an average of them was considered as the frequency of cavity depth oscillation at that operating condition. FFT was also applied to the time series of cavity width which failed to produce any definite frequency or pattern.

FFT of time series of cavity depth at lance height 0.12 m, bath height 0.15 m and flow rate 40 L/min.
The purpose of this analysis is to identify if it is possible to differentiate cavity modes on the basis of frequency and amplitude of change in cavity depth. Frequency of oscillation and amplitude at each cavity mode (i.e. dimpling, splashing, and penetrating) was considered as a “set” regardless of the lance height, gas flow rate and water bath height. An average frequency and amplitude of each mode was calculated. For both frequency and amplitude analysis, the set of dimpling, splashing and penetrating modes contained 7, 13 and 19 different experimental conditions respectively (stated in Table 3). Figure 11 shows that the frequency of cavity depth oscillation increased as cavity mode changed from dimpling (3.67 Hz) to splashing (5 Hz). In penetrating mode, frequency was found to be the highest which was 6.40 Hz. Therefore, it is clear that cavity oscillation became higher as the cavity mode changed from dimpling to penetrating.

Frequency of cavity oscillation in different cavity modes.
Figure 12 shows amplitude of the change of cavity depth in various cavity modes. In dimpling, the amplitude of change was very little (~0.0008 m) compared to that of splashing and penetrating mode. As cavity mode turned into splashing from dimpling mode with the droplet formation, amplitude of change in cavity depth became almost double to that of dimpling mode. In penetrating mode, the amplitude of cavity oscillation was 0.0018 m which was the highest of all the cavity modes.

Amplitude of cavity oscillation in different cavity modes.
For mechanical waves such as sound waves, water waves etc., the energy of one wavelength of a wave is calculated with the following formula22)
| (1) |
| (2) |
Now, from the FFT results, frequency and amplitude of cavity oscillation increased as the cavity mode changed from dimpling to splashing and splashing to penetrating. Frequency and amplitude of cavity oscillation was found higher in penetrating mode that that of dimpling and splashing. Therefore, from energy balance perspective, it can be concluded that more energy is used in oscillating the cavity in penetrating mode than that of splashing and dimpling modes. Though the results were not sufficient enough to identify various modes in terms of “one” dominant frequency as Lee et al.4) predicted and an averaging of frequency and amplitude was done, analysis of FFT clearly showed that how frequencies and amplitudes varied in different cavity modes and it was possible to associate a frequency with a specific cavity mode.
5.6. Height of Splash SheetsFrom images of 2000 frames per second, it was observed that “splash sheets” (as shown in Fig. 4(b)) were formed depending on the momentum of gas jet. The height of the splash sheets were found dependent on gas flow rate, lance height and weakly on water height in the bath. With increasing gas flow rate, height of these sheets grew (as shown in Fig. 13). It is reasonable as increasing gas flow rate means there is more energy to form these splash sheets. The work of Cullinan et al.17) supports this finding. In their work on splash of a liquid drop, it was found that the dimensional height of the crown (ratio of crown height to impinging droplet diameter) increased with increasing impact velocity.

Comparison of splash sheet height at lance height 0.120 m.
The height of the sheets was found slightly dependent on the water bath height. At lance height 0.120 m and bath height 0.20 m, the heights of the sheets were higher than that of bath height 0.15 m at the same lance height (as shown in Fig. 13). For example, the height of the sheets at 60 L/min and bath height 0.20 m was 0.005 m higher than that of sheets generated in bath height 0.15 m. Heights of splash sheets were presented at different Blowing numbers and constant bath height of 0.20 m in Fig. 14. It showed that at a constant lance height, increasing the Blowing number always increased the height of the sheets. As the lance height was decreased from 0.17 m to 0.10 m, the height of these sheets drastically decreased in general for all Blowing numbers. This is so because as the lance was placed closer to the bath, cavity mode changed from splashing to penetrating mode. At a constant Blowing number, the height of the splash sheets were found greater in splashing mode than those of penetrating mode. In penetrating mode, heights of the sheets decreased and therefore, splashing also reduced.

Height of splash sheets at different Blowing Numbers.
Existence of these splash sheets indicated an important aspect of splashing study. In steelmaking, sampling technique has been often used to estimate amounts of droplets present in the emulsion. Due to the formation of sheets, it is reasonable that if sampling is carried out close to the bath surface, sheets are collected into the sample pots which can lead to overestimation in the droplet generation rate. Detail investigation of this concept will be described in a future paper.
In this paper, droplet formation have been studied in detail with a cold model using a high speed camera. Image analysis and FFT technique has been used to investigate frequency and amplitude of cavity oscillation for a wide variety of experimental conditions. The summary of the findings are given below
(1) FFT analysis showed clear distinction among frequency and amplitude of oscillation in various cavity modes.
(2) Frequency and amplitude of cavity oscillation was found to be highest in penetrating mode among all the cavity modes.
(3) In penetrating mode, more energy is used in oscillating the cavity than that of splashing and dimpling mode due to highest frequency and amplitude of oscillation.
(4) High speed camera footage showed the formation of splash sheets. In penetrating mode, height of these sheets drastically decreased.
(5) Existence of splash sheets indicates that sampling position of the bath is a crucial issue and can give overestimation in splashing amount. To investigate this concept and quantify droplet generation in different cavity modes, a splashing study has been carried out as the continuation of the present investigation which will be discussed in a future paper. In addition, the relationships between operating conditions and cavity modes will be proposed in that paper.
The FFT investigation on different cavity modes indicates that penetrating mode is not energy efficient option for steelmakers from the view point of splash generation as energy is lost in oscillating the cavity rather than generating droplets.
d: Nozzle diameter (m)
D: Vessel diameter (m)
l: Vessel height (m)
H: Bath height (m)
L: Lance height (m)
N: Number of nozzles (–)
θ: Nozzle angle (°)
ρg: Density of gas at pressure 101325 Pa and temperature 273 K (kg/m3)
ρl: Density of liquid at pressure 101325 Pa and temperature 273 K (kg/m3)
Ug: Critical gas velocity (m/s)
U0: Gas velocity at nozzle exit (m/s)
Uj: Gas velocity at bath surface (m/s)
g: Gravitational acceleration (m/s2)
σ : Surface tension (N/m)
NB: Blowing Number (–)
Q: Gas flow rate at nozzle exit (L/min)
η: Constant (–)
α: Level of significance (–)
S: Standard deviation of samples (–)
σp: Standard deviation of population (–)
z: Standard score (–)
ME: Margin of error (m)
E: Energy of a one length of a wave (J)
μ: Mass per unit length of wave (kg/m)
ω: Angular frequency (Hz)
λ: Wavelength (m)
f: Frequency (Hz)
A: Amplitude (m)
Flow rate, Q (L/min) = 30;
Lance height, L (m) = 0.120;
Density of air and liquid was taken at 273 K and 101325 Pa pressure, as Subagyo et al.12) used this condition for calculation of Blowing Number.
Density of air, ρg (kg/m3) = 1.29;
Nozzle diameter, d (m) = 0.003;
Density of water, ρl (kg/m3) = 999.84;
Radius of the nozzle, r (m) = (d/2) = (0.003/2) = 0.0015;
Velocity at nozzle exit,
Impact velocity at bath surface24)
(Subagyo et al.12) used value of a = 0.07 for cold model experiments, 0.0382 for hot model data with no gas-metal reaction and 0.0393 for plant data with gas-metal reaction)
Critical gas velocity, Ug = ηUj = 0.44721 * 11.65 = 5.21 m/s (η = constant = 0.44721)
Blowing Number, NB
a. Sampling error calculation
As the sample size was only 30 for FFT analysis, estimation of sampling error in calculating cavity depth due to this sample size was also carried out.
For Flow rate 70 L/min, Lance height 0.12 m, bath height 0.15 m
Standard deviation of cavity depth in 30 images, S ≈ σp = 0.003 m
Taking confidence level 95% (α = .05)
z = 1.96 (at 1 – α /2 = 1 – 0.05/2 = 0.9750)
Margin of error,
It means that we are 95% confident that error in estimating mean of cavity depth is no more than 0.0011 m.
b. Image analysis error
In image analysis error, errors associated with measuring length from images were calculated. A known distance was measured by ImageJ and then it was compared with the true value of the distance.
The fast Fourier transform (FFT) is an efficient algorithm to compute discrete Fourier transform (DFT) and it’s inverse. The equation to solve DFT is given below
To solve DFT, the computation time is proportional to N2, the number of multiplications. It requires a huge amount of machine time for large N. Cooley and Tukey23) proposed FFT to solve DFT in less computing time. The computing speed is a time proportional to N log2N. The inbuilt FFT technique in OriginPro was used in the calculation of frequency and amplitudes. When applying FFT in OriginPro software, “rectangular weighting function” was used as a window.