Thermal Conductivity of Molten Slags: A Review of Measurement Techniques and Discussion Based on Microstructural Analysis

Abstract

In order to properly interpret the thermal conductivity of molten silicate slags, several different measurement methods are briefly reviewed, along with a discussion as to their respective advantages and limitations. In addition, a large number of thermal conductivity values measured by these methods are assessed, in order to evaluate their dependence on composition and temperature. The behavior of the thermal conductivity of molten silicate slags was found to show good agreement with well-focused analyses into its microstructure. Moreover, with an improved understanding of the microstructure of silicate slags, there is an apparent co-relation between thermophysical properties such as thermal conductivity, viscosity, and so forth.

1. Introduction

In many extractive metallurgical processes, the importance of molten slags cannot be overemphasized, not only as a by-product, but also as a major component of the processes. Clearly, the thermophysical properties of molten slags therefore need to be thoroughly understood in order to achieve optimal process performance. As one of the most important thermophysical properties, the thermal conductivity of molten slag has received much attention over the past few decades with regards to ladle slags and the continuous casting mold flux of the steelmaking process.^1,2,3)

Metallurgical slag is typically based on a silicate system, which is composed of ionic-bonded cations and covalent bonded anions. The slag composition is therefore expected to have a great influence on its microstructure and corresponding thermophysical properties. Mills suggested that the thermal conductivity of a molten slag at melting point is reduced with an increasing number of non-bridging oxygen ions;⁴⁾ whereas Hayashi et al. proposed that thermal conductivity is proportional to the slag viscosity, thus reflecting the slag microstructure, as shown in Fig. 1.^2,5) In spite of a number of integrated studies into the relationship between thermal conductivity and the structure of molten slags,^2,5,6,7) further clarification is still necessary for a complete understanding. For example, recently reported analyses of the microstructure of various slag systems using Fourier Transform-Infrared Spectroscopy (FT-IR), Raman Spectroscopy, Nuclear Magnetic Resonance (NMR) might provide further insight into the relationship between structure and thermal conductivity.^8,9,10)

Fig. 1.

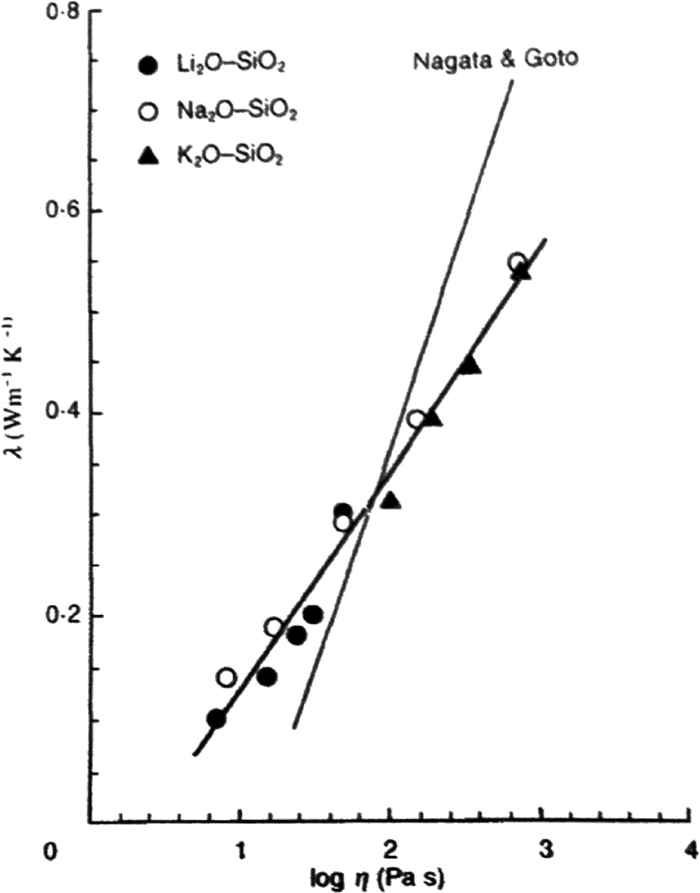
Relationship between thermal conductivities and viscosities of alkali silicates.⁴⁾

In this study, typical measurement methods for the thermal conductivity of molten slags, such as the hot-wire and laser flash methods, are briefly presented and evaluated. In addition, the influence of molten slag microstructure on the composition and temperature dependence of thermal conductivity is discussed with regards to selected microstructural analysis results.

2. Measurement Methods

2.1. Steady-state Methods

With steady-state measurement methods, thermal conductivity is determined from the temperature profile across a sample that is placed in direct contact with a heat source.¹¹⁾ Measurement time using such methods is relatively long, as a steady state of heat flux in the sample needs to be reached. Moreover, the thermal conductivity at high temperatures tends to be obtained as an apparent value, which includes other contributions such as radiation and convection.¹²⁾ These steady-state methods therefore have limitations in the application to liquid phases at high temperatures.

2.2. Non-steady-state Methods

The measurement is carried out by monitoring the temperature change of a sample over a short period of time with a constant supply of energy. Owing to the short measurement time, which is typically no longer than 30 s, and the relatively simple measurement setup, non-stationary methods such as the laser flash and hot-wire methods have been widely employed for measuring the thermal conductivity of molten slag.

In the laser flash method, the surface of a layered sample is exposed to a pulse-laser and the thermal response at the other side of the sample is simultaneously monitored by a detector. If the thickness of the sample is known, then the thermal diffusivity of the sample can be derived from the pulse shift and temperature change. The main advantages of this method are its short measurement time and wide applicable range of thermal diffusivity.¹¹⁾ Even though this particular method was originally designed for measuring the thermal diffusivity of solid materials,¹³⁾ it nonetheless can be extended to the measurement at high temperature liquid materials through many sufficient effort.

Based on the measurement principle of the laser flash method, Ohta and a number of other researchers have developed a three-layered laser flash method to effectively minimize heat loss during measurements.^14,15,16) In this, a molten sample is placed between upper and lower metal plates, which are an irradiated side and a detector side, respectively. These two plates enable precise adjustment of the sample thickness, which is often one of the most important issues during measurement at high temperature. Further development of this method has led to the creation of a differential three-layered method.¹⁴⁾ By carrying out two measurements at different sample thicknesses, the thermal diffusivity of the sample can be determined from the change in thermal response and the displacement of the top plate.

Another particular concern with the laser flash method is how to take into account the contribution of radiation heat transfer. In the three-layered laser flash method, the radiative heat flux on the surface of each plate, and the reflected heat flux between them, is expected to have a considerable influence on the thermal diffusivity measurement. Furthermore, when the molten sample is not completely transparent, part of the radiation heat may be absorbed into the molten sample, while the rest is transferred through it. Srinivasan et al. theoretically estimated this influence of radiation heat flux on the potential measurement error and found that measurement result can be corrected by proper consideration of various parameters;¹⁷⁾ despite the complicated calculations that are required.

These difficulties can be partly overcome by the design of the front-heating and front-detection laser flash method.^18,19) In this method, a molten sample is first placed in a platinum crucible, the bottom surface of which is then heated by a pulse-laser while the temperature change of the platinum surface is monitored. The temperature recovery of the bottom surface of the crucible is then analyzed to determine the thermal diffusivity of the sample. Unlike the three-layered method, both heating and detection takes place at the bottom surface of the crucible, while the upper surface of the sample is open. An absence of multiple reflections through the sample therefore means that the radiative heat flux can be considered only from the bottom surface of the crucible; however, an appropriate consideration of the radiative heat flux is still required. Moreover, Hasegawa et al. have pointed out that the influence of bubbles in the sample can be eliminated, thanks to the absence of a top plate on the surface of the sample.²⁰⁾ Various types of laser flash methods are schematically described in Fig. 2.

Fig. 2.

Schematic diagram showing the principles of various laser flash methods: (a) conventional,¹³⁾ (b) three layered,¹⁴⁾ (c) front-heating and front-detection.²⁰⁾

The hot-wire method can be distinguished from the laser flash method by its relatively low sensitivity to radiative heat transfer. As it is currently understood, it may be attributed to the far smaller surface area of the hot wire when compared to the platinum plate used in the laser flash method.²¹⁾ Menashe and Wakeham investigated the effect of radiation absorption and emission on heat conduction during measurement of thermal conductivity using the hot wire method.²²⁾ According to their simulation, the relative contribution of absorption into a sample was considered to be negligible compared to that of emission. Moreover, the increase in temperature caused solely by the radiative effect of emission turned out to be no larger than 0.005 K, which is significantly smaller than temperature change caused by conduction during hot-wire measurement. Proper control over convection in the molten sample, rather than radiation, may therefore be regarded as the more essential requirement. In addition Glaser et al. have determined the optimal measurement conditions to ensure better experimental reproducibility, particularly with regards to inhibiting convection.²³⁾

The transient hot wire method was originally designed more than 120 years ago for measuring the thermal conductivity of fluids at low temperatures.²⁴⁾ After being initially adapted by Murase and McBirney to measuring the thermal conductivity of igneous materials,²⁵⁾ Nagata and Susa further developed this technique in the early 1980s to apply to molten slag at high temperatures.^6,26,27,28) Initially, the Na₂O–SiO₂ slag system was selected for thermal conductivity measurements, taking advantage of its relatively low melting point.^{2,6,26,27,30,31,32)} Soon after, the hot wire method was also established for measuring the thermal conductivity of the CaO–Al₂O₃–SiO₂,^7,26,27,28) CaO–Al₂O₃–SiO₂–MgO,³¹⁾ and CaO–SiO₂–FeO_x slag systems.^32,33)

The fundamental measurement principle of the hot wire method can be described as follows: First, a thin thermo-resistor wire is placed vertically in the middle of a molten sample. Under a constant supply of electric power, heat is then generated from the hot wire at a constant rate and transfers into the sample surrounding it mainly by conduction. If we consider the sample as a semi-infinite cylindrical system, in which a line heat source is vertically placed, then the heat conduction equation can be written as follows:³⁴⁾   

$$\rho C_p\left(\frac{\partial T}{\partial t}+\nu \nabla T\right)=\lambda {\nabla }^{2}T+Q$$(1)

Here, Q corresponds to the heat generation per unit length of the hot wire. Solving this equation gives us:   

$$\mathrm{\Delta }T=\frac{Q}{4\pi \lambda }ln\frac{4at}{r^{2}C}=\frac{Q}{4\pi \lambda }\left(lnt+A\right)\mathrm{\hspace{0.17em} }\hspace{0.17em}\left(A:\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\right)$$(2)

where ΔT, r, a, and t are the temperature change of the hot wire, radius of the hot wire, thermal diffusivity of the sample and time, respectively. The value of C is equal to the exponential of the Euler constant, γ, and thus the thermal conductivity of the sample can be obtained from Q and the slope of ΔT versus the natural logarithm of time using the following relationship:   

$$\lambda =\frac{Q}{4\pi }/\frac{dT}{dlnt}$$(3)

A Pt-13%Rh wire is frequently employed as the hot wire for practical measurement, which plays roles of heater and sensor simultaneously. A typical measurement circuit is schematically drawn in Fig. 3, consists of a hot wire, a Galvanostat, a standard resistor and Pt conducting wire. By supplying a constant electric power to the hot wire, the voltage change of the hot wire can be continuously measured to determine the slope of ΔV versus lnt.

Fig. 3.

Schematic depicting the measurement apparatus for the hot wire method.⁵⁾

It has been acknowledged that molten silicate slags generally have an extraordinarily large Rayleigh number of ~10,^6,35) which can simply be regarded as the ratio between heat transfer by natural convection and by conduction. When the measurement time is sufficiently elapsed, the effect of convection becomes increasingly significant. It is, however, fortunate that this influence of convection appears to be distinguishable in a plot of ΔV versus lnt during measurement. As shown in Fig. 4,³⁶⁾ the voltage change starts to deviate from linearity after a few seconds due to the effect of convection. Hence, a linear range should be chosen from the curve using differentiation; and in doing so, the slope of ΔV versus lnt can be determined.

Fig. 4.

Typical voltage change of hot wire versus lnt for 0.33Na₂O-0.67SiO₂ at 1373 K.³⁶⁾

Since molten silicates are composed of cations and anions, one may consider that the current supplied to the hot wire will leak through the molten sample if its electrical conductivity is sufficiently high. In the thermal conductivity measurements of KNO₃–NaNO₃–NaNO₂ system heat-transfer-salts, Nagashima et al. utilized a Pyrex or quartz capillary tube filled with mercury as both the heating source and sensor, thereby pointing out that current leakage may occur though the capillary tube at 570 K.^37,38) However, in the case of heat-transfer-salts, decomposition of their components has the potential to cause gas evolution and corresponding convection; and thus the current leakage may be caused by chemical attack on the capillary tube. Recently, Hasegawa et al. pointed out that even in case of a molten CaO–Al₂O₃–SiO₂ slag, current leakage may occur during thermal conductivity measurements using the hot wire method.^20,39) To elucidate the possibility of current leakage from a Pt-Rh hot wire during thermal conductivity measurement of various molten slags, the resistivity of the Pt-Rh wire has been estimated at their respective measurement temperatures.⁴⁰⁾

In spite of the low resistivity of molten slag (0.01–0.05 Ohm·m),⁴¹⁾ the current passing through the slag sample is expected to be much less than that through the hot-wire (resistivity of 5.0–6.0 × 10^–7 Ohm·m).⁴²⁾ However, when molten slag contains transition metallic oxides with multiple valences, the electrical conductivity of the sample might be considerably high; and thus any current leakage would be need to be carefully considered.

3. Composition Dependence of Thermal Conductivity

In silicate-based slag, a Si atom is covalently bonded with tetrahedrally coordinated four oxygen atoms. In the melt, the SiO₄^4– tetrahedron tends to form a network of covalent bonds, which can be broken (depolymerized) by the existence of basic-oxide network modifiers. Since heat transfer by conduction in silicate melts is mostly carried out by phonon vibration, the thermal conductivity of a molten silicate slag is expected to be influenced by the relative quantities of ionic and covalent bonds, as determined by the slag composition.

Many researches into the thermal conductivity of molten silicate slags has started with an alkali oxide-silicate system, specifically the Na₂O–SiO₂ system^{2,6,26,27,30,31,32,43,44)} shown in Figs. 5, 6, 7, 8, 9. In Fig. 8, the thermal conductivity of this Na₂O–SiO₂ system is shown for relative molar fractions of 1:1 and 1:2. As the SiO₂ content increases, thermal conductivity increases, suggesting that the silicate structure strongly affects the heat transfer mechanism. Furthermore, this dependence seems to be more prevalent in those measurements using hot wire methods. For the K₂O–SiO₂ system, a similar compositional dependence of thermal conductivity also has been observed.⁴⁵⁾ Sukenaga et al. confirmed the structural modification of molten silicate slag by alkali oxides, on the basis of viscosity measurements and structural analysis using NMR.⁴⁶⁾ They further pointed out that the effect of alkali oxides on the viscosity of an aluminosilicate melt depends on the size of the alkali cation. More investigation and discussion of the thermal conductivity of these systems will therefore likely be meaningful in the sense of understanding the interrelationship between various thermophysical properties.

Fig. 5.

Thermal conductivity of 0.33Na₂O-0.67SiO₂ as a function of temperature (1).⁵⁾

Fig. 6.

Thermal conductivity of 0.33Na₂O-0.67SiO₂ as a function of temperature (2).⁶⁾

Fig. 7.

Thermal conductivity of 0.3Na₂O-0.7SiO₂ as a function of temperature.²⁹⁾

Fig. 8.

Thermal conductivity of the Na₂O–SiO₂ system as a function of temperature (1).^5,6,26)

Fig. 9.

Thermal conductivity of the Na₂O–SiO₂ system as a function of temperature (2).¹¹⁾

Fig. 10.

Thermal conductivity of the Na₂O–SiO₂ system as a function of temperature (3).²⁷⁾

The thermal conductivity of the molten CaO–Al₂O₃–SiO₂ system has been more frequently measured due to the practical applicability of such data to blast furnace slags. In most cases, the ratio of CaO (or sum of basic oxides) to SiO₂ (or sum of acidic oxides), is used as a composition index that determines the basicity of the molten slag. In this sense, the compositional dependence of the thermal conductivity seems to be more straightforward when compared to that of the Na₂O–SiO₂ system. Various data values for the thermal conductivity of the CaO–Al₂O₃–SiO₂ system are summarized in Figs. 11, 12, 13.^7,11,47) This reveals a tendency for the thermal conductivity to increases as the basicity of the slag decreases (i.e., more SiO₂ and less CaO), which is more or less valid for most of the results. In Fig. 14, the iso-thermal conductivity lines for various temperatures, which were determined using the hot wire method, confirms a strong dependence on the composition and slag basicity.

Fig. 11.

Thermal conductivity of the CaO–Al₂O₃–SiO₂ system as a function of temperature (1).⁷⁾

Fig. 12.

Thermal conductivity of the CaO–Al₂O₃–SiO₂ system as a function of temperature (2).¹¹⁾

Fig. 13.

Thermal conductivity of the CaO–Al₂O₃–SiO₂ system as a function of temperature using laser flash method.⁴⁷⁾

Fig. 14.

Iso-thermal conductivity lines of the CaO–Al₂O₃–SiO₂ system at: (a) 1673 K, (b) 1773 K, (c) 1873 K.⁷⁾

When depolymerization occurs in a silicate melt, the average number of disconnected oxygen atoms in tetrahedral network will increase. This can be expressed as the number of non-bridging oxygen atoms per tetrahedron, or NBO/T, which ranges from “0” with a complete network of SiO₂ to “4” with a fully depolymerized SiO₄^4– tetrahedra. Considering the characteristics of each oxide, Mill suggested that the NBO/T value of a silicate melt can be estimated from its composition.⁴⁸⁾ As with the basicity of the slag, the dependence of thermal conductivity on NBO/T in silicate melts is clearly shown in a number of published results,^33,48) as shown in Figs. 15 and 16.

Fig. 15.

Relationship between the thermal conductivity at liquidus temperature and NBO/T (1).⁴⁸⁾

Fig. 16.

Relationship between the thermal conductivity at liquidus temperature and NBO/T (2).³³⁾

In the CaO–Al₂O₃–SiO₂ system, Al₂O₃ is categorized as an amphoteric oxide that can behave as either a basic or acidic oxide depending on the overall composition. Consequently, Al₂O₃ can exist as either Al³⁺ or AlO₄^5– depending on the composition in a silicate melt. It can easily that expected ionic bonds between Al³⁺ and O^2– decreases, while covalent bond in AlO₄^5–. This amphoteric behavior of Al₂O₃ is evident in the thermal conductivity measurement of molten CaO–Al₂O₃–SiO₂ slags, as shown in Fig. 17.⁷⁾

Fig. 17.

Dependence of thermal conductivity on Al₂O₃ content at various CaO/SiO₂ ratios.⁷⁾

Park et al. also demonstrated the amphoteric behavior of Al₂O₃ in their measurements of the viscosity of a CaO–Al₂O₃–SiO₂ slag. Investigation into the structural modification using FT-IR spectroscopy,^49,50) as shown Figs. 18 and 19, revealed that the IR bands of the [SiO₄]-tetrahedra are broadened by a 10 wt% addition of Al₂O₃ addition; thus indicating polymerization of the network. When the Al₂O₃ addition was increased beyond 10 wt%, the appearance of an octahedral band (570 cm^–1) identified the presence of AlO₆, which is known to exhibit basic behavior. Zheng et al. confirmed this microstructural modification of the CaO–Al₂O₃–SiO₂ system with composition variation using Molecular Dynamics simulation.⁵¹⁾ This found that although the SiO₄ network may be depolymerized by initial Al₂O₃ addition, Si and Al are likely to subsequently coordinate together to form a new network cluster. By careful analyses of the microstructure of molten slags, the amphoteric behavior could be clearly understood and an interrelationship among the thermophysical properties of the molten silicate was verified.

Fig. 18.

Viscosities of CaO–SiO₂–Al₂O₃(–10MgO) slags at 1823 K as a function of Al₂O₃ content.⁴⁹⁾

Fig. 19.

IR transmittance of CaO–SiO₂–Al₂O₃ (CaO/SiO₂=1.3) slags with different Al₂O₃ contents as a function of wave number.⁴⁹⁾

The multi-valence nature of transition metal oxides may also influence the microstructure of silicate melts and their thermophysical properties. With particular experimental effort to control oxygen partial pressure, the effect of Fe valences on the local structure and the thermal conductivity has been clarified by Kang et al.³³⁾ Through microstructural analysis using Mössbauer spectroscopy, the relationship between microstructural properties (i.e., the valence and the coordination of the Fe ions) and the slag thermal conductivity could be reasonably explained. Nonetheless, more elaborate measurements and further consideration of the individual behaviors of various oxides is still necessary for a deeper understanding.

4. Temperature Dependence of Thermal Conductivity

Debye proposed that the thermal conductivity of a crystalline solid can be expressed using the kinetic theory of gas, as following equation:⁵²⁾   

$$\lambda =\frac{C_{V}vl}{3}$$(4)

where C_V, v, and l correspond to the heat capacity, the sound velocity in the sample and the phonon mean free path, respectively. According to Eq. (4), the thermal conductivity should be proportional to all these variables. Since the mean free path of phonons is inversely proportional to the absolute temperature, the thermal conductivity of the crystalline material will therefore decrease as the temperature rises.

In the case of silicate melts, the temperature dependence of the thermal conductivity had been investigated when the hot-wire method was applied.⁵³⁾ As it happens, a fairly good linear relationship between the thermal conductivity of 0.33CaO-0.67SiO₂ and 1/T in liquid region was reported by Nagata, as shown in Fig. 20.⁵⁴⁾ However, it has also been reported that the thermal conductivity of a molten CaO–Al₂O₃–SiO₂ slag exhibits a negative deviation from the expected linearity against 1/T.⁷⁾ This disagreement may imply that the theory of heat conduction in crystalline solid as expressed by Eq. (4) is not valid in the molten silicate. Moreover, Snyder et al. pointed out that the thermal conductivity of molten silicate deceases with increasing temperature according to the random collision theory suggested by Rao.^55,56) They confirmed that the thermal conductivities of room temperature liquids such as water, toluene and benzene decreased as temperature rises, even if the phonon mean free path hardly changes.

Fig. 20.

Temperature dependence of the thermal conductivity of 0.33Na₂O-0.67SiO₂.⁵⁴⁾

On the other hand, no noticeable temperature dependence has been observed in those values obtained by the laser flash method.^20,39) According to several previous researches using the laser flash method, the negligible temperature dependence of thermal conductivity of molten silicate was attributed to the constant mean free path, which will be equal to the unit cell size in fully depolymerized structure. In the laser flash method, however, the radiation effect on the heat transfer might be underestimated, resulting in the considerable difference in the temperature dependence.

If the network of a molten slag is depolymerized at an elevated temperature, phonon movement is subjected to scattering not only by harmonic vibration, but also by the depolymerization of network. Silicate slag samples quenched from different temperatures were analyzed by means of infrared absorption analysis in similar way to that mentioned in Section 3. At higher temperatures, the IR absorption patterns tend to shift to the higher NBO/T side, as shown in Fig. 21, thus indicating thermal depolymerization. Since this depolymerization can be regarded as thermally induced, the thermal conductivity, can be by an exponential expression:   

$$\lambda =Aexp\left(\frac{Q}{RT}\right)$$(5)

The temperature dependence of the thermal conductivities of various molten silicate slags is summarized in Fig. 22. The slope of the straight line was estimated to evaluate the apparent activation energy for the breaking of network bonds, which was found to be almost constant in the range of 150–170 kJ/mole. Since this falls into approximately the same order as the viscous activation energy of silicate melts,⁵⁷⁾ it may indicate the average Si–O bond breaking energy. At a constant basicity, it has been found that the activation energy for thermal conduction is smaller at lower SiO₂ contents. This decrease in the activation energy is likely to be caused by the increase in NBO/T with a lower population of [SiO₄]^– tetrahedra.

Fig. 21.

IR transmittance of 30 wt%CaO-18 wt%Al₂O₃-52 wt%SiO₂ melts at different temperatures as a function of wave number.⁷⁾

Fig. 22.

Temperature dependence of logarithm of the thermal conductivity for silicate melts where CaO/SiO₂ =0.9.

5. Conclusion

A review of recent progress in the thermal conductivity measurement of molten silicate slags was presented. As transient methods, the laser flash and hot-wire methods, were examined with regards to their respective features. In particular, the influence of radiative heat transfer should be carefully considered in the laser flash method, while the current leakage during the measurement using the hot-wire method may be responsible for error in the measurement. The resistivity of hot-wire, however, was turned out to be sufficient in a number of the thermal conductivity measurements of silicate slags. Thermal conductivity data available in the literature was also reviewed on the basis of microstructural analysis results. Furthermore, the effect of slag basicity, the amphoteric behavior of Al₂O₃, and the temperature dependence of thermal conductivity were all explained in relation to slag microstructure, with reasonable agreement between respective hypotheses.

Acknowledgements

The authors wish to thank Prof. M. Susa, Assoc. Prof. Y. Kobayashi, Assist. Prof. R. Endo, Tokyo Institute of Technology, Prof. H. Ohta, Ibaraki University, and Prof. H. Shibata, Tohoku University for providing useful information and constructive discussion. One of the authors (JL) further acknowledges the support afforded by the Industrial Strategy Technology Development (No. 10035258, Development of Process for Composition and Cooling Control of Molten Slag) through a grant provided by the Ministry of Knowledge Economy, Korea.

References

• 1)   A.  Yamauchi,  K.  Sorimachi,  T.  Sakuraya and  T.  Fujii: ISIJ Int., 33 (1993), 140.
• 2)   M.  Susa,  K. C.  Mills,  M. J.  Richardson,  R.  Taylor and  D.  Stewart: Ironmaking Steelmaking, 21 (1994), 279.
• 3)   S.  Ozawa,  M.  Susa,  T.  Goto,  R.  Endo and  K. C.  Mills: ISIJ Int., 46 (2006), 413.
• 4)   K. C.  Mills: Proc. 3rd Int. Conf. on Metallurgical Slags and Fluxes, Institute of Metals, London, (1988), 229.
• 5)   M.  Hayashi,  H.  Ishii,  M.  Susa,  H.  Fukuyama and  K.  Nagata: Phys. Chem. Glasses, 42 (2001), 6.
• 6)   M.  Susa,  S.  Kubota,  M.  Hayashi and  K. C.  Mills: Ironmaking Steelmaking, 28 (2001), 390.
• 7)   Y.  Kang and  K.  Morita: ISIJ Int., 46 (2006), 420.
• 8)   J. H.  Park,  D. J.  Min and  H. S.  Song: Metall. Mater. Trans. B, 35B (2004), 269.
• 9)   S.  Kashio,  Y.  Iguchi and  T.  Goto: Trans. Iron Steel Inst. Jpn., 20 (1980), 251.
• 10)   M.  Sakamoto,  Y.  Yanaba and  K.  Morita: J. Non-Cryst. Solids, 358 (2012), 615.
• 11)   K. C.  Mills and  M.  Susa: Thermal Conductivities of Slags, NPL Report DMM(A) Vol. 68, National Physical Laboratory, London, (1992).
• 12)   A. C.  Mikrovas,  S. A.  Argyropoulos and  L. D.  Sommerville: Iron Steelmaker, 18 (1991), 15.
• 13)   W. J.  Parker,  R. J.  Jenkins,  C. P.  Butler and  G. L.  Abbott: J. Appl. Phys., 32 (1961), 1679.
• 14)   H.  Ohta,  G.  Ogura,  Y.  Waseda and  M.  Suzuki: Rev. Sci. Instrum., 61 (1990), 2645.
• 15)   Y.  Waseda,  M.  Masuda and  H.  Ohta: Proc. of 4th Int. Symp. on Advanced Nuclear Energy Research, Japan Atomic Energy Research Institute, Kashiwa, Chiba, (1992), 298.
• 16)   H.  Ohta,  M.  Masuda,  K.  Watanabe,  K.  Nakajima,  H.  Shibata and  Y.  Waseda: Tetsu-to-Hagané, 80 (1994), 463.
• 17)   N. S.  Srinivasan,  X. G.  Xiao and  S.  Seetharaman: J. Appl. Phys., 75 (1994), 2325.
• 18)   H.  Ohta,  H.  Shibata,  A.  Suzuki and  Y.  Waseda: Symp. Fundamentals of Metallurgical Processing, eds. by C. Kaiura, C. Pickels, T. Utigard and A. Vahed, METSOC, Canada, (2000), 19.
• 19)   H.  Ohta,  H.  Shibata,  A.  Suzuki and  Y.  Waseda: Rev. Sci. Instrum., 72 (2001), 1899.
• 20)   H.  Hasegawa,  H.  Ohta,  H.  Shibata and  Y.  Waseda: High Temp. Mater. Proc., 31 (2012), 491.
• 21)   K. C.  Mills: The Estimation of Slag Properties, Southern African Pyrometallurgy 2011, Short Course Presentation, SAIMM, South Africa, (2011).
• 22)   J.  Menashe and  W. A.  Wakeham: Int. J. Heat Mass. Tran., 25 (1982), 661.
• 23)   B.  Glaser,  L.  Ma and Du Sichen: Steel Res., 84 (2013), 649.
• 24)   A. L.  Schieirmacher: Wiedemann Ann. Phys., 34 (1888), 122.
• 25)   T.  Murase and  A. R.  McBirney: Geol. Soc. Am. Bull., 84 (1974), 3563.
• 26)   K.  Nagata and  K. S.  Goto: Proc. of 2nd Int. Symp. on Metallurgical Slags and Fluxes, eds. by H. A. Fine and D. R. Gaskell, Metall. Soc. AIME, Warrendale, PA, (1984), 875.
• 27)   K.  Nagata,  M.  Susa and  K. S.  Goto: Tetsu-to-Hagané, 69 (1983), n.11, 1417.
• 28)   S.  Ishikuro,  K.  Nagata and  K. S.  Goto: Trans. Iron Stell Inst. Jpn., 21 (1981), B-13.
• 29)   M.  Susa,  K.  Nagata and  K.  Goto: Trans. Jpn. Inst. Met., 29 (1988), 133.
• 30)   K.  Ogino,  A.  Nishiwaki and  K.  Yamamoto: Tetsu-to-Hagané, 65 (1979), S683.
• 31)   B.  Glaser and  D.  Sichen: Metall. Mater. Trans. B, 44B (2013), 1.
• 32)   M.  Susa,  F.  Li and  K.  Nagata: Ironmaking Steelmaking, 20 (1993), 201.
• 33)   Y.  Kang,  K.  Nomura,  K.  Tokumitsu,  H.  Tobo and  K.  Morita: Metall. Mater. Trans. B, 43B (2012), 1420.
• 34)   H.  Carslow and  J.  Jaeger: Conduction of Heat in Solids, 2nd ed., Clarendon Press, Oxford, (1959).
• 35)   R. H.  Eric: J. South. Afr. Inst. Min. Metall., 104 (2004), 499.
• 36)   Y.  Kang and  K.  Morita: MOLTEN2009, 8th Int. Conf. on Molten Slags, Fluxes and Salts, Gecamin Ltd., Santiago, Chile, (2009).
• 37)   M.  Hoshi,  T.  Omotani and  A.  Nagashima: Rev. Sci. Instrum., 52 (1981), 755.
• 38)   T.  Omotani and  A.  Nagashima: Trans. Jpn. Soc. Mech. Eng., 48 (1982), 2034.
• 39)   H.  Hasegawa,  Y.  Hoshino,  T.  Kasamoto,  Y.  Akaida,  T.  Kowatari,  Y.  Shiroki,  H.  Shibata,  H.  Ohta and  Y.  Waseda: Metall. Mater. Trans. B, 43B (2012), 1405.
• 40)   Y.  Kang,  J.  Lee and  K.  Morita: Metall. Mater. Trans. B, 44B (2013), 1321.
• 41)  Slag Atlas, 2nd ed., Verlag Sthahleisen GmbH, Düsseldorf, (1995), 568, 591.
• 42)   W. F.  Roeser and  H. T.  Wensel: Temperature, Its Measurement and Control in Science and Industry (Appendix), Reinhold Publishing Corporation, New York, (1941).
• 43)   H.  Ohta,  Y.  Waseda and  Y.  Shiraishi: Proc. of 2nd Int. Symp. on Metallurgical Slags and Fluxes, Metall. Soc. AIME, Warrendale, PA, (1984), 866.
• 44)   M.  Kishimoto,  M.  Maeda,  K.  Mori and  Y.  Kawai: Proc. of 2nd Int. Symp. on Metallurgical Slags and Fluxes, eds. by H. A. Fine and D. R. Gaskell, Metall. Soc. AIME, Warrendale, PA, (1984), 891.
• 45)   H.  Ohta and  Y.  Shiraishi: Proc. of 2nd Int. Symp. on Metallurgical Slags and Fluxes, eds. by H. A. Fine and D. R. Gaskell, Metall. Soc. AIME, Warrendale, PA, (1984), 963.
• 46)   S.  Sukenaga,  N.  Saito,  K.  Kawakami and  K.  Nakashima: ISIJ Int., 46 (2006), 352.
• 47)   T.  Sakuraya,  T.  Emi,  H.  Ohta and  Y.  Waseda: J. Jpn. Inst. Met., 46 (1982), 1131.
• 48)   K. C.  Mills: ISIJ Int., 33 (1993), 148.
• 49)   J. H.  Park,  D. J.  Min and  H. S.  Song: Metall. Mater. Trans. B, 35B (2003), 269.
• 50)   J. H.  Park,  H.  Kim and  D. J.  Min: Metall. Mater. Trans. B, 39B (2008), 150.
• 51)   K.  Zheng,  Z.  Zhang,  F.  Yang and  S.  Sridhar: ISIJ Int., 52 (2012), 342.
• 52)   P.  Debye: Lectures on the Kinetic Theory of Matter and Electricity, B. G. Teubner, Leipzig, (1914), 46.
• 53)   S.  Ozawa,  R.  Endo and  M.  Susa: Tetsu-to-Hagané, 93 (2007), 416.
• 54)   K.  Nagata and  M.  Hayashi: CAMP-ISIJ, 16 (2003), 873.
• 55)   D.  Snyder,  E.  Gier and  I.  Carmichael: J. Geophys. Res., 99 (1994), 15503.
• 56)   M. R.  Rao: Phys. Rev., 59 (1941), 212.
• 57)   P. M.  Bills: J. Iron Steel Inst., 201 (1963), 133.