Electrical Conductivity Calculation of Molten Multicomponent Slag by Neural Network Analysis

Abstract

Only a few models for estimating electrical conductivity of molten slag have been developed, which are limited to systems with certain types of components. In this study, a new method for estimating the electrical conductivity of molten slag through neural network calculations is proposed and is compared with previous estimation approaches. The present estimation approach can reproduce the electrical conductivity of molten slag composed of SiO₂, CaO, MgO, MnO, Al₂O₃, FeO, Fe₂O₃, and Na₂O to an uncertainty of 30%. We found that the neural network calculation is applicable to various kinds of molten slag over wider mole fraction and temperature ranges than conventional models.

1. Introduction

The physicochemical properties of molten slag are an essential factor in the design of iron and steelmaking process. Hence, considerable efforts have been made to comprehensively understand the physicochemical properties of molten slag. In particular, research on the relationships between the physicochemical properties and structure of molten slag is considered to be important because the physicochemical properties of molten slag are strongly related to its complicated three-dimensional structure. Measurements of the electrical conductivity of slag have played an important role in accumulating current knowledge of the structure of molten slag.¹⁾ Thus, many researchers have measured the electrical conductivities of molten slag for a variety of slag systems, compositions, and temperatures.^{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33)} However, it is difficult to obtain all the necessary data for electrical conductivity by laboratory experiments, owing to the complex reactions of molten slag with surrounded materials at high temperatures.

To the best of our knowledge, four models for estimating the electrical conductivity of molten slag have been proposed by Jiao et al.,³⁴⁾ Lambert et al.,³⁵⁾ and Zhang et al.^36,37) Jiao et al.³⁴⁾ empirically derived equation for the electrical conductivity of SiO₂–CaO–MgO–MnO and Lambert et al.³⁵⁾ derived that for SiO₂–CaO–MgO–FeO at a particular temperature and composition. Zhang et al.^36,37) determined a relationship between the electrical conductivity and optical basicity and also found a relationship between the electrical conductivity and viscosity. They offered new interpretations of the electrical conductivity. The results derived from their equations are in good agreement with literature data for quaternary molten slag systems; SiO₂–CaO–MgO–Al₂O₃, SiO₂–CaO–MgO–MnO, and those partial sub-systems. These models can be applied only to systems with a limited number of components; however, slag arising from the steel industry contains several kinds of oxides with various mole fraction ratios. Therefore, the development of further models is essential for applications to processing industrial molten slag.

A neural network computation has recently been applied to estimate several kinds of physicochemical properties of molten slag.^38,39,40,41) Results calculated with a neural network have reproduced experimental data for a wide variety of molten slags with high accuracy. The viscosity and surface tension of the molten slag have been successfully modeled through neural network computations by Hanao et al.³⁸⁾ and Nakamoto et al.,³⁹⁾ respectively. In addition, sulfide, phosphate, phosphide, nitride, and carbide capacity predictions based on neural network computations have been achieved by Derin et al.^40,41) In the present work, we apply neural network computations to the estimation of electrical conductivity for molten slag in a multi component system composed of SiO₂, CaO, MgO, MnO, Al₂O₃, FeO, Fe₂O₃, and Na₂O to reproduce the experimental data with high precision and expand on the variety of molten slag systems.

2. Calculation of Electrical Conductivity of Molten Slag with Neural Network

A detailed explanation of the neural network computation is described elsewhere.^38,39,40,41) A layer type neural network, which includes an input layer, a middle layer and an output layer, is used in the present work, as shown in Fig. 1. When the summation of inputs multiplied by the weights exceeds a critical value, the input signal is transmitted through a sigmoid function to the middle layer as a new signal. Then, when the summation of the middle layer values multiplied by the weights exceeds another critical value in the middle layer, it is transmitted as a final output value to the output layer. The back propagation approach is used to minimize the error between the calculated value as an output value and the literature data as teaching data. Through the back propagation approach, the connection weights, W and V, and the critical values, h, are adjusted. The coefficient η determines the shape of the sigmoid curve. This process is called “learning.”

Fig. 1.

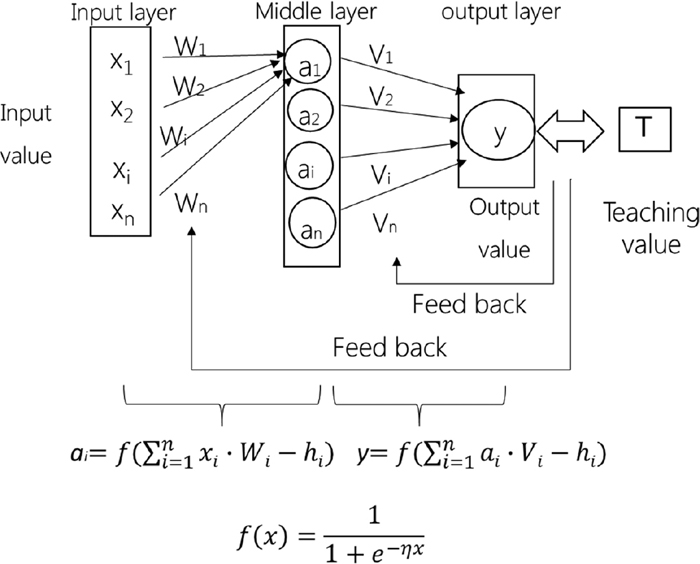
Schematic diagram of layered neural network used in neural network computation.

Original software for neural network computations developed by the Research Center of Computational Mechanics Inc., Osaka University, and Sumitomo Metal Industries Ltd.^40,41) was used in this study. The conditions and procedures of the present calculation are explained below. The input values are temperature and the concentrations of the mole fraction of Al₂O₃, CaO, SiO₂, FeO, Fe₂O₃, MgO, MnO, Na₂O and the output value is the electrical conductivity. The total number of literature values used in this study was 835 and we used data that represented both FeO and Fe₂O₃ concentrations in the treated slag. The data are based on the Slag Atlas,^{2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33)} and are listed in Table 1. We selected 752 data items of electrical conductivity (90% of total number) at random as teaching data to conduct the learning process. Here, we constructed a neural network for estimation of the electrical conductivity through a learning process based on 90% of the total data. The number of units in the middle layer ranged from 1 to 12, the learning number was 5000000, and the initial values which are related to the promotion of learning efficiency given in the product were used. The electrical conductivities calculated by the constructed neural network were compared with the remaining data (10% of total number) as test data to identify the applicability of the constructed network through learning. Finally, we examined the accuracy of the estimation of electrical conductivity by the neural network.

Table 1. Literature data used to estimate the electrical conductivity of molten slag.

system	Temperature (K)	Ref.
SiO2–Al2O3, CaO, FeO, Fe2O3 MgO, MnO, Na2O	1473–1973	2,3,4,5,6,7,8,9,10,11)
SiO2–Al2O3–CaO	1573–1773	2), 6), 12), 13)
SiO2–Al2O3–FeO	1553–1653	6), 14), 15)
SiO2–Al2O3–MgO	1813–2073	8), 16,17,18)
SiO2–Al2O3–Na2O	1273–1673	19), 20)
SiO2–CaO–FeO	2023–2043	6), 14), 21,22,23)
SiO2–CaO–Fe2O3	1558–1663	23)
SiO2–CaO–MnO	1673	5), 9), 10)
SiO2–CaO–Na2O	1273–1673	24)
SiO2–FeO–Na2O	1403–1543	25)
SiO2–MgO–MnO	1773	11)
SiO2–MgO–Na2O	1673–1873	26)
SiO2–Al2O3–CaO–MgO	1673–1873	8), 27,28,29,30,31)
SiO2–Al2O3–CaO–MnO	1673–1873	13), 27), 32)
SiO2–CaO–MgO–MnO	1773	11)
SiO2–Al2O3–CaO–FeO–MgO	1673–1873	33)

3. Results and Discussion

Figure 2 shows the average error of the difference between the experimental and calculated values with respect to the number of units in the middle layer. The average errors were calculated by Eq. (1):   

$$\mathrm{A}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{\hspace{0.17em} }\mathrm{e}\mathrm{r}\mathrm{r}\mathrm{o}\mathrm{r}=\frac{1}{N}\left({\sum }_{i=1}^N\frac{\left|{\sigma }_{\mathrm{C}\mathrm{a}\mathrm{l}}-{\sigma }_{\mathrm{E}\mathrm{x}\mathrm{p}}\right|}{{\sigma }_{\mathrm{E}\mathrm{x}\mathrm{p}}}\right)\times 100(\%)$$(1)

where σ_Exp is an experimental value referred to as teaching data in this study, σ_Cal is a value calculated by the neural network, and N is the number of the literature data. The average error of one unit in the middle layer shows a large value, i.e., approximately 28%. When the number of units increases, the average error monotonically decreases to approximately 5% at 12 units in middle layer. From these results, we confirmed that the accuracy in the estimation of the electrical conductivity of the slag by the neural network is improved by increasing the number of units in the middle layer. It is generally understood that a higher number of units in the middle layer has a higher number of connection weights to fit the calculated results to experimental values. However, a neural network with a large number of units in the middle layer potentially worsens the predictive performance for data, which are not used for ‘learning.’ Therefore, it is very important to decide the appropriate number of units, which satisfies not only the reproducibility in learning but also the prediction ability for unknown data. Thus, we attempt to determine the optimal number of units in the middle layer with the criterion as R², which is used to evaluate the number of variables in multi-linear regression.⁴²⁾   

$$R^2=\frac{\mathrm{\Sigma }{\left|{\sigma }_{\mathrm{C}\mathrm{a}\mathrm{l}}-{\overline{\sigma }}_{\mathrm{E}\mathrm{x}\mathrm{p}}\right|}^2}{\mathrm{\Sigma }{\left|{\sigma }_{\mathrm{E}\mathrm{x}\mathrm{p}}-{\overline{\sigma }}_{\mathrm{E}\mathrm{x}\mathrm{p}}\right|}^2}$$(2)

where ${\overline{\sigma }}_{\mathrm{E}\mathrm{x}\mathrm{p}}$ is the mean value of σ_Exp, and R² varies from 0 to 1. When the value of R² increases, the deviation between the calculated and experimental values becomes small over the composition range treated in this study, which represents the accuracy of the neural network computation. Figure 3 shows the relationship between R² and the number of units in the middle layer. The value of R² increases with increasing units, while R² is a roughly constant at approximately 0.966 above 7 units in the middle layer. As shown in Fig. 3, R² does not increase despite the increase in the number of units, when the number of units exceeds a particular number, i.e., 7. This means that the accuracy of the neural network does not change any more above 7 units in the middle layer even if the number of units increases. Finally, we decided the number of units in the middle layer to be 7 in the present calculation with the neural network.

Fig. 2.

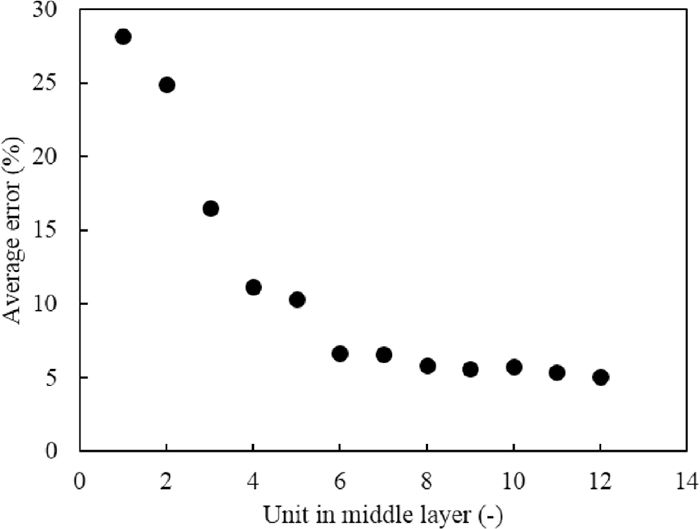
Change in average error with respect to the number of units in the middle layer.

Fig. 3.

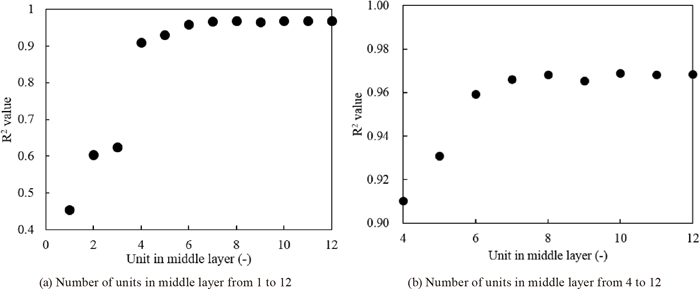
R² as a function of the units in the middle layer. Number of units in the middle layer ranging.

Figure 4 shows a comparison between the experimental value and the calculated value obtained by the neural network computation with 7 units in the middle layer. Most of the data have less than a 30% error between the experimental values and those calculated by the neural network. As Mills¹⁾ reported the error of the experimental values among different research groups ranges up to approximately 30%, thus, the error in our calculation with the neural network is considered to be reasonable. On the basis of the above results, we found that the electrical conductivity of the molten slag could be reproduced with the neural network.

Fig. 4.

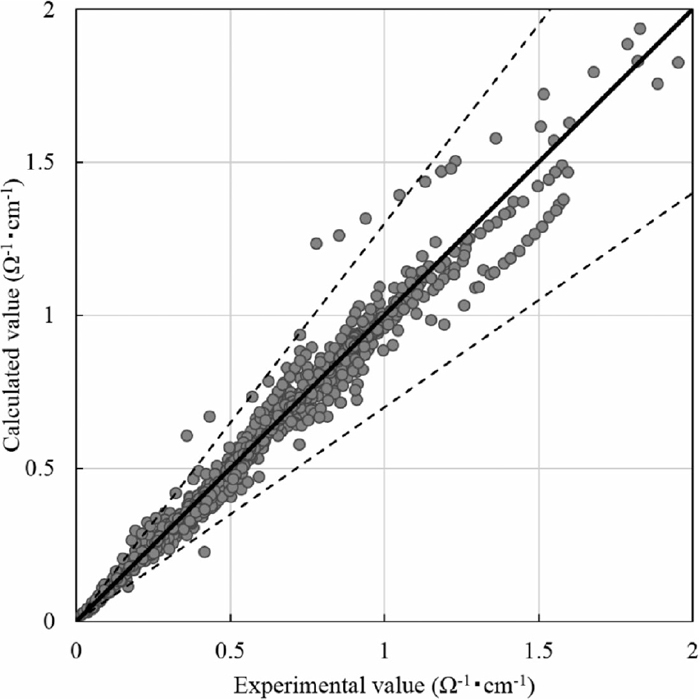
Comparison between experimental values of electrical conductivity and those calculated by neural network computation with 7 units in the middle layer.

Figure 5 shows a comparison between the experimental value and the calculated value obtained with the neural network computation with 7 units in the middle layer in terms of both teaching data and test data. Here, we identify the predictive performance of a neural network constructed under a learning process. In Fig. 5, solid circles express the electrical conductivity data used for learning, i.e., the teaching data, and solid triangles express electrical conductivity data, which were not used for learning, i.e. the test data. The error between the experimental value and the calculated value from the neural network was less than 30% even for the test data. These results mean that experimental data, which were not used for learning, were reproduced by the neural network computation with the unit number assessed by the R²-criterion.

Fig. 5.

Comparison between experimental values of electrical conductivity and those calculated by neural network computation, with 7 units in the middle layer, in terms of teaching data and test data.

To date four models have been proposed by Jiao et al.,³⁴⁾ Lambert et al.,³⁵⁾ and Zhang et al.^36,37) to reproduce the experimental values of electrical conductivity.

Jiao et al.³⁴⁾ proposed an estimation of the electrical conductivity of SiO₂–CaO–MgO–MnO slag from the mole fraction of the chemical components and temperature by the following equation.   

$$K=a+b\mathrm{\hspace{0.17em} }{X}_{\mathrm{C}\mathrm{a}\mathrm{O}},\mathrm{\hspace{0.17em} }+c\mathrm{\hspace{0.17em} }{X}_{\mathrm{M}\mathrm{g}\mathrm{O}},\mathrm{\hspace{0.17em} }+d\mathrm{\hspace{0.17em} }{X}_{\mathrm{M}\mathrm{n}\mathrm{O}}$$(3)

where K is the electrical conductivity, X_M is the mole fraction of M (CaO, MgO, MnO) and a, b, c, and d are coefficients, which are applicable only at 1773 K. Figure 6 shows a comparison between the experimental value of the molten slag and the calculated results of the neural network and by Jiao’s model at approximately 1773 K for SiO₂–CaO–MgO–MnO slag and its sub-systems. In Fig. 6, solid circles show the electrical conductivity of molten slag determined by the neural network, solid triangles show that of SiO₂–CaO–MgO–MnO slag determined by Jiao’s model, and open triangles show that of SiO₂–CaO, SiO₂–MgO, SiO₂–MnO, SiO₂–CaO–MnO, SiO₂–MgO–MnO slag, i.e., sub-systems of SiO₂–CaO–MgO–MnO slag, determined by Jiao’s model. As shown in Fig. 6, most data for the electrical conductivity of SiO₂–CaO–MgO–MnO slag estimated by Jiao’s model are within less than 30% error; however, only half the data for electrical conductivities of SiO₂–CaO, SiO₂–MgO, SiO₂–MnO, SiO₂–CaO–MnO, SiO₂–MgO–MnO slag estimated by this model are within less than 30% error. Conversely, the neural network is capable of estimating the electrical conductivity of both SiO₂–CaO–MgO–MnO slag and its sub-systems with less than 30% error. Therefore, our estimation by the neural network is more accurate than that of Jiao’s model.

Fig. 6.

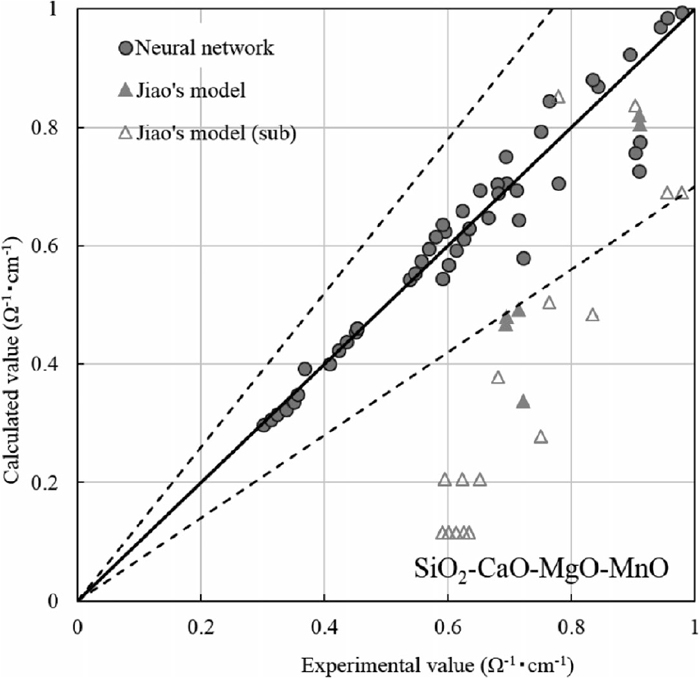
Comparison between experimental values of SiO₂–CaO–MgO–MnO slag electrical conductivity and sub-systems (SiO₂–CaO, SiO₂–MgO, SiO₂–MnO, SiO₂–CaO–MnO, SiO₂–MgO–MnO slag) electrical conductivity and those calculated by neural network and by Jiao’s model.

Lambert et al.³⁵⁾ proposed an estimation of the electrical conductivity of SiO₂–CaO–MgO–Fe₂O₃ slag from the mole fraction of the chemical components at approximately 1673 K as follows.   

$$\mathrm{L}\mathrm{o}\mathrm{g}K=0.697-2.835F$$(4)

where F is the silica ratio of the mole fraction in SiO₂–CaO–MgO–Fe₂O₃. This equation can be applied to SiO₂–CaO–MgO–Fe₂O₃ slag only at 1673 K. Figure 7 shows a comparison between the experimental value of the molten slag and those calculated by the neural network and by Lambert’s model at around 1673 K for SiO₂–CaO–MgO–Fe₂O₃ slag. In Fig. 7, solid circles show the electrical conductivity of the molten slag determined by the neural network and solid triangles show that of SiO₂–CaO–MgO–Fe₂O₃ slag determined by Lambert’s model. As shown in Fig. 7, the error between the experimental value and that calculated by Lambert’s model was greater than 30%, whereas the error between the experimental values and those calculated by the neural network were less than 30%. As shown in Fig. 7, the estimation by the neural network was more accurate than the estimation by Lambert’s model, and the neural network could be applied to SiO₂–CaO–MgO–Fe₂O₃ slag at different temperatures.

Fig. 7.

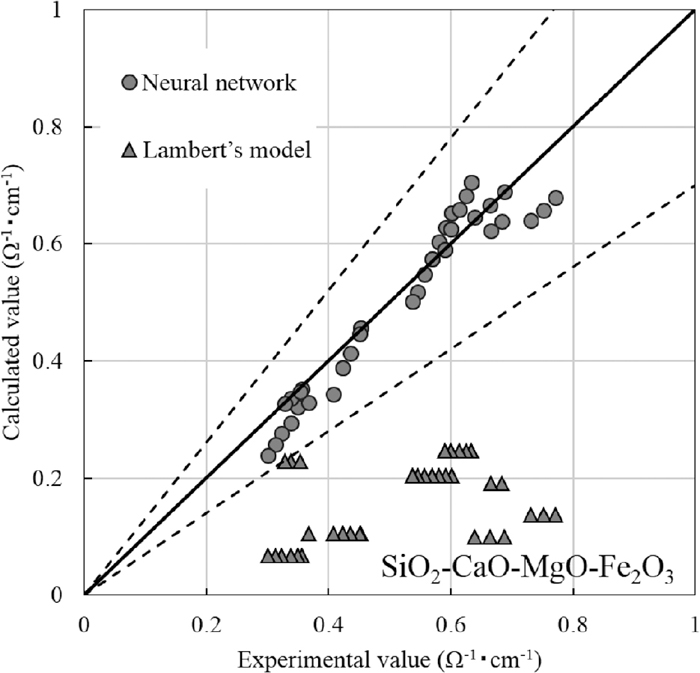
Comparison between experimental values of SiO₂–CaO–MgO–Fe₂O₃ slag electrical conductivity and those calculated by neural network and by Lambert’s model.

Zhang et al.³⁶⁾ proposed an estimation of the electrical conductivity of Al₂O₃–CaO–SiO₂–MgO and Al₂O₃–CaO–SiO₂ slag using the optical basicity. Zhang’s model is more suitable for the electrical conductivity estimation of molten slag than the models of Jiao or Lambert because melt structures are taken into account in Zhang’s model. The equations derived by Zhang et al. are expressed as Eqs. (5) and (6).   

$$\mathrm{L}\mathrm{n}K=\mathrm{l}\mathrm{n}A–B/(R\cdot T)$$(5)

  

$$B=m\cdot V+n,$$(6)

where A, m, n are constants, which are changed by chemical components and temperature, B is the activation energy, R is the gas constant, T is the temperature, and V is the optical basicity. In their model, the optical basicity of the slag was determined on the basis of Pauling electronegativity, as proposed by Duffy and Ingram.⁴³⁾ The optical basicity depends on the chemical composition. Their model is suitable for molten slag with V ranging from 0.58 to 0.67, because molten slag in this composition range is adapted to Eqs. (5) and (6).³⁶⁾ Figure 8 shows a comparison between the experimental electrical conductivity of the molten slag and that calculated by the neural network and Zhang’s model for Al₂O₃–CaO–SiO₂–MgO and Al₂O₃–CaO–SiO₂. In Fig. 8, solid circles show the electrical conductivity of the molten slag determined by the neural network; solid triangles show that of molten slag for V = 0.58–0.67, i.e., within the application region of Zhang’s model; open triangles show that of molten slag where V is less than 0.58 or more than 0.67, i.e., outside the application region of Zhang’s model. As shown in Fig. 8, in the application range Zhang’s model, the error between the experimental value of the molten slag and the value calculated by Zhang’s model is less than 30% error. However, Zhang’s model is not suitable for molten slag outside the application range of their model because the error between the experimental and calculated values was more than 30%, while the present neural network reproduces all data within less than 30% error. Our model can estimate the electrical conductivity of slag over a wider range of temperatures and mole fractions of various chemical components compared with the range of the Zhang’s model. Zhang et al.³⁷⁾ proposed another model that estimates the electrical conductivity of molten slag from the viscosity; however, we did not perform a comparison of their model based on viscosity and our calculation with the neural network in this study. This is because the viscosity of molten slag has a large experimental error, in general approximately ±20%,⁴⁴⁾ which can lead to a considerable scatter in the estimation of the electrical conductivity when viscosity is used for model calculations.

Fig. 8.

Comparison between experimental values of Al₂O₃–CaO–SiO₂–MgO and Al₂O₃–CaO–SiO₂ slag electrical conductivity and those calculated by neural network and by Zhang’s model. (inside application range: the value of optical basicity is ranged from 0.58 to 0.67.)

On the basis of the above results, we concluded that the present calculation with the neural network is applicable to the estimation of 22 types of molten slag systems over a temperature range of 1273–1943 K, as shown in Table 1, with less than 30% error. In SiO₂–CaO–MgO–MnO, SiO₂–CaO–MgO–Fe₂O₃, Al₂O₃–CaO–SiO₂–MgO and Al₂O₃–CaO–SiO₂ slag systems, the present neural network calculation reproduced the literature data over a wider range of compositions and temperatures than conventional models.

Finally, the iso-electrical conductivity lines were predicted in the liquidus area of the Al₂O₃–CaO–SiO₂ system and the result is shown in Fig. 9. In this figure, the calculated iso-electrical conductivity lines are drawn by solid lines and compositions where the experimental values are available are described by squares. The predicted iso-electrical conductivity lines well agreed with the reported experimental values, and indicated that the electrical conductivity decreases not only by SiO₂ addition but the molar ratio of Al₂O₃/CaO increases, thus its composition dependence is somewhat complicated. The latter tendency may correspond with the nature pointed by several authors^37,45,46) that the electrical conductivity of alkaline or alkaline-earth alminosilicate melts decreases by charge-compensated AlO₄ structure units formation, which will decrease the transportation ability of the Ca ions acting as the charge-compensator in the Al₂O₃–CaO–SiO₂ melt.

Fig. 9.

Iso-electrical conductivity lines in Al₂O₃–CaO–SiO₂ melt at 1773 K predicted by neural network computation.

4. Conclusions

We applied a neural network computation to the prediction of the electrical conductivity of molten slag in multi component systems. On the basis of the present results, neural network calculations precisely reproduced the experimental data for the electrical conductivity of the molten slag. The neural network was capable of accurately estimating the electrical conductivity of various types of slag over a wider range of compositions and temperatures than conventional models.

References

• 1)   K. C.  Mills and  B. J.  Keene: Int. Mater. Rev., 32 (1987), 1.
• 2)   T.  Hoster: Arch. Eisenhuttenwes., 54 (1983), 389.
• 3)   H.  Inouye,  J.  Tomlinson and  J.  Chipman: Trans. Faraday Soc., 49 (1953), 796.
• 4)  J. O’M. Bockris, J. A. Kitchener, S. Ignatowicz and J. W. Tomlinson: Discuss. Faraday Soc., 4 (1948), 265.
• 5)  J. O’M. Bockris, J. A. Kitchener, S. Ignatowicz and J. W. Tomlinson: Trans. Faraday Soc., 48 (1952), 75.
• 6)   A.  Adachi and  K.  Ogino: Molten Salts, 4 (1961), 151.
• 7)   K.  Mori and  Y.  Matsushita: Tetsu-to-Hagané, 38 (1952), 283.
• 8)   A.  Adachi and  K.  Ogino: Molten Salts, 7 (1964), 370.
• 9)   L.  Segers,  A.  Fontana and  R.  Winard: Trans. Inst. Min. Metall. Eng., 88 (1979), 53.
• 10)   L.  Segers,  A.  Fontana and  R.  Winard: Electrochim. Acta, 23 (1978), 1284.
• 11)   L.  Segers,  A.  Fontana and  R.  Winard: Can. Metall. Q., 22 (1983), 429.
• 12)   A. I.  Manakov,  B. M.  Lepinskikh,  O. I.  Bukmoyarov,  A. E.  Goncharov and  G. I.  Solovev: Izv. VUZ Chern. Met., 12 (1975), 14.
• 13)   S. O.  Bainsanov,  T. D.  Takenov,  T. G.  Gabdullin and  E. A.  Buketov: VINITI Tech. Report, (1981), 1770.
• 14)   K.  Narita,  T.  Onoye,  T.  Ishii and  K.  Uemura: Tetsu-to-Hagané, 61 (1975), 2943.
• 15)   L.  Bobok,  L.  Bodnar and  J.  Schmiedl: Hutn. Listy, 37 (1982), 419.
• 16)   J. H.  Downing and  L.  Urban: J. Met., (1966), 337.
• 17)   M. S.  Rennie,  D. D.  Howat and  P. R.  Jochens: J. South Afr. Inst. Min. Metall., (1972), 1.
• 18)   N. L.  Zhilo,  I. S.  Ostretsova,  G. V.  Charushnikova and  R. F.  Pershina: Izv. VUZ Chern. Met., 4 (1982), 35.
• 19)   G.  Bonetti: Riv. Stn. Sper. Vetro, 6 (1976), 241.
• 20)   Y.  Itai,  G.  Masuda,  K.  Mizoguchi and  Y.  Suginohara: Bull. Kyushu Inst. Technol., 41 (1980), 95.
• 21)   A.  Weijnarth: Trans. Electrochem. Soc., 65 (1934), 177.
• 22)   L.  Bodnar,  L.  Bobok and  J.  Schmiedl: Proc. 3rd Int. Conf. on Molten Salt Chemistry, Institute of Chemistry, Wydawn University, Wroclaw, (1979), 7.
• 23)   H. W.  Gudenau and  J.  Petry: Fachber. Huttenprax. Metallweiterverarb., 19 (1981), 32.
• 24)   H.  Wakabayashi and  R.  Terai: Yogyo Kyokaishi (J. Ceram. Soc. Jpn.), 91 (1983), 334.
• 25)   K.  Mori and  Y.  Matsushita: Tetsu-to-Hagané, 38 (1952), 444.
• 26)   M.  Kawahara,  Y.  Ozima,  K.  Morinaga and  T.  Yanagase: J. Jpn. Inst. Met., 42 (1978), 618.
• 27)   M.  Kato and  S.  Minowa: Trans. Iron Steel Inst. Jpn., 9 (1969), 39.
• 28)   S. B.  Sarkar: ISIJ Int., 29 (1989), 348.
• 29)   S. B.  Sarkar and  P. K.  Sen: Trans. Indian Inst. Met., 31 (1978), 276.
• 30)   S.  Nesterenko and  V. M.  Khomenko: Russ. Metall., 2 (1985), 42.
• 31)   H.  Winterhager,  L.  Greiner and  R.  Kammel: Forschungsbericht des Landes Nordrhein-Westfalen, Nr. 1630, Westdeutscher Verlag, Köln–Opladen, (1966).
• 32)   T. A.  Chubinidze,  G. D.  Maisuradze and  V. D.  Beider: Proc. Institute of Metallurgy, Academy of Science of the USSR: Physical Chemistry and Metallurgy of Manganese, Nauka, Moscow, (1983), 20.
• 33)   V. A.  Luganov,  M. E.  Turkeev and  T. K.  Ishchanov: Metall. Obogashch., 12 (1977), 75.
• 34)   Q.  Jiao and  N. J.  Themelis: Metall. Trans. B, 19 (1988), 133.
• 35)   J.  Lambert Bates: Proc. Conf. on High Temperature Sciences Related to Open-cycle, Coal-fired MHD Systems, U. S. Energy Research and Development Administration, Washington, D.C., (1977), 196.
• 36)   G. H.  Zhang and  K. C.  Chou: Metall. Mater. Trans. B, 41B (2010), 131.
• 37)   G. H.  Zhang and  K. C.  Chou: Metall. Mater. Trans. B, 43B (2012), 849.
• 38)   M.  Hanao,  M.  Kawamoto,  T.  Tanaka and  M.  Nakamoto: ISIJ Int., 46 (2006), 346.
• 39)   M.  Nakamoto,  M.  Hanao,  T.  Tanaka,  M.  Kawamoto,  L.  Holappa and  M.  Hamalainen: ISIJ Int., 47 (2007), 1075.
• 40)   B.  Derin,  M.  Suzuki and  T.  Tanaka: ISIJ Int., 50 (2010), 1059.
• 41)   B.  Derin,  E.  Alan,  M.  Suzuki and  T.  Tanaka: ISIJ Int., 56 (2016), 183.
• 42)   A. C.  Tamhane and  D. D.  Dunlop: Statistics and Data Analysis: From Elementary to Intermediate, Prentice Hall, London, (2000), 431.
• 43)   J. A.  Duffy and  M. D.  Ingram: J. Inorg. Nucl. Chem., 37 (1975), 1203.
• 44)   K. C.  Mills,  L.  Chapman,  A. B.  Fox and  S.  Sridhar: Scand. J. Metall., 30 (2001), 396.
• 45)   J. H.  Liu,  G. H.  Zhang and  K. C.  Chou: ISIJ Int., 55 (2015), 2325.
• 46)   H.  Wakabayashi,  R.  Terai and  H.  Yamanaka: Yogyo Kyokaishi (J. Ceram. Soc. Jpn.), 93 (1985), 209.