Control of Heterogeneous Nucleation in Carbon Steel by Magnesium Vapor Injection during Continuous Casting

Abstract

The behavior of magnesium vapor injected in the molten steel and the potential of magnesium vapor for the miniaturization of TiN were evaluated via continuous casting experiments. The position where magnesium vapor should be injected was determined through a non-steady state three-dimensional numerical simulation for molten steel flow in a tundish. The yield of magnesium in the molten steel was changed by the injection position. A high additive yield was achieved when magnesium vapor was injected between the immersion nozzle and the narrow wall of the tundish. The concentration of the soluble magnesium was maintained using a novel method that continuously added magnesium vapor into the molten steel in the tundish, which also ensured stable miniaturization of TiN.

1. Introduction

Recently, there have been an increasing global demand for the high-performance products of carbon steel. Some properties of the carbon steel final product are affected by the quality of continuous cast slabs. Therefore, it is necessary to refine the microstructure and fine inclusions for improving the quality of these slabs, and to minimize microsegregation during solidification.

Heterogeneous nucleation is one of the most effective methods to refine inclusions.^1,2,3) The nucleus is dispersed finely in molten steel and the inclusion generates on this nucleus heterogeneously. It is important to generate a heterogeneous nucleus with micro/nanoscale and disperse that nucleus under high density, without using expensive rare metals.

Previous study⁴⁾ reported that the refinement of TiN inclusion is possible using heterogeneous nucleation. Further, magnesium oxide is a suitable heterogeneous nucleus for TiN.^5,6,7,8,9)

Although several studies^10,11,12,13) have investigated magnesium vapor injection into molten steel and molten iron, these studies are limited to the batch process in a crucible or a ladle. The continuous injection of magnesium vapor into molten steel under continuous casting condition have not been investigated and reported.

When magnesium injection into molten pig iron is stopped, the concentration of magnesium in the molten pig iron decreases with time because of the evaporation of magnesium.¹⁴⁾ To generate continuously fine inclusions, it is important to maintain the concentration of magnesium in molten steel. The continuous injection of magnesium vapor into molten steel in the tundish and the solidification of magnesium oxide as a slab is an effective method to finely disperse magnesium oxide in the continuously cast slab. However, this method was not used in previous studies.

Further, molten steel flow in the tundish is complex. It is necessary to select the position for injecting magnesium into molten steel at a high yield ratio.

Therefore, this study employs a numerical simulation for molten steel flow in the tundish to determine the position of the magnesium vapor injection. Further, the effect of magnesium vapor injection into molten steel in the tundish is evaluated via an experiment using a continuous cast test machine.

2. Characteristics of Magnesium Vapor Injection into Molten Steel

In a previous study,⁴⁾ the authors used a Tammann furnace and a high-frequency induction furnace and obtained the following insights.

The reaction between magnesium and oxygen is given as follows.^15,16,17)   

$$Mg\left(g\right)\to \underset{\_}{Mg}$$(1)

  

$$\underset{\_}{Mg}+\underset{\_}{O}\to MgO$$(2)

  

$$K=\frac{P_{Mg}\times a_O}{a_{MgO}}=P_{Mg}\times a_O,a_{MgO}=1.0$$(3)

Here, P_Mg: vapor pressure, a_o: activity of oxygen, K: equilibrium constant, and a_MgO: activity of magnesium oxide. In Eq. (3), P_Mg or a_o becomes a governing factor depending on the method used to inject into molten steel. When a lump of magnesium is added into molten steel, the concentration of magnesium is determined using a_o and K. When the magnesium vapor injects into the molten steel, P_Mg becomes the governing factor and the effect of a_o reduces. Therefore, magnesium concentration in molten steel is increased by vapor injection. The reaction that progresses is balanced; however, it changes after vapor injection because of the variation in P_Mg. Further, K can be changed arbitrarily by changing P_Mg.

The P_Mg and K of magnesium have been studied previously,¹⁸⁾ and the value of K is 0.023 at 1873 K. In this study, this value of K is used to determine the magnesium concentration.

Figure 1 shows the relationship between the concentration and partial pressure of magnesium. The arrows indicate the range of magnesium concentration in vapor injection and lump addition. Since the concentration of magnesium is higher in vapor injection than that in lump addition, the partial pressure of magnesium is also higher. Since vapor injection into molten steel increases the partial pressure of magnesium, it is confirmed that vapor injection changes the chemical reaction actively.

Fig. 1.

Relationship between concentration and partial pressure of magnesium.

3. Analysis of Molten Steel Flow in the Tundish

Magnesium evaporates easily from molten steel because the evaporation temperature of magnesium is lower than that of molten steel and the vapor pressure is high. An effective approach to prevent magnesium from evaporating is to inject it into molten steel in the tundish and allow it to solidify rapidly in the continuous casting mold. Because the magnesium oxides remain in molten steel for a shorter time, it is therefore necessary to avoid the coarsening and coagulation of these oxides.

Further, if molten steel is poured into the mold from the ladle, the flow in the tundish becomes complex. Therefore, it is important to select the position of magnesium vapor injection in the tundish for pouring molten steel containing magnesium into the continuous casting mold.

Numerical simulation is employed for fluid flow in the tundish to change the position of magnesium vapor injection. Magnesium concentration at the top of the immersion nozzle is predicted to change with the position of magnesium vapor injection. These results indicate that the position of magnesium vapor injection for which the additive yield of magnesium becomes the highest is selected.

A non-steady three-dimensional numerical simulation of molten steel flow is employed to analyze magnesium vapor injected in the molten steel. The turbulent flow is evaluated using the large eddy simulation method.^19,20,21,22)

Figure 2 shows a schematic of the numerical simulation model. The shape of the tundish is assumed to be rectangular; molten steel poured into the tundish from the ladle flows into the immersion nozzle. Although a small amount of argon gas is fed to the immersion lance, it is assumed that only magnesium vapor is fed to the lance for simplifying the numerical simulation. The positions of magnesium injection are set at A, B and C, as shown in Fig. 2.

Fig. 2.

Numerical simulation model for molten steel flow in the tundish of the continuous casting machine. A, B C are the position of magnesium vapor injection, respectively.

The following equations are used in the numerical simulation.

Equation of continuity;   

$$\frac{\partial u_i}{\partial x_i}=0$$(4)

Equation of energy;   

$$\frac{\partial T}{\partial t}+\frac{\partial \left(u_{i}T\right)}{\partial x_i}=\frac{k}{\rho C_p}\frac{\partial }{\partial x_i}\left(\frac{\partial T}{\partial x_j}\right)$$(5)

Equation of diffusion;   

$$\frac{\partial C}{\partial t}+u_i\frac{\partial C}{\partial x_i}=\frac{\partial }{\partial x_i}{D}_{eff}\left(\frac{\partial C}{\partial x_i}\right)$$(6)

Equation of momentum;   

$$\begin{array}{l}{\displaystyle \frac{\partial u_i}{\partial t}}+{\displaystyle \frac{\partial }{\partial x_i}}\left(u_i{u}_j\right)=\\ -{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_i}}{\mu }_{eff}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)+\beta \left(T-T_L\right)g\end{array}$$(7)

  

$${\mu }_{eff}={\mu }_0+{\mu }_t\hspace{1em}{D}_{eff}=D_0+D_t$$(8)

  

$$S_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$(9)

  

$$\begin{array}{l}{\mu }_t={\left(C_S\mathrm{\Delta }\right)}^2\left|S\right|\hspace{1em}\mathrm{\Delta }={\left(\mathrm{\Delta }x\mathrm{\Delta }y\mathrm{\Delta }z\right)}^{\frac{1}{3}}\hspace{1em}{C}_S=1.0\\ \left|S\right|={\left(2S_{ij}{S}_{ji}\right)}^{\frac{1}{2}}\end{array}$$(10)

  

$$D_t=\frac{{\mu }_t}{\rho \times Sc}\hspace{1em}Sc=1.0$$(11)

Here, T: temperature (K), T_L: liquidus temperature (K), T_S: solidus temperature (K), k: thermal conductivity (Wm⁻¹K⁻¹), ρ: density (kg·m⁻³), ΔH: latent heat (J·kg⁻¹), C_p : specific heat (J·kg⁻¹·K⁻¹), f: solid fraction (−), t: time (s), u_i: flow velocity in direction i (ms⁻¹), p: pressure (Pa), β: thermal expansion coefficient, C: concentration of magnesium (mass%), D₀: diffusion coefficient of magnesium (m²s⁻¹), μ₀: viscosity (Pa·s) and g: acceleration of gravity (ms⁻²). The physical properties are listed in Table 1.

Table 1. Physical properties for calculation.

symbol	property	value	ref.
ρAr	density of an argon gas	1.78 (kgm−3)	26)
kAr	thermal conductivity of an argon gas	5.0×10−2 (Jm−1s−1K−1)	26)
μAr	viscosity of an argon gas	7.6×10−7 (kgm−1s−1)	27)
Cp,Ar	specific heat of an argon gas	5.22×10−4 (Jkg−1K−1)	24)
Tm	melting temperature of magnesium	922 (K)	26)
Tb	boiling temperature of magnesium	1363 (K)	26)
M	molar weight of magnesium	2.43×10−2 (kgmol−1)	26)
ρ	density of magnesium	1.74×103 (kgm−3)	26)
k	thermal conductivity of magnesium	1.0×102 (Jm−1s−1K−1)	26)
D0	diffusion coefficient of magnesium	3.0×10−9m2s−1	10)
Cp	specific heat of magnesium	1.36×103 (Jkg−1K−1)	26)
ΔH	heat of fusion of magnesium	1.07×102 (Jkg−1)	26)
ΔHv	heat of evaporation of magnesium	1.54×103 (Jkg−1)	26)
μ0	viscosity of molten steel	6.1×10−3(kgm−1s−1)	28)
R	gas constant	8.314 (JK−1mol−1)	26)

The density of the molten steel is obtained using the following equation obtained from the experiment.²³⁾   

$$\rho =7.02-7.50\times {10}^{-4}\left(T-T_L\right)\times {10}^3\mathrm{\hspace{0.17em} }kg\cdot m^{-3}$$(12)

Molten steel at a temperature of 1873 K is fed into the tundish from the ladle at a flow velocity of 2.3×10⁻² ms⁻¹ which corresponds to the casting speed. The molten steel in the tundish is assumed to flow to the immersion nozzle under the natural flow condition at a pressure of 0 Pa. A slip boundary condition between the molten steel and tundish wall is assumed.

The meniscus in the tundish is surrounded with argon gas under atmospheric pressure. It is necessary to consider the evaporation behavior of magnesium on the meniscus of molten steel in the tundish because magnesium can evaporate easily from molten steel. Further, to evaluate the amount of magnesium evaporated from molten steel, it is necessary to predict the mass transfer coefficient of magnesium between the meniscus and the atmosphere. In this study, the mass transfer coefficient is obtained experimentally.

4. Experimental Procedures

4.1. Experiment Using the High-Frequency Induction Furnace in the Vacuum Vessel

Magnesium can evaporate when magnesium dissolved in molten steel reaches the meniscus in the tundish. The amount of evaporated magnesium can be calculated using the mass transfer coefficient at the interface between the molten steel and the atmosphere. In this study, the mass transfer coefficient of magnesium was evaluated using the method employed in a previous study¹⁴⁾ for molten pig iron.

After stopping magnesium vapor injection into the molten pig iron, the change in the concentration of magnesium with time can be expressed as   

$$C=C_{max}exp\left(-\frac{k_{Mg}}{H}t\right)$$(13)

where, C: magnesium concentration (mass%), C_max: maximum concentration of magnesium when injection of magnesium vapor stopped (mass%), k_Mg: mass transfer coefficient of magnesium (m·s⁻¹), H: depth of molten steel and t: time (s).

Assuming Eq. (13) can be applied to molten steel, the mass transfer coefficient is evaluated from the experiment results obtained using a high-frequency induction furnace.

The high-frequency induction furnace was set in the vacuum vessel. The vessel was exhausted to vacuum, and then, it was filled with argon gas at a pressure of 9.9×10⁻² MPa below atmospheric pressure. The electrolytic iron and alloying metal were set in an MgO crucible and melted by induction heating. The chemical composition of the sample of 200 kg was Fe-0.06mass%C-0.95mass%Si-1.3mass%Mn-0.15mass%Al-0.16mass%Ti-0.038mass%O-0.0057mass%N. The temperature of molten steel was adjusted to 1873 K ± 5 K. The immersion lance is made of Mo–ZrO₂ cermet with an external diameter of 2.5×10⁻² m, an internal diameter of 1.0×10⁻² m and a length of 3.0×10⁻¹ m. The range of 1.0×10⁻¹ m from the end of the lance was immersed in the molten steel and heated. During and after injection of magnesium vapor, a sample for the analysis of magnesium concentration was obtained from the molten steel by using the immersion bomb sampler made of steel.

4.2. Advancing Condition of Magnesium Wire

It is necessary to examine the advancing conditions of a magnesium wire to generate magnesium vapor in the immersion lance. The relationship between the temperature and the advancing speed of magnesium wire into the lance was simulated through the heat transfer calculation.

The lance is heated to 1873 K by molten steel at the end of the distance of 1.0×10⁻¹ m. The magnesium wire advanced in the lance is vaporized by the heat of radiation.

The decrease in temperature caused by the flow of argon gas is determined by the heat transfer boundary condition from the Nusselt number.²⁴⁾   

$$Nu=\frac{hd}{k_{Ar}}=1.86\times {\left(Re\times Pr\times \frac{d}{L}\right)}^{\frac{1}{3}}$$(14)

  

$$Re=\frac{u{\rho }_{Ar}d}{{\mu }_{Ar}},\hspace{1em}Pr=\frac{{\mu }_{Ar}{C}_{p,Ar}}{k_{Ar}}$$(15)

Here, d: inner diameter of lance (m), L: length of lance (m), u: flow rate of an argon gas in lance (ms⁻¹), ρ_Ar: density of an argon gas (kgm⁻³), k_Ar: thermal conductivity of an argon gas (Jm⁻¹s⁻¹K⁻¹), μ_Ar: viscosity of an argon gas (kgm⁻¹s⁻¹), C_p,Ar: specific heat of an argon gas (Jkg⁻¹K⁻¹).

In addition, the high-temperature physical properties required in the heat transfer calculation are listed in Table 1.

4.3. Continuous Casting Test

Figure 3 shows the schematic of the experimental apparatus for continuous casting. The position of the tip of injection lance in the tundish was fixed based on the result of the numerical simulation; magnesium vapor was injected into the molten steel. Further, 2.4×10³ kg molten steel was used for the continuous casting test. The composition of steel is listed in Table 2. Electrolytic iron of low S grade and alloying materials were melted in the high-frequency induction furnace under argon gas atmosphere. The molten steel in the furnace was poured into the ladle. After moving the ladle on the tundish of the continuous casting machine, the molten steel was poured into the tundish from the bottom of the ladle. After the molten steel in the tundish reached a predetermined amount, the stopper on the immersion nozzle was moved upwards and the molten steel was poured into the mold and the casting was started. The amount of molten steel poured through the immersion nozzle was controlled to maintain the meniscus level in the mold, which changed with the opening space of the sliding gate based on the output of the eddy current sensor.

Fig. 3.

Schematic diagram of experimental setup for Mg injection into molten steel in the tundish of the continuous machine.

Table 2. Chemical composition of sample (mass%).

C	Si	Mn	P	S	Al	Ti	O	N
0.15	0.16	1.50	0.012	0.004	0.040	0.026	0.0040	0.0044

Magnesium vapor was injected into the molten steel from the end of the lance. The slab was 0.8 m wide and 0.1 m thick, and the casting speed was 0.8 ms⁻¹. When the yield ratio of magnesium vapor was assumed to be 100%, magnesium concentration in the molten steel was 5.5×10⁻³ mass%. The feeder of the magnesium wire was composed of a wire reel of magnesium, servomotor and speed meter, and it was set in the vessel under argon gas atmosphere. The lance was connected to the vessel using a flexible hose made of stainless steel. The flow rate of argon gas in the lance was adjusted to 1.0×10⁻⁶ m³ s⁻¹ by controlling the flow rate of argon gas fed into the vessel. When a large amount of argon gas is fed into the lance, the yield of magnesium seemed to decrease because of floatation with argon gas. However, it is though that the decrease in the yield of magnesium caused by the flow of argon gas is small under the experimental condition because a tiny amount of argon gas is fed into the lance.

The injection of magnesium vapor started at a length of 1.0 m of the slab and stopped at 2.4 m. By locating the starting and stopping positions of magnesium vapor injection into the molten steel, the change in magnesium concentration in the slab was evaluated. The injection period of magnesium vapor was 105 s. The magnesium concentration was evaluated by the chemical analysis of the samples that were obtained by drilling from the surface to a depth of 1.0×10⁻² m.

5. Results and Discussion

5.1. Experiment Using the High-Frequency Induction Furnace in the Vacuum Vessel

Figure 4 shows the analytical result of magnesium concentration. While magnesium vapor was injected continuously, the concentration of magnesium in the molten steel increased with time. After stopping the injection of magnesium vapor, a concentration of magnesium decreased gradually. It was assumed that the concentration of magnesium in the molten steel could be obtained using Eq. (13) after stopping magnesium vapor injection. The results of this experiment indicate that the mass transfer coefficient was 5.1×10⁻³ m·s⁻¹. Using this value, the amount of evaporated magnesium at the meniscus in the tundish was predicted.

Fig. 4.

The change of magnesium concentration with time in the molten steel. The equation expresses the magnesium concentration after stopping of magnesium vapor injection.

5.2. Numerical Simulation of Molten Steel Flow in the Tundish

It is important to understand the molten steel flow in the tundish to evaluate the behavior of magnesium injected in molten steel. Therefore, the streamline of the molten steel poured in the tundish from the ladle was simulated numerically.

Figure 5 shows the streamline of the molten steel in the tundish after 60 s of continuous casting without magnesium vapor injection.

Fig. 5.

Streamline of molten steel flow in the tundish without magnesium vapor. (Online version in color.)

The molten steel flow poured from the ladle reached the bottom of the tundish and turned around. Then, the flow spread in several directions inside the tundish, the downflow moved toward the immersion nozzle near the bottom wall of the tundish (streamline P); toward the side wall of the tundish; and then it turned in the direction of the meniscus (streamline Q); Further, the flow then moved toward the immersion nozzle near the narrow wall (streamline R) and the circulating flow near the narrow wall (streamline S).

Figure 6 shows the behavior of molten steel flow and the concentration distribution of magnesium in the tundish. The positions of magnesium injection are A, B and C as shown in Fig. 2. The molten steel flow shows the result at 60 s after the start of continuous casting. The concentration distribution of magnesium shows the result at 5 s after the beginning of injection.

Fig. 6.

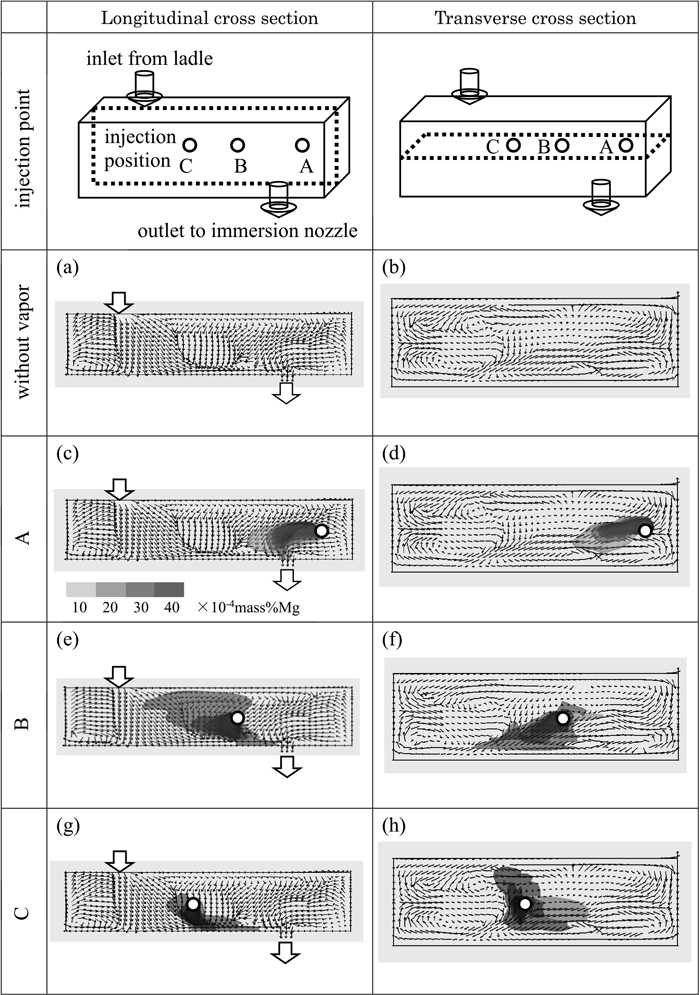
Fluid flow of molten steel and concentration distribution of magnesium in the longitudinal and transverse cross section of the tundish at 5 s after magnesium injection.

Figures 6(a) and 6(b) show the results of the numerical simulation for the molten steel flow shown in the arrow without magnesium vapor injection.

Figure 6(a) shows the molten steel flow at the cross section of the center of the tundish width. The molten steel flow from the ladle reached the bottom of the tundish and turned to the narrow wall, immersion nozzle and meniscus.

Figure 6(b) shows the molten steel flow at the cross section of the center of the tundish height. The molten steel flow was generated in both the longitudinal and latitudinal directions.

Figures 6(c) and 6(d) show the behavior of diffusion for magnesium when magnesium vapor is injected at position A. The region of molten steel that contained magnesium is shown in grey, ant it is divided into 10, 20, 30, 40×10⁻⁴ mass%.

Figure 6(c) shows the concentration distribution of magnesium at the cross section of the center of the tundish width. The molten steel that was contained magnesium flows toward the immersion nozzle.

Figure 6(d) shows the concentration distribution of magnesium at the cross section of the center of the tundish height. The molten steel with magnesium flows toward the immersion nozzle.

Figures 6(e) and 6(f) show the concentration distribution of magnesium when magnesium vapor is injected at position B.

Figure 6(e) shows the concentration distribution of magnesium at the cross section of the center of the tundish width. The molten steel that contained magnesium flows in the direction of the meniscus, ladle side, and slightly in the direction of the immersion nozzle.

Figure 6(f) shows the diffused region of magnesium at the cross section of the center of the tundish height. The molten steel flows toward one side of the tundish wall besides the immersion nozzle and ladle side.

Figures 6(g) and 6(h) show the concentration distribution of magnesium when magnesium vapor is injected at position C.

Figure 6(g) shows the molten steel flow that contained magnesium at the cross section of the center of the tundish width. The molten steel with magnesium flows toward the direction of both the immersion nozzle and ladle side.

Figure 6(h) shows the flow of molten steel with magnesium at the cross section of the center of the tundish height. The molten steel with magnesium flows in the direction of the immersion nozzle, wall side, and ladle side.

When magnesium vapor is injected at position A in the tundish, a large amount of the molten steel with magnesium flows in the direction of the immersion nozzle.

Figure 7 shows the ratio of magnesium concentration after 30 s of magnesium vapor injection into molten steel. This ratio was defined as the concentration at the joint part divided by the concentration at the injection lance. The larger the concentration ratio, the higher is the additive yield of magnesium.

Fig. 7.

The ratio of output to input for magnesium concentration at 30 s just after injecting magnesium vapor. The flow rate of argon gas in the lance: 1.0×10⁻⁶ m³s⁻¹.

Magnesium vapor is injected at positions A, B, and C, as shown in Fig. 2. The concentration ratio changes based on the position of magnesium vapor injection.

For position A, the concentration ratio was about 0.6, and its deviation was small. The concentration ratio deviates because of the non-steady state numerical simulation for the molten steel flow. Using this simulation, the velocity and direction of molten steel flow in the tundish changes consistently with time. For position B, the concentration ratio is 0.2 and the additive yield is small. The deviation of the concentration ratio is large because the change in the velocity of the molten steel flow at the injecting position is large. When magnesium vapor is injected at position C, the concentration ratio is 0.4 and its deviation is slightly large.

The results of the numerical simulations indicated that the concentration ratio at position A was the largest in the three cases Therefore, position A was selected as the position of magnesium vapor injection in the continuous casting test.

For position A, it is thought that the concentration distribution of magnesium in the continuously cast slab is negligible because the deviation of the concentration ratio at the top of the immersion nozzle is slightly. However, for position B and C, it is thought that the concentration distribution in the slab is large because the deviation of the concentration ratio is large.

5.3. Feeding Condition of Magnesium Wire

The temperature change in the magnesium wire advanced in the immersion lance was predicted by the heat transfer calculation.

Figure 8 shows the relationship between the distance from the lance and the advancing velocity of wire when the temperature of the magnesium wire core reaches 1373 K, thereby exceeding its boiling temperature. The higher the advancing velocity of the wire, the longer is the distance for the generation of magnesium vapor in the lance. The immersion depth of the lance in the continuous casting test was 1.0×10⁻¹ m. It is necessary to decrease the advancing velocity of wire below 6.0×10⁻² ms⁻¹. In this experiment, the insertion length of wire into the lance was reduced to less than one third of the total length of lance by adjusting the velocity to 1.7×10⁻² ms⁻¹.

Fig. 8.

The relationship between distance from lance entrance where Mg wire reaches 1373 K and Mg wire advancing speed.

Figure 9 shows the change in the core temperature of the wire based on the distance from the entrance of lance when the advancing velocity is 1.7×10⁻² ms⁻¹. It was confirmed that the temperature of the magnesium wire, which was advanced in the lance, increased with an increasing distance from the entrance, and it reached the boiling temperature of magnesium at approximately 3.0×10⁻² m; then, it generated magnesium vapor.

Fig. 9.

The calculated temperature profile in the core of magnesium wire in the lance.

5.4. Continuous Casting Test

The relationship between magnesium concentration and the injection timing of magnesium vapor into molten steel in the continuously cast slab is determined.

Figure 10 shows the result of the chemical analysis of the total magnesium, the soluble magnesium and total oxygen in the slab. When magnesium vapor was injected into molten steel, there was no splash. Hence, it was possible to inject magnesium vapor efficiently.

Fig. 10.

Relationship between (a) total magnesium and total oxygen concentration, (b) soluble magnesium concentration and distance from slab edge.

The concentration of both soluble magnesium and insoluble magnesium was measured using the method employed in a previous study.²⁹⁾ The sample of 0.5 g was dissolved using a solvent that was synthesized by mixing 20 mL triethanolamine, 1000 mL methanol, 1.0×10⁻² kg tetramethylammonium chloride, and 1.0×10⁻⁴ kg Ba. This solution was filtered by using a membrane filter of open pore of 1×10⁻⁶ m. The solution and the residue on a membrane filter were analyzed by using inductively coupled plasma (ICP).

The magnesium concentration in the solution corresponds to the soluble magnesium and the magnesium concentration in residue corresponds to insoluble magnesium. The total magnesium is equal to the sum of soluble and insoluble of magnesium.

The concentration of the total magnesium and soluble magnesium in the slab increased with an increase in the casting length after magnesium vapor injection.

The increase in the total magnesium concentration after injecting magnesium vapor is attribute to molten steel with magnesium being mixed with molten steel without magnesium. The total magnesium concentration after stopping the flow of magnesium vapor decreased because molten steel without magnesium was mixed with the molten steel with magnesium in the mold.

The ratio of the chemical analysis of magnesium concentration to the additive concentration is evaluated as shown in Fig. 7. That ratio obtained from the casting test was almost the same as that of the numerical simulation. The yield of magnesium in this experiment was as high as 60%, which is better than that of the conventional method.

The change in the soluble magnesium was different from that of the total magnesium, and it exhibited a constant value of 1.1×10⁻⁴ mass% after the injection of magnesium vapor. The concentration of the soluble magnesium in molten steel is determined by the balance of injection rate of magnesium vapor and evaporation rate of magnesium. As a result, the concentration of soluble magnesium became 1.1×10⁻⁴ mass%. The total magnesium reflects the composition of inclusion. Because the concentration of magnesium in the inclusion increased, it is thought that the total magnesium also increased.

The total oxygen shows the amount of the inclusion. Because the total oxygen was not soluble oxygen, it is thought that effect of magnesium deoxidation on the total oxygen was not able to be observed.

A slab of length 1 m was required when the concentration of total magnesium reached a constant value or a maximum value. However, in case of the soluble magnesium, this length was shorter at approximately 0.25 m. It was understood that the soluble magnesium was controlled easily. The analysis of the results of the numerical simulation indicated that molten steel injected with magnesium vapor, was poured in the mold immediately. By changing the injection rate of magnesium vapor in continuous casting, it was possible to control magnesium concentration in the slab. It is expected that magnesium vapor injection will become a new process to control magnesium concentration in the slab.

5.5. TiN in the Continuously Cast Slab

Magnesium oxide behaves similar to an effective heterogeneous nucleus of TiN. In this study, the continuous casting test was conducted using molten steel with a high concentration of titanium. Then, the behavior of the heterogeneous nucleation of TiN on magnesium oxide was examined after magnesium vapor injection into molten steel.

The square samples of 2.0×10⁻² m on one side were obtained from the slab at the center of the width and at a quarter thickness where magnesium vapor was injected. The samples were polished similar to mirror planes using an abrasive diamond compound 1 μm in diameter. Aabsolute alcohol was used as a lubricating liquid to polish the samples and inclusions were prevented from solving to water. The polished face of the samples was then etched with controlled potential electrolysis and TiN was introduced. The TiN was observed using FE-SEM with EDS. The solvent²⁵⁾ was synthesized by mixing 20 mL triethanolamine, 1000 mL methanol, 1.0×10⁻² kg tetramethylammonium chloride, and 1.0×10⁻⁴ kg Ba. The favorable electrolyte conditions were a voltage of 150 mV and an electric charge of 150C.

Figure 11 shows the FE-SEM image of TiN and magnesium oxide when magnesium vapor was injected into molten steel. From the result of the EDS analysis, the substance that existed in the core of the cubic TiN was spinel MgO·Al₂O₃.

Fig. 11.

The photograph of TiN with spinel by FE-SEM and EDS.

In the previous study,⁷⁾ it has been clarified that the spinel had the effect of heterogeneous nucleation. Moreover, it has been clarified that the spinel was generated at 0.04 mass% of aluminum concentration.³⁰⁾

The spinel became the heterogeneous nucleus of TiN similar to that in the previous studies.^5,6,7,8,9)

Figure 12 shows the relationship between the size of TiN and the distance from the bottom of the slab. The length of height and wide of hundred TiN on the sample surface were observed by using FE-SEM and the average size of TiN was obtained. Figure 10 shows that the TiN became smaller within the range of the soluble magnesium concentration and reached 1.1×10⁻⁴ mass%. The minimum size of TiN was about 200 nm. When magnesium concentration in the slab was less than 1.1×10⁻⁴ mass%, the size of TiN did not change before and after injecting magnesium vapor into the molten steel. When the spinel that plays a heterogeneous nucleus for TiN is used efficiently, it is important for the soluble magnesium concentration; however, the total magnesium concentration in the molten steel is increased by more than approximately 1.1×10⁻⁴ mass%.

Fig. 12.

The relationship between average size of TiN and distance from slab bottom.

It seems that the size of the spinel generated in the molten steel is small because magnesium vapor is a fine particle. When the size of a spinel is fine under the constant concentration of the soluble magnesium, the number of spinel becomes large. When the TiN nucleates around the spinel that behaves as a heterogeneous nucleus, the number of TiN increases and the size of TiN decreases.

As stated above, when magnesium vapor is added to molten steel, fine magnesium oxides are generated in the molten steel. TiN is generated heterogeneously on magnesium oxide and TiN in the continuous cast slab becomes fine when magnesium vapor is injected into the molten steel in the tundish.

The technique for injecting the metallic vapor into molten steel can thus be considered a new method for generating the inclusions and for fulfilling the demands of high performance for steel products.

6. Conclusions

Recently, high-performance products of carbon steel are demanded worldwide. Some properties of final carbon steel products are occasionally affected by the quality of steel slabs. Hence, the control of inclusions becomes important. The heterogeneous nucleus can generate the required inclusions.

In this study, the relationship between the generation behavior of TiN and magnesium vapor was clarified. From the continuous casting test machine, the following conclusions were obtained.

(1) Magnesium vapor injection into molten steel can increase the partial pressure of magnesium in the equilibrium reaction, and it is possible to achieve high concentration and a high yield of magnesium in molten steel simultaneously. When the experiment with the continuous casting test machine was conducted, it was clarified that magnesium concentration in the molten steel can be controlled by changing the amount of magnesium vapor.

(2) When magnesium vapor is injected into molten steel in the tundish and casted, the heterogeneous nucleus of TiN can be generated. Under the experimental conditions, the spinel MgO·Al₂O₃ behaves as the heterogeneous nucleus of TiN. The concentration of the soluble magnesium required for generating this nucleus is approximately 1.1×10⁻⁴ mass%.

(3) It is necessary to optimize the position of magnesium injection in the tundish to increase the additive yield of magnesium in molten steel. When magnesium vapor is injected at the position between the immersion nozzle and the narrow wall of the tundish, the additive yield of magnesium in the molten steel becomes large.

(4) In the continuous casting process, it is possible to use small amounts of vapor of additional metallic elements and inject this vapor into molten steel in the tundish. This method can be a new technique for the addition of a metallic element into molten steel.

References

• 1)   B. L.  Bramfitt: Metall. Trans., 1 (1970), 1987.
• 2)   T.  Ohashi,  T.  Hiromoto,  H.  Fujii,  Y.  Nuri and  K.  Asano: Tetsu-to-Hagané, 62 (1976), 614 (in Japanese).
• 3)   O.  Grong: Metallurgical Modelling of Welding, 2nd ed., Institute of Metals, London, (1997), 221.
• 4)   H.  Mizukami,  M.  Numata and  A.  Yamanaka: ISIJ Int., 56 (2016), 1420.
• 5)   G. V.  Pervushin and  H.  Suito: ISIJ Int., 41 (2001), 748.
• 6)   P.  Misra,  S.  Sridhar and  A. W.  Cramb: Metall. Mater. Trans. B, 32 (2001), 963.
• 7)   H.  Fujimura,  S.  Tsuge,  Y.  Komizo and  T.  Nishizawa: Tetsu-to-Hagané, 87 (2001), 707 (in Japanese).
• 8)   H.  Ohta,  R.  Inoue and  H.  Suito: ISIJ Int., 48 (2008), 294.
• 9)   K.  Isobe: ISIJ Int., 50 (2010), 1972.
• 10)   G. A.  Irons and  R. I. L.  Guthrie: Metall. Trans. B, 12 (1981), 755.
• 11)   J.  Yang,  K.  Okumura,  M.  Kuwabara and  M.  Sano: ISIJ Int., 42 (2002), 685.
• 12)   S.  Mukawa,  Y.  Ueshima,  M.  Sano,  J.  Yang and  M.  Kuwabara: ISIJ Int., 46 (2006), 1778.
• 13)   J.  Yang,  M.  Kuwabara,  T.  Sakai,  N.  Uchida,  Z.  Liu and  M.  Sano: ISIJ Int., 47 (2007), 418.
• 14)   G. A.  Irons,  C. W.  Chang,  R. I. L.  Guthrie and  J.  Szekely: Metall. Trans. B, 9 (1978), 151.
• 15)   H.  Itoh,  H.  Hino and  S.  Banya: Tetsu-to-Hagané, 83 (1997), 623 (in Japanese).
• 16)   G.  Okuyama,  K.  Yamaguchi,  S.  Takeuchi and  K.  Sorimachi: ISIJ Int., 40 (2000), 121.
• 17)   K.  Fujii,  T.  Nagasaka and  M.  Hino: ISIJ Int., 40 (2000), 1059.
• 18)   X.  Zhang, Q. Han and D. Chen: Metall. Trans. B, 22 (1991), 918.
• 19)   Z.  Qian and  Y.  Wu: ISIJ Int., 44 (2004), 100.
• 20)   B.  Zhao,  B. G.  Thomas,  S. P.  Vanka and  R. J.  O’Malley: Metall. Mater. Trans. B, 36 (2005), 801.
• 21)   F.  Wang,  B.  Li and  F.  Tsukihashi: ISIJ Int., 47 (2007), 568.
• 22)   J.  Zhang,  S.  Yang,  J.  Li,  W.  Yang,  Y.  Wang and  X.  Guo: ISIJ Int., 55 (2015), 1684.
• 23)   H.  Mizukami and  A.  Yamanaka: Tetsu-to-Hagané, 94 (2008), 507 (in Japanese).
• 24)   R. B.  Bird,  W. E.  Stewart and  E. N.  Lightfoot: Transport Phenomena, John Wiley & Sons, New York, (1976), 399.
• 25)   R.  Inoue and  H.  Suito: Progress in Research on Ultra Clean Steel, ISIJ, Tokyo, (1999), 348 (in Japanese).
• 26)  National Astronomical Observatory of Japan: Chronological Scientific Tables, Maruzen, Tokyo, (2019), 388 (in Japanese).
• 27)   G. H.  Geiger and  D. R.  Poirier: Transport Phenomena in Metallurgy, Addison-Wesley, Reading, MA, (1973), 7.
• 28)   Y.  Kawai and  Y.  Shiraishi: Handbook of Physico-chemical Properties at High Temperatures, ISIJ, Tokyo, (1988), 93.
• 29)   H.  Ohta and  H.  Suito: ISIJ Int., 46 (2006), 14.
• 30)   H.  Itoh,  M.  Hino and  S.  Banya: Tetsu-to-Hagané, 84 (1998), 85 (in Japanese).