Physical Modelling of Flow Phenomena Based on Simultaneous Similitude of Multiple Dimensionless Numbers

Abstract

Physical model experiments as well as numerical simulations are widely carried out to estimate flow phenomena of high-temperature liquid flow because it is difficult to observe or measure the high-temperature liquid flow directly. As for the physical modelling, similitude is an essential matter that has a great influence on the representation of real flow phenomena in the prototype. A commonsense of the physical modelling had been satisfying the similitude of one or two dimensionless numbers considering dominant forces influence on the objective flow phenomena. In this paper, physical modelling conditions required for the simultaneous similitude of multiple dimensionless numbers (SMDN) has been studied to enhance the accuracy of the flow phenomena representation. As a result, a simple relationship between physical properties of fluids and scale ratio of the physical model has become clear for the simultaneous similitude of the Froude, Reynolds, Galilei, capillary, Weber, Eötvös and Morton numbers. Then, rising velocity of bubbles has been investigated obtaining a result that the relative rising time of bubbles in the physical model corresponds well with that of the prototype under the SMDN condition. This result indicates physical models that satisfy the SMDN condition precisely represent flow phenomena of gas-liquid systems influenced by four forces; inertial force, gravitational force, viscous force and surface tension force, including bubble rising behavior as well as the bulk flow phenomena.

1. Introduction

Similitude is an essential matter of the physical modelling to represent the real phenomena. The Froude and Reynolds numbers of physical models are required to correspond with these of the real process to represent the bulk flow phenomena of the prototype. In addition, the Weber number similitude is required to represent surface flow or gas-liquid interfacial flow phenomena such as ripple waves or droplet/bubble formations. These three dimensionless numbers are the most important for the physical modelling of incompressible fluid.^1,2,3,4) However, it has been thought that simultaneous similitude of all criterial dimensionless numbers was very hard or impossible to realize.^5,6,7)

In the iron & steel industry, full-scale water model experiments are widely applied to represent the molten steel flow in the condition of the Froude and Reynolds numbers similitudes.^8,9,10,11) This is because the kinematic viscosity (η/ρ) of water is approximately equal to that of molten steel. On the other hand, the surface tension of water is small compared with that of molten steel. In addition, electro-magnetic devices are hard to apply to water models because of the low electric conductivity of water.

It is possible to solve these matters with molten metal models. Furthermore, recent new technologies of velocimetry such as UDV (Ultrasonic Doppler Velocimetry) can resolve the issue of molten metal model’s opacity.^12,13) However, conventional setups of molten metal models have been a combination of small scale ratios and the Froude number similitudes or two dimensionless numbers similitudes at most.^{2,5,12,13,14,15,16,17)} As a matter of record, there was no concept of multiple dimensionless numbers similitudes not only for the physical modelling of above-mentioned molten metal models and full-scale water models, but also for many scaled-down water models in the past articles published before 2010,^{3,18,19,20,21,22)} during 2011–2015^6,23,24,25) and after 2016.^{4,7,26,27,28,29,30,31,32,33,34,35,36)}

In this paper, the physical modelling condition has been studied for the precise representation of the real flow phenomena by establishing simultaneous similitude of the Froude, Reynolds, Weber, Galilei, capillary, Eötvös and Morton numbers. This multiple similitudes concept of the physical modelling has been named SMDN (Similitude of Multiple Dimensionless Numbers). Then specific physical modelling conditions (relationship of physical properties of fluids and scale ratios) have been researched that satisfies the SMDN condition, by which molten steel flow phenomena will be represented precisely.

Subsequently, bubble rising velocity has been investigated to validate the representation of bubbles behavior by physical models under the SMDN condition.

2. Relationship of Physical Properties and Scale Ratio for SMDN

The most important parameter of physical modelling, suite of dimensionless numbers, is the Froude number (Fr) and the Reynolds number (Re) to represent the bulk flow phenomena. In addition, the Weber number (We) cannot be ignored for the precise representation of the surface flow phenomena such as ripple waves, or droplet/bubble formations, etc.

These three dimensionless numbers are defined in Eqs. (1), (2a) and (3a),^37,38,39) in which the Froude number is defined as the square root of the ratio of the inertial/gravitational forces, the Reynolds number is the ratio of the inertial/viscous forces, and the Weber number is the square root of the ratio of the inertial/surface tension forces.   

$$\text{Fr}=\frac{V}{\sqrt{g\cdot L}}$$(1)

  

$$Re=\frac{\rho \cdot V\cdot L}{\eta }$$(2a)

  

$$\text{We}=V\sqrt{\frac{\rho \cdot L}{\sigma }}$$(3a)

Equation (2a) can be rearranged to Eq. (2b) applying kinematic viscosity ν = η/ρ. In the same manner, Eq. (3a) can be rearranged to Eq. (3b) applying a parameter ι = σ/ρ.   

$$\text{Re}=\frac{V\cdot L}{\nu }$$(2b)

  

$$\text{We}=V\sqrt{\frac{L}{\iota }}$$(3b)

Describing the prototype fluid (molten steel) with subscript 0, coincidence of the Froude numbers between the physical model and the prototype is expressed in Eq. (4). Here, λ is scale ratio of the physical model (L = λ·L₀).

The required flow velocity of the physical model V is then obtained in Eq. (5)⁸⁾ by rearranging Eq. (4).   

$$\text{Fr}=\frac{V_0}{\sqrt{g\cdot L_0}}=\frac{V}{\sqrt{g\cdot L}}=\frac{V}{\sqrt{g\cdot \lambda \cdot L_0}}$$(4)

  

$$V=\sqrt{\lambda }\cdot V_0$$(5)

In the same manner, similitude of the Reynolds number is expressed in Eq. (6). Scale ratio for the condition of the Froude and Reynolds numbers similitudes λ_FR is obtained in Eq. (7) by substituting Eq. (5) into Eq. (6).

It is clear from Eq. (7), that the physical model setup with a scale ratio equal to 2/3 power of the kinematic viscosity ratio is a specific condition for the Froude and Reynolds numbers similitudes. Namely, every fluid can be applied to represent the flow phenomena of any other fluids under the condition of the Froude and Reynolds numbers similitudes, provided that the fluids are incompressible Newtonian. For example, a physical model of the Froude and Reynolds numbers similitudes could be downsized by using a fluid of lower kinematic viscosity.   

$$\text{Re}=\frac{V_0\cdot L_0}{{\nu }_0}=\frac{V\cdot L}{\nu }=\frac{V\cdot \lambda \cdot L_0}{\nu }$$(6)

  

$${\lambda }_{FR}={\left(\frac{\nu }{{\nu }_0}\right)}^{\frac{2}{3}}$$(7)

Equality of the Weber numbers between the physical model and the prototype is expressed in Eq. (8) in the same manner as obtaining Eq. (6). The scale ratio for the condition of the Froude and Weber numbers similitudes; λ_FW is expressed in Eq. (9), obtained by substituting Eq. (5) into Eq. (8).

As described in Eq. (9), a physical model setup with a scale ratio equal to 1/2 power of the ratio of the parameter ι is a specific condition for the Froude and Weber numbers similitudes. That is to say, every fluid can be applied to represent the flow phenomena of any other fluids in the condition of the Froude and Weber numbers similitudes, provided that the fluids are incompressible.   

$$\text{We}=V_0\sqrt{\frac{L_0}{{\iota }_0}}=V\sqrt{\frac{L}{\iota }}=V\sqrt{\frac{\lambda \cdot L_0}{\iota }}$$(8)

  

$${\lambda }_{FW}={\left(\frac{\iota }{{\iota }_0}\right)}^{\frac{1}{2}}$$(9)

Subsequently, λ_FR in Eq. (7) and λ_FW in Eq. (9) should be equal in the condition of the Froude, Reynolds and Weber numbers similitudes. Accordingly, Eq. (10) is obtained to express a relationship of the physical properties for the simultaneous similitude of these three dimensionless numbers.

The relationship of the physical properties expressed in Eq. (10) is shown in Fig. 1.   

$$\frac{\iota }{{\iota }_0}={\left(\frac{\nu }{{\nu }_0}\right)}^{\frac{4}{3}}$$(10)

Fig. 1.

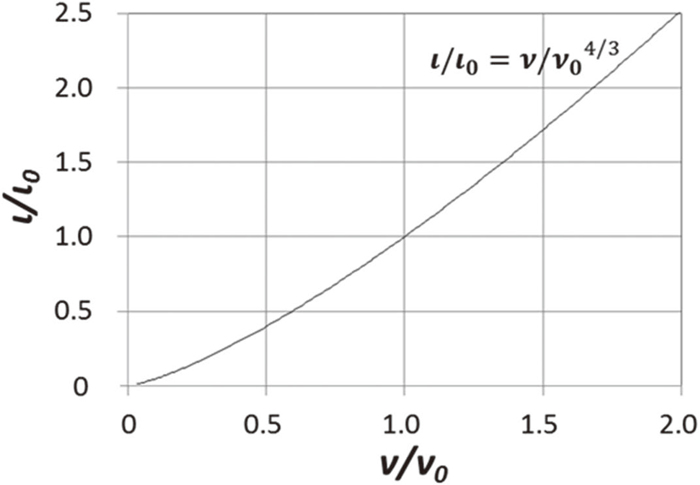
Relationship of physical properties for Fr, Re and We similitudes.

Furthermore, as a result of the Froude, Reynolds and Weber numbers similitudes, the Eötvös number (Eö) similitude and the Morton number (Mo) similitude are also actualized as described below.

As is described in the Clift, Grace and Weber’s chart that classifies the rising bubble shape,⁴⁰⁾ the Eötvös and the Morton numbers are dimensionless numbers that have a dominant influence on the bubble shape and bubble rising velocity.

The Eötvös number described in Eq. (11a),⁴⁰⁾ represents the ratio of the buoyancy/surface tension forces. If the density of the bubble is quite little compared with that of the surrounding fluid, Eq. (11a) can be rearranged to Eq. (11b). The subscript b is for the bubble in these Eqs.

The right side of Eq. (11b) can be rearranged in Eq. (12). It can be seen that d_b/L in Eq. (12) is always identical in value for both the prototype and the physical model $\left(\because \raisebox{1ex}{$d_b$}\!\left/ \!\raisebox{-1ex}{$L$}\right.=\raisebox{1ex}{$\lambda d_{b0}$}\!\left/ \!\raisebox{-1ex}{$\lambda L_0$}\right.=\raisebox{1ex}{$d_{b0}$}\!\left/ \!\raisebox{-1ex}{$L_0$}\right.\right)$. Subsequently, it is clear that the condition of the Eötvös number similitude is satisfied in the case of the Froude and Weber numbers similitudes.   

$$\mathrm{E}\ddot{\mathrm{o}}=\frac{g(\rho -{\rho }_b)\cdot d_b{}^2}{\sigma }$$(11a)

  

$$\mathrm{E}\ddot{\mathrm{o}}\approx \frac{g\cdot \rho \cdot d_b{}^2}{\sigma }$$(11b)

  

$$\frac{g\cdot \rho \cdot d_b{}^2}{\sigma }=\frac{V^2\cdot \rho \cdot L}{\sigma }\cdot \frac{g\cdot L}{V^2}\cdot {\left(\frac{d_b}{L}\right)}^2={\left(\frac{\text{We}}{\text{Fr}}\cdot \frac{d_b}{L}\right)}^2$$(12)

The Morton number described in Eq. (13),^1,41) consists of gravitational acceleration g and the physical properties of the fluid. Accordingly, the Morton number similitude is always established in the case that the fluid of the physical model and the prototype are the same. On the other hand, the physical properties should satisfy a specific relationship between two different fluids for the Morton number similitude.

As shown in Eq. (14), the Morton number defined in Eq. (13) completely comprises the Froude, Reynolds and Weber numbers.^1,41) As such, The Morton number similitude condition is always satisfied in the case of simultaneous dimensionless numbers similitudes of the Froude, Reynolds and Weber numbers.   

$$\text{Mo}=\frac{g\cdot {\eta }^4}{\rho \cdot {\sigma }^3}$$(13)

  

$$\frac{{\text{We}}^6}{{\text{Re}}^4\cdot {\text{Fr}}^2}=\frac{V^6\cdot {\rho }^3\cdot L^3}{{\sigma }^3}\cdot \frac{{\eta }^4}{{\rho }^4\cdot V^4\cdot L^4}\cdot \frac{g\cdot L}{V^2}=\text{Mo}$$(14)

Needless to say, any other combinations of inertial force, gravitational force, viscous force and surface tension force such as the ratio of the gravitational/viscous forces (Galilei number) or the viscous/surface tension forces (capillary number) are identical for the physical model and the prototype under the above mentioned SMDN condition.

3. Physical Model to Simulate Molten Steel Flow Phenomena under SMDN Condition

The purpose of this section is to realize a physical model that satisfies the SMDN condition to represent steel flow phenomena precisely. Here, the physical properties of molten Fe are substituted as representative molten steel properties.

Equation (10) is rearranged to Eq. (15) to indicate the relationship between kinematic viscosity ν = η/ρ and the parameter ι = σ/ρ of fluids applied for physical models. Subsequently, the physical properties of molten Fe in Table 1 are substituted into Eq. (15) as ν₀ and ι₀ to describe a line of the physical property relationship in Fig. 2.   

$$\iota ={\iota }_0{\left(\frac{\nu }{{\nu }_0}\right)}^{\frac{4}{3}}$$(15)

Table 1. Physical properties of liquid metals and water for Fig. 2.

	Melting point (°C)	Temperature of measurement (°C)	ρ(kg/m3)	η(Pa·s)	σ(N/m2)
Fe42,43)	1537	1550	7000	0.005	1.88
Hg44,45)	−38.9	20	13550	0.001568	0.4802
Bi46)	271	320	9986	0.001644	0.3758
Sn45,47)	232	280	6940	0.001971	0.5588
Cu48,49)	1085	1120	7968	0.003787	1.2496
Ga45,50)	29.8	50	6065	0.001532	0.7160
Zn50,51)	420	450	6532	0.003498	0.7552
Al52)	660	700	2300	0.0029	0.9
Water44)	0	30	996	0.0008	0.0712

Fig. 2.

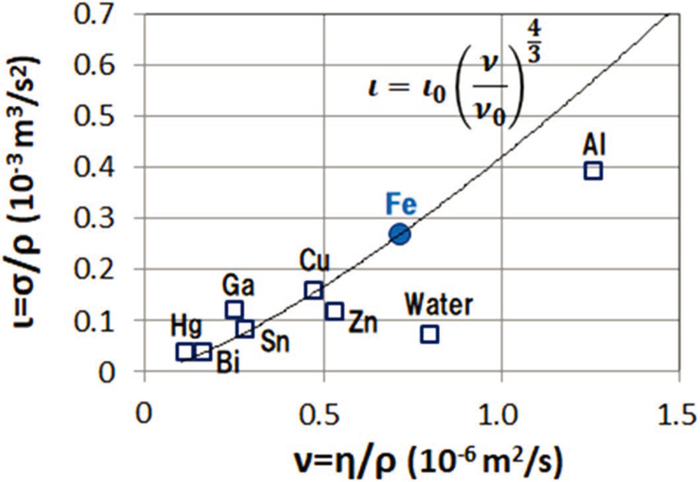
ν-ι relations of molten metals and water in Table 1 with line of SMDN condition for molten Fe. (Online version in color.)

If a fluid exists with the specific relationship between ν = η/ρ and ι = σ/ρ which satisfies Eq. (15), a physical model could be realized to represent molten Fe flow with the SMDN condition.

Figure 2 shows ν‐ι relationships of fluids listed in Table 1 and a line of Eq. (15) in which the physical properties of molten Fe are substituted. As is clear from Fig. 2, the ν‐ι relation of Hg, Bi, Sn, and Cu are located approximately on the line satisfying the SMDN condition. Especially, molten Sn is a safe and easy-to-treat fluid to construct a physical model.⁵³⁾ As compared with the conventional liquid metal models,^12,17) flow phenomena in the continuous casting molds will be represented more precisely by the physical models under the SMDN condition as shown in Table 2.

Table 2. Comparison of physical modelling similitudes.

	Conventional physical models			Physical model under SMDN condition
Fluid	Water	Hg17)	Sn60-Bi4012)	Sn	Cu
Experimental temperature	30°C	20°C	200°C	280°C	1120°C
Scale ratio	1.00	0.20	0.50	0.54	0.76
Relative Fr	1.0	1.0	0.6	1.0	1.0
Relative Re	0.9	0.6	1.0	1.0	1.0
Relative We	1.9	0.6	0.6	1.0	1.0
Relative Eo	3.8	0.3	0.9	1.0	1.0

It is not clear the reason why many molten metals have the specific properties satisfying the SMDN condition with each other. Further research is required on this fundamental matter, which presumably relates to the known periodicity of liquid metal when plotted against the atomic numbers.^54,55)

4. Rising Behavior of Bubbles in Physical Model under SMDN Condition

Inert gas injection is widely applied to continuous casting processes of steel to prevent clogging of refractory nozzles between tundish and mold. On the other hand, inert gas bubbles induce surface and internal defects of the cast slabs. Therefore, it is valuable to represent two-phase flow of bubbles and molten steel in the continuous casting mold for estimating the quality of slabs. Rising behavior of bubble is complicated influenced by the bubble deformation.⁴⁰⁾ The Eötvös and Morton numbers are the dimensionless numbers that have a dominant influence on the bubble shape and the bubble rising velocity. Accordingly, physical models that satisfy the SMDN condition were expected to represent bubble rising behavior with high accuracy.

Drag coefficient of bubble changes its value influenced by bubble shape and Reynolds number of bubble. This complicated change in value of the drag coefficient has been investigated by some researchers. Equation (16) shows Tomiyama’s equation⁵⁶⁾ which is one of the representative equations to express the drag coefficient of rising bubbles. On the other hand, Bozzano’s equation shown in Eqs. (17), (18), (19)⁵⁷⁾ has been devised to express the complicated change in value of the drag coefficient by a single function.

These equations were obtained by the experiments with water and some organic liquids, so it should be confirmed if these equations could apply to the molten metal systems.   

$$C_D=\text{max}\left[min\left\{\frac{24}{{\text{Re}}_b}(1+0.15{\text{Re}}_b{}^{0.685}),\mathrm{\hspace{0.17em} }\frac{72}{{\text{Re}}_b}\right\},\mathrm{\hspace{0.17em} }\frac{8}{3}\frac{\mathrm{E}\ddot{\mathrm{o}}}{\mathrm{E}\ddot{\mathrm{o}}+4}\right]$$(16)

  

$$C_D=f{\left(\frac{a}{r_e}\right)}^2$$(17)

  

$$f=\frac{48}{{\text{Re}}_b}\left(\frac{1+12{\text{M}}_{\text{o}}{}^{1/3}}{1+36{\text{M}}_{\text{o}}{}^{1/3}}\right)+0.9\frac{{\mathrm{E}\ddot{\mathrm{o}}}^{3/2}}{1.4(1+30{\text{M}}_{\text{o}}{}^{1/6})+{\mathrm{E}\ddot{\mathrm{o}}}^{3/2}}$$(18)

  

$${\left(\frac{a}{r_e}\right)}^2\cong \frac{10(1+1.3{\text{M}}_{\text{o}}{}^{1/6})+3.1\mathrm{E}\ddot{\mathrm{o}}}{10(1+1.3{\text{M}}_{\text{o}}{}^{1/6})+\mathrm{E}\ddot{\mathrm{o}}}$$(19)

Subsequently, rising velocity of bubbles has been investigated by a physical model experiment of molten metal system. Figure 3 shows experimental set-up to measure the rising velocity of bubbles. Ar bubbles were blown‐in the molten Sn bath by a L‐shaped lance made of SUS316 tube with a small nozzle hole at the tip of it. Detailed condition of the bubbling experiment is shown in Table 3. Depth range of the UDV measurement was 40–160 mm from the molten Sn surface. This shallow depth condition was to minimize the effect of the static pressure of molten Sn.

Fig. 3.

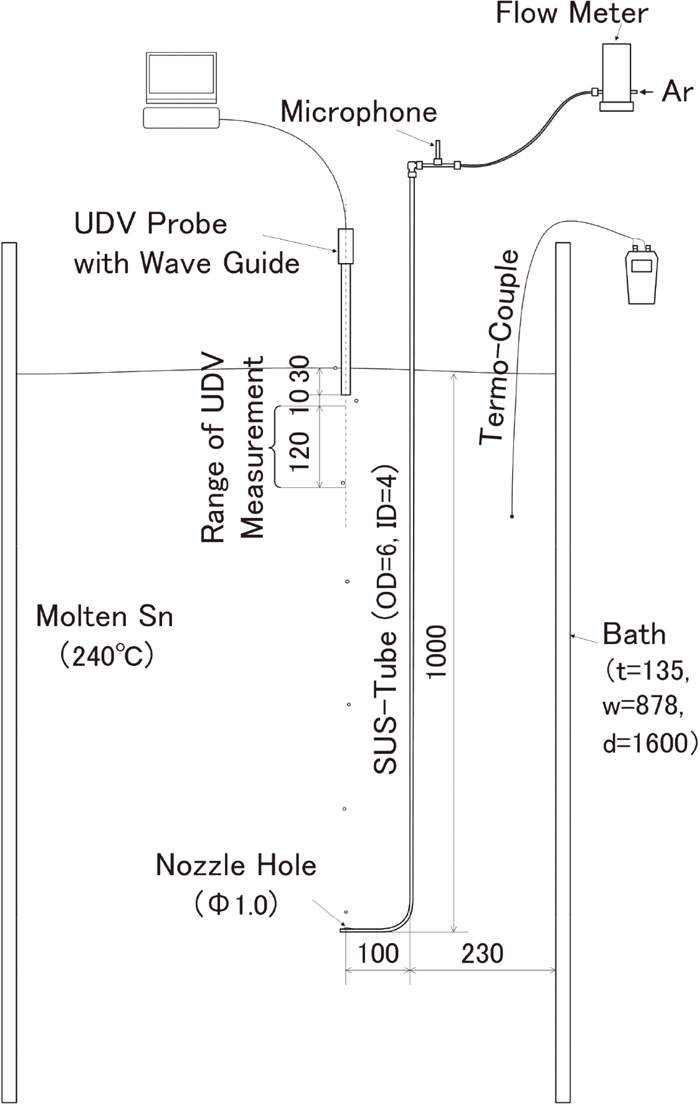
Schematic view of bubbling experiment apparatus.

Table 3. Condition of bubbling experiment (dimension in mm).

Liquid in bath	Molten Sn at 240°C
Bath size	Thickness = 135
	Width = 875
	Depth = 1600
Depth of bubbling lance	1000
Diameter of nozzle hole	1.0
Ar flow rate blown in from nozzle hole	0.6 Nl/min
	0.8 Nl/min
	1.0 Nl/min

Terminal velocity of bubbles was estimated as difference between average bubble rising velocity and average molten Sn velocity around bubbles. Both of the velocities were measured by ultra‐sonic Doppler velocimetry (UDV).^58,59,60,61) A set-up of the UDV (Ultra-sonic sensor with wave-guide⁶²⁾ and DOP4000 manufactured by Signal Processing SA, Lausanne, Switzerland) was used for the experiment. An example of obtained UDV signal distribution is shown in Figs. 4(a) and 4(b). Figure 4(a) is a 3D graph of raw output data from the UDV device to show a whole image of the UDV measurement. Figure 4(b) contains two cross-sections of Fig. 4(a) at two levels of depth. Three peaks of the bubble rising velocity approx. 300 mm/s and the basic upward velocity of molten Sn approx. 50 mm/s can be seen in Fig. 4(b). Both of the velocities were estimated as two peaks in the velocity histogram in the same manner as was confirmed by Eckert et al.^62,63) Table 4 and Fig. 5 shows results of the experiment. Then obtained data were compared with calculated values with Tomiyama’s and Bozzano’s equations in Fig. 6. As is clear from Fig. 6, Tomiyama’s equation represents the bubble rising velocity in molten Sn precisely.

Fig. 4(a).

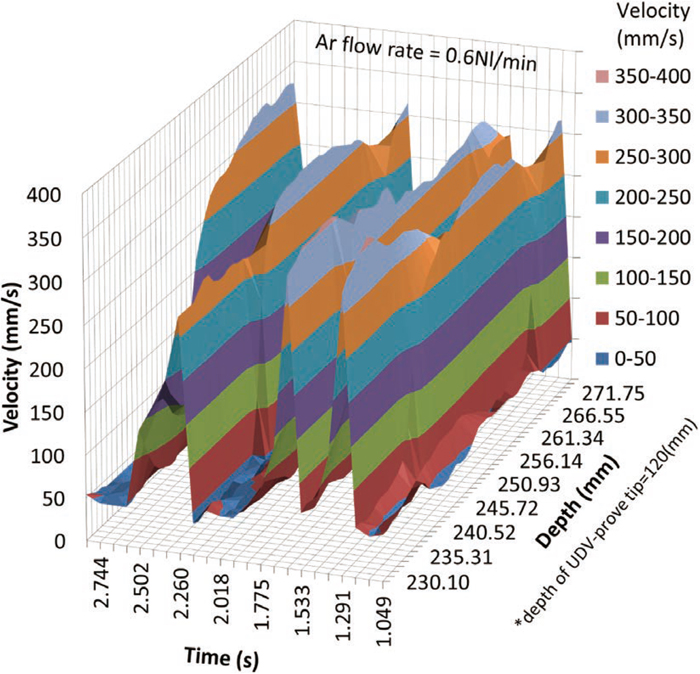
Example of UDV signal distribution.

Fig. 4(b).

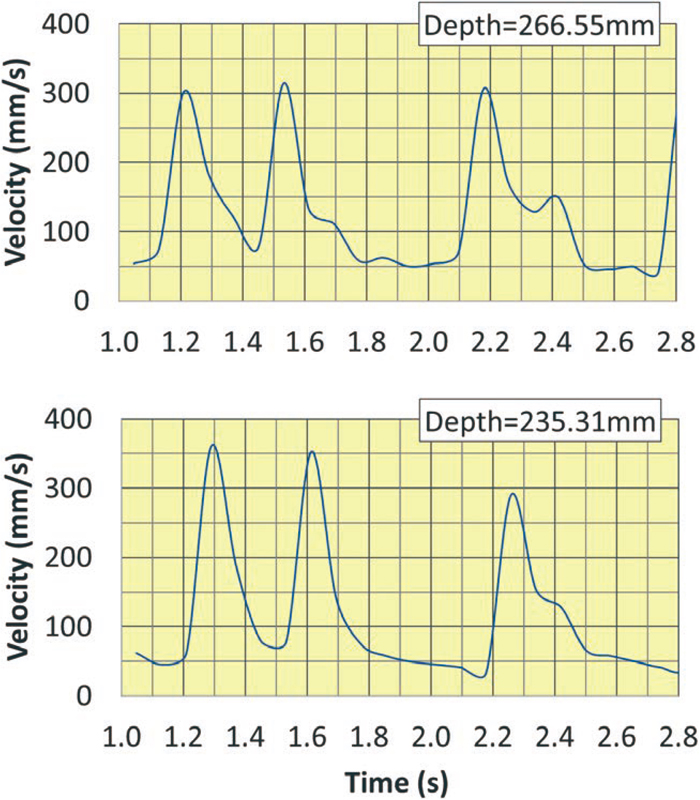
Example of UDV signal distribution indicating cross-sections of Fig. 4(a).

Table 4. Result of bubbling experiment.

Ar flow rate (Nl/min)	0.6	0.8	1.0
Frequency of bubble generation (Hz)	1.72	1.96	2.17
Diameter of equivalent spherical bubbles (mm)	2.69	2.83	2.96
Rising velocity of bubbles (m/s)	0.3080	0.3131	0.3258
Rising velocity of molten Sn (m/s)	0.0473	0.0521	0.0690
Terminal velocity of bubbles (m/s)	0.2607	0.2610	0.2568

Fig. 5.

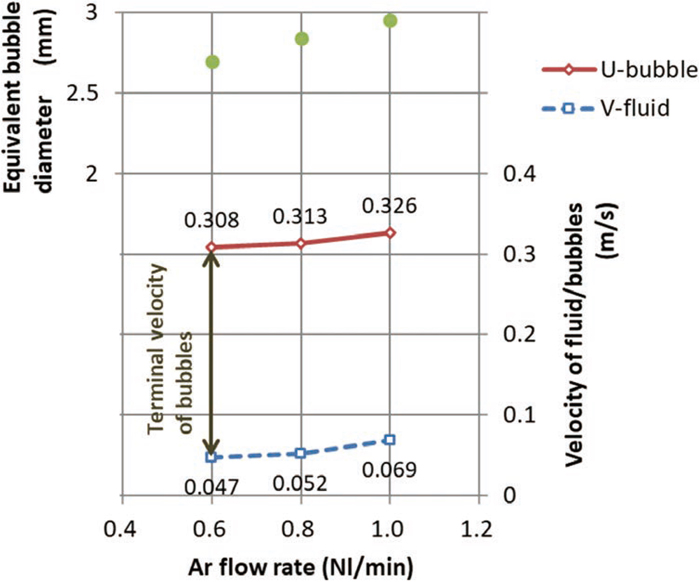
Result of bubbling experiment.

Fig. 6.

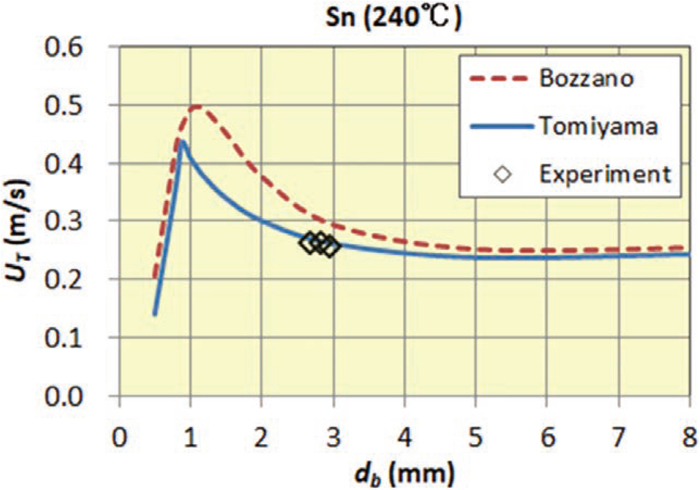
Experimental result of bubble terminal velocity compared with estimation formulas.

In addition, data of investigated bubble terminal velocity in Hg by a reliable past research⁶⁴⁾ was compared with these equations in Fig. 7. As shown in Fig. 7, these equations well represent the bubble terminal velocity in molten Hg. Particularly, Tomiyama’s equation was exceedingly precise.

Fig. 7.

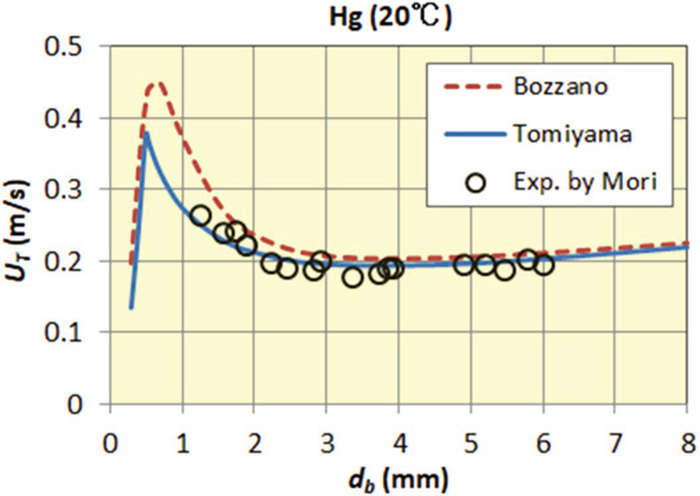
Experimental result of bubble terminal velocity of past research compared with estimation formulas. (Online version in color.)

Results of above mentioned studies show that Tomiyama’s equation can be extensively applied to molten metal systems. Then, we have calculated bubble rising velocity by these equation in molten Fe and molten Sn. Before comparing the bubble rising velocity in the prototype and the physical model, it should be noted that in the case of the Froude number similitude with the physical modelling scale ratio of λ. Flow velocity is described in equation (5; $V=\sqrt{\lambda }\cdot V_0$). Accordingly, time progression in the physical model will expand or contract as expressed in Eq. (20). For example, in the case of scale ratio λ = 0.5, time progression in the physical model will shrink $\sqrt{0.5}$ ≈ 0.71 times as compared with the real time progression. Specifically, a real flow phenomena occurred in 1 second will be represented in 0.71 second by the physical model with the scale ratio of 0.5 under the Froude number similitude.   

$$t=\frac{L}{V}=\frac{\lambda \cdot L_0}{V_0\sqrt{\lambda }}=\sqrt{\lambda }\cdot t_0$$(20)

Figure 8 shows relationship between bubble diameter in molten Fe and relative rising time (RRT) of bubbles under the SMDN condition of molten Sn model to represent molten steel system as described in Table 2 and Fig. 2. Data of bubble terminal velocity to obtain RRT in Fig. 8 were calculated by Tomiyama’s and Bozzano’s equations (Eqs. (16), (17), (18), (19)). RRT is the proportion between rising time of bubble in the prototype and rising time of bubble in the physical model experiment as expressed in Eq. (21) taking the time progression described in Eq. (20) into account. Here, U₀ means bubble rising velocity in the prototype (in molten Fe), U means bubble rising velocity in the physical model experiment (in molten Sn). Additionally, it should be noted that the bubble diameter d_b for U and bubble diameter d_b0 for U₀ are not same (d_b = λ·d_b0).   

$$RRT=\raisebox{1ex}{$\frac{L}{U}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{\lambda }\frac{L_0}{U_0}$}\right.=\raisebox{1ex}{$\frac{\lambda \cdot L_0}{U}$}\!\left/ \!\raisebox{-1ex}{$\sqrt{\lambda }\frac{L_0}{U_0}$}\right.=\frac{U_0\cdot \lambda }{U\cdot \sqrt{\lambda }}=\sqrt{\lambda }\frac{U_0}{U}$$(21)

Fig. 8.

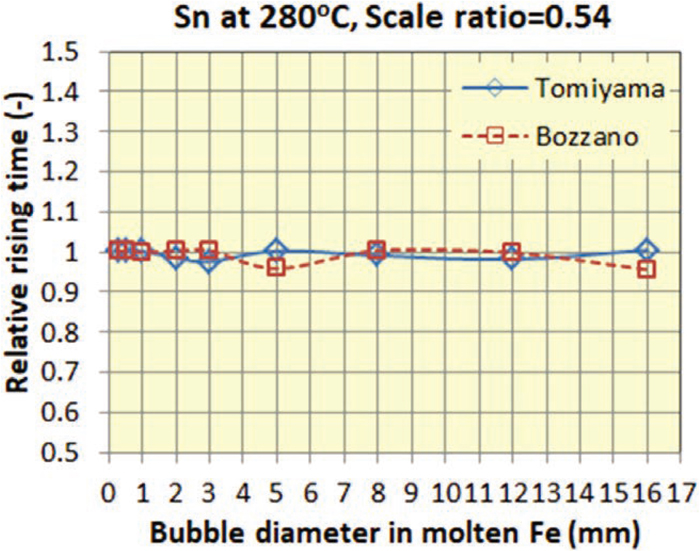
Relationship between relative rising time of bubble estimated by Tomiyama’s and Bozzano’s equations. (Online version in color.)

As shown in Fig. 8, estimated RRT were approximately 1.0 in a wide range of bubble size, which means that bubble terminal velocity in the prototypes will be precisely represented by the physical models under the SMDN condition. It is a reasonable result because the drag coefficient of Tomiyama’s equation (Eq. (16)) or Bozzano’s equation (Eqs. (17), (18), (19)) consist of three dimensionless numbers; the Reynolds, Eötvös and Morton numbers whose similitudes are satisfied under the SMDN condition.

Above-mentioned results indicate that the physical model experiments under the SMDN condition can represent bubble rising behavior of gas-liquid systems as well as the bulk flow phenomena. In addition, it is expected that many types of gas-liquid flow phenomena such as bubble formation influenced by surface tension, viscosity and flow inertia of liquid will be represented by physical models that satisfies the SMDN condition.

5. Conclusion

The condition of the physical modelling has been studied for the simultaneous similitudes of the Froude, Reynolds and Weber numbers. As a result, a simple relationship between density, viscosity, surface tension of fluids and scale ratio of the physical model were obtained by simple equations. Furthermore, it has become clear that the Eötvös and Morton number similitudes are established in the case of simultaneous similitudes of these three dimensionless numbers. To say nothing of the Galilei and capillary numbers. This multiple similitudes concept of physical modelling has been named SMDN (Similitude of Multiple Dimensionless Numbers).

Subsequently, physical properties of a number of liquids were investigated for the precise physical modelling to simulate the molten steel flow phenomena discovering some molten metals that satisfy the SMDN condition. Especially, molten Sn is a safe and easy-to-treat fluid to construct the physical models. It is not clear the reason why many molten metals have the specific properties satisfying the SMDN condition each other. Further researches are demanded on this matter.

Then rising velocity of bubbles in molten metal bath has been studied. As a result, it was confirmed that the relative bubble rising time in the prototype is precisely represented by physical models under the SMDN condition.

As a conclusion of above-mentioned study, the physical model experiments under the SMDN condition could represent many types of gas-liquid flow phenomena influenced by four forces; inertial force, gravitational force, viscous force and surface tension force, such as bubble formation or dispersion in molten metals as well as a single-phase molten metal flow. It is expected that the physical models under the SMDN condition will make a substantial contribution to the elucidation of flow phenomena of high-temperature fluids.

Symbols

V: Velocity of fluid

g: Gravitational acceleration

L: Characteristic length

ρ: Density

η: Viscosity

σ: Surface tension

ν: Kinematic viscosity

ι: σ/ρ

λ: Scale ratio

d: Diameter

r_e: Radius of equivalent spherical bubble

U: Bubble rising velocity

₀: Subscript for prototype

_b: Subscript for bubble

_T: Subscript for terminal velocity

References

• 1)   M.  Pfister and  H.  Chanson: J. Hydrodynam., 26 (2014), 291. https://doi.org/10.1016/S1001-6058(14)60032-9
• 2)   S.  Cho and  B.  Thomas: Metals, 9 (2019), 471. https://doi.org/10.3390/met9040471
• 3)   S.  Liu,  X.  Yang,  L.  Du,  L.  Li and  C.  Liu: ISIJ Int., 48 (2008), 1712. https://doi.org/10.2355/isijinternational.48.1712
• 4)   M.  Saternus and  T.  Merder: Metals, 8 (2018), 726. https://doi.org/10.3390/met8090726
• 5)   P.  Lopez,  P.  Jalali,  J.  Björkvall,  U.  Sjöström and  C.  Nilsson: ISIJ Int., 54 (2014), 342. https://doi.org/10.2355/isijinternational.54.342
• 6)   J.  Pieprzyca,  T.  Merder and  M.  Saternus: Metalurgija, 53 (2014), 327.
• 7)   M.  Saternus,  J.  Pieprzyca and  T.  Merder: Mater. Sci. Forum, 879 (2016), 1685. https://doi.org/10.4028/www.scientific.net/MSF.879.1685
• 8)   Y.  Sahai and  T.  Emi: ISIJ Int., 36 (1996), 1166. https://doi.org/10.2355/isijinternational.36.1166
• 9)   D.  Mazumdar and  R.  Guthrie: ISIJ Int., 39 (1999), 524. https://doi.org/10.2355/isijinternational.39.524
• 10)   K.  Moon,  W.  Choi,  M.  Isac,  R.  Guthrie and  H.  Nogami: ISIJ Int., 43 (2003), 1538. https://doi.org/10.2355/isijinternational.43.1538
• 11)   E.  Torres-Alonso,  R.  Morales,  S.  García-Hernández and  J.  Palafox-Ramos: Metall. Mater. Trans. B, 41 (2010), 583. https://doi.org/10.1007/s11663-010-9361-9
• 12)   K.  Timmel,  S.  Eckert,  G.  Gerbeth,  F.  Stefani and  T.  Wondrak: ISIJ Int., 50 (2010), 1134. https://doi.org/10.2355/isijinternational.50.1134
• 13)   K.  Timmel,  T.  Wondrak,  M.  Röder,  F.  Stefani,  S.  Eckert and  G.  Gerbeth: Steel Res. Int., 85 (2014), 1283. https://doi.org/10.1002/srin.201300034
• 14)   H.  Harada,  T.  Toh,  T.  Ishii,  K.  Kaneko and  E.  Takeuchi: ISIJ Int., 41 (2001), 1236. https://doi.org/10.2355/isijinternational.41.1236
• 15)   Y.  Tsukaguchi,  S.  Furuhashi and  M.  Kawamoto: ISIJ Int., 44 (2004), 350. https://doi.org/10.2355/isijinternational.44.350
• 16)   A.  Cramer,  S.  Eckert,  V.  Galindo,  G.  Gerbeth,  B.  Willers and  W.  Witke: J. Mater. Sci., 39 (2004), 7285. https://doi.org/10.1023/B:JMSC.0000048743.43663.e9
• 17)   B.  Li,  H.  Lu,  Z.  Shen,  X.  Sun,  Y.  Zhong,  Z.  Ren and  Z.  Lei: ISIJ Int., 59 (2019), 2264. https://doi.org/10.2355/isijinternational.ISIJINT-2018-866
• 18)   E.  Martinez,  M.  Maeda,  L.  Heaslip,  G.  Rodriguez and  A.  McLean: Trans. Iron Steel Inst. Jpn., 26 (1986), 724.
• 19)   S.  Singh and  S.  Koria: ISIJ Int., 33 (1993), 1228. https://doi.org/10.2355/isijinternational.33.1228
• 20)   J.  Kurobe and  M.  Iguchi: Mater. Trans., 44 (2003), 877.
• 21)   V.  Singh,  S.  Dash,  J.  Sunitha,  S.  Ajmani and  A.  Das: ISIJ Int., 46 (2006), 210. https://doi.org/10.2355/isijinternational.46.210
• 22)   L.  Zhang,  S.  Yang,  K.  Cai,  J.  Li,  X.  Wan and  B.  Thomas: Metall. Mater. Trans. B, 38 (2007), 63. https://doi.org/10.1007/s11663-006-9007-0
• 23)   M.  Warzecha: Metalurgija, 50 (2011), 147.
• 24)   L.  Sun,  J.  Li,  L.  An,  L.  Wang,  H.  Tang and  Y.  Gao: Proc. 8th Pacific Rim Int. Cong. on Advanced Materials and Processing, Springer, Cham, (2017), 3163.
• 25)   J.  Cloete,  G.  Akdogan,  S.  Bradshaw and  D.  Chibwe: J. South. Afr. Inst. Min. Metall., 115 (2015), 355.
• 26)   K.  Michalek,  K.  Gryc,  L.  Socha,  M.  Tkadlečková,  M.  Saternus,  J.  Pieprzyca,  T.  Merder and  L.  Pindor: Arch. Metall. Mater., 61 (2016), 257. https://doi.org/10.1515/amm-2016-0048
• 27)   M.  Salazar-Campoy,  R.  Morales,  A.  Nájera-Bastida,  V.  Cedillo-Hernández and  J.  Delgado-Pureco: Metall. Mater. Trans. B, 48 (2017), 1376. https://doi.org/10.1007/s11663-017-0918-8
• 28)   A.  Mabentsela,  G.  Akdogan and  S.  Bradshaw: J. South. Afr. Inst. Min. Metall., 117 (2017), 469.
• 29)   A.  Cwudziński: Metall. Res. Technol., 115 (2018), 101. https://doi.org/10.1051/metal/2017081
• 30)   K.  Zhang,  J.  Liu,  H.  Cui and  C.  Xiao: Metall. Mater. Trans. B, 49 (2018), 1174. https://doi.org/10.1007/s11663-018-1236-5
• 31)   Y.  Liu,  M.  Ersson,  H.  Liu,  P.  Jönsson and  Y.  Gan: Metall. Mater. Trans. B, 50 (2019), 555. https://doi.org/10.1007/s11663-018-1446-x
• 32)   X.  Jiang,  Z.  Cui,  M.  Chen and  B.  Zhao: Metall. Mater. Trans. B, 50 (2019), 782. https://doi.org/10.1007/s11663-019-01516-0
• 33)   J.  Pieprzyca,  T.  Merder,  M.  Saternus,  K.  Gryc and  L.  Socha: Arch. Metall. Mater., 64 (2019), 653. https://doi.org/10.24425/amm.2019.127594
• 34)   G. M.  de Souza,  A.  de Freitas Gomes de Mendonça and  R. P.  Tavares: REM: Int. Eng. J., 73 (2020), 531. https://doi.org/10.1590/0370-44672020730010
• 35)   A.  Cwudziński,  J.  Jowsa,  B.  Gajda and  A.  Hutny: Ironmaking Steelmaking, 47 (2020), 1188. https://doi.org/10.1080/03019233.2019.1708670
• 36)   M.  Bielnicki and  J.  Jowsa: Metall. Res. Technol., 117 (2020), 509. https://doi.org/10.1051/metal/2020055
• 37)   Y.  Tomita: Suirikigaku: Nagare-Gensyo-no-Kiso-to-Kouzou (New Edition of Fluid Engineering), Jikkyo Shuppan, Tokyo, (1982), 81 (in Japanese).
• 38)   Y.  Furuya,  M.  Murakami and  Y.  Yamada: Kaitei-Shinban Ryutai-Kougaku (New Edition of Fluid Engineering), Asakura Publishing, Tokyo, (1984), 57 (in Japanese).
• 39)   H.  Chanson: The Hydraulics of Open Channel Flow, 2nd ed., Butterworth-Heinemann, Oxford, UK, (2004), 257.
• 40)   R.  Clift,  J. R.  Grace and  M. E.  Weber: Bubbles, Drops, and Particles, Dover Publications, Inc., Mineola, NY, (2005), 27.
• 41)   M.  Pfister and  W. H.  Hager: J. Hydraul. Eng., 140 (2014), 02514001. https://doi.org/10.1061/(ASCE)HY.1943-7900.0000870
• 42)   A.  Kirshenbaum and  J.  Cahill: Trans. Metall. Soc. AIME, 224 (1962), 816.
• 43)   T.  Tanaka and  S.  Hara: Materia Jpn., 36 (1997), 47 (in Japanese). https://doi.org/10.2320/materia.36.47
• 44)  National Astronomical Observatory of Japan: Rika-Nenpyo Heisei 17 Nen (Chronological Scientific Tables 2005), Maruzen, Tokyo, (2004), 371 (in Japanese).
• 45)   A.  Kasama,  T.  Iida and  Z.  Morita: J. Jpn. Inst. Met., 40 (1976), 1030 (in Japanese). https://doi.org/10.2320/jinstmet1952.40.10_1030
• 46)   Y.  Plevachuk,  V.  Sklyarchuk,  G.  Gerbeth and  S.  Eckert: Int. J. Mater. Res., 101 (2010), 839. https://doi.org/10.3139/146.110357
• 47)   T.  Gancarz,  Z.  Moser,  W.  Gąsior,  J.  Pstruś and  H.  Henein: Int. J. Thermophys., 32 (2011), 1210. https://doi.org/10.1007/s10765-011-1011-1
• 48)   M.  Assael,  A.  Kalyva,  K.  Antoniadis,  R. M.  Banish,  I.  Egry,  J.  Wu,  E.  Kaschnitz and  W. A.  Wakeham: J. Phys. Chem. Ref. Data, 39 (2010), 033105. https://doi.org/10.1063/1.3467496
• 49)   T.  Matsumoto,  H.  Fujii,  T.  Ueda,  M.  Kamai and  K.  Nogi: Trans. JWRI, 34 (2005), 29. http://www.jwri.osaka-u.ac.jp/publication/trans-jwri/pdf/342-29.pdf
• 50)   M.  Assael,  I.  Armyra,  J.  Brillo,  S.  Stankus,  J.  Wu and  W.  Wakeham: J. Phys. Chem. Ref. Data, 41 (2012), 033101. https://doi.org/10.1063/1.4729873
• 51)   T.  Hogness: J. Am. Chem. Soc., 43 (1921), 1621. https://doi.org/10.1021/ja01440a026
• 52)   M.  Maniruzzaman and  M.  Makhlouf: Metall. Mater. Trans. B, 33 (2002), 305. https://doi.org/10.1007/s11663-002-0013-6
• 53)   K.  Fujita,  Y.  Tsukaguchi,  K.  Mishima and  N.  Okada: CAMP-ISIJ, 32 (2019), 161.
• 54)   T.  Iida and  R. I. L.  Guthrie: The Thermophysical Properties of Metallic Liquids: Vol. 1 - Fundamentals, Oxford University Press, Oxford, UK, (2015), 1.
• 55)   T.  Iida and  R. I. L.  Guthrie: The Thermophysical Properties of Metallic Liquids: Vol. 2 - Predictive Models, Oxford University Press, Oxford, UK, (2015), 1.
• 56)   A.  Tomiyama,  I.  Kataoka,  I.  Zun and  T.  Sakaguchi: JSME Int. J. Ser. B, 41 (1998), 472. https://doi.org/10.1299/jsmeb.41.472
• 57)   G.  Bozzano and  M.  Dente: Comput. Chem. Eng., 25 (2001), 571. https://doi.org/10.1016/S0098-1354(01)00636-6
• 58)   Y.  Takeda: Exp. Therm. Fluid Sci., 10 (1995), 444. https://doi.org/10.1016/0894-1777(94)00124-Q
• 59)   M.  Mori,  Y.  Takeda,  T.  Taishi,  N.  Furuichi,  M.  Aritomi and  H.  Kikura: Exp. Fluids, 32 (2002), 153. https://doi.org/10.1007/s003480100295
• 60)   H.  Kikura,  H.  Murakawa and  M.  Aritomi: Nagare, 27 (2008), 283 (in Japanese). https://doi.org/10.11426/nagare1982.27.283
• 61)   Y.  Takeda,  H.  Murakawa,  Y.  Murai and  Y.  Tasaka: Ultrasonic Doppler Velocity Profiler for Fluid Flow, ed. by Y. Takeda, Springer Japan, Tokyo, (2012), 1.
• 62)   S.  Eckert,  G.  Gerbeth and  V.  Melnikov: Exp. Fluids, 35 (2003), 381. https://doi.org/10.1007/s00348-003-0606-0
• 63)   C.  Zhang,  S.  Eckert and  G.  Gerbeth: Proc. 5th Int. Conf. on Multiphase Flow, JSMF, Osaka, (2004), 260.
• 64)   Y.  Mori,  K.  Hijikata and  I.  Kuriyama: J. Heat Transf., 99 (1977), 404. https://doi.org/10.1115/1.3450710