2022 Volume 62 Issue 1 Pages 38-47
2022 Volume 62 Issue 1 Pages 38-47
We proposed a novel numerical method for the reliable prediction of decarburization with CO2. In our method, mass, momentum, and energy conservation equations are solved simultaneously, where the reactive mass transfer, compressibility, and moving interface between gas and liquid are fully considered. In the decarburization reaction model, we assumed that the rate-limiting processes are the mass transfer in the gas phase and the interfacial reaction rate. Our method quantitatively well reproduced the total decarburization rates in the crucible of Nomura and Mori’s experiment (Trans. ISIJ, 13 (1973), 265.) using a jet of CO2–CO gas mixture. It was found that the interfacial reaction rate affected the local decarburization reaction rate and the concentration distribution of CO2 and CO near the gas–liquid interface. Thus, the consideration of the interfacial reaction rate is important for the accurate reproduction of the local decarburization phenomena by a gas jet of CO2.
To improve the performance of basic oxygen furnaces (BOFs), it is important to understand the complex dynamics in BOFs. In a BOF, supersonic gas jets of O2 are blown on a molten iron bath through a lance; consequently, impurities such as C, Si, Mn, and P are removed as CO–CO2 gas mixture and slag containing SiO2, MnO, and P2O5 through chemical reactions. The main role of BOFs is decarburization, which consumes approximately 100% of blown O2 in the main blowing stage, where the concentration of C in the bath is higher than approximately 0.3%.1) However, the details of the decarburization process are not well understood because of the complex interaction among many elementary processes, which involve the chemical reactions with the variable reaction rates coupled to the multiphase flow dynamics.
In order to understand the details of phenomena in BOFs, experiments have been conducted to observe and measure the inside of BOFs with a maximum temperature of over 2400 K2) and, more recently, simulations have been conducted using computational fluid dynamics (CFD). The main reaction sites for decarburization are typically presumed to comprise two zones, i.e., the impact zone, which is the surface of the cavity formed by the jet impinging on the molten iron bath, and the emulsion zone, where the droplets generated by the impinging jet, slag, and CO gas are mixed. For the emulsion zone, the mass percentage of metal droplets in the sampled emulsion has been experimentally investigated;3,4) however, the details are unclear owing to the complicated phenomena in the emulsion. For the impact zone, many studies have been conducted on the cavity formed by the jet. The relationship between the blowing conditions and the cavity shapes has been investigated by experiments with molten iron bath,5,6,7) cold models8,9,10,11,12) using water, glycerin, mercury, etc. and numerical simulations13,14,15,16) based on CFD. More recently, the cavity shape of a BOF was predicted by CFD, where the interaction among supersonic gas jets, molten iron, and slag was considered.17) However, the chemical reactions in the impact zone were not considered in the CFD models.
A reliable CFD model for the decarburization in the impact zone has not yet been established, although there are several related studies18,19,20) which consider decarburization with O2 (O2+2C=2CO) involving decarburization with CO2 (CO2+C=2CO) and post-combustion (CO+1/2O2=CO2), and studies21,22) which consider only decarburization with CO2. The chemical reaction models for the decarburization with O2 have not been sufficiently validated because the reaction rates of each of the three reactions, i.e., O2+2C=2CO, CO2+C=2CO, and CO+1/2O2=CO2, cannot be determined experimentally. For the decarburization with CO2, two CFD models (Cho et al.21) and Gao et al.22)) have been proposed so far, but neither of the two have considered both of the mass transfer in the gas-phase boundary layer and the interfacial chemical reaction rate, which would control the decarburization rate. Furthermore, their models were not validated under the high CO2 concentration condition, which is considered to be the case in actual BOFs from the model experiment with combustion in opposing flows of O2 and CO.23)
We herein propose a CFD solver, which fully couples governing continuum mechanics equations with a decarburization reaction model considering the mass transfer and the finite reaction rate on the gas-liquid interface, in order to elucidate the effects of each rate-limiting process. In this method, our pressure-based solver of mixed compressibility for two-phase flows24) was extended to treat reactive flows. The decarburization reaction model based on the model by Nomura and Mori25) was integrated into the CFD solver. The present method was validated by comparing the decarburization rates with those of Nomura and Mori’s element experiment.25)
After adding mass conservation equations for chemical species to the governing equations of compressible/incompressible gas–liquid two-phase flows,24) we obtained the following equations:
• transport equation for the color function to track the gas-liquid interface:
| (1) |
• mass conservation equations for chemical species in gas and liquid phases:
| (2) |
| (3) |
• mass conservation equation:
| (4) |
• momentum conservation equation:
| (5) |
• energy conservation equation:
| (6) |
We assumed that the density of molten iron was constant, i.e., ρl,0=7000 kg m−3,26) and the density of gas was expressed by the equation of state for ideal gas. We used Fick’s, Newton’s, and Fourier’s laws in the conservation equations of mass of the chemical species, momentum, and energy as follows:
The mass increase rates
The basic equations listed in Section 2.1 were solved using a multistep solution procedure for pressure–velocity–density coupling, as in OpenFOAM.37) In the solution procedure, after solving the transport equation of the color function Eq. (1) by isoAdvector scheme,38) the intermediate densities ρ*, (ρl,0αl)*, and (ρgαg)* were calculated based on the mass conservation equations as follows:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
The coupled solution method of the pressure, velocity, and density is based on the fractional-step method. The momentum conservation equation was solved using a two-step time-advancement scheme as follows:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
We developed a decarburization reaction model based on the model by Nomura and Mori,25) and integrated it into our CFD solver. The decarburization processes of molten iron by CO2 can be divided into two types of processes: chemical reactions at the gas–liquid interface and the mass transfer in the boundary layer. In the chemical processes, under the high concentration of C in molten iron, the rate-limiting reaction is assumed to be the direct reaction between CO2 and C at the gas–liquid interface described by:
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
The molar fluxes by mass transfer from the bulk to the gas–liquid interface, which move at the fluid velocity, N (mol m−2 s−1), are described as follows:
| (31) |
| (32) |
| (33) |
| (34) |
The following relations exist among the molar fluxes based on stoichiometric Eq. (26):
| (35) |
| (36) |
The increase rates of the species by the chemical reactions in Eq. (26),
| (37) |
| (38) |
| (39) |
| (40) |
In addition to the reaction model described above, a reaction model which assumes infinite reaction rate for the dissociative adsorption of CO2 was used. In the model, we assumed that CO2 is completely consumed at the gas–liquid interface because of the infinite reaction rate. Therefore, substituting
| (41) |
The time-stepping procedure of the governing equations (Eqs. (1), (2), (3), (4), (5), (6)), including the calculation of the decarburization reaction rate, is summarized as follows:
1. The color function for the liquid phase
2. The intermediate densities ρ*, (ρl,0αl)*, and (ρgαg)* were calculated using Eqs. (7), (8), (9).
3. The mass increase rates
4. The mass fractions of chemical species
5. The temperature Tn+1 was obtained by solving Eq. (15) after updating the specific heat at constant pressure
6. The density
7. The intermediate velocity U* was obtained from Eq. (16) after the viscosity was updated as μn+1.
8. The pressure pn+1 was obtained by solving Eq. (21).
9. The velocity Un+1, volumetric flow rate
10. The next time step was calculated based on steps 1 to 9 by updating the temporal index n with n+1.
The matrix solvers and spatial discretization schemes were selected considering the numerical stability and efficiency. The preconditioned conjugate gradient method was used for the pressure equation. Meanwhile, the preconditioned biconjugate gradient method was applied to solve the equations of energy and chemical species. The spatial derivatives for the diffusion terms were discretized using the second-order central-difference scheme. For the advection terms, the total variation diminishing scheme with the Sweby limiter43) was applied.
We simulated an experiment25) by Nomura and Mori using the apparatus shown in Fig. 1(a). In their experiment, a mixture of CO2–CO gas was blown through a nozzle of diameter 4.0 or 10.0 mm on a 0.4 kg molten iron with approximately 1.0 mass-percent carbon in a crucible of inner diameter 40 mm and height 100 mm. The temperature was maintained at 1873 K using an induction heater. The nozzle was 5.0 mm above the surface of molten iron. The decarburization rates were estimated by sampling the molten iron at constant intervals. The gas flow rates, q (m3 s−1), were in the range of 3.3–28.3×10−6 m3 s−1 at standard temperature 273.15 K and pressure 101.325 kPa (STP). The flow was assumed to be laminar because the Reynolds number of the gas jet was 150–1000. These experimental conditions are listed in Table 1.
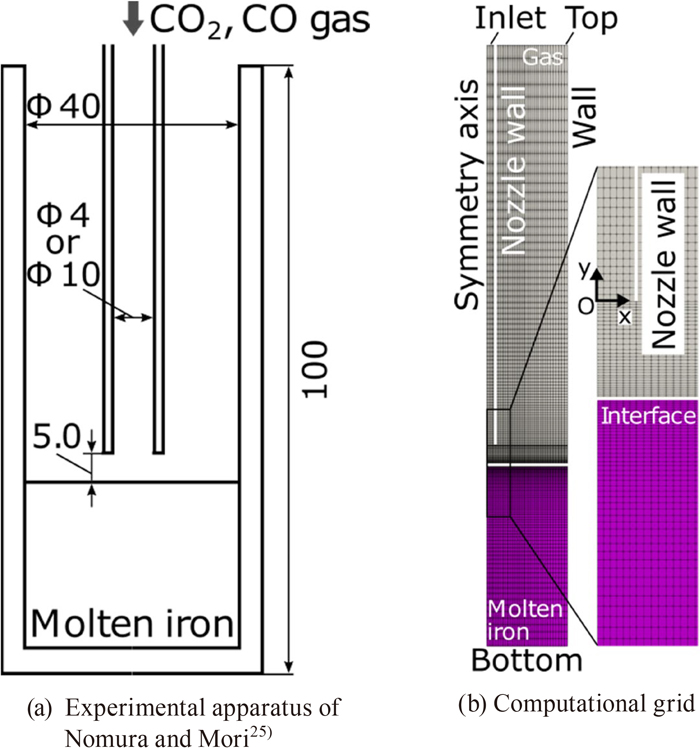
Schematic of the experimental apparatus of Nomura and Mori25) and computational grid. (Online version in color.)
| Mole fraction of CO2 in blowing gas (−) | 1.0, 0.7, 0.6, 0.0909, 0.0625 |
| Gas flow rate at STP (10−6 m3/s) | 3.3–28.3 |
| Temperature of blowing gas (K) | 300 |
| Pressure in atmosphere (kPa) | 101.325 |
| Weight of molten iron (kg) | 0.4 |
| Temperature of molten iron (K) | 1873 |
| Initial mass percent of carbon (%) | 1.0 |
The computational grid was axisymmetric and non-uniform, the spacings of which were smaller near the nozzle exit and the gas–liquid interface as shown in Fig. 1(b). The number of cells was 7920. The inner diameter of the nozzle, the inner diameter and height of the crucible, and the arrangement of the nozzle and the crucible were accurately represented in the grid. The induction heater was not considered, because the temperature in the molten iron can be regarded as uniform and 1873 K during our simulation time of 10 s under our boundary and initial conditions described below.
The boundary conditions were set as follows: At the inlet boundary, the mass flow rate, temperature, and mass fractions of species were specified. The top boundary was set as the free-flow boundary, where the velocity, temperature, and mass fractions were extrapolated from the values in the adjacent cells and the total pressure was specified. The wall and bottom boundaries were set to the no-slip and the adiabatic conditions.
In the entire region, we initially set the velocity to zero and the temperature to 1873 K. The initial pressure was set to 101.325 kPa in the gas phase and to the static pressure profile of the molten iron in the liquid phase. The initial mass fractions of chemical species in the gas were those of the blowing gas (e.g.,
A comparison of the budget of the inlet and outlet mass flow rates to the total mass increase in the system for C and O is shown in Fig. 2. The accumulated mass conservation errors of C and O at t =10 s were negligibly small and within 0.5% of the total mass of the inflow. At t =10 s the system was in a steady state, where the rate of change of the physical quantities had reached constant values.
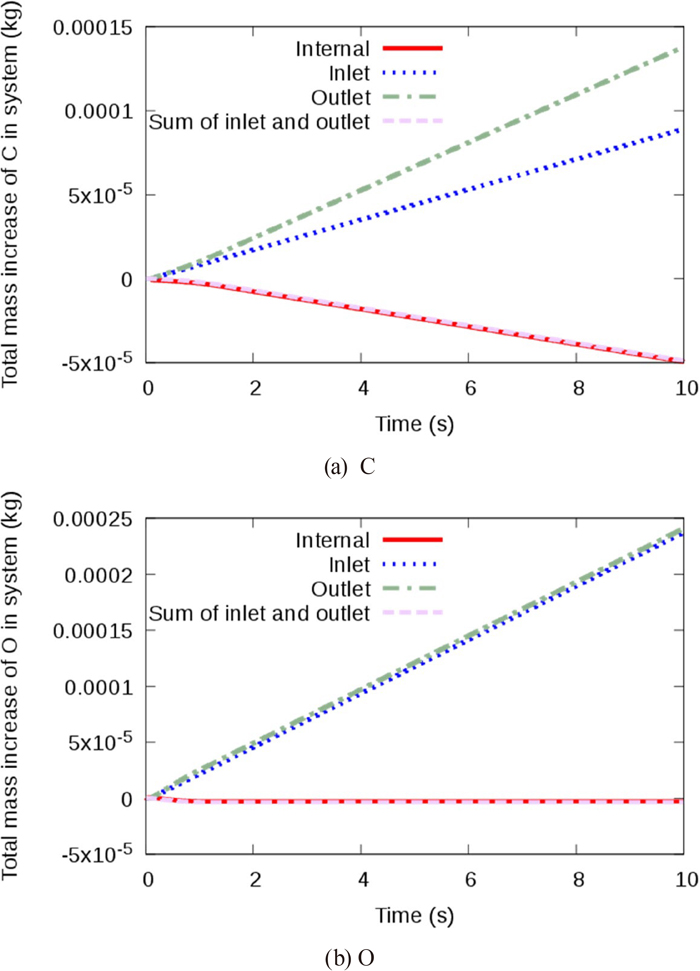
Comparison of budget of inlet and outlet mass flow rates to total mass increase in the system; the inner diameter of the nozzle was 4.0 mm, the blowing gas was pure CO2, and the gas flow rate was 1.7×10−5 m3 s−1 at the STP; the model with finite reaction rate for adsorption reaction of CO2. (Online version in color.)
A relationship between the decarburization rates and the grid spacings is shown in Fig. 3. As the grid spacings decreased, the decarburization rate converged to a constant value. The change in the decarburization rates was within 3% between grid spacings of 0.5 and 1.5 which were normalized by the original grid spacings. Therefore, the present calculation using a normalized grid spacings 1 is regarded as producing results with almost independent of the grid spacings.
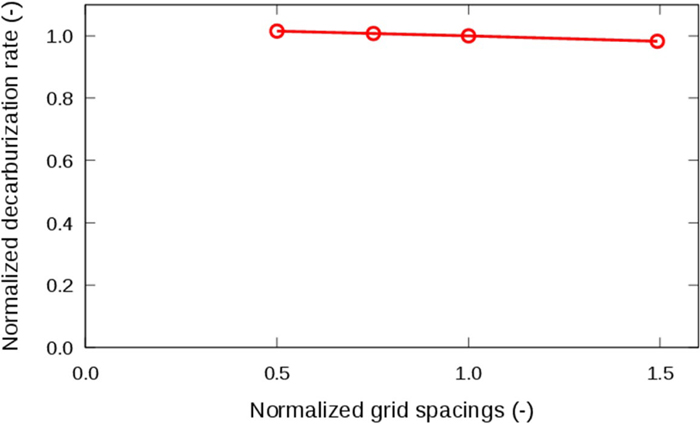
Relationship between decarburization rate and normalized grid spacings; the inner diameter of the nozzle was 4.0 mm, the blowing gas was pure CO2, and the gas flow rate was 1.7×10−5 m3 s−1 at the STP; the model with finite reaction rate for adsorption reaction of CO2. (Online version in color.)
A comparison of the calculated total decarburization rates by the models with finite reaction rate expressed by Eq. (29) or infinite reaction rate expressed by Eq. (41) for the dissociative adsorption reaction of CO2, with the experimental values25) is shown in Fig. 4. The total decarburization rates in the crucible were calculated by the summation of
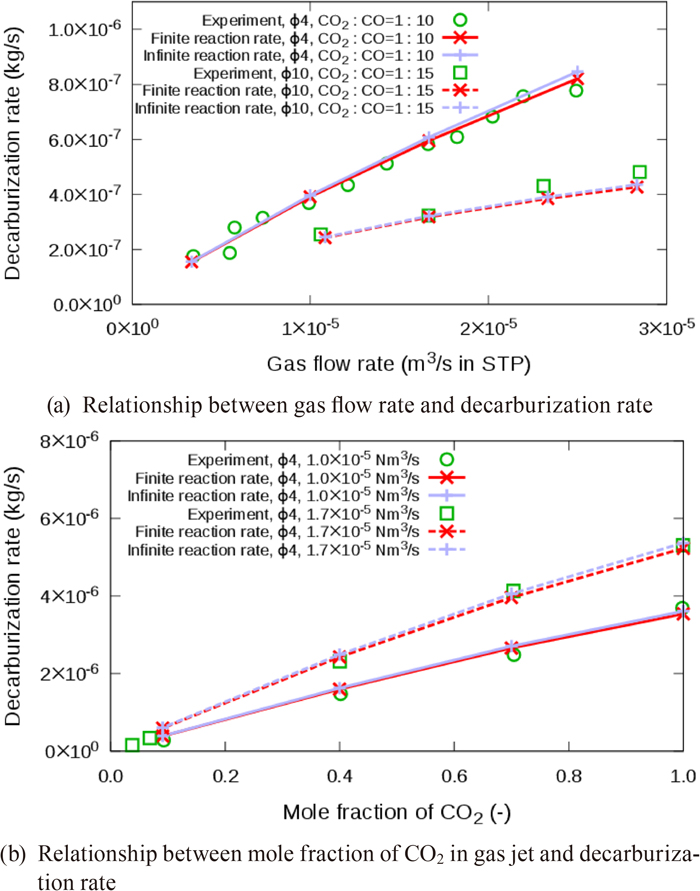
Comparison of calculated decarburization rates with experimental values.25) (Online version in color.)
The relationship between the gas flow rate and the reaction efficiency, which is defined by (Amount of CO2 consumed by decarburization)/(Supplied amount of CO2), is shown in Fig. 5. The calculated reaction efficiency was between 0.6–0.9 and decreases as increasing the gas flow rate. The trend was consistent with the experimental result.25)
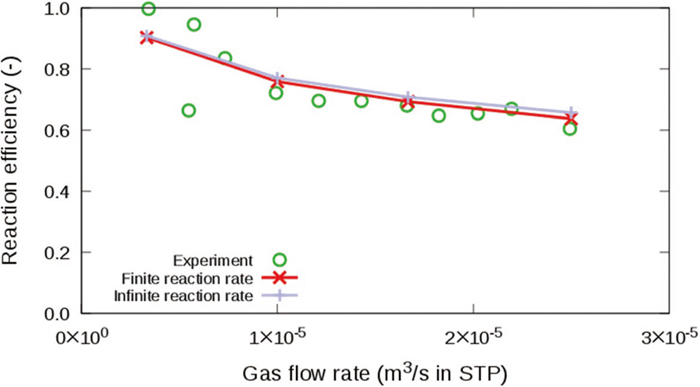
Relationship between gas flow rate and reaction efficiency; the inner diameter of the nozzle was 4.0 mm, the blowing gas was mixture of CO2 and CO in the ratio of 1:10.
Figure 6 shows snapshots of the distributions of velocity, temperature, and mass fractions of CO2, CO, and C at t =10 s using the model with the finite reaction rate for adsorption reaction of CO2. In the gas phase, CO2 gas jet impinged on the molten iron and spread radially along the almost flat gas–liquid interface, where it was consumed by the decarburization reaction. The CO gas generated by the decarburization reaction was advected in the radial direction with increasing its mass fraction. In the liquid phase, the low mass fraction of C was advected radially, hitting the crucible wall and flowing downward. The spatial variation of velocity and temperature in the liquid phase was much smaller than those in the gas phase. As the flow rate increased, the CO2 mass fraction increased because the reaction efficiency decreased as shown in Fig. 5. As the CO2 mass fraction of the jet increased, the velocity rising from the gas–liquid interface increased because the net flow rate was increased by the decarburization reaction. In addition, the temperature decreased due to the endothermic reaction of decarburization with CO2 as the CO2 mass fraction of the jet increased.
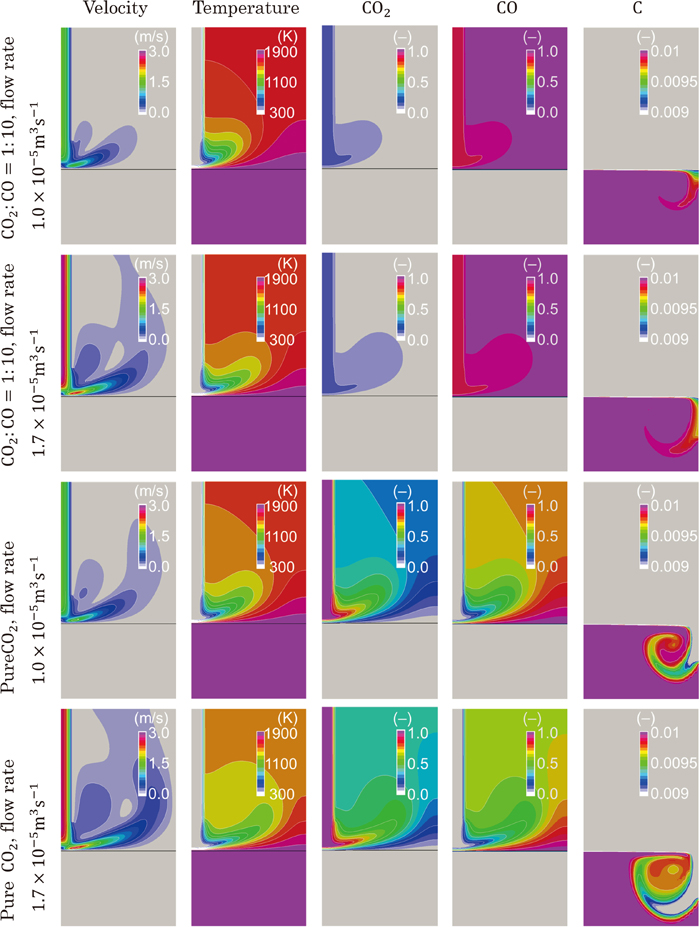
Distributions of velocity, temperature, and mass fraction of chemical species at t=10 s; black line is gas–liquid interface; the inner diameter of the nozzle was 4.0 mm; the model with finite reaction rate for adsorption reaction of CO2.
Figure 7 shows the radial profiles of reaction rates in the cells including gas–liquid interface at t =10 s using the model with the finite or infinite reaction rate for the adsorption reaction of CO2. Depending on the conditions, the reaction rates changed, but there were no significant differences in the profiles. Considering the finite reaction rate, the reaction rates in the jet impingement area were reduced compared to the case assumed the infinite reaction rate. Figure 8 shows the radial profiles of decarburization rate per unit radial length calculated by integrating the reaction rates of C in Fig. 7. In Fig. 8(d), the profiles calculated by the model with finite reaction rate was lower than that of the model with infinite reaction rate in the range below 10 mm radius and higher than that of the model with infinite reaction rate in the range above 10 mm radius. Under the other conditions, the same trend was observed: the reaction rate of the model with finite reaction rate was lower than that of the model with infinite reaction rate near the jet impingement area, and the reaction rate was higher than that of the model with infinite reaction rate in the area far from the jet impingement area. Therefore, the consideration of the finite reaction rate for the adsorption reaction of CO2 affects the local phenomena in decarburization although it does not have a significant impact on the total decarburization rate in the crucible as shown in Fig. 4.

Radial profiles of reaction rates per unit area of CO2, CO, and C on the gas-liquid interface; the inner diameter of the nozzle was 4.0 mm. (Online version in color.)
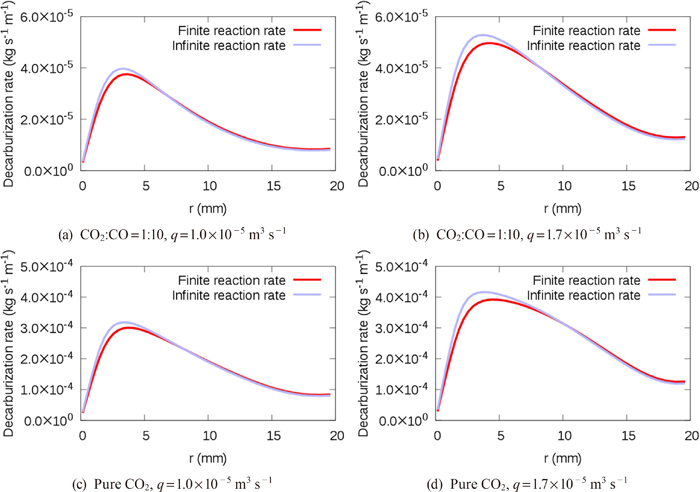
Radial profiles of decarburization rate per unit radial length on the gas-liquid interface; the inner diameter of the nozzle was 4.0 mm. (Online version in color.)
Figure 9 shows the radial profiles of mass fractions of CO2 and CO in the cells including gas–liquid interface at t =10 s using the model with the finite or infinite reaction rate for the adsorption reaction of CO2. Depending on the conditions, the mass fractions changed, but there were no significant differences in the profiles. The mass fraction of CO2 of the model with finite reaction rate was higher than that of the model with infinite reaction rate near the jet impingement area because the reaction rate was suppressed by the finite reaction rate as shown in Figs. 7 and 8. Figure 10 shows the vertical profiles of mass fractions of CO2 and CO on the central axis of the crucible at t =10 s using the model with the finite or infinite reaction rate for the adsorption reaction of CO2. The differences between the models were the same as in Fig. 9. As the flow rate increased, the thickness of the boundary layer decreased. The thickness of the boundary layer under the condition blowing the mixture gas of CO2 and CO in the ratio of 1:10 at the flow rate of 1.7×10−5 m3 s−1 was 0.625 mm, which was 1/1.2 times that under the condition blowing the mixture gas of CO2 and CO in the ratio of 1:10 at the flow rate of 1.0×10−5 m3 s−1. The rate of decrease in the boundary layer thickness was smaller than the rate of increase in the flow rate. This result corresponds to the low reaction efficiency at high flow rates shown in Fig. 5.
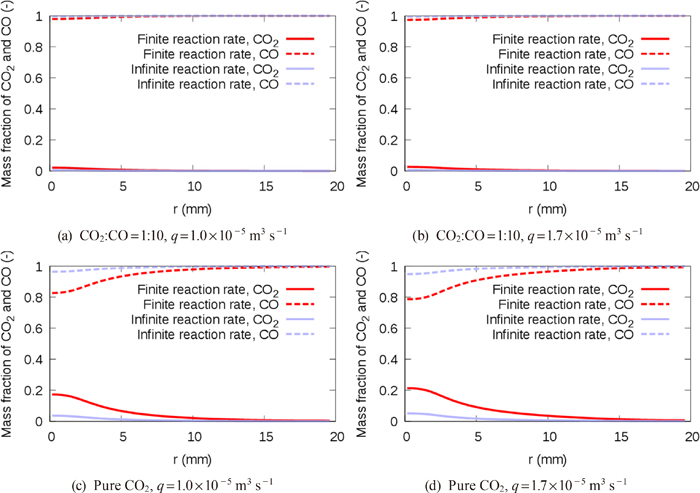
Radial profiles of mass fractions of CO2 and CO on the gas-liquid interface; the inner diameter of the nozzle was 4.0 mm. (Online version in color.)
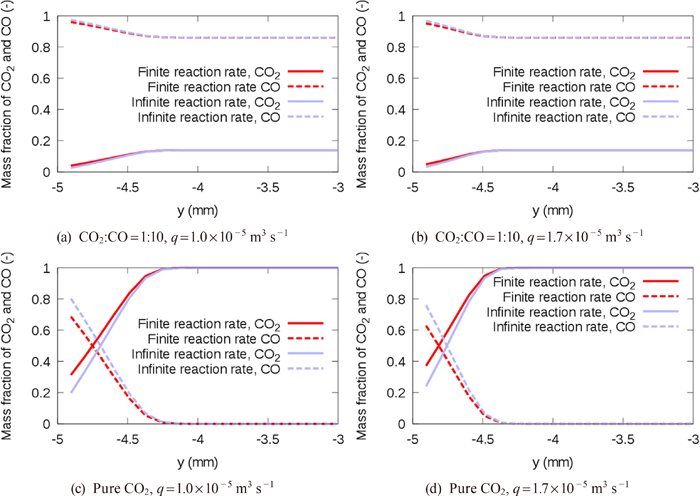
Vertical profiles of mass fractions of CO2 and CO on the central axis of the crucible; the inner diameter of the nozzle was 4.0 mm. (Online version in color.)
We proposed a novel simulation method for decarburization by CO2 considering the coupling between flow and decarburization reaction and assuming the mass transfer in the gas phase and the interfacial reaction rate, or the mass transfer alone as the rate-limiting factor. Our simulation method was validated by comparing the total decarburization rates in the system with the experimental values of Nomura and Mori.25) As a result, the total decarburization rates in the system were quantitatively reproduced over a wide range of CO2 concentration in the blown gas and flow rate, regardless of whether the interfacial reaction rate was considered as a rate-limiting factor or not. However, it was found that the interfacial reaction rate affected the local decarburization reaction rate and the concentrations of CO2 and CO. Therefore, it is important to consider the interfacial reaction rate for the accurate reproduction of the local decarburization phenomena by a gas jet of CO2.