Interaction Coefficients of Cu and Sn with Mn in Molten Iron at 1873 K

Abstract

Regarding the depletion of high-grade iron ore and an increase in steel scrap, a new ironmaking process that can utilize both low-grade iron ores and steel scraps is expected. When steel scrap is used as an iron source, tramp elements, such as Cu and Sn, are dissolved in hot metal. The tramp elements can affect the hot metal composition due to the thermodynamic interaction between tramp elements and other alloying elements. However, the thermodynamic interaction between Cu and Sn with Mn has not been known enough. In this work, the interaction coefficients between Cu and Sn with Mn were measured at 1873 K by a chemical equilibration technique using the liquid immiscibility of Fe and Ag as follows:

Moreover, the effects of scrap ratio (iron mass ratio of scrap to scrap and sinter) on hot metal and molten slag composition were thermodynamically analyzed considering the interaction coefficients measured in this work. When the scrap ratio was increased, the copper and tin contents of hot metal were increased, leading to the increase in the Mn content of the hot metal. However, the Mn content of hot metal was decreased by increasing the scrap ratio because the input amount of MnO was reduced.

1. Introduction

Reducing CO₂ emissions is one of the most critical issues for the Sustainable Development Goals (SDGs). Due to the increasing demand for steel products in developing countries, iron ore consumption has increased. In the developed countries, steel products have been accumulated in the society, and the products are recovered as steel scraps after their service life. Therefore, high-grade iron ore has been depleted,^1,2) and steel scrap is increasing. In Japan, 1.39 billion tonnes of steel products have been accumulated in the society until 2018,³⁾ and 26 million tonnes of the steel products, which is 2% of the steel stock, were recovered as steel scraps.⁴⁾ When the accumulation of steel products proceeds in the future, steel scrap will increase and exceed the crude steel production from natural iron resources by 2050.⁵⁾ Accordingly, a new ironmaking process is expected to utilize iron ores and steel scraps.⁶⁾ To achieve carbon neutrality utilizing steel scrap, a concept of a new iron and steel making system was proposed, which is called SMART.^7,8,9) In SMART, steel scrap is used as an iron source together with iron ores in the ironmaking process combined with a recycling system of CO₂. Packed Bed Type Partial Smelting Reduction Process (PSR)⁹⁾ is a promising ironmaking process that can utilize iron ores and steel scraps. Figure 1 shows the schematic of PSR. In PSR, iron ores, steel scraps, and coke are charged into a converter-type low-height shaft furnace equipped with tuyeres. Oxygen gas or air is introduced from the tuyeres, and reduction of iron ores and melting of steel scrap are simultaneously performed.^9,10) On the other hand, the steel scraps recovered from society contain impurity elements called tramp elements that are difficult to remove from molten iron by the current refining method. Daigo et al.¹¹⁾ reported that Cu, Sn, Ni, and Cr, which are the tramp elements, are often contained in steel scraps and inevitably dissolved in molten iron. Therefore, it is essential to control the thermodynamic activity of the elements, considering the coexistence of tramp elements.^12,13,14)

Fig. 1.

Schematic illustration of a PSR furnace (packed bed type partial smelting reduction process). (Online version in color.)

In the previous report,¹⁵⁾ an analysis model was developed to simulate the slag–metal reaction equilibrium considering the impurity elements in the steel scrap. The effects of the scrap ratio (iron mass ratio of scrap to scrap and sinter) on the hot metal and slag compositions were thermodynamically analyzed. Tramp elements in molten iron, which the slag cannot oxidize, will affect the redox equilibrium of other impurity elements due to the thermodynamic interaction between the tramp elements and other impurities. The author has measured interaction coefficients, which indicate the thermodynamic interactions of B, Co, and Ni with Cu¹²⁾ and of Mo, B, Ni, Ti, and Nb with Sn.¹³⁾ Tsuchiya et al.¹⁶⁾ proposed the discrimination method among conditions at the lower part of the blast furnace by distribution ratios of Si, Mn, and S between slag and hot metal, and Orimoto¹⁷⁾ estimated the temperature of the slag at the bottom of the blast furnace from the redox equilibrium of Mn. The redox equilibrium of Mn in the ironmaking process provides valuable information to know the thermal conditions in the furnace. Therefore, the thermodynamic interactions of tramp elements with Mn are essential. However, the interaction coefficients of Cu and Sn with Mn have not been reported. Therefore, those effects were ignored in the previous analysis. In this work, the interaction coefficients of Cu and Sn with Mn were measured at 1873 K. Furthermore, the measured values were applied to the analysis model developed by the authors,¹⁵⁾ and the effects of using scrap on the composition of the hot metal and slag were thermodynamically analyzed.

2. Experimental

The interaction coefficients between Cu and Sn with Mn were measured at 1873 K by a chemical equilibration technique using the liquid immiscibility of Fe and Ag.¹⁸⁾ Fe–Al–Mn alloy and Fe–Mn alloy were prepared from electrolytic iron and Mn regent in advance in a high-frequency induction furnace. The prepared alloys were cut and taken to the equilibrium experiments. The experimental conditions are listed in Table 1. In Table 1, “Sample” and “Initial mass” indicate the alloy used in the experiments and the total mass of the elements in the initial samples, respectively. The total mass of Fe and Ag was 10.0 or 7.0 g. Mn contents were controlled to be 0, 0.1, 0.3, 0.5, 1, 3, or 5 mass% by adjusting the amounts of Fe–Mn–Al alloy, Fe–Mn alloy, and electrolytic iron. The target contents of Cu and Sn were 0, 0.1, 0.3, 0.5, 1, 3, and 5 mass% and 0, 0.1, 0.2, 0.3, 0.4, and 0.5 mass%, respectively. To prevent the Al₂O₃ crucible from being reduced by Mn and the Mn contents from decreasing, Al was added into the Fe–Mn alloy in the experiments of No. 1–12, 28–47. The Al content of alloy was 0.2 mass%. Furthermore, in the experiments of No. 10–15, 42–50, the activity of MnO was maintained by adding 0.3 to 0.5 g of MnO–Al₂O₃ mixture so that the Fe phase was saturated with both Al₂O₃–MnO·Al₂O₃ phases. The MnO–Al₂O₃ mixture was prepared in the following procedures; Al₂O₃ and MnO regent powders were mixed in the ratio of 65mass%Al₂O₃-35mass%MnO, and the mixture was kept at 1873 K in argon for 24 h using an electric resistance furnace. Figure 2 shows a schematic diagram of the experimental apparatus and arrangement of materials. Three samples, contained in three alumina crucibles (o.d.: 15 mm, i.d.: 12 mm, height: 100 mm), were heated to 1873 K in a mullite tube (o.d.: 70 mm, i.d.: 60 mm, height: 1000 mm) in an electric resistance furnace. A larger alumina crucible (o.d.: 45 mm, i.d.: 38 mm, height: 100 mm) was used as an outer crucible. A carbon holder was placed on the alumina holder as a lid. The alloys and reagents were heated under argon to 1873 K and held for 5 h or 10 h to attain equilibrium. Subsequently, the alloys were withdrawn from the furnace and immediately quenched in water. The samples were carefully cut for chemical analyses. The Mn, Cu, Sn, and Al contents of the Fe and Ag phases were analyzed using Inductively Coupled Plasma Atomic Emission Spectroscopy (ICP-AES).

Table 1. Initial conditions and experimental result.

No.	M	Sample	MnO·Al2O3 (g)	Initial mass (g)					Experimental results (mass%)						Calculated mass (g)
									Fe phase			Ag phase
				Ag	Fe	Al	Mn	M	Al	Mn	M	Al	Mn	M	Al	Mn	M
1		Fe–Mn–Al	–	10.003	9.970	0.022	0.011	–	0.023	0.049	–	0.003	0.060	–	0.003	0.011	–
2			–	10.003	9.949	0.021	0.033	–	0.026	0.147	–	0.004	0.184	–	0.003	0.033	–
3			–	10.005	9.931	0.020	0.054	–	0.025	0.247	–	0.004	0.303	–	0.003	0.055	–
4			–	10.007	9.878	0.022	0.108	–	0.028	0.475	–	0.010	0.533	–	0.004	0.100	–
5			–	10.004	9.638	0.017	0.353	–	0.002	1.476	–	0.004	1.564	–	0.001	0.299	–
6			–	10.007	9.401	0.016	0.590	–	0.002	2.552	–	0.004	2.517	–	0.001	0.492	–
7			–	10.002	9.909	0.022	0.108	–	0.029	0.460	–	0.008	0.571	–	0.004	0.103	–
8	–		–	10.004	9.757	0.027	0.358	–	0.052	1.569	–	0.013	1.766	–	0.006	0.330	–
9			–	10.001	9.863	0.029	0.619	–	0.072	2.722	–	0.014	2.880	–	0.009	0.556	–
10			0.299	7.001	6.868	0.014	1.001	–	0.002	5.288	–	0.006	4.749	–	0.001	0.696	–
11		Fe–Mn–Al + Fe	0.302	7.005	6.935	0.007	0.500	–	0.001	2.478	–	0.000	2.523	–	0.000	0.349	–
12			0.301	7.001	6.969	0.004	0.251	–	0.001	1.221	–	0.003	1.385	–	0.000	0.182	–
13		Fe–Mn + Fe	0.505	7.004	9.962	–	0.979	–	0.002	4.540	–	0.000	4.358	–	0.000	0.758	–
14			0.493	7.001	9.983	–	0.457	–	0.001	1.854	–	0.000	2.073	–	0.000	0.330	–
15			0.502	7.004	9.983	–	0.131	–	0.001	0.463	–	0.000	0.592	–	0.000	0.088	–
16	Cu	Fe + Al	–	7.003	7.003	0.010	–	0.026	0.001	–	0.109	0.000	–	0.247	0.000	–	0.025
17			–	6.998	7.003	0.010	–	0.075	0.002	–	0.317	0.000	–	0.708	0.000	–	0.072
18			–	7.005	7.006	0.010	–	0.123	0.001	–	0.519	0.000	–	1.161	0.000	–	0.118
19			–	7.003	7.006	0.009	–	0.248	0.000	–	1.029	0.000	–	2.362	0.000	–	0.237
20			–	7.003	7.006	0.009	–	0.741	0.000	–	2.923	0.001	–	6.958	0.000	–	0.692
21			–	7.005	7.003	0.010	–	1.238	0.001	–	4.569	0.002	–	10.946	0.000	–	1.087
22	Sn	Fe + Al	–	7.000	6.999	0.010	–	0.034	0.000	–	0.050	0.000	–	0.424	0.000	–	0.033
23			–	7.001	6.997	0.010	–	0.069	0.000	–	0.110	0.000	–	0.826	0.000	–	0.066
24			–	7.002	7.001	0.010	–	0.135	0.000	–	0.222	0.000	–	1.589	0.000	–	0.127
25			–	7.002	6.999	0.011	–	0.204	0.000	–	0.340	0.000	–	2.435	0.000	–	0.194
26			–	6.997	6.998	0.010	–	0.273	0.000	–	0.460	0.000	–	3.260	0.000	–	0.260
27			–	7.004	6.996	0.010	–	0.339	0.000	–	0.581	0.000	–	3.820	0.000	–	0.308
28	Cu	Fe–Mn–Al	–	10.003	9.973	0.022	0.011	0.139	0.018	0.047	0.422	0.003	0.060	0.907	0.002	0.011	0.133
29			–	10.005	9.875	0.022	0.108	0.138	0.019	0.453	0.392	0.008	0.538	0.880	0.003	0.099	0.127
30			–	10.000	9.636	0.017	0.353	0.138	0.002	1.427	0.380	0.004	1.569	0.881	0.001	0.294	0.125
31			–	10.004	9.401	0.016	0.590	0.1385	0.001	2.459	0.379	0.005	2.500	0.879	0.001	0.481	0.124
32			–	10.000	9.967	0.022	0.011	0.352	0.024	0.046	1.043	0.005	0.058	2.387	0.003	0.010	0.343
33			–	10.001	9.951	0.021	0.033	0.353	0.010	0.137	1.060	0.000	0.183	2.421	0.001	0.032	0.347
34			–	10.003	9.901	0.053	0.108	0.353	0.137	0.465	0.990	0.043	0.582	2.340	0.018	0.104	0.332
35			–	10.005	9.654	0.048	0.354	0.352	0.113	1.547	0.984	0.032	1.817	2.279	0.014	0.331	0.323
36			–	10.004	9.464	0.048	0.594	0.353	0.131	2.757	0.974	0.039	2.954	2.318	0.016	0.556	0.324
37			–	10.007	9.822	0.029	0.360	0.132	0.033	1.557	0.390	0.009	1.779	0.888	0.004	0.331	0.127
38			–	10.004	9.794	0.029	0.615	0.132	0.006	2.556	0.359	0.000	2.715	0.893	0.001	0.522	0.124
39			–	9.999	9.969	0.022	0.022	0.353	0.019	0.081	1.061	0.004	0.099	2.344	0.002	0.018	0.340
40			–	10.003	9.951	0.025	0.033	0.352	0.039	0.142	1.053	0.010	0.179	2.371	0.005	0.032	0.342
41			–	10.002	9.930	0.029	0.054	0.353	0.049	0.233	0.995	0.011	0.303	2.368	0.006	0.053	0.336
42			0.503	10.002	9.808	0.020	1.429	0.353	0.002	5.441	0.915	0.001	5.302	2.283	0.000	1.064	0.318
43		Fe–Mn–Al + Fe	0.501	10.002	9.850	0.015	1.072	0.353	0.002	3.993	0.903	0.000	4.214	2.341	0.000	0.815	0.323
44			0.502	10.001	9.963	0.004	0.286	0.353	0.000	0.884	0.900	0.001	1.131	2.256	0.000	0.201	0.315
45	Sn	Fe–Mn–Al	0.301	7.000	6.861	0.014	1.000	0.339	0.002	5.312	0.610	0.000	4.907	3.636	0.000	0.708	0.296
46		Fe–Mn–Al + Fe	0.301	7.002	6.927	0.007	0.501	0.340	0.001	2.490	0.595	0.000	2.621	3.862	0.000	0.356	0.312
47			0.303	7.000	6.972	0.004	0.250	0.339	0.000	1.068	0.588	0.000	1.214	3.801	0.000	0.159	0.307
48		Fe–Mn + Fe	0.502	7.005	9.948	–	0.978	0.339	0.002	4.269	0.582	0.000	4.088	3.577	0.000	0.711	0.309
49			0.497	7.004	9.969	–	0.456	0.339	0.001	1.922	0.581	0.000	2.058	3.461	0.000	0.336	0.300
50			0.501	7.000	9.996	–	0.130	0.339	0.000	0.480	0.562	0.000	0.557	3.706	0.000	0.087	0.316

Fig. 2.

Schematic of the experimental apparatus and arrangement of materials. (Online version in color.)

3. Result and Discussions

3.1. Partitioning of Mn, Cu, and Sn between Molten Iron and Silver Phases

The experimental results are summarized in Table 1. “Calculated mass” is the total mass of the elements in both Fe and Ag phases after the experiments. It was found that the mass of Al was significantly decreased. In contrast, that of Mn was slightly decreased compared with “Initial mass”, which indicates that the reaction between Mn and alumina crucible was successfully suppressed. Because the Al content of the Ag phase was relatively low, in the range from 0.00 to 0.04 mass%, the effect of Al in the Ag phase was ignored in the following analysis. The partition ratios L of Mn, Cu, and Sn, which were defined as L_i = x_{i (in Ag)} / x_{i (in Fe)} (i: Mn, Cu, or Sn), were plotted in Figs. 3, 4, and 5 against x_{Mn (in Fe)}, x_{Cu (in Fe)} and x_{Sn (in Fe)}, respectively. The terms x_{i (in Fe)} and x_{i (in Ag)} are the mole fraction of element i in Fe and Ag phases, respectively. As shown in Figs. 3, 4, and 5, the partition ratio of Mn, Cu, or Sn deceased with increasing Mn, Cu, or Sn content in the Fe phase, respectively. When an element i in Fe(l) phase is equilibrated with that in Ag(l) phase, the activity relative to pure liquid in Fe(l) phase becomes equal to that in Ag(l) phase. This relationship is expressed as Eq. (1).   

$$ln{a}_{i\left(\text{in Fe}\right)}=ln{a}_{i\left(\text{in Ag}\right)}$$(1)

where a_{i(in Fe)} and a_{i(in Ag)} are the Raoultian activity of element i relative to pure liquid in Fe and Ag phases, respectively. In the Fe–M–Al–Ag system (M: Mn, Cu, and Sn), the activities of M in the Fe and Ag phases are expressed as follows:   

$$\begin{array}{l}ln{a}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}=ln{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}+ln{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ +{\rho }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^2+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\end{array}$$(2)

  

$$\begin{array}{l}ln{a}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}=ln{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}+ln{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ +{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\end{array}$$(3)

where ${\gamma }_{i\left(\text{in}\mathrm{\hspace{0.17em} }\alpha \right)}^{\text{o}}$ and ${\epsilon }_{i\left(\text{in}\mathrm{\hspace{0.17em} }\alpha \right)}^j$ are the activity coefficient of element i in the phase α (α: Fe(l) or Ag(l)) at infinite dilution, and the interaction coefficient of element j with i in the α phase, respectively. ${\rho }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}$ is the second-order self-interaction coefficient of the element M in Fe(l) phase. Only ${\rho }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ was considered in this work. Equation (4) is obtained from Eqs. (1), (2), (3).   

$$\begin{array}{l}ln\left(\frac{x_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)=ln\left(\frac{{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\rho }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^2\\ -{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ -{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\end{array}$$(4)

Fig. 3.

Concentration dependence of partition ratio of Mn between Fe(l) and Ag(l) phases at 1873 K.

Fig. 4.

Concentration dependence of partition ratio of Cu between Fe(l) and Ag(l) phases at 1873 K.

Fig. 5.

Concentration dependence of partition ratio of Sn between Fe(l) and Ag(l) phases at 1873 K.

The values of the interaction coefficients have been reported as follows: for Mn, ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}$ = 0.02¹⁹⁾ and ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}$ = 0.02.²⁰⁾ For Cu, ${\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ = −5.37¹⁹⁾ ${\rho }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ = 4.60,¹⁹⁾ ${\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}$, = −2.28.²¹⁾ For Sn, ${\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ = −0.29¹⁹⁾ and ${\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}$= 3.10.²²⁾ Equation (4) can be modified as Eq. (5).   

$$\begin{array}{l}ln\left(\frac{x_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)-{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\rho }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^2-{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ =-{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{M}}{x}_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ +\left\{ln\left(\frac{{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\right\}\end{array}$$(5)

The mutual solubilities in Fe–Ag binary system are reported to be x_{Ag(in Fe)} = 0.002 to 0.004 and x_{Fe(in Ag)} =0.006 to 0.017 at 1873 K.²³⁾ In a previous work by one of the authors in the Fe–Ag–Sn–M (M: Mo, B, Ni) system,¹⁴⁾ the solubility of Fe in Ag ranged from 0.002 to 0.017 and that of Ag in Fe from 0.003 to 0.004, which were almost the same values as those in Fe–Ag binary system, indicating that the Sn and M contents had no significant effect on the mutual solubilities in Fe–Ag system. These values are the saturated solubilities of Fe in the Ag phase and Ag in the Fe phase and are not considered to be significantly affected by small amounts of added element, i. Accordingly, in this work, the mole fractions of Fe in the Ag(l) phase (x_{Fe(in Ag)}) and Ag in Fe(l) phase (x_{Ag(in Fe)}) were assumed to be constant. Then, a linear relationship is expected when the left-hand side of Eq. (5) is plotted against x_{M(in Ag)}. The slope and the y-intercept corresponds to ${\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{M}}$ and $ln\left({\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}/{\gamma }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}\right)+{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}$, respectively. According to Eq. (5), the experimental results of the Fe–Mn–Al–Ag system (No. 1–15), Fe–Cu–Al–Ag system (No. 16–21), and Fe–Sn–Al–Ag system (No. 22–27), are plotted against x_{Mn(in Ag)}, x_{Cu(in Ag)} and x_{Sn(in Ag)}, respectively, in Figs. 6, 7, 8. In each figure, a linear relationship is found, and the following relationships were obtained from the linear approximation of the plots:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}=4.11\pm 0.40\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}=0.031\pm 0.003$$

  

$${\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-1.18\pm 0.07\text{,}\hspace{1em}{e}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-0.012\pm 0.001$$

  

$${\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=5.89\pm 1.62\text{,}\hspace{1em}{e}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=0.024\pm 0.006$$

  

$$\begin{array}{l}ln\left(\frac{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ =0.88\pm 0.017\end{array}$$

  

$$\begin{array}{l}ln\left(\frac{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ =1.47\pm 0.006\end{array}$$

  

$$\begin{array}{l}ln\left(\frac{{\gamma }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ =2.76\pm 0.035\end{array}$$

Fig. 6.

Determination of self-interaction coefficient of Mn in Ag(l) phase.

Fig. 7.

Determination of self-interaction coefficient of Cu in Ag(l) phase.

Fig. 8.

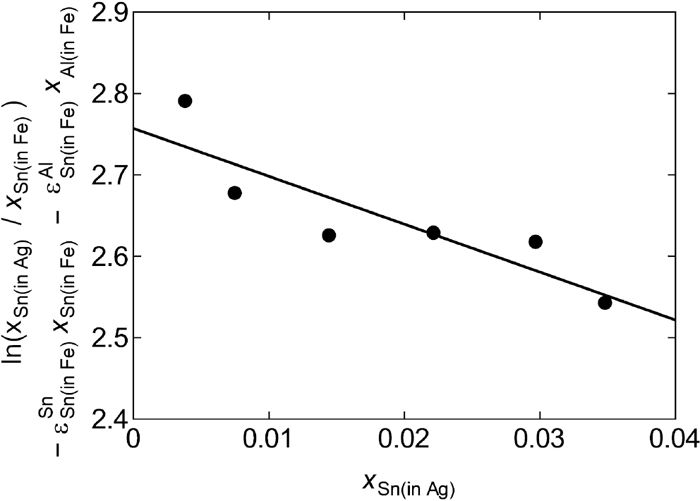
Determination of self-interaction coefficient of Sn in Ag(l) phase.

The interaction coefficients of the element j with i in the mass percent coordinates ($e_i^j$) are derived from those in the mole fraction coordinates (${\epsilon }_i^j$), using the following equation:   

$$e_{i\left(\text{in}\mathrm{\hspace{0.17em} }\alpha \right)}^j=\frac{1}{230}\left(\frac{M_{\alpha }}{M_j}{\epsilon }_{i\left(\mathrm{i}\mathrm{n}\mathrm{\hspace{0.17em} }\alpha \right)}^j+\frac{M_j-M_{\alpha }}{M_j}\right)$$(6)

where M_j, M_α (g/mol) are molar mass of the element j and the solvent α, respectively.

3.2. Interaction Coefficients of Cu and Sn with Mn

In the Fe–Mn–Cu–Al–Ag system, Eq. (4) is expressed as Eqs. (7) and (8) for Mn and Cu, respectively.   

$$\begin{array}{l}ln\left(\frac{x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)=ln\left(\frac{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ -{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ -{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\end{array}$$(7)

  

$$\begin{array}{l}ln\left(\frac{x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)=ln\left(\frac{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\rho }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^2\\ -{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ -{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\end{array}$$(8)

When R(Mn) and R(Cu) are defined as Eqs. (9) and (10), respectively, Eqs. (7) and (8) can be rearranged as Eqs. (11) and (12).   

$$\begin{array}{l}R\left(\text{Mn}\right)\equiv ln\left(\frac{x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)\\ -\left\{ln\left(\frac{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\right\}\\ -{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}-{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\end{array}$$(9)

  

$$\begin{array}{l}R\left(\text{Cu}\right)\equiv ln\left(\frac{x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)\\ -\left\{ln\left(\frac{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\right\}\\ -{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\rho }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^2+{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ -{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\end{array}$$(10)

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}=R\left(\text{Mn}\right)$$(11)

  

$${\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}=R\left(\text{Cu}\right)$$(12)

Because ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\alpha \right)}^{\text{Cu}}={\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\alpha \right)}^{\text{Mn}}$ (α: Fe or Ag), Eqs. (13) and (14) can be derived from Eqs. (11) and (12).   

$$\begin{array}{l}R\left(\text{Cu}\right)x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}-R\left(\text{Mn}\right)x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ ={\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}\left(x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\right)\end{array}$$(13)

  

$$\begin{array}{l}R\left(\text{Cu}\right)x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-R\left(\text{Mn}\right)x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ ={\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}\left(x_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\right)\end{array}$$(14)

Equations (13) and (14) expresses the linear relationship between the left-hand side of those equations and x_{Cu(in Ag)}x_{Mn(in Fe)}−x_{Mn(in Ag)}x_{Cu(in Fe)}, and the slopes correspond to ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ and ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}$, respectively. R(Mn) and R(Cu) were calculated by substituting the values obtained in section 3.1 into Eqs. (9) and (10). The relationship of Eqs. (13) and (14) were plotted in Figs. 9 and 10 from the experimental results of the Fe–Mn–Cu–Al–Ag system (No. 28–44). The interaction coefficients between Mn and Cu in Fe(l) and Ag(l) were determined respectively as follows:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-4.30\pm 0.78\text{,}\hspace{1em}{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-3.05\pm \mathrm{0.36.}$$

Fig. 9.

Determination of interaction coefficient of Cu with Mn in Fe(l) at 1873 K.

Fig. 10.

Determination of interaction coefficient of Cu with Mn in Ag(l) at 1873 K.

Similarly, in the Fe–Mn–Sn–Al–Ag system, R(Sn) was defined as Eq. (15), and Eqs. (16) and (17) were derived by replacing Cu with Sn in Eqs. (13) and (14).   

$$\begin{array}{l}R\left(\text{Sn}\right)\equiv ln\left(\frac{x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}}{x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}}\right)-\\ \left\{ln\left(\frac{{\gamma }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{o}}}{{\gamma }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{o}}}\right)+{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Ag}}{x}_{\text{Ag}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Fe}}{x}_{\text{Fe}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\right\}\\ -{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}{x}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}+{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}{x}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}-{\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Al}}{x}_{\text{Al}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\end{array}$$(15)

  

$$\begin{array}{l}R\left(\text{Sn}\right)x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}-R\left(\text{Mn}\right)x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}\\ ={\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}\left(x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\right)\end{array}$$(16)

  

$$\begin{array}{l}R\left(\text{Sn}\right)x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-R\left(\text{Mn}\right)x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\\ ={\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}\left(x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}\right)\end{array}$$(17)

Equations (16) and (17) expressed the linear relationship between the left-hand side of those equations and $x_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}-x_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}{x}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}$, and the slopes correspond to ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ and ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}$, respectively. R(Mn) and R(Sn) were calculated by substituting the values obtained in section 3.1 into Eqs. (9) and (15), and the relationship of Eqs. (16) and (17) were plotted in Figs. 11 and 12 from the experimental results of the Fe–Mn–Sn–Al–Ag system (No. 45–50). The interaction coefficients between Mn and Sn in Fe(l) and Ag(l) were determined as follows:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=-5.21\pm 0.55\text{,}\hspace{1em}{\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=-1.09\pm \mathrm{0.20.}$$

Fig. 11.

Determination of interaction coefficient of Sn with Mn in Fe(l) at 1873 K.

Fig. 12.

Determination of interaction coefficient of Sn with Mn in Ag(l) at 1873 K.

The interaction coefficients in the mole fraction coordinates were transformed to those in the mass percent coordinates, using Eq. (6). The derived values are summarized as follows:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-4.30\pm 0.78\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-0.016\pm 0.003$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-3.05\pm 0.36\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-0.026\pm 0.003$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=-5.21\pm 0.55\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=-0.008\pm 0.001$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=-1.09\pm 0.20\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=-0.004\pm 0.001$$

On the other hand, Eq. (18) can be derived for Fe-i-j ternary regular solution when the element i is dilute.^13,14,24)   

$${\epsilon }_{i\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^j=\text{ln}{\gamma }_{i\left(\text{in}\mathrm{\hspace{0.17em} }j\right)}^0-\text{ln}{\gamma }_{j\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0-\text{ln}{\gamma }_{i\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0$$(18)

The interaction coefficients of Cu and Sn with Mn in molten iron were calculated using Eq. (18) and were compared with the experimental values. The following values of activity coefficients are reported: ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0$ = 1.44 at 1843 K, ${\gamma }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0=$8.58 at 1873 K and ${\gamma }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0=$ 2.58 at 1873 K.¹⁹⁾ The activity coefficients of Mn in Cu and Sn were estimated to be ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Cu}\right)}^0$ = 0.70, ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Sn}\right)}^0=$0.80 at 1517 K from the activity data in molten Mn-Cu²⁵⁾ and Mn-Sn²⁶⁾ alloys. Assuming a regular solution, the values of the activity coefficients of Mn in Fe, Cu, and Sn were converted to those at 1873 K and were derived to be ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^0$ = 1.43, ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Cu}\right)}^0$ = 0.75, and ${\gamma }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Sn}\right)}^0$ = 0.83. Substituting these activity coefficients into Eq. (18), the interaction coefficients of Cu and Sn with Mn at 1873 K were estimated to be ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$=−2.8 and ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$=−1.5, respectively. Accordingly, in this work, it is found that the measured values of ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ and ${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ are more negative than those estimated from the regular solution model. The measured values are compared with the estimated ones in Fig. 13. The previous results summarized by one of the authors^13,14) are also shown in the figure. As a whole, it is found that the positive and negative signs of the estimated values reasonably agree with the measured ones. However, the absolute values are not exactly in agreement. Accordingly, it is not easy to estimate the interaction coefficients accurately, and it remains essential to measure those values by the equilibrium experiments.

Fig. 13.

Relationship between the measured ${\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ and ${\epsilon }_{\text{M}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ values at 1873 K and those derived from a regular solution model.

3.3. Thermodynamic Analysis of the Compositions of Hot Metal and Slag in the Ironmaking Process

3.3.1. Analysis Model

Using the analytical model developed in the previous work,¹⁵⁾ the effects of scrap ratio on hot metal and molten slag composition were thermodynamically analyzed considering the interaction coefficients $e_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ and $e_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ determined in this work. Taking the redox reaction of Mn as an example, the analysis model is described in this section. The reaction formula and equilibrium constant (K_Mn) of the redox reaction of Mn are expressed as Eqs. (19) and (20), respectively.   

$$\underset{\_}{\text{Mn}}+\underset{\_}{\text{O}}=\text{MnO}\left(\text{in}\mathrm{\hspace{0.17em} }\text{slag}\right)$$(19)

  

$$log{K}_{\text{Mn}}=log\frac{a_{\text{MnO}}}{a_{\text{Mn}}\times a_{\text{O}}}=12\mathrm{\hspace{0.17em} }760/T-5.62$$(20) ¹⁹⁾

where a_i (i: O, Mn) is the Henrian activity of i in molten iron relative to the infinite dilution and a_MnO is the activity of MnO relative to pure substance. The activity of O was calculated from the partial pressure of oxygen (P_O2) considering the equilibrium of Eq. (21).   

$$\frac{1}{2}{\text{O}}_2\left(\text{g}\right)=\underset{\_}{\text{O}}$$(21)

  

$$log{K}_{{\text{O}}_2}=log\frac{a_{\text{O}}}{P_{{\text{O}}_2}{}^{1/2}}=\frac{6\mathrm{\hspace{0.17em} }116}{T}+0.18$$(22) ¹⁹⁾

where K_O2 is the equilibrium constant of the reaction in Eq. (21). The activities of i (i: O, Mn) are expressed by Eq. (23), where f_i is the Henrian activity coefficient of i relative to the dilute solution in the mass percent coordinates.   

$$a_i=f_i\times {\left[\text{mass\%}i\right]}_{\text{in}\mathrm{\hspace{0.17em} }\text{Fe}}$$(23)

The activity coefficient of i is expressed by Eq. (24) using the interaction coefficients of the element i with j ($e_i^j$).   

$$log{f}_i={\sum }_{j\ne \text{Fe}}{e}_i^j{\left[\text{mass\%}j\right]}_{\text{in}\mathrm{\hspace{0.17em} }\text{Fe}}$$(24)

From the above equations, Eq. (25) is obtained for the equilibrium concentration of Mn.   

$$\begin{array}{l}log{\left[\text{mass\%Mn}\right]}_{\text{in}\mathrm{\hspace{0.17em} }\text{Fe}}+{\sum }_{j\ne \text{Fe}}{e}_{\text{Mn}}^j{\left[\text{mass\%}j\right]}_{\text{in}\mathrm{\hspace{0.17em} }\text{Fe}}\\ +\frac{1}{2}log{P}_{\text{O}2}+\text{log}{K}_{{\text{O}}_2}-log{a}_{\text{MnO}}+log{K}_{\text{Mn}}=0\end{array}$$(25)

By solving Eq. (25), the equilibrium concentration of Mn considering the interaction coefficients of Cu and Sn with Mn can be calculated.

Equations for the equilibrium concentrations of C, O, Si, S, P, and Fe in molten iron were obtained in the same method.¹⁵⁾ Furthermore, the mass conservation of Ca, Si, Al, Mg, Mn, Fe, S, P, Cu, Sn, Ni, and Cr were considered. For example, the mass conservation equation of Mn is expressed as Eq. (26).   

$$\begin{array}{l}{\left(\text{mass\%MnO}\right)}_{\text{in}\mathrm{\hspace{0.17em} }\text{slag}}\cdot W_{\text{slag}}+\frac{M_{\text{MnO}}}{M_{\text{Mn}}}{\left[\text{mass\%Mn}\right]}_{\text{in}\mathrm{\hspace{0.17em} }\text{Fe}}\\ \cdot W_{\text{hot}\mathrm{\hspace{0.17em} }\text{metal}}-W_{\text{MnO}\mathrm{\hspace{0.17em} }\text{total}}=0\end{array}$$(26)

where W_slag, W_metal, W_{j total}, and M_j denote the slag and hot metal masses and the total mass and molar mass of chemical component j, respectively. In addition, the total mass% concentration in each phase must be 100%. This relationship was also considered. A total of 21 equations were derived: seven equations for the equilibrium concentrations, 12 equations for the mass conservation, and 2 equations for the total mass% concentration. The variables are the concentrations of CaO, SiO₂, Al₂O₃, MgO, FeO, MnO, S, and P₂O₅ in the slag, and Fe, C, O, Si, Mn, S, P, Cu, Sn, Ni, and Cr in the hot metal, in addition to the masses of the slag and hot metal, in total 21. These nonlinear equations were simultaneously solved by a numerical method in this work. The equilibrium constants^19,27,28) used in the calculations are shown in Table 2. The solubility of C in Fe-C(l),²⁹⁾ the activity coefficients of C²⁸⁾ and Fe,³⁰⁾ the activities of oxides in slag,^{16,31,32,33,34)} and sulfide and phosphate capacities^35,36) are shown in Table 3. The interaction coefficients^13,14,19) are listed in Table 4. The values of which the temperature dependence was not reported were estimated from the values at the experimental temperature (T_exp.) by Eq. (27) assuming the regular solution.   

$$e_i^j\left(1\mathrm{\hspace{0.17em} }773\mathrm{\hspace{0.17em} }\text{K}\right)=\frac{T_{\text{exp}.}}{1\mathrm{\hspace{0.17em} }773}{e}_i^j\left(T_{\text{exp}.}\right)$$(27)

Table 2. Equilibrium constants used in this work.

$\underset{\_}{\text{C}}+\underset{\_}{\text{O}}=\text{CO}\left(\text{g}\right)$	$log{K}_{\mathrm{C}\mathrm{O}}=log\frac{a_{\mathrm{P}\mathrm{O}}}{a_{\mathrm{C}}\times a_{\mathrm{O}}}=\frac{1\mathrm{\hspace{0.17em} }168}{T}+2.07$	27)
$\mathrm{C}\left(\mathrm{s}\right)=\underset{\_}{\mathrm{C}}$ (carbon saturation)	$log{K}_{\text{C}}=log\frac{a_{\text{C}}}{a_{\text{C}\left(\text{s}\right)}}=\frac{1\mathrm{\hspace{0.17em} }180}{T}+2.20$	27)
$\underset{\_}{\text{Si}}+2\underset{\_}{\text{O}}={\text{SiO}}_2$ (in slag)	$log{K}_{\text{Si}}=log\frac{a_{\text{MnO}}}{a_{\text{Mn}}\times a_{\text{O}}}=\frac{30\mathrm{\hspace{0.17em} }110}{T}-11.40$	19)
$\underset{\_}{\text{Mn}}+\underset{\_}{\text{O}}=\text{MnO}$ (in slag)	$log{K}_{\text{Mn}}=log\frac{a_{\text{MnO}}}{a_{\text{Mn}}\times a_{\text{O}}}=\frac{12\mathrm{\hspace{0.17em} }760}{T}-5.62$	19)
$\text{Fe}\left(\text{l}\right)+\underset{\_}{\text{O}}=\text{FeO}$ (in slag)	$log{K}_{\text{Fe}}=log\frac{a_{\text{FeO}}}{a_{\text{Fe}}\times a_{\text{O}}}=\frac{6\mathrm{\hspace{0.17em} }150}{T}-2.604$	19)
$\frac{1}{2}{\text{O}}_2\left(\text{g}\right)=\underset{\_}{\text{O}}$	$log{K}_{{\text{O}}_2}=log\frac{a_{\text{O}}}{P_{{\text{O}}_2}^{1/2}}=\frac{6\mathrm{\hspace{0.17em} }116}{T}+0.18$	19)
$\frac{1}{2}{\text{S}}_2\left(\text{g}\right)=\underset{\_}{\text{S}}$	$log{K}_{\text{S}}=log\frac{a_{\text{O}}}{P_{\text{S}}^{1/2}}=\frac{6\mathrm{\hspace{0.17em} }535}{T}-0.964$	19)
$\frac{1}{2}{\text{P}}_2\left(\text{g}\right)=\underset{\_}{\text{P}}$	$log{K}_{{\text{P}}_2}=log\frac{a_{\text{O}}}{P_{{\text{P}}_2}^{1/2}}=\frac{8\mathrm{\hspace{0.17em} }236}{T}+0.28$	19)

Table 3. Thermodynamic data of activities and capacities used in this work.

Thermodynamic data	Reference
$log{x}_{\text{C}\mathrm{\hspace{0.17em} }\text{satd}.\left(\text{binary}\right)}=-12.728/T+0.727logT-3.049$	29)
$log{f}_{\text{C}}=\left(\frac{4\mathrm{\hspace{0.17em} }530}{T}\right)\left[T+4\cdot {10}^{-4}\left(T-1\mathrm{\hspace{0.17em} }770\right)\right]\left(2-x_{\text{C}}\right)\cdot x_{\text{C}}+log\left\{\left(M_{\text{Fe}}\left(1-x_{\text{C}}\right)+M_{\text{C}}{x}_{\text{C}}\right)/M_{\text{Fe}}\right\}$	28)
$log{\gamma }_{\text{Fe}}=\left(-1\mathrm{\hspace{0.17em} }700/T-0.36\right)\cdot {\left\{x_{\text{C}}\left(1-x_{\text{C}}\right)\right\}}^2$	30)
$a_{{\text{SiO}}_2}=4.634x_{{\text{SiO}}_2}{}^3-0.7552x_{{\text{SiO}}_2}{}^2$	32, 33)
$a_{\text{MnO}}=\left(\text{\%MnO}\right)\times \left\{5.9\left(\left(\text{\%CaO}\right)+1.4\left(\text{\%MgO}\right)\right)/\left({\text{\%SiO}}_2\right)+1.6\right\}\times {10}^{-3}$	16, 33)
$log{a}_{{\text{Fe}}_t\text{O}}=log{x}_{{\text{Fe}}_t\text{O}}+0.366\left(x_{\text{CaO}}+0.6x_{\text{MgO}}\right)/\left(x_{{\text{SiO}}_2}+1.8x_{{\text{Al}}_2{\text{O}}_3}\right)+1\mathrm{\hspace{0.17em} }748.5/T+0.921$	34)
$log{C}_{{\text{S}}^{2-}}=1.39\left(x_{\text{CaO}}+x_{\text{MgO}}/2\right)/\left(x_{{\text{SiO}}_2}+x_{{\text{Al}}_2{\text{O}}_3}/3\right)-6\mathrm{\hspace{0.17em} }911/T-1.649$	35)
$log{C}_{{\text{PO}}_4^{3-}}=2.60\left\{\left(\text{\%CaO}\right)+0.33\left(\text{\%MnO}\right)+0.55\left(\text{\%MgO}\right)-0.90\left({\text{\%Fe}}_t\text{O}\right)-0.77\left({\text{\%PO}}_{2.5}\right)\right\}/\left({\text{\%SiO}}_2\right)+40\mathrm{\hspace{0.17em} }400/T-6.48$	36)

Table 4. Interaction coefficients of elements in iron $e_i^j$ at 1773 K used in this work.

i	$e_i^{\text{C}}$	$e_i^{\text{O}}$	$e_i^{\text{Si}}$	$e_i^{\text{Mn}}$	$e_i^{\text{S}}$	$e_i^{\text{P}}$	$e_i^{\text{Cu}}$	$e_i^{\text{Sn}}$	$e_i^{\text{Ni}}$	$e_i^{\text{Cr}}$
C	0.000	0.000	0.029	−0.003	0.036	0.030	0.006	0.010	0.004	−0.005
O	−0.001	−1750/T +0.76	−0.070	−0.021	−0.141	0.074	−0.014	−0.012	0.006	−0.058
Si	0.061	−0.126	0.109	−0.015	0.070	0.095	0.0152	0.017	0.005	−0.0003
Mn	−0.030	−0.088	−1838/T +0.964	0.000	−0.049	−0.057	−0.017*	−0.009*	−0.008	0.0041
S	0.089	−0.285	0.077	−0.027	−120/T +0.018	0.036	−0.009	−0.005	0.000	−94.2/T +0.04
P	0.069	0.137	0.105	−0.030	0.035	0.057	−0.033	0.013	0.003	−0.019
Cu	0.015	−0.069	0.029	−0.019*	−0.022	−0.070	−0.021	−86.9/T +0.0336	−0.001413)	0.019
Sn	0.243	−0.116	0.059	−0.024*	−0.029	0.037	−162.4/T +0.0627	0.0018	−0.03014)	0.016
Ni	0.003	0.011	0.006	−0.008	−0.004	0.002	−0.000913)	−0.01214)	0.001	−0.0003
Cr	−0.037	−0.1997	−0.004	0.004	−0.020	−0.035	0.017	0.009	0.0002	−0.0003

_ : values in carbon saturated Fe(l) ($e_C^i$ were estimated from the influence of element i on the solubility of carbon in molten iron, $e_i^C$ were calculated from $e_C^i$ as $e_i^C=\frac{M_i}{M_C}{e}_C^i+\frac{1}{100\mathrm{\hspace{0.17em} }ln\mathrm{\hspace{0.17em} }10}\frac{M_C-M_i}{M_C}$)

*  : This work

3.3.2. Effect of Scrap Amount on the Compositions of Hot Metal and Slag

The raw materials data are needed for the analysis model described in section 3.3.1. The estimated compositions of the sinter, coke, and steel scraps are summarized in Table 5. The composition of the sinter reported by T. Natsui et al.³⁷⁾ was used in the calculation. The composition of coke was estimated from the values in the study of T. Yamamoto et al.¹⁰⁾ and the ash composition reported by T. Miyagawa.³⁸⁾ The composition of steel scrap was estimated from the analyzed values of C, Si, S, and P content of low carbon steel.³⁹⁾ In cases 1 and 2, only Cu or Sn was considered a tramp element to study its effect on the equilibrium compositions of slag and hot metal. The concentration of Cu or Sn was varied as 0.1, 0.5, 1, 5, and 10 mass%, respectively. In case 3, the contents of Cu, Sn, Ni, and Cr were estimated from the average concentrations in the steel bar investigated by I. Daigo et al.⁴⁰⁾ The scrap ratio (SR) was defined by Eq. (28).   

$$SR=\frac{{\left(\text{mass}\mathrm{\hspace{0.17em} }\text{of}\mathrm{\hspace{0.17em} }\text{Fe}\right)}_{\text{in}\mathrm{\hspace{0.17em} }\text{scrap}}}{{\left(\text{mass}\mathrm{\hspace{0.17em} }\text{of}\hspace{0.17em}\text{Fe}\right)}_{\text{in}\mathrm{\hspace{0.17em} }\text{sinter}}+{\left(\text{mass}\mathrm{\hspace{0.17em} }\text{of}\mathrm{\hspace{0.17em} }\text{Fe}\right)}_{\text{in}\mathrm{\hspace{0.17em} }\text{scrap}}}$$(28)

Table 5. Estimated composition of (a) sinter, (b) coke, and (c) steel scrap.

(a) sinter37) (mass%)
T. Fe	FeO	CaO	SiO2	Al2O3	MgO	MnO	S	PO2.5	CaO/SiO2
58.3	7.75	8.61	4.37	1.72	1.45	1.24	0.058	0.058	1.97

(b) coke10,38)
Ash (mass%)	Ash composition (mass%)
	SiO2	Al2O3	Fe2O3	CaO	MgO	PO2.5	S	Others
10.5	50.7	36	4.4	2.7	0.5	2.0	0.54	1.6

(c) steel scrap39,40) (mass%)
	C35)	Si35)	Mn35)	S35)	P35)	Cu	Sn	Ni	Cr	Fe
Case 1	0.043	0.012	0.19	0.007	0.015	0.1–10.0				balance
Case 2							0.1–10.0
Case 3						0.27836)	0.01736)	0.07236)	0.17536)

Firstly, the effect of Cu or Sn content of steel scrap on the partition ratio of Mn between slag and hot metal was discussed. The coke rate, temperature, and scrap rate were 420 kg/t-hot metal, 1773 K, and 0.5, respectively. Effects of Cu and Sn contents of steel scrap on the partition ratio of Mn between slag and hot metal ([mass%Mn] in hot metal/(mass%MnO) in slag) are shown in Figs. 14 and 15, respectively. The Mn partition ratio increased by increasing the contents of both Cu and Sn in the scrap. Because both of the interaction coefficients of Cu and Sn with Mn are negative, Cu and Sn decrease the activity of Mn in hot metal. Therefore, Cu or Sn enrichment in scrap increases the Mn concentration in hot metal because MnO in the slag is more easily reduced. This result indicates that the partial pressure of oxygen estimated from the Mn partition ratio becomes higher than the hot metal excluding Cu and Sn. In addition, because the absolute value of $e_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}$ is larger than $e_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}$ in the interaction coefficient, the effect of Sn on Mn concentration is small when Cu and Sn have the same concentration.

Fig. 14.

Effect of Cu content of steel scrap on partition ratio of Mn between slag and hot metal. (Online version in color.)

Fig. 15.

Effect of Sn content of steel scrap on partition ratio of Mn between slag and hot metal. (Online version in color.)

Secondly, the coke rate was determined to be 420 kg/t-hot metal, and SR was varied from 0 to 0.5 at 0.1 intervals. The effect of SR on hot metal and molten slag composition was analyzed at P_O2 ranging from 10⁻¹⁶ to 10⁻¹⁰ atm at 1773 K. Figure 16 shows the effect of SR on the equilibrium concentrations of MnO and Mn in slag and hot metal, respectively. The Mn contents are represented by bold lines along the vertical axis on the left, and those of MnO are represented by thin lines along the vertical axis on the right. As P_O2 was increased, Mn content of hot metal was decreased, and MnO content of slag was increased due to the oxidation as can be seen in Fig. 16. When SR is increased, Cu and Sn contents of hot metal increase, leading to the increase in Mn content because the values of the interaction coefficients of Cu with Mn and Sn with Mn are negative. However, the input amount of MnO is decreased with increasing the SR because the Mn content of the sinter is higher than that of steel scrap. Therefore, it was found that the concentrations of both MnO in slag and Mn in hot metal decreased as SR increased.

Fig. 16.

Effect of scrap ratios on the equilibrium concentration of MnO in slag and Mn in hot metal at P_O2 ranging from 10⁻¹⁶ to 10⁻¹⁰ atm at 1773 K. (Online version in color.)

4. Conclusions

Interaction coefficients of Cu and Sn with Mn were measured at 1873 K by a chemical equilibration technique using the liquid immiscibility of Fe and Ag. Furthermore, the effects of the scrap ratio on the compositions of the hot metal and slag were thermodynamically analyzed, considering the interaction coefficients measured in this work. The conclusions are summarized as follows:

(1) The self-interaction coefficients of Mn, Cu, and Sn in the Ag phase at 1873 K were determined as follows:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Mn}}=4.11\pm 0.40\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Mn}}=0.031\pm 0.003$$

  

$${\epsilon }_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-1.18\pm 0.07\text{,}\hspace{1em}{e}_{\text{Cu}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-0.012\pm 0.001$$

  

$${\epsilon }_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=5.89\pm 1.62\text{,}\hspace{1em}{e}_{\text{Sn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=0.024\pm 0.006$$

(2) The interaction coefficients of Cu and Sn with Mn in Fe(l) and Ag(l) phases at 1873 K were obtained as follows:   

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-4.30\pm 0.78\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Cu}}=-0.016\pm 0.003$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-3.05\pm 0.36\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Cu}}=-0.026\pm 0.003$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=-5.21\pm 0.55\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Fe}\right)}^{\text{Sn}}=-0.008\pm 0.001$$

  

$${\epsilon }_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=-1.09\pm 0.20\text{,}\hspace{1em}{e}_{\text{Mn}\left(\text{in}\mathrm{\hspace{0.17em} }\text{Ag}\right)}^{\text{Sn}}=-0.004\pm 0.001$$

(3) When the mass ratio of the scrap in the iron source increases, the Cu content of hot metal increases, leading to the increase in the Mn content because the value of the interaction coefficients of Cu and Sn with Mn is negative. However, the input amount of MnO is decreased with increasing the mass ratio of scrap because the Mn content of the sinter is higher than that of steel scrap. Therefore, it was found that the concentrations of both MnO in slag and Mn in hot metal decreased as the mass ratio of scrap was increased.

Acknowledgments

This study was supported by JSPS KAKENHI Grant Numbers JP20JI0432 and JP18H03405.

References

• 1)   T.  Murakami: Bull. Iron Steel Inst. Jpn., 22 (2017), 621 (in Japanese).
• 2)   T.  Maeda,  M.  Matsuo,  K.  Ohno and  K.  Kunitomo: Tetsu-to-Hagané, 103 (2017), 238 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2016-073
• 3)  The Japan Ferrous Raw Materials Association: Accumulated quantity estimation of Japan, http://tetsugen.or.jp/kiso/5chikujapan.htm, (accessed 2021-05-22) (in Japanese).
• 4)  The Japan Ferrous Raw Materials Association: Pig iron, Iron and steel scrap supply and demand (Fiscal year), http://tetsugen.or.jp/kiso/3jyukyu1nendo.htm, (accessed 2021-05-22) (in Japanese).
• 5)  The Japan Iron and Steel Federation: JISF long-term vision for climate change mitigation, a challenge towards zero-carbon steel (rev. in 2019), https://www.jisf.or.jp/en/activity/climate/documents/JISFLong-termvisionforclimatechangemitigation_text.pdf, (accessed 2022-3-10).
• 6)   K.  Kato and  H.  Ono: J. Jpn. Soc. Exp. Mech., 22 (2022), 4 (in Japanese). https://doi.org/10.11395/jjsem.22.4
• 7)   K.  Suzuki,  K.  Hayashi,  K.  Kuribara,  T.  Nakagaki and  S.  Kasahara: ISIJ Int., 55 (2015), 340. https://doi.org/10.2355/isijinternational.55.340
• 8)   K.  Hayashi,  S.  Kasahara,  K.  Kuribara,  T.  Nakagaki,  X. L.  Yan,  Y.  Inagaki and  M.  Ogawa: ISIJ Int., 55 (2015), 348. https://doi.org/10.2355/isijinternational.55.348
• 9)   S.  Hisashige,  T.  Nakagaki and  T.  Yamamoto: ISIJ Int., 59 (2019), 598. https://doi.org/10.2355/isijinternational.ISIJINT-2018-355
• 10)   T.  Yamamoto,  Y.  Ujisawa,  H.  Ishida and  K.  Takatani: ISIJ Int., 39 (1999), 705. https://doi.org/10.2355/isijinternational.39.705
• 11)   I.  Daigo,  K.  Tajima,  H.  Hayashi,  D.  Panasiuk,  K.  Takeyama,  H.  Ono,  Y.  Kobayashi,  K.  Nakajima and  T.  Hoshino: ISIJ Int., 61 (2021), 498. https://doi.org/10.2355/isijinternational.ISIJINT-2020-377
• 12)   H.  Ono and  M.  Nakamoto: Bull. Iron Steel Inst. Jpn., 23 (2018), 253.
• 13)   H.  Ono,  T.  Maeda and  H.  Konishi: Tetsu-to-Hagané, 104 (2018), 121 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2017-068
• 14)   H.  Ono, H. O and S. Fujiwara: Tetsu-to-Hagané, 105 (2019), 363 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2018-119
• 15)   K.  Kato and  H.  Ono: ISIJ Int., 61 (2021), 2979. https://doi.org/10.2355/isijinternational.ISIJINT-2021-281
• 16)   N.  Tsuchiya,  S.  Taguchi,  Y.  Takada and  K.  Okabe: Tetsu-to-Hagané, 63 (1977), 1791 (in Japanese). https://doi.org/10.2355/tetsutohagane1955.63.12_1791
• 17)   T.  Orimoto: Nippon Steel Tech. Rep., 123 (2020), 119.
• 18)   H.  Ono,  T.  Miki and  M.  Nakamoto: Tetsu-to-Hagané, 105 (2019), 344 (in Japanese). https://doi.org/10.2355/tetsutohagane.TETSU-2018-148
• 19)  The Japan Society for the Promotion of Science, The 19th Committee on Steelmaking: Steelmaking Data Sourcebook, Gordon and Breach Science Publishers, New York, (1988), 35, 39, 111, 125, 145, 273.
• 20)   M.-K.  Paek,  J.-M.  Jang,  M.  Jiang and  J.-J.  Pak: ISIJ Int., 53 (2013), 973. https://doi.org/10.2355/isijinternational.53.973
• 21)   K.  Sugiyama,  S.  Ueda,  X.  Gao,  S.  Kim and  S.  Kitamura: ISIJ Int., 57 (2017), 625. https://doi.org/10.2355/isijinternational.ISIJINT-2016-676
• 22)   K.  Sugiyama,  S.  Ueda,  X.  Gao,  S.  Kim and  S.  Kitamura: ISIJ Int., 60 (2020), 2147. https://doi.org/10.2355/isijinternational.ISIJINT-2019-550
• 23)   L. J.  Swartzendruber: Bull. Alloy Phase Diagr., 5 (1984), 560. https://doi.org/10.1007/BF02868316
• 24)   K.  Hori,  K.  Kato and  H.  Ono: ISIJ Int., 62 (2022), 405. https://doi.org/10.2355/isijinternational.ISIJINT-2021-395
• 25)   P. J.  Spencer and  J. N.  Pratt: Trans. Faraday Soc., 64 (1968), 1470. https://doi.org/10.1039/TF9686401470
• 26)   P. J.  Spencer and  J. N.  Pratt: Trans. Metall. Soc. AIME, 242 (1968), 1709.
• 27)   T.  Fuwa and  J.  Chipman: Trans. AIME, 218 (1960), 887.
• 28)   A.  Rist and  J.  Chipman: Rev. Metall., 53 (1956), 796. https://doi.org/10.1051/metal/195653100796
• 29)   F.  Neumann and  H.  Schenck: Arch. Eisenhüttenwes., 30 (1959), 477. https://doi.org/10.1002/srin.195903065
• 30)   J.  Chipman: Metall. Trans., 1 (1970), 2163. https://doi.org/10.1007/BF02643430
• 31)   D. A. R.  Kay and  J.  Taylor: J. Iron Steel Inst., 201 (1963), 67.
• 32)   K.  Tamura,  K.  Ono and  N.  Nishida: Tetsu-to-Hagané, 67 (1981), 2635 (in Japanese). https://doi.org/10.2355/tetsutohagane1955.67.16_2635
• 33)   K. P.  Abraham,  M. W.  Davies and  F. D.  Richardson: J. Iron Steel Inst., 196 (1960), 82.
• 34)   T.  Arato,  M.  Tokuda and  M.  Ohtani: Tetsu-to-Hagané, 68 (1982), 2263 (in Japanese). https://doi.org/10.2355/tetsutohagane1955.68.15_2263
• 35)   A. S.  Venkatradi and  H. B.  Bell: J. Iron Steel Inst., 207 (1969), 1110.
• 36)   A.  Sobandi,  H. G.  Katayama and  T.  Momono: ISIJ Int., 38 (1998), 781. https://doi.org/10.2355/isijinternational.38.781
• 37)   T.  Natsui,  K.  Nakano,  Y.  Matsukura,  K.  Sunahara,  Y.  Ujisawa and  T.  Inada: Tetsu-to-Hagané, 99 (2013), 267 (in Japanese). https://doi.org/10.2355/tetsutohagane.99.267
• 38)   T.  Miyagawa: J. Fuel Soc. Jpn., 58 (1979), 940 (in Japanese). https://doi.org/10.3775/jie.58.11_940
• 39)   I.  Saeki,  T.  Ikeda,  K.  Ohno,  T.  Sato and  S.  Kurosawa: Tetsu-to-Hagané, 97 (2011), 12 (in Japanese). https://doi.org/10.2355/tetsutohagane.97.12
• 40)   I.  Daigo and  Y.  Goto: Tetsu-to-Hagané, 100 (2014), 756 (in Japanese). https://doi.org/10.2355/tetsutohagane.100.756