Experiment and Conformation of Non-sinusoidal Oscillation Waveform Function for Continuous Casting Mold

Abstract

Mold oscillation is a key technology of steel continuous casting. Sinusoidal oscillation and non-sinusoidal oscillation are widely used in actual production. Non-sinusoidal oscillation has many advantages compared with the sinusoidal oscillation, such as it can reduce the depth of oscillation mark, and make slab demoulding easily. But the maximum acceleration of non-sinusoidal oscillation is higher, which will result in the larger inertia force, influence on the service life and running smoothly of the oscillator. The modification ratio of the non-sinusoidal oscillation is bigger, the impact and noise of the oscillator are more serious especially when the mold arrives at the top and bottom position. To control the maximum acceleration of the non-sinusoidal oscillation waveform, a novel waveform function with three sections was proposed. And the displacement, velocity and acceleration curves were continuous and smooth, which had no rigid and flexible impact. Thus, it had good dynamic characteristics and realized the switching between the sinusoidal and the non-sinusoidal oscillation. Then the proposed oscillation waveform function was realized by a mechanical oscillator with double servomotors arranged symmetry. Meanwhile, the angular speed of the servomotor to realize the oscillation waveform was presented and the tested curves were obtained by the experiment. The experiment results show that the oscillation waveform can be realized well, the vertical maximum acceleration of the proposed function is reduced by 13.6%, which is helpful to reduce the inertia force, enhance the motion stability and prolong the service life of the oscillator.

1. Introduction

Mold sinusoidal oscillation can effectively improve the slab surface quality, and the advance methods are high frequency and small amplitude. However, the high frequency reduces the oscillation period, while the negative strip time is shortened, the positive strip time is also restricted. In contrast, mold non-sinusoidal oscillation can reduce the negative strip time and increase the positive strip time which is useful to reduce the depth of the oscillation mark, increase the consumption of the slab slag, reduce the friction force and improve the lubrication environment between the mold and the slab. Meanwhile, the larger negative strip distance is helpful to remove the slab from the mold strongly and the smaller positive strip velocity reduces the slab shell tensile stress of mold meniscus. Thus, non-sinusoidal oscillation is regarded as the best oscillation mode.^1,2,3,4,5)

The core of the non-sinusoidal oscillation is the waveform function, which have two types of entirety and section. Suzuki⁶⁾ and Kang et al.⁷⁾ proposed the entirety oscillation waveforms, which were composed of the sine functions. Zhang et al.^8,9,10) proposed the composite entirety oscillation waveform, which was constructed by the composition of two sine functions and realized by the oscillator of double eccentric shafts. Li,^11,12) Ren^13,14) and Liu et al.^15,16,17) proposed the entirety oscillation waveforms realized by the non-circular gears. Ma^18,19) and Hong et al.,^20,21) proposed the entirety oscillation waveform function of Fourier expansion. Although the entirety oscillation waveform functions have good dynamic characteristics, it is difficult to construct and the modification ratio has the limitation value against the slab surface improvement further. To extend the range of the modification ratio for meeting various kinds of steel, enhance the casting speed and improve the slab surface quality, the section functions had been presented. Li et al.²²⁾ proposed the five section functions, the curves of the displacement, velocity and acceleration were smooth and continuous, which had good dynamic characteristics. However, the maximum acceleration was larger, which would result the bigger inertia force of the oscillator and influence the movement stability. Meng,^23,24) Sun²⁵⁾ and Zhang et al.²⁶⁾ also determined the five section functions, and the acceleration curves had the inflecting points, which was unhelpful to run smoothly for the oscillator. Zhang et al.^27,28) proposed the seven section functions, which aimed at reducing the maximum acceleration, but the parameters were too many and it was inconvenient to control and optimization. Zhou et al.^29,30) also proposed the seven section functions. Although the structure was simple and the maximum acceleration was lower, the acceleration curves had the inflecting points, which were unhelpful for the oscillator running smoothly.

In brief, the maximum acceleration values of the above mentioned oscillation waveform functions are larger. To reduce the maximum acceleration and ensure the acceleration cure smooth, a new non-sinusoidal oscillation waveform function with three sections is constructed, which is simple, has good dynamic characteristics and large range of parameters changed. And the modification ratio of non-sinusoidal oscillation is zero, the sinusoidal oscillation is realized.

2. Oscillation Waveform Function Analysis

2.1. Sinusoidal Oscillation Waveform Function

The sinusoidal oscillation is widely used and is convenient to be realized. Its functions are expressed as follows.

The displacement function is

  

$$s_z=hsin(2\pi ft)$$(1)

The velocity function is

  

$$v_z=2\pi fhcos\left(2\pi ft\right)$$(2)

The acceleration function is

  

$$a_z=-4{\pi }^2{f}^{2}hsin\left(2\pi ft\right)$$(3)

where h is amplitude, mm, t is time, s, f is oscillation frequency, Hz, s_z, v_z, a_z are the displacement, velocity and acceleration of sinusoidal oscillation respectively, mm, mm/s, mm/s².

The displacement and velocity curves of different oscillation modes are shown in Fig. 1. From Fig. 1(a), it can be seen that the peak time of non-sinusoidal oscillation waveform lags behind the sinusoidal oscillation waveform in the front half a period. Thus the modification ratio of non-sinusoidal oscillation waveform is defined as

  

$$\alpha =\frac{4t_z}{T}$$(4)

where α is modification ratio of non-sinusoidal oscillation, t_z is time-delay, s, T is oscillation period, s, f = 1/T.

Fig. 1. Waveform curves of different oscillation modes (a) Displacement curve (b) Velocity curve. (Online version in color.)

2.2. Non-sinusoidal Oscillation Waveform Function Construction

When the mold reaches the top or the bottom, the maximum acceleration will result the reversing impact and noise because of the inertia force. The time zones of the maximum acceleration are nearby t_C and t_E. To reduce the maximum acceleration and based on the best oscillation mode of the mold, a smooth curve (BCDEF) was designed into the piecewise oscillation waveform function which was constructed with three sections. It is easy to control and has the larger ranges of parameters changed. And the velocity curve is smooth and continuous, shown in Fig. 1(b), where the AB and FG are straight lines, BCDEF is cosine. The waveform functions can be expressed as follows.

The velocity function is

  

$$v=\{\begin{array}{ll}{v}_B\hfill & 0\le t\le t_B\hfill \\ -mcos\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]-m+v_B\hfill & t_B\le t\le t_F\hfill \\ v_B\hfill & t_F\le t\le T\hfill \end{array}$$(5)

where $t_C=\frac{1+\alpha }{4f}$, $t_F=\frac{1}{f}-t_B$, k ≥ 1. The parameters of k, v_B and m will be solved, the solution process is as follows.

When the mold moves form the time 0 to t_C, the displacement is h, then

  

$${\int }_0^{t_B}{v}_{B}dt+{\int }_{t_B}^{t_C}\left\{-mcos\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]-m+v_B\right\}dt=h$$(6)

To process

  

$$-\frac{msin\left[2\pi kf\left(t_C-\frac{1}{2f}\right)\right]}{2\pi kf}+\left(v_B-m\right)t_C+m{t}_B=h$$(7)

When the mold moves from the time t_C to $\frac{1}{2f}$, the displacement is −h, it yields

  

$${\int }_{t_C}^{\frac{1}{2f}}\left\{-mcos\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]-m+v_B\right\}dt=-h$$(8)

Further calculation

  

$$\frac{\left(v_B-m\right)}{2f}+\frac{msin\left[2\pi kf\left(t_C-\frac{1}{2f}\right)\right]}{2\pi kf}-\left(v_B-m\right)t_C=-h$$(9)

Considering the Eqs. (7) and (9), thus the implicit equation of k is obtained as

  

$$kcos\left[\frac{k\pi \left(\alpha -1\right)}{2}\right]+k=1$$(10)

When the mold arrives at the point C, the velocity is 0, then

  

$$-mcos\left[2\pi kf\left(t_C-\frac{1}{2f}\right)\right]-m+v_B=0$$(11)

  

$$v_B=mcos\left[\frac{k\pi \left(\alpha -1\right)}{2}\right]+m$$(12)

Submitting the Eq. (12) into the Eq. (7), it has

  

$$m=\frac{4\pi kfh}{\pi k(\alpha -1)cos\left[\frac{k\pi (\alpha -1)}{2}\right]-2sin\left[\frac{k\pi (\alpha -1)}{2}\right]}$$(13)

The displacement function is

  

$$s=\{\begin{array}{ll}{v}_{B}t\hfill & 0\le t\le t_B\hfill \\ \frac{-msin\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]}{2\pi kf}+\left(v_B-m\right)t+c_1\hfill & t_B\le t\le t_F\hfill \\ v_B\left(t-\frac{1}{f}\right)\hfill & t_F\le t\le T\hfill \end{array}$$(14)

where c₁ will be calculated, the calculation process is as follows.

When the mold moves at the time t_B, the displacement function is continuous for the Eq. (14), thereby

  

$$v_B{t}_B=\frac{-msin\left[2\pi kf\left(t_B-\frac{1}{2f}\right)\right]}{2\pi kf}+\left(v_B-m\right)t_B+c_1$$(15)

  

$$c_1=m{t}_B$$(16)

The acceleration function is

  

$$a=\{\begin{array}{ll}0\hfill & \mathrm{\hspace{0.17em} }0\le t\le t_B\hfill \\ 2\pi kfmsin\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]\hfill & t_B\le t\le t_F\hfill \\ 0\hfill & t_F\le t\le T\hfill \end{array}$$(17)

where s, v and a are the displacement, velocity and acceleration of non-sinusoidal oscillation, mm, mm/s, mm/s², m and k are waveform coefficients. v_B is the velocity of point B, t, t_B, t_C, t_F are time, s, f is oscillation frequency, Hz, h is amplitude, mm, α is modification ratio of non-sinusoidal oscillation.

When the modification ratio is different values, the three section functions curves of non-sinusoidal oscillation waveform are shown in Fig. 2 with h = 6 mm, f = 2 Hz. Where α is 0, the non-sinusoidal oscillation is switched to the sinusoidal oscillation. It can be seen from the Fig. 2 that the displacement, velocity and acceleration curves are smooth and continuous, which have no rigid and flexible impact, are helpful to move smoothly for the mold oscillator. Compared with the oscillation waveform of the proposed and the five section functions, shown in Fig. 3, it can be seen from Fig. 3 that the maximum acceleration of the proposed is smaller with the parameters of h=6 mm, α=20%, f=2 Hz, which can effectively reduce the inertia force, the impact and the noise of the oscillator, increase the stability of movement, especially when the mold arrives at the top and bottom.

Fig. 2. Non-sinusoidal oscillation waveforms of three section functions (a) Displacement curves (b) Velocity curves (c) Acceleration curves. (Online version in color.)

Fig. 3. Acceleration curves of three and five section functions. (Online version in color.)

3. Non-sinusoidal Oscillator and Rotate Rules of Servomotor

An oscillator driven by double servomotors is used to realize the non-sinusoidal oscillation waveform, shown in Fig. 4, which can make the parameters of modification ratio and oscillation frequency adjusted on line. And the amplitude is also changed with the oscillator stop. To exhibit the working principle of mold oscillator more clearly, based on the structural symmetry of the oscillation system, half a model of the oscillation table driven by the eccentric shaft through the linkage is presented in Fig. 5.

Fig. 4. Mold non-sinusoidal oscillator. (Online version in color.)

Fig. 5. Sketch of oscillating table driven by the eccentric shaft.

From Fig. 5, it is obtained that the vertical displacement of the point A for the eccentric shaft is expressed as

  

$$s_A=\delta sin({\omega }_{p}t)$$(18)

where δ, ω_p are the eccentricity and the angular speed of the eccentric shaft respectively, mm, rad/s, s_A is the vertical displacement of the point A, mm.

It also can be seen from Fig. 5 that the vertical displacement of the point B can be considered the similar as the point A. Because the linkage length of AB is far longer than the eccentric distance OA. Thus considering the Eqs. (10) and (14), the eccentric shaft angular speed can be determined as

  

$${\omega }_p=\frac{v}{\sqrt{{\delta }^2-s^2}}$$(19)

Since the eccentric shaft connects with the servomotor through the reducer and coupling, according to the transmission rule of the oscillation system, the angular speed ω of the servomotor continuously rotating in a single direction is expressed as

  

$$\begin{array}{l}\omega =\\ \{\begin{array}{ll}\frac{i{v}_B}{\sqrt{h^2-{(v_{B}t)}^2}}\hfill & 0\le t\le t_B\hfill \\ \left|\frac{i\left\{-mcos\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]-m+v_B\right\}}{\sqrt{h^2-{\left\{-\frac{m}{2\pi kf}sin\left[2\pi kf\left(t-\frac{1}{2f}\right)\right]+(v_B-m)t+c_1\right\}}^2}}\right|\hfill & t_B\le t\le t_F\hfill \\ \frac{i{v}_B}{{\sqrt{h^2-\left[v_B\left(t-\frac{1}{f}\right)\right]}}^2}\hfill & t_F\le t\le T\hfill \end{array}\end{array}$$(20)

where i is the transmission ratio of planet reducer, i=7.

When the modification ratios of the non-sinusoidal oscillation waveform are different constants, the angular speed curves of the servomotor are shown in Fig. 6 with oscillation frequency equaling 2 Hz. From Fig. 6, it can be seen that the angular speed curves of the servomotor are continuous and smooth. The three section functions of non-sinusoidal oscillation waveform can be realized as the servomotor rotates according to the Eq. (20). If the parameters of oscillation frequency and modification ratio are changed, the angular speed of the servomotor should be calculated again. Then the oscillation waveform with parameters modified can be realized.

Fig. 6. Angular speed curves of the servomotor. (Online version in color.)

4. Non-sinusoidal Oscillator Experiment and Results

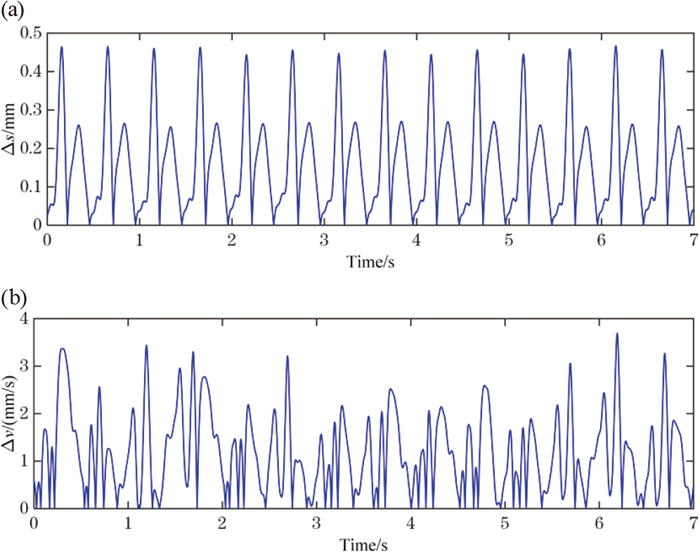
The oscillation table driven by double servomotors moves in a single direction. To demonstrate the oscillation waveform realized well and the feasibility of the oscillator, the oscillation parameters of two sides were measured. And the oscillation waveform cures were tested by using the sensors of displacement, velocity and acceleration with the parameters of h=6 mm, f=2 Hz, α=20%, shown in Fig. 7. From Fig. 7, it can be seen that the curves of left and right for the displacement, velocity and acceleration are essentially in agreement, so the proposed oscillation waveform can be achieved well. To exhibit the consistence of both sides oscillation curves precision and the effectiveness of the experimental oscillator, the displacement and velocity error of left and right are shown in Fig. 8. And the maximum displacement and velocity error are less than 0.5 mm and 4 mm/s, which are caused by the error of mechanical process and the control accuracy of electrical components. If the both aspects are improved, the curve accuracy will be improved. The acceleration curves of different directions were tested, shown in Fig. 9. The acceleration value of the horizontal direction along the leaf spring is close to 0. The acceleration at transverse direction to the leaf spring is reduced by 71.4% compared with Ref [11], shown in Fig. 9(a). From Fig. 9(b), it can be seen that the maximum acceleration of the three section functions in the vertical direction is evidently lower than the Ref [11], which can enhance the movement smoothness and reduce the inertia force of the oscillator. Thus the proposed oscillation waveform function is effective to cope with the reversing impact of the oscillator and has broad application prospects.

Fig. 7. Oscillation waveforms tested of piecewise functions (a) Displacement curves (b) Velocity curves (c) Acceleration curves. (Online version in color.)

Fig. 8. Curve errors (a) Displacement error (b) Velocity error. (Online version in color.)

Fig. 9. Acceleration curves of different directions (a) Horizontally perpendicular to the leaf spring direction (b) Vertical direction. (Online version in color.)

5. Conclusions

A novel non-sinusoidal oscillation waveform function is constructed with the maximum acceleration considered to handle the reversing impact of the oscillator. The waveform function consists of three sections. At the connection points of each two sections the displacement, velocity and acceleration curves are smooth and continuous. So it has no rigid and flexible impact. Besides, the maximum acceleration is lower, which can reduce the inertia force of the mold moving at the top and bottom, increase the running smoothness of the oscillator. The proposed oscillation waveform function was realized on the mechanical prototype driven by servomotors in the laboratory. The experimental results show that the oscillation waveform tested is in agreement with the theory oscillation waveform. So the servomotor angular speed curves given in this paper is accurate. And at the transverse direction and the vertical direction of the leaf spring, the tested accelerations of the proposed function are reduced by 71.4% and 13.6% than that of reference [11] respectively. During the experiment, it could be found that the reversing impact and noise were lower. So the oscillation waveform function could prolong the service life and enhance the movement stability of the oscillator.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors are especially grateful to the announce reviewer, whose advice will be helpful to the paper. Meanwhile, the authors also thank the Hebei Provincial Natural Science Foundation of China (Granted No. E2020203128, F2020203105), Hebei Provincial Education Department Higher Education Science and Technology Program (NATURAL SCIENCE) (Granted No. ZD2021106, ZD2022012), Central Government Guided Local Science and Technology Development Fund Project (Granted No. 236Z1601G), Key Research and Development (R&D) Plan of Hebei Province (Granted No. 21327102D), Science and Technology Program of Qinhuangdao (Granted No. 202301A316).

References

• 1)   L. P.  Zhang,  X. K.  Li,  Y. F.  Yao and  L. D.  Yang: Ironmak. Steelmak., 37 (2010), 204. https://doi.org/10.1179/030192309X12573371383677
• 2)   Z.  Ma,  Y. M.  Fang,  J. X.  Li,  L.  Liu and  Q.  Li: ISIJ Int., 60 (2020), 628. https://doi.org/10.2355/isijinternational.ISIJINT-2019-342
• 3)   Y. F.  Yao,  J. X.  Li and  Y. M.  Fang: Chin. J. Mech. Eng., 28 (2015), 1269. https://doi.org/10.3901/CJME.2015.0714.093
• 4)   J.  Yang,  X. N.  Meng and  M. Y.  Zhu: ISIJ Int., 58 (2018), 2071. https://doi.org/10.2355/isijinternational.ISIJINT-2018-169
• 5)   W. L.  Wang,  X. K.  Long,  H. H.  Zhang and  P. S.  Lyu: ISIJ Int., 58 (2018), 1695. https://doi.org/10.2355/isijinternational.ISIJINT-2018-275
• 6)   M.  Suzuki,  H.  Mizukami,  T.  Kitagawa,  K.  Kawakami,  S.  Uchida and  Y.  Komatsu: ISIJ Int., 31 (1991), 254. https://doi.org/10.2355/isijinternational.31.254
• 7)   G. P.  Kang,  G.  Shin and  C. G.  Kang: J. Mech. Sci. Technol., 21 (2007), 421. https://doi.org/10.1007/BF02916303
• 8)   X. Z.  Zhang,  C.  Zhou,  P. F.  Liu and  J.  Guan: China Mech. Eng., 27 (2016), 3125 (in Chinese).
• 9)   X. Z.  Zhang,  H. T.  Zhu,  A. K.  Tieu,  H. B.  Xie,  X. Z.  Du,  X. K.  Li and  C. X.  Dou: Adv. Mater. Res., 264–265 (2011), 337. https://doi.org/10.4028/www.scientific.net/AMR.264-265.337
• 10)   X. Z.  Zhang and  X. K.  Li: Heavy Mach., 4 (2005), 20 (in Chinese).
• 11)   X. K.  Li,  X. M.  Wu,  Y. M.  Fang,  Z. Q.  Xu,  X. R.  Zheng and  D. M.  Zhang: Chin. J. Mech. Eng., 36 (2000), 67 (in Chinese).
• 12)   H. P.  Yang,  X. K.  Li,  X. Z.  Zhang and  T.  Jin: Chin. J. Mech. Eng., 43 (2007), 207 (in Chinese).
• 13)   T. Z.  Ren and  C.  Liu: Chin. J. Mech. Eng., 17 (2004), 606. https://doi.org/10.3901/CJME.2004.04.606
• 14)   T. Z.  Ren,  B. W.  He,  J. J.  Chen and  X.  Jin: Chin. J. Mech. Eng., 45 (2009), 269 (in Chinese).
• 15)   D. W.  Liu and  T. Z.  Ren: China Mech. Eng., 24 (2013), 327 (in Chinese).
• 16)   D. W.  Liu,  L. M.  Luo,  G. H.  Wang and  X.  Jin: China Mech. Eng., 28 (2017), 2608 (in Chinese).
• 17)   D. W.  Liu,  T. Z.  Ren and  X.  Jin: China Mech. Eng., 26 (2015), 2325 (in Chinese).
• 18)   C. W.  Ma: Contin. Cast., (2014), 22 (in Chinese).
• 19)   C. W.  Ma,  H. X.  Wang,  Z.  Li,  W. H.  Feng and  C.  Zhang: Foundry Technol., 34 (2013), 214 (in Chinese).
• 20)   Q. H.  Hong and  D. C.  Hu: Heavy Mach., 3 (2008), 15 (in Chinese).
• 21)   Q. H.  Hong and  D. C.  Hu: J. Shanghai Inst. Technol., 8 (2008), 94 (in Chinese).
• 22)   X. K.  Li,  Q. X.  Zhu,  X. R.  Zheng,  D. M.  Zhang and  X. W.  Zeng: Iron Steel, 33 (1998), 26 (in Chinese).
• 23)   X. N.  Meng and  M. Y.  Zhu: China Mech. Eng., 18 (2007), 1779 (in Chinese).
• 24)   X. N.  Meng and  M. Y.  Zhu: Chin. J. Process Eng., 6 (2006), 91 (in Chinese).
• 25)   D. J.  Sun,  B.  Wang and  C. P.  Wang: Heavy Mach., 4 (2012), 42 (in Chinese).
• 26)   W.  Zhang and  Z. L.  Zhang: Foundry Technol., 35 (2014), 1081 (in Chinese).
• 27)   X. Z.  Zhang,  Q. G.  Liu,  W.  Huang and  Y. M.  Fang: Iron Steel, 49 (2014), 42 (in Chinese).
• 28)   X. Z.  Zhang,  Y. M.  Fang and  H. Y.  Wang: China Mech. Eng., 24 (2013), 3375 (in Chinese).
• 29)   C.  Zhou,  C.  Yang,  X. Z.  Zhang,  F.  Wang and  Y. L.  Yu: Mech. Solids, 56 (2021), 1114. https://doi.org/10.3103/S002565442106025X
• 30)   C.  Zhou,  X. Z.  Zhang,  F.  Wang and  S. B.  Ren: Complexity, (2020), 4165689. https://doi.org/10.1155/2020/4165689