本研究では,マーク付き多次元Hawkes過程を用いて高頻度注文板内で観測される複数イベントを表現し,それぞれの自己励起性および相互励起性を検証するとともに,イベントにおけるマークの大きさがHawkes過程の強度関数に与えるインパクトの大きさについて分析を行う.具体的には,価格の上昇及び下降を伴う約定に加えて,中心価格の変動を伴うビッド及びアスク注文を4系列のイベントとして定義し,そのときの取引数と注文数をマークとしたマーク付き4次元Hawkes過程を提案している.そしてこのモデルを東証一部上場の複数銘柄に当てはめ,それぞれのパラメータ推定を行う.次に,推定されたパラメータを利用して時系列と銘柄間の比較を行い,各イベントの自己励起性,及びイベント間の相互励起性についての特徴を明らかにする.さらに,マークがHawkes過程の強度関数に与える影響の有無とその大きさについて分析を行う.
近年,情報通信技術の発達や情報処理機器の高性能化に伴い,世界中の金融市場において取引システムの高速化や,取引データの時間解像度の向上が図られている.日本の株式市場においても,2010年に東京証券取引所がアローヘッドを導入して以来,注文処理の高速化やデータの時間解像度の向上が続いている.2019年7月現在,東証より配信されるリアルタイム情報であるFLEX Fullデータはマイクロ秒単位で記録されている.
これらの現状を踏まえ,日中データと呼ばれる,日次以上の頻度で取引が記録されたデータを用いた実証分析が行われている.宇野,柴田(2012)は2010年1月に稼働したアローヘッドの導入初期の影響を分析している.その後も,田代,川口(2017)や保坂(2014),林,佐藤(2016)などが高頻度データの実証分析を行っている.高頻度領域で観測される諸現象は,市場参加者にとって取引の意思決定を行う際に重要な情報となる.取引速度の高速化に伴い,データの時間解像度も高くなり続けていることから,このような研究は今後も継続し続けることが重要である.
高頻度データの詳細な分析が可能になったことで,金融分野においてはそれ以前には見られなかった現象が次々と報告されている.例えば,株式市場においては開場直後と閉場直前に取引が集中し,そのボラティリティが大きくなる傾向があることが明らかとなった.同様の現象は,為替市場において主要通貨の取引市場の昼間時間においても観測されている.この現象は日内季節性と呼ばれ,高頻度データが明らかにしたスタイライズド・ファクトの代表例である.また,Goodhart and Figliuoli (1991)は,米ドルと主要外国通貨の分次為替データを用いて,高頻度領域において収益率に強い負の自己相関が存在することを明らかにしている.高頻度金融データのモデリングについては,例えば,統計数理の2017年第65巻第1号を参照(川崎,荻原(2017))すると良い.
高頻度データの中でも,個々の約定や注文が記録されているティックデータの分析は重要である.ティックデータは,市場や個別銘柄における価格形成の過程そのものを反映したデータであり,これらを分析することにより投資家の行動をダイレクトに検証することが出来る.この分野の実証分析では,ビッド・アスク・バウンス現象と呼ばれる,取引価格が短時間に上下する現象が報告されている.LeBaron (1994)は,米ドル・スイスフランの為替ティックデータを用いて,収益率の負の自己相関とビッド・アスク・バウンス現象について分析を行い,ティック領域においてはどちらも観測されるが,1時間次データにおいては負の自己相関が消失することを示している.
年次や月次,日次で集計されるデータと比較した日中データの特徴は,得られるデータの時点が等間隔ではなく,そのことに留意したモデル化が求められることである.標準的な時系列モデルの多くは,通常,時間に対して等間隔にデータが並んでいることを前提としているため,不等間隔に観測値が並ぶ高頻度データを用いる際は何らかの前処理を行う必要がある.そして,採用する前処理は,元のデータがもつ本来の情報を棄損しないように処理する必要がある.一方で,連続時間モデルを想定し,不等間隔の観測値を,その間隔の長さも考慮した上でモデル化する手法が存在する.その代表的なモデリングの一つが,点過程によるモデリングである.点過程によるモデリングは,時間間隔そのものをモデルとしているため,不等間隔データをそのまま用いることができる特徴をもつ.したがって,高頻度データのモデリングに点過程を用いることは自然な応用と考えられる.
本研究で取り上げるHawkes過程は1971年にAlan G. Hawkesにより提唱された点過程の一種である(Hawkes (1971)).最初は,地震学の分野において本震の後に余震が伝播していく様子を表現するモデルとして提唱された.点過程における点の発現頻度(単位時間当たりの点の発現確率)である強度関数に自己励起性と呼ばれる性質を持たせていることが特徴である.具体的には,点過程の強度関数の中に,過去に発生した事象がその後の強度に正のインパクトを与えるような項が含まれている.また,Hawkes過程は多次元モデルへと拡張することができ(例えば,国友,江原,栗栖(2017)参照),その場合には自己励起性とともに,複数の強度関数が互いに正のインパクトを与え合うような相互励起性をもつ点過程を表現することが可能となる.
Hawkes過程は神経科学(Reynaud et al. (2013)),生態学(Balderama et al. (2012)),情報科学(Rizoiu et al. (2017))など,地震学以外の分野にも積極的に応用されている.金融分野への応用は2000年代に始まり,Bacry et al. (2015)によれば,Hawkes過程を金融分野へと応用した先がけがBowsher (2007)によって行われた.金融市場で発生する金融商品の価格変動や信用リスクの伝播(監物,中川(2019))といった事象は,多数の要素が相互に影響しあっており複雑な様相を呈していることから,事象の相互関係を簡潔に記述,解釈することができるHawkes過程は金融分野においても有用なモデルと考えられている.金融市場における高頻度取引が盛んとなり,その分析の重要性が増大した昨今,Hawkes過程を用いたファイナンスの研究は非常に盛んである.近年では,Quantitative Finance のVolume 18, 2018で“Hawkes Processes in Finance”の特集が組まれていおり,Hawkes自身によるレビュー(Hawkes (2018))も報告されている.またBacryらによるサーベイ(Bacry et al. (2015))も参考になる.本研究で取り上げる,Hawkes過程を注文板データのモデリングに用いた研究としては,Achab, M. et al. (2018),Large (2007),Martins and Hendricks (2016)などが挙げられる.
以上の現状を踏まえ,本研究では,多次元のHawkes過程によるモデリングをベースとして,さらに注文量や取引量も考慮したモデルを提案する.実際に市場参加者が注文を行う際は,価格変動の履歴だけでなく,注文板上に表示されている注文枚数も鑑みた意思決定をしている可能性が高い.したがって,本研究では,高頻度注文板データに対して,注文/取引の発生時刻をタイムスタンプとして,注文量/取引量をマークとして付与したマーク付き多次元Hawkes過程を用いたモデリングを行う.具体的には以下で述べるように,高頻度注文板内で観測される4種類のイベントの自己励起性及び相互励起性を分析するとともに,各イベントに伴うマークの大きさが強度関数に与えるインパクトの大きさについて分析を行う.これにより,重要なイベントが起こったときの注文量がその後の取引行動に与える影響の有無とその大きさを分析することが可能となる.
マーク付きHawkes過程をファイナンスの分野に応用した先行研究は未だ限られているのが現状である.例えば,Embrechts et al. (2011)やLee and Seo (2017)は2次元のマーク付きHawkes過程を用いた研究を行っている.2次元を越えるモデルを用いた金融の実証研究は筆者の知る限りまだない.また,マーク付きHawkes過程を注文板データの分析に応用した例も筆者の知る限りまだ存在しておらず,本研究の実証結果はその意味においては最初の研究と位置づけられる.
本研究は,以下の意味で市場参加者に有用な情報を提供できる.第1に本研究結果を利用することで,注文板上のイベントの発生履歴や注文量,取引量が将来のイベント発生確率に対して与える影響を考慮して,注文のタイミングや注文量についてより良い意思決定を行えるようになる可能性がある.特に高頻度取引業者と呼ばれる,コロケーションシステムやアルゴリズム取引を行う業者の場合,市場に与えるインパクトを常に考慮しながらマーケットメイキングを行うため,本研究の結果は取引アルゴリズムの改定を行う際に有意義な示唆を含んでいると期待される.第2に,本研究のアプローチは,各銘柄の注文数とその後の取引活動の関連を明らかにすることから,とりわけマークの大きさが強度関数へ大きなインパクトを持つ銘柄に関して大口取引への注意を促すなど,市場の安定性に興味がある取引所にとっても重要な示唆を与えることができる.
本研究では東京証券取引所が提供する高頻度電文データFLEX Fullを使用し,データセットの中から,東証一部上場銘柄のうち,約定回数が多く,かつ異なる業種の銘柄を複数選択する.次に各銘柄について(1)価格上昇を伴う約定イベントの系列,(2)価格下降を伴う約定イベントの系列,(3)中心価格の変動を伴うビッド注文イベントの系列,(4)中心価格の変動を伴うアスク注文イベントの系列,に対してマーク付き4次元Hawkes過程によるモデリングを行う.選択する4つのイベントは,Hawkes過程を用いた注文板の分析を行ったLarge (2007)やMartins and Hendricks (2016)を参考にしており,これらは,価格の弾力性や価格形成に大きな影響を及ぼすような注文板上のイベントと考えられているものである.Cont et al. (2014)は,高頻度注文板データを用いた分析により,株価変動のダイナミクスの大部分は最良気配値の不均衡により引き起こされると結論付けている.
本研究の実証分析の結果として,価格変動を伴う約定のマークの大きさは,強度関数に対して正のインパクトを与えることが明らかになる.一方で,約定を伴わずに最良気配を変化させる注文のマークの大きさは,銘柄によっては強度関数にインパクトを与えない結果になっている.これは当該時間において市場参加者が意思決定をする際に最良気配枚数を考慮に入れていない可能性を示唆している.
本研究の構成は以下の通りである.セクション2では,マーク付きHawkes過程の導入を行い,パラメータの推定法について記述する.セクション3では,本研究で用いるデータの構造およびその前処理について簡潔に説明する.セクション4では,実証分析の結果とその解釈について議論する.最後に,セクション5は本論文の結言である.
マーク付きHawkes過程は,図1のように,イベントの発生時点とそのイベントに紐づくマークを点過程として表現するモデルである.このセクションでは,Liniger (2009)を参考として,マーク付きHawkes過程の定義や諸性質について説明を行ったうえで,最尤推定法を用いたパラメータの推定について述べる.一般のマーク付き点過程に関する議論はDaley and Vere-Jones (2008)を参照されたい.

図1 2次元のマーク付きHawkes過程の例
最初にいくつかの表記を導入する.$\mathcal{T}, \mathcal{X}$をそれぞれ完備可分距離空間とする.ある加算集合$\mathcal{I}$の元$i \in \mathcal{I}$に対して,観測されたイベントをトリプレット$(t_i,d_i,x_i)$で表す.$t_i\in \mathcal{T}$はイベントが観測された時刻,$d_i\in \{1,...,d\},\ d\in \mathbb{Z}_+$はイベントの系列番号,$x_i \in \mathcal{X}$はイベントのマークの大きさを表す.このとき,$d_i=j$である集合は$\{(t_i,x_i)\}$は$\mathcal{T} \times \mathcal{X}$上のマーク付き点過程$N=\{(t_i,x_i)\}$である.また,任意の有界ボレル集合$A\in \mathcal{B}(\mathcal{T})$に対して,点過程$N$に関して,マークを考えない基底過程$N_{g_j}(A)=N(A \times \mathcal{X})<\infty$も点過程となる.以降,便宜上$N_{g_j}(A)=N_j(A)$と書く.
フィルター付きの確率空間$(\Sigma, \mathcal{F}, P, \{ {\mathcal{F}}_{t} \})$を定義し,この確率空間上で定義される点過程$N_j(t)$が,フィルトレーション$\mathcal{F}_t$に関する適合過程であるとする.このとき,$N_j(t)$の強度関数$\lambda_j(t)$は次のように定義される.
| \begin{equation*} \lambda_j(t){\rm d}t:=\mathbb{E}[N_j(t+{\rm d}t)-N_j(t)|\mathcal{F}_{t-}]. \end{equation*} |
ただし,$\mathcal{F}_{t - }: = \sigma \left( {\bigcup\nolimits_{s < t} {{\mathcal{F}_s}} } \right)$,すなわち時点$t>0$の直前までの事象に対する$\sigma$加法族と定義している.また,$\lambda_j(t)$は,各時点$t$において正の値を持つ確率過程である.マーク付き$d$次元Hawkes過程$N$のもとで,第$j$番目,$j \in \{1,...,d\}$の点過程$N_j$の強度関数$\lambda_j(t)$は次式で定義される.
| \begin{equation} \lambda_j(t):=\eta_j+\sum^d_{k=1}\theta _{jk}\int_{(-\infty,t)\times \mathbb{R}}\omega _j(t-s)g_k(x)N_k({\rm d}s\times {\rm d}x),\qquad \qquad t \in \mathbb{R}. \end{equation} | (1) |
ただし,$\omega_j:\ \mathbb{R}_+ \to \mathbb{R}_+$,$g_k:\ \mathbb{R}_+ \to \mathbb{R}_+$,$k\in \{1,...,d\}$,$\eta_j \geq 0$,$\theta_{jk} \geq 0$とする.(1)式中の$\boldsymbol{\eta} = \{ \eta _{j} \}$はベースライン強度と呼ばれ,強度関数のうち自己励起性および相互励起性による影響を受けない項である.本研究の場合,ベースライン強度は過去のイベントから誘発されたイベントとは無関係に発生する系列の強度を意味している.すなわち,$\eta _{j}$の値が大きいほど,取引に誘発されたのではない,その銘柄自身の基礎的な取引需要が大きいと考えられる.また,$\boldsymbol{\Theta}=(\theta_{jk}:\ j,k\in {1,...,d})$によって定義される$d\times d$行列$\boldsymbol{\Theta}$は分枝行列(Branching matrix)と呼ばれ,その要素$\theta_{jk}$は系列$k$で発生したイベントが系列$j$へ及ぼす影響の大きさを意味している.そして,$j=k$の場合は自己励起の影響を,$j\neq k$の場合は相互励起の影響を表している.
マーク付きHawkes過程では,マークが従う分布(マーク分布)は,過去のイベントの発生時点とは独立であると考える.すなわち,第$j$番目の点過程$N_j$が与えられたとき,マークの確率変数$\boldsymbol{X}_j\in \mathbb{Z}$は点過程の履歴とは独立な確率密度関数$f_j$をもつとする.一方,(1)式の右辺第二項のうち,$g_k(\cdot)$はインパクト関数と呼ばれ,マークの大きさが強度関数に及ぼすインパクトを表す関数である.$g_k>1$の場合には,発生したイベントのマークサイズが強度へ与えるインパクトを,マークを考慮しないときに比べて増大させることを意味し,反対に$g_k<1$の場合には,発生したイベントのマークサイズが強度へ与えるインパクトを,マークを考慮しないときに比べて減少させることを意味する.そして,$g_k=1$はマークがイベントの発生頻度に影響を与えないことを意味する.本研究では,インパクト関数としてLee and Seo (2017)が提案している以下のような線形関数を仮定する.
| \begin{equation} g_j(x):=\frac{1+(x_k-1)p_j}{\mathbb{E}\left[1+(x_j-1)p_j \right]}. \end{equation} | (2) |
最後に,(1)式の$\omega_j(\cdot)$はカーネル関数と呼ばれ,あるイベントのインパクトが時間とともに減衰する速さを表す関数である.代表的なカーネル関数には,指数カーネル(Exponential kernel)とべき乗カーネル(Powerlaw kernel)があり,それぞれ次のような関数形で与えられる.
| \begin{equation*} \begin{split} 指数カーネル&:\qquad\qquad \omega_j(t)=\alpha_j e^{-\alpha_j t}.\\ べき乗カーネル&:\qquad\qquad \omega_j(t)=\frac{\alpha_j}{(1+\alpha_j t)^{1+\beta_j}}. \end{split} \end{equation*} |
べき乗カーネルはその関数の形状から,地震の発生といった,あるイベントのインパクトが長い時間にわたって残留する場合に有効である.一方,指数カーネルはインパクトが短時間で減衰する場合に有効である.また,指数カーネルを用いる場合,$(N_j(t),\lambda_j(t))$がマルコフ過程となることから,強度関数を再帰的に計算することが可能となる.Hawkes (2018), Oakes (1975)の指摘にあるように,これは計算時間の点で利点となる.本研究では,高頻度データであるティックデータを用いる点,多次元Hawkes過程の強度関数の計算時間を考慮して,指数カーネルを採用する.
次に,強度関数に対応する点過程の存在と唯一性について述べる.(1)式で表される強度関数が次の2つの条件を満たす場合には,対応する点過程が唯一存在することが知られている.
ここで,分枝行列$\boldsymbol{\Theta}$のスペクトル半径${\rm Spr}(\boldsymbol{\Theta})$は$\boldsymbol{\Theta}$の固有値の最大値で定義される.詳細は例えばLiniger (2009)のTheorem 1.16,及びTheorem 6.55とその証明を参照されたい.
2.2 マーク付きHawkes過程のパラメータの推定本研究では最尤推定法を用いて,多次元のマーク付きHawkes過程のパラメータ推定を行う.尤度関数を定義するため,最初に,推定区間$D$における補正項$\Lambda_j(t)$を導入する.区間$D=[T_*,T^*]$において観測される多次元点過程の補正項を
| \begin{equation} \Lambda_j(t)=\int_{T_*}^t \lambda_j(s) {\rm d}s, \qquad {\rm for} \ j \in \{1,\ldots,d\}, \end{equation} | (3) |
と定義する.マーク付きHawkes過程の補正項は,2つの式(1),(3)より
| \begin{equation} \Lambda_j(t)=\eta_j(t-T_*)+\sum_{k=1}^d\theta_{jk}\int_{(-\infty,t)\times \mathbb{R}}\left[\bar{\omega}_j(t-u)-\bar{\omega}_j(T_*-u)\right] g_k(x)N_k({\rm d}u \times {\rm d}x), \end{equation} | (4) |
となる.ただし,$\bar{w}_j(t)=\int_0^t w_j(s)ds=1-e^{-\alpha_j t}$と置いている.
いま,推定区間$D$を用いてマーク付きHawkes過程のパラメータを推定することを考える.このとき,対数尤度関数は,
| \begin{equation} {\rm log}L=\sum^d_{j=1}\int_{[T_*,T^*]\times \mathbb{R}}{\rm log}\lambda_j(t)N_j({\rm d}t\times {\rm d}x)+\sum_{j=1}^d\int_{[T_*,T^*]\times \mathbb{R}}{\rm log}f_j(x)N_j({\rm d}t\times {\rm d}x)-\sum_{j=1}^d\Lambda_j(T^*), \end{equation} | (5) |
と表せる.また,指数カーネルのもとで,強度関数$\lambda_j(t)$は,
| \begin{eqnarray} \lambda_j(t)&=&\eta_j+\sum^d_{k=1}\theta_{jk}\int_{(-\infty,t)\times \mathbb{R}}\alpha_je^{-\alpha_j(t-s)}g_k(x)N_k({\rm d}s\times {\rm d}x)\nonumber \\ &=&\eta_j+e^{-\alpha_j(t-r)}\sum^d_{k=1}\theta_{jk}\int_{(-\infty,r)\times \mathbb{R}}\alpha_je^{-\alpha_j(r-s)}g_k(x)N_k({\rm d}s\times {\rm d}x)\\ &+&\sum^d_{k=1}\theta_{jk}\int_{[r,t)\times \mathbb{R}}\alpha_je^{-\alpha_j(t-s)}g_k(x)N_k({\rm d}s\times {\rm d}x)\nonumber \\ &=&\eta_j+e^{-\alpha_j(t-r)}\left[ \lambda_j(r)-\eta_j \right] +\sum^d_{k=1}\theta_{jk}\int_{[r,t)\times \mathbb{R}}\alpha_je^{-\alpha_j(t-s)}g_k(x)N_k({\rm d}s\times {\rm d}x),\nonumber \end{eqnarray} | (6) |
と変形できる.これは,過去の1時点における$\lambda_j(r)$を用いて再帰的に計算可能であることを示している.
推定区間$D$において観測されたデータを$(t_1,d_1,x_1,\ldots,t_m,d_m,x_m,\ldots,t_n,d_n,x_n)$とおく.このとき,(5)式の推定量${\rm log}\hat{L}$は以下のように書くことができる.
| \begin{equation} {\rm log}\hat{L}=\sum_{m=1}^n{\rm log}\hat{\lambda}_{d_m}(t_m)+\sum_{m=1}^n{\rm log}f_{d_m}(x_m)-\sum^d_{j=1}\hat{\Lambda}_j(T^*). \end{equation} | (7) |
ここで,強度関数の推定量 $\hat{\lambda}_j(t_i)$は,(6)式より,
| \begin{equation*} \left\{ \begin{aligned} &\hat{\lambda}_j(t_1)=\eta_j\\ &\hat{\lambda}_j(t_i)=\eta_j+e^{-\alpha_j(t_i-t_{i-1})}\left[\hat{\lambda}_j(t_{i-1})-\eta_j\right] +\theta_{j,d_{i-1}}\alpha_je^{-\alpha_j(t_i-t_{i-1})}g_{d_{i-1}}(x_{i-1}), \mathrm{for}\; \mathrm{all}\;2\geq i \geq n, \end{aligned} \right. \end{equation*} |
である.また,補正項の推定量 $\Lambda_j(T^*)$は,(4)式より,
| \begin{equation*} \hat{\Lambda}_j(T^*)=\eta_j(T^*-T_*)+\sum^n_{m=1}\theta_{j,d_m}\bar{w}_j(T^*-t_m){d_m}(x_m), \end{equation*} |
と表される.
本研究においては,分析目的を達成しつつ,推定されるパラメータの数を適切にコントロールし,推定値の安定性を確保するために,次の2つの追加の仮定を行ったうえで実際の推定作業を行う.第1に,本研究ではマークの大きさ自体の分析は行わないため,特定の分布$f_j$を想定しない.すなわち,(7)式の右辺第2項はマークの大きさ$x_m$の確率密度関数の項になっているが,この項は影響を与えないとして最尤推定を行う.同様の想定は,Liniger (2009)やLee and Seo (2017)においてもなされている.第2に,全ての$j$について$\alpha_j=\alpha$とした上で推定を行う.これは取り上げる全ての系列に関してその減衰率が同じと想定していることを意味している.
本セクションの最後に,マーク付きHawkes過程のフィッティングの良さを評価するために残差過程(Residual process)を導入し,Ogata (1988)による時間変更定理の概要を述べる.時間変更定理を用いてHawkes過程の強度過程から残差過程を作成し,それがポアソン過程に近いかどうかを評価することで,本研究で提案するHawkes過程がどれだけ観測されるデータにフィットしているかを確認することができる.
いま,区間$D=[T_*,T^*]$において,マーク付きHawkes過程に従う配列$\{(t_i,d_i,x_i)\},\ i\in \{1,\ldots,n\}$が観測されるとする.このとき,各要素が次のように定義される配列$\boldsymbol{\tau}=\{ \tau_1,\ldots,\tau_n \}$を考える.
| \begin{equation*} \tau_i:=\Lambda_{d_i}(t_i). \end{equation*} |
ここで$\Lambda_{d_i}(t_i)$の各パラメータには,それぞれの推定値が代入される.さらに,$j\in \{1,...,d\}$に対し,$d_i=j$を満たす$i$に従って$\tau_i$を抽出した配列${\rm Res}_j$を残差過程と呼ぶ.時間変更定理の主張は,このとき${\rm Res}_j$がそれぞれが独立で強度が1の斉次ポアソン過程に従うというものである(Daley and Vere-Jones (2008), Embrechts et al. (2011)).仮に設定したHawkesモデルが不適切であれば,計算された残差過程はポアソン過程からかけ離れたものになる.
このセクションでは,パラメータ推定に使用するデータとその前処理の概略を記述する.本研究で利用するFLEX Fullデータは東京証券取引所が提供するリアルタイム情報サービスであり,具体的には日本取引所グループの取引システムであるアローヘッドより配信される電文データのことである.FLEX Fullデータには現在値,売買高,売買代金,全気配値段・数量・注文件数,引け条件付注文数量及び件数がタイムスタンプとともに記録されている.
3.1 注文板データFLEX Fullデータは電文形式の注文フローデータであると同時に,注文板データと見なすこともできる.すなわち,特定の1銘柄についてある時刻までの残存気配データに注目するとき,注文板を再現することが可能である.最初に,データの前処理の手順について説明を行う前に,注文板および注文板上の情報変化を記録した注文板データについて概要を記述する.
株式市場における注文板とは,ある1銘柄の株式について市場参加者が行った売買注文の集合である.注文板に表示される注文は指値注文と呼ばれ,市場参加者がいくらで(気配価格),どれだけの株式を(気配数量),売り(アスク)または買い(ビッド)を取引サーバに送信したものである.表1は,注文板上の変化を再現した仮想例である.表1の左側は,ある時刻に注文板に表示されている指値注文を表している.このとき,アスク側の最安値の気配及びビッド側の最高値の気配を最良気配値と呼ぶことが一般的である.FLEX Fullデータの仕様では板中心という呼称が用いられている.中央は,左側から1時点後の注文板を表している.1,999円での買い注文が16枚入っていることがわかる.このとき,「最良買い気配値が変化した」または「買い気配の板中心が動いた」という.右側は,中央からさらに1時点後の注文板を表している.2,001円に存在していた25枚の気配が消失しており,最良売り気配値が2,002円に移動していることがわかる.売り(買い)気配の消失が発生したとき,考えられる原因は2点ある.1つ目は,即時約定の買い(売り)注文が入ったときである.即時約定注文は成行注文とも呼ばれ,価格を指定せずに数量のみを指定して行う注文であり,注文した瞬間に最良気配値での約定(取引成立)を伴う.2つ目は,2,001円上に存在していた25枚の指値注文が注文者によりキャンセルされたときである.なおFLEX Fullデータでは,前者は「取引成立に伴う気配の変化」として,後者は「取引成立を伴わない気配の変化」として記録されるため,データ上区別することが可能である.
| Ask | Price | Bid | Ask | Price | Bid | Ask | Price | Bid | ||
| 45 | 2,004 | 45 | 2,004 | 45 | 2,004 | |||||
| 54 | 2,003 | 54 | 2,003 | 54 | 2,003 | |||||
| 67 | 2,002 | 67 | 2,002 | 67 | 2,002 | |||||
| 25 | 2,001 | 25 | 2,001 | 2,001 | ||||||
| 2,000 | 2,000 | 2,000 | ||||||||
| 1,999 | 1,999 | 16 | 1,999 | 16 | ||||||
| 1,998 | 13 | 1,998 | 13 | 1,998 | 13 | |||||
| 1,997 | 29 | 1,997 | 29 | 1,997 | 29 | |||||
| 1,996 | 32 | 1,996 | 32 | 1,996 | 32 |
FLEX Fullデータの1日分のデータ量は約5$\sim$10GBであり,図2のように改行のない1行,50$\sim$100億文字のテキストデータで配信される.そのため,そのままでは分析に用いることができず,いくつかの前処理のステップを踏まなくてはならない.電文内には注文情報のほかに配信サーバー用の制御コードなども含まれているため,分析に必要な情報を抽出する前に以下の2ステップの前処理を行っている.

図2 FLEX Fullデータサンブル, 2019年5月31日
まずはじめに,東証一部上場銘柄の中から,トヨタ自動車株式会社(以下,トヨタ),楽天株式会社(以下,楽天),ソニー株式会社(以下,ソニー),ソフトバンクグループ株式会社(以下,ソフトバンク),国際石油開発帝石株式会社(以下,国際帝石),丸紅株式会社(以下,丸紅),三井不動産株式会社(以下,三井不動産)の計7社を分析対象とする.これらは,(1)約定回数が多く,(2)業種の被りがないように,の2点に注意しながら選択している.約定回数が多い銘柄を選択した主な理由は,本研究で利用するHawkesモデルにおいては,取引が活発で,十分な数の日中データが記録されるようなものが適しているからである.実際,予備検証において,本研究のモデルである4次元マーク付きHawkes過程の場合,ウィンドウサイズがおよそ$n<500$では推定する解が収束せず,$500\leq n\leq 750$においてもデータによっては収束せず,$n\geq1000$で解が安定して収束することが,経験的に明らかとなっている.一方,業種間の偏りの排除に関しては,業種に依存しない形での分析を行う意図があることの反映である.パラメータ推定に使った推定区間は,2019年5月7日から2019年5月31日の間の19営業日分を基本とする.FLEX fullデータは原則,1つの電文内には1つの銘柄にかかわる情報のみが記録される.したがって,1銘柄の電文のみを抽出すると図3のようになる.

図3 トヨタ(7203)の注文データより一部抜粋したもの,2019年5月31日
本研究では,系列データとして,以下の4種類のイベントを用いる.イントロダクションにも述べた通り,これらは価格の弾力性や価格形成に大きな影響を及ぼすような注文板上のイベントであることが指摘されている.
銘柄内の全取引データから,系列1$\sim$4に該当するイベントを時刻$t_i$,取引量または注文量$x_i$と共に抽出し,整理すると表2のようになる.最後に,ウィンドウ幅を1000行分に設定したうえで,開場直後,休憩前後および閉場直前の30分にさしかからないように分割し,前処理プロセスを終了する.
| $t_i$ | $d_i$ | $x_i$ |
| 40802.269840 | 4 | 3400 |
| 40802.775807 | 4 | 200 |
| 40802.777521 | 4 | 3500 |
| 40802.778404 | 4 | 100 |
| 40804.913212 | 2 | 4000 |
| 40807.846515 | 3 | 500 |
| 40808.070171 | 3 | 2100 |
| 40808.880469 | 4 | 200 |
| 40808.884333 | 4 | 2100 |
| 40808.885131 | 4 | 100 |
| 40815.461708 | 2 | 1000 |
| 40817.941131 | 1 | 7000 |
| 40820.119268 | 1 | 22000 |
| 40820.122510 | 4 | 200 |
このセクションでは,東京証券取引所のFlex Fullデータををマーク付き4次元Hawkes過程に当てはめたときの,パラメータの推定結果を提示し,その考察を行う.
4.1 Hawkes過程によるモデリングの有効性の検証最初に,Hawkes過程のフィッティングに関する検証を行い,モデリングの有効性について議論する.時間変更定理に基づき,残差過程に対するバーコードプロットとQ-Qプロットを用いて,Hawkes過程のフィッティングの良さを評価する.いずれも,残差過程がどれだけ斉次ポアソン過程に近いかを評価する手法である.
4.1.1 バーコードプロット図4は,2019年5月31日のトヨタの8001番目から9000番目のデータに対してフィッティングを行った結果を示したバーコードプロットである.図4(a)から図4(d)のそれぞれの図において,横軸は時間を縦軸はイベントの発生を表している.また,中段は元データ,上段は元データの先頭50サンプル分を抽出したもの,そして下段が時間変更の処理を行った後のバーコードプロットを表している.4つの系列データのグラフから共通して読み取れる第1の特徴は,元データ(中段)のグラフには,明らかにイベントの発生頻度に偏りが含まれることである.イベントの発生が集中している箇所は,その時間帯において注文または取引が集中したことを表す「クラスタリング現象」と呼ばれる現象を反映していると考えられる.実際に,元データを拡大した上段のグラフを見ても,イベントの発生のクラスタリングが確認できる.第2の特徴は,時間変更後のイベントの発生頻度(下段)は,ところどころクラスタリング現象が発生しているように見える箇所があるものの,概ね均一に分散されていることである.このことは,時間変更処理により,変更後の点過程がポアソン過程に近づいていることを示唆している.

図4 トヨタの株価に関する4 系列のバーコードプロット

図5 トヨタの株価に関する4 系列のQ-Qプロット
点過程$N$が強度1の斉次ポアソン過程に従う場合,そのデュレーション,すなわち隣り合うイベントの時間間隔は,強度1の標準指数分布に従う.この性質を利用し,時間変更後の点過程のデュレーションの経験分布と,標準指数分布を比較するためにQ-Qプロットという手法を用いる.Q-Qプロットは,横軸に想定している分布の分位点を,縦軸に比較するデータの経験分布の分位点をプロットすることにより,経験分布がどれだけ想定の分布の形状に近いかを評価するときに用いられる手法の一つである.
図5は,トヨタの2019年5月31日の前処理後データのうち,8001番目から9000番目のデータに対して時間変更を行い,Q-Qプロットを作図したものである.$d_1$から$d_4$のどの系列においても,低い分位点の部分においてはデュレーションはおおむね標準指数分布に従っているように見える.一方,分布の裾部分に関しては標準指数分布とは乖離した値をとる結果ではあるが,これはLu and Abergel (2018)やEmbrechts et al. (2011)の結果にも見ることできる.本研究はHawkes過程のフィッティングの精度向上を主たる目的とした研究ではないが,分布の裾部分のフィッティングを改善し,さらに正確なモデリングを可能にすることはHawkes過程のモデリング上の課題であるといえる.しかしながら,裾以外の部分においては良好なフィッティング結果になっており,用いたデータに対するモデルとしてマーク付きHawkes過程が有用であるといえる.
4.2 時系列方向の分析 4.2.1 日中,週内の分析ここでは,日内,及び週内でHawkes過程のパラメータがどのように推移していくのかを検証する.具体的にはウィンドウ幅を$1000$とし,100データずつ開始と終了をずらしながらフィッティングを行うことでパラメータの推定値がどのように変化するのかを検証する.分析には2019年5月23日から5月28日の4営業日分のトヨタのデータを用いる.
まず初めに,ベースライン強度$\boldsymbol{\eta}=\{\eta_1,\eta_2,\eta_3,\eta_4\}$の変化について検証する.Hawkes過程の強度は$\boldsymbol{\eta}$の値のみで決まるわけではないため,他のパラメータの影響も考慮する必要がある.しかしながら,$\boldsymbol{\eta}$はHawkes過程の強度関数の最低値を表すパラメータであるため,ベースライン強度の値を見ることでイベントの発生頻度が最低どの程度存在しているのかを確認することができる.図6は,4営業日それぞれの1日内でベースライン強度$\boldsymbol{\eta}$が時間とともにどのように推移するかをまとめたグラフである.4つのグラフを比較するため,縦軸のスケールを統一して描いている.いずれのグラフでも$\boldsymbol{\eta}$はゆるやかに変化しており,大きな値の変化は観測されていない.このサンプル期間では,5月27日(月)は他の3営業日に比べてすべてのパラメータが相対的に高い水準で推移しているものの,5月28日(火)には5月23日(木)や5月24日(金)の水準に戻っている.また,Hawkes過程の系列$\eta_i, i=1,\ldots,4$の大きさを比較すると,約定を伴わない注文のベースライン強度$\eta_3,\eta_4$の方が,約定を伴うベースライン強度$\eta_1,\eta_2$よりも,総じて大きな値を取っていることが分かる.この結果は,過去の板情報の変化に反応して起こる励起的な取引を除いた場合,約定よりも気配変化の方が発生の強度が高いことを意味している.

図6 トヨタに関する$\boldsymbol{\eta}$の推定値の変化:2019年5月24日から28日,$n=1000,w=100$
次に,分枝行列$\boldsymbol{\Theta}$の時系列変化に着目する.$\boldsymbol{\Theta}$は強度関数の中で自己励起性及び相互励起性を表現するパラメータである.すなわち,$\boldsymbol{\Theta}$の要素$\theta_{jk}$は系列$k$で発生したイベントが系列$j$の強度関数に与えるインパクトの大きさを指す.例えば,$\theta_{11}$は系列1(直前の約定からの価格上昇を伴う約定)から系列1へのインパクト(自己励起性)を表しており,$\theta_{12}$は系列2(直前の約定からの価格下降を伴う約定)から系列1へのインパクト(相互励起性)を表している.図7は,4営業日それぞれの1日内で,分枝行列の16要素それぞれの値が,時間とともにどのように推移するかをまとめたグラフである.図より,$\boldsymbol{\Theta}$の各要素はそれぞれ緩やかに変化しており,$\boldsymbol{\eta}$の時と同様,大きな値の変化は観測されていないことが分かる.次に,行列要素の大小関係に着目すると,4営業日ともに$\theta_{31},\theta_{42},\theta_{33},\theta_{44}$が,その他の要素と比較して大きな値を取っていることが分かる.すなわち,自己励起性については系列3(約定を伴わない最良買い気配値の変化)と系列4(約定を伴わない最良売り気配値の変化)が系列1(価格上昇を示す取引),系列2(価格下落を示す取引)と比べて相対的に大きいことが分かる.一方,相互励起性については,系列1から系列3に与えるインパクトと,系列2から系列4に与えるインパクトが大きいことを意味している.
続いて,カーネル関数のパラメータ$\alpha$の変化を検証する.$\alpha$はイベントの発生が強度関数に与えるインパクトの減衰速度を表現したパラメータであり,その数値が大きいほどインパクトが時間経過に対して急速に減衰することを意味する.インパクトの値がイベント発生時の半分になるまでの時間を半減期といい,指数カーネルの場合,その半減期は$\frac{{\rm log}2}{\alpha}$である.$\alpha$の時系列変化をプロットしたものが図8である.ベースライン強度$\boldsymbol{\eta}$や分枝行列$\boldsymbol{\Theta}$のケースと同様,$\alpha$ の値も,日内において急激に値が変化する様子は見られない.一方で,他の2つのケースと異なる特徴として,$\alpha$の値は日によってその水準が異なっていることが挙げられる.このサンプルでは,5月28日の値は他に比べて高い水準にある.減衰の効果を定量的に見るために,それぞれの日内で$\alpha$に関する平均値を計算し,それを元にその半減期を求めると,5月23日が0.013秒,5月24日が0.014秒,5月27日が0.012秒であるのに対し,5月28日は0.0082秒とおよそ2/3となっている.
最後に,マークの大きさが系列に与える影響を分析するため,(2)式のインパクト関数$g_j$のパラメータ$p_j$の変化を見る.(2)式より$p_j$は,マークの大きさ$x$とその平均$\mathbb{E}[x_j]$との乖離の感度を表すパラメータであると解釈できる.つまり,$p_j$が大きいほど,あるイベントのマークが平均を上回ったときに強度関数へのインパクトを増大させ,下回ったときには減少させる.図9は,それぞれの営業日ごとに,時間軸に対して$\boldsymbol{p}$の変化をプロットしたグラフである.これによると,$p_1,p_2$はその他のパラメータと比較して一日の中でも大きく変動している箇所があり,週内での値の変化も大きい.一方で$p_3,p_4$に関しては,0に近い値を取る箇所が多く,$p_1,p_2$とは明らかに異なる挙動を示している.このことは,約定を伴うイベントにおけるマーク(注文数)はその後のイベントに影響を与えるが,約定を伴わないマークは,その後のイベントにあまり影響を与えないことを示唆している.

図7 トヨタに関する${\boldsymbol{\Theta}}$の推定値の変化:2019年5月24日から28日,$n=1000,w=100$
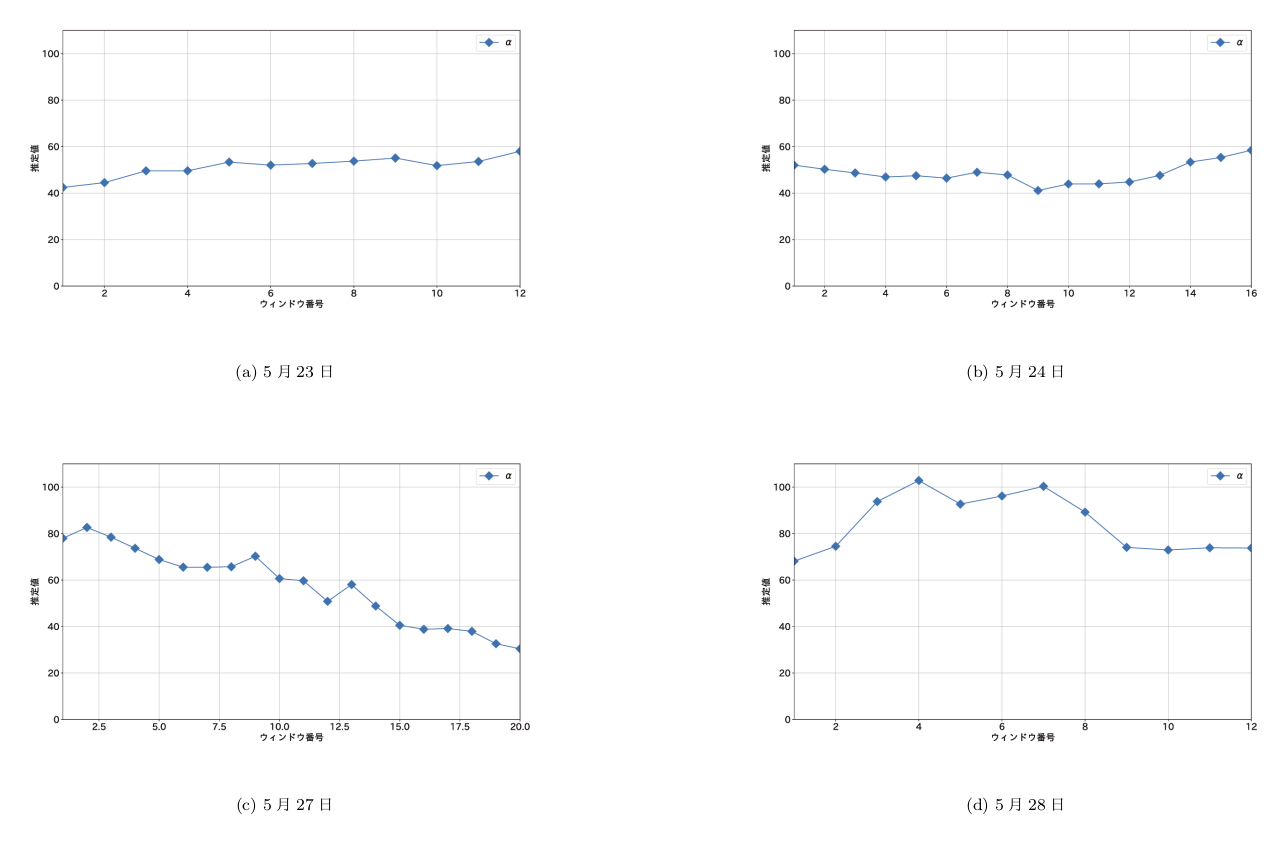
図8 トヨタに関する${\alpha}$の推定値の変化:2019年5月24日から28日,$n=1000,w=100$

図9 トヨタに関する$\boldsymbol{p}$の推定値の変化:2019年5月24日から28日,$n=1000,w=100$
この節では,各月のパラメータ推定値の平均が1年間でどのような変動をするのかに注目する.これは,4.2.1で検証した日内及び週内のパラメータ推定値の変化をさらに長いタイムスパンで確認することを意図している.データは2018年6月1日から2019年5月31日のトヨタの注文板データを用いる.それぞれの月において各パラメータ推定値の平均の変動を示したものが図10である.図10(a)は$\boldsymbol{\eta}={\eta_j},\ j\in\{1,...,4\}$,図10(b)は$\boldsymbol{\Theta}=\theta_{jk},\ j,k\in\{1,...,4\}$,図10(c)は$\alpha$,図10(d)は$\boldsymbol{p}=p_j,\ j\in\{1,...,4\}$の推定値の月ごとの変化を示している.まず$\boldsymbol{\eta}$に注目すると,$\eta_1$と$\eta_2$,$\eta_3$と$\eta_4$はそれぞれ同じような値を示している.$\eta_1$は価格上昇を伴う約定,$\eta_2$は価格下降を伴う約定のベースライン強度を示すパラメーターであることから,価格上昇と価格下降を伴う約定のベースライン強度は同じように変動している.すなわち,自己励起性及び相互励起性を除いた場合,価格上昇と価格下を伴う約定はほぼ同じ頻度で発生するということがわかる.次に${\boldsymbol{\Theta}}$に注目すると,先の結果と同様に$\theta_{31},\theta_{33},\theta_{42},\theta_{44}$の値が他のパラメータに比べて大きくなっており,1年を通じて同じ傾向がみられる.最後に,$\boldsymbol{p}$の値の変化に注目すると,$p_2$や$p_4$は月によっては前月比0.5倍から2倍に変動していることがわかる.$\boldsymbol{p}$はインパクト関数内のパラメータであるので,この結果からマークの大きさが強度関数に与えるインパクトの大きさは銘柄を固定しても月によって変動する可能性があるといえる.

図10 トヨタの月ごとの推定値の平均値の変化
次に,クロスセクション,すなわち複数の銘柄に関する実証を行い,銘柄間の比較を行う.楽天,ソニー,トヨタ,ソフトバンク,国際帝石,丸紅,三井不動産の計7つの銘柄それぞれについて,5月7日から5月31日の19営業日分のサンプルを,ウィンドウサイズを$1000$としてセクション3で説明した前処理を行った後にパラメータ推定を行う.
| $\eta_{j}$ | $\mathbb{E}[x_j]$ | $\alpha$ | |||||||
| 銘柄 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 楽天 | .100 | .097 | .047 | .039 | 121.1 | 142.0 | 26.3 | 23.1 | 80.3 |
| ソニー | .233 | .235 | .205 | .206 | 48.0 | 48.8 | 8.5 | 8.8 | 86.8 |
| トヨタ | .0976 | .0881 | .161 | .147 | 42.7 | 44.8 | 8.0 | 7.2 | 84.7 |
| ソフトバンク | .190 | .190 | .137 | .125 | 45.5 | 43.6 | 8.4 | 7.9 | 96.8 |
| 国際帝石 | .0932 | .0874 | .268 | .257 | 43.6 | 41.3 | 5.6 | 5.7 | 112 |
| 丸紅 | .102 | .0884 | .125 | .118 | 53.4 | 52.6 | 7.4 | 6.6 | 94.4 |
| 三井不動産 | .0503 | .0520 | .0737 | .0627 | 42.2 | 44.9 | 5.6 | 5.6 | 82.7 |
表3は,ベースライン強度$\eta_j$, 各系列のマークの大きさの平均値$\mathbb{E}[x_j]$,そしてカーネル関数のパラメータ$\alpha$の推定値の平均値をまとめたものである.最初に,ベースライン強度$\eta_j$の大きさについて考察する.表3の値からまず明らかとなるのは,銘柄によってベースライン強度の水準が異なるということである.本研究で選択した銘柄の中では,ソニーのベースライン強度がいずれの系列も最も大きく,続いてソフトバンクグループがそれに続く.それに対して,約定に関係する系列1,2は三井不動産のベースライン強度が最も小さく,気配値の変化に関連する系列3,4については楽天のそれが最も小さい.一方で,それぞれの銘柄ごとに見ると,ベースライン強度の水準は概ね同じ水準を取っている.唯一,国際帝石は約定に関するベースライン強度が低い水準なのに対して,気配値の変化に関する強度が大きい.ベースライン強度が取引に誘発されたのではない基礎的な取引需要に対応していると考えるならば,銘柄ごとにその水準に違いが出ることには説明がつくと考えられる.
マークサイズの期待値表3の$\mathbb{E}[x_j]$は,各系列ごとのマークの大きさの期待値を表している.この値は,(2)式のインパクト関数$g_i$を計算するときに用いられるため,その推定値として推定区間ごとの各系列におけるイベント発生時のマークの大きさ(注文数の大きさ)の平均値を利用する.
系列間の比較をすると,どの銘柄においても系列1と2,系列3と4の平均サイズはほぼ同じあり,全て,系列1,2のサイズが大きい.また,銘柄間の比較においては,楽天のマークの平均サイズが他と比べて非常に大きいことが読み取れる.この事実は,約定が行われないスプレッドの外に追加の注文を出す場合には,小さいサイズでの注文が出されていることを意味している.
カーネル関数のパラメータ$\alpha$表3の最後の列は,各銘柄ごとのカーネル関数のパラメータ$\alpha$の値の平均値を記している.7銘柄の中では,国際帝石の$\alpha$が$112$で最も大きく,楽天が$80.3$で最も小さい.すなわち,国際帝石の取引のインパクトが比較的短い時間に消えるのに対し,楽天のそれは長い時間残る傾向がある.
分枝行列続いて,分枝行列$\boldsymbol{\Theta}$の結果について考察する.図11と図12は,分枝行列$\boldsymbol{\Theta}^\top$をヒートマップとして表現したものであり,内部にはその数値が書かれている.ヒートマップは,縦軸が発生したイベントの系列,横軸がインパクトを受ける系列が対応しており,色が濃いほどインパクトが大きいことを表している.
7つの図に共通する特徴として$\theta_{31}, \theta_{42}, \theta_{33}, \theta_{44}$の部分が濃い,すなわちインパクトが大きいことが分かる.この事実は,自己励起性に関しては,約定価格の方向にかかわらず,約定というイベントそれ自体は,次の約定にはあまり影響を与えてないが,約定されない気配値の変化は,その後の気配値の変化を同じ方向に加速させる傾向があると解釈可能である.一方の相互励起性については,系列1,すなわち価格上昇を伴う約定が,系列3の最良買い気配値の変化を伴う系列に影響を与える傾向があることを示唆している.また,系列2,すなわち価格下落を伴う約定は,系列4の最良売り気配値の変化を伴う系列に影響を与える傾向があることを示唆している.つまり,相互励起性に関しては,価格が上昇する局面においては買い手(ビッド)の行動が活発になる一方で,価格が下落する局面では売り手(アスク)側の行動が活発になる傾向があると解釈できる.以上の特徴は,濃淡はあるものの選択した7銘柄全てに現れていることから,銘柄にかかわらず板を使った取引に備わる特徴である可能性が高い.

図11 $\boldsymbol{\Theta}^\top$の推定値のヒートマップ1

図12 $\boldsymbol{\Theta}^\top$の推定値のヒートマップ2
次に,マークの大きさが強度関数に与える影響に関して,銘柄間の比較分析を行う.本研究ではインパクト関数として(2)式を利用している.この関数は切片が$\frac{1-p_j}{\mathbb{E}\left[1+(x_j-1)p_j \right]},$係数が$\frac{p_j}{\mathbb{E}\left[1+(x_j-1)p_j \right]}$の一次関数である.つまり,インパクト関数は,パラメータ$p_j$とともに,マーク$x$の期待値$\mathbb{E}[x_j]$にも依存する.
表4は,銘柄ごとに,系列別にパラメータ$p_j$の推定値をまとめた表である.代表値として平均値と中央値の両方を示している.表5は,東証一部で取引されている7銘柄の基本情報をまとめたものである.本研究の実証分析で用いた2019年5月は全体としては株価が下降傾向にあったことが確認できる.また取り上げた7銘柄の株式の出来高は十分に大きいことも分かる.また,図13(a)から図13(d)は系列1から系列4のそれぞれについて,横軸にマークの大きさ(注文サイズ),縦軸にインパクト関数$g_j$を描写したグラフである.これらのグラフにより,インパクト関数の効果を銘柄間の比較分析することが出来る.これら4つのグラフより共通に読み取れる傾向としては,第1に,全ての銘柄の全ての系列において,マークはインパクト関数に正の影響を与えていることである.この結果はLee and Seo (2017)による2011年のニューヨーク証券取引所におけるIBMのティックデータを用いたマーク付きHawkes過程を用いた分析結果と整合的である.第2に,おおよその傾向として,それぞれの銘柄ごとで系列1と系列2のインパクト関数は比較的似ており,同様に系列3と系列4のインパクト関数は比較的似ている.すなわち,約定が発生する注文は,価格変動の向きにかかわらず同じようなインパクト関数を持つ場合が多い.同じように,板中心が変化する注文もまた類似のインパクト関数を持つ場合が多い.そして,約定が発生する場合のインパクトとはその効果が異なるケースが多いと推察できる.
次に,銘柄間の比較を行うと,約定を伴う注文に対応する系列1,2に関しては,ソフトバンクのインパクト関数が比較的大きくて,楽天のそれが小さい.一方,板中心が変化する注文に対応する系列3,4に関しては,三井不動産とソフトバンクのインパクト関数が大きい.
| 系列ごとの$p_{j}$の平均値 | 系列ごとの$p_{j}$の中央値 | $p_{j}=0$の割合($\%$) | ||||||||||
| 銘柄 | $1$ | $2$ | $3$ | $4$ | $1$ | $2$ | $3$ | $4$ | $1$ | $2$ | $3$ | $4$ |
| 楽天 | 1.20e-2 | 7.40e-3 | 6.85e-3 | 1.20e-2 | 1.04e-2 | 6.21e-3 | 6.59e-3 | 1.18e-2 | 0.0 | 0.0 | 0.0 | 0.0 |
| ソニー | 2.02e-2 | 2.92e-2 | 5.42e-3 | 2.81e-3 | 1.79e-2 | 2.17e-2 | 2.81e-10 | 8.95e-11 | 0.0 | 0.0 | 58.5 | 66.7 |
| トヨタ | 2.60e-2 | 2.41e-2 | 3.90e-3 | 2.29e-2 | 1.68e-2 | 1.62e-2 | 2.02e-4 | 2.09e-7 | 0.0 | 0.0 | 42.9 | 49.2 |
| ソフトバンク | 4.25e-2 | 3.60e-2 | 1.61e-2 | 2.25e-2 | 3.14e-2 | 2.25e-2 | 6.60e-3 | 1.39e-2 | 0.0 | 0.0 | 26.2 | 19.0 |
| 国際帝石 | 1.04e-2 | 1.03e-2 | 1.24e-2 | 1.17e-2 | 7.55e-2 | 7.33e-3 | 3.64e-3 | 6.71e-4 | 6.4 | 5.3 | 42.2 | 47.6 |
| 丸紅 | 8.12e-3 | 5.77e-3 | 6.02e-2 | 1.12e-1 | 6.34e-2 | 4.27e-3 | 2.80e-11 | 8.05e-3 | 1.4 | 2.7 | 63.0 | 31.5 |
| 三井不動産 | 2.31e-2 | 1.72e-2 | 2.29e-2 | 2.94e-2 | 1.38e-2 | 1.53e-2 | 1.53e-2 | 1.48e-2 | 0.0 | 0.0 | 29.2 | 29.2 |
より詳細に表4をみると,系列1,2に関しては,若干の順序にずれはあるものの,総じて,その期間の株価の水準が高い銘柄ほど$p_1, p_2$の値が大きい傾向があることが分かる.本研究で取り上げた銘柄においては,単元株数が全て100株であることを考えると,株価の水準の大小は,最低購入代金の大小を意味する.したがって,最低購入代金が大きいほど$p_1, p_2$の値が大きくなる傾向がある.このことより,売り買いいずれの方向においてもマーク1単位の経済的インパクトが大きい銘柄ほど$p_j$の値も大きくなっているといえる.次に,系列3,系列4に注目すると,平均値と中央値の乖離が激しいことが分かる.これは,推定された$p_3, p_4$の値がほぼ0に等しいケースが多数発生していることが原因である.表4の最後の4列は,サンプルの中で$p_j$の推定値がほぼゼロ(絶対値が$10^{-6}$以下)の割合を示した値である.この表より,楽天を除く6銘柄では,$20%$から$67%$の割合で$p_3, p_4$の値がゼロとなっている.すなわち,たとえ中心価格の変動を伴うビッド及びアスク注文があっても,約定を伴わないイベントにおいてはマークの大きさが強度関数にインパクトを与えていない場合が相当割合あることになる.また中央値の欄から明らかなように,$p_3, p_4$が非ゼロの場合でも,それらの値は$p_1, p_2$より小さい.以上の結果は,マークの大きさが影響を受けるのは主として約定された場合で,約定が伴わない場合にはその可能性は比較的小さく,ある場合にもそのインパクトは小さいと考えられる.約定を伴わない指値注文は,後にキャンセルすることもでき,その場合には注文行動が価格には全く反映されないことを考えると,この結果は理にかなっていると考えることが出来る.同時に,本研究では直接調査していないが,注文がキャンセルされる可能性が投資家の間で認識されていることを示唆している.
上記の分析は,唯一楽天には全く当てはまらない.すなわち,楽天の$p_3, p_4$の値は常に非ゼロであり,かつその大きさも$p_1, p_2$と同水準である.楽天が他の銘柄と異なる結果になった真の原因は不明であるが,楽天が他の6銘柄と異なっている点がいくつかある.第1に,表3から明らかなように,楽天の1回のイベントに対応する取引のサイズは他の銘柄それと比べて著しく高い.第2に,他の6銘柄が東京証券取引所が提供するTOPIX100と呼ばれる,TOPIX銘柄の中でも時価総額および流動性の高い大型株100銘柄の構成銘柄となっているのに対して,楽天はその構成銘柄とはなっていない.機関投資家など,特定のカテゴリーの市場参加者にとって,特に流動性の視点からTOPIX100構成銘柄に含まれているか否かは,彼らの実行する投資戦略に影響を与える可能性があると考えることができる.その意味において,楽天がほかの6銘柄と異なった投資家層で取引されている可能性がある.第3に,表5より,楽天の呼値1単位のリターンが最も大きい.すなわち,他の銘柄と異なり,リターンの観点から見て楽天の株価は相対的には滑らかには動かず,離散的に動く傾向がある.この事実もまた投資家の取引戦略に影響を与える可能性がある.以上の違いはあくまで推論であり,科学的な根拠としては不十分であるが,投資家層や投資戦略の違いを生み出す要因としての可能性がある.したがってこの点に関しては,さらなる研究を積み重ねる必要があると考えられる.

図13 系列1から系列4のインパクト関数
| 2019年5月の株価 | 呼値 | 呼値1単位の | ||||
| 銘柄名 | 始値 | 終値 | リターン | 出来高 | (円) | リターン(%) |
| 楽天 | $1,241$ | $1,235$ | $-3.9$ | $223,570,550$ | $1$ | $.038$ |
| ソニー | $5,500$ | $5,257$ | $-2.0$ | $135,357,900$ | $1$ | $.008$ |
| トヨタ | $6,855$ | $6,384$ | $-3.1$ | $98,152,400$ | $1$ | $.007$ |
| ソフトバンク | $11,870$ | $10,250$ | $-6.4$ | $132,442,000$ | $1$or$5$ | $.004$ or $.021$ |
| 国際帝石 | $1,066.5$ | $878.8$ | $-8.4$ | $136,364,600$ | $0.1$ | $.005$ |
| 丸紅 | $794.1$ | $683.4$ | $-6.5$ | $136,252,900$ | $0.1$ | $.006$ |
| 三井不動産 | $2,594.5$ | $2,631.5$ | $0.6$ | $65,147,200$ | $0.5$ | $.008$ |
本研究では,マーク付き多次元Hawkes過程を用いて東京証券取引所で取引されている複数の銘柄に関する高頻度注文板データのモデリングを行った.第一に,時間変更定理を用いて残差過程を導出し,モデルの有効性の確認を行った.続いて,4系列のイベントに関するマーク付き多次元Hawkes過程のパラメータをそれぞれ導出し,強度関数の観点からそれぞれの銘柄の特性を議論した.本研究の実証研究の結果,推定されたパラメータは,銘柄や推定区間により変動はするものの,概ね安定的である事が確認できた.さらに,次の事実が観測できた.まず,分枝行列の情報より,約定というイベントに対する自己励起性は小さいのに対し,約定されない気配値の変化に対する自己励起性は相対的に大きい.一方,相互励起性に関しては,価格上昇を伴う約定が最良買い気配値の変化を伴う系列に,価格下落を伴う約定は最良売り気配値の変化を伴う系列に大きな影響を与えている.次にマークの大きさとして注文量を考え,それがその後の強度関数にどのような影響を与えているかについての実証を行った.まず,約定時のマークの大きさは強度関数に正のインパクトを与えることが明らかとなった.また,影響の大きさについては,分枝行列の場合と異なり,最良気配値の変化よりは,約定イベントの方が相対的にインパクトの大きさが大きいことが明らかとなった.また,多くの銘柄においては最良気配値の変化イベントにおいて,注文量の大きさはほとんどインパクトを与えないということも観測された.
今後の研究としては,以下の課題が考えられる.第1は,フィッティング向上のためのモデルの精緻化の可能性である.本研究では,重要と考えられる4つのイベントを系列として取り上げたが,板の変化という視点から見ると他にも様々なイベントが発生している.これらの情報を取り込むことで注文板のさらに複雑な挙動をモデル化することができる.また,本研究では技術的な観点から,いくつかの単純化を行っているが,そのような単純化を行わないモデルも考えることが可能である.ただし,いずれの場合にでも推定されるパラメータが不安定化する可能性には注意する必要がある.第2に,インパクト関数の形状をさらに明らかにする目的で,実証分析に基づく最適なインパクト関数の導出が挙げられる.本研究においては一次関数のインパクト関数を用いたが,より良いフィッティング精度をもたらすインパクト関数の存在は否定できない.マークの大きさが強度関数に与えるインパクトは,データから直接観測することができない情報であるが,より実際のデータに即したインパクト関数を導出することが期待される.第3に,本研究では複数の銘柄で1週間から1年間のデータを用いた実証を行っているが,本研究で導き出された知見がその他の銘柄や異なる期間でも安定的に現れる特徴なのかを調べることは大変興味深い.また,それらの特徴がどのようなメカニズムで現れるかについてのさらなる検証を行うことも重要な今後の課題である.
本研究を進めるにあたり,慶應義塾大学ビジネススクール教授の林高樹先生から数多くの貴重な助言をいただきました.加えて,論文の査読者の方からも貴重なご意見を多数いただきました.また,高頻度電文データFLEX Fullデータの提供に関しましては,株式会社日本取引所グループの皆さまに大変お世話になりました.ここに御礼申し上げます.
* 本研究は,科研費基盤研究B (YYK5B02) の助成を受けている.