本研究は,外国為替証拠金取引業務におけるロールオーバー戦略について検討した.一般に実務においては流動性の観点より,受渡し日が短いトゥモローネクストでロールオーバーするのが一般的である.しかし理論的には金利のタームプレミアムを考慮すると,1週間や3週間など長期のフォワード取引を活用することにより受取りスワップポイントの上乗せを期待できる.しかし稀に短期のスワップ金利が急騰する場合があり,その際に長期フォワード取引を選択していれば高いスワップポイントを逃してしまう.そこで我々は機械学習によって長期のフォワード取引を積極的に選ぶべきタイミングを検出し,短期のトゥモローネクストおよびより長期のフォワード取引を組み合わせた混合戦略を提案する.このタイミングは,対象通貨における為替相場のみならず,株式・債券・商品先物など様々な要因が非線形的に影響すると考えられる.またフォワードレートは一般的にカバー付き金利平価説によって定式化できるが,突発的な政治経済情勢などの変化によって,現実のフォワードレートは理論値から乖離する可能性がある(Du et al. (2018a)).その結果,タームプレミアムの逆転現象(短期と長期のフォワード取引から得られるスワップ金利の逆転現象)も実際に度々観測される.本研究ではこのような状況を踏まえ,理論値からの乖離に影響を与えうる要因を説明変数とし,機械学習によって適切なフォワード期間を選択するための判別モデルを構築した.教師データとして過去の最適解を学習し,その後の判別を行った結果,約70%の正答率を実現できた.さらに獲得したスワップポイントのリスクリターン比によれば,我々の混合戦略は長期のフォワード取引と同等の安定性を維持したまま,短期のトゥモローネクストと同等の収益性を実現できた.
外国為替証拠金(Foreign Exchange Trading: FX)取引では,約定の2営業日後に現物の受渡しを行うルールがある.しかし一般的に取引額は高額に及ぶため,FX業者など非銀行が毎回現物を用意するのは非現実的である.そこで長期に渡りドル円を買い持ちしたい場合,約定の翌日にドル円を売り,さらに同時に新規にドル円を買う.つまり売り取引と買い取引を同時に行い,決済日を繰り延べする.これをロールオーバーといい,ロールオーバーを繰り返すことで現物の受渡しを無期限化できる.さらにロールオーバー時にトゥモローネクスト(以下,トムネ)や1週間フォワードといった,受渡し日を自由に長期化できるフォワード取引を組み合わせることでスワップポイントを獲得できるようになる1.外国為替取引において通貨ごとに金利が異なり,この金利差はスワップポイントとして表される.通常の経済状況では決済日までの期間が長いほど金利が高くなるタームプレミアムが考えられるため,決済日が長期に及ぶフォワード取引の方が多くのスワップポイントを獲得しやすい2.しかし流動性リスクや在庫管理業務の観点により,実務においては受渡し日が短いトムネでロールオーバーするのが一般的である.
本研究ではロールオーバーにおける長期のフォワード取引の選択について分析する.フォワードレートと金利の関係については一般的にカバー付き金利平価説(Covered Interest rate Parity: CIP)によって定式化できる.2008年のグローバル金融危機以前はCIPからの乖離は一時的という報告が多くの研究でなされてきた(Taylor (1987), Fletcher and Taylor (1996), Takezawa (1995), Akaram et al. (2008))3.さらにLustig et al. (2011)やMenkhoff et al. (2012)など為替ポートフォリオの研究においても,CIPが成立していることを前提でポジションを構築することが一般的に行われている.しかしグローバル金融危機以降はCIPからの乖離が大きく,また継続することがBaba and Packer (2009), Du et al. (2018a), Cerutti et al. (2021)などで報告されている.その理由としてBaba and Packer (2009)では金融機関同士のカウンターパーティーリスク,Du et al. (2018a)では金融危機後の銀行への規制,Cerutti et al. (2021)では上記の要因に加え,非伝統的金融政策が重要な役割を果たしていることが指摘されている.加えてDu et al. (2018b)とAvdjiev et al. (2019)は金融危機以後は米ドルによる資金調達コストが上昇していることを示している.以上のようにCIPからの乖離について近年市場構造が変化しており,大きな注目を集めている.
我々は上述の先行研究のようにCIPからの乖離の要因を検証するのではなく,ロールオーバー戦略の効率化を目的とする.本研究ではロールオーバーを行う金融機関は,トムネでのロールオーバーを複数回行うか,あるいはより長期の先物でロールオーバーを行うかを選択する.この選択を決定するモデルに機械学習を用いる.近年,機械学習によるモデルの有効性がファイナンスの研究においてもクレジットリスク(Khandani et al. (2010), Butaru et al. (2016)),株価リターン(Gu et al. (2020)),債券リターン(Bianchi et al. (2021))で有効性が示されている.本研究では機械学習の中でもChen and Guestrin (2016)により提案されたXGBoostを用いる.XGBoostはNobre and Neves (2019)やYe and Schuller (2021)で示されているように非線形な市場の構造を捉えるのに適している.マクロ経済変数と為替の収益機会についても非線形の関係があることが知られているため4,XGBoostにより通常の線形モデルでは捉えきれない非線形性を捉えることが期待される.なお本論文は,著者らの研究成果(雉子波・杉本・酒本・鈴木 (2021))に,追加実験を行ったうえで改訂したものである.
本稿に用いる数式記号を表1に示す.
カバー付き金利平価とは,どの通貨で資産を保有しても収益率が同じになることを仮定した為替レートの決定理論である.ドル円市場を例とすると,
| (1) |
| (2) |
しかし実際のフォワードレー
| (3) |
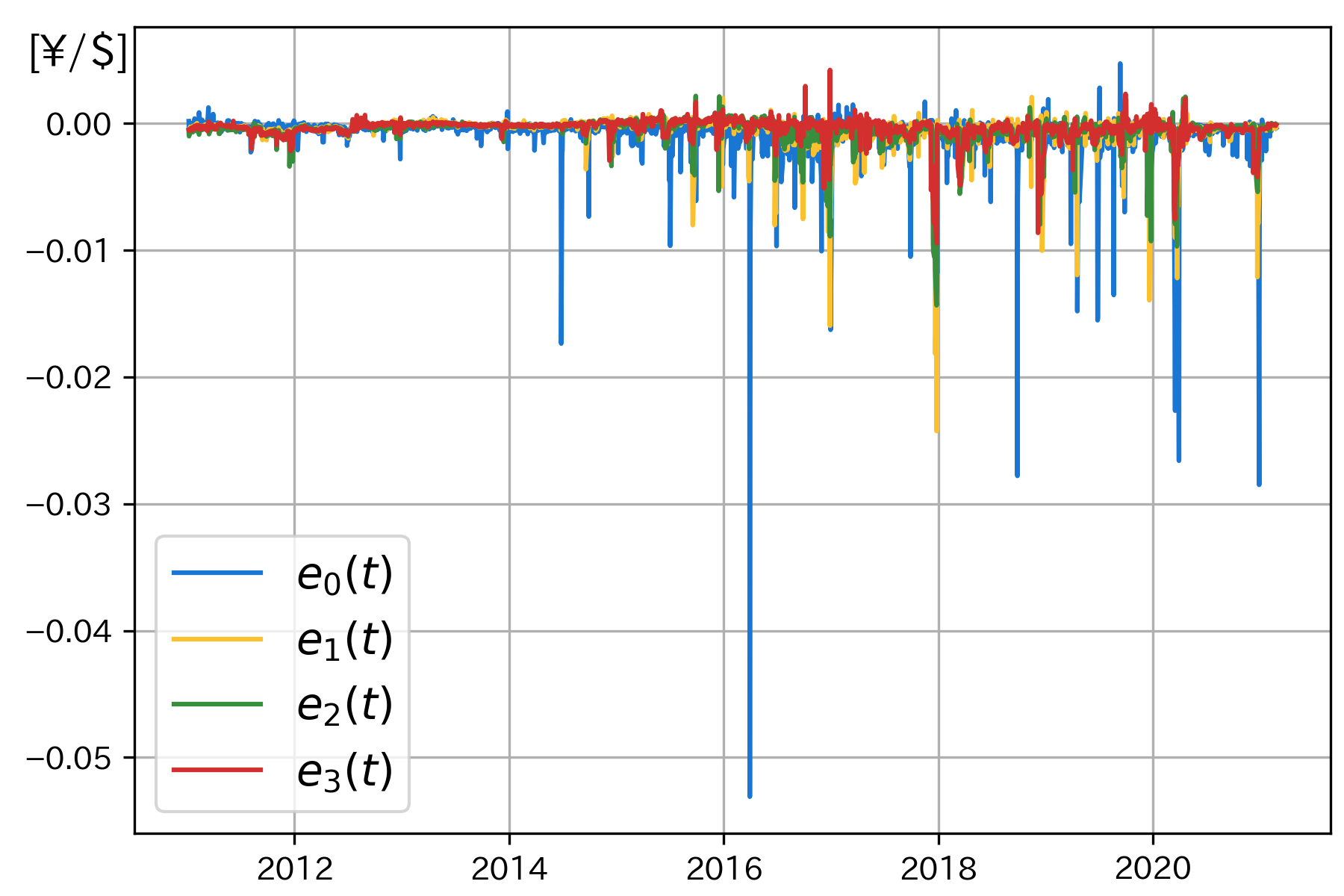
図1 カバー付き金利平価(理論値)からの乖離
| 記号 | 意味 |
| フォワード日数 | |
| フォワードレートの実測値 | |
| フォワードレートの理論値 | |
| 理論値からの乖離: |
|
| スポットレート | |
| スワップポイント: |
|
| 日本のLIBOR金利(年率) | |
| 米ドルのLIBOR金利(年率) | |
| 内外金利差: |
|
| 変数の時間変化: |
本稿は最も基礎的な設定として,トムネ(
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
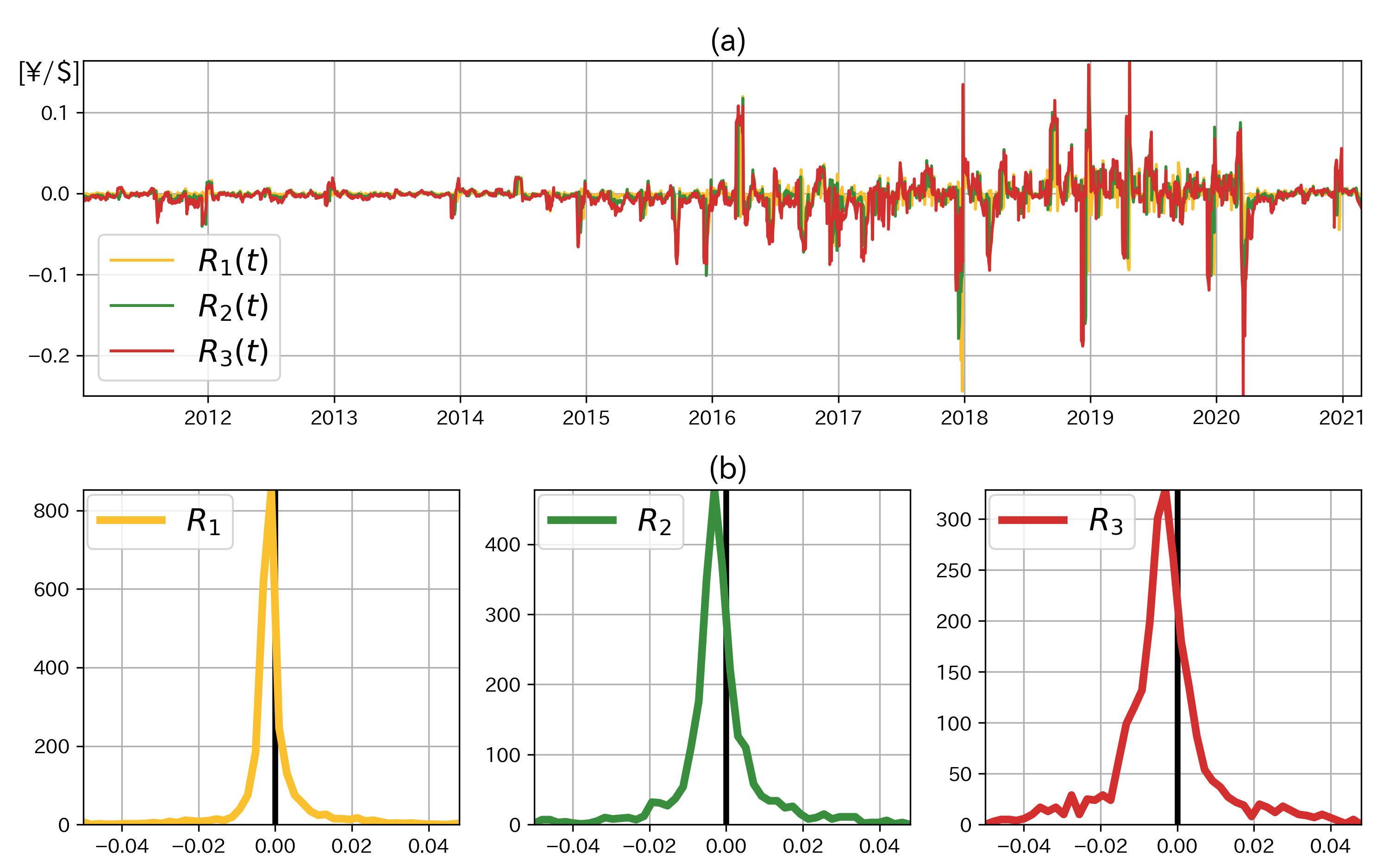
図2 (a) 目的変数
次に,
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
式(9)を構成する各要因 (
これらの乖離には自己相関構造が存在するため,現在までに確定している乖離のヒストリカルデータが機械学習にとって有用だと考えられる (仮説1).しかし2章で考察したように,乖離は為替の受給変化の影響を受けるため,様々な金融市場に関する説明変数も有用だと考えられる(仮説2).さらに金融システムは複雑系であるため,機械学習においては線形モデルより非線形モデルの方が有用だと考えられる7(仮説3).次章において,この3つの仮説を検証する.
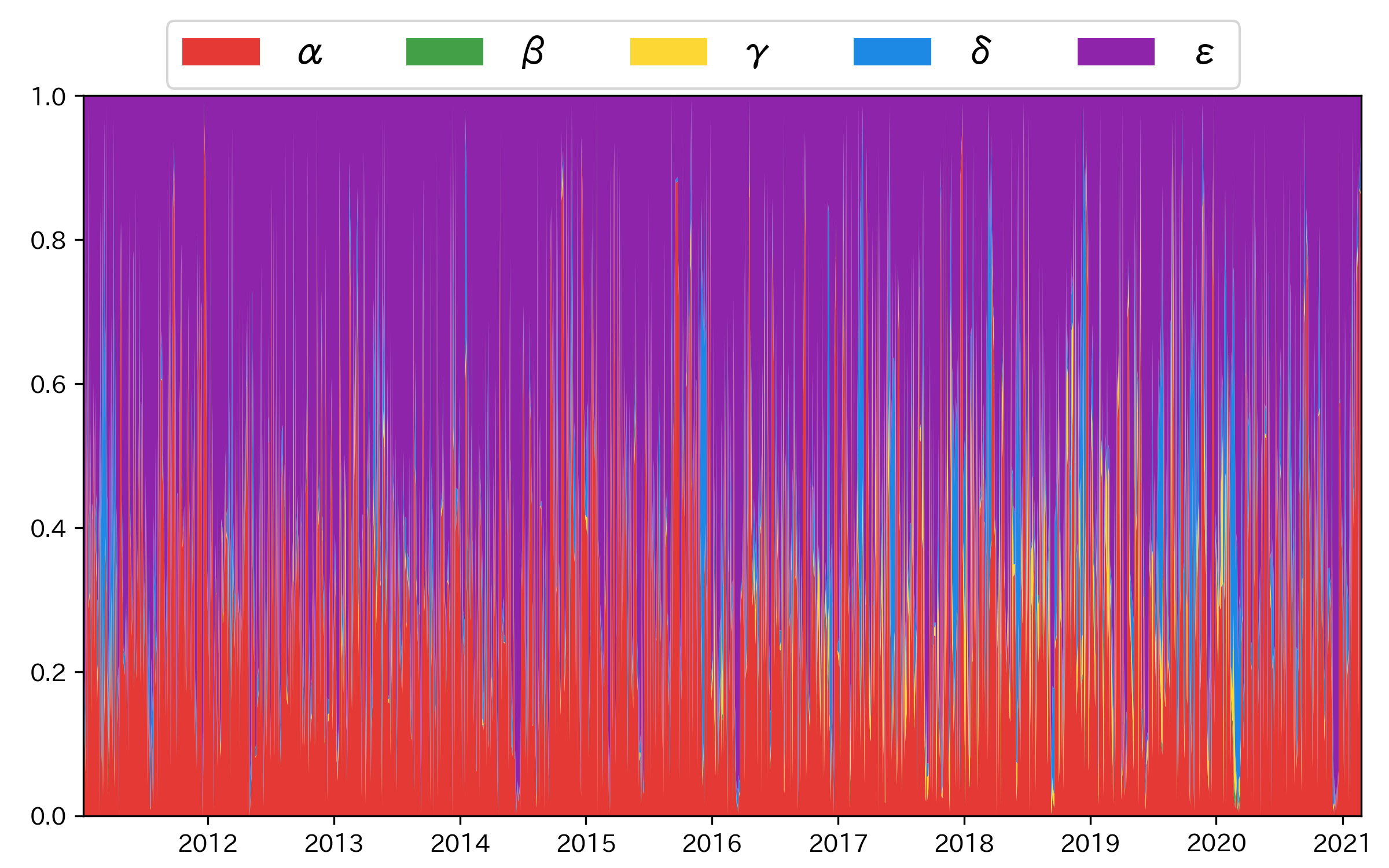
図3 要因分解の混合割合(ただし

図4 (a) 乖離
仮説3を検証するために,線形モデルと非線形モデルを比較する.本研究は2クラス判別問題であるため,線形モデルとして「線形判別分析」「ロジスティック回帰 (正則化なし)」「ロジスティック回帰 (L1正則化あり)」「ロジスティック回帰 (L2正則化あり)」「サポートベクターマシン (線形カーネル)」の5モデルを用いる.なお正則化は,多重共線性や過学習を緩和する効果を期待している.比較対象となる非線形モデルについてもモデル数を揃えつつ,代表的な「k近傍法」「ニューラルネットワーク」「サポートベクターマシン (多項式カーネル)」「サポートベクターマシン (RBFカーネル)」「XGBoost」の5モデルを用いる.Pythonのライブラリとして,XGBoostには「xgboost 1.3.3」を用い,それ以外には「scikit-learn 0.24.1」を用いた.なお一般的なモデリング性能を評価すべく,ハイパーパラメータはデフォルト値を用いた.それらの詳細を付録2に示す.
2014年1月〜2021年1月を機械学習の評価期間とし,毎日動的に再学習することでモデルパラメータを更新する.各評価日
| 式(9)中の時刻 |
|
| 期待超過スワップポイント | |
| 国内外の金利差 | |
| スポットレート | |
| 理論値からの乖離 | |
| フォワード日数 | |
| 目的変数 |
|
| 実現超過スワップポイント | |
| 実現スワップポイント | 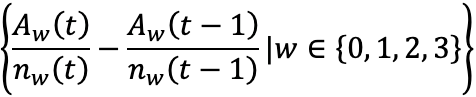 |
| 乖離 |
|
| 乖離のヒストリカル合計値 | 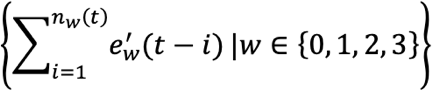 |
| スポットレート |
|
| 変化率 | 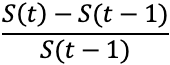 |
| モメンタム | 変化率の平均値(直近25日) |
| ボラティリティ | 変化率の標準偏差(直近25日) |
| VIX指数 | |
| CVIX指数 | |
| 金利に関する変数 | |
| 内外金利差 | |
| 物価に関する変数 | |
| WTI原油先物価格 | |
| CRB原材料価格指数 | |
| CRB金属サブ指数 | |
| CRB食品サブ指数 | |
| 国債に関する変数 | |
| 米国債金利(3ヶ月) | |
| 米国債金利(2年) | |
| 米国債金利(10年) | |
| 日本国債金利(3ヶ月) | |
| 日本国債金利(2年) | |
| 日本国債金利(10年) | |
| 景気に関する変数 | |
| TOPIX指数 | |
| S&P500指数 | |
| World Stock指数 | |
| 金スポット価格 | |
| ドルインデックス | |
| 円インデックス | |
3章の仮説を鑑み,機械学習に用いる説明変数を表2に示す.時刻
図5に,評価期間における各モデルのROC曲線およびAUCを示す.ROC曲線はTPR(True Positive Rate: 真陽性率)とFPR(False Positive Rate: 偽陽性率)のトレードオフを示し,その下方面積を表すAUC(Area Under the Curve) 値が大きいほど判別性能に優れている.結果として,いずれの

図5 ROC曲線とAUC値: (a)

図6 XGBoostにおける説明変数の重要度(ただし
次に仮説1,2の検証として,XGBoostに用いた各説明変数の重要度(Feature importance)を図6に示す.この重要度の算出には,xgboostライブラリのget_scoreメソッドにて「importance_type='gain'」と設定した11.オリジナルのXGBoost(Chen and Guestrin (2016))は決定木を構成するため,ノード毎の分割基準に各説明変数をランダムに割り当て,ノード分割によって低減できた不純度(ジニ係数など)の差分を情報利得(gain)として算出する.XGBoost全体を学習した後,説明変数毎に複数の情報利得が得られるため,説明変数毎に情報利得を平均化することで各説明変数の重要度を算出した.なお比較のため,各時刻
XGBoostによる判別モデルを実務に活用することを想定し,どの程度の収益改善を期待できるのか検証する.その際にベストな運用パフォーマンスを実現すべく,Optuna(Akiba at el. (2019))によりXGBoostのハイパーパラメータを最適化した.その評価指標として,検証期間におけるLog損失を最小化するハイパーパラメータを選択した.表3にハイパーパラメータの探索範囲を示す.未記載のハイパーパラメータはデフォルト値を用いた.その他,評価期間や評価日
| random_state | |
| max_depth | |
| min_child_weight | |
| gamma | |
| colsample_bytree | |
| subsample |
図7に評価期間の混同行列を,表4に評価スコアを示す.提案手法の評価スコアはより長期の長期フォワードを対象にするほど向上している.これは図5の各

図7 混同行列: (a)
| 取引手法 | 正答率 | 再現率 | 適合率 | F値 |
次に,獲得したスワップポイント
| (15) |
表5に,獲得したスワップポイント集合
まず,常にトムネを選択する場合(
さらに表6に,リターンとリスクの詳細を示す.なお,
| (16) |
結果として,平均値については提案手法と常にトムネを選択する場合が高リターンであり,提案手法で混合するフォワード取引を長期化するほど平均値は向上している.これは常に長期フォワードを選択する場合も同様であり,タームプレミアムによる恩恵だと考えられる.標準偏差については,中心極限定理により常に長期フォワードを選択する場合が低リスクであり,常にトムネを選択する場合が高リスク,提案手法はその中間である.しかし下方リスクのみに着眼すると,提案手法のリスクリターン比(平均値/半偏差)は,常に長期フォワードを選択する場合と同等である.つまり現実的には,提案手法は常に長期フォワードを選択する場合と同等の低リスク水準を実現しつつ,常にトムネを選択する場合と同等の高リターンを獲得できる混合戦略と言える.
| 取引手法 | 最小値 [¥/10Lot] |
25パーセンタイル [¥/10Lot] |
中央値 [¥/10Lot] |
75パーセンタイル [¥/10Lot] |
最大値 [¥/10Lot] |
| 常にトムネのみ ( |
|||||
| 常に1週間フォワードのみ ( |
|||||
| 常に2週間フォワードのみ ( |
|||||
| 常に3週間フォワードのみ ( |
|||||
| 提案手法 (混合戦略 |
|||||
| 提案手法 (混合戦略 |
|||||
| 提案手法 (混合戦略 |
| 取引手法 | 平均値 [¥/10Lot] |
標準偏差 [¥/10Lot] |
平均値/ 標準偏差 |
半偏差 [¥/10Lot] |
平均値/ 半偏差 |
| 常にトムネのみ ( |
|||||
| 常に1週間フォワードのみ ( |
|||||
| 常に2週間フォワードのみ ( |
|||||
| 常に3週間フォワードのみ ( |
|||||
| 提案手法 (混合戦略 |
|||||
| 提案手法 (混合戦略 |
|||||
| 提案手法 (混合戦略 |
フォワードレートの理論値(カバー付き金利平価)からの乖離に着眼し,より多くのスワップポイントを獲得できるフォワード取引を機械学習により判別した.その際に,長期フォワード取引による追加的なスワップポイントを目的変数とし,これを解析的に要因分解することで機械学習モデルを設計した.特に要因分解を通じて,理論値からの乖離の高い影響力や非線形モデルの必要性を認識し,乖離に影響し得る様々な金融市場に関する説明変数を採用した.実データ分析を通じてこれらの妥当性を検証したところ,広範な説明変数が機械学習に寄与している様子や,非線形ダイナミクスを表現できるXGBoostの導入により線形なロジスティック回帰よりも判別精度を向上できることを確認した.実運用を想定したシミュレーションにおいては,本判別モデルによる正答率やF値は約
なお1章で述べたように,実務においては流動性や在庫管理に伴う業務リスクも考慮しつつ長期のフォワード取引を選択する必要がある.そこで今後の課題として,このような業務リスクとタームプレミアムのトレードオフを考慮しつつ,最適なフォワード取引を判別する.さらにリスクの観点から,ドル円市場のみならず新興国市場についても検証する.
ここで,
最終式にて
が得られる.
4章の機械学習に用いたハイパーパラメータを以下に示す.各項目の意味については,ライブラリの説明サイト(scikit-learn: https://scikit-learn.org/0.23/,XGBoost: https://xgboost.readthedocs.io/en/release_1.3.0/parameter.html)を参照されたし.
| 線形判別分析 | l1_ratio | None | |
| solver | svd | ロジスティック回帰(L2正則化あり) | |
| shrinkage | None | penalty | l2 |
| priors | None | dual | False |
| n_components | None | tol | 1e-4 |
| stor_covariance | False | C | 1.0 |
| tol | 1.0e-4 | fit_intercept | True |
| covariance_estimator | None | Interccept_scaling | 1 |
| ロジスティック回帰(正則化なし) | class_weight | None | |
| penalty | none | random_state | 0 |
| dual | False | solver | lbfgs |
| tol | 1e-4 | max_iter | 100 |
| C | 1.0 | multi_class | auto |
| intercept_scaling | 1 | verbose | 0 |
| class_weight | None | warm_start | False |
| random_state | 0 | n_jobs | None |
| solver | lbfgs | l1_ratio | None |
| max_iter | 100 | サポートベクターマシン(線形カーネル) | |
| multi_class | auto | C | 1.0 |
| verbose | 0 | kernel | linear |
| warm_start | False | degree | 3 |
| n_jobs | None | gamma | scale |
| l1_ratio | None | coef0 | 0.0 |
| ロジスティック回帰(L1正則化あり) | shrinking | True | |
| penalty | l1 | probability | True |
| dual | False | tol | 1e-3 |
| tol | 1e-4 | cache_size | 200 |
| C | 1.0 | class_weight | None |
| fit_intercept | True | verbose | False |
| intercept_scaling | 1 | max_iter | -1 |
| class_weight | None | decision_function_shape | ovr |
| random_state | 0 | break_ties | False |
| solver | liblinear | random_state | 0 |
| max_iter | 100 | k近傍法 | |
| multi_class | auto | n_neighbors | 5 |
| verbose | 0 | weights | uniform |
| warm_start | False | algorithm | auto |
| n_jobs | None | leaf_size | 30 |
| metric | minkowski | p | 2 |
| metric_params | None | gamma | scale |
| n_jobs | None | coef0 | 0.0 |
| ニューラルネットワーク | shrinking | True | |
| hidden_layer_sizes | (100, ) | probability | True |
| activation | relu | tol | 1e-3 |
| solver | adam | cache_size | 200 |
| alpha | 0.0001 | class_weight | None |
| batch_size | auto | verbose | False |
| learning_rate | constant | max_iter | -1 |
| learning_rate_init | 0.001 | decision_function_shape | ovr |
| power_t | 0.5 | break_ties | False |
| max_iter | 200 | random_state | 0 |
| shuffle | True | XGBoost | |
| random_state | 0 | booster | gbtree |
| tol | 1e-4 | verbosity | 1 |
| verbose | False | validate_parameters | false |
| momentum | 0.9 | nthread | not set |
| nesterovs_momentum | True | disable_default_eval_metric | false |
| early_stopping | False | eta | 0.3 |
| validation_fraction | 0.1 | gamma | 0 |
| beta_1 | 0.9 | max_depth | 6 |
| beta_2 | 0.999 | min_child_weight | 1 |
| epsilon | 1e-8 | max_delta_step | 0 |
| n_iter_no_change | 10 | subsample | 1 |
| max_fun | 15000 | sampling_method | uniform |
| サポートベクターマシン(多項式カーネル) | colsample_bytree | 1 | |
| C | 1.0 | colsample_bylevel | 1 |
| kernel | poly | colsample_bynode | 1 |
| degree | 3 | lambda | 1 |
| gamma | scale | alpha | 0 |
| coef0 | 0.0 | tree_method | auto |
| shrinking | True | sketch_eps | 0.03 |
| probability | True | scale_pos_weight | 1 |
| tol | 1e-3 | updater | grow_colmaker |
| cache_size | 200 | refresh_leaf | 1 |
| class_weight | None | process_type | default |
| verbose | False | grow_policy | depthwise |
| max_iter | -1 | max_leaves | 0 |
| decision_function_shape | ovr | max_bin | 256 |
| break_ties | False | predictor | auto |
| random_state | 0 | objective | binary:logistic |
| サポートベクターマシン(RBFカーネル) | base_score | 0.5 | |
| C | 1.0 | eval_metric | logloss |
| kernel | poly | seed | 0 |
| degree | 3 | seed_per_iteration | false |
本研究の遂行にあたり有益なご助言を頂いた,外貨ex byGMO株式会社の市川 佳彦氏やホ エルデン氏に感謝申し上げます.なお本稿の内容は筆者個人の見解であり,所属組織の公式見解ではありません.本研究の一部はJSPS科研費(20K11969)の助成により行われました.
1 マネックス証券: https://info.monex.co.jp/fx/fx-plus/rule/swap.html(参照日: 2021.9.7)
2 例えばGürkaynak and Wright (2012)などを参照.
3 一方,カバーなし金利平価(Uncovered Interest rate Parity: UIP)は乖離することが多く,収益機会となることが報告されてきた.Fama (1984), Bekaert and Hodrick (1993), Engel (1996), Lustig and Verdelhan (2007), Menkhoff et al. (2012)などを参照.
4 Bansal (1997), Bansal and Dahlquist (2000), Baillie and Kim (2015), Sakemoto (2019)を参照.
5
6 マネックス証券: https://info.monex.co.jp/fx/fx-plus/rule/swap.html(参照日: 2021.9.7)
7 混合割合が微小であるが,
8 1ヶ月間の平均的な営業日数に相当する.各国で祝日数が異なるため土日のみを除いた暦日数を12ヶ月で割ると21.7日になる.
9 後述するROC曲線の下方面積を意味する.
10
11 Python API Reference: https://xgboost.readthedocs.io/en/latest/python/python_api.html(参照日: 2021.12.25)
12 結果として1週間フォワードのみ(