概要

機械学習技術の発展により, 近年では深層強化学習を用いたポートフォリオ構築モデルが提案されている．しかしながら深層強化学習は計算負荷が高いため, 先行研究では少数の投資対象銘柄を対象にしており, また非常に短い間隔でのリバランス問題としてモデルが構築されている．本論文では, 大きな資金を運用する機関投資家の資産運用に利用可能なモデルを構築することを目的として, 広範な投資対象銘柄, 取引コスト（回転率, 流動性）, 月次程度のリバランス間隔などを考慮した深層強化学習モデルを提案する．国内株式市場の株式データを用いた実証分析の結果, 提案したモデルは大型・中型500銘柄の投資対象銘柄を現実的な時間で取り扱うことができ, 構築したポートフォリオは先行研究で利用されている深層強化学習モデルや標準的な機械学習モデルを用いたものに比べ高い有効性を有していることを示した．

1　はじめに

従来，資産運用，特に年金などの大規模な資金を運用する株式運用には平均・分散モデルのような数理最適化モデルを使用し，リターンとリスクのバランスの取れた運用を行うことが一般的であった．このようなポートフォリオ最適化モデルについては，古くから実務的・理論的研究が数多く行われており，様々な運用モデルも提案されている（山本（2008））．

これに対し近年，機械学習技術の発展によりこれらの技術を金融市場予測や資産運用に応用する流れが加速しており，学術の面ではもちろん伝統的な金融企業や新興のフィンテック企業などから様々なサービスが提供され始めている．

機械学習は教師あり学習，教師なし学習，強化学習の大きく３つに分類することができる．教師あり学習はその名の通り学習データに対し正解となるデータ（教師データ）を与え，それをもとに学習を行う方法である．回帰問題や分類問題に用いられ，金融市場予測では株価やインデックスの価格やトレンドの予測に応用されている（Luigi et al.(2018)，Gudelek et al.(2017)）．特に近年のファイナンス分野の研究として，Gu et al. (2020)ではニューラルネットワークやランダムフォレストなどの機械学習手法を用いて，米国の個別銘柄の92の属性情報と翌月の株価リターンの関係を分析している．約60年のデータを用いてモデル構築と検証を行った結果，特にニューラルネットワークを用いて期待リターンを作成し，それに基づく運用を行うことで高い有効性が得られることを示している．ただし，これらの手法では構築するポートフォリオの回転率を考慮することが難しく，月次で100%以上の回転率が必要であることも指摘している．またBianchi et al. (2021)では債券リターンとイールドカーブ情報や128のマクロ経済指標との関係をGu et al. (2020)と同様に解析しており，ニューラルネットワークの有効性を示している．

教師なし学習は教師あり学習とは異なり，教師データを用いない学習方法であり，データの特徴の抽出，表現の変換などに用いられる．クラスタリングや次元圧縮に使用され，金融市場予測ではパターンマッチングなどに応用されている（Heryadi et al.(2017)，Roy et al.(2018)）．

強化学習は教師あり学習，教師なし学習を合わせた性質を持っており，学習データのみを用いると同時に，与えられた報酬を最大化することを目指して学習を行う方法である．具体的にはある環境内におけるエージェント（人工知能）が，現在の状態を観測し，それをもとに行動を選択し，その結果として環境からフィードバックとして報酬を受け取る．そしてエージェントは受け取った報酬を元に行動選択の原理（方策）を改善するという方法である．強化学習の中でも特に状態の観測や行動の選択において深層学習モデルを使用する深層強化学習は，回転率や取引コストを考慮することも可能なことから金融市場予測においてポートフォリオ最適化に応用されており，投資のロボットアドバイザーや自動運用へのニーズの高まりを背景に3つの分類の中でも特に注目を集めている．

深層強化学習をポートフォリオ最適化に応用する研究は今まで多く実施されている．Jiang et al. (2017)は深層強化学習をポートフォリオ最適化に応用した代表的な研究である．この研究ではEnsemble of Identical Independent Evaluators (EIIE)という独自の深層学習ネットワークを考案し，暗号資産12銘柄を30分毎にリバランスを行うモデルを構築した．その結果，Li and Hoi (2014)で提案されているそれまでに提案された取引モデルと比べて，高いリターンが得られることを実証している．これ以降EIIE モデルは多くの研究で参照されている ．Jiang and Liang (2017)ではConvolutional Neural Network（CNN）をベースに構築されたネットワークを利用し，暗号資産12銘柄を30分毎にリバランスして運用しパフォーマンスを計測した．Gao et al. (2020)ではEIIEを拡張したネットワークを構築し，米国株式5銘柄を1日毎にリバランスして運用するモデルを，Soleymani and Paquet (2020)ではオートエンコーダーとCNNを組み合わせたネットワークを構築し，米国株23銘柄を1日毎にリバランスして運用するモデルを提案した．またAdbelKawy et al. (2021)ではDeep Belief Network（DBN）とLong Short Term Memory（LSTM）を組み合わせたネットワークを構築し，米国株5銘柄を1日毎にリバランスして運用し，パフォーマンスを計測した．いずれの研究も深層強化学習モデルの高い有効性を示している．

このように近年，深層強化学習をポートフォリオ最適化に応用した研究がいくつか行われているが，それらはすべて少数銘柄を投資対象として高頻度の取引を行うことを前提としており，大規模な資金を運用する機関投資家の資産運用に適用することは困難である．通常機関投資家は，大量の資金を投資するため数十から数百程度の銘柄を保有しており，取引コストも大きくかかることから概ね1か月から3か月に1回程度の銘柄組み換え（リバランス）を行うことが多い（Sun et al. (2006)）．このため現在提案されている深層強化学習を用いた資産運用方法の利用は非現実的となっている．

特に投資対象銘柄数を拡大して深層強化学習を利用することは，深層強化学習の計算負荷が高いため困難であり，近年の先行研究を見ても数十銘柄を取り扱うことが限界であることが分かる．一方，国内の株式市場における投資対象銘柄は約3000銘柄であり，一般的に機関投資家の投資対象となる流動性の高い大型・中型銘柄に絞っても500銘柄である ．

そこで本論文では，Bozinovski and Fulgosi (1976)で提案されている転移学習を利用した深層強化学習モデルを提案し，500銘柄を対象とした深層強化学習ポートフォリオが構築可能となることを実証する．提案した手法を用いることで現実的な時間で広範な投資対象銘柄を取り扱った資産運用モデルを構築できる点は，先行研究にない重要な新規性である．さらに国内株式市場の流動性の高い大型・中型500銘柄を投資対象銘柄として，リバランス頻度，回転率や流動性，保有銘柄数，取引コストなどの現実的な制約条件を踏まえたうえでモデル構築と実証分析を行い，機関投資家が実際に運用可能な条件下で深層強化学習の有効性を明らかにする．本論文を通して，年金などの大規模な資金を運用する機関投資家に対する深層強化学習の利用可能性が明らかになるものと考える．

本論文の構成は以下のとおりである．第2章では本論文で提案するモデルのもととなる深層学習にLSTMを用いた深層強化学習モデルについて説明を行う．第3章では，広範な投資対象銘柄を取り扱うための提案として転移学習を用いた深層強化学習モデルを提案する．第4章では，国内株式市場のデータを用いて計算機実験について説明し，提案した深層強化学習モデルが実務的な制約条件の下で有効に機能することを示す．最後に第5章では結論と今後の課題について記す．

2　LSTMを用いた深層強化学習のフレームワーク

本章では，提案する深層強化学習モデルについて強化学習部分，深層学習部分に分けて説明したのち，深層強化学習モデルについて説明する．

2.1 方策関数ベースの強化学習

強化学習の学習方法（アルゴリズム）は大きく価値関数ベースと方策関数ベースに分類される．価値関数ベースの学習は，最適な価値関数を学習し，その関数のもとで最適な行動を選択する方法である．この学習方法の場合，一般的にエージェントが取れる行動空間が離散的な場合に限られてしまうため，投資ウェイトのような連続的な行動を決定するには不向きである．

それに対し，方策関数ベースの学習は，行動の選択自体を関数として近似し，与えられた価値関数を最大とする行動を直接学習する．そのため，投資ウェイトのような連続的な値を最適化するのに向いているといわれている．これより本論文では方策関数ベースの強化学習を採用した．

図1に本論文で行ったポートフォリオ最適化を強化学習で行う流れを示した．

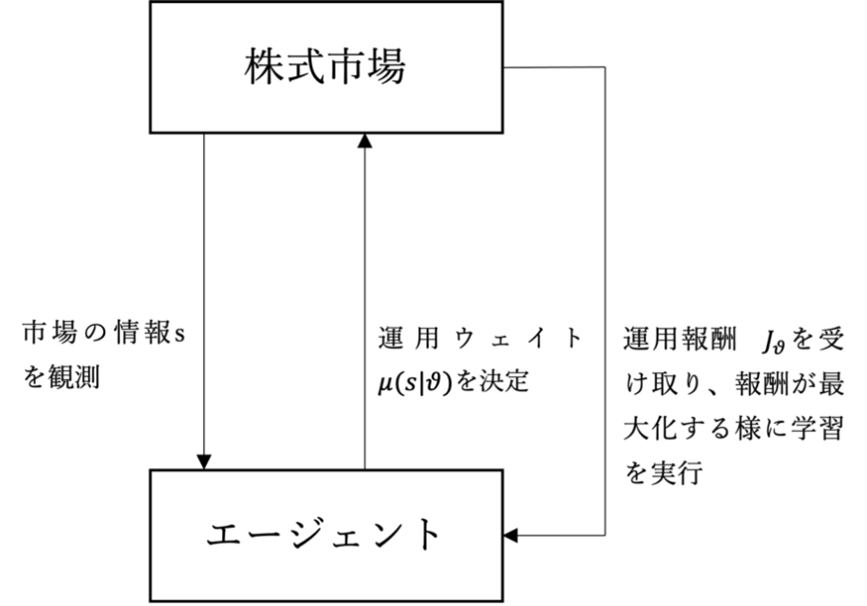
図1．強化学習をポートフォリオ最適化に応用する際の流れ

ここでエージェントとは認知，判断，行動を行う主体であり，ポートフォリオを決定する主体である．エージェントは株式市場から市場の情報$s$（株式データなど）を観測し，自身が管理するパラメータを$\vartheta$とする運用ウェイト決定関数$\mu$をもとに投資ウェイト$\mu \left(s\right|\vartheta )$を決定して運用を行う．その結果フィードバックとして株式市場から報酬$J_{\vartheta }$（翌期の株価上昇/下落から得られる投資収益など）を受け取り，この報酬を最大化する様に，運用ウェイト決定関数のパラメータ$\theta$を更新する．このようなエージェントと株式市場の相互作用を繰り返すことによりエージェントの最適化を行う．

2.2 強化学習モデルの定式化

本論文では，Jiang et al. (2017)に倣い過去の株価を情報として用いて投資ウェイトを決定する問題として定式化を行った．

時点$t$における投資対象$n$資産の日次収益率を${\mathit{y}}_t=\left(y_{1,t},y_{2,t},\dots ,y_{n,t}\right)$とし，時点$t$におけるパフォーマンス計測用の翌期までの株価収益率を$r_t^{+1}=\left(r_{1,t}^{+1},r_{2,t}^{+1},\dots ,r_{n,t}^{+1}\right)$と定義する¹．これにより，時点$t$における市場の情報${\mathit{s}}_t$，行動${\mathit{w}}_t$，報酬関数$J_{\theta }$は以下の様に表すことができる．

  

$${\mathit{s}}_t=\left({\mathit{y}}_{t-D},{\mathit{y}}_{t-D+1},\dots ,{\mathit{y}}_{t-1},{\mathit{y}}_t\right)$$(1)

  

$${\mathit{w}}_t=\left(w_{1,t},w_{2,t},\dots ,w_{n,t}\right)=\mu \left({\mathit{s}}_t|\theta \right)$$(2)

  

$$J_{\theta }=\sum _{t=1}^T\{\log (\sum _{i=1}^n{(r}_{i,t}^{+1}+1)w_{i,t}-tc\sum _{i=1}^n\left|w_{i,t}^0-w_{i,t}\right|)-\lambda {‖{\mathit{w}}_t‖}^2\}$$(3)

ただし，$D$は学習する過去の株価収益率の使用期間を示し，$tc$は取引コストペナルティ，$\lambda$は正則化ペナルティ，$T$は運用期間，$w_{i,t}^0$はリバランス前のウェイトであり$w_{i,t}^0={(r}_{i,t-1}^{+1}+1)w_{i,t-1}/{\sum }_j{(r}_{j,t-1}^{+1}+1)w_{j,t-1}$とする．また$s_t$は投資対象である全$n$銘柄の直近$D$日間の株価収益率を並べた行列，$w_t$は運用ウェイトベクトル，$J_{\theta }$はエージェントの一連の投資行動による報酬（スカラー値）を表しており，運用期間における取引コストを考慮したポートフォリオの総収益の対数効用に正則化項を追加したものである．2.1節で説明した通り，強化学習は(3)式で定義される運用期間のリターンやコストを考慮して最も効率的な運用ウェイトを決定する．本論文では先行研究に倣い$D=250，T=48$とした．

2.3 LSTMネットワークを用いた深層学習モデル

次に図1におけるウェイト決定関数$\mu \left(s\right|\vartheta )$を決定するための深層学習モデルについて説明する．深層学習ネットワークには様々なものが提案されている．その中でもポートフォリオ最適化を深層強化学習で行うJiang and Liang (2017)やSoleymani and Paquet (2020)ではCNNを用いており，AdbelKawy et al. (2021)ではLSTMを用いている．株価データは代表的な時系列情報を持ったデータであるため，本論文では時系列データの時間情報をネットワークに反映できるLSTMを採用した．

LSTMとはHochreiter and Schmidhuber (1997)によって導入されたネットワークであり，時系列データの学習を得意とする自己ループにより内部の状態を次の時刻に伝播させるリカレントネットワーク（RNN）の1種である．LSTMは忘却ゲート，出力ゲート，入力ゲートといわれる3つのゲートで情報を制御することにより，RNNの学習の問題であった勾配消失問題を解決でき，長期の時系列データの学習を可能とするという特徴を持っている．

LSTMを用いて株価の予測を行うモデルを提案する研究も行われており，Fischer and Krauss (2018)では，LSTMを用いたリターン予測モデルを米国の500の株式を用いて構築し，それに基づいた投資を行うことで高いリターンが得られることを実証している．具体的には入力を過去240日の日次収益率とし，中間層の次元を25としたLSTMネットワークで株価の上昇/下落を予測するモデルを構築している．

本論文の投資対象もFischer and Krauss (2018)と同様の個別株式であることから，中間層の次元も同様に25次元として設定した．

2.4 深層強化学習モデル

これより，提案する深層強化学習モデルの詳細なアーキテクチャを以下のように定義する．

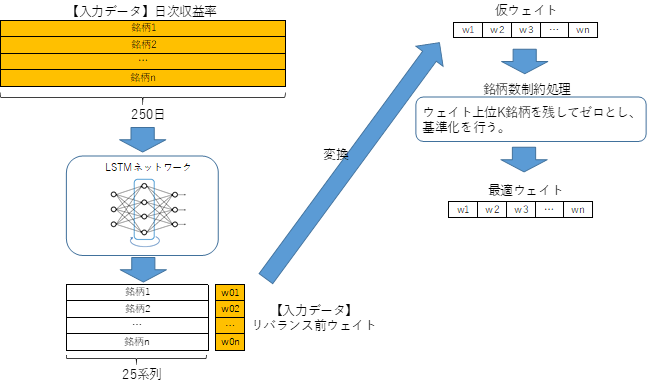
図2　深層強化学習モデルのアーキテクチャ

図2の提案モデルは全投資対象銘柄の過去250日の日次収益率行列とリバランス前のウェイトベクトルを入力とし，はじめに日次収益率行列をLSTMにより25次元のデータに集約したうえで，強化学習モデルによって仮ウェイトベクトルを計算する．さらに実務上許容できない銘柄数の保有を回避するために保有銘柄数をKに絞り込んだうえで合計1のウェイトに変換するネットワークとなっている．このウェイトの評価関数値(3)を評価し，それが高くなるように学習を行っていく．

しかしながら，提案したモデルは強化学習モデルの中に深層学習を含んだ複雑なネットワーク構造を持っており，計算負荷が非常に高い．先行研究においてもJiang and Liang (2017)は12銘柄，Soleymani and Paquet (2020)は23銘柄を投資対象としており，本論文で対象とする国内株式市場の大型・中型500銘柄を取り扱うことはほぼ不可能である．そこで本論文では転移学習を用いることでこの問題を解決する．

3 転移学習を用いた深層強化学習モデルの拡張

本章では提案モデルの計算負荷を軽減するための転移学習の利用について説明する．

3.1 転移学習

転移学習とはBozinovski and Fulgosi (1976)で考案された学習⽅法で，あるタスクを学習する際に，予め別タスクで学習させたモデルを組み合わせることにより学習の効率化を計る⽅法のことである²．本論文の場合，LSTMを事前に学習させ，そのパラメータ値を固定したうえで深層強化学習を行うことになる．

転移学習のメリットとしてはまず短時間でモデルを学習できる点が挙げられる．深層強化学習の学習時に⼀部学習済みのモデルを組み入れることにより，その部分のパラメータの最適化が必要なくなるため，より短い時間で学習することができる．また転移学習は一種のパラメータの制約条件とみなすことができるため，モデルへ正則化の効果をもたらすとされている．これらの理由から，本論文では深層強化学習に転移学習を取り入れることを提案する．

3.2 LSTMを用いたリターン予測モデル

転移学習を行うためにはLSTMを事前に学習する必要があり，そのためにLSTM単体でモデルを構築する必要がある．本論文ではLSTMを用いたリターン予測モデルを構築したFischer and Krauss (2018)をもとにモデルを構築した．

Fischer and Krauss (2018)では，入力として米国約500銘柄の過去240日の日次収益率を用いており，出力を投資対象銘柄を翌日の収益率の大きさで2分類した0-1データとしてLSTMネットワークで学習を行っている．その際，中間層の次元は25次元としており，出力層の変換にはsoftmax関数を使用している．また全銘柄のLSTMのパラメータを同じにするという制約を設けることで過学習を抑制し，シンプルでありながら高い予測精度を実現した．

本論文でもFischer and Krauss (2018)を踏襲する形でモデルを構築するが，出力に関しては翌1か月の収益率の大きさで5分類したone-hotデータ³を用いている．これは空閑ら (2010)，山本ら (2020)など機関投資家の利用を意識してファクター分析を行っている先行研究において，標準的なスプレッドリターン分析として5分類が使用されていることから決定しており，機関投資家のポートフォリオ構築を目的としている本論文では適切であると思われる．

つまり，提案するリターン予測モデルは過去250日の日次収益率をLSTMネットワークで25次元に圧縮し，それをsoftmax関数により変換することで，翌1か月の収益率で分類される5クラスの所属確率が計算できる仕様になっている（図3）．

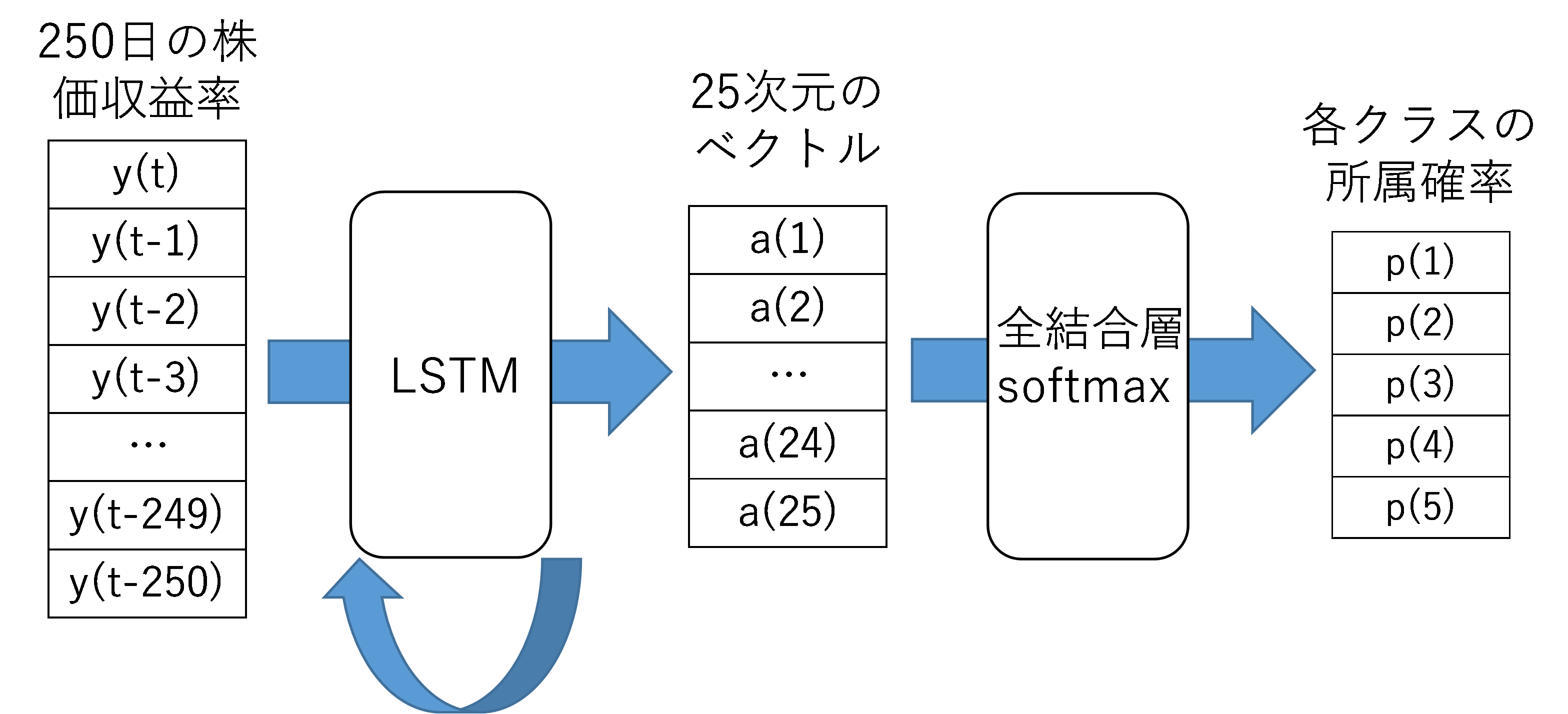
図3　LSTMを用いたリターン予測モデル．

3.3 転移学習を用いた提案深層強化学習モデル

これより本論文で提案する転移学習を用いた提案深層強化学習モデルは図4のようになる．

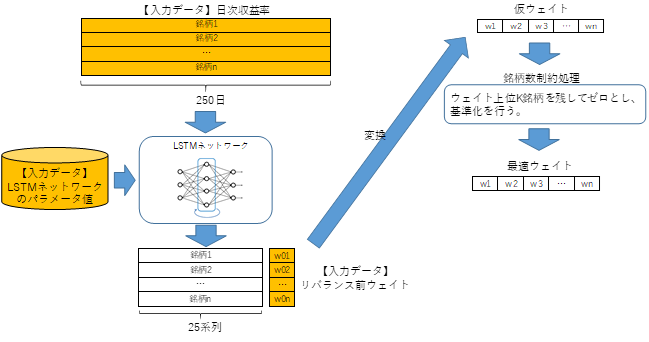
図４　提案モデルのアーキテクチャ

提案モデルは図3のLSTMによるリターン予測モデルにより学習したLSTMネットワークを強化学習モデルに取り込むことで，計算負荷を軽減しているモデルである．またリターンの予測や運用評価は月次リターンで行っており，評価関数の(3)式では運用期間のリターンの他に取引コストも考慮している．さらに多すぎる銘柄を保有しないための保有銘柄数に関する制約も考慮できるモデルであり，現実の運用を意識したモデルになっている．

3.4 提案モデルの学習方法

次に提案モデルの学習方法について説明する．提案モデルは転移学習を行うLSTM部分の学習と強化学習部分の学習に分かれているため，それぞれについて説明する．

3.4.1 LSTMを用いたリターン予測モデルの学習方法

Fischer and Krauss (2018)では過去240日の日次収益率データを用いて翌日の株価収益率を予測する株価予測モデルをLSTMを用いて構築しており，その際学習データとして約1000日の日次収益率を利用している．本論文でも同様に過去4年間（約1000日）の日次収益率データを使用した．

学習データについては，まずある投資対象銘柄について250日の日次収益率と翌20日間の株価収益率に基づくone-hot（所属クラス）データを1つの学習データとし，それを学習期間4年間（約1000日）の中で1日ずつずらしたものを使用した．つまり投資対象銘柄500，学習期間1000日の場合，1つの銘柄につき731の学習データが作成され，全銘柄で約36万の学習データを用いてLSTMのパラメータを学習することになる．ここで入力データである株価収益率は全銘柄4年間分の日次収益率を1セットとした平均と標準偏差で基準化を行っている．

LSTM ネットワークの学習に用いる最適化手法にはRMSProp⁴を採⽤した．RMSPropは通常，RNN 系のネットワークに適した手法であることが知られているため⼀般的にLSTM の学習に⽤いられている（Chollet (2016)）．また，Gal and Ghahramani (2016)に従い，訓練時の各パラメータ更新時に⼊⼒ユニットの⼀部を⼀定割合ランダムにドロップし，オーバーフィッティングのリスクを削減することができるrecurrent dropout機構を適⽤した．ドロップする割合はFischer and Krauss (2018)に倣い0.1 とした．学習回数については早期停⽌を利⽤して動的に制御した．早期停⽌とは，学習データセットを学習セットと検証セットの2つに分割し，学習エポックごとに学習セットを⽤いてパラメータを学習する．次に学習したパラメータを⽤いて検証セットの損失関数を計算することで汎化性能を検証し，そしてある⼀定回数（エポック）の間，検証損失が改善されない場合，学習を終了とする学習⽅法である．早期停⽌を実⾏することで過学習を抑制することができる．本論文では学習セットと検証セットの割合を8:2とし，5回連続で検証損失が改善されない場合，学習終了とした．

3.4.2 強化学習の学習方法

強化学習の学習には，3.4.1節と同様に学習期間4年間（T=48）とし，入力データは過去250日の日次収益率を使用した．LSTMと同様，入力データは全銘柄4年間分の日次収益率を1セットとした平均と標準偏差で基準化を行っている．

また取引コスト係数$\mathrm{tc}$=0.05，正則化項のペナルティλ=0.3とした．そしてランダムに選んだ時点から最大48期間の月次取引での運用を行い，評価関数(3)式を高めるようにパラメータをミニバッチ学習した⁵．その際，学習回数は10000としており，パラメータ最適化のアルゴリズムについては現在様々なモデルで広く使われているAdam⁶を利⽤した．

4 計算機実験

本章では提案した深層強化学習モデルに対し，国内株式市場の株価データを用いて行った計算機実験の結果について説明する．

4.1 分析設定

本論文では国内株式市場に上場する流動性の高い大型・中型銘柄（500銘柄）を対象に提案した深層強化学習モデルを適用した⁷．使用したデータは2001年1月から2020年の1月までの株価であり，株価から計算される日次収益率をモデルの入力データとした．バックテストを行う際には毎年12月末に過去4年間のデータを用いて提案モデルのパラメータを最適化し，そのパラメータを用いて翌1年間のポートフォリオを構築した（図5）．またパフォーマンス評価の際には取引コストを片側0.25%として評価し，リバランス間隔は1ヵ月とした．

図5．バックテストのイメージ

また大型銘柄から中型，小型銘柄になるとサイズ区分内の銘柄数も多くなり，流動性も低くなることから銘柄間の格差が大きくなる．そのため，投資対象全銘柄でポートフォリオを学習すると規模の小さなサイズ区分の銘柄に偏ったポートフォリオを構築してしまい，現実的な運用を行うことができないことが予想される．

本論文では運用金額の大きい機関投資家が運用可能なポートフォリオの構築を目的としていることから，この問題を解決するために市場を大型（時価総額上位100位以内），中型（時価総額上位101位から500位），小型（時価総額501位以降）に分解した．そして，大型・中型の市場から20銘柄，60銘柄のポートフォリオを構築し，それらを市場の時価総額ウェイトで合わせたものを運用ポートフォリオとした．また深層強化学習による銘柄選択効果の追加的な検証として，小型市場でも100銘柄のポートフォリオを構築した⁸（図6）．このように市場を分けて学習することで，大型銘柄も必ず保有するバランスの取れたポートフォリオを構築することができる．また大型，中型，小型は市場の評価が異なることから，超過収益の源泉も異なる可能性が高い．市場を分けることでそのような超過収益の源泉の違いもモデルに取り込むことが可能になる．

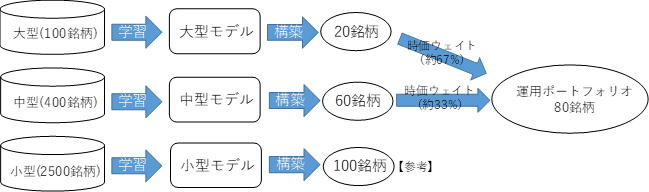
図6．ポートフォリオ構築のイメージ

これより，本論文で提案したモデルは大規模な資金を運用する機関投資家が考慮する必要のある取引コスト，流動性，売買タイミング，保有銘柄数などを考慮したうえで最適な運用ポートフォリオを決定できるモデルとなっている．

なお本論文で使用した計算機は表1の通りである．

表1．計算機スペック

4.2 計算効率に関する検証

はじめに提案モデルの投資対象銘柄数に対する拡張性を，学習時間の観点から検証するために，2018年末の学習データを用いて，投資対象銘柄数を30〜500まで段階的に増やした場合の学習時間を計測した．比較として，Jiang et al. (2017)で提案された図2の深層学習をCNNとしたEIIE CNNと図2のEIIE LSTMを構築した．EIIE CNNやEIIE LSTMは40000回の学習が必要とされているが，今回はモデルの拡張性に関する検証であるため，学習回数を1000回とした．表2に各モデルの計算時間を記す．

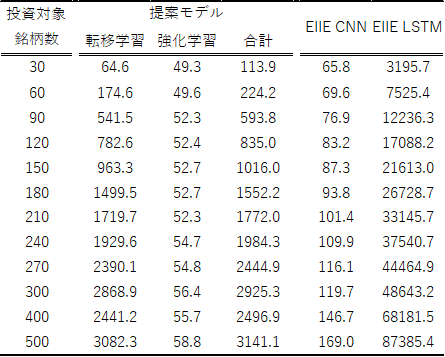
表2．提案モデルの計算時間(秒)

表2よりまずEIIE LSTMの学習時間が⾮常に長く，その他のモデルと比べて投資対象銘柄数の上昇に対する学習時間の増加率も高いことがわかる．国内株式市場の大型・中型銘柄500を想定した場合，実際に利用する際には学習回数を増やす必要があることからEIIE LSTMは⼤規模な投資対象銘柄を扱うことが困難であると⾔える．EIIE LSTMとEIIE CNNはモデルの学習器がCNNであるかLSTMであるかの違いのみであり，モデルアーキテクチャに大きな違いはないことや，⼀般的にLSTMはCNNより学習時間がかかることから，LSTMを強化学習モデルに組み込むことは⼤規模な投資対象銘柄を扱う上で容易ではない．しかし，提案モデルの学習時間はEIIE CNNよりは長いものの，EIIE LSTMに比べ20倍から30倍程度の速さであり，より大きな投資対象銘柄を取り扱うことができる．これは転移学習によりLSTMのパラメータを固定化することによって生じた学習時間短縮の効果であり，LSTMのような学習時間が長くなるネットワークでも転移学習を⽤いることで⼤規模な投資対象銘柄を深層強学習モデルに組み入れることが可能であること⽰している．

4.3 学習回数に関する検証

次に提案モデルの学習回数の検証を行うために，2018年末の投資対象銘柄500銘柄に対し，40000回の学習を行ってモデルの損失関数（報酬関数の負の値）が収束するまでにかかる学習回数を観測した．この検証において，提案モデルの比較としてEIIE CNNを利⽤しており，EIIE LSTMについては現実的な時間内で500銘柄の投資対象銘柄を使⽤して学習することが困難であるため除外した．結果を図7に⽰す．

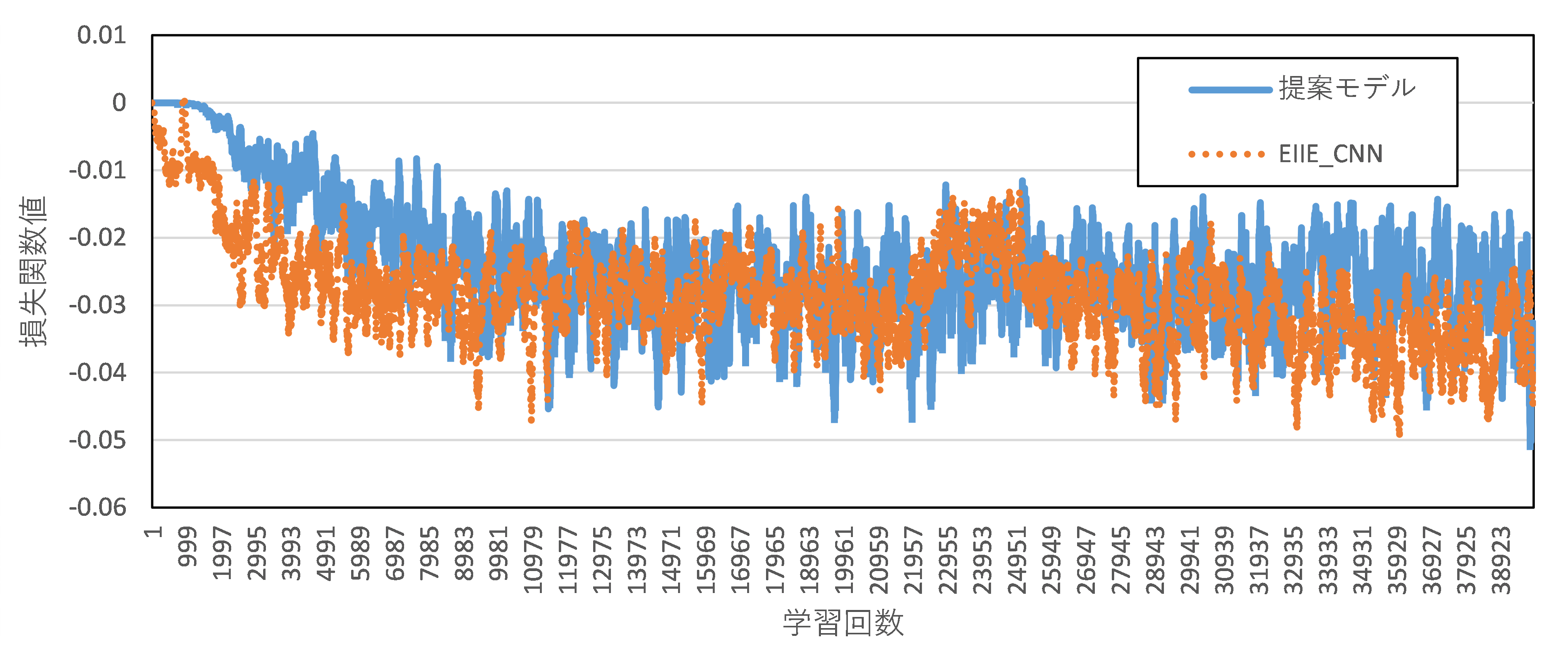
図7．学習回数と損失関数値の関係

図7より，損失関数値が収束している回数については提案モデルが約10000 回，EIIE CNNが約6000 回であり，提案モデルの計算は10000回程度の学習回数で十分であることがわかる．

4.4 バックテストによるパフォーマンス検証

次に本論文で提案した深層強化学習モデルを用いて国内株式市場でバックテストを行い，そのパフォーマンスを評価した結果について説明する．本モデルの有効性を示すために代表的な深層学習や機械学習モデルの6つの手法，及びTOPIXを比較対象とした．以下に比較した手法について説明する．

①CNNベースの深層強化学習モデル（CNN EIIE）

Jiang et al. (2017)で提案されたモデルであり，5.2節，5.3節で使用した深層強化学習モデル．図2の深層強化学習のネットワークをCNNに変更したモデル．入力データ，学習方法，サイズ区分による分割などは提案モデルと同様とした．

②LSTMを用いたリターン予測モデル（LSTM）

3.2節で説明したLSTMを用いたリターン予測モデルを直接使用して投資を行ったモデルであり，Fischer and Krauss (2018)で提案されたモデル．本モデルを使用することで各銘柄に1か月後のリターンクラスの予想所属確率が算出される（図3）．最も高いリターンクラスの所属確率が高い上位K銘柄（大型20銘柄，中型60銘柄）を等ウェイトで保有したポートフォリオを運用ポートフォリオとした．入力データ，学習方法，サイズ区分による分割などは提案モデルと同様とした．

③CNNを用いたリターン予測モデル（CNN）

3.2節で説明したLSTMを用いたリターン予測モデルのネットワーク構造にCNNを使用したモデルである．ポートフォリオの構築方法，入力データ，学習方法，サイズ区分による分割などはLSTMと同様とした．

④ニューラルネットワークを用いたリターン予測モデル（NN）

Krauss et al. (2017)で有効性が確認されたモデル．入力データは過去250日の日次収益率のうち直近20日間に40日前，60日前，…，240日前の日次収益率${\mathit{s}}_t=\left({\mathit{y}}_{t-240},{\mathit{y}}_{t-220},\dots ,{\mathit{y}}_{t-40},{\mathit{y}}_{t-20},{\mathit{y}}_{t-19},\dots ,{\mathit{y}}_{t-1},{\mathit{y}}_t\right)$のみを使用している．これは次元の呪いの影響を緩和する効果をもたらすとされている．ニューラルネットワークの隠れ層は2であり，全結合層でそれぞれ15次元，10次元に集約する処理を行い，最後にsoftmax関数を用いた全結合層でLSTMモデルと同様の5クラスの所属確率を算出するモデルである．学習データの作成方法，ポートフォリオの構築方法，サイズ区分による分割などはLSTMと同様とした．

⑤ランダムフォレストを用いたリターン予測モデル（RFM）

Krauss et al. (2017)で使用されてたモデルであり，入力データはNNと同様である．LSTMと同様の学習データを作成し，全銘柄共通で1か月後のリターンクラスの所属確率を学習させた．決定木の数などのハイパーパラメータに関してはグリッドサーチで探索を行った．ポートフォリオの構築方法，サイズ区分による分割などはLSTMと同様とした．

⑥ロジスティック回帰を用いたリターン予測モデル（Logit）

Krauss et al. (2017) で使用されてたモデルであり，多項ロジスティック回帰を用いてLSTMと同様の学習データから全銘柄共通で1か月後のリターンクラスの所属確率を推計した．ポートフォリオの構築方法，サイズ区分による分割などはLSTMと同様とした．

これらのモデルを用いて2005年1月から2019年12月までバックテストを行った．表3，図8に比較したモデルの通期のバックテストのパフォーマンスを示す．

表3．パフォーマンスサマリー

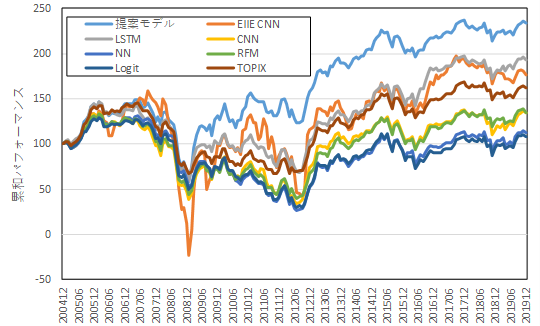
図8．累和パフォーマンス

表3，図8より，提案モデルのパフォーマンスは比較したすべてのモデルに比べて高く，安定していることが分かる．特に深層学習，機械学習モデルの中でTOPIXを上回るパフォーマンスとなっているのは提案モデルとEIIE CNN，LSTMだけであり，CNNはTOPIXを下回っていることから，LSTMと強化学習によるポートフォリオ構築はどちらも1か月リバランスという先行研究に比べて長期の運用期間でも機能することが明らかになった．また提案モデルとLSTM，EIIE CNNとCNNを比較するとパフォーマンスが改善しているだけでなく，回転率が低下していることが分かる．これは強化学習に取引コストペナルティを取り入れているため売買回転率を抑制した中で最適なポートフォリオを構築しているからである．

取引コストについては0.25%としたが，現実の取引コストは機関投資家の運用規模や市場の流動性に影響を受ける．そこで取引コストを0%から2.0%まで変更した場合の提案モデルのリターンとリスク・リターン比を図9に示す．

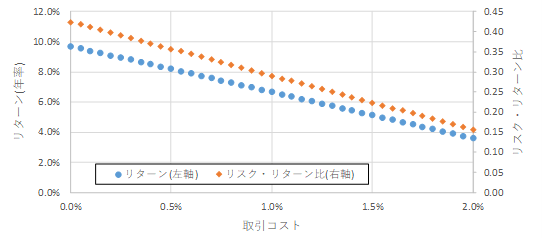
図9．取引コストと提案モデルのパフォーマンスの関係

図9より，リターンがベンチマークであるTOPIX以下となるのは取引コストが1.8%以上，リスク・リターン比は1.4%以上の場合である．つまり極端に大きな取引コストにならない限り，提案モデルはTOPIXに対して高い有効性を保つことができる．これは深層強化学習による回転率の考慮が取引コストを意識する投資家にとって非常に有効であることを意味している．

これより提案した深層強化学習モデルは，流動性や取引コスト，リバランスタイミングなど実務的な制約条件を考慮した上でも安定したパフォーマンスを得られる実務的に使用しやすいモデルであることが分かった．

次に提案モデルの有効性の詳細を確認するため，年別にパフォーマンスを分析した結果を表4に示す．ここで色がついている部分はTOPIXよりも高いリターンが得られているモデルを示している．

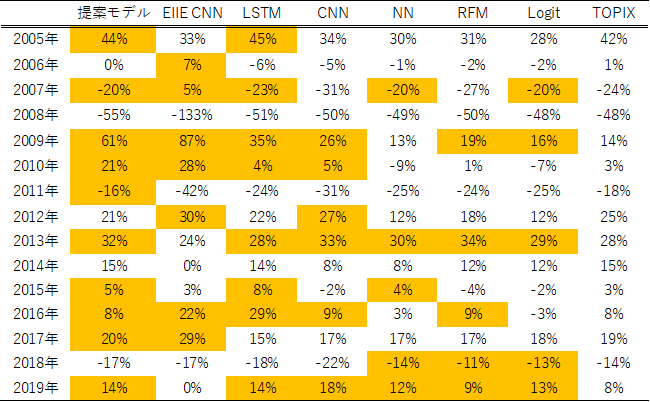
表4．各モデルの年別パフォーマンス

表4より，提案モデルは約7割の年でTOPIXを上回るパフォーマンスを得られており，年や相場環境に関わらず有効性が高いといえる．特に提案モデルはTOPIXに劣後している年でも最大7%，それ以外は1%から4%程度の差であり，TOPIXに大きく劣る局面は少ないことが分かる．正則化などポートフォリオを安定化させる手法を取り入れていること，サイズ分割をすることでTOPIXから大きく乖離したポートフォリオとならないことが要因として考えられる．

次にモデルを分割した大型，中型，小型それぞれの区分のパフォーマンスを表5に示す．ここでTOPIXはTOPIX Large，TOPIX Mid，TOPIX Small指数を示している．小型株についてはこれまでの分析ではポートフォリオには含めていないが，深層強化学習のポートフォリオ構築効果を追加的に検証するための参考値として記載した⁹．そのため取引コストは大型中型と同じ0.25%としている．

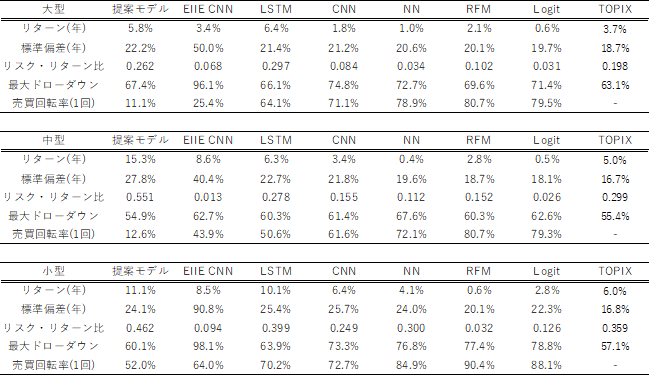
表5．サイズ別パフォーマンス

表5より，提案モデルはすべてのサイズ区分でTOPIXよりも有効性が高いことが分かる．大型区分ではLSTMに若干劣後しているが，売買回転率はLSTMの1/6程度であり，運用のしやすさを考慮すると提案モデルも有効性が高いと思われる．特に興味深い点は，一般的に効率性が高く超過リターンを獲得することが難しい大型区分でTOPIXを上回る効果が得られることである．EIIE CNNはTOPIXよりも劣後しており，LSTMは上回っていることから，LSTMのリターン予測能力が大型区分でも機能していることが分かる．また表3，表4の分析には小型株は投資対象外としているが，分析期間のTOPIX LargeとTOPIX SmallではTOPIX Smallが年間2.3%ほど高く，小型株効果が確認される¹⁰．提案モデルは小型株効果以上のリターンを大型・中型区分で獲得していることを示している．

4.5 ポートフォリオの特性分析

本節では提案モデルで構築されたポートフォリオの特性を確認するために，表6のファクターを用いてポートフォリオのファクター属性値を計算した¹¹．ファクター属性値は毎月末にファクター値をクロスセクション基準化したものである¹²．そして提案モデルから得られたポートフォリオで加重和することでポートフォリオのファクター属性値を算出した．つまり，ファクター値がプラスであるほどTOPIXに対してプラスのファクター属性を持つことを示している．ポートフォリオのファクター属性値を年別に平均した値を図10に示す．

表6．使用したファクターの定義

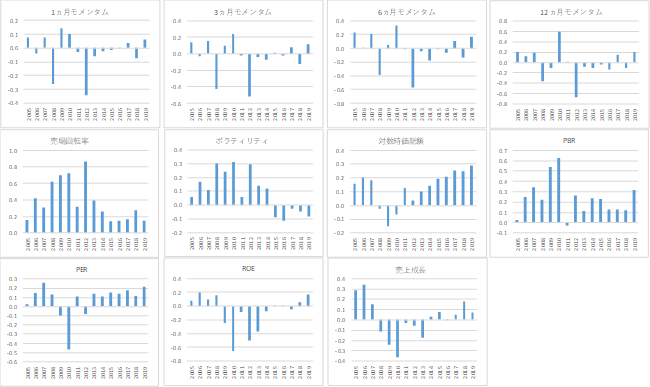
図10．年別ポートフォリオファクター属性値

図10より，過去の株価属性は短期も長期もモメンタム，リバーサルの一貫した特徴はなく，学習結果に応じでポートフォリオ属性が変化していることが分かる．次に売買回転率についてはプラスであり，対数時価総額もほとんどの年でプラスの値をとっている．つまりほとんどの年で大型で流動性のある銘柄でポートフォリオを構築していることになる．これはサイズ区分で分割してポートフォリオを構築した効果であり，実務的に運用しやすいポートフォリオであるといえる．またボラティリティについては2014年までプラス，それ以降マイナス，PBR，PERは概ねプラスの値をとっていることから平均的なファクター属性として過去は株価の変動の高い割高銘柄，直近は値動きが安定している割高銘柄を保有していることが分かる．

国内株式市場では久保田・竹原 (2007)が割安株効果が強いことを指摘しているが，Arnott et al. (2021)では近年世界的に安株効果が低下していることを指摘している．そこでクオンツ運用で代表的に利用されてきた割安株効果と提案モデルの割安属性の関係性を分析する．具体的にはKenneth French Data Libraryにある日本のファクターリターンのうち割安株リターンを取得し，年平均値を算出する¹³．その値と図10のPBRをまとめた結果を図11に示す．

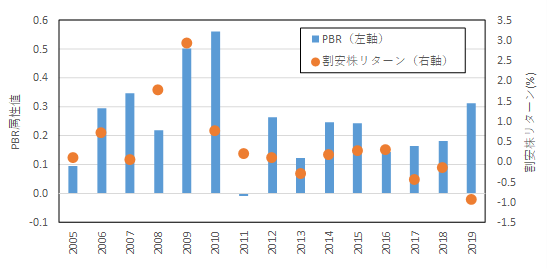
図11．ポートフォリオのPBR属性と割安株効果の関係

図11より，平均的に割安株効果が高い2008年や2009年であってもPBR属性値が高く割安株特性が低いことが分かる．また近年割安株リターンは下がっているもののPBR属性を大きく高めているわけではないことが分かる．このように深層強化学習で得られた最適ポートフォリオは割安株効果の大小に関わらず割高銘柄で構成されており，クオンツ運用で標準的に構築されるポートフォリオとは異なる属性を持つものと思われる．さらにこれらのポートフォリオ属性は年別で変動しており，一貫したものではない．つまり標準的なファクター投資では再現できない戦略である．これらの特徴は，深層強化学習で株価の系列から従来のファクター投資では得られない特性を抽出した効果である可能性があり，新しい投資手法として興味深い結果である．

次に提案した戦略を標準的なファクター投資戦略と比較することで，新たな投資手法としての実現可能性を考察する．ここで標準的なファクター戦略として，MSCIが公表しているMSCIモメンタム指数，MSCI最小分散指数，MSCIクオリティ指数，MSCI Value Weighted指数，MSCI高配当指数を使用した．構築する投資対象銘柄はMSCI Japan Standardとした¹⁴．これらの指数と提案モデルのリターンのMSCI Japan 指数に対する超過リターンを計算し，そのパフォーマンスを計算した結果を表７に示す．

表7．MSCI指数との比較（対MSCI Japan超過ベース）

表７より，提案モデルは比較した指数に比べ超過リターン，インフォメーションレシオ（IR）が最も高いことが分かる．提案モデルはコスト控除後のパフォーマンスであることから，標準的なファクター戦略と比較して十分高い効果が得られているということができる．また特徴的なのは提案モデルと他の指数との相関係数である．相関が高い戦略はなく，ほとんどの戦略とはマイナス，または若干の正の相関となっている．ファクター分析で得られた結果と同様，深層強化学習によるポートフォリオは従来のファクター戦略とは異なる特性を持つ戦略であり，その有効性が高いだけでなく，超過収益の源泉の分散化の意味でも非常に効果的な戦略となっていることが分かる．

4.6 ロバストテスト

これまで示してきた結果はあるパラメータの結果であるため，ロバスト性を確認するためにいくつかのパラメータを変化させたうえでバックテストを行い，そのパフォーマンスを評価した．具体的には入力の日次収益率を過去80日間とし，評価関数(3)式の取引コスト係数$tc$と正則化項ペナルティ$\lambda$，大型・中型・小型区分で選択する銘柄数$K$を変化させている．ここで取引コスト係数は評価関数(3)式の回転率にかかるペナルティであり，バックテストの取引コストは0.25%を使用している．バックテストの通期のパフォーマンスを表8に示す．色付きがこれまでの分析で使用したデフォルト値である．

表8．取引コスト係数とパフォーマンスの関係

表9．正則化ペナルティとパフォーマンスの関係

表10．保有銘柄数とパフォーマンスの関係

表8から表10より，まず入力データの期間を80日と短期にしても，表3のすべてのモデル，市場指数に対して有効性が確認できた．入力情報を削減することで深層強化学習が読み取る情報が少なくなるものの，十分に高い効果が得られている．またその他のパラメータを変化させてもポートフォリオのパフォーマンスは大きく変わらず，ほとんどのケースで他のモデルを上回っている．これは提案した深層強化学習モデルがパラメータの値によらず株価の特性を抽出していることが原因であり，その結果提案モデルが設定したパラメータ値に大きく依存せず安定した結果を得られると考えられる．

5 まとめと今後の課題

本論文では運用金額の大きい機関投資家の資産運用が利用可能な条件の下で深層強化学習を用いたポートフォリオ構築モデルを提案した．具体的には広範な投資対象銘柄数，1か月のリバランス頻度，取引コスト（回転率，流動性），投資銘柄数を考慮したモデルである．先行研究で提案されている深層強化学習によるポートフォリオ構築モデルは計算負荷が高いことから数十銘柄の投資対象銘柄を扱い，長くて日次のリバランスを行う高頻度の取引を目的としていた．

それに対し，本論文では転移学習を利用して，学習器をモデルの外で学習させる深層強化学習モデルを提案し，広範な投資対象銘柄に対して深層強化学習を用いたポートフォリオ構築が可能であることを示した．さらに学習を翌月の株価収益率を対象に行うことや，市場をサイズ区分で分割して学習することでリバランス間隔や流動性の制約も考慮できることを示した．

実証分析では，国内株式市場の大型・中型500銘柄を用いて提案したモデルで実用的な時間で深層強化学習が可能であることを示した．また得られたポートフォリオでバックテストを行い，先行研究で提案されている深層強化学習モデルや標準的な機械学習モデルに比べて，パフォーマンスが安定しており高い有効性を有していることを実証した．この主な要因は分類器で使用したLSTMが国内株式市場の1か月程度の株価の予測に対して高い有効性を持っていることであり，それに対し強化学習を用いて回転率や投資銘柄数を制御してポートフォリオを構築することでより効率的な運用を実現できるモデルとなっている．特に流動性が高く，効率性も高い大型区分で有効性が高いことは本論文の重要な発見である．

また得られたポートフォリオのファクター分析を行い，株価から学習したポートフォリオが結果的に割高銘柄に投資を行っており，標準的なクオンツ投資とは異なる銘柄を保有していることを明らかにした．またMSCIのスマートベータ指数とパフォーマンスを比較した結果，パフォーマンスが優れているだけでなく，他の指数との相関が低いことを確認した．これは提案したモデルの有効性が高いだけでなく，超過収益の源泉の分散化にも有益であることを示しており，従来の投資手法とは異なる手法として深層強化学習を利用できる可能性が十分にあるといえる．

今回の研究では転移学習に利用するモデルとしてシンプルなモデルを用いたが，機械学習ブームにより日々新たなモデルが開発されている現状を踏まえると，他にも様々なモデルで検証する余地がある．また，今回は終値データのみを使用したが今後は終値以外の株価データやテキストデータなど様々な種類のデータを利用したネットワークの構築も今後の課題である．

謝辞

本研究は日本学術振興会の基盤研究(C) 22K04604.の助成を受けている．

脚注

1 パフォーマンス計測が月次であれば，$r_t^{+1}$は時点$t$から翌1カ月先までの株価収益率を指す．

2 転移学習は，厳密にはInstances-base, Mapping-base, Network-base, Adversarial-baseに分類できるが，本論文ではNetwork-baseの転移学習について扱う（Tan et al.(2018)）．

3 例えばクラス2に所属している場合，one-hotベクトルは(0,1,0,0,0)となる．

4 最適化パラメータは$\alpha$=0.001，$\mathrm{\beta }$=0.9とした．

5 詳細はJiang et al. (2017)を参照．

6 最適化パラメータは$\alpha$=0.001，${\mathrm{\beta }}_1$=0.999，${\mathrm{\beta }}_2$=0.9とした．

7 一般的に小型株は機関投資家が運用するには流動性が低いため今回の分析からは除外した．

8 東証の大型，中型，小型の区分も同様の区分けとなっている．それぞれの時価総額ウェイトは約60%，30%，10%である．

9 本論文で提案する転移学習を用いた深層強化学習は2500の投資対象銘柄でも現実的な計算時間で求解を行うことができる．

10 Fama and French (2012)では1989年から2011年の期間で日本では小型株効果が確認されないことを示している．本論文とは分析期間が異なることから結果に違いがあると考えられる．

11 過去1ヵ月，3ヵ月の株価収益率は逆符号値とし，リバーサルとして使用することが多いが，本論文では分かりやすいようにモメンタムで統一した．

12 毎月末東証1部上場銘柄の時価総額を使用した加重平均と全銘柄の単純標準偏差を計算し，ファクター値から平均を引き，標準偏差を割ることで算出した．東証1部上場銘柄の時価加重平均を引くことで，ファクター属性値ゼロがTOPIXに近い属性であることを示している．

13 http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.htmlから取得．割安株リターンはBE/MEのHighからLowを引いた値として定義した．

14 MSCI Standardは大型、中型銘柄で構成される投資対象ユニバースであり，約350銘柄、時価総額で日本株式市場の85%をカバーしている（MSCI (2017)）．

参考文献

• 空閑健一・山本零・石川敦啓 (2010),「新興国株式市場における割安株投資の有効性検証」, 『証券アナリストジャーナル』, 48(9), 38-49.
• 久保田敬一・竹原均 (2007), 「Fama-Frenchファクターモデルの有効性の再検証」, 『現代ファイナンス』, 22, 3-23.
• 山本零 (2008), 「ポートフォリオ最適化」,『MTECジャーナル特別号：フィナンシャル・テクノロジーの過去・現在・未来』, 153-192.
• 山本零・川代尚哉・栗田昌孝 (2020), 「決算短信と四季報テキスト情報の投資戦略への利用可能性検証」, 『ジャフィ―・ジャーナル』, 18, 46-62.
• MSCI (2017),「MSCI指数ハンドブック」.
• Abdelkawy, R., Abdelmoez, W. M., and Shoukry, A. (2021), “A synchronous deep reinforcement learning model for automated multi-stock trading,” Progress in Artificial Intelligence, 10, 83-97.
• Arnott, R. D., Harvey, C. R., Kalesnik, V., and Linnainmaa, J. T. (2021), “Reports of value's death may be greatly exaggerated,” Financial Analysts Journal, 77(1), 44-67.
• Bianchi, D., Büchner, M., and Tamoni, A. (2021), “Bond risk premiums with machine learning,” Review of Financial Studies, 34(2), 1046-1089.
• Bozinovski, S., and Fulgosi, A. (1976), “The influence of pattern similarity and transfer of learning upon training of a base perceptron B2,” Proceedings of Symposium Informatica, 3-121.
• Chollet, F. (2016). “Keras,” https://github.com/fchollet/keras.
• Fama E. F., and French, K. R. (2012), “Size, value, and momentum in international stock returns,” Journal of Financial Economics, 105(3), 457-472.
• Fischer, T., and Krauss, C. (2018), “Deep learning with long short-term memory metworks for financial market predictions,” European Journal of Operational Research, 270(2), 654-669.
• Gal, Y., and Ghahramani, Z. (2016), “A theoretically grounded application of dropout in recurrent neural networks,” Proceeding in Advances in Neural Information Processing Systems, 1019-1027.
• Gao, Z., Gao, Y., Hu, Y., Jiang, Z., and Su, J. (2020), “Application of deep q-network in portfolio management,” Proceeding in 2020 5th IEEE International Conference on Big Data Analytics, 268-275.
• Gu, S., Kelly B. and Xiu, D. (2020), “Empirical asset pricing via machine learning,” Review of Financial Studies, 33(5), 2223-2273.
• Gudelek, M. U., Boluk, S. A., and Ozbayoglu, A. M. (2017), “A deep learning based stock trading model with 2-D CNN trend detection,” Proceeding in 2017 IEEE Symposium Series on Computational Intelligence.
• Heryadi, Y., Leslie, H., and Warnars, H. S. (2017), “Learning temporal representation of transaction amount for fraudulent transaction recognition using CNN, stacked LSTM, and CNN-SLTM,” Proceeding in 2017 IEEE International Conference on Cybernetics and Computational Intelligence.
• Hochreiter, S., and Schmidhuber, J. (1997), “Long short-term memory,” Neural Computation, 9(8), 1735-1780.
• Jiang, Z., and Liang, J. (2017), “Cryptocurrency portfolio management with deep reinforcement learning,” Proceeding in 2017 Intelligent Systems Conference, 905-910.
• Jiang, Z., Xu, D., and Liang, J. (2017), “A deep reinforcement learning framework for the financial portfolio management problem,” arXiv preprint arXiv:1706.10059.
• Krauss, C., Do, X. A., and Huck, N. (2017), “Deep neural networks, gradient-boosted trees, random forests: statistical arbitrage on the S&P 500,” European Journal of Operational Research, 259(2), 689-702.
• Li, B., and Hoi, S. C. H. (2014), “Online portfolio selection: A survey,” ACM Computing Surveys, 46(3), 1-36.
• Luigi, T., Elena, M. V., and Vincenzo L. (2018), “Replicating a trading strategy by means of LSTM for financial industry applications,” IEEE Transactions on Industrial Informatics, 14(7), 3226-3234.
• Roy, A., Sun, J., Mahoney, R., Alonzi, L., Adams, S., and Beling, P. (2018), “Deep learning detecting fraud in credit card transactions,” Proceeding in Systems and Information Engineering Design Symposium.
• Soleymani, F., and Paquet, E. (2020), “Financial portfolio optimization with online deep reinforcement learning and restricted stacked autoencoder - DeepBreath,” Expert Systems with Applications, 156, 1-16.
• Sun, W., Fan, A. Chen, L. W., Schouwenaars, T., and Albota, M. A. (2006),　“Optimal rebalancing for institutional portfolios,” Journal of Portfolio Management, 32(2), 33-43.
• Tan, C., Sun, F., Kong, T., Zhang, W. Yang, C., and Liu, C. (2018), “A survey on deep transfer learning,” Artificial Neural Networks and Machine Learning ‒ ICANN 2018, 270-279.