Estimation of 95% confidence intervals for the coefficient of variation using the Boot-Strap method: Comparison of interindividual variability of laboratory values in healthy subjects in eight Asian cities

Abstract

統計的計算法であるBoot-Strap（BS）法をExcel VBAで作成し，変動係数（CV%）の95%信頼区間（95%CI_CV）およびその区間幅（95%CI_RANGE）を推定することを目的とした。BS法の実行に用いるデータ数を50，反復計算回数を100回に設定した。1回のBS法実行に必要な時間は約3秒であった。95%CI_CVの推定には，反復計算で得られるCV%の分布における平均と2.5および97.5パーセンタイル値を用いた。大阪，香港，ハノイなどアジア地区8都市における健常基準個体の臨床検査12項目について，それぞれの95%CI_CVを比較すると，γGT，トリグリセリドおよびIgAで都市間差が認められた。一方，都市間で95%CI_CVに有意差は認められないものの，95%CI_RANGEが都市によって大きく異なる項目が認められた。そこで，各都市の緯度を特徴値として95%CI_RANGEとの関係を検証すると，アルカリ性フォスファターゼ（ALP）でのみ有意な負の相関関係が認められた（r = −0.727, p = 0.041）。しかし，この関係は，血液型がBまたはO型で分泌型の場合に血清中での活性値が高値を呈する小腸型ALPに起因するものであった。すなわち，都市の緯度と95%CI_RANGEの有意な相関関係は，血液型の分布が交絡することによる疑似相関であると考察された。BS法による95%CI_CVの推定は，煩雑な計算を必要とせず，測定法評価や個体間差に対するより積極的な考察に対して有用であると考えられる。

Translated Abstract

95% confidence intervals for the coefficient of variation (95%CI_CV) were estimated by the boot-strap (BS) method. The BS method was independently implemented using Excel VBA. The sample size for BS method was set to 50, and the number of iterations was set to 100. The 95% CI_CV was estimated from the mean and 2.5 and 97.5 percentile values of the distribution of CV% calculated by the BS method. The 95% CI_CVs were compared for 12 clinical laboratory tests of healthy reference individuals across eight Asian cities, including Osaka, Hong Kong, and Hanoi. The results showed significant intercity differences in γGT, triglycerides and IgA. Conversely, a significant correlation was found only in ALP between the latitude of each city and the range of the 95% confidence intervals (r = −0.727, p = 0.041). However, this relationship was a pseudo-correlation, with small intestinal ALP, whose activity in serum is increased in blood types B and O, being a confounding factor. Estimation of 95% CI_CV by the BS method is practical in that it does not require complex calculations and is extremely useful for measurement method evaluation and assessment of interindividual differences.

I　 はじめに

観測データの標準偏差（SD）をその平均で除することにより算出される変動係数（CV）は，測定法評価における再現性や，個体間における測定データのバラつきの指標として多用されている。SDも平均からのデータのバラつきの程度を表す統計量であるが，平均や単位の異なる群間でその大きさを比較することに意味はない。これに対して，CVは平均1単位あたりの標準偏差の大きさを意味しており，平均の異なる群間でその大小関係を比較することができる。また，測定データの標準偏差と平均は同単位であるのでCVは無単位であり，単位の異なる群間においてもその大きさを比較することが可能となる。すなわち，CVは平均と単位で標準化された統計量である。

一方，異なる群間でのCVの差の有意性を検証するためには，有意水準を5%とすると，CVの95%信頼区間（95%CI_CV）を推定する必要があり，1930年代より検討されている^1),2)。しかし，その推定には複雑な数学的展開が必要となり，少なくとも臨床検査の分野でCVの有意差検定について議論されることはほとんどない。

そこで本研究では，統計的計算法であるBoot-Strap（BS）法³⁾により，複雑な計算を必要としない95%CI_CVとその信頼区間の幅（95%CI_RANGE）を推定するとともに，アジア地区8都市における健常人臨床検査成績の個人間差を95%CI_CVで比較することを目的とした。なお，以下，算出されたCVは100倍したCV%で示した。

II　 方法

1． BSの実行プロセス⁴⁾

Excel Visual Basic for Applications（VBA）によるBSマクロを独自に作成した。Figure 1にBSマクロの実行プロセスを示す。例として10個の観測データ（オリジナルデータ；OD）が得られたとすると，それぞれのデータに連続した番号を割り当てる。そして，オリジナルデータと同数の乱数を発生させ，各乱数に対応したデータをリサンプリングする。このとき，リサンプリングデータの重複は許容する。次にリサンプリングデータより目的とする統計量（本研究ではCV%）を算出する。BS法ではこのプロセスを数十回から数百回反復計算する。例では反復計算回数（Cycle数）を100回としているので，算出される100個のCV%の分布より95%CI_CVを推定する。なお，〈補足〉としてBSマクロのプロシージャの主要部分を記載した。

Figure 1　 BSマクロの実行プロセス

OD数を10とした場合，1～10の10個の乱数を発生させ，重複を許容して各乱数に対応するODをリサンプルする。

2． 95%CI_CVの推定法

以下に示す4種類の方法（A, B, C, D）で95%CI_CVを推定し，95%CI_RANGEを比較した（［　］内の左：信頼区間下限，右：信頼区間上限）。

A：CV%の分布の平均をM，標準偏差をSDとして，

$[M-\mathrm{1.96SD}\mathrm{\text{，}}M+\mathrm{1.96SD}]$を95%CI_CVとする。

B：CV%の分布の2.5パーセンタイル値を2.5%点，97.5パーセンタイル値を97.5%点として，

$\left[2.5\mathrm{\text{\%点，}}97.5\text{\%点}\right]$を95%CI_CVとする。

C：Bと同様にパーセンタイル値より，

$[2\times \mathrm{M}-\mathrm{97.5\%}\text{点，}\mathrm{2}\times \mathrm{M}-\mathrm{2.5\%}\text{点}]$を95%CI_CVとする。

D：標本平均値を標本標準偏差で除した統計量が非心t分布にしたがうことを利用した概算式による推定⁵⁾。

n個のサンプルから算出された変動係数をcvとして，以下に示す範囲を95%CI_CVとする。

  

$$\left[\frac{\mathrm{\text{CV}}}{1+\sqrt{\frac{2}{\mathrm{n}}}}\mathrm{\text{,}}\frac{\mathrm{\text{CV}}}{1-\sqrt{\frac{2}{\mathrm{n}}}}\right]$$

ただし，n ≥ 20，母平均が母標準偏差よりも十分に大きい，母集団の正規性が担保できる，などが適用条件となる。

3． 使用データベース

日本7地域および，ソウル，北京，香港など，アジア地区7都市における健常基準個体を対象として調査，作成されたデータベース「アジア地区共有基準範囲設定国際プロジェクト2009」⁶⁾から，Table 1に示す肝機能関連，脂質関連，および免疫関連項目の12項目の男性データを用いた。本データベースは，臨床検査の国際的な標準化と歩調を合わせるために，山口大学 市原清志教授を研究代表としたプロジェクトにおいて，健常人3,540（日本国内2,084，国外1,456）名を対象として主要臨床検査95項目について作成されたものである。

Table 1　解析対象とした臨床検査項目

肝機能関連項目	脂質関連項目	免疫関連項目
AST	HDL-コレステロール（HDL-C）	IgG
ALT	LDL-コレステロール（LDL-C）	IgM
γGT	トリグリセリド（TG）	IgA
アルカリ性フォスファターゼ（ALP）	総コレステロール（TCHO）	C4

III　 結果

1． BS法の実行条件

反復計算回数を100回に固定し，OD数を10から100とした場合のそれぞれ100個のCV%の中央値，最小および最大値を比較した。母集団がほぼ正規分布とみなせるTCHOと，典型的な対数正規分布に従うTGにおいても，OD数が50以上で中央値，最大値と最小値，およびその幅：Rangeがほぼ収束する傾向にあった（Figure 2）。以上の結果からOD数を50と設定した。

Figure 2　 OD数の設定

反復計算回数を100回に固定し，OD数を変化させたときの100個のCV%の分布における最大・最小，および中央値。

次に，OD数を50に固定しTCHOとTGで反復計算回数を検証すると，Figure 3に示すように，反復計算回数を増やすことによりRangeが上昇する傾向にあったが，実用性を考慮して反復計算回数を100回に設定した。ちなみに，上述の実行条件で1回のBS実行に要する時間は一般的なスペックのパソコンで約3秒である。

Figure 3　 反復計算回数（Cycle数）の設定

OD数を50に固定し，Cycle数を変化させたときのCV%の分布における最大・最小，および中央値。

2． CV%の分布の正規性

反復計算より得られたCV%の分布から，その95%CI_CVを推定するためには，分布の正規性が担保されている必要がある。そこで，TCHOとTGにおいて上述の実行条件で得られたCV%の分布の正規性をカイ2乗検定で確認すると，TCHOでχ² = 7.785（p = 0.169），TGでχ² = 0.595（p = 0.988）と正規性が確認された。また，正規確率プロットでは両項目ともに累積確率2.5%～97.5%の範囲でプロットの直線性が確認された。

3． 95%CI_CV推定法の比較

Table 2に4種類の95%CI_CV推定法で求めた95%信頼区間および95%CI_RANGEを示す。理論概算法であるD法は，OD（n = 50）より算出される推定値であり，また項目によっては測定値が正規分布に従っていない場合があるが，A～C法との比較のために表に提示した。

Table 2　95%CI_CV推定法の比較

	A法	B法	C法	D法	OD, CV%*
AST	14.9–22.4	14.7–22.3	15.0–22.6	15.8–23.6	18.9
	7.5	7.6	7.6	7.8
ALT	32.7–50.6	32.3–49.6	33.6–51.0	35.5–53.3	42.6
	17.9	17.3	17.4	17.8
γGT	40.0–53.5	39.9–53.2	40.3–53.6	39.2–58.8	47.0
	13.5	13.3	13.3	19.6
ALP	18.2–26.5	17.3–25.5	19.1–27.3	19.2–28.2	23.0
	8.3	8.2	8.2	9.0
HDL-C	16.1–29.7	16.1–29.4	16.4–29.7	19.9–30.0	23.9
	13.6	13.3	13.3	10.1
LDL-C	14.9–22.8	15.0–22.7	15.0–22.7	16.0–23.9	19.2
	7.9	7.7	7.7	7.9
TG	42.3–56.8	41.6–55.6	43.6–57.5	41.8–62.7	50.2
	14.5	14.0	13.9	20.9
TCHO	15.0–22.0	13.0–21.7	15.4–24.0	16.0–24.0	19.2
	7.0	8.7	8.6	8.0
IgG	14.0–21.9	14.1–21.3	14.6–21.8	15.5–23.2	18.6
	7.9	7.2	7.2	7.7
IgM	32.6–47.1	32.5–47.2	32.6–47.2	32.9–49.4	39.5
	14.5	14.7	14.6	16.5
IgA	27.6–39.5	26.6–38.8	28.3–40.4	28.5–42.8	34.2
	11.9	12.2	12.1	14.3
C4	19.2–27.3	19.5–26.5	19.9–27.0	19.6–29.3	23.5
	8.1	7.0	7.1	9.7

各項目の上段：95%CI_CV　下段：95%CI_RANGE

*OD（n = 50）でのCV%

結果として，CV%の分布の平均と標準偏差から信頼区間を推定するA法よりも，パーセンタイル値より推定するB，C法で95%CI_RANGEが狭くなる傾向にあった。また，D法では他の推定法に比べて信頼区間幅が広く推定される傾向にあった。以上の結果より，CV%の分布のパーセンタイル値および平均を推定のパラメータとするC法により95%CI_CVを推定することとした。

4． アジア8都市間における95%CI_CVの比較

北京，ソウル，大阪，台北，香港，ハノイ，ジャカルタ，およびクアラルンプール（K.L.）の8都市の健常基準個体について，Table 1に示した検査項目の95%CI_CVを比較した。Figure 4に都市間で95%CI_CVに重なりが認められなかった，すなわち有意水準5%でCVの平均値に有意差（都市間差）があると判断された3項目を示す。一方，都市間で95%CI_CVに有意差は認められないものの，その区間幅（95%CI_RANGE）が都市によって大きく異なる項目が認められた。これは各都市における基準個体の生活習慣，気候，人種の違いに起因するものと考えられたため，各都市の気候に影響する特徴値として地理的緯度に着目し，全項目における95%CI_RANGEとの関係を検証した。

Figure 4　 アジア地区8都市間における95%CI_CVの比較

*都市間で95%CI_CVに重なりが認められない場合，有意水準5%でCVの平均に有意差があると判断した。

5． 各都市の緯度と95%CI_CVの関係

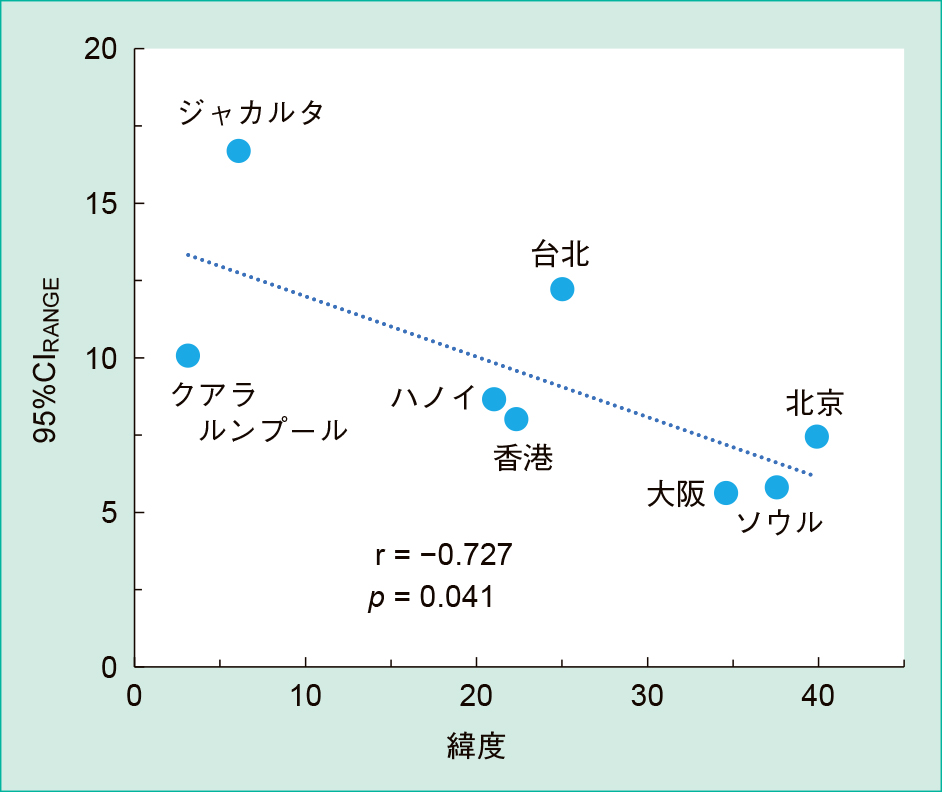
その結果，Figure 5に示すように，ALPにおいてのみ，緯度と95%CI_RANGEの間にr = −0.727（p = 0.041）とn = 8ではあるが有意な負の相関性が認められ，緯度の低い都市ほどCV%の信頼区間幅が有意に広い傾向にあった。ここで，ALPのJSCC法では小腸型ALPに対する反応性が高い試薬処方が採用されており，血液型がBまたはO型で分泌型の場合，正常な状態でも小腸型ALPにより高値を呈することが指摘されている⁷⁾。今回の検討に利用したALPはJSCC法での測定値である。そこで，データベースより各都市の基準個体に占めるBまたはO型の割合を求め，これと緯度および95%CI_RANGEの関係を確認すると，Figure 6に示すように有意ではないがB，O型の割合が高い都市では95%CI_RANGEが広い傾向にあり，一方，緯度との関係では，ソウル，大阪，台北，香港，ハノイのプロットがほぼ一直線上に位置していた。

Figure 5　 ALPにおける緯度と95%CI_RANGEの関係

Figure 6　 血液型がBまたはO型の割合と95%CI_RANGE，緯度の関係

IV　 考察

Efronによって発案されたBS法は，シミュレーションや数値計算を乱数により実行するモンテカルロ法⁸⁾を，計算機を用いた大量の反復計算で置き換えた統計的計算法であり，理論的，数学的アプローチが困難であった問題に対して極めて有用な解析法として注目されている⁸⁾。一方，CV%は測定（観測）データのバラつきや個体間差の指標として重要な統計量であるが，少なくとも臨床検査の分野において，CV%の信頼区間についての研究は多くは見当たらない。これはMcKay¹⁾やVangel²⁾によってカイ2乗分布による95%CI_CVの近似法が報告されているが，極めて複雑な計算が必要となることなど，実用性の面における問題に起因しているものと考えられる。この点について稲田⁵⁾は，簡易な定義式における95%CI_CV推定法を提案しており，測定データのバラつきや個体間差についてのより積極的な考察に貢献できるものと期待される。そこで，本研究では複雑な数式の展開を必要としないExcelマクロで実行可能なBS法による95%CI_CVの推定を試みた。

今回作成したBS法におけるOD数を50と設定した。当初は，より小数のデータ数を予想していたが，電解質のように個人間差の小さな検査項目や，健常な状態でも個人間差が大きな検査項目に対応するためには妥当なデータ数であると考えられる。これに対して，測定法の再現性評価のためのCV%では，Table 2に示した検査項目におけるCV%よりも低い10%以下の精度が議論の対象となることが多いため，OD数や反復計算回数など測定法評価に特化したBS法の実行条件の設定が必要であると考えられる。

アジア8都市間における95%CI_CVの比較では，γGT，TGおよびIgAで有意な都市間差が認められた。これは基準個体の生活習慣や生活環境の違いに起因するものと考えられるが，現時点ではその原因を特定するには至っていない。一方，95%CI_RANGEについては生活環境（気温）に影響する各都市の緯度との間にALPにおいてのみ有意な関係が認められた。しかし，緯度とALPの95%CI_RANGEは独立した変量であり，血液型がBまたはO型の場合に出現する高分子小腸型ALP（HIAP）により，他の血液型グループに比べてALP活性が約23%高値を呈することが報告されている。すなわち，HIAPにより健常な状態でも個人差が大きくなることが指摘されている⁷⁾。そこで基準個体におけるB，O型の割合に着目すると，95%CI_RANGEとは（+）方向の，また緯度との間には（−）方向の関係が認められた。以上の結果を考え合わせると，ALPにおける緯度と95%CI_RANGEとの相関性は，B，O型の割合が95%CI_RANGEに示す（+）の効果と，緯度に対する（−）の効果による血液型の分布を交絡因子した疑似相関であると考えられる。

V　 結語

BS法による変動係数の95%信頼区間の推定は，複雑な計算を必要とせず，また短時間で推定可能であり，異なる群間における変動係数の大小関係だけでなく，その差の有意性を検証できることから，測定法評価や個体間差に対するより積極的な考察に極めて有用であると考えられる。

なお，本論文の要旨は第64回日臨技近畿支部医学検査学会にて発表した。

〈補足〉

以下にBSマクロプロシージャの主要部分を記載する。

Set WS = Worksheets("Sheet1")

Sam = UserForm1.TextBox1.Text  ‘ OD数

SamN = Sam + 1

Cyc = UserForm1.TextBox2.Value  ‘ 反復計算回数

Cyc = Cyc + 1

WS.Range("C2:C1000").Value = " "  ‘ 乱数列

WS.Range("D2:D1000").Value = " "  ‘ リサンプルデータ列

WS.Range("G2:G20000").Value = " "  ‘ リサンプルデータCV%の平均

‘ 乱数の発生

For i = 2 To SamN

CelNo = "C" & i

Randomize

WS.Range(CelNo) = Round((Sam − 1) * Rnd + 1)

Next i

‘ リサンプリング

For t = 2 To SamN

CelNo1 = "C" & t

CelNo2 = "D" & t

WS.Range(CelNo2) = Application.WorksheetFunction. VLookup​(Range(CelNo1), Range("A:B"), 2, False)

Next t

WS.Cells(RowPos, ColPos) = WS.Range("L1")

RowPos = RowPos + 1

Cnt = Cnt + 1

Loop

COI開示

本論文に関連し，開示すべきCOI 状態にある企業等はありません。

文献

• 1)   McKay  AT: Distribution of the coefficient of variation and the extended “t” distribution. J Royal Stat Soc, 1932; 95: 695–698.
• 2)   Vangel  MG: Confidence intervals for a normal coefficient of variation. The American Statistician, 1996; 50: 21–26.
• 3)   Efron  B: Bootstrap methods: Another look at the jackknife. The Annals of Statistics, 1979; 7: 1–26.
• 4)   吉原  健一：ブートストラップ法による推測方法．ブートストラップ法を用いたデータ解析，36–41，培風館，東京，2009.
• 5)   稲田  政則：変動係数の95%信頼区間の概算法．日本臨床検査自動化学会会誌，2018; 43: 601–607.
• 6)   Ichihara  K: The Asian project for collaborative derivation of reference intervals: (1) strategy and major results of standardized analytes. Clin Chem Lab Med, 2013; 51: 1429–1442.
• 7)   松下  誠，他：血清アルカリホスファターゼ活性と血液型との関係．臨床化学，2001; 30: 217–222.
• 8)  小西 貞則，他：ブートストラップ．計算統計学の方法，1–3．朝倉書店，東京，2013.