第13章　時系列解析

古賀 秀信

doi:10.14932/jamt.24J1-13

Abstract

本稿は，臨床研究における時系列解析の重要性とその手法について述べる。臨床検査データは，複数回にわたり測定されることが一般的であり，時系列の特性を無視して単純な比較を行うことは，誤った結論を導く可能性が高い。このようなデータは，患者ごとに階層的な構造を持つため，通常の統計解析ではデータの変動を過小評価する可能性がある。この問題に対処するためには，マルチレベル分析を適用し，階層構造を考慮することが重要である。また，ある時点を境に治療手順やルールが変更された場合，その後のアウトカムの変化を解析するためには，分割時系列解析（ITSA）を用いることが有効である。特に，検査値などの連続変数においては，治療閾値を基準にアウトカムの変化を解析する回帰不連続デザインが適している。一方，周期性やノイズを含む時系列データの解析には，移動平均法，自己相関分析，ARIMAモデル（自己回帰和移動平均モデル）などの手法が用いられる。これらの手法は，データの時間的変動を考慮し，短期的な変動や長期的なトレンド，周期性などを明らかにすることができる。特にARIMAモデルは，自己回帰成分と移動平均成分を組み合わせることで，時系列データのトレンドや季節性を効率的に捉えることが可能であり，予測や変動の分析に適している。時系列解析の本質は，データの時間的構造を適切に評価し，時間軸に沿った変化を考慮して解析を行うことで，予測精度を向上させる点にある。本稿では，これらの解析手法が臨床研究における結果の信頼性向上や，データ解析の精度を高める上で不可欠であることを実際の事例に適用した例を挙げながら解説する。

臨床検査データは，複数回測定されることが多く，時系列の特性を無視して比較を行うことは誤った結論を導く可能性が高い。そのため，階層構造を考慮したマルチレベル分析の使用を検討する。また，ある時点の前後のアウトカムの変化には，分割時系列解析（ITSA）や回帰不連続デザインが適している。

一方，周期性やノイズを含む時系列データの解析には，移動平均法，自己相関分析，ARIMAモデル（自己回帰和移動平均モデル）などの手法が用いられる。時系列解析の本質は，データの時間的構造を適切に評価し，時間軸に沿った変化を考慮して解析を行うことで，予測精度を向上させる点にあるが，これらの手法は，データの時間的変動を考慮し，短期的な変動や長期的なトレンド，周期性などを明らかにすることができる。特にARIMAモデルは，自己回帰成分と移動平均成分を組み合わせることで，時系列データのトレンドや季節性を効率的に捉えることが可能であり，予測や変動の分析に適している。

I　分割時系列デザイン

分割時系列解析（interrupted time series analysis；以下，ITSA）は，集団における介入効果の評価として用いられる手法で，準実験デザイン手法の一つと考えられている。既に実施されている何らかの介入の効果を，種々の理由により無作為化していない（無作為化できない）人や対象集団全体に制御を加えないで，後ろ向きに評価しなければならないこともある¹⁾。医療現場における業務改善や臨床研究では，以下のような場面が想定される。

①診療報酬改定前後における薬剤使用量の変化

②パス導入前後の平均在院日数の変化

③業務改善前後のアウトカムの比較

④その他

イタリアでは，2005年から受動喫煙の健康への悪影響を制限する目的で，すべての屋内公共施設で喫煙を禁止する規制を導入した。Figure 1は2002年から2007年までのシチリア島（イタリア）における急性冠症候群の入院率を示したものである。

Figure 1　シチリア島（イタリア）における受動喫煙防止政策前後の急性冠症候群の入院率の推移

政策を施した2005年を境に入院率に変化を認めることが読みとれる。時系列とは，時間の経過と共に繰り返し（通常は等間隔で）採取された，集団上の連続した一連の観測値であり，ITSAを用いた研究では，興味のある特定の結果の時系列が，既知の時点における介入によって，変化を認めることを確認するために使用される。ITSAでは少なくとも3つのデータが必要である。

・アウトカム変数

件数，連続変数，2値のいずれでもよい。

・時間変数

単位は日，月，年など種類を問わない。

・介入の有無（介入なし0，介入あり1）

また，ITSAでは介入によってどのような影響があると想定されるのかを事前に決めておく必要がある。Figure 2はインパクトモデル（影響モデル）と呼ばれるもので，6つが紹介されている¹⁾。本稿では，カウントデータ（件数）を用いた最も簡単な事例を紹介する。

Figure 2　分割時系列解析のインパクトモデル

Table 1は最も簡単なデータセットで，介入の有無（X），時間経過（T）とカウントデータのアウトカム（Y）が記載されている。実際のITSAでは以下のようなモデルを立てる。

Table 1　最も簡単な分割時系列のサンプルデータ

count (Y)	month (T)	count (Y)	month (T)	intervention (X)
73	1	83	30	0
66	2	85	31	0
79	3	82	32	0
73	4	86	33	0
76	5	84	34	0
73	6	89	35	0
76	7	89	36	0
74	8	83	37	1
72	9	80	38	1
81	10	83	39	1
80	11	82	40	1
86	12	88	41	1
89	13	76	42	1
77	14	77	43	1
85	15	74	44	1
77	16	78	45	1
78	17	84	46	1
76	18	85	47	1
77	19	91	48	1
75	20	102	49	1
77	21	86	50	1
83	22	98	51	1
88	23	89	52	1
93	24	96	53	1
91	25	84	54	1
81	26	81	55	1
94	27	88	56	1
84	28	84	57	1
92	29	94	58	1

Y_t = β₀ + β₁T + β₂Xt + β₃TXt

β₀は時間T = 0におけるベースラインを，β₁は介入前の回帰直線の傾斜を，β₂は介入によるレベルの変化を，β₃は介入後の回帰直線の傾斜の変化を示している。Figure 3は実際の解析結果である。破線は介入前の状態が介入後も続いたと仮定した場合の回帰直線（反事実）で，縦線以降の実線は介入後の回帰直線である。

Figure 3　分割時系列解析のインパクトモデル

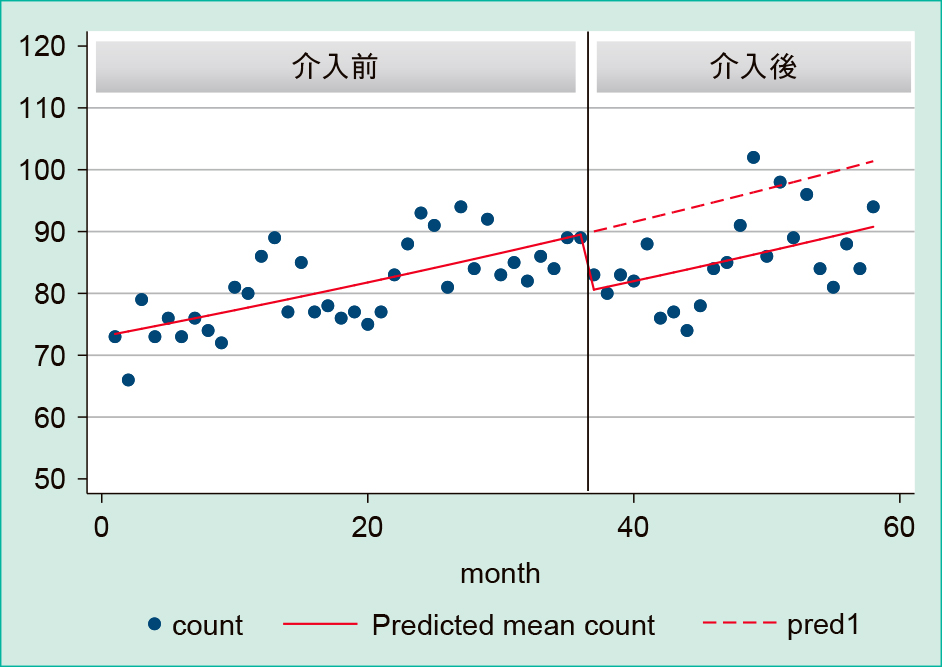
Figure 4はStataで解析を行った結果である。Coef.はcoefficientの略で回帰係数に相当する。[_t]は時間経過におけるアウトカムの変化量を示しているが，1ヶ月毎に0.45増加すること示している（p < 0.001）。[_37]は介入による変化量を示している（37は37ヶ月を示している）。介入によってアウトカムが約9.43有意に（p < 0.001）減少することを示している。[_x_t37]は介入後の介入と時間の交互作用であり，介入後の回帰直線の傾きの違いを示す。p値は0.70であり交互作用は認めず，介入後の回帰直線の傾斜に変化がないことを示している（介入後の回帰係数は0.52）。

Figure 4　 ITSA解析結果

医療現場では，2年に一度の診療報酬改定，4月からの医師や職員の入れ替わり，周知や対策実施の前後変化といった時間経過を無視できない比較は多い。このような場合，ITSAは有効な手法である。実際の解析は，RもしくはStataといった解析ソフトが必要である。前者のRは無料であり，文献¹⁾にはRおよびStataの解析コードが公開されている。個人でチャレンジするのも良いが，統計に精通したスタッフも研究メンバーに加えることで，質もスピードも向上する。

II　マルチレベル分析

高齢者の肺炎患者における検査値や入院時の所見とアウトカムの関係を解析（多変量解析）する場合を考える。高齢者の肺炎は比較的ポピュラーな疾患であり，必ずしも同一診療科が担当するとは限らない。一般内科，呼吸器内科，総合診療科，老年内科をはじめ，他の診療科でも治療を行うことがある。しかし，これらを全て含めて解析を行うと，正しい結果が導き出せない可能性がある。治療ガイドラインはあっても，主治医によって少なからず治療方針の「クセ」のようなものがあるかもしれない。また，診療科の方針によっても治療方針が異なり，患者のアウトカムに影響を与えている可能性があるからである。Table 2はそれらの関係を表で示したものであり，診療科の中に医師は所属しているが，患者データは診療科・医師という階層構造の中に属したデータであることが分かる。このようなデータを「階層構造を持つデータ」という。また，同一患者で上腕部と足関節部での血圧測定，上腕部の血圧の複数回測定や定期的な上腕部血圧の測定など，同一個体で複数回測定する際は，それらのデータは個人内でくくられたデータであり「ネストされた構造を持つデータ」という²⁾。同じ主治医から治療を受けた患者や，同一個体から複数回測定されたデータは似ており，グループ内で相関があるという。階層構造を持つデータやネストされた構造を持つデータは，マルチレベル分析を行わなければならない。考慮しないで通常の解析を行えば，本当は差がないのに差があると結論付けてしまうαエラーを増大させてしまう原因となる¹⁾。このような階層構造，ネストされた構造を持つデータの分析をマルチレベル分析multi-level analysisという。階層線形モデルhierarchical linear model，混合効果モデルmixed effect model，変量効果モデルrandom effect modelとも呼ばれることもある。

Table 2　診療科・主治医の階層構造

id	A診療科			B診療科		C診療科	D診療科
id	A1医師	A2医師	A3医師	B1医師	B2医師	C1医師	D1医師
1	●
2			●
3				●
4	●
5							●
:	:	:	:	:	:	:	:
n					●

目的変数（連続変数）をY，説明変数をX，回帰係数をβ，切片をα，誤差をε，患者を識別する添え字をjとすれば以下の式となる。

Y_j = α + βX_j + ε_j

これに診療科，施設といった水準を考え（iで表す），分布を与えれば以下のように表すことができる。

Y_ij = (α_i + δ_i) + βX_ij + ε_ij

このような診療科，施設に影響を与える効果を変量効果（random effect）という（これに対し，Xのような通常の水準は固定効果（fixed effect）という）。

Table 3とFigure 5は，仮想であるがメタボリック症候群の地域住民に運動プログラムを6ヶ月間施行した際の体重推移である（5名）。これらのデータは個人にくくられたデータであり，マルチレベル解析が必要である。

Table 3　運動療法後の体重推移（5名）

id	month	weight	id	month	weight	id	month	weight
1	1	84	3	1	84	5	1	87
1	2	81	3	2	85	5	2	90
1	3	78	3	3	84	5	3	89
1	4	74	3	4	81	5	4	87
1	5	75	3	5	85	5	5	85
1	6	73	3	6	82	5	6	83
2	1	77	4	1	91
2	2	76	4	2	90
2	3	75	4	3	92
2	4	76	4	4	87
2	5	73	4	5	89
2	6	72	4	6	87

Figure 5　運動療法中の体重推移（6名）

Figure 6はマルチレベルを無視して行った通常の回帰分析であるが，係数は −1.074と経過によって減少傾向にあるが有意ではない（p = 0.101）。

Figure 6　回帰分析の結果

Figure 7はマルチレベル分析を用いて行った結果であるが，係数は −1.074と同じであるが，有意となっている（p < 0.001）。また，同時に尤度比検定も行っているがこちらも有意（p < 0.001）となっており，マルチレベル分析の結果を支持するものである。

Figure 7　マルチレベル分析の結果

検査データも外来・入院問わず，時系列での推移を追うことが多く，このような場合，マルチレベル分析を行わなければならない。統計ソフトとしてRや市販の有料ソフトがあるが，統計に精通したスタッフと共同で行うことが望ましい。

III　回帰不連続デザイン

分割時系列デザインと似た手法のひとつに回帰不連続デザイン（regression discontinuity design; RDD）がある。血圧，コレステロールや血糖値（HbA1c）がガイドラインの提唱する治療域を超えた場合，臨床現場では治療を開始する。

回帰不連続デザインを用いた代表的な研究を紹介する。HIVに感染した場合，CD4陽性Tリンパ球数が200（cells/μL）未満となると日和見感染を起こしやすくなることが知られている⁴⁾。Figure 8は文献⁵⁾から引用した南アフリカのHIV患者における初回CD4測定値と頻度のヒストグラムである。分布に特に偏りはない。

Figure 8　初回CD4測定値の頻度

一方，Figure 9は，X軸は初回CD4測定値で同じで，Y軸が死亡率となっている。当時の治療閾値であった200（cells/μL）を境に曲線が不連続であることが分かる。CD4陽性リンパ球が低下すると日和見感染を起こしやすくなるため死亡率は高くなるが，200（cells/μL）を境に一旦死亡率が低下している。抗レトロウイルス療法（antiretroviral therapy; ART）を開始したからである。このように検査値のような連続変数とガイドライン等で定められている閾値とアウトカムがあれば，このような研究が可能になる。ちなみに現在では，CD4陽性Tリンパ球数の数に関係なく，全てのHIV患者に対して治療を行うようにガイドラインが改められている⁶⁾。

Figure 9　初回CD4測定値と死亡率

［臨床診断・治療］

・高血圧診断とNa摂取量に及ぼす影響

・コレステロール値（脂質代謝異常症治療）と動脈硬化

［有害物質の摂取・曝露］

・飲酒開始年齢（20歳）と自殺・うつ病

［医療政策］

・医療費負担割合（70歳）と受診率・死亡率

・診療報酬改定前後における受療行動／処方の変化

このように臨床検査値をはじめ，年齢を用いても同様の研究を行うことができる。

IV　移動平均法

移動平均（moving average）とは，株価，気温や降水量など時系列で測定されるデータの変動をなだらかにすることで，データの傾向を把握しやすくする方法である。移動平均には以下のような種類が知られているが，ここでは，単純移動平均と加重移動平均について紹介する。

単純移動平均（simple moving average; SMA）

加重移動平均（weighted moving average; WMA）

指数移動平均（exponential moving average; EMA）

修正移動平均（modified moving average; MMA）

三角移動平均（triangular moving average; TMA）

単純移動平均とは，平均を求める範囲をずらしながら平均をとって，データを平滑化する方法である。以下は，7月の最高気温（℃）を想定して作成した架空のデータである。

26.0，25.3，26.2，27.1，29.7，28.9，29.7，29.5，29.5，29.8，29.9，31.2，31.8，31.9，32.3，32.6，33.9，33.7，34.0，33.2，31.1，31.6，32.4，31.7，33.7，32.4，32.5，32.3，33.6，34.9，35.0

7月の最高気温の平均は，以下の式のように31.2（℃）であるが，気温は上昇しているのか，横ばいなのかといった最高気温の変化については把握できない。

(25.0 + ... + 35.0)/31 = 31.2

一方，移動平均は，例えば5日間で平均を求めるとした場合，1日～5日，2日～6日，3日～7日のように1日ずらしていくことで求めることができる。

(26.0 + 25.3 + 26.2 + 27.1 + 29.7)/5 = 26.9

(25.3 + 26.2 + 27.1 + 29.7 + 28.9)/5 = 27.4

(26.2 + 27.1 + 29.7 + 28.9 + 29.7)/5 = 28.3

……

(32.5 + 32.3 + 33.6 + 34.9 + 35.0)/5 = 33.6

この機能はMicrosoft Excelのアドイン機能の一つである「データ分析」メニューに実装されている。

加重移動平均とは，直近のデータに重みを置いた平均である。1日～5日のデータであった場合，以下のように，初日には1を，2日目には2，直近である5日には5を掛けて，5ではなく1 + 2 + 3 + 4 + 5の合計である15で割って計算する。

{(26.0*1) + (25.3*2) + (26.2*3) + (27.1*4) + (29.7*5)}/15 = 26.9

Figure 10は，実際にExcelで，5日間の移動平均および加重移動平均を算出し，折れ線グラフで示したものであるが，日々のデータをプロットするよりも移動平均の方が気温の変動がなだらかで把握しやすく，7月は最高気温が上昇していることが容易に理解できる。

Figure 10　最高気温データの推移と移動平均・加重移動平均

このような時系列データに対して，一定のウィンドウサイズ（上記の5日間の移動平均気温の例であれば5）を適用することで単純移動平均を得ることができるが，これは，画像処理等でよく用いられている畳み込み処理（convolution process）と同じである。畳み込み演算は，信号処理や画像処理などの分野で広く使われており，時系列データの平滑化や特徴抽出にも応用されている。移動平均を求めることでデータのノイズを減らし，データ全体の傾向を把握しやすくなる。

指数平滑法は，加重移動平均と似ており，直近のデータに重みを置き，過去のデータになるほど重みを軽くする方法でその重みは指数関数的に減少する。

Table 4は7月の1日から7日までの気温を指数平滑法で求めたもので，当日の気温は下式で求めることができる。

Table 4　指数平滑法で求めた気温

日	実測気温（℃）	平滑化指数（α）
日	実測気温（℃）	0.1	0.3	0.5	0.7	0.9
1日	26.0
2日	25.3	26.0	26.0	26.0	26.0	26.0
3日	26.2	25.9	25.8	25.7	25.5	25.4
4日	27.1	26.0	25.9	25.9	26.0	26.1
5日	29.7	26.1	26.3	26.5	26.8	27.0
6日	28.9	26.4	27.3	28.1	28.8	29.4
7日	29.7	26.7	27.8	28.5	28.9	29.0

α × 前日の気温 + (1 − α) × 前日の予測値

αは平滑化指数といい，0 < α < 1の値をとり，0に近いほど過去の経過を，1に近いほど直前の実績重視した予測となる^*)。実際，α = 0.1の場合，7日の気温の予測は26.7℃であるのに対し，α = 0.9では29.0℃となっており，後者において予測ができている。

V　自己相関分析

自己相関とは，その名の通り自分のデータとの相関である。Table 5は，24時間毎に同じ気温が繰り返される架空のデータである。

Table 5　自己相関データ

	時刻	気温	lag0	lag1	lag2	lag3	lag12	lag24
1日	0:00	20.0	20.0
	1:00	20.5	20.5	20.0
	2:00	21.0	21.0	20.5	20.0
	3:00	21.5	21.5	21.0	20.5	20.0
	4:00	22.0	22.0	21.5	21.0	20.5
	5:00	22.5	22.5	22.0	21.5	21.0
	6:00	23.0	23.0	22.5	22.0	21.5
	7:00	23.5	23.5	23.0	22.5	22.0
	8:00	24.0	24.0	23.5	23.0	22.5
	9:00	24.5	24.5	24.0	23.5	23.0
	10:00	25.0	25.0	24.5	24.0	23.5
	11:00	25.5	25.5	25.0	24.5	24.0
	12:00	26.0	26.0	25.5	25.0	24.5	20.0
	13:00	26.5	26.5	26.0	25.5	25.0	20.5
	14:00	27.0	27.0	26.5	26.0	25.5	21.0
	15:00	26.5	26.5	27.0	26.5	26.0	21.5
	16:00	26.0	26.0	26.5	27.0	26.5	22.0
	17:00	25.5	25.5	26.0	26.5	27.0	22.5
	18:00	25.0	25.0	25.5	26.0	26.5	23.0
	19:00	24.5	24.5	25.0	25.5	26.0	23.5
	20:00	24.0	24.0	24.5	25.0	25.5	24.0
	21:00	23.5	23.5	24.0	24.5	25.0	24.5
	22:00	23.0	23.0	23.5	24.0	24.5	25.0
	23:00	22.5	22.5	23.0	23.5	24.0	25.5
2日	0:00	20.0	20.0	22.5	23.0	23.5	26.0	20.0
	1:00	20.5	20.5	20.0	22.5	23.0	26.5	20.5
	2:00	21.0	21.0	20.5	20.0	22.5	27.0	21.0
	3:00	21.5	21.5	21.0	20.5	20.0	26.5	21.5
	4:00	22.0	22.0	21.5	21.0	20.5	26.0	22.0
	5:00	22.5	22.5	22.0	21.5	21.0	25.5	22.5
	6:00	23.0	23.0	22.5	22.0	21.5	25.0	23.0
	7:00	23.5	23.5	23.0	22.5	22.0	24.5	23.5
	8:00	24.0	24.0	23.5	23.0	22.5	24.0	24.0

このデータを1時間ずらしたデータを考えてみる。このずれをラグ（lag）といい，1時間ずらしたデータをlag1，2時間ずらしたデータをlag2，……とする。元のデータとlagデータとの相関をとると以下のようになる。

Lag0：自己相関係数1.00

Lag1：自己相関係数0.94

Lag2：自己相関係数0.82

Lag3：自己相関係数0.65

……

Lag12：自己相関係数−0.95

……

Lag24：自己相関係数1.00

Table 5のようなデータであった場合，lagは24の倍数のときに最大となり，lag12，lag36，lag60，……のときに最小となる，24時間毎の周期性を持ったデータであることが分かる。Lagを横軸，実測値とlagとの自己相関係数を縦軸に示した図をコレログラムという。周期性がある場合，コレログラムは特徴的なパターンを示すが，周期性がない場合は際立った特徴を示さない。

VI　 ARIMA（自己回帰和移動平均）

ARIMA（自己回帰和分移動平均）とは，autoregressive integrated moving averageの略であり，以下の3つで構成されている。

・自己回帰（AR）

・和分（I）

・移動平均（MA）

自己回帰（AR）は，過去の値に依存する現在の値のモデル化，和分（I）はデータのトレンドのモデル化ならびに移動平均（MA）は，過去の誤差に依存する現在の値をモデル化で，これらを組み合わせることで，様々な種類の時系列データを効果的に予測することが可能となる。

Table 6のようなデータ（Excel形式）を，Python（Google Colaboratory）を用いてARIMAモデルを行うことを考えてみる。

Table 6　PythonでARIMAモデルを行う気温データ

DateTime	Temperature
2024-07-01 00:00	28.5
2024-07-01 01:00	18.6
2024-07-01 02:00	15.4
2024-07-01 03:00	28.6
:	:
2024-07-31 00:00	23.0

# インポート

import pandas as pd

from statsmodels.tsa.arima.model import ARIMA

# データの読込み

file_path ='/content/drive/MyDrive/●●●●.xlsx'

data = pd.read_excel(file_path)

# データの整形

data['DateTime'] = pd.to_datetime(data['DateTime'])

data.set_index('DateTime', inplace=True)

# ARIMAモデルおよびパラメータの指定と実行

model = ARIMA(data, order=(5, 1, 0))

model_fit = model.fit()

# サマリの表示

model_summary = model_fit.summary()

print(model_summary)

モデルの係数と残差の解釈は以下の通り（Figure 11）。

Figure 11　 ARIMAモデルの解釈

・coef：各自己回帰項の係数

・std err：係数の標準誤差

・z：z統計量

・p > |z|：p値

・[0.025 0.975]：95%信頼区間

・Ljung-Box（L1）（Q）：残差の自己相関

例では自己相関がないと仮定できる（p = 0.90）

・Jarque-Bera（JB）：残差の正規性を評価

例では，正規性を仮定できる（p = 0.67）

・Heteroskedasticity（H）：残差の分散の一貫性

例では一貫性があると仮定できる（p = 0.99）

・Skew：歪度（0に近いほど正規分布に近い）

・Kurtosis：尖度（3に近いほど正規分布に近い）

この読み込ませたデータに基づいて，24時間の予測を行ってみると，Figure 12のようになる。

Figure 12　 ARIMAモデルによる予測

# 24時間後の予測

forecast_steps = 24

forecast = model_fit.forecast(steps=forecast_steps)

model_summary, forecast

実際，ARIMAを用いるには，R，Pythonならびに市販の統計ソフトが必要になるが，時系列データそのものともいえる臨床検査データを積極的に活用し，様々なエビデンスを創出していくために，我々臨床検査技師は，活用できるようにしておく必要がある。

以上，時系列データ解析として，分割時系列デザイン，マルチレベル分析，回帰不連続デザイン，移動平均法，自己相関分析およびARIMAモデルについて概説した。臨床検査技師が行う観察研究においても十分活用できる。分割時系列デザインや回帰不連続デザインは「準実験デザイン」とも呼ばれ，疫学・臨床疫学分野で注目を浴びている。しかし，実際使用するに際して難解であることも多く，研究者と統計担当とのコラボレーションが必要である。

COI開示

本論文に関連し，開示すべきCOI 状態にある企業等はありません。

文献

1) Bernal JL et al.: Interrupted time series regression for the evaluation of public health interventions: A tutorial, Int J Epidemiol, 2017; 46: 348–355.
2) 藤野義久，他：Part I準備編・Part II統計モデル．保険医療従事者のためのマルチレベル分析活用ナビ，2–34，診断と治療社，東京，2013.
3) 丹後俊郎，他：4.4 母数モデルと変量モデル．新版医学統計学ハンドブック，78–79，朝倉書店，東京，2018.
4) 令和5年度厚生労働行政推進調査事業費補助金エイズ対策政策研究事業　HIV感染症および血友病におけるチーム医療の構築と医療水準の向上を目指した研究班：抗HIV治療ガイドライン（2024年3月発行）III 抗HIV治療の基礎知識．https://hiv-guidelines.jp/2024/part03-2.htm（2025年2月4日アクセス）
5) Bor J et al.: Regression discontinuity designs in epidemiology: Causal inference without randomized trial. Epidemiology, 2014; 25: 729–737.
6) 令和5年度厚生労働行政推進調査事業費補助金エイズ対策政策研究事業　HIV感染症および血友病におけるチーム医療の構築と医療水準の向上を目指した研究班：抗HIV治療ガイドライン（2024年3月発行）IV 抗HIV治療の開始時期（成人、慢性期）．https://hiv-guidelines.jp/2024/part04-1.htm（2025年2月4日アクセス）
7) マネジメントクラブ：需要予測の方法．https://media.management-club.jp/data-juyo-yosoku-20190601/#title6 （2024年6月23日アクセス）

Corresponding author

Register with J-STAGE for free!

count (Y)	month (T)	count (Y)	month (T)	intervention (X)
73	1	83	30	0
66	2	85	31	0
79	3	82	32	0
73	4	86	33	0
76	5	84	34	0
73	6	89	35	0
76	7	89	36	0
74	8	83	37	1
72	9	80	38	1
81	10	83	39	1
80	11	82	40	1
86	12	88	41	1
89	13	76	42	1
77	14	77	43	1
85	15	74	44	1
77	16	78	45	1
78	17	84	46	1
76	18	85	47	1
77	19	91	48	1
75	20	102	49	1
77	21	86	50	1
83	22	98	51	1
88	23	89	52	1
93	24	96	53	1
91	25	84	54	1
81	26	81	55	1
94	27	88	56	1
84	28	84	57	1
92	29	94	58	1

id	month	weight	id	month	weight	id	month	weight
1	1	84	3	1	84	5	1	87
1	2	81	3	2	85	5	2	90
1	3	78	3	3	84	5	3	89
1	4	74	3	4	81	5	4	87
1	5	75	3	5	85	5	5	85
1	6	73	3	6	82	5	6	83
2	1	77	4	1	91
2	2	76	4	2	90
2	3	75	4	3	92
2	4	76	4	4	87
2	5	73	4	5	89
2	6	72	4	6	87

count (Y)	month (T)	count (Y)	month (T)	intervention (X)
73	1	83	30	0
66	2	85	31	0
79	3	82	32	0
73	4	86	33	0
76	5	84	34	0
73	6	89	35	0
76	7	89	36	0
74	8	83	37	1
72	9	80	38	1
81	10	83	39	1
80	11	82	40	1
86	12	88	41	1
89	13	76	42	1
77	14	77	43	1
85	15	74	44	1
77	16	78	45	1
78	17	84	46	1
76	18	85	47	1
77	19	91	48	1
75	20	102	49	1
77	21	86	50	1
83	22	98	51	1
88	23	89	52	1
93	24	96	53	1
91	25	84	54	1
81	26	81	55	1
94	27	88	56	1
84	28	84	57	1
92	29	94	58	1

id	month	weight	id	month	weight	id	month	weight
1	1	84	3	1	84	5	1	87
1	2	81	3	2	85	5	2	90
1	3	78	3	3	84	5	3	89
1	4	74	3	4	81	5	4	87
1	5	75	3	5	85	5	5	85
1	6	73	3	6	82	5	6	83
2	1	77	4	1	91
2	2	76	4	2	90
2	3	75	4	3	92
2	4	76	4	4	87
2	5	73	4	5	89
2	6	72	4	6	87

count (Y)	month (T)	count (Y)	month (T)	intervention (X)
73	1	83	30	0
66	2	85	31	0
79	3	82	32	0
73	4	86	33	0
76	5	84	34	0
73	6	89	35	0
76	7	89	36	0
74	8	83	37	1
72	9	80	38	1
81	10	83	39	1
80	11	82	40	1
86	12	88	41	1
89	13	76	42	1
77	14	77	43	1
85	15	74	44	1
77	16	78	45	1
78	17	84	46	1
76	18	85	47	1
77	19	91	48	1
75	20	102	49	1
77	21	86	50	1
83	22	98	51	1
88	23	89	52	1
93	24	96	53	1
91	25	84	54	1
81	26	81	55	1
94	27	88	56	1
84	28	84	57	1
92	29	94	58	1

id	month	weight	id	month	weight	id	month	weight
1	1	84	3	1	84	5	1	87
1	2	81	3	2	85	5	2	90
1	3	78	3	3	84	5	3	89
1	4	74	3	4	81	5	4	87
1	5	75	3	5	85	5	5	85
1	6	73	3	6	82	5	6	83
2	1	77	4	1	91
2	2	76	4	2	90
2	3	75	4	3	92
2	4	76	4	4	87
2	5	73	4	5	89
2	6	72	4	6	87