2015 Volume 1 Pages 5-8
2015 Volume 1 Pages 5-8
Conformational analysis was conducted for a hexakis-N-methylformamide nickel(II) complex cation, [Ni- (NMF)6]2+ [hexakis(N-methylformamide-κO)nickel(II) dication], by the semi-empirical PM6 method and the Density Functional Theory (DFT) method, using 54 possible conformers obtained by the Computational Group Theory (CGT) method as initial structures. In the preliminary structural optimization by the PM6, all of the initial structures converted to only two conformers, pseudo-S6 and pseudo-D3 conformers. Subsequently, the structures of the two conformers were optimized by the DFT method, and the pseudo-S6 conformer was found to be more stable than the pseudo-D3 conformer by 1.8 ~ 2.2 kcal mol–1. From the energy difference, the pseudo-S6 conformer was found to be practically the only species at room temperature. This result is consistent with the crystal structure.
When six monodentate ligands bind to a metal ion in bent forms (Figure 1), how many conformational isomers exist for the octahedral metal complex? It is worth answering this question when the structure cannot be determined experimentally and we need to determine the structure computationally. That is because any molecular computations require initial structures, and we should consider all the possibilities in order not to make mistakes.

An octahedral complex with six ligands in bent forms.
It is not easy to find all the possible structures [1,2,3,4]; however, we previously investigated [5] all the possible isomers of a hexakis-methylamine nickel(II) complex cation [Ni(CH3NH2)6]2+ [hexakis-(methylamine-κN)nickel(II) dication] by computational group theory (CGT) method [6]. We showed there are 36 meridional diastereomers and 16 bisected diastereomers, where the meridional diastereomers have six methylamine ligands on the edges of the N6 octahedron around the nickel(II) ion, and the bisected diastereomers have their six ligands bisecting the edges. Both groups of diastereomers are mutually exclusive and collectively exhaustive. A relationship between the 36 meridional diastereomers and the 30 edge configurations for m = 6 [7] is as follows: if we consider putting six arrows from each apex of an octahedron, the 30 edge configurations are reduced to 23 configurations (Table 1); considering the directions of arrows subsequently, the number of real arrow edge configurations becomes 38. The corresponding point groups of the real arrow edge configurations are also summarized in Table 1.
| Symmetry | Number of edge configurations(m = 6) [7] | Number ofpossible edge configurations for arrow edge configurations | Number of real arrow edgeconfigurations |
| C1 | 14 | 12 | 24C1 |
| C2’ | 2 | 2 | C1, 2C2 |
| Cs | 2 | 1 | C1 |
| Cs’ | 2 | 1 | C1’ |
| C3 | 1 | 1 | 2C3 |
| D2’ | 1 | 1 | C2 |
| C 2v | 2 | 1 | Cs |
| C2v’ | 1 | 0 | – |
| C2v” | 2 | 1 | C2 |
| C2h | 1 | 1 | Ci |
| D3d | 2 | 2 | 2S6, D3 |
| Sum | 30 | 23 | 38 |
We also previously investigated the isomers of [Ni(DMF)6]2+ (DMF = N,N-dimethylformamide) [3]; however, we eliminated unfavorable structures empirically to reduce the number of possible isomers. Therefore, in the present study, in order not to rely on the empirical elimination method, we investigated isomers of a related hexakis-N-methylformamide nickel(II) complex cation,[Ni(NMF)6]2+[hexakis(N-methylformamide-κO)nickel(II) dication] (NMF = N-methylformamide), using CGT method.
All the possible conformers were obtained using previous tables (Tables 2 and 3) [5] obtained by the CGT method [6]. Computational molecular structures were constructed using Winmostar software [8].
| No | Example | Point Group |
| A1 | [ [y], [-z], [-y], [z], [-x], [x] ] | D3 |
| A2 | [ [y], [z], [-x], [y], [z], [-x] ] | C3 |
| A3 | [ [y], [-x], [-x], [-z], [-z], [y] ] | C3 |
| A4 | [ [y], [z], [x], [-y], [-z], [-x] ] | S6 |
| A5 | [ [y], [-z], [x], [-y], [z], [-x] ] | S6 |
| A6 | [ [y], [-x], [x], [-z], [-x], [x] ] | C2 |
| A7 | [ [y], [-z], [y], [z], [-x], [-x] ] | C2 |
| A8 | [ [y], [-x], [-y], [-y], [-z], [y] ] | C2 |
| A9 | [ [y], [z], [-y], [-z], [-x], [x] ] | C2 |
| A10 | [ [y], [-x], [x], [-y], [x], [-x] ] | Ci |
| A11 | [ [y], [-x], [y], [-z], [-x], [y] ] | C1 |
| A12 | [ [y], [-x], [-x], [-z], [-x], [y] ] | C1 |
| A13 | [ [y], [-x], [y], [-z], [z], [y] ] | C1 |
| A14 | [ [y], [-x], [-x], [-y], [-z], [-x] ] | C1 |
| A15 | [ [y], [-x], [y], [-y], [-z], [y] ] | C1 |
| A16 | [ [y], [-x], [-x], [-y], [x], [-x] ] | Cs |
| A17 | [ [y], [-x], [-y], [z], [-x], [-y] ] | C1 |
| A18 | [ [y], [-z], [-x], [-y], [-z], [-x] ] | C1 |
| A19 | [ [y], [-z], [-y], [-y], [-z], [-x] ] | C1 |
| A20 | [ [y], [-z], [y], [-y], [-z], [-x] ] | C1 |
| A21 | [ [y], [z], [-x], [-y], [-z], [-x] ] | C1 |
| A22 | [ [y], [-x], [x], [-z], [-x], [y] ] | C1 |
| A23 | [ [y], [-x], [-y], [z], [-x], [x] ] | C1 |
| A24 | [ [y], [-x], [y], [-z], [-x], [x] ] | C1 |
| A25 | [ [y], [z], [-x], [-z], [z], [-y] ] | C1 |
| A26 | [ [y], [-z], [-x], [-y], [x], [-x] ] | C1 |
| A27 | [ [y], [-z], [y], [-z], [-x], [x] ] | C1 |
| A28 | [ [y], [-x], [-y], [-y], [-z], [-x] ] | C1 |
| A29 | [ [y], [-z], [-y], [-z], [-x], [x] ] | C1 |
| A30 | [ [y], [-x], [y], [-y], [-z], [-x] ] | C1 |
| A31 | [ [y], [-x], [x], [-y], [-z], [-x] ] | C1 |
| A32 | [ [y], [-x], [-x], [-z], [z], [-y] ] | C1 |
| A33 | [ [y], [-x], [y], [-y], [z], [-x] ] | C1 |
| A34 | [ [y], [-z], [y], [-y], [x], [-x] ] | C1 |
| A35 | [ [y], [-x], [x], [-y], [z], [-x] ] | C1 |
| A36 | [ [y], [-x], [-y], [-y], [x], [-x] ] | C1 |
| A37 | [ [y], [-z], [-x], [-y], [x], [-y] ] | C1 |
| A38 | [ [y], [z], [-x], [-y], [x], [-y] ] | C1 |
| No | Example | Point Group |
| B1 | [ [y+z], [x-z], [x-y], [-y-z], [-x+z], [-x+y] ] | D3d |
| B2 | [ [y+z], [-x-z], [x-y], [y+z], [-x-z], [x-y] ] | D3 |
| B3 | [ [y+z], [-x+z], [-x-y], [-y-z], [x-z], [x+y] ] | S6 |
| B4 | [ [y+z], [x-z], [-x+y], [-y-z], [-x+z], [x-y] ] | C2h |
| B5 | [ [y+z], [-x+z], [x-y], [-y-z], [-x+z], [x-y] ] | C2 |
| B6 | [ [y+z], [-x+z], [x-y], [y-z], [-x+z], [-x-y] ] | C2 |
| B7 | [ [y+z], [x-z], [-x-y], [-y-z], [x+z], [-x+y] ] | C2 |
| B8 | [ [y+z], [-x+z], [-x-y], [-y-z], [x+z], [x-y] ] | C2 |
| B9 | [ [y+z], [-x+z], [x-y], [y-z], [-x-z], [x-y] ] | C2 |
| B10 | [ [y+z], [x-z], [-x+y], [-y-z], [-x+z], [-x+y] ] | Cs |
| B11 | [ [y+z], [-x-z], [x-y], [-y-z], [-x+z], [x-y] ] | C1 |
| B12 | [ [y+z], [-x+z], [x-y], [y-z], [-x+z], [x-y] ] | C1 |
| B13 | [ [y+z], [-x-z], [-x+y], [-y+z], [-x-z], [x+y] ] | C1 |
| B14 | [ [y+z], [-x+z], [-x-y], [-y-z], [x+z], [-x+y] ] | C1 |
| B15 | [ [y+z], [-x-z], [-x+y], [-y-z], [-x+z], [x-y] ] | C1 |
| B16 | [ [y+z], [-x+z], [x-y], [-y+z], [-x-z], [x+y] ] | C1 |
All of the initial conformers were optimized using MOPAC2012 [9] program based on the semi-empirical PM6 method [10], and the resulting conformers were optimized based on the Density Functional Theory (DFT) method computation. DFT computations were performed using GAMESS program [11,12] on FUJITSU PRIMERGY CX400 (TATARA computer) at Kyushu University. Structural optimizations were performed with LC-BOP/6-31G, LC-BOP/6-31G*, LC-BOP/6-31G**, LC-BLYP/6-31G, LC-BLYP/6-31G*, and LC-BLYP/6-31G** [13]. Molecular structures were drawn using Winmostar software [8].
All of the possible initial structures for the hexakis-N-methylformamide nickel(II) complex cation, [Ni(NMF)6]2+, were obtained based on the previous tables (Tables 2 and 3). Note that we describe, for example, a conformer shown in Figure 2B as [ [y], [-z], [-y], [z], [-x], [x] ]; meridional planes are described as [y], [-z], and so on; bisected planes are described as [y+z], [x-z], and so on. In this way, 38 meridional conformers, A1-A38, and 16 bisected conformers, B1-B16, were obtained.

Numbering system (A) and an example of a conformer (B).
Using the semi-empirical PM6 method, all of the 54 conformers, A1-A38 and B1-B16, were optimized. [It is noted that among PM5, PM6, and PM7, only PM6 gave a reasonable structure for the present nickel(II) complex. That is, Ni-O-C-N moiety is known to be planar (dihedral angle Ni-O-C-N ~180°) for the related formamide complexes [14,15]; however, PM5 and PM7 gave deformed structures (dihedral angle Ni-O-C-N ~140° or ~220°).] Surprisingly, all the isomers converted to either of only two conformers, C1 and C2, as summarized in Table 4. Subsequently, conformers C1 and C2 were structurally optimized by the DFT method. (We chose LC-BOP and LC-BLYP, because they previously gave reasonable results [16].) The finally obtained structures are shown in Figure 3, and the energy differences are listed in Table 5. The most stable and the second most stable conformers, C1 and C2, have pseudo-S6 structure and pseudo-D3 structure, respectively.
| No | Point Group | Initial structure |
| C1 | pseudo-S6 (C1) | [A3-A5, A7, A8, A10-A16, A21, A22, A24, A27-A37, B1, B3, B4, B8, B14, B15] |
| C2 | pseudo-D3 (C1) | [A1, A2, A6, A9, A17-A20, A23, A25, A26, A38, B2, B5-B7, B9-B13] |
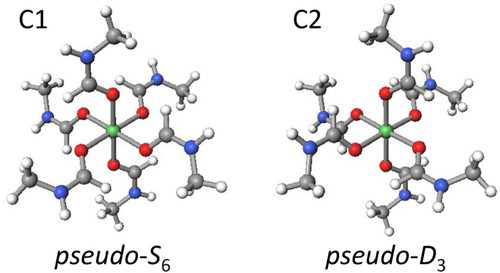
Optimized conformers for [Ni (NMF)6]2+ complex cation (LC-BOP/6-31G).
| DFT method | Energy difference [E(C2) − E(C1)] |
| LC-BOP/6-31G | 2.876 |
| LC-BOP/6-31G* | 1.900 |
| LC-BOP/6-31G** | 1.849 |
| LC-BLYP/6-31G | 3.110 |
| LC-BLYP/6-31G* | 2.284 |
| LC-BLYP/6-31G** | 2.173 |
The energy differences between the conformers were concluded to be 1.8~2.2 kcal mol–1 (Table 5), and if the ratios of the conformers are estimated using the Boltzmann’s distribution law (kT product is 0.596 kcal mol–1 at 300 K), the ratio of conformer C1 is more than 96%. Therefore, conformer C1 (pseudo-S6) is practically the only species at room temperature.
3.3 Comparison with crystal structureThe crystal structure of [Ni(NMF)6](BPh4)2 was determined by single-crystal X–ray method [15]. In the crystal, there were two types of [Ni(NMF)6]2+ cations, A and B (Figure 4), and both have pseudo-S6 structure. Therefore, the present computational investigation is consistent with the crystal structure.

Two types of [Ni(NMF)6]2+ cations (A and B) observed in a single crystal [15].
In this study, the structures of [Ni(NMF)6]2+ complex cation were computationally obtained, and the result was consistent with the crystal structure. At the beginning, 54 possible conformers were obtained by the CGT method. Subsequently, the 54 conformers were structurally optimized by the semi-empirical PM6 method to obtain only two conformers, pseudo-S6 conformer and pseudo-D3 conformer. After the subsequent optimization by the DFT method, the energy difference indicated that the pseudo-S6 conformer is considered to be practically the only species at room temperature. This result is consistent with the fact that only the pseudo-S6 conformer was found in the crystal structure.
This work was supported by JSPS KAKENHI Grant Number 15K05445. Financial support by Yamagata University is also acknowledged. A copy of the MOPAC2012 program was provided by Professor J. J. P. Stewart. The technical support on Tatara computer was provided by Dr. Yuichi Inadomi at Kyushu University.