Reconstruction of Four-Body Statistical Pseudopotential for Protein-Peptide Docking

Abstract

We constructed the four-body statistical pseudopotential proposed by Krishnamoorthy and Tropsha, which is a type of coarse-grained potential previously used for protein-peptide docking, using different data sets. The first data set is composed of crystal structures of proteins that satisfy the conditions specified using PISCES, a protein sequence culling server. The second data set consists of crystal structures of protein-protein complexes obtained from the PDBbind-CN database. The four-body potential has 44275 patterns of scores, depending on the type of amino acid in the quadruplet of residues and the continuity of amino acid in the sequence of protein or peptide. While the PISCES-based data set covers almost all patterns, docking simulations revealed that both potentials provided comparable accuracy in reproducing experimentally determined peptide binding poses.

1 INTRODUCTION

The COVID-19 pandemic caused by SARS-CoV-2 required rapid drug development. Docking simulations have been used to screen drug candidates, contributing to the acceleration of the drug development [1]. In the development of antibody drugs, a technology that can find sequences binding predominantly to the epitope of viral spike proteins would be useful. The docking simulation is expected to be a candidate for such a technology.

Krishnamoorthy and Tropsha developed a four-body statistical pseudopotential for evaluating protein stability [2]. Aita et al. applied it to the protein-peptide docking [3]. Our group has also developed a program for protein-peptide docking simulations using the four-body coarse-grained potential. Unfortunately, it has become clear that the potential constructed in the literature [2] cannot reproduce experimentally measured binding poses of protein-peptide complexes with sufficient accuracy when used as is [3, 4].

The four-body coarse-grained potential is statistically determined based on a data set consisting of a large number of protein structures. Therefore, the docking result could be strongly influenced by the contents of the data set. In this study, we aimed to improve the accuracy of the docking simulation using the four-body statistical pseudopotential by constructing the potentials from different data sets and comparing the docking results.

2 METHOD

2.1 Four-Body Statistical Pseudopotential

Tropsha and co-workers coarse-grained the protein structure by Delaunay tessellation as a set of tetrahedra consisting of quadruplets, namely, representative points of four amino acid residues [2, 5]. Each tetrahedron is classified into one of the classes α = 0, 1, 2, 3, or 4 according to the continuity in the sequence of amino acid residues (Figure 1).

Figure 1.

 Five classes of tetrahedra considered in the four-body pseudopotential.

The class of α = 0 means that each of the four residues in the protein/peptide sequence is not adjacent to the others. α = 1 means that two residues are consecutive in the sequence, and the others are separated. α = 2 is the case where two sets of two consecutive residues are present. As for α = 3, three residues are consecutive, and the remaining one is separated. α = 4 means that all the residues are consecutive.

Let i, j, k, and l denote the types of amino acid residues constituting the quadruplet and α denote the class. The score Q of the coarse-grained potential is defined by equation (1) [2].

  

$Q_{i,j,k,l}^{\text{α}}=\log \left[\frac{f_{i,j,k,l}^{\text{α}}}{P_{i,j,k,l}^{\text{α}}}\right]$(1)

$f_{i,j,k,l}^{\text{α}}$ is the probability that the type of amino acid residues is i, j, k, and l when selecting one at random from the tetrahedra of class α in the data set. $P_{i,j,k,l}^{\text{α}}$ is the probability that the type of amino acid residue is i, j, k, and l and the class is α when four amino acid residues in the data set are randomly selected. The explicit formula of $P_{i,j,k,l}^{\text{α}}$ is given by equation (2).

  

$P_{i,j,k,l}^{\text{α}}=C{a}_i{a}_j{a}_k{a}_l{P}_{\text{α}}$(2)

a_i, a_j, a_k, and a_l are the ratio of the amino acid residues i, j, k, and l in the data set, respectively. P_α is the probability that the class is α when one of the tetrahedra are randomly selected from the data set. By treating each amino acid residue in the quadruplet as a duplicate combination, the coefficient C is given by equation (3).

  

$C=\frac{4!}{{\text{Π}}_{\upsilon =1}^{\eta }{t}_{i_{\upsilon }}!}$(3)

η is the number of the types of amino acids in the quadruplet (1 ≤ η ≤ 4), and $t_{i_{\upsilon }}$ is the number of type $i_{\upsilon }$ residues in the quadruplet.

According to the literature [2], the four-body pseudopotential was constructed using two data sets, one of which was based on a list of protein chains from the CulledPDB directory with 2.2 Å resolution and 30% maximum sequence identity. Another set of protein chains with a resolution no more than 2.5 Å and a maximum sequence identity of 25% was selected from the Sequence Unique Database. The former contained 1653 chains and the latter 967 chains.

We utilized PISCES [6, 7], which is a protein sequence culling server, to obtain a list of protein chains at a resolution of 2.5 Å, a maximum sequence identity of 25%, and a maximum R-value of 0.30. This resulted in a list of 10529 protein chains, based on which we downloaded PDB files from the Protein Data Bank [8, 9] to construct the potential. Hereafter, this data set and the corresponding four-body potential are referred to as PISCES25. The large number of protein chains reflects the increase in the number of entries to the Protein Data Bank during the last two decades. We prepared another data set using a database of biomolecular complexes. 2477 structures of protein-protein complexes registered in the PDBbind-CN database version 2020 [10] were adopted as the components of data set. This data set and corresponding four-body potential is referred to as PDBbind.

2.2 Docking Simulation

The PepSet Benchmark [11] was used to evaluate the accuracy of the docking simulation. This benchmark set contains 185 protein-peptide complexes, where peptides range in length from 5 to 20 residues. In this study, the docking simulations of 13 complexes with 5 peptide residues were performed using our in-house program. We excluded 5ggp, 5kds, and 6f4s because the experimental structure shows the existence of a small molecule near the position of the peptide. An explicit treatment of such a molecule is not subject to the protein-peptide docking based on the four-body pseudopotential considered in this study.

In our docking simulations, peptide binding poses were searched with the protein structures fixed. The protein surface was defined by the Defpol [12] or MSMS [13, 14] method. In the Defpol method, atomic radii of carbon, hydrogen, nitrogen, oxygen, and sulfur were set to 1.462, 1.135, 1.392, 1.332, and 1.741 Å, respectively. The default setting of the program [14] was used for the atomic radii in the MSMS method. Density and high density of triangulation in the MSMS method were 10.0 vertex/Ų, and the probe radius was 2.0 Å. Search points were placed at 2.15 Å from the surface.

Proteins were coarse-grained by Delaunay tessellation and represented as a set of tetrahedra with C_α atoms as vertices. Peptides were also treated as coarse-grained models with C_α atoms as representative points. One of the five amino acid residues comprising the peptide was placed at a search point, and the score of the tetrahedra formed by the placed residue and the residues of the protein were evaluated. The placement and evaluation were performed for all the residues. For the top 5% of search points for each residue (Residue 1 in Figure 2), the adjacent amino acid residue in the peptide sequence was placed at a search point, and the score of the tetrahedra consisting of the placed residue and the residues of the protein was evaluated (Residue 2 in Figure 2). For the two search points with the highest scores, the position of the next amino acid residue was searched in the same way (Residue 3 in Figure 2). All the remaining amino acid residues are similarly processed to obtain peptide binding poses. The search is proceeded from the initially placed residue to the N-terminal of the peptide, and then from the remaining residue adjacent to the initially placed one to the C-terminal.

Figure 2.

 An example of the tree structure for searching four binding poses. The number on the node represents the score of the residue placed at the search point.

The search for binding poses after the first residue is placed is represented as a tree structure (Figure 2). The search does not proceed any further except for the two nodes with the highest scores. When the low-score nodes are removed, the tree structure becomes a binary tree, and the number of leaves is at most 2 to the power of N − 1, where N is the number of amino acid residues in the peptide.

For all the peptide binding poses obtained from the docking simulations, the difference in the peptide position from the experimental structure was evaluated by Geometric center To Geometric center Distance (GTGD) and Root Mean Squared Deviation (RMSD).

  

$\text{GTGD}=\left|\frac{1}{N}\sum _{i=1}^N{r}_i-\frac{1}{N}\sum _{i=1}^N{r}_i^{\text{exp}}\right|$(4)

  

$\text{RMSD}=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left|r_i-r_i^{\text{exp}}\right|}^2}$(5)

N is the number of amino acid residues in the peptide, r_i is the coordinate of the C_α atom at the i-th amino acid residue, and $r_i^{\text{exp}}$ is the coordinate of the C_α atom at the i-th amino acid residue in the experimental structure. The minimum values of GTGD determined for each complex and those of RMSD were used as a measure of accuracy.

3 RESULTS AND DISCUSSION

3.1 Analysis of Data sets and Potential Scores

This subsection focuses on the features of the data sets used to construct the potentials. Figure 3 shows the percentages of amino acids counted from the data set. The differences of both data sets are small except for alanine and serine. The overall trends with respect to the type of amino acid are similar to the frequency of the proteome isoelectric point database consisting of about 23.9 billion amino acid residues [15]. Figure 4 shows the percentage of the tetrahedron classes counted from the data set. The difference in appearance rates at α = 3 and α = 4 may be due to the fact that tetrahedra composed of amino acid residues between polypeptide chains do not belong to α = 4, which means that four residues are consecutive on the amino acid sequence of one polypeptide chain.

Figure 3.

 The frequency of amino acids in the data set for the four-body statistical pseudopotential.

Figure 4.

 The frequency of tetrahedron classes in the data set for the four-body statistical pseudopotential.

The score of the four-body pseudopotential expressed in equation (1) has 8855 combinations of amino acids and 5 classes, which means that there are totally 44275 patterns of i, j, k, l, and α. We investigated the number of combinations which are not present in the dataset (Table 1).As for the PISCES-based data set, different sequence identity thresholds were examined. A sequence identity (%) is expressed as the number associated with “PISCES.” Obviously, the number of non-emerging patterns correlates with the number of data, which is the number of protein chains or that of the protein-protein complexes. For the PISCES25 data set, the number of missing combinations was 30 out of 44275, indicating that the data set is comprehensive. The PDBbind data set has 439 combinations that are not present in the dataset.

Table 1. Comparison of the datasets with respect to size and non-emerging tetrahedron patterns.

	Number ofdata	Number of non-emerging patterns of tetrahedra
PISCES30	14535	22
PISCES25	10529	30
PISCES20	6842	72
PISCES15	4528	135
PDBbind	2477	439

Scores are not determined from equation (1) for ijklα combinations that are not present in the data set, because $f_{i,j,k,l}^{\text{α}}$ = 0. In such cases, a finite value of the score (−1.20) was set for the feasibility of docking simulations. We point out the difference of the constructed potentials in the score. They are only weakly correlated as shown in Figure 5.

Figure 5.

 Comparison between the potential scores from the PISCES25 data set and those from the PDBbind dataset.

3.2 Docking Simulation

Before comparing the binding poses from different potentials, we investigate whether search points are properly placed using an algorithm that generates molecular surfaces. The docking simulation was performed with the protein surface defined either by the Defpol method or by the MSMS method. Table 2 lists the number of search points and binding poses obtained from the docking simulation for each of the 13 protein-ligand complexes.

Table 2. The number of search points and obtained binding poses.

	Defpol			MSMS
	Searchpoint	Binding pose		Searchpoint	Binding pose
1jq8	3138	11242		2705	7760
1mf4	3221	11142		2769	9587
1nvq	4853	17184		5437	15881
1v1t	3829	14179		3769	13984
2aij	5125	18113		5367	14797
2hpl	2490	8823		2062	6930
3fp2	6523	22219		10732	33731
3hds	4468	16045		4595	15003
4hdq	5241	17779		6526	19879
4ny3	5362	19508		5871	21320
4×3o	4989	16274		5842	18845
5e33	7630	24926		12119	35596
5onp	5471	18325		6034	20214

In the case of the Defpol method, the GTGD and RMSD minima averaged over the 13 complexes were 3.031 and 5.116 Å, respectively. Those for the MSMS method were 1.935 and 4.201 Å, respectively. Figure 6 plots the minimum values of GTGD and RMSD for the 13 complexes. The horizontal axis represents the case of adopting the Defpol method to define the protein surface, and the vertical axis represents the case of the MSMS method. The MSMS method generally provided similar or slightly smaller values than the Defpol method, whereas the values can differ significantly. In the case of the complex of PDBID 5e33 [16] (Figure 7), the GTGD and RMSD of the Defpol method were quite large (> 17 Å), in contrast with the good result of the MSMS method.

Figure 6.

 Comparison of the Defpol and MSMS methods in terms of the smallest GTGDs and RMSDs (Å).

Figure 7.

 The experimental structure of 5e33. The protein is described in the ribbon model with a molecular surface, and the peptide is described in the wireframe model.

All the binding poses obtained from the docking simulations of the complex with PDBID 5e33 are shown in Figure 8. The Defpol method resulted in the peptide binding poses outside of the protein because it did not place search points inside the protein. The MSMS method placed search points in the inner cavity of the protein, which caused the peptide binding poses inside the protein, resulting in qualitative agreement with the experimental structure. The difference in the ability to place search points originates in the difference in the algorithms used to generate the molecular surface. In the Defpol method, an ellipsoid is created outside the molecule, and it is brought close to each atom of the protein. The MSMS method, on the other hand, generates the surface by rolling a probe on atoms with certain radii, which is suitable for grooves on the molecular surface and cavities inside the molecule.

Figure 8.

 Peptide binding poses (shown in light blue) of 5e33 obtained by the docking simulation using (a) Defpol method and (b) MSMS method. The pink lines represent the coarse-grained protein structure by Delaunay tessellation as a set of tetrahedra consisting of quadruplets.

Figure 9 plots the minimum values of GTGD and RMSD for the 13 complexes. The horizontal axis represents the case of the protein chains based on PISCES, and the vertical axis represents the protein-protein complexes in PDBbind as the data set used to construct the coarse-grained potential. The two and three complexes resulted in significantly different (> 1 Å) GTGD and RMSD values, respectively. The GTGD and RMSD minima of the potential constructed from PDBbind were 1.620 and 4.343 Å, respectively, on average for the 13 complexes, which were comparable to the values of PISCES25 (1.935 and 4.201 Å as mentioned above).

Figure 9.

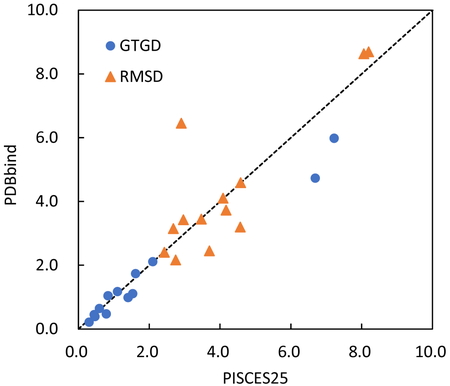
 Comparison of the data sets in terms of the smallest GTGDs and RMSDs (Å).

The results presented up to here were obtained when the search of binding poses proceeds by adopting the best and second-best cases in score when an amino acid residue is placed at search points. The result of the search can be expressed as a binary tree. We defined this case as N = 2 and performed the docking simulations for N = 1 and N = 3, the latter of which corresponds to a ternary tree. Table 3 shows the minimum values of GTGD and RMSD averaged for the 13 complexes. As the value of N increases, the best binding pose became closer to the experimental structure. In addition, the accuracy in the binding pose, i.e., the smallest GTGD or RMSD was not strongly dependent on the four-body potential.

Table 3. Averaged values of the smallest GTGDs and RMSDs (Å) from the docking simulations employing top-N search points.

	Dataset	N = 1	N = 2	N = 3
GTGD	PISCES25	2.343	1.935	1.526
	PDBbind	2.200	1.620	1.503
RMSD	PISCES25	5.027	4.201	3.770
	PDBbind	5.174	4.343	3.783

4 CONCLUSION

We constructed the four-body statistical pseudopotential, a type of the coarse-grained potential previously used for protein-peptide docking. The Defpol and MSMS methods were investigated as a technique to represent protein surfaces for the placement of search points, with the latter providing better results. Two data sets were prepared to determine the score of the potential. The data set obtained using PISCES is superior because of the small number of non-emerging patterns of tetrahedra. Although the PDBbind data set was small in amount of data, the constructed potential was comparable in docking accuracy to the PISCES-based potential.

Acknowledgments

The docking simulations were performed using the HPC cluster of Information and Media Center, Toyohashi University of Technology.

REFERENCES

• [1]   K. Gao, R. Wang, J. Chen, L. Cheng, J. Frishcosy, Y. Huzumi, et al., Chem. Rev., 122, 11287 (2022). , doi:10.1021/acs.chemrev.1c00965 PMID:35594413
• [2]   B. Krishnamoorthy, A. Tropsha, Bioinformatics, 19, 1540 (2003). , doi:10.1093/bioinformatics/btg186 PMID:12912835
• [3]T. Aita, K. Nishigaki, Y. Husimi, Comput. Biol. Chem., 34, 53 (2010). , doi:10.1016/j.compbiolchem.2009.10.005
• [4]S. Matsumoto, H. Goto, unpublished.
• [5]   R. K. Singh, A. Tropsha, I. Vaisman, J. Comput. Biol., 3, 213 (1996). , doi:10.1089/cmb.1996.3.213 PMID:8811483
• [6]   G. Wang, R. L. Dunbrack, Jr., Bioinformatics, 19, 1589 (2003). , doi:10.1093/bioinformatics/btg224 PMID:12912846
• [7]   PISCES, A Protein Sequence Culling Server,http://dunbrack.fccc.edu/pisces/.
• [8]   Nucleic Acids Res., 47, D520 (2019). doi:10.1093/nar/gky949
• [9]   RCSB PDB, https://www.rcsb.org/.
• [10]   PDBbind-CN database, http://www.pdbbind.org.cn/.
• [11]   G. Weng, J. Gao, Z. Wang, E. Wang, X. Hu, X. Yao, et al., J. Chem. Theory Comput., 16, 3959 (2020). , doi:10.1021/acs.jctc.9b01208 PMID:32324992
• [12]C. S. Pomelli, J. Tomasi, J. Comput. Chem., 19, 1758 (1998).
• [13]M. F. Sanner, A. J. Olson, J. C. Spehner, Biopolymers,38, 305 (1996). ,
• [14]   MSMS, https://ccsb.scripps.edu/msms/.
• [15]L. P. Kozlowski, Nucleic Acids Res., 50, D1535 (2022). , doi:10.1093/nar/gkab944
• [16]P. Kumar, V. Reithofer, M. Reisinger, S. Wallner, T. Pavkov-Keller, P. Macheroux, K. Gruber, Sci. Rep., 6, 23787 (2016). , doi:10.1038/srep23787