2016 Volume 2 Article ID: 2016-0001
2016 Volume 2 Article ID: 2016-0001
MagSaki(Tetra) software was developed for the purpose of analyzing the magnetic susceptibility data of tetranuclear octahedral high-spin cobalt(II) complexes. The software enables the analyses six types of tetranuclear cobalt(II) structures, including cubane and defect dicubane structures, to obtain magnetic parameters: the interaction parameters, J, J’, J”, and J”’, the spin-orbit coupling parameter, λ, the orbital reduction factor, κ, and the axial splitting parameter, Δ.
The magnetic properties of some high-spin cobalt(II) complexes are difficult to interpret because of the effects of the ligand field and the spin-orbit coupling [1]. Earlier, Lines [2] and Figgis [3] developed a way to analyze
the magnetic properties of mononuclear octahedral high-spin cobalt(II) complexes by considering an axially distorted ligand field and spin-orbit coupling. Although they showed the importance of considering the distorted ligand field, the distortion had never been considered for dinuclear octahedral high-spin cobalt(II) complexes until Sakiyama developed susceptibility equations for the dinuclear systems [4,5,6,7].
For the purpose of analyzing the magnetic properties of high-spin cobalt(II) complexes conveniently, a series of computational programs, MagSaki software series, has been developed for mononuclear, dinuclear, and trinuclear systems [8,9,10]. A magnetic susceptibility equation was recently developed for tetranuclear octahedral high-spin cobalt(II) complexes [11], including the cubane and defect dicubane structures (Figure 1). In this paper, a MagSaki(Tetra) software is reported, which was developed for the purpose of analyzing the magnetic properties of tetranuclear high-spin cobalt(II) complexes.
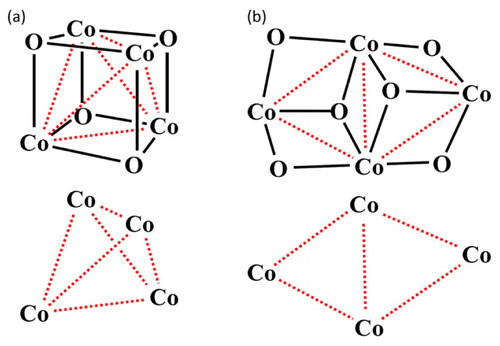
Tetranuclear cubane (left) and defect dicubane (right) structures.
The main symbols for the magnetic parameters are summarized in Table 1.
| Symbol | Unit | Meaning |
| J, J’, J”, J”’ | cm–1 | Interaction parameters |
| T | K | Absolute temperature |
| TIP | cm3 mol–1 | Temperature-independent paramagnetism |
| v | – | Distortion parameter defined as Δ/(κλ) |
| Δ | cm–1 | Axial splitting parameter |
| κ | – | Orbital reduction factor |
| λ | cm–1 | Spin-orbit coupling parameter |
| μeff | μB | Effective magnetic moment |
| χA | cm3 mol–1 | Atomic magnetic susceptibility |
| χM | cm3 mol–1 | Molar magnetic susceptibility |
The software was developed using REALbasic software [12] on a KOHJINSHA SA5 SX04A computer (OS: Windows XP Home edition).
As well as the previous MagSaki software series [8,9,10], the MagSaki(Tetra) software imports the temperature dependence data of magnetic susceptibility, χA versus T data (χA = χM/4 for tetranuclear cobalt(II) complexes), and displays a χA versus T graph and an effective magnetic moment μeff versus T graph. The software can calculate theoretical χA and μeff values for six types of tetranuclear cobalt(II) structures, including cubane and defect dicubane structures, and also displays the theoretical curves of χA and μeff on the graph. The software can optimize magnetic parameters to fit the theoretical curve to the observed data.
In addition to the calculation modes of the MagSaki(A) software, the MagSaki(Tetra) software has six calculation modes for tetranuclear high-spin cobalt(II) species. The most symmetrical tetranuclear structure belongs to a Td point group (Figure 2), and in this case, six interactions between cobalt(II) ions are equivalent. Hereafter, the interaction pattern of the Td structure is called <6> because there are six interactions but there is only one type of interactions, J (Table 2). When the tetranuclear structure deforms, the symmetry is decreased; main deformation patterns are described in Figure 2, and the abbreviations of the interaction patterns are summarized in Table 2. For example, in the case of tetranuclear cubane structure, the symmetry of Co4 unit is Td, and the interaction pattern is <6>; in the case of symmetrical tetranuclear defect dicubane structure, the symmetry of Co4 unit is D2h (D2h − 2), and the interaction pattern is <141>. The MagSaki(Tetra) software is capable of analyzing the various types of tetracobalt(II) structures, although using only six calculation modes: <6>, <51>, <42>, <141>, <321>, and <1221>. The magnetic susceptibility equation is described in Reference 11.

Main deformation patterns of tetranuclear structure.
| Symmetry | Number of types of interactions | Type of interactions | Abbreviation of the pattern |
| Td | 1 | 6J | <6> |
| C3v | 2 | 3J, 3J’ | <33> |
| D3h | 2 | 3J, 3J’ | <33> |
| S4 | 2 | 4J, 2J’ | <42> |
| D4h | 2 | 4J, 2J’ | <42> |
| D2 | 3 | 2J, 2J’, 2J” | <222> |
| D2h − 1 | 3 | 2J, 2J’, 2J” | <222> |
| C2v | 3 | J, 4J’, J” | <141> |
| D2h − 2 | 3 | J, 4J’, J” | <141> |
| C2 | 4 | J, 2J’, 2J”, J”’ | <1221> |
| C2h | 4 | J, 2J’, 2J”, J”’ | <1221> |
| - a | 1 | 5J, J’ | <51> |
| - a | 3 | 3J, 2J’, J” | <321> |
a Not for any realistic structures, but useful for analysis; for example, <51> corresponds to the J = J' case for <141>, and <321> corresponds to the J = J' case for <1221>.
Some of the theoretical χAT versus T curves have been already reported for the tetranuclear cobalt(II) complexes of mode <6> [11]. In this paper, some other theoretical curves for square-shaped and parallelogram-shaped tetranuclear cobalt(II) complexes (Figure 3) are demonstrated in Figures 4 and 5. It is noted that the χAT value is temperature-dependent due to the spin-orbit coupling even when there are no interactions between cobalt(II) ions; the no-interaction curve is shown in black in each graph. In the case of square-shaped tetranuclear cobalt(II) complexes of D4h symmetry, mode <42> is appropriate, considering four J interactions and two J’ interactions (Figure 3a). The variation of J changes the theoretical curve when J’ is positive (+10 cm–1) (Figure 4a); however, the effect is small when J’ is negative (−10 cm–1) (Figure 4b).

Square-shaped (a) and parallelogram-shaped (b) models.

Theoretical χAT versus T curves for tetranuclear cobalt(II) complexes of square shape with the variation of J when J’ > 0 (a) and when J’ < 0 (b). [The curves represent from the bottom (J/ cm–1, J’/ cm–1) = (−10, +10), (−5, +10), (0,0), (0, +10), (+5, +10), and (+10, +10), respectively for (a) and (J/ cm–1, J’/ cm–1) = (−10, −10), (−5, −10), (0, −10), (+5, −10), (+10, −10), and (0,0), respectively for (b), when λ = −170 cm–1, κ = 0.9, and Δ = 0 cm–1.]
In the case of parallelogram-shaped tetranuclear cobalt(II) complexes, mode <1221> is appropriate, considering one J interaction, two J’ interactions, two J” interactions, and one J”’ interaction (Figure 3b). When only J’ is negative, the complex is considered as two coupled dinuclear cobalt(II) complexes. Therefore, the χAT curve is exactly equal to that of a dinuclear complex, and the χAT value reaches zero in the low-temperature range (the red curve in Figure 5a). On the other hand, when only J is negative, the complex is considered as one coupled dinuclear cobalt(II) complex and two magnetically isolated mononuclear cobalt(II) complexes. In this case, the χAT value (one quarter of χMT value) reaches one half of the monomer, corresponding to two magnetically isolated cobalt(II) ions, in the low-temperature range (the orange curve in Figure 5a).

Theoretical χAT versus T curves for tetranuclear cobalt(II) complexes of parallelogram shape. [The curves represent from the bottom (J/ cm–1, J’/ cm–1, J”/ cm–1, J”’/ cm–1) = (0, −10, 0, 0) [red], (−10, 0, 0, 0) [orange], and (0, 0, 0, 0) [black] when λ = −170 cm–1, κ = 0.9, and Δ = 0 cm–1 (a), (J/ cm–1, J’/ cm–1, J”/ cm–1, J”’/ cm–1) = (−50, −10, 0, 0) [blue], (−40, −10, 0, 0), (−30, −10, 0, 0), (−20, −10, 0, 0), (−10, −10, 0, 0), (0, −10, 0, 0) [red], and (0, 0, 0, 0) when λ = −170 cm–1, κ = 0.9, and Δ = 0 cm–1 (b), when λ = −170 cm–1, κ = 0.9, and Δ = −1530 cm–1 (c), and when λ = −170 cm–1, κ = 0.9, and Δ = +1530 cm–1 (d).]
When J’ is fixed to −10 cm–1 in a parallelogram-shaped tetranuclear cobalt(II) complex, the variation of J (−50 to −10 cm–1) was demonstrated (Figure 5b). When J becomes smaller and the antiferromagnetic interaction becomes larger, a characteristic two-step shape appears due to the two thermally distributed states, while χAT decreases monotonously when J is close to zero due to only one thermally distributed state. The axial splitting parameter, Δ, is zero in Figure 5b, but when Δ changes, the shapes of the curves change (Figures 5c and 5d). The Δ parameter is negative in Figure 5c, and positive in Figure 5d. Since the curve shape depends on the Δ parameter, which indicates the degree of distortion, considering the distortion of the octahedral ligand field is important in magnetic data analysis.
The software can optimize magnetic parameters to fit the theoretical curve to the observed data. Using the software, several data have been analyzed [11,13].
The software (MagSaki(Tetra) 2100W) will run on Windows computers.
This work was supported by JSPS KAKENHI Grant Number 15K05445. Financial support by Yamagata University is also acknowledged.