2018 Volume 4 Article ID: 2017-0042
2018 Volume 4 Article ID: 2017-0042
In the present work, phase diagrams in (pressure, temperature) space were calculated for water, oxygen, propane and lithium, employing van der Waals (vdW) equations of state, similar to an approach previously employed for argon. These calculations allowed the triple point temperatures to be obtained. The experimentally-determined triple point pressure values (p3) normalized by the critical point pressure (pc) (that is, p3/pc) are known to exhibit a significant correlation with the normalized triple point temperature (T3/Tc), and the present results reproduce this correlation qualitatively. This work also demonstrated that the low-density solid, high-density solid, liquid and gas-phases of water produce a phase diagram similar to that of the ice-water system.
In a previous study, we obtained the three-phase equilibrium diagram for argon using van der Waals (vdW) equations of state (EOS) [1]. A novel aspect of this work was the introduction of a vdW equation of state for a solid-gas system in addition to the ordinary vdW EOS [2]. The solid was treated as a condensed phase with a higher density than the liquid, with a stronger effective attractive interaction in the solid phase than in the liquid phase. Because a solid-gas2 EOS [1] has the same form as the original liquid-gas EOS [2] with different coefficients, the gas, liquid and solid phases are treated uniformly in the calculation of the thermodynamic properties. The universality of this EOS will be tested in this paper.
This same concept was applied to the present model of water as a low-density solid and high-density solid. Although there are many ice structures in the real system [3], only two types of solid were assumed for the sake of simplicity in the calculations in this study [3,4,5]. In Figure 1, the experimentally observed triple point pressure (p3) normalized by the critical point pressure (pc) (that is, p3/pc) is plotted as a function of the normalized triple point temperature (T3) (that is, T3/Tc) [5,6,7,8,9,10,11,12,13,14]. This Figure uses the vapor pressure at the melting point for those instances for which the triple point pressure has not been reported. It is evident that p3/pc becomes very small as T3/Tc decreases. In this study, water, oxygen, propane and lithium were all examined using the vdW technique, and the results of these theoretical calculations are compared with experimental data. These substances are selected to see how the vdW EOS can reproduce the normalized pressure p3/pc in a wide normalized temperature T3/Tc range. Another reason for the selection is the variety in chemical properties.
The melting line of ice at low pressures (P < 200 MPa) has a negative tangent, as in the equation below [2,3,4,5].
| (1) |
This results from the following inequality for the volume per particle, V/N,
| (2) |
For this reason, solid water at standard pressure is referred to as low-density ice. Many types of high-density ice have been identified [3], although here we assume only one type of high-density solid so as to simplify the calculations. The ice VII and VIII have about twice the density of low density ice case. The present high-density solid is a model of ice VII and VIII.
According to previously published work [1], the following set of equations of state can be employed for the pressure, p, and the internal energy, U, of the water system, in which the vdW coefficients ε ( = a/b) and b are used.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
The parameter b in equation (3) has a meaning of hard sphere volume of the molecule in the liquid state. For this reason the volume of liquid must satisfy the inequality mentioned in equation (3). The first term in equations (4), (6) and (8) is the kinetic energy in the internal energy, the second term is the density-dependent potential energy, and the other terms are the density-independent potential energy. The average of potential energy has also kinetic energy term which depends on the degree of freedom. Water molecule has translational and rotational degrees of freedom. An adjustable parameter is assumed in the case of the internal energy of the solid.
In Figure 2, the pressure values are plotted as functions of the normalized number density (Nb/V) at T = 0.125 ε/k for three states. Here, the high-density solid, the liquid and the low-density solid-states appear as the density decreases, because of the inequality associated with the van der Waals coefficient b, as below.
| (9) |

The pressure, p, of water as a function of the number density, N/V, at T = 0.125 ε/k. The high density solid, solid and liquid branches are compared.
Figure 3 presents the internal energy per particle, U/N, as functions of the normalized number density at T = 0.125 ε/k. The internal energy of the high-density solid is seen to be lowest in the region of highest density, while the liquid phase is energetically stable in the intermediate density region around 0.826 < Nb/V < 1 and the low-density solid is stable in the region 0.758 < Nb/V < 0.826.

The internal energy per particle, U/N, of water as a function of the number density, N/V, at T = 0.125 ε/k. The high-density solid, solid and liquid branches are compared.
The entropy differences, ΔS, were calculated using the first law of thermodynamics, as in a previous study [1]. The origin for S was selected as follows.
| (10) |
The entropy difference, ΔS, is called as S, hereafter. The resulting S values are summarized in Figure 4 as functions of the normalized number density, Nb/V, at T = 0.125 ε/k. The S values are evidently minimized near the density boundaries, as follows.
| (11) |

The entropy per particle, S/N, of water as a function of the number density, N/V, at T = 0.125 ε/k. The high density solid, solid and liquid branches are compared.
In contrast, S becomes very large at the low-density limit, such that the following holds true.
| (12) |
As a result, the Gibbs energy, G, is sufficiently low in the low-density limit, as shown in Figure 5, which plots the number density dependence of G at T = 0.125 ε/k. The pressure (Figure 2) and the Gibbs energy (Figure 5) both exhibit a so-called vdW loop.

The Gibbs energy per particle, G/N, of water as a function of the number density, N/V, at T = 0.125ε/k. The high density solid, solid and liquid branches are compared.
In each case, the phase boundary was obtained numerically in the same manner as reported in a previous paper [1]. There are two types of triple points in this system, one of which is the low pressure triple point seen in Figure 6, for which the triple point temperature is 0.125 ε/k. The Gibbs energy per particle, G/N, is plotted as a function of pressure at this temperature in Figure 6, and it can be seen that the solid, liquid and gas branches all cross at the point labeled “T3.” The associated triple point pressure, p3, is given below.
| (13) |

The Gibbs energy per particle, G/N, of water, as a function of the pressure, p, at T = 0.125 ε/k in the triple point region. The solid branch crosses with the gas and liquid branches at the point labeled T3.
Figure 6 shows the following inequalities.
| (14) |
The second triple point is the high-pressure triple point at (T3H, p3H) as shown in Figure 7, and as given below.
| (15) |

The Gibbs energy per particle, G/N, of water, as a function of the pressure, p, at T = 0.100 ε/k in the triple point region. The high density solid branch crosses with the solid and liquid branches at the point labeled T3.
The inequalities around the high-pressure triple point are as follows.
| (16) |
The vdW coefficients ε ( = a/b) and b can be determined from the experimental critical temperature, Tc, and the critical pressure, pc [4], using the following equation and the resulting values are shown in Table 1.
| (17) |
| substance | a/(Jm3) | ε/J | (ε/k)/K | b/m3 | (ε/b)/Pa |
| H2O | 1.53E-48 | 3.01E-20 | 2.18E+03 | 5.06E-29 | 5.96E+08 |
| O2 | 3.81E-49 | 7.20E-21 | 5.22E+02 | 5.29E-29 | 1.36E+08 |
| C3H8 | 2.59E-48 | 1.72E-20 | 1.25E+03 | 1.50E-28 | 1.15E+08 |
| Li | 1.17E-47 | 1.50E-19 | 1.09E+04 | 7.78E-29 | 1.86E+09 |
The calculated phase diagram is compared with the experimental data [3,4,5] in Figure 8, where it is evident that the calculated melting temperature is suitably close to the observed value. Although the estimated triple point pressure is not as low as the experimental value, the overall features of the calculated phase diagram are similar to those of the experimental diagram, even when using simple vdW equations of state.

The liquid-gas-phase boundary shown in Figure 6 was obtained using the same procedure reported in a previous paper (see Figure 6 in ref.1). This crossing point was determined using only the original vdW equations of state, and so included a reduced vapor pressure curve which is a universal function of the reduced temperature in the vdW model. This function is referred to as Pv, and is plotted in Figure 9. The right hand end of this curve provides the critical point (Tc, pc).
| (18) |

The vapor pressure function, vapor_pressure (T/(ε/k) function of the temperature, T, in the vdW equation of state (see Eq. (18)).
The following set of equations of state was assumed for the pressure, p, and the internal energy, U, of the oxygen system.
| (19) |
| (20) |
| (21) |
| (22) |
The G/N vs. p plot at the triple point temperature, T3 = 0.1 ε/k, is provided in Figure 10. This Figure demonstrates the following inequality regarding the second gas (Gas2) branch, which appears at the low-density limit of the solid-gas equation of state.
| (23) |

The Gibbs energy per particle, G/N, of oxygen as a function of the pressure, p, at T = 0.100 ε/k in the triple point region. The solid branch crosses with the gas and liquid branches at the point labeled T3.
The vdW coefficients ε ( = a/b) and b are determined from the experimental critical temperature, Tc, and the critical pressure, pc [4], as shown below. The values of ε and b are presented in Table 1.
| (24) |
The calculated phase diagram for oxygen is provided in Figure 11 in (p, T) space. The experimental phase diagram exhibits many solid structures; however, the fine structure is not clear in the log-scale plot in Figure 11. The experimental sublimation pressure is very low. Despite this, the calculated phase diagram is seen to be generally similar to the experimental diagram.

The sublimation pressure is close to the curve obtained by extrapolation of the vapor pressure curve. This is because the sublimation pressure is determined from the point at which the solid and gas branches cross, as shown in Figure 12. The liquid branch is seen to be almost parallel to the solid branch, while the gas branch has a larger tangent than the liquid and the solid ones. For this reason, the crossing pressure values are relatively similar, such that the extended vapor pressure is very close to the sublimation pressure.

The Gibbs energy per particle, G/N, of oxygen as a function of the pressure, p, at T = 0.07 ε/k in the sublimation pressure region. The solid branch crosses with the gas branch, while the liquid branch crosses nearby.
Propane has a low triple point temperature relative to the critical temperature of hydrocarbons (Figure 1). The propane case is shown below:
| (25) |
For this reason, the propane phase diagram was examined in this study.
The following set of equations of state was assumed for the pressure, p, and the internal energy, U, of the propane system. The characteristic terms in this set are the energy parameter, 4εb, and the size parameter, 0.8b, in the solid equation of state, which differ from the terms in the argon equation of state [1].
| (26) |
| (27) |
| (28) |
| (29) |
The G/N vs. p plot at the triple point temperature T3 = 0.06 ε/k is shown in Figure 13, from which it is evident that the relative triple point temperature is lower than those of argon [1], water (Figure 6) and oxygen (Figure 10). The calculated relative value of propane is shown below:
| (30) |

The Gibbs energy per particle, G/N, of propane as a function of the pressure, p, at T = 0.06ε/k in the triple point region. The solid branch crosses with the gas and liquid branches at the point labeled T3.
The van der Waals coefficients ε = (a/b) and b can be obtained using the experimental critical temperature, Tc, and the critical pressure, pc, as below [4]. The values of ε and b are shown in Table 1.
| (31) |
The calculated phase diagram for propane is shown in Figure 14, compared with the experimental results [10,11]. The calculated p3 is small but not as low as the experimental value [4], as shown below.
| (32) |
| (33) |

Although the present theoretical work is based on very simple vdW equations of state, the calculated phase diagram generally matches the main features of the experimental version.
Lithium has the lowest normalized triple point temperature in Figure 1, although the critical values are estimated from experimental data [12], as below.
| (34) |
The triple point temperature was estimated based on the melting point [6].
The following set of equations of state was assumed for the pressure, p, and the internal energy, U, of the lithium system. Because lithium atoms are spherical, the same equations of state as were formerly employed for argon were used as a starting point.
| (35) |
| (36) |
| (37) |
| (38) |
Figure 15 presents the G/N vs. p plot at the triple point temperature T3 = 0.04 ε/k. Here, the triple point temperature is lower than those determined for argon [1], water (Figure 6), oxygen (Figure 10) and propane (Figure 13). The following inequalities are evident from this Figure.
| (39) |
| (40) |
| (41) |
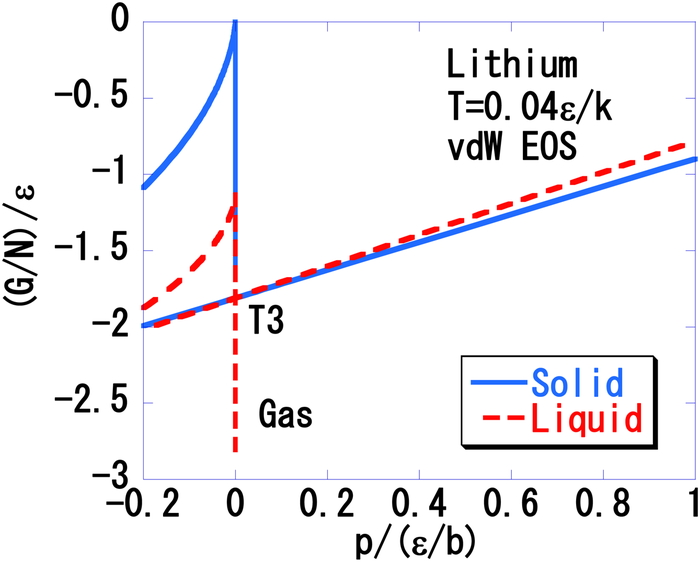
The Gibbs energy per particle, G/N, of lithium as a function of the pressure, p, at T = 0.04 ε/k in the triple point region. The solid branch crosses with the gas and liquid branches at the point labeled T3.
The van der Waals coefficients ε ( = a/b) and b were determined from the experimental critical temperature, Tc, and the critical pressure, pc [4], as below. The values of ε and b are shown in Table 1.
| (42) |
The calculated phase diagram for lithium is provided in Figure 16. These values are also compared with experimental results [4,6,11,12,13]. The high-pressure region (P > 1 GPa) was not an aspect of the current work [14] but, outside this region, the main features of the experimental phase diagram are well reproduced by the calculations using simple vdW equations of state.

The calculated normalized triple point temperature and pressure are compared with the experimental values in Table 2. There is a good concordance in the case of the triple point temperature, although the agreement is only qualitative in the case of the triple point pressure. The reason for this outcome can be seen in Figure 9, which plots a universal function in vdW equations of state.
| substance | T3/Tc | p3/pc | ||
| vdW | exp | vdW | exp | |
| Ar [1] | 0.47 | 0.582 | 0.02 | 0.0142 |
| H2O | 0.42 | 0.422 | 8.E-03 | 2.8E-05 |
| O2 | 0.34 | 0.352 | 1.E-03 | 4.E-05 |
| C3H6 | 0.20 | 0.230 | 2.E-06 | 4.E-11 |
| Li | 0.135 | 0.141 | 4.E-10 | 3.E-16 |
Examples of the Microsoft Excel worksheets used to calculate the phase transition boundaries are provided in the electronic Appendix to this paper.
The phase diagrams of water, oxygen, propane and lithium were obtained by thermodynamics calculations using the van der Waals equations of state. The new development in this work is the introduction of a solid-gas equation of state with the same functional form as that for the liquid-gas system. The gas, liquid and solid phases are treated uniformly in the calculation of the thermodynamic properties. The universality of this EOS was confirmed in a wide range of chemical substances.
The author would like to thank Prof. Hironori Ogata for valuable discussions. The author also wishes to acknowledge the Research Center for Computing and Multimedia Studies at Hosei University for providing computing resources.