Extension of a van der Waals Equation of State to the Solid-liquid-vapor Phases of a Lennard-Jones System

Abstract

An existing van der Waals (vdW) equation of state (EOS) based on hard-sphere repulsions during intermolecular interactions was extended to a Lennard-Jones (LJ) system. Specifically, an EOS for a perfect solid and liquid v5 (Y. Kataoka and Y. Yamada, J. Comput. Chem. Jpn.,12, 181–189 (2013)) was simplified to satisfy the Rigby conditions for a generalized vdW EOS. The phase diagram of argon was reproduced in pressure-temperature space using this extended EOS, and a phase diagram in temperature-density space was also generated and found to be qualitatively consistent with the LJ system.

1 INTRODUCTION

Molecular liquids and solids are typically considered as Lennard-Jones (LJ) systems [1,2] and are often modeled using molecular dynamics (MD) and Monte Carlo simulations [3,4,5,6]. Molecular simulations such as these can provide many of the physical properties for a given local state [3,4]. However, global thermodynamic properties are determined using an equation of state (EOS). For this reason, simulation results are usually summarized by a complex EOS involving numerous coefficients [7,8], although our own group has previously reported simpler EOS’s [9,10,11,12,13,14,15] based on MD simulations.

The van der Waals (vdW) EOS is one of the simplest that may be used to describe a liquid-gas-phase transition. In prior work, a vdW EOS and a new solid-gas2 vdW EOS were derived for the solid-liquid-vapor phase transition [16]. The resulting phase diagram in p-T space was found to be qualitatively similar to the results obtained from simulations and free energy calculations [16]. However, the phase diagram in T-density space exhibited a solid-liquid phase boundary for which the tangent was not in agreement with the results of free energy calculations [17]. This inconsistency was attributed to the hard core repulsion included in the vdW EOS.

In the present work, the vdW EOS was extended to a LJ system in association with a continuous interaction function. The LJ potential (u (r)) may be expressed as a function of the interatomic distance (r) using the equation   

$u\left(r\right)=4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$(1)

where ε is the depth of the potential well and σ is the separation at which u (σ) = 0. ε and σ are in units of energy and length, respectively.

This work begins with our simple EOS for a LJ system [14], based on MD simulations, following which the vdW EOS is extended to obtain a generalized vdW EOS [18]. The resulting phase diagrams in p-T space and T-density space are subsequently compared with the results of experimental studies on argon [19,20,21], simulations [22,23,24,25,26,27] and free energy calculations [16,28].

2 EXTENSION OF THE VAN DER WAALSEQUATION OF STATE

The temperature and density dependence of the internal energy and pressure were determined by MD simulations involving a LJ system and the super-cooled liquid state was also examined [14]. The sum of the average kinetic and potential energies at 0 K and the temperature-dependent potential energy was employed as the internal energy term in the EOS, while the temperature-dependent average potential energy term was assumed to be a linear function of the temperature and its coefficient was expressed as a polynomial function of the number density. The pressure was expressed in a similar manner, such that it satisfied the thermodynamic EOS. Using this approach, the phase equilibrium conditions for argon were determined numerically. The Gibbs energy value thus calculated provides a reasonable transition pressure for argon’s three-phase equilibrium state [14]. The resulting EOS is that for a perfect solid and liquid v5 [14] and is shown below.   

$U(V,T)=\frac{3}{2}NkT+U_e(V,0K)+g\left(V\right)NkT$(2)

  

$p=\frac{NkT}{V}-{\left(\frac{\partial U_{\text{e}}\left(V,0\text{ K}\right)}{\partial V}\right)}_T+f\left(V\right)NkT+\left(\frac{dg\left(V\right)}{dV}\right)NkT\ln \left(kT\right)$(3)

Here, U is the internal energy, p is the pressure, T is the temperature, k is the Boltzmann constant, and N is the number of particles. The terms $U_e(V,0K)$, $g\left(V\right)$ and $f\left(V\right)$ are functions of volume and ln () signifies the natural logarithmic function. The last term in equation (2) is included to satisfy the thermodynamic EOS [1].

The generalized vdW EOS derived by Rigby is written as follows.   

$p=\frac{NkT}{V}\beta \left(\rho \right)-\alpha \left(\rho \right)$(4)

Here, α(ρ) and β(ρ) are functions of the number density but do not depend on temperature, and the volume dependent term in g(V) in equations (2) and (3) is neglected to satisfy the Rigby conditions. For simplicity, the higher order terms in f(V) are also neglected. Thus the extended vdW EOS’s for a LJ system (vdW-LJ) are as below.   

$p_f(V,T)=\frac{NkT}{V}+\varphi \frac{NkT}{V}\left(4.8\frac{{\sigma }^3}{v}\right)-\frac{\partial U_e{}_{,f}(V,0\text{ K})}{\partial v}$(liquid) (5)

  

$U_f(V,T)=3NkT+U_e{}_{,f}(V,0\text{ K})$(liquid) (6)

  

$\frac{U_{\text{e}}{}_{\text{,f}}(V,0\text{ K})}{N\epsilon }=\left(1.5\frac{{\sigma }^{18}}{v^6}-9\frac{{\sigma }^3}{v}\right)$(liquid) (7)

  

$p_s(V,T)=\frac{NkT}{V}+\gamma \frac{NkT}{V}\left(6\frac{{\sigma }^3}{v}\right)-\frac{\partial U_e{}_{,s}(V,0\text{ K})}{\partial v}$(solid) (8)

  

$U_s(V,T)=3NkT+U_e{}_{,s}(V,0\text{K})$(solid) (9)

  

$\frac{U_{\text{e}}{}_{\text{,s}}(V,0\text{ K})}{N\epsilon }=6\left(1+\frac{1}{128}\right)\frac{{\sigma }^{12}}{v^4}-12\left(1+\frac{1}{5}\right)\frac{{\sigma }^6}{v^2}$(solid) (10)

  

$v=\frac{V}{N}$(11)

Here, the temperature-dependent part of the average of the potential energy of the system is assumed to be (3/2)NkT based on the harmonic oscillator approximation, and ϕ and γ are adjustable parameters with values of approximately 1.

3 THERMODYNAMIC QUANTITIES

The entropy change for reversible isothermal expansion and heating at constant volume to the next change of state was calculated based on the first law of thermodynamics, as in the equations below [1].   

$\begin{array}{c}\Delta S\equiv S(V_f,T_i)-S(V_i,T_i)=Nk\ln \left(\frac{V_f}{V_i}\right)+\left(F\left(V_f\right)-F\left(V_i\right)\right)Nk+3Nk\ln \left(\frac{T_f}{T_i}\right)\\ F\left(v\right)\equiv \int f\left(v\right)dv\end{array}$(12)

Here, the initial state is as shown in the following equations.   

$T_i=\frac{\epsilon }{k},V_i=N{v}_{\max }$(13)

  

$S_0\equiv S_i=Nk\ln \left(N{v}_{\max }\right)+F\left(N{v}_{\max }\right)Nk+3Nk\ln \left(\frac{\epsilon }{k}\right)$(14)

The volume (v_max) term in these equations is sufficiently large compared to the unit volume, σ³, and the temperature is expressed in units of ε/k. The function F(V) is assumed to have a value of zero in the initial state (see equations (3), (5) and (8)) and, as a result, the entropy change has the following form.   

$\Delta S(Nv,T)\equiv S(Nv,T)-S_0=Nk\ln \left(\frac{v}{{\sigma }^3}\right)+F\left(v\right)Nk+3Nk\ln \left(\frac{kT}{\epsilon }\right)$(15)

Hereafter, the entropy change from this S₀ value is expressed simply as the entropy, S.

The other thermodynamic quantities were obtained using standard procedures [1]. The critical temperature was adjusted based on the MD results as [25]   

$Tc=1.321\epsilon /k$(16)

, while assigning   

$\varphi =1.1081$(17)

.

The critical constants were obtained by solving the following equation.   

${\left(\frac{\partial p}{\partial V}\right)}_T={\left(\frac{{\partial }^{2}p}{\partial V^2}\right)}_T=0$(18)

The critical constants derived in this manner are compared with the simulation results in Table 1, from which it is evident that the present results are similar to those obtained using a perfect EOS for a liquid and solid v8 [15]. These calculated critical constants are reasonable because of the simplicity of the present model.

Table 1.  The critical LJ system constants as determined using various EOS's and MD simulations.

	Tc/(ε/k)	pc/(ε/σ3)	Vc/σ3
This work	1.321	0.227	2.49
EOS v8 [15]	1.321	0.219	2.57
EOS [7]	1.313	0.13	3.22
EOS [8]	1.340	0.141	3.22
MD [26]	1.321	0.129	3.16

4 PHASE EQUILIBRIUM IN P–T SPACE

The conditions at the equilibrium between phases 1 and 2 in p-T space can be expressed as in equation (17).   

$\begin{array}{c}{p}_1(V_1,T)=p_2(V_2,T),\\ \frac{G_1(V_1,T)}{N_1}=\frac{G_2(V_2,T)}{N_2}\end{array}$(19)

A vdW-LJ EOS is a function of volume and temperature; therefore, equation (17) can be solved numerically [10], and the (G/N)p graphs for both branches were plotted using the volume per particle as an auxiliary variable as shown in Figure 1. The electronic appendix to this paper provides some example worksheets for such calculations.

Figure 1.

 The Gibbs energy per particle, G/N, for argon as a function of the pressure, p, at T = 0.692 ε/k in the triple point region, as determined using the vdW-LJ EOS. The liquid (L) and solid (S) branches are compared at several temperatures. The solid branch crosses with the gas and liquid branches at the point indicted by T3. Both gas and liquid branches are colored blue in this Figure, however the low density part of Eq. (5) corresponds to gas branch.

The (G/N)p plots in the case of the triple point are shown in Figure 1. In this Figure, the adjustable parameter, γ, was assigned as   

$\gamma =1.031$(20)

, and the triple point temperature, T3, was adjusted based on the free energy calculation results to be [17]   

$T3=0.692\epsilon /k$(21)

.

In order to compare the calculated phase diagram in p-T space with that of argon experimentally obtained, the potential parameters ε and σ were selected based on the following two equations.   

$Tc=1.321\epsilon \text{/}k=150.72\text{ K}$(22)

  

$pc=0.227\epsilon /{\sigma }^3=4.86\text{ MPa}$(23)

The potential parameters are shown in Table 2, while the phase diagram in p-T space is presented in Figure 2. The agreement is seen to be satisfactory because of the simplicity of the present EOS. In fact, the calculated melting curve is very close to the experimental data [20,21], and also in good agreement with the results of free energy calculations [17]. The vapor pressure curve generated using the vdW-LJ EOS is also consistent with that previously reported, based on the EOS [8]. Finally, the present sublimation pressure obtained from the vdW-LJ EOS is in good agreement with that obtained from the free energy calculations [17]

Table 2.  The LJ potential parameters for argon.

ε/J	(ε/k)/K	ε/m	(ε/σ3)/MPa
1.58E-21	114.1	4.19E-10	21.4

Figure 2.

 The Ar phase diagram in p-T space, comparing the results obtained from calculations using the vdW-LJ EOS with the results of experimental studies [19,20,21], the EOS [8] and free energy calculations [17].

Table 3 compares the critical constants. In the case of the critical volume, the relative error is 46%, which is attributed to the error in equation (23). The critical pressure, expressed in units of ε/σ³, also exhibits a significant relative error of 76% compared to the MD result. This error indicates a presently unidentified shortcoming of our simplified EOS.

Table 3.  A comparison of the calculated critical constants with experimental data.

	Tc/K	pc/MPa	Vc(cm3/mol)
This work	150.72	4.86	110
vdW [16]	150.72	4.86	97
exp [21]	150.72	4.86	75.25

The calculated triple point values are compared with the experimental data in Table 4. As noted, the triple point temperature was adjusted based on the free energy calculation results. However, our value was still lower than the experimental T3. For this reason, the calculated p3 is also lower than the experimental value. The large error in the molar volume at the triple point (V3f) may result from the error in equation (23), as discussed in relation to Vc.

Table 4.  A comparison of the calculated triple point values with experimental data. The molar volume of the liquid at T3 is given here in the form of V3f.

	T3/K	p3/MPa	V3f(cm3/mol)
This work	79.0	0.015	51
vdW [16]	70.0	0.087	39
exp [21]	83.8	0.06893	28.2

The configurational entropy values are compared with the results of free energy calculations [17] in Figure 3. The configurational entropy, Sc, is the entropy other than the contribution of the kinetic energy and is obtained from the following equation.   

$Sc=S+\frac{3}{2}NkT\ln (T/(\epsilon /k\left)\right)$(24)

Figure 3.

 The configurational entropy per particle, Sc/N, as a function of the temperature at the solid-liquid transition as determined using the vdW-LJ EOS. The results are compared with those obtained from free energy calculations [22].

The absolute value has no meaning when comparing configurational entropy values because the entropy origin is not always the same in the two methods (that is, when using the vdW-LJ EOS or MC and MD simulations). Therefore, only the temperature dependence of Sc is compared herein. At the gas-liquid phase boundary, Sc changes rapidly while, in contrast, the change in Sc as a function of temperature along the liquid-solid phase boundary is minimal. Figure 3 also demonstrates that the calculated values are consistent with the results of the free energy calculations [17].

The values for the average of the potential energy, U_e, at the phase boundary are compared with data from Refs [8,17]. in Figure 4. Along the gas-liquid phase boundary, the calculated values are consistent with the reported values [8], although the tangents at the liquid-solid phase boundary are overly steep in comparison with the results of free energy calculations [17]. This divergence is attributed to over-simplification in the pressure EOS (the second term on the right-hand side of equations (5) and (8)). An analysis of the MD results produced two higher order terms [14] but, these are neglected in the present work for the sake of simplicity.

Figure 4.

 The average potential energy entropy per particle, Ue/N, as a function of the temperature at the solid-liquid transition as determined using the vdW EOS. The results are compared with those obtained from free energy calculations [22].

5 PHASE EQUILIBRIUM IN T–N/V SPACE

Figure 5 shows the temperature–number density phase boundaries determined using the vdW-LJ EOS along with a comparison of the calculated results [8,17]. This Figure shows the densities of the equilibrated phases on the phase boundary plotted in Figure 2 as functions of temperature. At temperatures below Tc, the calculated phase boundaries are in reasonably good agreement. However, the liquid-solid transition boundaries exhibit a systematic deviation from those of the LJ system obtained from free energy calculations [17]. As noted when discussing Figure 4, this lack of coincidence may result from the over-simplification of the pressure EOS in equations (5) and (8), in which the higher order terms were neglected.

Figure 5.

 The Ar phase diagram in T, N/V space, comparing the results obtained from calculations using the vdW-LJ EOS with results of the EOS [8] and free energy calculations [17]. This phase diagram shows the density as a function of temperature on the phase boundary shown in Figure 2. The abbreviation SL means the phase boundary of the solid and the liquid phases.

However, Figure 5 is qualitatively consistent with the LJ results, in contrast to the case of a simple vdW EOS incorporating hard core repulsion [16].

6 THERMODYNAMIC PROPERTIES ATCONSTANT TEMPERATURE

Pressure is plotted as a function of number density in Figure 6, in which the results from the liquid-gas EOS and solid-gas2 EOS are compared at several temperatures. This Figure displays the so-called vdW loop. Figure 7 plots the internal energy against the number density at 0 K because the density dependence of the liquid and solid is the same at 0 K in the present model (see equations (6) and (9)). The minimum values of $U_{\text{e}}{}_{\text{,f}}(V,0\text{ K})/N\epsilon$ and $U_{\text{e}}{}_{\text{,s}}(V,0\text{ K})/N\epsilon$ are summarized in Table 5, and the entropy, S, is plotted as a function of number density at T = 0.692 ε/k in Figure 8. This Figure demonstrates that S becomes very large when approaching the low density limit, as predicted by equation (13).

Figure 6.

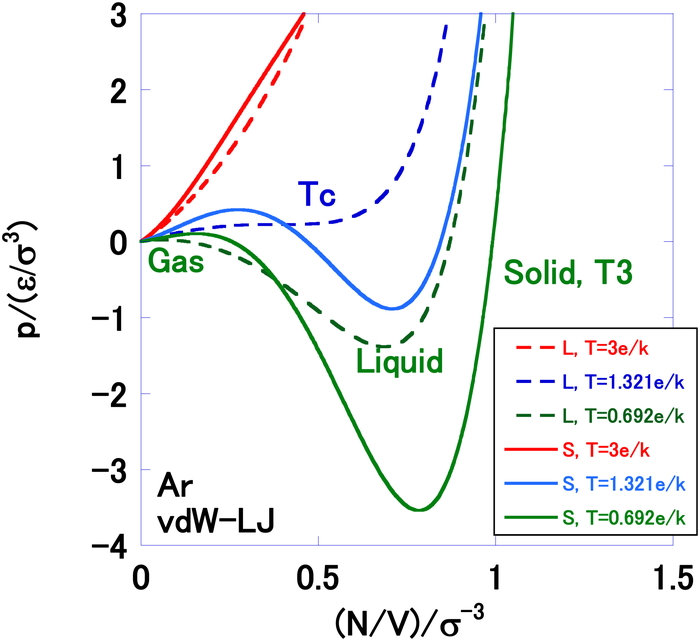
 Pressure, p, as a function of the number density, N/V, as determined using the vdW-LJ EOS. The liquid (L) and solid (S) branches are compared at several temperatures.

Figure 7.

 Internal energy per particle, U/N, as a function of the number density, N/V, as determined using the vdW-LJ EOS. The liquid (L) and solid (S) branches are compared at T = 0.

Table 5.  The minimum values of U_e.f and U_e,s.

v/σ3	Ue,f (V,0 K)/Nε	v/σ3	sU(V,0 K)/Nε
1	−7.5	0.9164	−8.573

Figure 8.

 Entropy per particle, S/N, as a function of the number density, N/V, at T = 0.692 ε/k as determined using the vdW-LJ EOS. The liquid (L) and solid (S) branches are compared at T = 0.692 ε/k.

The Gibbs energy is plotted as function of number density at T = 0.692 ε/k in Figure 9, from which it can be seen that the Gibbs energy falls to a very low value when approaching the low density limit. Comparing Figures. 6 and 9, the crossing point labeled T3 in Figure 1 can be seen to be reasonable.

Figure 9.

 Gibbs energy per particle, G/N, as a function of the number density, N/V, as determined using the vdW EOS. The liquid (L) and solid (S) branches are compared at T = 0.692 ε/k.

7 CONCLUSION

The vdW EOS was extended to a LJ system, and the EOS for a perfect solid and liquid v5 [14] was simplified to satisfy Rigby’s condition for a generalized vdW EOS. In this manner, the phase diagram of argon was reproduced in p-T space, and the phase diagram in T-N/V space was found to be qualitatively consistent with the LJ system.

Acknowledgment

The author would like to thank Prof. Hironori Ogata for valuable discussions and to gratefully acknowledge the Research Center for Computing and Multimedia Studies at Hosei University for the use of computer resources.

REFERENCES

• [1]   P. W. Atkins, Physical Chemistry, Oxford Univ. Press, Oxford (1998).
• [2]   D. A. McQuarrie, Statistical Mechanics, Harper Collins (1976).
• [3]   M. P. Allen, D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford (1992).
• [4]   R. J. Sadus, Molecular Simulation of Fluids: Theory, Algorithms and Objective-Orientation, Elsevier, Amsterdam (1999).
• [5]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 13, 115 (2014). doi:10.2477/jccj.2013-0023
• [6]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 13, 257 (2014). doi:10.2477/jccj.2014-0016
• [7]   J. K. Johnson, J. A. Zollweg, K. E. Gubbins, Mol. Phys., 78, 591 (1993). doi:10.1080/00268979300100411
• [8]   J. Kolafa, I. Nezbeda, Fluid Phase Equilib., 100, 1 (1994). doi:10.1016/0378-3812(94)80001-4
• [9]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 10, 98 (2011). doi:10.2477/jccj.H2308
• [10]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 11, 81 (2012). doi:10.2477/jccj.2011-0030
• [11]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 11, 165 (2012). doi:10.2477/jccj.2012-0006
• [12]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 11, 174 (2012). doi:10.2477/jccj.2012-0009
• [13]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 12, 101 (2013). doi:10.2477/jccj.2012-0027
• [14]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 12, 181 (2013). doi:10.2477/jccj.2013-0007
• [15]   Y. Kataoka, Y. Yamada, J. Comput. Chem. Jpn., 13, 130 (2014). doi:10.2477/jccj.2014-0002
• [16]   Y. Kataoka, J. Comput. Chem. Jpn., submitted.
• [17]   M. A. Barroso, A. L. Ferreira, J. Chem. Phys., 116, 7145 (2002). doi:10.1063/1.1464828
• [18]   M. Rigby, Q. Rev. Chem. Soc., 24, 416 (1970). doi:10.1039/qr9702400416
• [19]   K. Clusius, K. Weigand, Z. Phys. Chem., B Chem. Elem. Proz. Aufbau Mater., 46, 1 (1940).
• [20]   R. K. Crawford, W. B. Daniels, Phys. Rev. Lett., 21, 367 (1968). doi:10.1103/PhysRevLett.21.367
• [21]   CRC Handbook of Chemistry and Physics. Ed., D. R. Lide, CRC press, Boca Raton (1995).
• [22]   J. P. Hansen, L. Verlet, Phys. Rev., 184, 151 (1969). doi:10.1103/PhysRev.184.151
• [23]   D. A. Kofke, J. Chem. Phys., 98, 4149 (1993). doi:10.1063/1.465023
• [24]   R. Agrawal, D. A. Kofke, Mol. Phys., 85, 43 (1995). doi:10.1080/00268979500100921
• [25]   H. Okumura, F. Yonezawa, J. Chem. Phys., 113, 9162 (2000). doi:10.1063/1.1320828
• [26]   H. Okumura, F. Yonezawa, J. Phys. Soc. Jpn., 70, 1990 (2001). doi:10.1143/JPSJ.70.1990
• [27]   M. A. van der Hoef, J. Chem. Phys., 117, 5092 (2002). doi:10.1063/1.1498462
• [28]   A. Ahmed, R. J. Sadus, J. Chem. Phys., 131, 174504 (2009). , doi:10.1063/1.325368619895022