2019 Volume 5 Article ID: 2017-0044
2019 Volume 5 Article ID: 2017-0044
An absolute quantitative analysis method has been recently developed as a third generation polymerase chain reaction method “PCR” for fractionated DNA. The method is designed to determine the number of DNA molecules in target DNA samples by counting the number of PCR products obtained from fractionated DNA. We applied EXCEL Macro to perform the conversion of two dimensional orthogonal coordinate (x, y) fluorescent signal plot data obtained by digital PCR device to two dimensional polar coordinate (r, θ) fluorescent signal plot data, followed by analyzing the angle (θ) histogram of plot data without overlapping of plot data occurring by two dimensional orthogonal coordinate (x, y) histogram. The analysis made it possible to identify gene mutation and count the number of DNA molecules with mutation faster and easier.
It has been demonstrated that data from digital PCR analysis [1,2,3,4], in which wild type and mutant type are labeled with a probe/Hexachloro Fluorescein (HEX) and a probe/Fluorescein Amidite (FAM), respectively, generate almost 15,000–20,000 fluorescent signals, the results of which are recorded in the two dimensional orthogonal coordinate (x, y) to determine the extent of target gene amplification [5]. It is possible to detect the presence of gene mutation and the rate of mutation with high sensitivity in an extremely small amount of target sample by plotting the intensity of mutant type (Mt) with HEX fluorescent signal in the x-axis and wild type (Wt) with FAM fluorescent signal in the y-axis in two dimensional orthogonal coordinate (x, y) (Figure 1). It is, however, difficult to show the distribution status in two dimensional orthogonal coordinate (x, y) histogram without overlapping of the plots between no DNA template control (NTC) region and Mt region or NTC region and Wt region, resulting in the need for two separate histograms created from x (HEX) axis direction and y (FAM) axis direction. In this study, it is possible to observe all fluorescent signal plots in angle (θ) histogram without the overlapping, where the histogram was created based on the value of angle (θ) of the converted two dimensional polar coordinate (r, θ) [6], which was prepared by converting from the data in the two dimensional orthogonal coordinate (x, y) by EXCEL. The origin of the converted two dimensional polar coordinate (r, θ) was moved to the gravity point of the triangle consisting of each center of Mt region, Wt region and NTC region. Therefore, it is possible to determine gene mutation easily and accurately as well as determine mutation rate by applying the polar coordinate approach.

Fluorescent signal plots of dPCR by two dimensional orthogonal coordinates (x, y). Sample is ALK wild type/resistant mutation type (L1196M) DNA. A; Mutation Type region (Mt region), B; No Template Control region (NTC region), C; Wild Type region (Wt region). HEX (Hexachloro Fluoresein); a probe for Wild type DNA, FAM (Fluorescein Amidite); a probe for Mutation type DNA. HEX fluorescent signals are plotted in x axis and FAM fluorescent signals are plotted in y axis.
It has been generally demonstrated that the extent of the target gene amplification could be monitored by plotting the intensity of fluorescence signals of Wt/HEX in the x axis and those in Mt/FAM in the y axis in two dimensional orthogonal coordinate (x, y). The extent of occurrence frequency was only determined by histogram. It is, however, difficult to count the accurate number of Mt/FAM fluorescent signals in x axis histogram, because of overlapping signals of NTC with those of Mt/FAM (Figure 2). Similarly, it was also difficult to count the accurate number of Wt/HEX fluorescent signals in y axis histogram, because of overlapping signals of NTC with those of Wt/HEX (Figure 3). Therefore, the distribution condition of Mt/FAM and Wt/HEX fluorescent signals by one histogram is difficult to observe in two dimensional orthogonal coordinate (x, y) without any overlapping signals.

Histogram of two dimensional orthogonal coordinate (HEX axis). Sample is ALK wild type/resistant mutation type (L1196M) DNA. In histogram of x (HEX) axis, A (Mt region) is overlapped with B (NTC region), therefore HEX fluorescent signal plot numbers of A (Mt region) can’t be counted accurately. Two separate histograms of x (HEX) axis and y (FAM) axis are needed to calculate the fluorescent signal plot numbers of A (Mt region) and C (Wt region).

Histogram of two dimensional orthogonal coordinate (FAM axis). Sample is ALK wild type/resistant mutation type (L1196M) DNA. In histogram of y (FAM) axis, C (Wt region) is overlapped with B (NTC region) like the case of Figure 2, therefore FAM fluorescent signal plot numbers of C (Wt region) can’t be counted accurately. Two separate histograms of x (HEX) axis and y (FAM) axis are needed to calculate the signal plot numbers of A (Mt region) and C (Wt region), as same as the caption in Figure 2.
The origin (x = 0, y = 0) in two dimensional orthogonal coordinate (x, y) was moved to the gravity of A (Mt region), B (NTC region) and C (Wt region), and then, two dimensional orthogonal coordinate (x, y) were converted to two dimensional polar coordinate (r, θ) (Figure 4). In the two dimensional polar coordinate (r, θ), all plots are observed by (θ) histogram without any overlapping (Figure 5). The gravity was obtained by cluster analysis method of three elements (k = 3), such as A (Mt region), B (NTC region) and C (Wt region). The gravity calculation was executed automatically by EXCEL Macro [7] for k-means clustering method [8,9,10], a typical dividing-optimization method. The explanation for conversion equation from two dimensional orthogonal coordinate (x, y) to two dimensional polar coordinate (r, θ) is described in Appendix A (Conversion from two dimensional orthogonal coordinate (x, y) to two dimensional polar coordinate (r, θ)) and the consideration for angle setting in converting to two dimensional polar coordinate (r, θ) is described in Appendix B (Consideration for the angle setting (0°– 360°) in converting from two dimensional orthogonal coordinate (x, y) to two dimensional polar coordinate (r, θ)), an example of EXCEL Macro for the conversion is described in Appendix C (Conversion from two dimensional orthogonal coordinate (x, y) to two dimensional polar coordinate (r, θ) by EXCEL Macro), respectively.

Conversion of dPCR fluorescent signal plots from two dimensional orthogonal coordinate (x, y) to two dimensional polar coordinate (r, θ). Origin (x = 0, y = 0) for two dimensional polar coordinate (r, θ) is moved to the gravity of the three regions A (Mt region), B (NTC region) and C (Wt region). After the origin moving, two dimensional orthogonal coordinates (x, y) are converted to two dimensional polar coordinates (r, θ) using converting equation as below.
r =SQRT (X^2+Y^2)
θ =DEGREES (ATAN (Y/X))
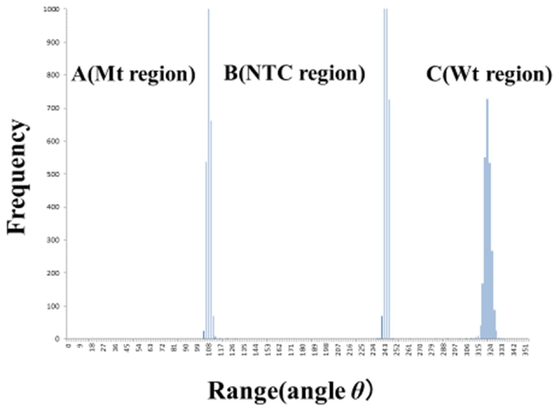
Histogram of two dimensional polar coordinate (θ, 0°– 360°). Sample is ALK wild type/resistant mutation type (L1196M) DNA. Frequency of the three regions A (Mt region), B (NTC region) and C (Wt region) by histogram of two dimensional polar coordinate (θ, 0°– 360°) can be observed accurately without any overlapping at the two dimensional orthogonal coordinate (x, y) case, such as Figures 2, 3. Therefore the fluorescent signal plot numbers of A (Mt region), B (NTC region) and C (Wt region) are counted accurately and automatically using by the EXCEL Macro program.
After the coordinate converting, the number of fluorescent signal plots in the A (Mt region), B (NTC region) and C (Wt region) are calculated automatically using the normal distribution probability density function “NORMDIST” in EXCEL at each of 90%, 95% and 99% confidence interval, the gene mutation is determined by existence of fluorescent signal plots in the Mt region, and the gene mutation rate is calculated by Mt fluorescent signal plots/(Mt fluorescent signal plots + Wt fluorescent signal plots). In Figure 6, the EXCEL Macro program execution result of ALK wild type/resistant mutation type (L1196M) DNA (10,000copies) is shown, and in Figure 7, the EXCEL Macro program execution result of ALK wild type/resistant mutation type (L1196M) DNA (Mt/Wt;10/1,000 copies) is shown respectively.

Result of EXCEL macro program execution using by converted two dimensional polar coordinate (r, θ). Sample is ALK wild type/resistant mutation type (L1196M) DNA (10,000copies). Fluorescent signal plot numbers of A (Mt region) and C (Wt region) are calculated accurately at the same time, those plot numbers are shown in the table right upper side. In this case, gene mutation is detected by the existence of fluorescent signal plots in A (Mt region), and the gene mutation rates are 51.7% (2315/4475), 52.1% (2475/4747) and 51.8% (2568/4954) at each confidence interval 90%, 95% and 99%, respectively. “center” in table is expressing each center coordinate (x, y) of A, B and C region, respectively. Inside, middle and outside elliptical graphs are expressing the areas at each confidence interval 90%, 95% and 99%, respectively.

Result of EXCEL macro program execution using by converted two dimensional polar coordinate (r, θ). Sample is ALK wild type/resistant mutation type (L1196M) DNA (Mt/Wt:10:1,000copies). Fluorescent signal plot numbers of A (Mt region) and C (Wt region) are calculated accurately at the same time, those plot numbers are shown in the table right upper side. In this case, though the number of the fluorescent signal plots is very few, gene mutation is observed by existence fluorescent signal plots in A (Mt region), and the gene mutation rates are 1.1% (6/528), 1.3% (7/555) and 1.2% (7/565) at each confidence interval 90%, 95% and 99%, respectively. “center” in table is expressing each center coordinate (x, y) of A, B and C region, respectively. Inside, middle and outside elliptical graphs are expressing the areas at each confidence interval 90%, 95% and 99%, respectively, as same as Figure 6.
It is possible to judge promptly and easily whether target gene mutations are present by visualizing genetic analysis fluorescent signal plots data through the following processing procedure of EXCEL VBA MACROS analysis except that the Steps 1) and 9) were input and evaluated manually.
[Operating Procedure]1) Data uptake two dimensional orthogonal coordinate (x, y)
2) Determine centroids for corresponding A (Mt region), B (NTC region) and C (Wt region) by k-means clustering method
3) Determine the gravity point of triangle formed by the centroids for A (Mt region), B (NTC region) and C (Wt region)
4) Parallel move of the origin of two dimensional orthogonal coordinate (x, y) to the gravity point
5) Conversion to two dimensional polar coordinate (r, θ)*
* r=SQRT (X^2+Y^2), θ =DEGREES (ATAN (Y/X))
6) Histogram preparation based on (θ) degrees
7) Calculate the number of fluorescent signal plots distributed in A (Mt region), B (NTC region) and C (Wt region) within 90%, 95% and 99% confidence interval by NORMDIST function
8) Re-conversion** to two dimensional orthogonal coordinate (x, y) and elliptical graph of 90%, 95% and 99% confidence interval display
** x=r*COS (RADIANS (θ)), y=r*SIN (RADIANS (θ))
9) Determine gene mutation and calculate gene mutation rates within 90%, 95% and 99% confidence interval, respectively
In quantitative analysis from histograms in HEX (x axis) and FAM (y axis), it is difficult to show each distribution state of the fluorescent signal plots in A (Mt region), B (NTC region) and C (Wt region) at the same time, due to overlapping of fluorescent signal plots in A (Mt region) with those in B (NTC region) or C (Wt region) with B (NTC region) so far. Therefore, the origin (x = 0, y = 0) was moved to the gravity point inside of the triangle consisting of A (Mt region), B (NTC region) and C (Wt region), and the two dimensional orthogonal coordinate (x, y) were converted to the two dimensional polar coordinate (r, θ). It is confirmed that this approach made it possible to show separately all fluorescent signal plots of the three regions such as A (Mt region), B (NTC region) and C (Wt region) in histogram at one time without any overlapping and easy to count the number of fluorescent signal plots in A (Mt region) and C (Wt region). Furthermore, we consider that employing an automated processing from coordinate conversion to graphic visualization of results by EXCEL Macro is useful for identifying mutation occurrence and mutation rate promptly. For the future, we are hoping to develop a more convenient genetic analysis method by processing more samples using the method described here.