Analyses of Optical Gains and Oscillation Wavelengths for Quantum Cascade Lasers Using the Nonequilibrium Green’s Function Method

Abstract

We have succeeded in improving the gain of the base quantum cascade laser (QCL) through experiments and device simulations using the nonequilibrium Green’s function (NEGF) method, and we investigate the factor that increases the gain by reducing the thickness of the barrier by 10%. Specifically, we analyzed the minibands (Wannier–Stark states), density of states (DOS), and electron density that contribute to the emission. The results show that the gain enhancement is due to the increase in the electron density of the quantum wells in the active region and the increase in the oscillator strength between the minibands that contribute to the emission. Quantum mechanical calculation like the NEGF method is very effective for mesoscopic systems such as the active layer of QCL.

1 INTRODUCTION

Quantum cascade laser (QCL) is a semiconductor laser that emits mid- and far-infrared rays. The active layer of QCL is a mesoscopic system consisting of multiple layers of In_xAl_(1-x)As/In_yGa_(1-y)As. Its oscillation wavelength can be controlled by changing the material and thickness of the layer [1]. By making the active layer multistaged, it is possible to reuse electrons that had already contributed to the laser emission and to achieve high quantum efficiency and high output.

Currently, the QCL has been applied to various fields such as semiconductor processes, optical frequency combs, combustion diagnosis of engines, the discovery of drugs and explosives, and life science [2,3,4,5,6,7]. Since its wavelength is in the infrared region, the application to trace gas analysis and remote gas detection is particularly noticeable [8, 9]. To achieve this, a QCL with a wavelength suitable for such measurements is required. In addition, with such trace substance detection and remote gas detection, higher sensitivity is expected by increasing the output. Since the amount of laser absorption is measured in the detection of trace substances, the laser must propagate along a long optical path. To develop a laser with such a high output and a wavelength suitable for measurement, it is effective to use a simulation method that can predict the oscillation wavelength and gain.

In the simulation, the Schrödinger equation is first solved to calculate the eigenvalues and eigenfunctions, that is, the energies and the wavefunctions. The laser light intensity is then calculated from the upper and lower level lifetimes and the transition probabilities between the upper and lower levels. To reproduce them and calculate the oscillation wavelength and gain with high precision in the simulation, how the electron dynamics are calculated is important. QCL skillfully applies the electron dynamics such as the optical transition of electrons between subbands in the conduction band of the active layer and electron transport to the next active layer by the tunnel effect in the miniband of the injector region. Calculation methods of such electron dynamics are, for example, the rate equation [10], the MC method [11], and the nonequilibrium Green’s function (NEGF) method [12,13,14]. This work is based on the NEGF method.

In the rate equation and MC approaches, the electron density distribution and the transition of electrons from the upper level to the lower level can only be calculated semi-classically [15]. On the other hand, in the calculation using the NEGF, they can be calculated quantum mechanically [16,17,18,19,20]. Furthermore, by determining the self-energy of electron scattering, we can easily add the effect of electron scattering on the electron distribution. Not only can the gain be calculated accurately, it is also possible to reflect the effects of operating temperature and strain.

We ran the simulations that incorporate the NEGF method for the calculation of electron dynamics in QCLs [21,22,23,24]. In previous work [25], the active layers of the QCLs were designed to increase the gain using a simulator, and it was shown that the output could be improved by thinning the barrier of the active region. As a result of evaluating a QCL of this structure, the EL emission intensity was found to be increased 1.4-fold compared with the QCL of the base structure. In this work, to check the correctness of input and output, the current–voltage (IV) characteristic was also verified. The calculated values of the IV characteristic well reproduced the tendency of the measured values. Furthermore, the calculated values of the oscillation wavelength by the NEGF method were in good agreement with the measured values. The wavelengths were explained from the energy difference of the minibands (Wannier–Stark states), which mainly contributes to the emission. We also analyzed the origin of the gain from the density of states (DOS), electron density, and oscillator strength. The NEGF calculations are found to be very useful in computational chemistry for the mesoscopic system, such as the active layer of QCL.

The novelty of this work is that the cause of the improvement was analyzed in detail from the minibands (the eigenstates of the Schrödinger equation without accounting for Poisson equation), the density of states, electron density, and oscillator strength.

2 THEORETICAL METHODS

2.1 Composition simulator

The nextnano.NEGF software (nextnano GmbH) [26] was used for calculating the optical gains, IV characteristics, and the oscillation wavelengths of QCLs [21,22,23,24].

Figure 1 shows the calculation flow in the simulation. The simulator uses field-periodic boundary conditions. In this way, the simulation accounts for an infinite periodic structure, with a periodic electric field. First, the single-band effective mass Schrödinger equation is solved in real space. As a second step, the scattering coupling terms are calculated for each of the mechanisms (longitudinal polar-optical phonons scattering, charged impurities scattering, interface roughness scattering, alloy disorder scattering, and electron-electron scattering). Acoustic phonons scattering is not in general efficient and is neglected in this work. Assuming that the unperturbed Hamiltonian is ${\hat{H}}_0$ (^ indicates that it is an operator) and the perturbation term for the electron scattering is ${\hat{H}}_{\text{scatt}}$, the Hamiltonian $\hat{H}$ in the Schrödinger equation is expressed by   

$\begin{array}{c}\hat{H}={\hat{H}}_0+{\hat{H}}_{\text{scatt}} ,\end{array}$(1)

where ${\hat{H}}_0$ is an exactly solvable part. ${\hat{H}}_{\text{scatt}}$ contains impurity, phonon, or electron-electron scattering matrix elements and is solved perturbatively.

Figure 1.

 The calculation process of NEGF simulator. In NEGF Solver, the lesser Green’s function G^< is calculated in a self-consistent field. The calculation is iteratively performed until the value converges to the set threshold value.

Then, the main part of the calculation consists of the self-consistent NEGF solver. We start to find an initial guess of the lesser Green’s function G^< by solving the Schrödinger equation, where G^< is also called the correlation function. Next, the Poisson equation is solved to find the mean-field electrostatic potential, and the retarded self-energy Σ^R and the lesser self-energy Σ^< are calculated. Σ^R and Σ^< can be expressed by [27]   

$\begin{array}{c}{\Sigma }^R=G^R{D}^R+G^R{D}^{<}+G^{<}{D}^R,\end{array}$(2)

  

$\begin{array}{c}{\Sigma }^{<}=G^{<}{D}^{<},\end{array}$(3)

where D^R and D^< are the sums of retarded and lesser Green’s functions of the environment.

The retarded Green’s function G^R is derived using the Dyson equation expressed by   

$\begin{array}{c}{G}^R=\frac{1}{E-{\hat{H}}_0-{\Sigma }^R}.\end{array}$(4)

Here, E is the energy. Using the Keldysh equation shown as equation (5), we obtain the lesser Green’s function G^<,   

$\begin{array}{c}{G}^{<}=G^R{\text{Σ}}^{<}{G}^A,\end{array}$(5)

where G^A is an advanced Green’s function. G^A and G^R are Hermitian conjugates, i.e., G^A = [G^R]^†. G^< obtained from equation (5) is compared with the initial G^<, and the calculation is repeated until it converges to the set threshold. That is, G^< is obtained by a self-consistent method. The electron density matrix is obtained from G^<. The current density is directly calculated, as well as the electron density. Based on the electron density matrix, the optical gain and the current of the QCL are calculated. The energy-resolved density matrix $\rho \left(E\right)$ is   

$\begin{array}{c}\rho \left(E\right)=-\frac{i}{2\pi }\int dE{G}^{<}\left(E\right).\end{array}$(6)

The electron density is given by the diagonal term of ρ(E). The spectral function, i.e., DOS, is the imaginary part of the retarded Green’s function G^R.

By using the NEGF method, both quantum transport effects (i.e., coherent transport effects such as resonant tunneling) and scattering mechanisms can be accounted for. This makes it suitable for QCL simulations [28,29,30].

From a series of calculations, the relationship between the energy (wavelength) and the gain is calculated. The oscillation wavelength of the laser is determined as the wavelength that maximizes the gain. By using the NEGF method, it is possible to perform the calculation while taking into consideration of the effects of the strain and electron scattering on the crystal lattice corresponding to the operating temperature of the QCL.

2.2 Optical gain

This subsection is based on Grange’s commentary [31]. The optical gain is obtained as follows [32,33,34]. The gain self-consistent calculation calculates the linear response to the input AC electromagnetic field. It is performed for each possible frequency (photon energy) within the gain calculation. In this case, the perturbation due to an AC electric field along z(coordinate in growth direction) is considered. The perturbating Hamiltonian is:   

$\begin{array}{c}{\hat{H}}_{AC}=ez\delta F{e}^{-i\omega t}\end{array}$(7)

in the Lorenz gauge, where e is the elementary charge, F is the electric field, $\omega$ is the angular frequency, and t is the time. The response Green’s function $\text{δ}{G}^{<}\left(\omega ,E\right)$ is calculated within linear response theory. According to Wacker [32], the Green’s function linear responses are:   

$\begin{array}{c}\begin{array}{c}\delta G^R\left(\omega ,E\right)\\ =G^R\left(E+\frac{h\omega }{2\pi }\right)\left({\hat{H}}_{AC}+\delta {\Sigma }^R\left(\omega ,E\right)\right)G^R\left(E\right),\end{array}\end{array}$(8)

and   

$\begin{array}{c}\text{δ}{G}^{<}\left(\omega ,E\right)=G^R\left(E+\frac{h\omega }{2\pi }\right){\hat{H}}_{AC}{G}^{<}\left(E\right)\\ +G^{<}\left(E+\frac{h\omega }{2\pi }\right){\hat{H}}_{AC}{G}^A\left(E\right)\\ +G^R\left(E+\frac{h\omega }{2\pi }\right)\delta {\Sigma }^R\left(\omega ,E\right)G^{<}\left(E\right)\\ +G^R\left(E+\frac{h\omega }{2\pi }\right)\delta {\Sigma }^{<}\left(\omega ,E\right)G^A\left(E\right)\\ +G^{<}\left(E+\frac{h\omega }{2\pi }\right)\delta {\Sigma }^A\left(\omega ,E\right)G^A\left(E\right).\end{array}$(9)

In the self-consistent gain calculation, the 3 last terms in equation (9) are accounted for. Indeed, to account for them, the self-energies $\delta \Sigma \left(\omega ,E\right)$ need to be calculated from $\text{δ}{G}^{<}\left(\omega ,E\right)$, requiring a self-consistent loop.

From this Green’s function response, the AC conductivity is calculated as   

$\begin{array}{c}\sigma \left(\text{ω}\right)=\frac{\delta j\left(\omega \right)}{\delta F}.\end{array}$(10)

Here,   

$\begin{array}{c}\delta j\left(\text{ω}\right)=Tr\left(G^{<}J\right),\end{array}$(11)

where J is the current operator.

The bulk dielectric constant is assumed to be given by the Lyddane-Sachs-Teller relation [35]:   

$\begin{array}{c}\begin{array}{c}{ϵ}_r^{bulk}\left(\omega \right)\\ ={ϵ}_{\infty }+\left({ϵ}_{\infty }-{ϵ}_{static}\right)\frac{{\omega }_{TO}}{{\omega }^2-{\omega }_{TO}^2},\end{array}\end{array}$(12)

where ${ϵ}_{\infty }$ is the dielectric constant at very high frequencies, ${ϵ}_{static}$ is the static dielectric constant, and ${\omega }_{TO}$ is the transverse optical phonon frequency. In the self-consistent gain calculation, the quantity which is calculated is the AC conductivity $\text{σ}\left(\text{ω}\right)$. The complex dielectric constant is then:   

$\begin{array}{c}{ϵ}_r\left(\omega \right)={ϵ}_r^{bulk}\left(\omega \right)-i\frac{\sigma \left(\omega \right)}{\omega {ϵ}_0},\end{array}$(13)

where ${ϵ}_0$ is the vacuum permittivity. Finally, the gain is   

$\begin{array}{c}g\left(\text{ω}\right)=-\frac{Re\left(\sigma \left(\omega \right)\right)}{{ϵ}_r\left(\omega \right)}.\end{array}$(14)

When the oscillator strength between the subbands contributing to the photoemission is stronger, the gain is also higher. At the same time, the gain is higher when the population inversion is achieved. Thus, increasing the gain requires two contradictory conditions.

3 RESULTS AND DISCUSSION

3.1 The active layer of QCL

To obtain experimental values of electroluminescence (EL) emission intensity, IV characteristics, and oscillation wavelengths, a prototype was made using the structure reported by Evans et al. [36], and these physical properties were measured.

The materials of our prototype are Ga_0.331In_0.669As for the wells and Al_0.638In_0.362As for the barriers. In this structure, one period of the active layer consists of 22 layers, the injection region is from the 1st to 14th layers, and the active region is from the 15th to 22nd layers. The injection region is doped with Si (its concentration is 2.0 × 10¹⁶ cm⁻³). The thicknesses in nanometers for one period are as follows: 2.8, 1.7, 2.5, 1.8, 2.2, 1.9, 2.1, 2.1, 2.0, 2.1, 1.8, 2.7, 1.8, 3.8, 1.2, 1.3, 4.3, 1.3, 3.8, 1.4, 3.6, 2.2, where values for the barriers are in bold and those for wells are in normal font. The underlined thicknesses represent the doped layers. This structure is denoted as APL91. The device structure has a ridge width of 15 µm and a length of 4 mm. Figure 2 shows the conduction band of APL91. Electrons are injected from the injection region into the upper subband of the active region, and they drop to the lower subband through the intersubband transition. Photoemission occurs at that time.

Figure 2.

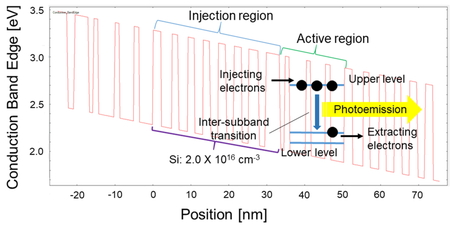
 Conduction band of APL91. The material is Ga_0.331In_0.669As for the wells and Al_0.638In_0.362As for the barriers. See the text for the thicknesses. Photoemission occurs when electrons drop from the upper subband to the lower subband of the active region

3.2 Gain and EL emission intensity

We attempted to design a high-power active layer for QCLs using the NEGF method [25]. The design was based on the structure shown in Figure 2 [35]. The thicknesses of barriers in the active region are changed to achieve high gain. Many cases were calculated while adjusting parameters, such as net strain, calculation range, and convergence condition.

Simulations with various parameters were performed based on physical considerations. The structure with the noticeable change in gain was that in which the thicknesses of the barriers in the active region were varied. The calculated gains of this design are shown in Figure 3. When the barriers in the active region were reduced, the gain increased, and a maximum gain that is 1.28 times that in APL91 is observed. On the other hand, in the structures in which the thicknesses of barriers are increased, the gains are lower than those in APL91.

Figure 3.

 Dependence of gain on barrier thickness. As the thickness of the barrier of the active region is reduced, the gain increases.

Based on calculation results, for measuring EL, we fabricated devices with 10% thinner barriers in the active region (−10% device) and APL91. The device length is 2 mm and the ridge width is 100 μm. The device is soldered onto a Cu/W mount. We used the Nicolet8700 Thermo Scientific to measure the EL spectrum. The emitted light is focused by a mirror, and the EL intensity is measured by MCT (HgCdTe) detector. The prototypes were operated at a frequency of 100 kHz, a pulse width of 300 nm (duty 3%), and 77 K.

Figure 4 shows the EL spectra of the prototypes. The horizontal axis represents wavelength and the vertical axis represents EL emission intensity. Good emission is observed in the −10% device. The wavelengths of APL91 and the −10% device are 4.53 μm and 4.77 μm, respectively. The EL emission intensities are 1.50 and 2.05, respectively. In other words, the EL emission intensity of the −10% device increased 1.37 times that of APL91. Although slightly larger than the value obtained in the simulation, a strong EL emission intensity was achieved as calculated.

Figure 4.

 EL spectra of APL91 and prototype with 10% thinner barriers (−10% device).

The simulator needs to be able to reproduce not only the gain but also the electrical characteristic of the device with high accuracy. IV characteristic is a typical electrical characteristic. To verify the accuracy of the simulator, we focused on the IV characteristic and compared the simulated and experimental values. The prototype in Subsect. 3.1 was used again to obtain experimental values of the IV characteristic.

We measured the peak current and voltage, but the simulator outputs the relationship between current density and voltage, so the current was converted to current density from the ridge width and device length for comparison. Figure 5 shows the simulation and experimental results of the IV characteristic. Although the shape of the curves is slightly different, values are relatively close, and both of them show an increase in voltage as the current density increases. In the simulation, it is assumed that all the input voltage is applied to the active layer. Therefore, although there is a slight difference between the measured and calculated values, we judged that this level of difference was sufficient to achieve the purpose of this work.

Figure 5.

 Experimental and calculated values of current density versus voltage characteristics.

3.3 Analysis of wavelength and gain

High outputs can be expected from the structure with thin barriers in the active region, but if the structure is markedly changed, fabricating the prototype becomes difficult because the net strain increases as the thickness decrease. Therefore, the wavelengths were calculated for a structure with a 10% thinner barrier (−10% structure) and a structure with a 10% thicker barrier (+10% structure).

Figure 6 shows the minibands (Wannier-Stark states) of APL91 at a voltage of 400 mV per period and a temperature of 300 K. The Wannier-Stark states correspond to the eigenstates of the Schrödinger equation without accounting for Poisson equation (i.e., electrostatic mean-field). All three structures consist of 14 minibands. The minibands that contribute to the emission and their energy differences are shown in Figure 7. Which miniband mainly contributes to the emission was determined from the oscillator strength. The main contribution to the emission was level 4 to level 6 transition. Let Δ_emi be the energy difference between level 4 and level 6. The energy difference Δ_emi of APL91 is 264.2 meV, which is 4.697 μm when converted to wavelength. Δ_emi values of the −10% structure and +10% structure are 251.5 meV (4.934 μm) and 272.0 meV (4.562 μm), respectively. The wavelength for the −10% structure is longer because Δ_emi of the −10% structure is smaller than that of APL91. Similarly, Δ_emi of the +10% structure is larger than that of APL91, so the wavelength of the +10% structure is shorter.

Figure 6.

 The minibands (Wannier-Stark states) of APL91 at a voltage of 400 mV per period and a temperature of 300 K. The Wannier-Stark states correspond to the eigenstates of the Schrödinger equation without accounting for the Poisson equation.

Figure 7.

 The minibands that contribute to the emission and their energy differences at a voltage of 400 mV per period and a temperature of 300 K for (a) APL91, (b) −10% structure, and (c) +10% structure.

Figure 8 shows the calculated wavelengths. Since the experimental wavelength of APL91 is 4.708 μm [28], the calculated value is in good agreement with the experimental one. −10% structure had a slightly longer wavelength than APL91. On the other hand, the wavelength was shortened in +10% structure. In Figure 4, the oscillation wavelength of −10% structure is 4.77 μm, which is in good agreement with the simulation results.

Figure 8.

 Oscillation wavelengths are dependent on barrier thickness.

Figure 9 shows DOSs at a voltage of 400 mV per period and a temperature of 300 K for APL91, −10% structure, and +10% structure. The DOS of a system is a physical quantity describing the number of states for each energy level that can be occupied by the system within a small energy interval. If the DOS is high at an energy level, it means that many states can occupy that energy level, and if the DOS is zero, it means that the system cannot occupy that energy level. The product of DOS and Fermi–Dirac distribution gives the electron density. −10% structure, which shows a higher gain than APL91, can occupy more states in the active region, whereas +10% structure, which shows a lower gain than APL91, has fewer states that can be occupied in the active region.

Figure 9.

 Density of states (DOS) for (a) APL91, (b) −10% structure, and (c) +10% structure.

Electron densities at a voltage of 400 mV per period and a temperature of 300 K are shown in Figure 10. In the electron density diagram, the electron density is higher in the well adjacent to the thick barrier of the injection region. Electrons are injected from this well into the active region. In addition, large values of electron density are distributed in the upper and lower subbands of the active region. Strong luminescence is generated as a result of these electron density distributions. Comparing the electron densities of APL91 and −10% structure, the electron density of −10% structure is higher in the upper subband of the second well and the lower subband of the fourth well of the active region. This is most likely contributing to the higher gain of −10% structure. Both structures achieve the population inversion in the wells of the active region, so high gains are obtained. The overall electron density distribution of +10% structure is lower than that of APL91 and −10% structure, especially in the active region, which contributes to the emission, and this may be the reason for the low gain of +10% structure.

Figure 10.

 Electron densities for (a) APL91, (b) −10% structure, and (c) +10% structure.

The populations of minibands of upper and lower levels for APL91 are 0.109 and 0.054, respectively. On the other hand, the populations of minibands of upper and lower levels of the −10% device are 0.121 and 0.054, respectively. Both APL91 and the −10% device achieve population inversion, but the degree of inversion is larger in the −10% device. It is thought to be the reason why the EL emission intensity of the −10% device increased. In addition, the oscillator strength between the upper level 4 and lower level 6 represents the likelihood of inter-subband transition. The unnormalized oscillator strengths of APL91 and the −10% device are 14.7 and 15.7, respectively; the −10% device is stronger. This may have also contributed to the increased EL intensity.

4 CONCLUSION

As one of the important targets for mesoscopic systems in computational chemistry, we selected a QCL and calculated the physical properties, i.e., optical gains, the IV characteristic, and the oscillation wavelengths using the NEGF method. The active layer was designed to increase the gain. It was shown that the output could be improved by reducing the barrier thicknesses in the active region. The reasons for the increase in gain were analyzed using DOS and electron density. DOS and electron density in the active region of −10% structure are increased compared to APL91, which is the origin of the gain enhancement. We fabricated QCL devices with the improved structure and the base structure, and evaluated their output wavelengths and EL emission intensities. As a result, the wavelengths of our prototypes were found to be in good agreement with the calculated values. The origins of the wavelength variation were analyzed using energy differences of the minibands Δ_emi. Δ_emi is the smallest in −10% structure, and as a result, the oscillation wavelength is the longest in −10% structure. DOS and electron density in the active region, and oscillator strength between level 4 and level 6 are the largest in −10% structure, resulting in a higher gain.

It was found that NEGF calculations are very useful in analyzing the properties and validating novel structures of QCL.

ACKNOWLEDGMENTS

This work was supported by Innovative Science and Technology Initiative for Security (Grant Number JPJ004596), ATLA, Japan.

SUPPLEMENTARY MATERIALS

Material data and adjustments of parameters

REFERENCES

• [1]   J. Faist, F. Capasso, D. L. Sivco, C. Sirtori, A. L. Hutchinson, A. Y. Cho, Science, 264, 553 (1994). , doi:10.1126/science.264.5158.553 PMID:17732739
• [2]   J. Faist, Quantum Cascade Laser (Oxford University Press, United Kingdom, 2013).
• [3]   A. Hugi, G. Villares, S. Blaser, H. C. Liu, J. Faist, Nature, 492, 229 (2012). , doi:10.1038/nature11620 PMID:23235876
• [4]   J. Faist, G. Villares, G. Scalari, M. Rösch, C. Bonzon, A. Hugi, et al., Nanophotonics, 5, 272 (2016). doi:10.1515/nanoph-2016-0015
• [5]   J. Ye, S. T. Cundiff, Femtosecond Optical Frequency Comb: Principle, Operation, and Applications (Springer, Norwell, MA, 2005).
• [6]   A. M. Weiner, Ultrafast Optics (Wiley, New York, 2009).
• [7]   R. F. Curl, F. Capasso, C. Gmachl, A. A. Kosterev, B. McManus, R. Lewicki, et al., Chem. Phys. Lett., 487, 1 (2010). doi:10.1016/j.cplett.2009.12.073
• [8]   I. F. Howieson, Laser Focus World, 47, 33 (2011).
• [9]   J. B. McManus, M. S. Zahniser, D. D. Nelson, J. H. Shorter, S. Herndon, E. Wood, et al., Opt. Eng., 49, 111124 (2010). doi:10.1117/1.3498782
• [10]   S. L. Lu, L. Schrottke, S. W. Teitsworth, R. Hey, H. T. Grahn, Phys. Rev. B, 73, 033311 (2006). doi:10.1103/PhysRevB.73.033311
• [11]   R. C. Iotti, F. Rossi, Rep. Prog. Phys., 68, 2533 (2005). doi:10.1088/0034-4885/68/11/R02
• [12]   J. Schwinger, J. Math. Phys., 2, 407 (1961). doi:10.1063/1.1703727
• [13]   L. P. Kadanoff, G. Baym, Quantum Statistical Mechanics (W. A. Benjamin, Inc., Menlo Park, California, 1962).
• [14]   L. V. Keldysh, Sov. Phys. Jetp-USSR, 20, 1018 (1965).
• [15]   C. Jirauschek, T. Kubis, Appl. Phys. Rev., 1, 011307 (2014). doi:10.1063/1.4863665
• [16]   S. Datta, Electronic Transport in Mesoscopic Systems (Cambridge University Press, New York, 1995) Chap. 8.
• [17]   S. Datta, Quantum Transport: Atom to Transistor (Cambridge University Press, New York, 2005).
• [18]   S. Datta, Superlattices Microstruct., 28, 253 (2000). doi:10.1006/spmi.2000.0920
• [19]   T. Miyoshi, M. Ogawa, H. Tsuchiya, Nanoerekutoronikusu No Kiso (Nano Electronics) (Baifukan, Tokyo, 2007).
• [20]   S. C. Lee, F. Banit, M. Woerner, A. Wacker, Phys. Rev. B, 73, 245320 (2006). doi:10.1103/PhysRevB.73.245320
• [21] T. Grange, Physical Review B 92, 241306–31–5 (2015).
• [22]   T. Grange, Appl. Phys. Lett., 105, 141105 (2014). doi:10.1063/1.4897543
• [23]   T. Grange, Phys. Rev. B, 89, 165310 (2014). doi:10.1103/PhysRevB.89.165310
• [24]   T. Grange, D. Stark, G. Scalari, J. Faist, L. Persichetti, L. Di Gaspare, et al., Appl. Phys. Lett., 114, 111102 (2019). doi:10.1063/1.5082172
• [25]   S. Takagi, H. Tanimura, T. Kakuno, R. Hashimoto, K. Kaneko, S. Saito, Proceedings of the 8th International Conference on Photonics, Optics and Laser Technology, in Valletta, Malta (2020).
• [26] nextnano.NEGF software can be purchased from the website of nextnano GmbH.
• [27]   H. Haug, A.-P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors (Springer, Berlin, 1996).
• [28]   T. Kubis, P. Vogl, J. Phys. Conf. Ser., 193, 012063 (2009). doi:10.1088/1742-6596/193/1/012063
• [29]   T. Kubis, C. Yeh, P. Vogl, A. Benz, G. Fasching, C. Deutsch, Phys. Rev. B, 79, 195323 (2009). doi:10.1103/PhysRevB.79.195323
• [30]   T. Kubis, S. R. Mehrotra, G. Klimeck, Appl. Phys. Lett., 97, 261106 (2010). doi:10.1063/1.3524197
• [31]   https://nextnano-docu.northeurope.cloudapp.azure.com/dokuwiki/doku.php?id=qcl:optics
• [32]   A. Wacker, Phys. Rev. B, 66, 085326 (2002). doi:10.1103/PhysRevB.66.085326
• [33]   S. C. Lee, A. Wacker, Phys. Rev. B, 66, 245314 (2002). doi:10.1103/PhysRevB.66.245314
• [34]   F. Banit, S. C. Lee, A. Knorr, A. Wacker, Appl. Phys. Lett., 86, 041108 (2005). doi:10.1063/1.1851004
• [35]   R. H. Lyddane, R. G. Sachs, E. Teller, Phys. Rev., 59, 673 (1941). doi:10.1103/PhysRev.59.673
• [36]   A. Evans, S. R. Darvish, S. Slivken, J. Nguyen, Y. Bai, M. Razeghi, Appl. Phys. Lett., 91, 071101–1 (2007).