Relativistic DFT Calculations of Changes in NMR Chemical Shifts in Aqueous Solutions of Heavy-Metal Nitrates

Abstract

The NMR chemical shifts for metal ions in aqueous solutions of inorganic salts often change with the solution concentration. These changes are referred to herein as dilution–concentration (dc) shifts. For main-group elements, the dc shifts generally increase with increasing atomic number. We calculated the dc shifts for various metal and nonmetal ions in aqueous nitrate solutions of elements in periods 5 and 6 by the DFT method based on the spin–orbit ZORA Hamiltonian. The calculation results revealed that the dc shifts of metal and nonmetal ions with the outermost shell electron configuration of 6s² are primarily determined by the changes in the spin–orbit interaction terms of the shielding constants. Furthermore, the spin densities of the Pb(II) ions in aqueous lead nitrate solutions under an external magnetic field were calculated using the matrix/modified Dirac–Kohn–Sham Hamiltonian, which confirmed the presence of Fermi contacts between the spin-polarized electrons and the lead nucleus. When a suitable threshold for visualizing the spin density was set, there was no Fermi contact in the infinite dilution state, whereas the upward-spin electron was in Fermi contact with the lead nucleus in the saturation state. There have been few reports of the NMR chemical shifts of heavy atoms in terms of Fermi contacts with relativistically spin-polarized electrons. We succeeded in clarifying how the dc shifts occur on the hydrated ions of heavy atoms by visualizing the Fermi contact of spin-polarized electrons with heavy-metal nuclei.

1 INTRODUCTION

The NMR resonance lines measured for the solvated ions in aqueous solutions of various inorganic salts exhibit concentration-dependent chemical shift changes [1,2,3,4,5,6,7,8]. In this paper, we comprehensively investigate the changes in NMR chemical shifts that occur when measuring the same solvated ions at two different concentrations; we refer to such changes in the NMR chemical shifts as dilution–concentration (dc) shifts. The dc shifts between the two concentrations corresponding to infinite dilution and saturation are mainly considered in this work.

The dc shifts of metal ions generally increase with increasing atomic number. For example, the dc shifts of Pb(II) ions, where lead is a period 6 element, in aqueous nitrate solutions are larger than those of lighter metals in aqueous nitrate solutions [8]. It is likely that relativistic effects are closely related to this atomic number dependence of dc shifts.

The relativistic effects observed for the NMR resonance lines of heavy nuclei and their adjacent nuclei have been well known as “heavy-atom effects” since the early days of NMR spectroscopy. For example, normal halogen dependence (NHD) [9, 10] and inverse halogen dependence (IHD) [11] are familiar phenomena originating from such heavy-atom effects [9]. In the 1960s, Nakagawa and co-workers demonstrated using third-order Rayleigh–Schrödinger perturbation theory that the heavy-atom effects observed for the resonance lines of some alkyl halides can be ascribed to spin polarization; the resonance shifts caused by the heavy atoms were referred to as spin polarization shifts [9]. In the 1980s, four-component formalisms started to be used in theoretical calculations of the heavy-atom effects [6, 12,13,14], while Pyykkö and co-workers reported the heavy-atom effect on the heavy atom itself (HAHA effect) [6].

For the theoretical study of the dc shifts, it is important to elucidate the hydration structures of the solvated ions based on solution chemistry. Experimental results indicate that the dominant hydration structure of a solvated ion at infinite dilution is distinct from that at saturation. Nancollas demonstrated that the change in conductivity of aqueous lead nitrate solutions can be explained by rapid exchange between an aquated lead ion and a Pb(NO₃)⁺ ion complex [15]. Recently, on the basis of this exchange equilibrium, the chemical shifts of ²⁰⁷Pb in aqueous lead nitrate solutions were calculated and the experimental values were accurately reproduced [10].

Pb(II) ions are known to have a hydrated structure in which the water molecules are coordinated in a hemidirected manner, which is also the case for Sn(II), Tl(I), and Bi(III) ions [16]. It has also been demonstrated that at infinite dilution the hemidirected structure of a solvated lead ion changes into a holodirected structure in which the nitrate ion and water molecules are omnidirectionally situated around the metal center [17]. The same solvation structures were applied to calculate the NMR chemical shifts for bismuth ions in aqueous solutions of bismuth nitrate [18].

In this work, to elucidate the role of relativistic effects in the dc shifts, we calculated the NMR chemical shifts of various solvated ions in aqueous solutions of nitrate salts, including the ions of both metal and nonmetal elements in periods 5 and 6. The NMR shielding constants were calculated by unrestricted density functional theory (DFT) using the spin–orbit zeroth-order regular approximation (SO-ZORA) [19,20,21] Hamiltonian to obtain the theoretical values of the dc shifts. The results revealed that for metal and nonmetal ions with the 6s orbitals as the highest occupied atomic orbitals, the dc shifts are governed by the power relationship between the paramagnetic shielding terms and the spin–orbit interaction terms.

In addition, to elucidate the relation between the spin polarization on the solvated ions and the dc shifts, we calculated and visualized the spin densities for the solvated Pb(II) ions and Cs(I) ions in the presence of an external magnetic field using a matrix/modified Dirac–Kohn–Sham (mDKS) Hamiltonian. These calculation results revealed the major factors responsible for the dc shifts of Pb(II) ions. Finally, we show that there exists a close relation between the spin–orbit interaction terms and the Fermi contact interactions of the shielding constants, which has not been reported in previous studies of the spin–orbit HAHA (SO-HAHA) effect.

2 THEORY

In solution NMR, the resonance frequency ν_NMR is determined by the gyromagnetic ratio of an observed nucleus γ, the external static magnetic field B₀, and the shielding constant of the nucleus σ_N:   

${\text{ν}}_{\text{NMR}}=\frac{\left|\text{γ}\right|}{2\text{π}}\left(1-{\sigma }_{\text{N}}\right)B_0$(1)

.

The NMR shielding constant is defined as a tensor expressed as a 3 × 3 array based on the molecular coordinate system x, y, z. In solutions, the molecules rotate randomly, so the NMR resonance lines appear at the isotropic values ${\sigma }_{\text{N}}=1/3({\sigma }_{\text{N},xx}+{\sigma }_{\text{N},yy}+{\sigma }_{\text{N},zz})$.Based on the second-order Rayleigh–Schrödinger perturbation theory, Ramsey showed that the shielding constant ${\sigma }_{\text{N},tu}$ has the following relationship with the energy $E\left(B_0,{\mu }_{\text{N}}\right)$ of a nucleus in the external static magnetic field $B_0$:   

${\sigma }_{\text{N},tu}={\frac{{\partial }^{2}E\left(B_0,{\mu }_{\text{N}}\right)}{\partial B_{0,t}\partial {\mu }_{\text{N},\text{u}}}|}_{B_0={\mu }_{\text{N}}=0}\left(t,u=x,y,z\right)$(2)

, where ${\mu }_{\text{N}}$ is the magnetic moment of the observed nucleus.

The shielding constant can be broken down according to the shielding mechanism as follows:   

${\sigma }_{\text{N}}={\sigma }_{\text{dia}}+{\sigma }_{\text{para}}+{\sigma }_{\text{SO/FC}}+{\sigma }_{\text{SO/SD}}+{\sigma }_{\text{others}}$(3)

, where ${\sigma }_{\text{dia}}$ and ${\sigma }_{\text{para}}$ are the shielding terms due to Larmor diamagnetism and Van Vleck paramagnetism, respectively. In relativistic systems, additional shielding terms ${\sigma }_{\text{SO/FC}}$ and ${\sigma }_{\text{SO/SD}}$ are added. The ${\sigma }_{\text{SO/FC}}$ term originates from the Fermi contact between the electrons in the valence orbital, which are spin-polarized by the spin–orbit interaction, and the observed nucleus. The spin-dipole term ${\sigma }_{\text{SO/SD}}$ is neglected in this paper because it is very small in solution NMR because of the random and rapid rotation of the molecules.

The Kohn–Sham DFT equation can be written as   

$\left[T+V^{\text{KS}}\right]{\phi }_i={\epsilon }_i{\phi }_i$(4)

, where $T$ is the kinetic energy operator, $V^{\text{KS}}$ is the local Kohn–Sham potential, and ${\epsilon }_i$ and ${\phi }_i$ are a spinor energy and a spinor orbital, respectively [22]. For the ZORA method, $T$ is given by   

$T^{\text{ZORA}}=\sigma \cdot p\frac{{\text{c}}^2}{2{\text{c}}^2-V^{\text{KS}}}\sigma \cdot p$(5)

, where σ denotes the Pauli matrices, p is the momentum of an electron, and c is the speed of light. For the calculation of the NMR shielding constant, p is replaced by the generalized momentum $\pi =p+\frac{A_0}{\text{c}}+\frac{A_N}{\text{c}}$, where $A_0$ is the vector potential of the external static field and $A_N$ is the vector potential of the nucleus. The formalism of the NMR shielding constant within the SO-ZORA is provided in references [23, 24].

In addition, the electron spin densities of molecules in the static magnetic field, which are strongly related to ${\sigma }_{\text{SO/FC}}$, were also calculated. The spin densities were calculated using the mDKS Hamiltonian based on the following four-component Dirac kinetic energy operator:   

$T^{\text{Dirac}}=\sigma \cdot p\frac{{\text{c}}^2}{2{\text{c}}^2+{\epsilon }_i-V^{\text{KS}}}\sigma \cdot p$(6)

. The electron spin density of a molecule is given by the following equation:   

$\rho =\text{Tr}\left[{\left(X^{\text{RKB}}\right)}^{†}\Sigma X^{\text{RKB}}D\right]$(7)

, where $X^{\text{RKB}}$ is the matrix composed of atomic orbital functions under the restricted kinetic balance (RKB) condition [25], $\Sigma =\left(\begin{array}{cc}\sigma & 0\\ 0& \sigma \end{array}\right)$, and $D$ is a matrix determined by the Hartree–Fock potential and kernel. The explicit forms of $X^{\text{RKB}}$ and $D$ are given elsewhere [25]. The studies [26,27,28] of the spin–orbit heavy-atom effects on light atoms (SO-HALA effect) have shown that the electron spin density is proportional to the ${\sigma }_{\text{SO/FC}}$ term of the spectator NMR atoms.

3 METHODS

All nitrate salts were purchased from Tokyo Chemical Industry Co., Ltd. and used without further purification. Deuterium oxide (99%) was purchased from Wako Pure Chemical Industries Ltd. Aqueous solutions of the nitrate salts were prepared in the concentration range from 0.01 to 1 mol/kg in 10% D₂O, which was obtained by diluting D₂O with H₂O. NMR spectra were recorded at 295 K on a JEOL ECA500 spectrometer operating at 500 MHz for ¹H. The π/2 pulse lengths for the observed nuclei were set to10 μs by adjusting the radio-frequency field attenuator. The recycle delays were in the range of 1–5 s. The number of co-added free induction decays varied from 8 to 2048 depending on the concentration. The NMR spectra for each nitrate salt were referenced to the lowest resonance frequency observed in the aqueous solutions.

For aqueous nitrate solutions in the infinite dilution state, hydrates in which only water molecules are bound to the central cations are dominant. In contrast, in the saturated state, the central ions of some of the hydrates are bound to nitrate ions. Hereinafter, the hydration structures corresponding to these two states will be referred to as the dilution model and the concentration model, respectively.

The initial structures of the dilution models were determined for each individual electron configuration of the outermost shells, based on previous reports [17, 29,30,31,32,33,34,35,36,37], as follows: The initial hydration structures of Rb(I) [33], Sr(II) [34], Cs(I), and Ba(II) [34] ions, in which the outermost shells of the metal ions have the s²p⁶ configuration, were set to square antiprismatic geometry with eight bound water molecules. The initial hydration structures of Cd(II) [31, 32], In(III) [36], Sn(IV), Sb(V), Hg(II) [35], Tl(III) [37], Pb(IV), and Bi(V) ions, in which the outermost shells of the metal ions have the s²p⁶d¹⁰ configuration, were set to octahedral geometry [17] with six bound water molecules. The initial hydration structure of Ag(I) ions was set to tetrahedral geometry [17, 30]; the calculation results for hydrates of Au(I) ions are not presented in this paper because no optimized hydration structure was obtained. The outermost shells of In(I), Sn(II) [17], Sb(III), Te(IV), I(V), Tl(I) [17], Pb(II) [16, 17, 29], Bi(III) [18], Po(IV), and At(V) ions have the s² electron configuration; the initial hydration structures of Sb(III), Te(IV), I(V), Pb(II), Bi(III), Po(IV), and At(V) ions were set to hemidirected structures [17] with seven bound water molecules; the initial hydration structures of In(I), Sn(II), and Tl(I) ions were set to the structures with fourteen bound water molecules, because for In(I), Sn(II), and Tl(I) ions, the initial structures with less than fourteen water molecules did not lead to optimized structures.

To obtain the concentration models for solvated ions with the square antiprismatic geometry in their dilution models, we used the initial structure with a nitrate ion placed between the upper and lower planes of the antiprismatic structure. For solvated ions with the octahedral geometry in their dilution models, one of the water molecules was replaced by a nitrate ion to generate the initial structure for the concentration model. For the solvated ions with the hemidirected structure in their dilution models, a nitrate ion was placed around the central ion such that the initial structure for the concentration model was holodirected.

The DFT optimization of these initial structures was performed using ADF 2019 [38] with the basis functions of DZ [39] for H atoms, TZP [39] for O and N atoms, and TZ2P [39] for the central ions. For the density functional (also referred to as the exchange-and-correlation (XC) functional), we used the long-range corrected hybrid functional ωB97X [40, 41]. For the relativistic effects, the scalar relativistic effects and the spin–orbit interaction were included in the calculations by using the SO-ZORA Hamiltonian. To make the relativistic effect near the nucleus more pronounced, a Gaussian distribution model [42] was used for the nuclear charge distribution. To introduce the solvent effect, the COSMO/water scheme [43] was employed. For the structural optimization algorithm, the Hessian-based quasi-Newton-type Broyden–Fletcher–Goldfarb–Shanno (BFGS) was used. All of the optimized structures are listed in Tables S1–S46 in the Supporting Information.

The NMR shielding constants [44, 45] of the central ions in the structure-optimized hydrates in aqueous solution were determined by unrestricted DFT calculations in ADF 2019. In the NMR calculations, we used the GGA functional BP86 [46, 47] and the hybrid functionals B3LYP [48,49,50] and PBE0 [51]. Although several functionals [52] have been proposed for NMR calculations, the purpose of the present study is to investigate the effect of the solution state on the chemical shifts of heavy atoms. Therefore, rather than NMR-specific functionals, we used B3LYP and PBE0, which are widely used in general quantum chemical calculations and have been verified for accuracy. In addition, to estimate the difference between GGA functionals and the hybrid functionals, BP86 was used. The spin polarization direction due to the spin–orbit interaction was set as “non-collinear”, and gauge-independent atomic orbitals (GIAO) were adopted to avoid the problem of gauge-dependent calculation results.

The ReSpect program (version 5.1.0) [53] with the B3LYP XC functional was used to calculate the spin density. For the basis functions, we used upc-1 [54] for H atoms, dyall-vdz [55,56,57] for O and N atoms, and dyall-cvtz [55,56,57] for the central ions. Relativistic effects were introduced into the calculations at the four-component level by the mDKS Hamiltonian. A Gaussian distribution model for the nuclear charge distribution and GIAO were used in these calculations. Gauss View 6 [58] was used to visualize the calculation results.

4 RESULTS AND DISCUSSION

Figure 1 presents the experimentally measured dc shifts for the metal ions in selected aqueous nitrate solutions. Although these experimental results do not precisely correspond to the calculated chemical shift differences between the dilution and concentration models, we can observe the trend in the variation of the dc shifts throughout the periodic table. Figure 1 shows that the metal ions with the s²p⁶ electron configuration for the outermost shell, such as Rb(I) and Cs(I) ions, exhibit small dc shifts, whereas those with electron configurations of s²p⁶d¹⁰, such as Cd(II) and Hg(II) ions, and s², such as Pb(II) ions, display large dc shifts.

Figure 1.

 Experimentally measured dc shifts for metal ions in selected aqueous nitrate solutions. The chemical shifts of the metal ions were measured at several concentrations ranging from 0.01 to 1 mol/kg, and the absolute value of the maximum change in chemical shift for each ion is plotted. The horizontal axis indicates the nature of the metal ions and the period to which they belong. The expressions show the outermost shell electron configurations of the metal ions, where n denotes the period. Note that the experimental value for Hg (II) refers to mercury perchlorate rather than mercury nitrate.

Figure 2 summarizes the calculated dc shifts for metal and nonmetal ions in aqueous nitrate solutions of elements in periods 5 and 6, excluding most of the transition metals. We can see that the main features of the experimental results shown in Figure 1 are reproduced in Figure 2. There are quantitative differences between the experimental and calculated values of the dc shifts. This is because not only at 0.01 mol/kg or 1 mol/kg but also at any concentration the chemical shift is observed under equilibrium due to the rapid exchange between the complexes corresponding to the dilution and concentration models [59]. That is, the reason is that the solution states of 0.01 mol/kg and 1 mol/kg do not correspond to the dilution and concentration models, respectively.

Figure 2.

 Calculated dc shifts for metal and nonmetal ions in aqueous nitrate solutions of elements in periods 5 and 6, excluding most of the transition elements. The difference in chemical shifts between the dilution and concentration models for each ion is plotted. ${\delta }_{\text{calc}}^{\left(\text{dc}\right)}$ is given by ${\delta }_{\text{calc}}^{\left(\text{dc}\right)}={\sigma }_{\text{total}}^{\left(\text{d}\right)}-{\sigma }_{\text{total}}^{\left(\text{c}\right)}$, where ${\sigma }_{\text{total}}^{\left(i\right)}$ (i = d or c) are the total shielding constants for the dilution and concentration models, respectively. ${\delta }_{\text{dia}}^{\left(\text{dc}\right)}$, ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$, and ${\delta }_{\text{SO}/\text{FC}}^{\left(\text{dc}\right)}$ are given by ${\delta }_{\text{dia}}^{\left(\text{dc}\right)}={\sigma }_{\text{dia}}^{\left(\text{d}\right)}-{\sigma }_{\text{dia}}^{\left(\text{c}\right)}$, ${\delta }_{\text{para}}^{\left(\text{dc}\right)}={\sigma }_{\text{para}}^{\left(\text{d}\right)}-{\sigma }_{\text{para}}^{\left(\text{c}\right)}$, and ${\delta }_{\text{SO}/\text{FC}}^{\left(\text{dc}\right)}={\sigma }_{\text{SO}/\text{FC}}^{\left(\text{d}\right)}-{\sigma }_{\text{SO}/\text{FC}}^{\left(\text{c}\right)}$, respectively. Here, ${\sigma }_{\text{dia}}^{\left(i\right)}$ and ${\sigma }_{\text{para}}^{\left(i\right)}$ (i = d or c) denote the diamagnetic and paramagnetic shielding constants, respectively, and ${\sigma }_{\text{SO}/\text{FC}}^{\left(i\right)}$ (i = d or c) denotes the shielding constant based on the spin–orbit interactions and Fermi contact interactions. The superscript letters in brackets denote the two models. Below the horizontal axis, the XC functionals used to calculate the dc shifts and the outermost shell electron configurations are shown.

In terms of functional dependence, only BP86 shows a tendency to differ significantly from the other functionals in some of the results (Figure 2). We calculated the chemical shifts of the dilution model for Pb(II) with the three functionals using tetramethyllead as a reference material, and only B3LYP and PBE0 displayed good agreement with the literature values [59]. Therefore, a functional dependence exists for BP86, and it is appropriate to base our discussion on the values obtained with B3LYP and PBE0.

We will first discuss the difference between the metal ions with the outermost shell electron configuration of s²p⁶, for which ${\delta }_{\text{para}}^{\left(\text{dc}\right)}={\sigma }_{\text{para}}^{\left(\text{d}\right)}-{\sigma }_{\text{para}}^{\left(\text{c}\right)}$ hardly changes, and the metal and nonmetal ions with the outermost shell electron configuration of s²p⁶d¹⁰ or s², for which ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$ changes.

The metal ions with the outermost shell electron configuration of s²p⁶ have ${\sigma }_{\text{para}}^{\left(\text{d}\right)}$and ${\sigma }_{\text{para}}^{\left(\text{c}\right)}$values of approximately −50 to −250 ppm. This is attributed to their stable noble-gas-like electron configurations and the lack of mixing of excited states into the valence orbitals. The small ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$, which is the difference between ${\sigma }_{\text{para}}^{\left(\text{d}\right)}$and ${\sigma }_{\text{para}}^{\left(\text{c}\right)}$, can also be ascribed to the stable electron configuration of the ions and the small change in the valence orbitals that occurs upon the binding of a nitrate ion.

For the metal and nonmetal ions with the outermost shell electron configuration of s²p⁶d¹⁰ or s², the absolute values of ${\sigma }_{\text{para}}^{\left(\text{d}\right)}$and ${\sigma }_{\text{para}}^{\left(\text{c}\right)}$ are larger than those of the ions with the outermost shell electron configuration of s²p⁶. For example, for Pb(IV), ${\sigma }_{\text{para}}^{\left(\text{d}\right)}$and ${\sigma }_{\text{para}}^{\left(\text{c}\right)}$ calculated with B3LYP are −2877 and −2714 ppm, respectively; for Pb(II), these are −1121 and −991 ppm. On the other hand, for Cs(I) these are −76 and −60 ppm. This is likely attributable to the greater mixing of p and d characters into the valence orbitals of the ions with the outermost shell electron configuration of s²p⁶d¹⁰ or s² compared to the those of the ions with the outermost shell electron configuration of s²p⁶.

The paramagnetic terms ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$ of the ions with the outermost shell electron configuration of s²p⁶d¹⁰ or s² are negative except for the results for In(I), Sn(II), and Tl(I) with all three functionals and those for Sb(III), Te(IV), Bi(III), and Po(IV) with BP86. In both groups, when a nitrate ion binds to the central metal ion, the number of electrons on the metal ion increases. This likely lead to the explanation of the negative values of ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$ observed for most of the ions besides the exceptions noted above. However, the data in this paper are insufficient to support this assertion, and calculations such as population analysis are necessary for confirmation.

For the metal ions with the outermost electron configuration of s²p⁶d¹⁰, the absolute values of ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$ increase with the oxidation number of the ions. The optimized structures of these ions show that the bond distances between the central ions and other molecules decrease with increasing oxidation number. Because the approximate expression of the paramagnetic shielding constant includes the reciprocal of the mean distance between the nucleus and the nearby electrons, the decrease in the bond distances expands ${\sigma }_{\text{para}}^{\left(\text{d}\right)}$and ${\sigma }_{\text{para}}^{\left(\text{c}\right)}$, and the difference between them, ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$, is also expanded. The systematic changes in ${\delta }_{\text{para}}^{\left(\text{dc}\right)}$ observed for the ions with the outermost shell electron configuration of s²p⁶d¹⁰ can be explained as described above.

The reason why a tendency for the paramagnetic terms to have physical meaning emerges in the present analysis requires further study, and it is too early to draw any conclusions from the current data. Because the paramagnetic terms by GIAO include the contribution of the normal paramagnetic terms [60], these terms likely make the dominant contributions in the normal paramagnetic terms.

For metal ions with an outermost shell electron configuration of 6s², changes in both the paramagnetic shielding terms and the ${\sigma }_{\text{SO/FC}}$ terms govern the dc shifts. To the best of our knowledge, this is the first report of calculation results showing that the ${\sigma }_{\text{SO/FC}}$ term, which originates from the magnetism due to the relativistic phenomena of spin–orbit couplings, changes with the concentration of solvated ions in aqueous solution. In other words, the ${\sigma }_{\text{SO/FC}}$ term varies with changes in the structures of the solvated ion complexes. It has been generally considered that the ${\sigma }_{\text{SO/FC}}$ terms of heavy atoms or heavy ions do not vary in response to changes in complex structures [28]. However, in the present study, it was found that the ${\sigma }_{\text{SO/FC}}$ terms are significantly influenced by the changes in complex structure that occur in heavy ions with the outermost shell electron configuration of 6s². The ${\sigma }_{\text{SO/FC}}$ term is highly dependent on the s character of the valence orbitals [61]. Hence, the s character of the valence orbitals of the hydrated heavy ions with the outermost shell electron configuration of 6s² is considered to be changed by the bonding with a nitrate ion, resulting in the large changes in the ${\sigma }_{\text{SO/FC}}$ term as shown in these results.

The ${\sigma }_{\text{SO/FC}}$ term originates from the Fermi contact between the spin-polarized valence electrons and the observed nucleus, where the spin polarization is caused by the spin–orbit interaction that emerges in the presence of an external magnetic field. To investigate the connection between the dc shifts and the spin polarization, we calculated the spin densities for the dilution and concentration models of Pb(II) ions in the presence of an external magnetic field using the mDKS Hamiltonian.

Figure 3 shows the calculated spin densities for the two models of Pb(II) ions. We found that when the threshold of the spin density visualization was set to 8.742 × 10⁻⁵ a.u. or greater, there was no Fermi contact in the dilution model, and only in the concentration model was the upward-spin electron in Fermi contact with the metal nucleus. In the concentration model, the magnetic dipole of the polarized electron spin reduces the local magnetic field of the metal nucleus more than in the dilution model. Therefore, the dc shift due to the spin–orbit interaction is negative on the δ scale. The direction of this chemical shift change is consistent with the experimental and calculated dc shifts presented in Figures. 1 and 2.

Figure 3.

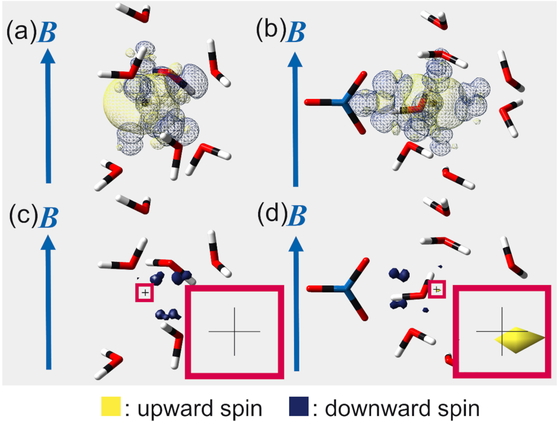
 Fermi contacts between the nuclei of Pb(II) ions and spin-polarized electrons in aqueous nitrate solutions. The arrows indicate the direction of the external magnetic field. Panels (a) and (c) depict the spin density around the nucleus of a Pb(II) ion in the dilution model, while panels (b) and (d) show the spin density around the nucleus of a Pb(II) ion in the concentration model. The densities of upward and downward spins are depicted in yellow and navy, respectively. The thresholds for the spin density visualization are 1 × 10⁻⁶ a.u. in panels (a) and (b) and 8.742 × 10⁻⁵ a.u. in panels (c) and (d). In panels (c) and (d), the areas near the centers of the lead nuclei are magnified in the lower right squares. When the threshold value was less than 8.742 × 10⁻⁵ a.u., the upward spins in Fermi contact with the lead nuclei were confirmed in both the dilution and concentration models. When the threshold value was set to 8.742 × 10⁻⁵ a.u. or greater, the upward spin in Fermi contact with the lead nucleus was confirmed only in the concentration model. In the concentration model, the spin density near the center of the lead nucleus was visible until the threshold value reached 1.298 × 10⁻⁴ a.u.

For comparison, the spin densities were calculated for the dilution and concentration models of Cs(I) ions, for which the ${\sigma }_{\text{SO/FC}}$ terms remain almost unchanged. Figure 4 shows the calculated spin densities. We observed a small difference in the spin density between the two models for the Cs(I) nuclei through a comparison of panels (c) and (d). However, it was found that the change in spin density on the Cs(I) nuclei does not lead to a large dc shift, because the difference in the spin density on the Cs(I) nuclei was more than an order of magnitude smaller than that on the Pb(II) ions.

Figure 4.

 Fermi contacts between the nuclei of Cs (I) ions and spin-polarized electrons in aqueous nitrate solutions. The arrows indicate the direction of the external magnetic field. Panels (a) and (c) depict the spin density around the nucleus of a Cs (I) ion in the dilution model, while panels (b) and (d) show the spin density around the nucleus of a Cs (I) ion in the concentration model. For the sake of clarity, the densities of the upward spins only are depicted in yellow. The thresholds for the spin density visualization are 1 × 10⁻⁶ a.u. in panels (a) and (b) and 2 × 10⁻⁶ a.u. in panels (c) and (d). In panels (c) and (d), the areas near the centers of the Cs (I) nuclei are magnified in the lower right squares. When the threshold value was greater than 2.722 × 10⁻⁵ a.u., the spin density was not observed. Because the maximum value of the threshold at which the spin density could be observed was 2.722 × 10⁻⁵ a.u., Cs (I) ions have smaller spin polarization than Pb(II) ions in the external magnetic field.

From the results of Figures 3 and 4, it is apparent that the changes in the ${\sigma }_{\text{SO/FC}}$ terms shown in the calculations of the dc shifts for the Pb(II) and Cs(I) ions correspond to the changes in the spin densities on the observed nuclei. These results regarding the spatial distributions of valence electrons in the molecular spinors are considered to be strongly related to the conventional theory that the s character of valence orbitals affects the ${\sigma }_{\text{SO/FC}}$ terms. Detailed analysis of the valence orbitals, such as through spin–orbit-induced electron deformation density (SO-EDD) [27, 28] analysis, will be presented in the near future.

5 CONCLUSION

We have studied the effects of spin–orbit interactions on the dc shifts of metal and nonmetal ions in aqueous nitrate solutions of elements belonging to periods 5 and 6, primarily through quantum chemical calculations. For the solvated ions with outermost shell electron configurations of s²p⁶, s²p⁶d¹⁰, and s², the dc shifts increased in that order for a given period, which was confirmed by both calculations and experiments.

We further investigated the components of the NMR shielding constants through calculations using the SO-ZORA Hamiltonian. It was found that for metal ions with an outermost shell electron configuration of s²p⁶d¹⁰, the dc shifts were determined by the changes in the dominant paramagnetic shielding terms, whereas for metal and nonmetal ions with an outermost shell electron configuration of s², the dc shifts were determined by the changes in both the paramagnetic shielding and spin–orbit interaction terms.

We also calculated the spin densities, which are induced by both the external magnetic field and spin–orbit interactions, for the dilution and concentration models of selected metal ions using the mDKS Hamiltonian. These calculations were applied to examine the spin-polarized electrons in Fermi contact with the ionic nuclei. These calculations ultimately revealed distinct changes in the spin densities on the nuclei of Pb(II) ions with the outermost shell electron configuration of s² between the dilution and concentration models. These results provide a clear explanation for one of the origins of the changes in the spin–orbit interaction terms in the shielding constants calculated using the SO-ZORA Hamiltonian.

In previous studies of the SO-HALA effects, it has been pointed out that changes in the molecular structure lead to changes in the ${\sigma }_{\text{SO/FC}}$ terms for light atoms. For heavy ions with an outermost shell electron configuration of s² in aqueous nitrate solutions, the changes in hydration structures with concentration correspond to the changes in the molecular structures of the systems containing light atoms. It can thus be concluded that for such heavy ions, the changes in hydration structures induce changes in the ${\sigma }_{\text{SO/FC}}$ terms, resulting in substantial dc shifts.

SUPPORTING INFORMATION AVAILABLE

Optimized structures for various solvated ions in aqueous nitrate solutions.

Acknowledgments

We are grateful to Dr. Ayaki Sunaga for helpful discussions and comments on the manuscript. We gratefully acknowledge the work of past members of our laboratory, Takumi Yokoyama, Tatsuki Sato, and Kenta Tasaki. We would also like to thank the ReSpect program team for kindly providing the ReSpect program, especially Dr. Michal Repisky for responding to us via email.

REFERENCES

• [1]   C. Deverell, R. E. Richards, Mol. Phys., 10, 551 (1966). doi:10.1080/00268976600101491
• [2]   G. E. Maciel, J. K. Hancock, L. F. Lafferty, P. A. Mueller, W. K. Musker, Inorg. Chem., 5, 554 (1966). doi:10.1021/ic50038a013
• [3]   E. G. Bloor, R. G. Kidd, Can. J. Chem., 46, 3425 (1968). doi:10.1139/v68-569
• [4]   R. J. Kostelnik, A. A. Bothner-By, J. Magn. Reson., 14, 141 (1974). doi:10.1016/0022-2364(74)90268-6
• [5]   M. Munataka, S. Kitagawa, F. Yagi, Inorg. Chem., 25, 964 (1986). doi:10.1021/ic00227a016
• [6]   U. Edlund, T. Lejon, P. Pyykko, T. K. Venkatachalam, E. Buncel, J. Am. Chem. Soc., 109, 5982 (1987). doi:10.1021/ja00254a015
• [7]   N. Altounian, A. Glatfelter, S. Bai, C. Dybowski, J. Phys. Chem. B, 104, 4723 (2000). doi:10.1021/jp000130u
• [8]   N. Nakagawa, M. Okazaki, N. Motohiro, T. Yamazaki, N. Nagashima, J. Uzawa, H. Seki, Y. Kubota., The International Symposium on Nuclear Magnetic Resonance, (2011).
• [9]   N. Nakagawa, S. Sinada, S. Obinata, The 6th Annual Meeting of the NMR Society of Japan, (1967).
• [10]   Y. Nomura, Y. Takeuchi, N. Nakagawa, Tetrahedron Lett., 10, 639 (1969). doi:10.1016/S0040-4039(01)87770-4
• [11]   S. Moncho, J. Autschbach, Magn. Reson. Chem., 48, S76 (2010). , doi:10.1002/mrc.2632 PMID:20586110
• [12]   N. C. Pyper, Chem. Phys. Lett., 96, 204 (1983). doi:10.1016/0009-2614(83)80492-8
• [13]   P. Pyykkö, Chem. Phys., 74, 1 (1983). doi:10.1016/0301-0104(83)80001-9
• [14]   Z. C. Zhang, G. A. Webb, J. Mol. Struct. THEOCHEM, 104, 439 (1983). doi:10.1016/0166-1280(83)80193-6
• [15]   G. H. Nancollas, J. Chem. Soc. Resumed, 1458 (1955). doi:10.1039/jr9550001458
• [16]   I. Persson, Pure Appl. Chem., 82, 1901 (2010). doi:10.1351/PAC-CON-09-10-22
• [17]   F. Alkan, T. Small, S. Bai, A. Dominowski, C. Dybowski, J. Struct. Chem., 57, 369 (2016). doi:10.1134/S0022476616020189
• [18]   A. Antušek, M. Repisky, M. Jaszuński, K. Jackowski, W. Makulski, M. Misiak, Phys. Rev. A, 98, 052509 (2018). doi:10.1103/PhysRevA.98.052509
• [19]   E. van Lenthe, E. J. Baerends, J. G. Snijders, J. Chem. Phys., 99, 4597 (1993). doi:10.1063/1.466059
• [20]   E. van Lenthe, E. J. Baerends, J. G. Snijders, J. Chem. Phys., 101, 9783 (1994). doi:10.1063/1.467943
• [21]   E. van Lenthe, A. Ehlers, E. J. Baerends, J. Chem. Phys., 110, 8943 (1999). doi:10.1063/1.478813
• [22]   W. Kohn, L. J. Sham, Phys. Rev., 140, A1133 (1965). doi:10.1103/PhysRev.140.A1133
• [23]   S. K. Wolff, T. Ziegler, J. Chem. Phys., 109, 895 (1998). doi:10.1063/1.476630
• [24]   S. K. Wolff, T. Ziegler, E. van Lenthe, E. J. Baerends, J. Chem. Phys., 110, 7689 (1999). doi:10.1063/1.478680
• [25]   S. Komorovsky, P. J. Cherry, M. Repisky, J. Chem. Phys., 151, 184111 (2019). , doi:10.1063/1.5121713 PMID:31731859
• [26]   R. J. F. Berger, M. Repisky, S. Komorovsky, Chem. Commun., 51, 13961 (2015). , doi:10.1039/C5CC05732A PMID:26243659
• [27]   J. Vícha, S. Komorovsky, M. Repisky, R. Marek, M. Straka, J. Chem. Theory Comput., 14, 3025 (2018). , doi:10.1021/acs.jctc.8b00144 PMID:29676906
• [28]   J. Vícha, J. Novotný, S. Komorovsky, M. Straka, M. Kaupp, R. Marek, Chem. Rev., 120, 7065 (2020). , doi:10.1021/acs.chemrev.9b00785 PMID:32574047
• [29]   A. M. Kuznetsov, A. N. Masliy, G. V. Korshin, J. Mol. Model., 24, 193 (2018). , doi:10.1007/s00894-018-3726-4 PMID:29974247
• [30]   I. Persson, K. B. Nilsson, Inorg. Chem., 45, 7428 (2006). , doi:10.1021/ic060636c PMID:16933947
• [31]   H. Ohtaki, T. Radnai, Chem. Rev., 93, 1157 (1993). doi:10.1021/cr00019a014
• [32]   G. Johansson, Adv. Inorg. Chem., 39, 159 (1992). doi:10.1016/S0898-8838(08)60260-3
• [33]   P. D’Angelo, I. Persson, Inorg. Chem., 43, 3543 (2004). , doi:10.1021/ic030310t PMID:15154820
• [34]   I. Persson, M. Sandström, H. Yokoyama, Z. Naturforsch. A, 50, 21 (1995). doi:10.1515/zna-1995-0105
• [35]   I. Persson, L. Eriksson, P. Lindqvist-Reis, P. Persson, M. Sandström, Chem. Eur. J., 14, 6687 (2008). , doi:10.1002/chem.200800225 PMID:18563768
• [36]   P. Lindqvist-Reis, A. Muñoz-Páez, S. Díaz-Moreno, S. Pattanaik, I. Persson, M. Sandström, Inorg. Chem., 37, 6675 (1998). , doi:10.1021/ic980750y PMID:11670798
• [37]   J. Glaser, G. Johansson, Acta Chem. Scand. A, 36, 125 (1982). doi:10.3891/acta.chem.scand.36a-0125
• [38]   G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders, T. Ziegler, J. Comput. Chem., 22, 931 (2001). doi:10.1002/jcc.1056
• [39]   E. V. Lenthe, E. J. Baerends, J. Comput. Chem., 24, 1142 (2003). , doi:10.1002/jcc.10255 PMID:12759913
• [40]   J. D. Chai, M. Head-Gordon, J. Chem. Phys., 128, 084106 (2008). , doi:10.1063/1.2834918 PMID:18315032
• [41]   J. D. Chai, M. Head-Gordon, Phys. Chem. Chem. Phys., 10, 6615 (2008). , doi:10.1039/b810189b PMID:18989472
• [42]   J. Autschbach, ChemPhysChem, 10, 2274 (2009). , doi:10.1002/cphc.200900271 PMID:19670399
• [43]   C. C. Pye, T. Ziegler, Theor. Chem. Acc. 101, 396 (1999). doi:10.1007/s002140050457
• [44]   G. Schreckenbach, T. Ziegler, J. Phys. Chem., 99, 606 (1995). doi:10.1021/j100002a024
• [45]   M. Krykunov, T. Ziegler, E. van Lenthe, Int. J. Quantum Chem., 109, 1676 (2009). doi:10.1002/qua.21985
• [46]   A. D. Becke, Phys. Rev. A, 38, 3098 (1988). doi:10.1103/PhysRevA.38.3098
• [47]   J. P. Perdew, Phys. Rev. B, 33, 8822 (1986). , doi:10.1103/PhysRevB.33.8822 PMID:9938299
• [48]   A. D. Becke, J. Chem. Phys., 98, 5648 (1993). doi:10.1063/1.464913
• [49]   C. Lee, W. Yang, R. G. Parr, Phys. Rev. B, 37, 785 (1988). , doi:10.1103/PhysRevB.37.785 PMID:9944570
• [50]   P. J. Stephens, F. J. Devlin, C. F. Chabalowski, M. J. Frisch, J. Phys. Chem., 98, 11623 (1994). doi:10.1021/j100096a001
• [51]   J. P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett., 77, 3865 (1996). , doi:10.1103/PhysRevLett.77.3865 PMID:10062328
• [52]   T. W. Keal, D. J. Tozer, J. Chem. Phys., 119, 3015 (2003). doi:10.1063/1.1590634
• [53]   M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina, V. G. Malkin, J. Chem. Phys., 152, 184101 (2020). , doi:10.1063/5.0005094 PMID:32414255
• [54]   F. Jensen, J. Chem. Phys., 115, 9113 (2001). doi:10.1063/1.1413524
• [55]   K. G. Dyall, Theor. Chem. Acc., 129, 603 (2011). doi:10.1007/s00214-011-0906-z
• [56]   K. G. Dyall, Theor. Chem. Acc., 108, 365 (2002). doi:10.1007/s00214-002-0396-0
• [57]   K. G. Dyall, Theor. Chem. Acc., 115, 441 (2006). doi:10.1007/s00214-006-0126-0
• [58]   GaussView, Version 6.1, R. Dennington, Todd A. Keith, John M. Millam, Semichem Inc., Shawnee Mission, KS, (2016).
• [59]   P. G. Harrison, M. A. Healy, A. T. Steel, J. Chem. Soc., Dalton Trans., 1845 (1983). doi:10.1039/DT9830001845
• [60]   G. Schreckenbach, Theor. Chem. Acc., 108, 246 (2002). doi:10.1007/s00214-002-0379-1
• [61]   M. Kaupp, O. L. Malkina, V. G. Malkin, P. Pyykkö, Chem. Eur. J., 4, 118 (1998).