On the Proposed Triangle Test Used as a Preference Test

1. 緒言

同一のサンプルAを2つと1つの異なるサンプルBをパネリストに示し, 3つのうち異なったものをひとつ指摘させることによって識別の可能性を調べる, いわゆる3点識別テストは食品官能検査においてしばしば用いられる. テストに当ってはサンプルAとBは識別できないという帰無仮説H₀をおいて, この結果としてパネリスト中A2個のうちひとつを選ぶものの数, Bを選ぶものの期待値はそれぞれ全体の2/3, 1/3になるとして, AB間の識別は有意に可能であるという対立仮説H₁に対して検定を行う. パネリストは2点識別よりも集中を要求されるためにより信頼性のあるデータがとれる可能性もあると考えられている. （これについては本論文とは別のところで考えることにする.）

さて, このような 3点識別テストが嗜好テストに先立って行われ, 3点識別テスト直後に更にパネリストに対して2種のサンプルの間の好みの差を問ういわゆる3点嗜好テストも亦しばしば行われる. ここで嗜好テストとは片方のサンプルがもう一つのサンプルより有意に好まれるかどうかを調べることが目的であるとしよう.

識別テストを行った後に嗜好テストを行うことについては一方には心理的要因も含めていくつかの理由から批判がある[たとえばStone and Sidel]. しかし実際にはそれにも係わらずこれは広く行われている. 実際, 官能検査のテキストブックとしてしばしば参考にされる佐藤（統計的官能検査法, 1985）, 日科技連官能検査委員会編（新版官能検査ハンドブック, 1973）にもここに述べた「3点嗜好試験」についての記述がある.これらのテキストブックは良く読まれているために, 国内の論文についてテキストブックの記述を間違って適用しているものが散見されるので注意を喚起したい.

たとえば佐藤（統計的官能検査法）p.97には「毛糸AとBの手ざわりに対する好みを比較するためにN=288人に対して3点嗜好法を実施したところ, 210人が正しく奇数試料を指摘し, その正答者のうちa=110人がAを好み, b=100人がBを好むと答えた. A, B間に（好みに）差があると言えるか.」という例題8.2がある. （変数名はあとの議論のわかりやすさのために変えてある.）

これを解析するのに著者はまず識別は有意であるかの二項検定を行い, 危険率5%で識別はされるという結論を得る. 次に同じ仮説H₀のもとでさらに「好みに差がない」という帰無仮説H₀'をたて, 好みに有意に差があるという対立仮説H₁'に対して検定を行っている.

仮説H₀のもと, 前段の識別テストでたまたま正答する確率は1/3, そこでたまたま正答してAを選ぶ者, たまたま正答してBを選ぶ者の数の期待値はそれぞれ全パネリストの1/6と考えて検定を行う. 例題で言うと仮説H₀のもとで正答の予想は288/3=96, 誤答の予想は192. そこでたまたまAまたはBを選ぶ者の数は48となる. そこで

  

よって統計量

  

を取るとこれは自由度2の分布に従うから

X²=62²/48+52²/48+114²/192=204.1 p.98（8.3）

これは（ν=2, 0.1%）=13.816より大であるから帰無仮説H₀'は捨てられ, 好みには差があると結論している. （これと同じ記述は日科技連官能検査委員会編, 新版官能検査ハンドブックp.253にもある.）

しかし識別テストに正答したパネリスト中, Aを好むと答えたものの数, Bを好むと答えたものの数の期待値が全パネリストの1/6になるためには仮説H₀'が成立するのみならず仮説H₀も成立たなければならないことは明らかである. すなわち識別ができなかったと仮定した場合だけである. すなわち2段目のテストの検定で棄却される仮説はあくまでも識別ができないというH₀と, 好みに差がないというH₀'の積である. だからこれが棄却されてもすぐAとBの間に好みの差があるという結論を導くことはできない. このことはたとえば上の例題で仮に正答且つAを好むもの, 正答且つBを好むものがそれぞれ105人であったとしてもX²=203.1で帰無仮説が捨てられる事から明らかである.

2. いくつかのこころみ

この小論の主旨は上に引用したテキストブックに従って解析を行い, 嗜好に関して間違った結論―すなわち2つのサンプル間に好みに差があったという―を導いている論文が散見されるのに対して警告を行うことにあるが, では仮に上の例のようなデータが既にあったときにAとBの間に好みの差があるかを検定するにはどうすればよいのかを単純に数学的な手続として考えてみよう. これには方法は色々考えられると思われるが, ここでは筆者の考えた3つの方法について述べてみたい.

N人中区別できない人の出現率を今pとおく. 3点識別法というテストの性格によって, 区別できない人のうちで, 1/3はたまたま正答し, 2/3は誤答することが期待される. よってこれらの出現率は各々p/3, 2p/3である. （図参照）

  

区別できる人はすべて正答すると考えて良い. よって今, 誤答する人の出現率eは2p/3である.

出現率がp/3であった区別できないがたまたま正答した人は, 区別できないという特性から, その半分, a'=p/6はAを好むと答え, 同じくb'=p/6はBを好むと答えることが当然期待される.

我々の実際の興味の対象である出現率が1-pの区別できる人の好みはAとBに分かれている. 今このうちで割合qの人がAを好み, 割合1-qの人がBを好むとしよう. qこそが我々の知りたい量である. よって区別できてAを好む人の出現率aはa=q（1-p）で, また区別できてBを好む人の出現率bはb=（1-q）（1-p)であらわされる.

正答してAを好むとした人は, 区別できてAを好むとした人（出現率a）と, たまたま正答してAを選んだ人（出現率a'）の和であり, その出現率を〈a〉と書くと, これは

〈a〉=a+a'=p/6+q(1-p), （1）

同じように正答してBを好むとした人の出現率〈b〉は

〈b〉=b+b'=p/6+(1-q)(1-p). （2）

となる.

2. 1 尤度比による検定

これらの人数の分布が三項分布に従うと考えると, A, BはそれぞれN〈a〉, N〈b〉の出現値であることに注意すれば, その確立分布から尤度は

  

で与えられる. これを最大にするp, qを知るためにこの対数をとり, 連立方程式

  

  

を解いてp, qの最尤値       ,       が

  

のように求められる. この結果はほぼ予想通りであろう. 以上を用いて尤度比検定を行う. H₀のもとではq=1/2であるから, 統計量

  

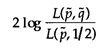を考えるとこれがH₀のもとでは自由度1のΧ²-分布に従うと考えられる. pとqすなわちパネルの中に区別できない人がどれくらいいるか, とABのいずれが好まれるかは全く独立と考えている.

佐藤（統計的官能検査法）の具体例にこの方法を適用してみよう. A, B, Eの実現値それぞれ 110, 100, 78を（3）に代入して計算するとこの量は0.4764となる. P(Χ²＞0.4764, ν=1) = 0.490であるから. H₀は棄却できないという結論を得る. （Z₀=0.690に相当）

2. 2　適合度検定

この方法においては積極的にこの問題の誤差である, 区別できないがたまたま正答した人数を評価することを試みる.

一般にN人中出現率rの人があるグループに属するとき, その人数の期待値はrNである. その人数の実現値Rからrを推定すると

  

また標本出現率       の分散（統計量）とその推定値は

  

で与えられるということを用いる.

N人中誤答者の実現値をEとしたとき, 誤答者の出現率eの推定値êは（4）より

  

で与えられる. 区別できる人はすべて正答すると考えて良いので, 誤答する人の出現率は前節に述べたことから

e=2p/3　（7）

である.

出現率p/3の区別できないがたまたま正答してAをえらんだ人, 区別できないがたまたま正答してBをえらんだ人の実現値は知られていないが, 仮に分ったとするとその標本出現率の分散σ_chan²とその推定値はともに（5）より

  

で与えられるはずである.

ちなみに区別できない人全体の標本出現率の分散は同じ考え方から

  

である. （これはあとで使う）

前節で述べたように, 正答してAを好むとした人は, 出現率aの区別できてAを好むとした人と, 出現率p/6の区別できないがたまたま正答してAを好むとした人の和である. すなわち

a=〈a〉－a'=〈a〉－p/6　（9）

さらに（7）から

a=〈a〉－e/4　（10）

であり, この推定値は

  

で与えられる.

さて（10）の関係, あるいは（11）を用いて区別できてAを好む人数を推定した時, これに伴う誤差を考えてみよう. 区別できる能力とA, Bに対する好みはこのモデルでは独立と考えるので, 区別できてAを好むとした人の標本出現率の分散σ_u²は, 正答してAを好むとした人全体の標本出現率の分散σ_〈n〉²と, 区別できないがたまたま正答してAを好むとした人の標本出現率の分散σ_chan²の和であると考えられる. すなわち

σ_â²=σ_〈u〉²+σ_chan²　（12）

（5）より

  

これと（8）より

  

同様に区別できてBを好むとした人の出現率b=〈b〉-e/4の推定値       は, Bを好むとした人の実現値がBならば（11）と同様に(B-E/4)/Nである. さらにその標本出現率の分散σ_B²も（14）と同様に

  

で与えられる.

H₀：a=bのもとではa=bの期待値は

  

となる. ここでeは分っていないのでその実現値E/Nで近似した. また, このとき〈a〉=〈b〉=(1－e)/2である. そこで推定出現率を (1－E / N)/2とすると, このときの区別できないがたまたま正答してAまたはBを好むとした人の標本出現率の分散は次式で与えられる.

  

よって正答してAまたはBを好むとした人の標本出現率の分散は

  

で与えられる.

全体N人中区別できてAを好むとした人の出現率aの推定値は(A-E/4)/Nであり, 同じく区別できてBを好むとした人の出現率bの推定値は(B-E/4)/Nである. H₀のもとではa=bの期待値は1/2-3E/4N, 標本出現率の分散は

  

であることが分った. これを用いて近似的に正規分布を仮定して

  

なる統計量がΧ²-分布に従うとしてH₀：好みに差がない, H₁：好みに有意の差ありということでΧ²検定を行う. このモデルにおいては, 全数がNという条件の他にeの実現値E/Nを計算に用いている. それ故, 上の統計量の従うΧ²-分布の自由度は1であると考えられる.

  

このモデルは多項, すなわち色々なカテゴリーのパネルのうち, 区別できてAを選んだ人, 同じく区別できてBを選んだ人の2項を抜出して適合度検定を試みたものである. その場合, 各項の人数の分散の評価に関する誤差は高次のものと思われるが, 実際にカテゴリーに属する人と, H₀が成立つときの人の数の差の評価にはeの実現値E/Nを用いている. それともう一つ指摘すべき事としては, 区別できないがたまたま正答してAを好むとした人に関する誤差σ_chan²と区別できないがたまたま正答してBを好むとした人に関する誤差σ_chan²とから2σ_chan²がでてきているが, これには少々議論が必要に思われる. 統計学的に考えてpがまず決っているとすれば, この2つの誤差が独立で2σ_chan²というのは正しい. 一方でいま決っているのはEであって, その解析には色々なpの場合が考慮されるべきであると考えると, その各々のpの場合についてもやはりa'とb'の独立性は言えるが, これらの寄与をすべて重ねるとすると, pが大きいとa'もb'も小さく, 逆にpが小さいとa'もb'も大きくなりその結果としてa'とb'には見かけの相関がでてくる. この考え方が正しいかどうかはもう少し議論が必要であるが, これに基づいて筆者が上に与えられた例について当ってみるとこの寄与はそれほど大きくはないがある程度2σ_chan²に当る項を小さくする. つまりH₀の棄却を助ける方向に働く事が分った.

2. 3　区別できない人の予測値を用いる方法

前節末に記した, このデータでは, Eは決っているが, 解析には色々なpの場合が考慮されるべきであるという考え方を押し進める. このテストの性格からして, N人中区別できない人の割合がpなら, 区別できなくて誤答する人の割合は2p/3である. では区別できなくて誤答する人の実現値がEなら, 区別できない人全体の人数はいくらか.

この人数Pの分布は

P(P)=_PC_E(2/3)^E-1(1/3)^P-E

=P_{NegativeBinomial Distribution}(P－E;E+1, 2/3)　（21）

なる負の二項分布に従うことが容易に示せる.

P人が区別できず, そのうちE人は誤答し, P-E人は正答する. 正答する人を確率1/2で分割する. Aを好むとする人数n_a'の分布は

P_Binomial (n_a' ;P－E, 1/2)

なる二項分布に従う.

区別できた人の予想値はN-Pである. これがq対1-qに分割されることになる. そこで区別できてAを好む人数n_aの分布は

P_Binomial(n_a;N－P, q)

に従う. 従って区別できない人がP人の時, 正答してAを選ぶ人がA人になる確率は

  

で与えられる. ここで仮定からこのとき区別できてBを選ぶ人の数はN-A-Eである.

Eから予想されるPは色々の値があって上述の分布をするので. 実際のAの分布は

  

で与えられることが分る. この総和は実際に直接計算できる.

さて, いまq=1/2というH₀を導入しよう. H₁はq≠1/2とする. すると（23）式は

dist(A)=P_Binomial(A;N－E, 1/2)　（24）

に簡単化されてしまう. これは少々気持が悪いが, はじめからN人から誤答するE人を除いて残りを出現率1/2で区別できてAを選ぶ人, Bを選ぶ人に2分したのと同じだという事である. そこで実例としてA, B, Eの実現値それぞれ110, 100, 78をとって計算する.

  

を計算すると0.5347となる. また正規分布で近似すれば

  

A=109.5とするとP(|z₀|＞0.621)=0.535でいずれにしてもH₀は棄却できない.

3. 考察

以上3つの異なった方法でこの問題を扱ってみた. いずれにしても結論はこの例においてはH₀は棄却できないことになるが, 棄却できない割合については大まかに一致しているものの少しの差がある.

1の方法　Z₀=0.690

2の方法　Z₀=0.767

3の方法　Z₀=0.621

議論の問題の少なさという点から言うと1の方法が一番すっきりしている. しかし人によっては尤度比というものが本当に仮説の検定に使えるかどうかと言う点で疑問を感ずるかもしれない. その点で2の方法が一番この問題の構造に立入って評価をしていると思われる. 具体例に対応するz₀の値にしても一番大きくなっている. ただその節の最後に記したような問題点が指摘できる.

3の方法は 2の方法の中で色々なpの場合が考慮されるべきであるという問題に対処するために具体的なモデルとして扱ったものであるが, q≠1/2というH₁に対しq=1/2というH₀を導入すると, 結果としてはじめから全数をN-Eとし, 確率を1/2とした二項分布になってしまい, これが我々が行おうとしている検定に相当しているのかどうかちょっと心配になる. 具体例に対応するz₀の値にしても3つの方法の中で一番小さくなっている.

この問題の面白いところは次の点にある. 識別試験で誤答をした人を全部除いてしまって正答者のみで統計を取ると言うしばしば行われる手法を使うと, そこには区別できなかったがたまたまA, またはたまたまBを選んでしまった人の数が単純に誤差として入ってきてしまう. せっかくテストを行ったのに識別試験で誤答した人からのデータを捨ててしまうのは勿体ないと思われる所から色々な改良案が提案された [たとえばJ. G. Davis and H. L. Hanson, N. T. Gridgemanなど]. しかしこれらの改良案においては3点嗜好法の大きい長所であるサンプルの違いの内容をパネルに明示しないで行えると言う利点を放棄しなければならず, また結果の処理についても加重をかけてデータ処理を行う等煩雑になると言う難点がある. しかし考えてみると, 誤答者を含む区別できなかった人には, 区別できなかったというところから規定される一定の構造があって, その情報は誤答者数という形で現れていて, この情報をうまく使えばしばしば行われる手法の場合より, 時によってはずっと多くの情報量を統計的手段によって引出すことができる可能性があるということである. 筆者はこれを扱うのに本稿中で3つの方法を試みた.

以上の手続は識別テストの結果と嗜好テストの結果が互いに独立と考えて問題を機械的に扱ったが, 統計学的見地から見てもこれは疑問なしとしない.

また, テストを計画する段階においては, 緒言中で述べたように, 識別テストを行った後に嗜好テストを行うことについては批判があることを考慮に入れることが必要であると思われる.

本文の作成に当り, 京都産業大学理学部 辻井芳樹教授に色々と有益な示唆を頂いた. 篤く感謝したい.

引用文献

• J.G.Davis and H. L. Hanson(1954): Sensory test methods. I. The triangle intensity (T-1) and related test systems for sensory analysis. Food Technol., 8, 335-339 .
• N. T. Gridgeman(1970): A reexamination of the two-stage triangle test for the perception of sensory differences. J. Food Sci., 35, 87-91.
• 日科技連官能検査委員会編（1973）：新版官能検査ハンドブック, p. 252-253, 日科技連出版社,
• 佐藤信（1985）：統計的官能検査法, pp. 93-100, 日科技連出版社.
• H. Stone and J. L. Sidel(1985): Sensory evaluation practices, p. 188, Academic Press.