Particle Filtering and Gaussian Mixtures – On a Localized Mixture Coefficients Particle Filter (LMCPF) for Global NWP

Abstract

In a global numerical weather prediction (NWP) modeling framework we study the implementation of Gaussian uncertainty of individual particles into the assimilation step of a localized adaptive particle filter (LAPF). We obtain a local representation of the prior distribution as a mixture of basis functions. In the assimilation step, the filter calculates the individual weight coefficients and new particle locations. It can be viewed as a combination of the LAPF and a localized version of a Gaussian mixture filter, i.e., a “Localized Mixture Coefficients Particle Filter (LMCPF)”.

Here, we investigate the feasibility of the LMCPF within a global operational framework and evaluate the relationship between prior and posterior distributions and observations. Our simulations are carried out in a standard pre-operational experimental set-up with the full global observing system, 52 km global resolution and 10⁶ model variables. Statistics of particle movement in the assimilation step are calculated. The mixture approach is able to deal with the discrepancy between prior distributions and observation location in a real-world framework and to pull the particles towards the observations in a much better way than the pure LAPF. This shows that using Gaussian uncertainty can be an important tool to improve the analysis and forecast quality in a particle filter framework.

1. Introduction

Let us consider a state space ℝⁿ of dimension n ∈ ℕ, an observation space ℝ^m of dimension m ∈ ℕ and a sequence of observations y_k ∈ ℝ^m at points in time t_k for time index k = 1, 2, 3, …. Based on a prior distribution , at time t_k, the task of Bayesian data assimilation is to calculate a posterior probability distribution at time t_k. States and observations are linked by the equation   

with the true state vector at time t _k, some observation error ∈_k and the observation operator H : ℝⁿ → ℝ^m. Usually, the prior is estimated from earlier analysis steps, from which the distribution is propagated through time to some recent analysis time t_k based on some numerical model M.

The approximation of a general prior distribution by an ensemble of states, also known as a set of particles, has a long tradition in mathematical stochastics, see for example Bain and Crisan (2009). It is also well-known, that sampling as usually carried out by Markov Chain Monte Carlo (MCMC) methods (Anderson and Anderson 1999; Bain and Crisan 2009; Crisan and Rozovskii 2011) works well in low dimensions, but when we sample in a high-dimensional space (where high usually refers to dimensions above n = 5), the methods basically collapse, since the number of necessary samples to find some probability different from zero grows exponentially with the dimension (van Leeuwen 2010; Snyder et al. 2008, 2015; Bickel et al. 2008). Alternative methods based on particular approximations of the prior and posterior have been developed, with the Ensemble Kalman Filter (EnKF) (Evensen 1994, 2009; Evensen and van Leeuwen 2000) and the Local Ensemble Transform Kalman Filter (LETKF) by Hunt et al. (2007) as important and widely used methods for high-dimensional filtering. These methods, however, rely on the approximation of the prior by a Gaussian, which is a strong limitation when applied to highly non-linear dynamical systems as either global or high-resolution Numerical Weather Prediction (NWP).

Different routes to carry out non-Gaussian assimilation have been taken by the filtering community for example with Gaussian mixtures (Anderson and Anderson 1999), locally applied Gaussian mixtures (Bengtsson et al. 2003) or by the development of particular filters such as the GIGG filter of Bishop (2016). For an overview of different ensemble-based data assimilation methods, we refer to Vetra-Carvalho et al. (2018) and van Leeuwen et al. (2019). An alternative route has been chosen by the 4D-VAR community with an ensemble of 4D-VARs based on perturbed observations, compare Klinker et al. (2000).

Over the past years particle filters have become mature enough to be used for very-high-dimensional non-Gaussian filtering, compare van Leeuwen (2009, 2015); Farchi and Bocquet (2018) and van Leeuwen et al. (2019) for recent reviews. Localization for particle filters is used by Reich and Cotter (2015); Poterjoy and Anderson (2016); Penny and Miyoshi (2016) and Potthast et al. (2019). Instead of the localization Kawabata and Ueno (2020) have used an adaptive observation error estimator to avoid the filter collapse in a regional mesoscale model. Particle filters have been successfully used for full-scale NWP systems. In particular, in Poterjoy et al. (2017) a localized particle filter has been studied for a regional NWP model over the US. The team Frei and Künsch (2013) developed a hybrid Ensemble Kalman Particle Filter which Robert et al. (2017) has tested for the regional COSMO NWP model. The Localized Adaptive Particle Filter (LAPF) described in Potthast et al. (2019) has been tested for the global ICON NWP model. The LAPF (Potthast et al. 2019) has shown to provide reasonable assimilation results for an global atmospheric data assimilation for the ICON model in quasi-operational setup. It has been successfully run for a month of assimilations with 10⁶ degrees of freedom (52 km global resolution) and shows a stable behavior synchronizing the system with reality.

Here, our starting point is the investigation of the behavior of the LAPF with respect to errors in the prior distribution . By studying the statistics of the observations vector mapped into ensemble space, we will show that in many cases the model forecasts show significant distance to the observations, and the particle filter based on a limited number of delta distributions does not pull the particles close enough to the observations when the move of particles is only achieved through adaptive resampling.

To allow individual particles to move towards the observations, we further develop the LAPF by bringing ideas from Gaussian mixtures into its framework. We reach this goal by including model and forecast uncertainty for each particle, as for example suggested by the Low-Rank Kernel Particle Kalman Filter (LRKPKF) of Hoteit et al. (2008), compare also Liu et al. (2016a) and Liu et al. (2016b). The basic idea is to consider each particle to be a Gaussian where its width is representing its uncertainty. This means we study a prior distribution given by a Gaussian (or more general radial basis function RBF) mixture. Then, the prior has the form   

with constants for the individual Gaussian basis functions with mean x^(b,ℓ) and covariance G and a normalization constant c, which in this case is given by c = 1/L. For this approximation, and when the observation operator H is linear, we can explicitly calculate the posterior distribution as a corresponding Gaussian mixture, i.e.,   

with some matrix [calculated e.g., in Chapter 5.4 of Nakamura and Potthast (2015)], constants w_ℓ given by   

with as explicitly calculated by Eq. (40) in Schenk et al. (2022), with temporary analysis states , with   

and with the components   

The constant will normalize the integral of p^(a) to one, but not individual terms q^{(a, ℓ)} given by (1.5). If there are no further constraints to the variables, the ℓ-th posterior particle can be directly drawn with relative probability w_ℓ from the distribution component q^{(a, ℓ)}(x) leading to an analysis ensemble member x^{(a, ℓ)}. This drawing process is carried out based on localization, adaptivity and the transformation into ensemble space as developed for the LAPF (Potthast et al. 2019); details will be described in Sections 2.1 and 2.2. As for other particle filters, the posterior particles will be calculated by an ensemble transform matrix, with details worked out in Section 2.2. For each posterior ensemble member, based on the prior Gaussian mixture, this matrix defines transformation coefficients arising from the weights of each particle. The name Local Mixture Coefficients Particle Filter (LMCPF) has been used to distinguish from other localized particle filter methods. For example, Reich and Cotter (2015) present Localized Particle Filter (LPF) versions, which include sophisticated optimal transport properties. A further LPF method is introduced by Penny and Miyoshi (2016) and the LAPF (already implemented at the German Weather Service in 2014¹) is presented by Potthast et al. (2019). We note that the choice for G of formula (1.2) as a scaled version of the ensemble correlation matrix of Hunt et al. (2007), i.e., , resembles the choices made for the LETKF (Hunt et al. 2007) and leads to very efficient code.

We will investigate the usefulness of the Gaussian uncertainty within the particle filter in very high-dimensional systems, leading to moves or shifts of the particles towards the observations. Statistics of these shifts will be shown, demonstrating that for this global atmospheric NWP system the uncertainty plays an important role. Further, our numerical results show that the LMCPF is a particle filter with a quality comparable to the LETKF for state-of-the-art real-world operational global atmospheric NWP forecasting systems. This will be demonstrated by numerical experiments based on an implementation of the particle filter in the operational data assimilation software suite DACE² of Deutscher Wetterdienst (DWD).

The LMCPF is introduced in Section 2, where we first summarize the ingredients we build on in Section 2.1. Then, an elementary Gaussian filtering step in ensemble space is described in Section 2.2. Finally, the full LMCPF method is presented in Section 2.3. We describe the high-dimensional experimental environment for our development and evaluation framework for numerical tests in Section 3. The numerical results for the global weather forecasting model ICON are shown in Section 4. We study the statistics of the relationship of observations and the ensemble as well as the corresponding statistics of the shift vectors of the Gaussian particles of the LMCPF. We show the large improvements with respect to standard NWP scores which the LMCPF can achieve compared to the LAPF. Additionally, we present case studies comparing the LMCPF forecast scores to the operational LETKF.

2. Localized Mixture Coefficients Particle Filter (LMCPF)

The basic idea of a Bayesian assimilation step is to calculate a posterior distribution p^(a) (x) for a state x ∈ ℝⁿ based on a prior distribution p^(b) (x) for x ∈ ℝⁿ, some measurement y ∈ ℝ^m and a distribution of the measurement error p (y | x) of y given the state x. The famous Bayes formula calculates   

with normalization constant c such that .

Our setup for data assimilation is to employ an ensemble {x^(b,ℓ) ∈ ℝⁿ, ℓ = 1, …, L} of states, which are used to estimate or approximate p^(b) (x). The basic analysis step of data assimilation is to construct an analysis ensemble {x^(a,ℓ) ∈ ℝⁿ, ℓ = 1, …, L} of analysis states, which approximate p^(a) (x) in a way consistent with the approximation of p^(b) (x) by x^(b,ℓ), ℓ = 1, …, L. The above idea is common to both the Ensemble Kalman Filter (EnKF) and to particle filters. We employ the notation   

for the matrix of ensemble differences to the ensemble mean x̄ defined by   

For the ensemble differences in observation space we employ   

with the mean ȳ defined by   

and   

From now on we will use X for X^(b) and Y for Y^(b) for brevity. In the case of a linear observation operator we have ȳ = H x̄ and Y = HX. Usually, for EnKFs, the approximation of the covariance matrix is chosen to be based on the estimator   

The estimator B can also be written as . Usually, in this case the prior is approximated by   

with B⁻¹ well defined³ for all x = x̄ + Xβ with some vector β ∈ ℝ^L. The normalization constant c_B can be calculated based on a matrix which consists of an orthonormal basis of N (X)^⊥ ⊃ ℝ^L of dimension 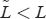by   

where det (Φ^TX^TXΦ) is the Gramian of the injective mapping , i.e., the determinant of the Gram matrix Φ^TX^TXΦ. The approximation of the classical particle filter is   

with the delta distribution δ(·) and a normalization constant c = 1/L. A well-known idea is to employ Gaussian mixtures [c.f. Hoteit et al. (2008); Liu et al. (2016a, b)], i.e., use the approximation   

where G_ℓ ∈ ℝ^n×n is some symmetric and positive definite matrix which describes the uncertainty of the individual particle, is a normalization constant for each of the Gaussians under consideration and c is an overall normalization constant.

• • The matrix G_ℓ is the covariance of each Gaussian and can be seen as a measure for the short-range forecast error consisting of model error and some of the uncertainty in the initial conditions beyond the distribution of the ensemble of particles itself. We will discuss the important role of G_ℓ in several places later, when we describe the LMCPF and its numerical realization. In particular, we will investigate the situation where G_ℓ is a multiple of the covariance matrix B defined above.
• • The Gaussian mixture filter can be seen as a generalization of the classical particle filter, where instead of a delta distribution a Gaussian around each prior particle is employed to calculate the posterior distribution and draw from it. Here, we will employ localization and adaptivity as developed for the LAPF in combination with the mixture concept within the LMCPF.

2.1 The localized adaptive particle filtering ingredients and preparations

The goal of this section is to collect, prepare and summarize all components employed for the LMCPF. For the following derivation we assume linearity of H, we will discuss the form of the equations in the case of non-linear H later. Then, we have Y^T = X^TH^T and with the standard estimator for the covariance matrix is given by B = γXX^T. We will later use B as measure of uncertainty of individual particles, then using the scaling   

with a parameter κ > 0 scaling the standard covariance matrix. Following standard arguments as in Hunt et al. (2007); Nakamura and Potthast (2015) or Potthast et al. (2019), this leads to the Kalman gain   

with invertible observation error covariance matrix R ∈ ℝ^m×m We note that we have   

by elementary calculations. We also note that I + γ Y^TR⁻¹ Y is invertible on ℝ^L and R + γ Y Y^T is invertible on ℝ^m by assumption on the invertibility of R. Then, multiplying (2.14) by (I + γ Y^TR⁻¹ Y)⁻¹ from the left and by (R + γ Y Y^T)⁻¹ from the right we obtain   

Now, (2.15) can be used to transform (2.13) into   

This can be used to calculate the covariance update step of the Kalman filter in ensemble space as follows. We derive   

For collecting the formulas we now move back to using X^(b) for X. The analysis ensemble X^(a) which generates the correct posterior covariance by B^(a) = γX^(a)(X^(a))^T is given by   

where the matrix I + γY^TR−¹ Y ∈ ℝ^L×L lives in ensemble space, it is symmetric and invertible by construction, for all γ > 0.

The localized ensemble transform Kalman filter (LETKF) following Hunt et al. (2007) based on the square root filter for calculating the analysis ensemble can be written as   

with   

and   

with   

The above equations are carried out at each analysis grid point where the matrix R is localized by multiplication of each entry with a localization function depending on the distance of the variable to the analysis grid point Hunt et al. (2007). Using   

the full update of the LETKF ensemble can be written as   

where we define the sum of a vector (here x̄^(b) or γX^(b)w) plus a matrix (here X ^(b)W) by adding the vector to each column of the matrix.

For non-linear observation operator H as in (18) of Hunt et al. (2007) the operator K is defined by the last line of (2.13), see also (2.16) and the ensemble transform by (2.21) with W by (2.22). This basically corresponds to an approximate linearization of H in observation space based on the differences y^(b,ℓ)−ȳ

2.2 An elementary Gaussian filtering step in ensemble space

Let us consider a Bayesian assimilation step (2.1) based on the approximation of the prior p^(b) (x) as a Gaussian mixture (2.11). We first describe the steps in general, then derive the ensemble space version of he equations. To each particle, we attribute a distribution with covariance G, i.e., we define   

which is normalized according to Eqs. (4.5.28) of Nakamura and Potthast (2015). Then, the full prior is a Gaussian mixture.   

with (i.e., we choose the variance uniform for all ℓ) and with some normalization constant in this case. Bayes formula leads to the posterior distribution   

x ∈ ℝⁿ, with a normalization constant , here different from the normalization constant in (2.26). We note that the terms in round brackets constitute individual Gaussian assimilation steps. In the case where H is linear or approximated by its linearization H, the posterior of each of these terms can be explicitly calculated the same way as for the Ensemble Kalman Filter. Following Nakamura and Potthast (2015), Section 5.4, we define   

and   

Then, we know that   

with constants w_ℓ given by (1.4). Since c_ℓ does not depend on ℓ, the constants are irrelevant for the resampling step and will be removed by the normalization step. Note that the constants w_ℓ, ℓ = 1, …, L, are extremely important, since they contain the relative weights of the individual posterior particles with respect to each other. They should not be ignored! Here, we first describe the full posterior distribution, which is now given by   

In the case of the classical particle filter, the Gaussians become δ-distributions c_ℓδ [x − x^(b,ℓ)] with weights c_ℓ = 1. In this case, the individual posterior weights w_ℓ are given by the likelihood of observations   

This choice will also be a reasonable approximation in the case of small variance G of the Gaussians under consideration in comparison with the distance y − H [x^(b,ℓ)]. In the general Gaussian case, the weights can be calculated from (1.4). For our numerical experiments we use non-zero G with some positive variance, and tested both the exact weights (1.4) or approximate weights w_ℓ given by (2.32).

In Fig. 1 we show a comparison of the normalized approximative weights (2.32) as dashed lines and the normalized exact determined weights (1.4) as solid lines, for a selected point of the full NWP model described in Sections 3 and 4. Here, each ensemble member (L = 40) is described by a different color. For this plot we varied the parameter κ, described in (2.12), between 0 and 5. Figure 1 shows how the normalized approximative weights differ from the normalized exact weights. We have carried out experiments both with the exact and approximate weights, we found that overall the results with exact weights show a better performance.

Fig. 1.

We show a comparison between the normalized approximative weights calculated as in (2.32) versus the normalized exact calculated weights (1.4). The solid lines show the normalized exact determined weights and the dashed lines the normalized approximative weights. The colors vary for different ensemble members (L = 40). On the x-axis we show the value for κ of (2.12), on the y-axis the values of the weights.

Let us now describe the ensemble space transformation of the above equations. The ensemble space as a subset of the state space is spanned by X given in (2.2). Our ansatz for the model error covariance is γXX^T with some scaling factor γ. We note that for the LETKF, . Here, γ > 0 can be any real number. We will provide some estimates for what γ can be in a global NWP model setup in our numerical part in Section 4. In the transformed space this leads to the covariance γI ∈ ℝ^L×L to be used for the ensemble transform version of (2.27). Recall the ensemble transformation x − x̄ = Xβ, x^(ℓ) − x̄ = Xe_ℓ and x − x^(ℓ) = X (β − e_ℓ) for ℓ = 1, …, L, where e_ℓ is the standard unit vector with one in its ℓ-th component and zero otherwise leading to   

We note that X^T (XX^T)⁻¹X = I is true only on the subspace N(X)^⊥, but we can employ the arguments used to justify Eq. (15) of Hunt et al. (2007) to use the covariance γ⁻¹ I in ensemble space for the prior term. For the observation error term of (2.27) in ensemble space ℝ^L we use Eq. (11) of Potthast et al. (2019), i.e., we have   

with norming constant ĉ, for ℓ = 1,…, L, where P is the orthogonal projection onto span{Y} with respect to the scalar product in ℝ^m weighted by R⁻¹; it is defined in Eq. (10) of Potthast et al. (2019) and Lemma 3.2.3 of Nakamura and Potthast (2015) to be given by   

As in (13)–(15) of Potthast et al. (2019) the right-hand side of (2.34) can be transformed into   

with   

We now carry out (2.28) and (2.29) in ensemble space based on (2.13) and (2.14), leading to the new mean of the posterior distribution for the ℓ-th particle prior distribution   

and the new covariance matrix of this distribution   

independent of ℓ when G = γXX^T is independent of ℓ. This means that we obtain   

with β^(α,ℓ) given by (2.38) and given by (2.39) for the posterior distribution of the ℓ-th particle in ensemble space. We denote the term   

as the shift vector for the ℓ-th particle in ensemble space, i.e., in (2.38). The use of the model error γI corresponding to γXX^T for this particle in ensemble space leads to this shift in the analysis. The shift has important effects:

1. 1. it moves the particle towards the observation in ensemble space,
2. 2. by the use of particle uncertainty, it constitutes a further degree of freedom which can be used for tuning of a real system.

One of the major advantages and problems at the same time of the LAPF as well as a classical particle filter is that the particles are taken as they are. If the model has some local bias, i.e., if all particles have a similar behavior and do not fit the observation well, then there is no inherent tool in the classical particle filter or the basic LAPF to move the particles towards the observation - this move is only achieved by selection of the best particles, closest to the observation. By resampling and rejuvenation, effectively the whole ensemble is moved towards the observation. Here, with the introduction of uncertainty of individual particles into the assimilation step, this is already carried out for each individual particle by calculating a posterior mean β^(α,ℓ) in (2.38) of the posterior component q^{(a, ℓ)}(β) given by (2.40) for the model error prior distribution q^(b,ℓ) attributed to each particle (2.25).

2.3 Putting it all together: the full LMCPF

Here, we now collect all steps to describe the full LMCPF assimilation step and data assimilation cycle. The LMCPF assimilation cycle is run analogously to the LETKF or LAPF assimilation cycle, i.e., we start with some initial ensemble x ₀^(a,ℓ) at time t₀. Then, for time steps t_k, k = 1, 2, 3, … we

1. (1) carry out a propagation step, i.e., we run the model forward from time t _k−1 to t _k for each ensemble member, leading to the background ensemble x_k^(b,ℓ) at time t _k.
2. (2) Then, at each localization point ξ on a coarser analysis grid we carry out the localized ensemble transform (2.37), calculating C and A. Localization is carried out as for the LETKF and LAPF, i.e., the matrix R is weighted depending on the distance of each of its observations to the analysis point.
3. (3) We now carry out a classical resampling step following Section 3d of Potthast et al. (2019). This leads to a matrix   
   
   i, ℓ = 1,…,L, draw r_ℓ ~ U([0, 1]), set R_ℓ = ℓ − 1 + r_ℓ, with accumulated weights and ∈ R^L×L defined by (2.42) with entries one or zero reflecting the choice of particles. As for the LETKF and LAPF this is carried out at each localistion point ξ on a coarser analysis grid to ensure that the weight matrices only change on scales on the order of the localization length scale. Here, we use instead of for brevity.
4. (4) The posterior matrix given by (2.39) and the shift vectors β^(shift,ℓ) given by (2.41) for ℓ = 1, …, L are calculated for each localization point ξ. We define   
   

   Then, if we want the shift given by the ℓ th-particle, we obtain it by the product W^(shift)e_ℓ. If we have a selection matrix for which each column with index ζ, ζ = 1,…,L, contains some particle e_ℓ with ℓ = ℓ (ζ), which has been chosen to be the basis for the corresponding new particle, we obtain the shifts for these particles by the product . According to the analysis equation (2.38) the new coordinates in ensemble space are calculated by   

   

5. (5) For each particle we now carry out an adaptive Gaussian resampling or rejuvenation step. The rejuvenation is carried out the same way as described in Section 3e and 3f of Potthast et al. (2019), i.e., we first calculate   
   
   at each localization point, with the actual ensemble covariance matrix and with the observation minus background statistics d_o−b = y_k − ȳ_k where ȳ_k denotes the ensemble mean in observation space described in (2.5) at time t_k⁴ Then we scale ρ by some function   
   
   where the constants ρ⁽⁰⁾, ρ⁽¹⁾, c₀, and c₁ are tuning constants. We note that temporal smoothing is applied to ρ as usual for LETKF or LAPF. Let N ∈ ℝ^L×L be a matrix with entries drawn from a normal distribution, i.e., each entry is taken from a Gaussian distribution with mean zero and variance 1. This is chosen uniformly for all localization points ξ on the analysis grid . Then, the rejuvenation plus shift step is carried out by   
   

   Again, we note that and are functions of physical space with chosen from the analysis grid .

6. (6) The matrices W are calculated at each analysis point ξ on a coarser global analysis grid . We now interpolate the matrices onto the full model grid .
7. (7) Finally we calculate the analysis ensemble (2.23) by   
   

Comparing (2.48) with (2.24) we observe some similarities and some differences. The LETKF does not know the selection reflected by the matrix , instead it transforms the ensemble by its matrix W. Both know a shift term, for the LETKF it is given by w, for the LMCPF by , shifting each particle according to model error (here taken proportional to ensemble spread), where the LETKF shifts according to the full ensemble spread. The LMCPF also takes into account that part of the ensemble spread which is kept during the selection process. Further, it employs adaptive resampling around each remaining shifted particle. This helps to keep the filter stable and achieve an appropriate uncertainty described by o − b statistics.

3. Experimental Environment: the global ICON model

3.1 The ICON model

We have carried out experiments testing the LMCPF algorithm in the global ICON (ICOsahedral Nonhydrostatic) model, i.e., the operational global NWP model of DWD, compare Zängl et al. (2014) and Potthast et al. (2019) for further details on the systems. ICON is based on an unstructured grid of triangles generated by subdivision from an initial icosahedron. The operational resolution is 13 km for the deterministic run and 26 km for the ensembles both for the data assimilation cycle and the ensemble prediction system (EPS). The upper air prognostic variables such as wind, humidity, cloud water, cloud ice, temperature, snow and precipitation live on 90 terrain-following vertical model levels from the surface up to 75 km height. In the operational setup, we have 265 million grid points. We also note that there are further prognostic variables on the surface and on seven soil levels, in particular soil temperature and soil water content, as well as snow variables, sea ice fraction, ice thickness and ice surface temperature of ICON's integrated sea-ice model.

The data assimilation for the operational ensemble is carried out by an LETKF based on Hunt et al. (2007). We run a data assimilation cycle with an analysis every 3 hours. Forecasts are calculated based on the analysis for 00 UTC and 12 UTC, with 180 hours forecast lead time. For the operational system, forecasts with shorter lead times of 120 hours for 06 UTC and 18 UTC and 30 hours for 03, 09, 15 and 21 UTC are calculated. The ensemble data assimilation cycle is run with L = 40 members.

For the experimental setup of our study, we employ a slightly lower horizontal resolution of 52 km for the ensemble and 26 km for the deterministic run (in the operational setup a part of the observations quality control is carried out within the framework of the deterministic run, we keep this feature for our particle filter experiments). An incremental analysis update with a window of t ∈ [−90 min, 90 min] around the analysis time for starting the model runs is used. The analysis is carried out for temperature, humidity and two horizontal wind components, i.e., for four prognostic variables per grid point. This leads to n = 6.6 ·. 10⁶ free variables at each ensemble data assimilation step. Forecasts are only carried out for 00 UTC and 12 UTC. We employ L = 40 members for the experimental runs as well.

3.2 Comparison in an operational framework

For testing and developing algorithms in the operational framework, the tuning of basic algorithmic constants is a crucial part. The task of testing in a real-world operational setup is much more intricate than for what is usually done when algorithms are compared in a simulation-only small-scale environment. In particular for new algorithms, the whole model plus assimilation cycled NWP system needs a retuning and it is difficult to compare one algorithmic layer only within a very complex system with respect to its performance. To compare two algorithms A and B, there are two important points to be taken into account:

1. (1) Tuning Status of the Methods. There might be a raw or default version of the algorithms, but when you compare scores with the task of showing that some algorithm is better than the other, you need to compare tuned algorithms. In principle, you have to tune algorithm A to give the best results and then you have to tune algorithm B to give the best results and then compare the results of tuned A and tuned B. If A has been tuned for several years, but B is raw, the results give you insight into the tuning status of A and B, but not necessarily of the algorithms as such! So we have to be very careful with generic conclusions.
2. (2) Quality Control of Obervations. When you compare two algorithms for assimilation or two models, verification provides a variety of scores. But verification with real data needs quality control of these data, since otherwise scores are mainly determined by outliers, and one broken device can make the whole verification result completely useless. But how is the data quality controlled? Usually we employ o − f (observation minus first guess) statistic and remove observations which are far away from the model first guess. This leads to an important point: each algorithm A and B needs to use its own quality control. If model biases change between A and B, you will have a different selection of ‘good’ observations.

     But how do you compare two systems which employ different observations? One solution can be to use observations for comparison which passed both quality controls. A second method is to verify each algorithm separately and then compare the scores (this is what is done with World Meteorological Organization (WMO) score comparisons between global models). A third method is to try to use ‘independent’ observations. But these also need some quality control, and since they are not linked to any of the forecasting systems, it is unclear in what way their use in verification helps to judge a particular algorithm or to compare two algorithms.

For our experiments, we compare the LMCPF with the LAPF and the LETKF. The LETKF has a relatively advanced tuning status. LAPF has been mildly tuned and the LMCPF is relatively new. We carried out several tuning steps to try to make LMCPF and LETKF comparable. Further, we employ quality control for the observations in each system separately. Verification of the o − f statistics is based on each system independently. Here, one important performance measure is the number of observations which passes the quality control. If this number is larger for B than for A, we can conclude that the system fits better to the observations, which is a good indicator for the quality of a short-range forecast. For comparison of forecasts the joint set of observations is used, those which pass both the quality control of algorithm A and algorithm B.

4. Numerical results

The goal of this numerical part is, firstly, to investigate the relationship between the observation vector mapped into ensemble space and the ensemble distribution. Secondly, we show since the LMCPF moves particles based on the Gaussian uncertainty of individual particles, it bridges the gap between forecast ensemble and observations. Furthermore we study its distribution. The third part shows results of observation - first guess (o − f) statistics for the LMCPF with different choices for κ > 0 compared to the LETKF and the LAPF. Fourthly, we investigate the evolution of ensemble spread with different parameter settings. In the last part we demonstrate the feasiblity of the LMCPF as a method for atmospheric analysis and subsequent forecasting in a very high-dimensional operational framework, demonstrating that it stably runs for a month of global atmospheric analysis and forecasting.

4.1 Distributions of observations in ensemble space

In a first step, we study (a) the distance between the observation and the ensemble mean and (b) the minimum distance between the observation and the ensemble members. In ensemble space, for distance calculations an appropriate metric needs to be used. Recall that ℝ^m with dimension m is the observation space and ℝ^L with dimension L the ensemble space. Given a vector β ∈ ℝ^L in ensemble space, the distance corresponding to the physical norm in observation space, which is relevant to the weight calculation of the particle filter, is calculated by   

where ⟨·, ·⟩ denotes the standard L²-scalar product in ℝ^m or ℝ^L, respectively. The notation ⟨·, ·⟩_D with some positive definite matrix D denotes the weighted scalar product ⟨·, D ·⟩ and , here with either R⁻¹ in ℝ^m or A in ℝ^L. Note that for A to be positive definite we need L ≤ m.

The matrix A including the standard LETKF localization in observation space has been integrated into the data assimilation coding environment. Here, we show results from an LMCPF one month experiment studying one assimilation step at 00 UTC of May 6, 2016. The cycle has been started May 1, such that the results illustrate a situation where the spin-up period is over and LMCPF spread has reached a steady state (compare Fig. 8).

At each analysis grid point ξ of some coarse global analysis grid we have a matrix A [see (2.37)], L = 40 ensemble members and one projected observation vector C ∈ ℝ^L [see (2.37)]. This leads to a total of N_ω = 10890 samples ω numbering the analysis grid points in a given height layer, e.g., for 850 hPa. The distance of the observations to the ensemble mean is given by   

where the metric A is chosen to be consistent with (2.37). The minimal distance of the observations vector to the ensemble members is given by   

with ω = 1,…,N_ω, where we employed (4.1) and where we note that in ensemble space the ensemble members x^(b,j) − x̄ are given by the standard unit normal vectors e_j, j = 1, …, L.

To analyze the role of moving particles towards the observation in ensemble space, in Fig. 2 we show global histograms for d_C and d_min for three height levels of approximately 500, 850, and 1000 hPa. When the distribution of both d_C and d_min are similar, i.e., the distribution of the minimal distance of the observation to the ensemble members and the distribution of the distance of observations to the ensemble mean are comparable, it indicates that we have a well-balanced system. To understand the particular form of the distributions, we compare it with simulations of random draws of a Gaussian distribution in a 40 dimensional space shown in Fig. 3. When you draw from a Gaussian with mean zero and standard deviation σ = 4, we obtain Fig. 3a. The behavior of the histograms of the norms of the points drawn changes significantly if we consider mixtures with different variances in different space directions. Figures 3a–e shows different distributions with variances given by   

where the constant η ∈ (4, 15, 30, 40, 50) has been chosen to achieve a maximum around 4 and different decay exponents ν ∈ (0, 0.5, 1, 2, 3) have been tested. The distributions of Fig. 2 correspond to a decay exponent between ν = 1 and ν = 2. How much is this reflected by the eigenvalue distributions for the matrices A? We have carried out a fit to the eigenvalue decay of A for a selection of analysis points. The constant η is obtained by using j = 1, which leads to σ₁ = η. Taking the logarithm on both sides now yields   

A fit of ν can be obtained for example by division through log (j) and taking the mean of the remaining right-hand side. The distribution of the resulting exponents is displayed in Fig. 3f. The results find exponents between 0.7 and 2.2. The corresponding distributions are those shown in Figs. 3c and 3d, which are quite close to the distributions of d_C found in the empirical particle-filter generated NWP ensemble in Fig. 2.

Fig. 2.

We show global histograms of d_C and d_min defined in (4.2) and (4.3) for three different pressure levels: 500 hPa in (a) and (d), 850 hPa in (b) and (e), and 1000 hPa in (c) and (f), with d_C in (a)–(c) and d_min in (d)–(f). Shown are statistics for the LMCPF with κ = 25 for May 6, 00 UTC.

Fig. 3.

We show simulations of distributions of random draws in an L = 40 dimensional space, with different mixtures of variances given by formula (4.4), here with η ∈ (4, 15, 30, 40, 50) and ν ∈ (0, 0.5, 1, 2, 3) in (a) to (e). A histogram of the fit of exponents ν as in (4.4) to the eigenvalue decay of the matrices A for a selection of 1000 points is shown in (f). The fit is obtained from the mean of exponents derived from formula (4.5).

4.2 The move of particles

At a second step, we want to investigate the capability of the LMCPF to move particles towards the observation by testing different choices of κ > 0 given by (2.12). In Fig. 4 we compare histograms of the norm of the mean ensemble shift in ensemble space for pressure level 500 hPa, determined for May 6, 00 UTC. The four histograms show the statistics for the three filters in different settings: a) LAPF, b) LMCPF with κ = 1, c) LMCPF with κ = 2.5, and d) LMCPF with κ = 25.

Fig. 4.

We show global histograms of the norm of the mean ensemble shift at pressure level at 500 hPa. On the x-axis we show the norm of shift of mean vectors in ensemble space and on the y-axis we show the frequency. We display the histogram for (a) the LAPF, (b) the LMCPF with κ = 1, (c) the LMCPF with κ = 2.5, and (d) shows the LMCPF with κ = 25. The pink line displays the median, which is also shown on the top of each plot. Shown are the statistics for May 6, 00 UTC.

There are two effects seen in Fig. 4. First, we see the distribution of average shifts or moves of the ensemble mean generated by the LAPF and the LMCPF with three different choices κ controlling the size of the uncertainty used for each particle. The mean shift increases if the uncertainty increases, i.e., from κ = 1 to κ = 2.5 and κ = 25. To develop an understanding of the relative size of this shift let us look at the one-dimensional version of formula (2.41) given by   

with background variance b and observation error variance r, reflecting the size of the particle move. When we, for example, choose r = 4 and b = 16, as we would get with typical values for the error of 2ms⁻¹ for wind measurements and an ensemble standard deviation of 4 m s⁻¹, and then study κ ∈ (1, 2.5, 10, 25), we obtain factors of size s (κ) ∈ (0.8, 0.9, 0.97, 0.99). If the observation has a distance of 3.6 to the ensemble mean, as seen in Fig. 2, this would make the means observed in Fig. 4 plausible. For small κ = 1 here the particle move is 0.8 times the innovation, for large κ = 25 it is 0.99 times the innovation y − H(x^(b)). In Fig. 4 we observe this behavior with the median of the ensemble increments being median = 2.62 in (a) to median = 3.54 in (d).

As a final step of this part, we want to investigate not only the overall distribution of the particle moves, but relate the size of the average particle move to the distance of the observation to the ensemble mean. Figure 5 shows scatter and density plots for the LMCPF with different particle uncertainty. We employ the same values for κ as in Fig. 4, (a) and (d) with κ = 1, (b) and (e) with κ = 2.5, (c) and (f) show results for κ = 25. Displayed are statistics for the average particle move vs. the difference of the observation vectors from the ensemble mean, all for the pressure level at 500 hPa.

Fig. 5.

We show scatter and density plots of the average particle move versus the distance of the observation vector to the ensemble mean, all for the pressure level 500 hPa in ensemble space. On the x-axis we can see the norm of the observation distance to ensemble mean and on the y-axis we show the average size of the corresponding particle move. We display statistics for the LMCPF with different particle uncertainty, for each setting a scatter plot and a density plot which shows high density of points in a better way. (a) and (d) show the statistics for κ = 1, (b) and (e) for κ = 2.5 and (c) and (f) for κ = 25, all for May 6, 00 UTC.

The results of Fig. 5 show that clearly the move of the particles is related to the necessary correction as given by the distance of the observation to the individual particle. There is a clear correlation of the average move to the observation discrepancy with respect to the ensemble mean. If we would investigate each particle individually in one dimension, all points would be on a straight line with slope given by (4.6). The situation in a high-dimensional space with non-homogeneous metric is more complicated as reflected by Fig. 5. The figure confirms that the method is working as designed.

4.3 Assimilation cycle quality assessment of the LMCPF

Here, studying standard global atmospheric scores for the analysis cycle we investigate the quality of the LMCPF by testing different choices of κ > 0, investigate the interaction effects between particle uncertainty, ensemble spread and adaptive spread control and compare it to the way the LETKF moves the mean of the ensemble. For this aims we show two figures.

Figure 6 shows the functionality of the LMCPF by a display of the analysis and the first guess errors for upper air temperature for an ICON assimilation step, comparing the LETKF and the LMCPF with exact and approximate weights, respectively. Here, in the first line we show statistics for the LMCPF (blue line) with exact weights and κ = 2.5 compared to the LETKF (red line). The left panel shows the number of observations which passed quality control, the middle panel shows the root mean square error (RMSE) of observation minus first guess statistics (o − f) (also known as observation - background (o − b) statistics) and the right panel shows the RMSE for observations minus analysis statistics (o − a). The blueish shading shows areas with lower values for the LMCPF in comparison to the LETKF. The second row shows the comparison of the LMCPF with exact (blue lines) and approximate (red lines) weights.

Fig. 6.

We show the observation verification of upper air temperature measured by airplanes, in particular the first guess and analysis scores. The three columns show the number of observations which passed quality control, the RMSE for o − f statistics and the RMSE for o − a statistics for the LMCPF with exact weights (blue line) compared to the LETKF (red line) in the first row and the LMCPF (blue line) with exact weights compared to the LMCPF with approximate weights (red line) in the second row. We display results for one global assimilation step at 00 UTC of January 1st, 2022.

It can clearly be seen that with respect to o − f scores the LMCPF is able to outperform the LETKF in case studies with one assimilation step when an appropriate size of the uncertainty of each particle, here given by the size of κ, is found. The experiments demonstrate that the exact weights yield better results than the approximate weights.

The numerical experiments prove that the particle uncertainty enables the LMCPF to move the background ensemble towards the observation in a way comparable to or even better than the LETKF. This effect remains active during model propagation and can also be observed for the first guess statistics and for forecasts with short lead times. Here, the LMCPF is able to outperform the operational version of the LETKF.

In Fig. 7 we show a comparison of analysis cycle verification for a full one month period of LMCPF, LAPF and LETKF experiments. The columns are showing the same statistics as in Fig. 6. The first row in Fig. 7 shows the differences between LETKF (red line) and LMCPF with exact weights and κ = 2.5 (blue line) for a full month of cycling (January 2022). The second row shows the comparison of LAPF (red line) and LMCPF with with approximate weights and κ = 2.5 (blue line) for one month (May 2016). Again, the blueish shading indicates lower numbers or RMSE values for the experiment (LMCPF), the yellowish shading indicates lower values for the reference (LETKF resp. LAPF).

Fig. 7.

Again, we show some observation verification statistics for upper air temperature measured by airplanes. We show the same statistics as in Fig. 6 but for experiments carried out for the period one month each. In the upper row the comparison between LETKF (red line) and LMCPF (blue line) with exact weights is shown for January 2022, in the lower row we show the comparison between LAPF (red line) and LMCPF (blue line) in May 2016.

Row one shows that the LMCPF with particle uncertainty given by κ = 2.5 can outperform the LETKF for short lead times, which is very important for practical applications. Here the LMCPF is up to 2.5 % better than the LETKF for the o − f statistics. In this experiment, for some levels in the atmosphere the o − a and o − f statistics of the LMCPF are up to 0.5 % worse than the LETKF. The amount of data which passes quality control is quite similar for all methods under consideration, however, at some levels we loose up to 1.1 % of observations in comparison with the LETKF. This is an effect of quality control based on the ensemble spread - a smaller ensemble spread as we observe for the particle filter leads to less observations passing quality control. In the second row of Fig. 7 we show the statistics of LAPF (Potthast et al. 2019) vs. LMCPF. Here we can clearly see that the LMCPF shows much better upper air scores than the LAPF. It clearly shows the importance of allowing a movement of particles towards the observations by using particle uncertainty.

Overall we conclude that with respect to the verification of the analysis cycle the LMCPF with particle uncertainty given by κ = 2.5 is comparable to the LETKF, with some levels to be better, some to be worse, overall differences mostly below 3 %. The upper air verification for the analysis cycle of the LMCPF in operational setup is more than 10 % better than for the LAPF.

4.4 The evolution of the ensemble spread

It is an important evaluation step to investigate the stability of the LMCPF for global NWP over longer periods of time. To this end, we have run a period of one month. We compare the particle spread evolution of the LMCPF, the LAPF and LETKF in Fig. 8. All experiments were started with an ensemble which consists of 40 identical copies of the particles, i.e., with an ensemble in degenerate state. Thus, here the tests also evaluate the capability of the whole system to resolve degeneracy and return to an ensemble with reasonable stable spread.

Fig. 8.

The evolution of the ensemble spread is shown for three filters and six different parameter choices for the LMCPF for a time period of both one month (LETKF - black, LAPF - blue, LMCPF - red) and for one week for different parameter choices for the LMCPF (see Table 1). The x-axis shows the period in one day steps. The y-axis shows the upper air temperature at ICON model level 64 (≈ 500 hPa) in Kelvin. The first row shows the mean of the spread, the second row the minimum and the third row the maximum.

In a sequence of experiments we have tested the ability of the LMCPF to reach and maintain a particular ensemble spread using a combination of the choice of κ with a posterior covariance inflation   

for each particle with replacing in (2.48), which is used to generate the analysis ensemble by random draws. We also note that for the random draw of (2.46) we employed bounds given by c₀ and c₁. The parameter combinations chosen for six different experiments over one week are compiled into Table 1. The corresponding spread evolution is visualized in Fig. 8. The results show that, starting with an initial ensemble of identical particles, after some spin-up phase of 2–3 days all particle filters reach their particular spread level and keep it stable over a longer period of time. We carried out selected longer term studies comparing the behavior of the LMCPF (red), the LAPF (blue) and the LETKF (black) over a period of one month.

The control of the ensemble spread is a delicate topic. A larger ensemble spread does not necessarily lead to better forecast scores, measured by RMSE (Skill) of the ensemble mean or its standard deviation (SD), defined as the RMSE after the bias has been subtracted. With the ability to control separately the strength of the adaptive resampling and the ability of the filter to pull the particles towards the observations, we have independent parameters at hand to adapt the approximations to a real-world situation. At the same time, the way the assimilation step of the LMCPF pulls the ensemble to the observations is based on both the size of the particle uncertainty, which itself is depending on the ensemble spread, and within the cycled environment on the adaptive resampling. Of course, it would be desirable to develop tools to estimate the real uncertainty adequate for each particle, and to keep all parts of the system consistent. We expect this to lead to much further research and discussions, which are beyond the scope of this work.

4.5 Forecast quality of the LETKF and LMCPF experiments

As the last part of the numerical results, we study the quality of longer forecasts based on the analysis cycle of the LMCPF with κ = 2.5 and compare it to the LETKF based forecasts in Fig. 9 and to forecasts based on the LAPF analysis cycle in Fig. 10. For this purpose, forecasts were run twice a day at 00 UTC and 12 UTC. In Fig. 9 we display upper air verification for the LMCPF (dashed lines) with exact weights and for the LETKF (solid lines). The different colors identify the different lead times, from one day up to one week. The first row shows the upper air temperature and the second row shows the verification of pressure forecasts. The first panel shows the Continuous Ranked Probability Score (CRPS), the second panel the Standard Deviation (SD), the third panel the Root Mean Square Error (RMSE) and the last panel shows the Mean (ME). For CRPS, SD and RMSE it is the aim to receive statistics as low as possible; for the Mean (= Bias) it is the goal to reach zero. We used the same observations for verification in both experiments.

Fig. 9.

We display forecast scores for the LMCPF (dashed) with exact weights and the LETKF (bold lines) calculated for January 2022. Shown are the continuous rank probability score (CRPS), the standard deviation (SD), the RMSE and the mean (ME). First row shows the upper air temperature, the second row shows pressure forecast verification. The colors indicate the different lead times from one day to 7 days.

Fig. 10.

Exemplarily for relative humidity and upper air temperature we show the improvement of the LMCPF with approximate weights (dashed) compared to the the LAPF (bold lines) for May 2016.

Studying the results shown in Fig. 9, we observe that forecast scores are very similar for LMCPF and LETKF for the upper air temperature. For pressure forecast the bias (ME) for the LMCPF is mostly smaller than for the LETKF below 50 hPa.

In Fig. 10 we show the same statistics as in Fig. 9 focussing on relative humidity and upper air temperature for the comparison of LMCPF and LAPF, where here we used the approximate weights or both to study the effect of the shifts only. Here, it can be clearly seen that the LMCPF shows lower RMS errors than the LAPF for both variables and for all levels. For relative humidity the LMCPF is clearly better for the shorter lead times up to three days, but with less prominence it still outperforms the LAPF for the longer lead times up to one week. For the upper air temperature the RMSE statistics are clearly better for the LMCPF for all lead times. It is worth noting that the biases for the two particle filters show a quite similar behavior.

These results altogether demonstrate that using particle uncertainty is an important ingredient for improving first guess and forecast scores of the particle filter.

5. Conclusions

In this work we develop the use of a Gaussian mixture within the framework of the Localized Adaptive Particle Filter (LAPF) introduced in Potthast et al. (2019), as an approximation to model and forecast particle uncertainty in the prior and posterior distributions. The filter, following earlier ideas of Hoteit et al. (2008) and Liu et al. (2016a, b) constructs an analysis distribution based on localized Gaussian mixtures, whose posterior coefficients, covariances and means are calculated based on the prior mixture given by the ensemble first guess and the observations. The analysis step is completed by resampling and rejuvenation based on the LAPF techniques, leading to a Localized Mixture Coefficients Particle Filter (LMCPF). In contrast to the LAPF the LMCPF is characterized by a move or shift of the first guess ensemble towards the observations, which is consistent with the non-Gaussian posterior distribution based on a Bayesian analysis step, and where the size of the move is controlled by the size of the uncertainty of individual particles.

We have implemented the LMCPF in the framework of the global ICON model for numerical weather prediction, operational at Deutscher Wetterdienst. Our reference system to test the feasibility of ideas and demonstrate the quality of the LMCPF is the LETKF implementation operational at DWD, which generates initial conditions for the global ICON Ensemble Prediction System ICON-EPS. We have shown that the LMCPF runs stably for a month of global assimilations in operational setup and for a wide range of specific LMCPF parameters. Our investigation includes a study of the distribution of observations with respect to the ensemble mean and statistics of the distance of ensemble members to the projection of the observations into ensemble space. We also study the average size of particle moves when uncertainty is employed for individual Gaussian particles within the LMCPF and provide an analytic explanation of the histogram shapes with a comparison to the eigenvalue distribution of the matrices A on which the particle weights are based.

We show that the upper air first guess errors of the LMCPF and LETKF during the assimilation cycle are very similar within a range of plus-minus 1–3 %, with the LMCPF being better below 850 hPa and the LETKF being better in some range above. Forecast scores for a time-period of one month have been calculated, demonstrating as well that the RMSE of the ensembles is comparable for upper air temperature, relative humidity, wind fields and pressure (2–3 %). The size of the mean spread of the LMCPF strongly depends on parameter choices and is usually stable after a spin-up period.

In several shorter case studies we demonstrate that by varying the parameter choices, we can achieve better first guess RMSE for the LMCPF in comparison to the LETKF, which shows that for very short range forecasts the quality of the method can be comparable to or better than that of the LETKF. While reaching a break-even point for operational scores with a new method establishes an important mile-stone, we need to note that there are many open and intricate scientific questions here with respect to the choice of parameters for the Gaussian mixture and their inter-dependence as well as about the control of an optimal and correct ensemble spread both in the analysis cycle and for the forecasts.

Overall, with the LMCPF we demonstrate significant progress compared to the localized adaptive particle filter (LAPF) for numerical weather prediction in an operational setup, demonstrating that the LMCPF has reached a stability and quality comparable to that of the LETKF, while allowing and taking care of diverse non-Gaussian distributions in its analysis steps.

Clearly, there is much more work to be done. The automatic choice of current tuning parameters is an important topic. Also, in further steps we will take a look at the quality control. Currently, the LMCPF and the LETKF are using the same observation quality control, but the LMCPF seems to need a more accurat approach. Furthermore, we have implemented the LAPF and LMCPF in the Lorenz 63 and Lorenz 96 models and are studying the characteristics of the particle filters in low-dimensional systems.

Acknowledgments

The research has been supported by the Innovation in Applied Research and Development (IAFE) grant of the German Ministry for Transport and Digital Infrastructure BMVI. The authors thank Dr. Harald Anlauf and Dr. Andreas Rhodin from DWD for much support working on the DACE data assimilation coding environment.

Data Availability Statement

The datasets generated and analyzed in this study are not publicly available since they contain large amount of model fields and operational observations, but are available from the corresponding author on reasonable request as far as possible.

Footnotes

¹ Shown by German Climate Computing Center DKRZ Git Records.

² Data Assimilation Coding Environment.

³ The standard arguments, see Lemma 3.2.1 of Nakamura and Potthast (2015), show injectivity of XX^T on R(X): XX^TXβ = 0 with β ∈ ℝ^L yields X^T Xβ ∈ N (X) ⋂ R(X^T) = R(X^T)^⊥ ⋂ R(X^T), thus X^TXβ = 0. The same argument for Xβ ∈ N (X^T) yields Xβ = 0, thus XX^T is injective on R (X). For surjectivity we consider v ∈ R(X), i.e., v = Xw with w ∈ R^L = N (X) ⨁ N (X)^⊥ = N (X) ⨁ R (X^T), such that w = w₁ + w₂ with w₁ ∈ N (X) and w₂ = X^Tβ with some β ∈ ℝⁿ = R (X) + R (X)^⊥. Repeating the last argument leads to a β₁ ∈ R (X) with w = X^Tβ₁ and thus surjectivity. Invertibility of B is thus shown.

⁴ The R matrix is taken from operations, where it is estimated based on standard Desrozier statistics. Usually ρ is kept between a minimal and maximal positive value, e.g., 0.7 and 1.5 for operations to account for statistical outliers in the estimator.

References

•  Anderson,  J. L., and  S. L.  Anderson, 1999: A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts. Mon. Wea. Rev., 127, 2741–2758.
•  Bain,  A., and  D.  Crisan, 2009: Fundamentals of Stochastic Filtering. Stochastic Modelling and Applied Probability, vol. 60, Springer, 403 pp.
•  Bengtsson,  T.,  C.  Snyder, and  D.  Nychka, 2003: Toward a nonlinear ensemble filter for high-dimensional systems. J. Geophys. Res., 108, D24, doi:10.1029/2002JD002900.
•  Bickel,  P.,  B.  Li, and  T.  Bengtsson, 2008: Sharp failure rates for the bootstrap particle filter in high dimensions. Pushing the Limits of Contemporary Statistics: Contributions in Honor of Jayanta K. Ghosh. vol.3, IMS Collections, 318–329.
•  Bishop,  C. H., 2016: The GIGG-EnKF: Ensemble Kalamn filtering for highly skewed non-negative uncertainty distributions. Quart. J. Roy. Meteor. Soc., 142, 1395–1412.
•  Crisan,  D., and  B.  Rozovskii, 2011: The Oxford Handbook of Nonlinear Filtering. Oxford University Press, 1063 pp.
•  Evensen,  G., 1994: Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res., 99, 10143–10162.
•  Evensen,  G., 2009: Data Assimilation: The Ensemble Kalman Filter. Earth and Environmental Science, Springer, 307 pp.
•  Evensen,  G., and  P. J.  van Leeuwen, 2000: An ensemble Kalman smoother for nonlinear dynamics. Mon. Wea. Rev., 128, 1852–1867.
•  Farchi,  A., and  M.  Bocquet, 2018: Comparison of local particle filters and new implementations. Nonlinear Processes Geophys., 25, 765–807.
•  Frei,  M., and  H.  Künsch, 2013: Bridging the ensemble Kalman and particle filters. Biometrika, 100, 781–800.
•  Hoteit,  I.,  D.-T.  Pham,  G.  Triantafyllou, and  G.  Korres, 2008: A new approximate solution of the optimal nonlinear filter for data assimilation in meteorology and oceanography. Mon. Wea. Rev., 136, 317–334.
•  Hunt,  B. R.,  E. J.  Kostelich, and  I.  Szunyogh, 2007: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Phys. D, 230, 112–126.
•  Kawabata,  T., and  G.  Ueno, 2020: Non-Gaussian probability densities of convection initiation and development investigated using a particle filter with a storm-scale numerical weather prediction model. Mon. Wea. Rev., 148, 3–20.
•  Klinker,  E.,  F.  Rabier,  G.  Kelly, and  J.-F.  Mahfouf, 2000: The ECMWF operational implementation of four-dimensional variational assimilation. III: Experimental results and diagnostics with operational configuration. Quart. J. Roy. Meteor. Soc., 126, 1191–1215.
•  Liu,  B.,  B.  Ait-El-Fquih, and  I.  Hoteit, 2016a: Efficient kernel-based ensemble Gaussian mixture filtering. Mon. Wea. Rev., 144, 781–800.
•  Liu,  B.,  M. E.  Gharamti, and  I.  Hoteit, 2016b: Assessing clustering strategies for Gaussian mixture filtering a subsurface contaminant model. J. Hydrol., 535, 1–21.
•  Nakamura,  G., and  R.  Potthast, 2015: Inverse Modeling. IOP Publishing, 506 pp.
•  Penny,  S. G., and  T.  Miyoshi, 2016: A local particle filter for high-dimensional geophysical systems. Nonlinear Processes Geophys., 23, 391–405.
•  Poterjoy,  J., and  J. L.  Anderson, 2016: Efficient assimilation of simulated observations in a high-dimensional geophysical system using a localized particle filter. Mon. Wea. Rev., 144, 2007–2020.
•  Poterjoy,  J.,  R. A.  Sobash, and  J. L.  Anderson, 2017: Convective-scale data assimilation for the weather research forecasting model using the local particle filter. Mon. Wea. Rev., 145, 1897–1918.
•  Potthast,  R.,  A.  Walter, and  A.  Rhodin, 2019: A localized adaptive particle filter within an operational nwp framework. Mon. Wea. Rev., 147, 345–362.
•  Reich,  S., and  C.  Cotter, 2015: Probabilistic Forecatsing and Bayesian Data Assimilation. Cambridge University Press, 308 pp.
•  Robert,  S.,  D.  Leuenberger, and  H. R.  Künsch, 2017: A local ensemble transform Kalman particle filter for convective-scale data assimilation. Quart. J. Roy. Meteor. Soc., 144, 1279–1296.
•  Schenk,  N.,  R.  Potthast, and  A.  Rojahn, 2022: On two localized particle filter methods for Lorenz 1963 and 1996 models. Front. Appl. Math. Stat., 8, doi:10.3389/fams.2022.920186.
•  Snyder,  C.,  T.  Bengtsson,  P.  Bickel, and  J.  Anderson, 2008: Obstacles to high-dimensional particle filtering. Mon. Wea. Rev., 136, 4629–4640.
•  Snyder,  C.,  T.  Bengtsson, and  M.  Morzfeld, 2015: Performance bounds for particle filters using the optimal proposal. Mon. Wea. Rev., 143, 4750–4761.
•  van Leeuwen,  P. J., 2009: Particle filtering in geophysical systems. Mon. Wea. Rev., 137, 4089–4114.
•  van Leeuwen,  P. J., 2010: Nonlinear data assimilation in geosciences: An extremely efficient particle filter. Quart. J. Roy. Meteor. Soc., 136, 1991–1999.
•  van Leeuwen,  P. J.,  Y.  Cheng, and  S.  Reich, 2015: Nonlinear Data Assimilation. Frontiers in Applied Dynamical Systems: Reviews and Tutorials, vol. 2, Springer Cham, 130 pp.
•  van Leeuwen,  P. J.,  H. R.  Künsch,  L.  Nerger,  R.  Potthast, and  S.  Reich, 2019: Particle filters for high-dimensional geoscience applications: A review. Quart. J. Roy. Meteor. Soc., 145, 2335–2365.
•  Vetra-Carvalho,  S.,  P. J.  van Leeuwen,  L.  Nerger,  A.  Barth,  M. U.  Altaf,  P.  Brasseur,  P.  Kirchgessner, and  J.-M.  Beckers, 2018: State-of-the-art stochastic data assimilation methods for high-dimensional non-Gaussian problems. Tellus A, 70, 1–43.
•  Zängl,  G.,  D.  Reinert,  P.  Rípodas, and  M.  Baldauf, 2014: The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Quart. J. Meteor. Soc., 141, 563–579.