Geometry of Rainfall Ensemble Means: From Arithmetic Averages to Gaussian-Hellinger Barycenters in Unbalanced Optimal Transport

Abstract

It is well-known in rainfall ensemble forecasts that ensemble means suffer substantially from the diffusion effect resulting from the averaging operator. Therefore, ensemble means are rarely used in practice. The use of the arithmetic average to compute ensemble means is equivalent to the definition of ensemble means as centers of mass or barycenters of all ensemble members where each ensemble member is considered as a point in a high-dimensional Euclidean space. This study uses the limitation of ensemble means as evidence to support the viewpoint that the geometry of rainfall distributions is not the familiar Euclidean space, but a different space. The rigorously mathematical theory underlying this space has already been developed in the theory of optimal transport (OT) with various applications in data science.

In the theory of OT, all distributions are required to have the same total mass. This requirement is rarely satisfied in rainfall ensemble forecasts. We, therefore, develop the geometry of rainfall distributions from an extension of OT called unbalanced OT. This geometry is associated with the Gaussian-Hellinger (GH) distance, defined as the optimal cost to push a source distribution to a destination distribution with penalties on the mass discrepancy between mass transportation and original mass distributions. Applications of the new geometry of rainfall distributions in practice are enabled by the fast and scalable Sinkhorn-Knopp algorithms, in which GH distances or GH barycenters can be approximated in real-time. In the new geometry, ensemble means are identified with GH barycenters, and the diffusion effect, as in the case of arithmetic means, is avoided. New ensemble means being placed side-by-side with deterministic forecasts provide useful information for forecasters in decision-making.

1. Introduction

Nowadays, ensemble forecasts play a vital role in numerical weather prediction. With advanced high-performance computing, the number of ensemble members is anticipated to continue increasing in the future. Therefore, it is important to extract useful information from a large number of individual forecasts that give equally possible realizations. The standard technique in ensemble forecast is to reduce all ensemble members to a small number of important fields, such as quantile and probabilistic maps, ensemble means and spreads, and ensemble clusters. Quantile and probabilistic maps turn the high-dimensional probability distribution from an ensemble forecast into scalar quantities derived from one-dimensional marginal distributions at grid points. In contrast, ensemble means and ensemble clusters retain the high dimensionality of forecast fields and their coherent structures, but only show typical representatives of all ensemble members. This is the multivariate nature of the latter approach that makes the resulting forecast fields more interesting and complicated in use. At the same time, it opens rooms for new interpretations and explorations. In this study, we demonstrate this interesting problem with the ensemble mean.

The ensemble mean is chosen due to its simplicity, which is, in fact, the arithmetic average of all forecast members. This operator tends to filter out random noise but, at the same time, diffuse informative processes in individual members, leading to a smooth mean field. The diffusion effect is noticeably clear when this operator is applied to rainfall. The resulting rain field tends to spread out and is noticeably different from each member. Figure 1 illustrates this phenomenon with 20 rainfall forecasts over Kyushu Japan from the mesoscale ensemble prediction system MEPS of the Japan Meteorology Agency (JMA) (Ono et al. 2021) using the JMA's operational limited area model ASUCA (Ishida et al. 2022). The arithmetic mean of 20 rainfall distributions differs greatly from the deterministic forecast. As a result, ensemble means of rainfall are rarely used in practice.

Fig. 1

(a) Accumulated precipitations observed by radars and rain gauges between 00-09 JST on July 4th, 2020. (b) The corresponding 5-km deterministic forecast by ASUCA started at 18 JST on July 4th, 2020. (c) The corresponding 5-km ensemble mean forecast by MEPS started at 18 JST on July 4th, 2020.

Figure 2a conceptually explains this fact using two one-dimensional rainfall distributions with the same shapes but a small displacement error. We expect that the mean should retain a similar shape with its location between the locations of the two individual distributions. However, the arithmetic average yields an undesirable result: a bimodal distribution with peaks much smaller than those of the two members. Furthermore, the mean distribution covers a wide area spreading from the left leg of the first member to the right leg of the second member. Although this explanation is employed in a one-dimensional space, it can be carried out in higher spaces without any significant difference.

Fig. 2

(a) A one-dimensional simple model explaining the undesirable behavior of ensemble means: two identical rainfall distributions (circles) with a displacement error result in an ensemble mean distribution (squares) with two modes, which is far from the expected mean (triangles). (b) The same distributions when viewed under cumulative forms.

An important reason for using the ensemble mean as a representative forecast is that if the probability distribution of forecasts is a multivariate normal distribution, the forecast mean also gives the mode of this probability distribution. As a result, the forecast mean becomes the most probable forecast and can be taken as the best approximation of the true state. Under this assumption, the expected error between the ensemble mean and the observation is proved to be proportional to the reciprocal of the square root of the number of ensemble members (see Appendix). Thus, by increasing the number of ensemble members, we expect to obtain a more accurate forecast through the ensemble mean. However, this is not the case even with a relatively large number of ensemble members, as observed in Fig. 3a (1000 members in this case). Instead of two-dimensional rainfall distributions, the problem is simplified by only plotting the time series of 1-hour precipitation averaged over the Ichifusa catchment in Kyushu Japan. The forecasts are obtained from a 1000-member ensemble prediction system LETKF1000 (Duc et al. 2021) using the JMA's former operational limited area model NHM (Saito et al. 2006). Like the two-dimensional case, the ensemble mean does not show a similar pattern as the corresponding time series from the observations. However, intriguingly, if we plot the time series of accumulated rainfall instead of rain rates (Fig. 3b), the ensemble mean becomes nearly identical to the accumulated rainfall observations. This striking fact has been observed in several studies using a large number of ensemble members (Kobayashi et al. 2020, 2023) without any adequate explanation.

Fig. 3

(a) Time series of the 1-hour precipitation averaged over the Ichifusa catchment as forecasted by LETKF1000. The ensemble mean, the GH barycenter, and the observations are denoted by triangles, squares, and stars, respectively. (b) The same forecasts when viewed under cumulative forms.

Geometrically, if we consider each distribution with n elements as a point in an n-dimensional space ℝⁿ. the ensemble mean is simply the center of mass or the barycenter of all members, assuming that all members have the same mass. Figure 3b implies that if we want to retain the meaning of the ensemble mean as a bary-center, we need to work in the space of cumulative rainfall distributions. In other words, the appropriate use of the ensemble mean of rainfall in one-dimensional cases is with accumulated rainfall distributions rather than rain rate distributions. We can easily verify the validity of this hypothesis with the simple example in Fig. 2a. Figure 2b plots the cumulative distributions corresponding to the distributions in Fig. 2a. As expected, the cumulative distribution of the expected mean lies between the two cumulative distribution members. However, what is notable here is that in cumulative forms, the expected mean is nearly identical to the arithmetic mean of the inverses of the cumulative distributions. Note that in Fig. 2b, since the cumulative distributions are one-to-one maps, their graphs also represent their inverses, in which time is considered as a function of cumulative rainfall.

Figure 2b suggests the following procedure to find the expected ensemble mean for any number of one-dimensional distributions:

1. (1) Transforming all distributions to the space of inverses of cumulative distributions;
2. (2) Calculating the arithmetic mean in the transformed space;
3. (3) Transforming the resulting ensemble mean back to the space of distributions.

Of course, the important problem is how we can justify such a procedure with a robust theoretical base. Note that Fig. 2b demonstrates the first two steps (1) and (2) of this procedure, while Fig. 2a demonstrates the last step (3).

The above procedure shows a potential way of finding expected ensemble means in high-dimensional cases. Thus, all we need is to find an appropriate space in which the ensemble mean retains its meaning as barycenters while being robust to the diffusion effect in the presence of displacement errors among members. However, an attempt to extend cumulative distributions from one-dimensional cases to high-dimensional cases does not work since it is unclear how to define a high-dimensional cumulative field from a high-dimensional distribution. A natural question is whether this space exists at all in general cases. It is noted that even in one-dimensional cases, the arithmetic average operator only makes sense if all one-dimensional distributions have the same total mass. This means that even in the simplest cases, the existence of such a space is still questionable.

In this study, we show that the theory of optimal transport (OT) (Villani 2009; Santambrogio 2015; Peyré and Cuturi 2019) proposes an elegant solution to this problem. Instead of working in a transformed space, we continue to stick with the space of rainfall distributions but endowed with a new geometry. Thus, the similarity between any distributions is no longer measured by the normal Euclidean distance but is replaced by a new distance defined in the context of OT. In particular, this distance becomes the normal Euclidean distance between inverses of cumulative distributions in one-dimensional cases. The theory of OT relevant to this study, i.e., unbalanced OT, is presented in the next section. The barycenters, resulting from the new geometry of rainfall distributions defined by unbalanced OT, are described and analyzed in Section 3. Finally, Section 4 summarizes the main points of this study and discusses some potential applications.

2. Unbalanced optimal transport

Although OT has been successfully applied in many fields of data science, there is only a limited number of applications of OT in geosciences (Farchi et al. 2016; Métivier et al. 2016; Yang et al. 2018; Sambridge et al. 2022). However, it is worth noting that in recent years, we have seen an increase in studies using OT in geophysical data assimilation (Reich and Cotter 2015; Feyeux et al. 2018; Li et al. 2018; Tamang et al. 2021; Vanderbecken et al. 2023). In order to make OT accessible to the meteorology community, the theory of OT will be adapted to rainfall distributions and simplified in this section. A more rigorous treatment for probabilistic distributions can be found in Villani (2009) and Santambrogio (2015). Our mathematical treatment in this section mainly follows Peyré and Cuturi (2019).

Let two vectors denote two rainfall distributions with the same total rain mass over the same domain D. We consider rainfall in the same domain, however, in the theory of OT, two distributions need not be on the same domain. We call a matrix a transport plan that moves a to b in the sense that the element P_ij denotes the rain mass from bin i to bin j. A bin corresponds to a grid box in the domain. For mass conservation, we impose two constraints on the elements of P

  

  

where 1 denotes a vector with all elements equal to one. From the constraints (1), it is easy to verify that the total rain mass is conserved

  

Associated with P, we have a matrix whose element C_ij denotes the transportation cost from bin i to bin j.

The original theory of OT seeks the OT plan P* that minimizes the following objective function

  

subject to the constraints (1) where the symbol ⟨ ⟩ denotes the inner product of two matrices. With the linear constraints (1), the linear programming problem (3) is convex and therefore has a global minimum. This formulation is known as the Kantorovich problem in OT (Kantorovich 1942), an extension of the Monge problem in which mass splitting is not allowed (the entire mass from a bin is moved to another bin). What is the connection between the optimal cost L_C (a, b) and the geometry of rainfall distributions?

The connection follows from an important theorem: if 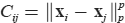where is the Minkowski distance of order p between two grid points x_i, x_j, then L_C (a, b) induces a distance between a and b, which is called the p-Wasserstein distance

  

We replace C with D^p in (4) to emphasize that the new distance is defined by using the Minkowski distance as the transportation cost. Also, recall that the Minkowski distance of order 2 is the familiar Euclidean distance. In order to be a distance, the distance function has to be positive, symmetric, and has to obey the triangular inequality. The p-Wasserstein distance usually does not have an analytic form, and can only be estimated numerically.

However, for one-dimensional distributions, W_p (a, b) has a closed form given by

  

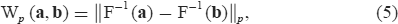where F⁻¹ (a) denotes the inverse of the cumulative distribution constructed from a. Thus, when p = 2, i.e., 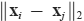is the Euclidean distance between x_i and x_j, the 2-Wasserstein distance is identical to the Euclidean distance between F⁻¹ (a) and F⁻¹ (b). This fact supports our averaging operation in Fig. 2b, where we take the arithmetic mean of two inverses of cumulative distributions. This step is equivalent to taking the barycenter c of two distributions a and b with respect to the 2-Wasserstein distance

  

Of course, in practice, we avoid minimizing (6) by simply taking the average of F⁻¹ (a) and F⁻¹ (b), and transform it back to the space of distributions.

Recall that the OT problem (3) strictly requires the same total mass between a and b. However, rainfall distributions from different ensemble members rarely satisfy this condition. Therefore, rainfall distributions cannot be considered in the same Wasserstein space. This limitation prevents the application of OT for rainfall distributions. Clearly, the averaging operation does not make sense in Fig. 2b if the two cumulative distributions have two different heights.

There are many attempts to relax the requirement of the same total mass in OT. The most successful approach is known under the name unbalanced optimal transport (UOT) (Frogner et al. 2015; Chizat et al. 2018a; Liero et al. 2018), which relaxes the objective function (3) with the new form

  

where τ is the marginal relaxation parameter that penalizes the discrepancy between mass transportation and original mass distributions. This discrepancy is measured with the Kullback-Leibler (KL) divergence

  

The existence of the term b_i − a_i in (8) is due to unequal total mass between a and b. Thus, (7) replaces the strong constraints (1) with weak constraints through the marginal relaxation terms, and controls these constraints by τ. It can be verified that (7) reduces to (3) in the limit τ → ∞ under the total mass constraint .

Like the 2-Wasserstein distance, when is the square of the Euclidean distance, the optimal cost (7) defines a distance between a and b, called the Gaussian-Hellinger (GH) distance

  

However, unlike W_p (a, b), GH (a, b) can only be estimated numerically even for one-dimensional distributions. Using this new distance, we can estimate the barycenter of an ensemble of rainfall distributions 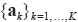from the following minimization problem

  

In other words, we seek the distribution b that minimizes the averaged GH distances from b to all a_k. Figure 4 illustrates this barycenter problem by showing GH-barycenters of two different rainfall distributions in terms of both volumes and spreads. The computation is employed by using the algorithm described in the next section.

Fig. 4

Dependence of regularized GH barycenters on (a) the entropic regularization parameter, and (b) the marginal relaxation parameter. The GH barycenters are estimated from two different rainfall distributions in terms of both volumes and spreads using the Sinkhorn-Knoop algorithm.

3. Regularized Gaussian-Hellinger barycenters

The most common method to solve the linear programing problem (3) is the simplex algorithm. In general, the computational complexity of the simplex method is which limits the applications of OT in practice. Recall that n denotes the size of the vectors a, b, which is the number of grid points in the domain D. With the introduction of the marginal relaxation, the UOT minimization problem (7) is no longer a linear programing problem. The closed solution exists when distributions have Gaussian forms (Janati et al. 2020). Blondel et al. (2018) proposed to solve this using the L-BFGS-B algorithm with the squared norm in place of the KL divergence. Sato et al. (2020) provided an effective solution when distributions have a tree structure. Chapel et al. (2021) showed that (7) can be turned into a non-negative linear regression problem, and solved with non-negative matrix factorization. However, what makes UOT applicable in practice is the introduction of entropic regularization into UOT, leading to scalable and fast algorithms.

The idea of adding an entropic regularization term into (3) has been proposed by Cuturi (2013) to make the problem strictly convex and, therefore, simpler to solve. In particular, regularization enables the use of the fast Sinkhorn-Knopp algorithm (Sinkhorn and Knopp 1967; Benamou et al. 2015) with the complexity to approximate the optimal plan. This idea has been introduced into UOT by Chizat et al. (2018b) to derive matrix scaling algorithms for UOT problems in the vein of the Sinkhorn-Knopp algorithm. Thus, we regularize the minimization problem (7) by adding an entropic regularization term

  

where ε is the entropic regularization parameter, and H (P) represents the entropy of P

  

The regularized GH distance associated with the regularized UOT problem (11) is expressed as GH^ε(a, b), which transforms our barycenter problem (10) to

  

By letting ε go to zero in minimizing (13), we obtain the GH barycenter of the original barycenter problem (10).

The matrix scaling algorithm developed by Chizat et al. (2018b) for the barycenter problem (13) is reproduced here with some adaptations

  

Repeat:

  

  

  

Until convergence

Output: b

The symbol ∅ in (14a) and (14c) denotes the element-wise division operator. The matrix K is the element-wise exponential matrix of −C/ε. It is worth noting that this algorithm is prone to numerical underflow and overflow when s is small. Therefore, it is better to work with , than K, u_k, v_k. This strategy is known as the log-domain Sinkhorn-Knopp algorithm.

Figure 4 shows the impact of the entropic regularization and the marginal relaxation on approximations of GH barycenters using Algorithm 1. Due to the fact that OT plans become less sparse under the entropic regularization, ε with large values cause the mass spread in approximated GH barycenters, as illustrated in Fig. 4a. This implies that to avoid the diffusion effect, ε should be set to small values. However, if ε are too small, the Sinkhorn-Knopp algorithm will suffer from numerical underflow and overflow, and fail to terminate. For the marginal relaxation τ, it is interesting to see that when a large mass discrepancy is enabled, i.e., τ are small, the UOT barycenter problem leads back to a distribution similar to the arithmetic mean of two ensemble members. Therefore, τ should be set to large values to avoid arithmetic means. However, if τ are too large, the algorithm will converge slower due to ϕ ~ 1. The settings of ε = 10⁻⁴ and τ = 10 will be applied in all the computations using Algorithm 1.

When applying the matrix scaling algorithm to two-dimensional rainfall distributions, the most challenging issue is the exponential increase in computational costs. For the one-dimensional case in Fig. 4, the size of the problem is n = 100. Let us consider two-dimensional distributions with the same size in each direction. The problem size becomes n = 100² = 10⁴, leading to an increase of 10⁸/10⁴ = 10⁴ times in the computational cost. Notice that the computation cost in Algorithm 1 is mainly dominated by the matrix-vector products, Kv_k and , which takes operations. In order to mitigate the huge computational cost in two-dimensional cases, we model K as a tensor product , so that the matrix-vector products can be done in each x and y direction separately. As a result, the computation cost reduces to resulting in 10² time increase in the computational cost as compared to one-dimensional cases, which is affordable in practice.

Figure 5 shows the GH barycenters for consecutive 3-hour precipitation from 00 to 09 JST on July 4th, 2020, estimated from 20 members of MEPS. Corresponding deterministic forecasts and arithmetic means are also plotted for comparison. Clearly, all GH barycenters avoid the diffusion effect as observed in the arithmetic means. Furthermore, the GH barycenters provide additionally useful information for the deterministic forecasts by showing locations where all members disagree with the deterministic forecasts, therefore, overconfidence from the deterministic forecasts may be avoided. This information is important for forecasters in decision-making.

Fig. 5

Consecutive 3-hour precipitation between 00–09 JST on July 4th, 2020 forecasted by MEPS with the deterministic forecasts (left columns), the ensemble means (right columns), and the GH barycenters (center columns).

Objective verification using the Fractions Skill Score (FSS) (Roberts and Lean 2008) is performed to quantify the performances of the two kinds of bary-centers in addition to the deterministic forecasts. The verification results are shown in Fig. 6. Clearly, for the arithmetic means, due to the diffusion effect, their FSSs drop rapidly to zero when the rainfall thresholds increase. This means the GH barycenters outperform the arithmetic means for intense rain. However, the arithmetic means are not entirely worse than the GH barycenters. At the rainfall thresholds smaller than 10 mm (3h)⁻¹, the arithmetic means yield forecasts slightly better than the GH barycenters. The reason can be traced back to Fig. 1, where a large rainfall area is forecasted by the arithmetic means (Fig. 1c) because the diffusion effect is unexpectedly in accordance with the observed rainfall area (Fig. 1a). In contrast, individual forecasts similar to the deterministic forecasts tend to predict a rainfall area much smaller than that of the observations. As a result, the GH barycenters become slightly worse than the arithmetic means in predicting the rainfall area.

Fig. 6

FSSs of the MEPS forecasts of consecutive 03-hour precipitation given by the deterministic forecasts, the ensemble means, and the GH bary-centers between 00–09 JST on July 4th, 2020 over Kyushu. A fixed spatial scale of 15 km is used for all forecasts.

The computing program for the barycenters in Fig. 5 is parallelized along the direction of ensemble members, i.e., each processor only works with a subset of ensemble members. With 20 Intel Xeon processors and the domain consisting of 311 × 242 grid points, each GH barycenter takes three minutes to calculate. The running time can be accelerated considerably if parallelization in the x and y directions is employed. Since all GH barycenters are independent with respect to different lead times, they can be produced in parallel. This enables GH barycenters to be deployed in real-time.

4. Discussions and conclusions

It is well-known in rainfall ensemble forecasts that ensemble means suffer substantially from the diffusion effect resulting from the averaging operator. Therefore, ensemble means are usually not comparable with any ensemble members, and as a result, are rarely used in practice. The use of the arithmetic average to compute ensemble means is equivalent to the definition of ensemble means as centers of mass of all ensemble members where each member is considered as a point in a high-dimensional Euclidean space. This study uses the limitation of ensemble means as evidence to support the viewpoint that the geometry of rainfall distributions is not the familiar Euclidean space, but a different metric space associated with a certain distance. The rigorously mathematical theory underlying this space has already been developed in the theory of OT with various applications in other disciplines, of which objects are the same kind of distributions as rainfall distributions.

In the theory of OT, all distributions are required to have the same total mass. This requirement is, of course, rarely satisfied in rainfall ensemble forecasts. We, therefore, develop the geometry of rainfall distributions from an extension of OT called UOT. This geometry is associated with the GH distance defined in UOT. This distance is the optimal cost to push a source distribution to a destination distribution with penalties on the mass discrepancy between mass transportation and original mass distributions. The applications of the new geometry of rainfall distributions in practice are enabled by the fast and scalable Sinkhorn-Knopp algorithms, in which GH distances or GH barycenters can be approximated in real-time. By replacing arithmetic means with GH barycenters, the diffusion effect is avoided. Furthermore, new ensemble means, with respect to the GH distance, being placed side-by-side with deterministic forecasts provide useful information for forecasters in decision-making.

A new view on the geometry of rainfall distributions should provide solutions for a broader range of problems, not limited to ensemble means. We now try to tackle the reason underlying the resemblance of the ensemble means and the observations for one-dimensional cumulative distributions in Fig. 3b that is left in the introduction. In the metric space defined by the GH distance, GH barycenters are expected to approach observations with increasing the number of ensemble members. Recall that the 2-Wasserstein distance is equivalent to the Euclidean distance of inverses of cumulative distributions. This suggests that to grasp the convergence with respect to the GH distance, a distance similar to the 2-Wasserstein distance, GH barycenters should be plotted in cumulative forms. As expected, Fig. 7 shows that when the number of ensemble members increases from 20 (MEPS) to 100 (LETF100) and 1000 (LETKF1000) (see Duc et al. 2001, for detailed descriptions of the three ensemble prediction systems), the GH barycenters gradually approach the observations. However, what is more surprising is that the arithmetic means also converge to the GH barycenters. This explains why the arithmetic means converge to the observations in Fig. 3b.

Fig. 7

As Fig. 3b but with the ensemble forecasts of (a) MEPS, (b) LETKF100, and (c) LETKF1000. Figure 3b is reproduced in Fig. 7c for comparison. The number of ensemble members increases from 20 in MEPS to 100 and 1000 in LETKF100, and LETKF1000, respectively.

Since arithmetic means are, in fact, Euclidean barycenters, this raises a question on how we explain the convergence of two barycenters with increasing the number of ensemble members. In general, it is easy to show a counter-example for this property, e.g., many pairs of ensemble members with a fixed Wasserstein mean in Fig. 2b. Therefore, we hypothesize that this is a special property of rainfall ensemble forecasts in numerical weather prediction. In order to provide evidence for this hypothesis, Fig. 8 plots two-dimensional GH barycenters and arithmetic means from the same ensemble forecast systems in Fig. 7. Clearly, the arithmetic means again become nearly identical to the GH barycenters when the number of ensemble members reaches 1000. Thus, two-dimensional rainfall distributions also show evidence for this property as in one-dimensional distributions. Of course, this hypothesis should be verified for more cases.

Fig. 8

As Fig. 5 but with the accumulated precipitation between 00–09 JST on July 4th, 2020 and forecasts from three ensemble forecast systems: (a, b, c) MEPS, (d, e, f) LETKF100, and (g, h, i) LETKF1000.

What are the other potential applications of the UOT-based geometry of rainfall distributions? In this study, we use ensemble means to illustrate one of the potential applications of the new geometry. However, it is important to verify the performance of GH barycenters in comparison with deterministic forecasts or traditional ensemble means. This verification is usually quantified by objective verification scores as demonstrated in Fig. 6 with FSS. Due to its nature as a similarity measure, the GH distance should be a natural verification score in rainfall verification. Also, ensemble means do not make sense if forecasts show a bimodal probability distribution. In such cases, clustering needs to be deployed first, and clusters are represented by appropriate representatives. Then, the clustering can use the GH distance as a similarity measure, while clusters can be expressed by their corresponding GH barycenters. We will address these problems in the near future.

Data Availability Statement

The datasets and source codes generated and/or analyzed in this study are available at https://github.com/leducvn/uot4ens.

Acknowledgments

This work was supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) through the Program for Promoting Researches on the Supercomputer Fugaku JPMXP1020351142 ‘Large Ensemble Atmospheric and Environmental Prediction for Disaster Prevention and Mitigation’ (hp200128, hp210166, hp220167), and JST Moonshot R&D project (grant no. JPMJMS2281).

Appendix: Statistics of the forecast skill

In this section, all quantities are given in observation space. First, we suppose that an ensemble forecast with K ensemble members is equivalent to K samples randomly drawn from a multivariate normal distribution , where x_f is the forecast mean, and Q is the forecast error covariance. Thus, any ensemble member x_k can be written under the form

  

where ε_k is a realization of forecast errors . The corresponding observation y is assumed to be the true state x_t, which is unknown, contaminated by observation errors

  

where ε_o is a realization of observation errors , and R is the observation error covariance.

We define the forecast skill to be the difference between the ensemble mean and the observation y

  

where we use (A1) and (A2) to obtain the last expression. Clearly, s is a random variable, and it is straightforward to calculate its statistics

  

  

The right-hand sides of (A4) and (A5) are derived using the fact that are independent.

In order to get the final forms of (A4) and (A5), we need to make an assumption on the true state x_t. Since x_f is the mode of the probability distribution of the forecasts , we assume that x_f is a good approximation of x_t

  

This means rather than a random variable, x_t is considered as a fixed quantity given approximately by x_f. Under this assumption, (A4) and (A5) respectively become

  

  

If observation errors R are negligible compared to forecast errors Q, (A8) points out that asymptotically converges to y with the error being proportional to .

The assumption (A6) can be further relaxed only by requiring x_t to follow the same probability distribution of the forecasts

  

where ε_t is a realization of forecast errors . This means x_t is considered as a random variable now, and is indistinguishable from all ensemble members. Under this assumption, (A4) and (A5) respectively become

  

  

Again, if observation errors R are negligible, (A11) represents the well-known spread-skill relationship in ensemble forecast.

References

•  Benamou,  J.-D.,  G.  Carlier,  M.  Cuturi,  L.  Nenna, and  G.  Peyré, 2015: Iterative Bregman projections for regularized transportation problems. SIAM J. Sci. Comput., 37, A1111–A1138.
•  Blondel,  M.,  V.  Seguy, and  A.  Rolet, 2018: Smooth and sparse optimal transport. Proceeding of International Conference on Artificial Intelligence and Statistics, 880–889.
•  Chapel,  L.,  R.  Flamary,  H.  Wu,  C.  Févotte, and  G.  Gasso, 2021: Unbalanced optimal transport through non-negative penalized linear regression. Proceeding of 35th Conference on Neural Information Processing Systems, 18 pp. [Available at https://arxiv.org/abs/2106.04145.]
•  Chizat,  L.,  G.  Peyré,  B.  Schmitzer, and  F. X.  Vialard, 2018a: Unbalanced optimal transport: geometry and Kantorovich formulation. J. Functional Anal., 274, 3090–3123.
•  Chizat,  L.,  G.  Peyré,  B.  Schmitzer, and  F. X.  Vialard, 2018b: Scaling algorithms for unbalanced transport problems. Math. Comput., 87, 2563–2609.
•  Cuturi,  M., 2013: Sinkhorn distances: Lightspeed computation of optimal transport. Adv. Neural Inf. Process. Syst., 26, 2292–2300.
•  Duc,  L.,  T.  Kawabata,  K.  Saito, and  T.  Oizumi, 2021: Forecasts of the July 2020 Kyushu heavy rain using a 1000-member ensemble Kalman filter. SOLA, 17, 41–47.
•  Farchi,  A.,  M.  Bocquet,  Y.  Roustan,  A.  Mathieu, and  A.  Quérel, 2016: Using the Wasserstein distance to compare fields of pollutants: Application to the radio-nuclide atmospheric dispersion of the Fukushima-Daiichi accident. Tellus B, 68, 31682, doi:10.3402/tellusb.v68.31682.
•  Feyeux,  N.,  A.  Vidard, and  M.  Nodet, 2018: Optimal transport for variational data assimilation. Nonlinear Processes Geophys., 25, 55–66.
•  Frogner,  C.,  C.  Zhang,  H.  Mobahi,  M.  Araya, and  T. A.  Poggio, 2015: Learning with a Wasserstein loss. Adv. Neural Inf. Process. Syst., 2053–2061.
•  Ishida,  J.,  K.  Aranami,  K.  Kawano,  K.  Matsubayashi,  Y.  Kitamura, and  C.  Muroi, 2022: ASUCA: the JMA operational non-hydrostatic model. J. Meteor. Soc. Japan, 100, 825–846.
•  Janati,  H.,  B.  Muzellec,  G.  Peyré, and  M.  Cuturi, 2020: Entropic optimal transport between unbalanced gaussian measures has a closed form. Adv. Neural Inf. Process. Syst., 33, doi:10.48550/arXiv.2006.02572.
•  Kantorovich,  L. V., 1942: On translation of mass. Dokl. AN SSSR, 37, 227–229 (in Russian).
•  Kobayashi,  K.,  L.  Duc,  T.  Oizumi, and  K.  Saito, 2020: Ensemble flood simulation for a small dam catchment in Japan using nonhydrostatic model rainfalls. Part 2: Flood forecasting using 1600-member 4D-EnVarpredicted rainfalls. Nat. Hazards Earth Syst. Sci., 20, 755–770.
•  Kobayashi,  K.,  L.  Duc,  T.  Kawabata,  A.  Tamura,  T.  Oizumi,  K.  Saito,  D.  Nohara, and  T.  Sumi, 2023: Ensemble rainfall–runoff and inundation simulations using 100 and 1000 member rainfalls by 4D LETKF on the Kumagawa River flooding 2020. Prog. Earth Planet. Sci., 10, 5, doi: 10.1186/s40645-023-00537-3.
•  Li,  L.,  A.  Vidard,  F.-X.  Le Dimet, and  J.  Ma, 2018: Topological data assimilation using Wasserstein distance. Inverse Problems, 35, 015006, doi:10.1088/1361-6420/aae993.
•  Liero,  M.,  A.  Mielke, and  G.  Savaré, 2018: Optimal entropy-transport problems and a new Hellinger-Kantorovich distance between positive measures. Inventiones Mathematicae, 211, 969–1117.
•  Métivier,  L.,  R.  Brossier,  Q.  Mérigot,  E.  Oudet, and  J.  Virieux, 2016: Measuring the misfit between seismograms using an optimal transport distance: Application to full waveform inversion. Geophys. J. Int., 205, 345–377.
•  Ono,  K.,  M.  Kunii, and  Y.  Honda, 2021: The regional modelbased Mesoscale Ensemble Prediction System, MEPS, at the Japan Meteorological Agency. Quart. J. Roy. Meteor. Soc., 147, 465–484.
•  Peyré,  G., and  M.  Cuturi, 2019: Computational optimal transport: With applications to data science. Foundations and Trends^® in Machine Learning, 11, 355–607.
•  Reich,  S., and  C.  Cotter, 2015: Probabilistic Forecasting and Bayesian Data Assimilation. Cambridge University Press, 308 pp.
•  Roberts,  N. M., and  H. W.  Lean, 2008: Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon. Wea. Rev., 136, 78–97.
•  Saito,  K.,  T.  Fujita,  Y.  Yamada,  J.  Ishida,  Y.  Kumagai,  K.  Aranami,  S.  Ohmori,  R.  Nagasawa,  S.  Kumagai,  C.  Muroi,  T.  Kato,  H.  Eito, and  Y.  Yamazaki, 2006: The operational JMA nonhydrostatic mesoscale model. Mon. Wea. Rev., 134, 1266–1298.
•  Sambridge,  M.,  A.  Jackson, and  A. P.  Valentine, 2022: Geophysical inversion and optimal transport. Geophys. J. Int., 231, 172–198.
•  Santambrogio,  F., 2015: Optimal Transport for Applied Mathematicians. Progress in Nonlinear Differential Equations and Their Applications, No. 87, Birkhäuser, New York, 380 pp.
•  Sato,  R.,  M.  Yamada, and  H.  Kashima, 2020: Fast unbalanced optimal transport on a tree. Adv. Neural Inf. Process. Syst., 33, doi:10.48550/arXiv.2006.02703.
•  Sinkhorn,  R., and  P.  Knopp, 1967: Concerning nonnegative matrices and doubly stochastic matrices. Paci. J. Math., 21, 343–348.
•  Tamang,  S. K.,  A.  Ebtehaj,  P. J.  van Leeuwen,  D.  Zou, and  G.  Lerman, 2021: Ensemble Riemannian data assimilation over the Wasserstein space. Nonlinear Processes Geophys., 28, 295–309.
•  Vanderbecken,  P. J.,  J.  Dumont Le Brazidec,  A.  Farchi,  M.  Bocquet,  Y.  Roustan,  É.  Potier, and  G.  Broquet, 2023: Accounting for meteorological biases in simulated plumes using smarter metrics. Atmos. Meas. Tech., 16, 1745–1766.
•  Villani,  C., 2009: Optimal Transport: Old and New. Springer Verlag, Berlin, 976 pp.
•  Yang,  Y.,  B.  Engquist,  J.  Sun, and  B. F.  Hamfeldt, 2018: Application of optimal transport and the quadratic Wasserstein metric to full-waveform inversion. Geophysics, 83, R43–R62.