Do Dry GCMs Generate QBO-like Oscillation?

Abstract

The effect of vertical discretization methods and vertical resolution on Quasi-Biennial Oscillation (QBO)-like oscillations that can occur in mechanistic General Circulation Models (dry GCMs) is investigated. Two models are compared. One model uses the spectral method in the horizontal direction but the finite difference method in the vertical direction (VFD model), while the other is a three-dimensional spectral model that uses the spectral method for discretization in both the horizontal and vertical directions (3DS model). Both models include horizontal hyperdiffusion, simple Newtonian cooling and Rayleigh friction, but as they are dry models, they do not include the effects of moist convection, and no explicit vertical diffusion is used, following a previous study. Long-term numerical integrations of these models show that the 3DS model does not generate QBO-like oscillations at the vertical resolution settings used. On the other hand, the VFD model generates QBO-like oscillations at low vertical resolution, but no QBO-like oscillations at higher vertical resolution. Wavenumber-frequency spectral analyses of wave disturbances show that, in the VFD model, the amplitude of the waves at the sigma-level near the central altitude of the QBO-like oscillations is highly dependent on the vertical resolution of the model. Analyses of the wave contribution to the vertical momentum fluxes and additional numerical experiments show that in the higher vertical resolution setting, steady eastward zonal winds form above the altitude corresponding to the tropopause, and these zonal winds suppress the upward propagation of eastward moving waves. Transformed Eulerian mean analyses are also done for the results of the VFD models to investigate the contribution of the residual circulation and the wave-mean-flow interaction to the QBO-like oscillation.

1. Introduction

The Quasi-Biennial Oscillation (QBO) is a periodic reversal in the direction of the zonal mean zonal wind with a downward shift in the phase of the zonal wind in the tropical stratosphere. This phenomenon was discovered by Ebdon (1960), Ebdon and Veryard (1961), and Reed et al. (1961), and subsequent theoretical work by Lindzen and Holton (1968) proposed the basic mechanism of this phenomenon, namely that such oscillations are caused by the wave-mean-flow interaction. The waves considered in that theory were gravity waves, but Holton and Lindzen (1972) updated the theory to consider Kelvin waves and mixed Rossby-gravity (MRG) waves, which had by then been identified. Regarding which types of waves actually drive the QBO, Dunkerton (1997) used a two-dimensional numerical model to show that Kelvin waves and MRG waves alone cannot provide enough momentum flux to cause oscillations with realistic period and structure due to the presence of Brewer-Dobson upwelling in the real atmosphere, and that gravity waves play an important role in driving the QBO. Indeed, recent studies using modern high-resolution General Circulation Models (GCMs) and reanalysis data have shown that not only large-scale waves such as Kelvin and MRG waves, but also small-scale gravity waves are important in driving the QBO. and that for the zonal mean zonal wind acceleration, both Kelvin waves and small-scale gravity waves contribute to the eastward acceleration, while gravity waves are mainly responsible for the westward acceleration (see Anstey et al. 2022, the latest comprehensive review of the QBO, and references therein).

The waves driving the QBO are thought to be mainly excited by moist convection in the tropics, and the studies using modern GCMs mentioned above have naturally included the moist process in their models. In contrast, Yao and Jablonowski (2015, hereafter referred to as YJ2015) performed numerical experiments with four dry dynamical cores, which are options in NCAR’s Community Atmosphere Model, version 5 (CAM5), and showed that QBO-like oscillations can be obtained. The four dynamical cores were, the spectral transform semi-Lagrangian (SLD) model, finite-volume (FV) model, spectral transform Eulerian (EUL) model, and spectral element (SE) model, and there simple Newtonian temperature relaxation and Rayleigh friction were incorporated (hereafter, we refer to dynamical cores with these effects as dry GCMs). YJ2015 investigated how the choice of dynamical core affects the generation of QBO-like oscillations. Whereas three of the four dry GCMs used in that study, SLD, EUL, and SE models, generated QBO-like oscillations with largely different amplitudes and periods, the FV model did not generate QBO-like oscillations. In YJ2015, the cause of the difference in the occurrence/non-occurrence of QBO-like oscillations was explored to some extent, with the FV model where QBO-like oscillations did not occur clearly having less wave activity than the other three models, and this was thought to be the cause of the difference in the occurrence/non-occurrence of QBO-like oscillations. However, it is not clear what was responsible for such a difference in the magnitude of wave activity, although some analysis of the instability of the calculated fields was done there. Furthermore, there is a possibility that the solutions without QBO-like oscillations, i.e., with less wave activity, could be the true solution if we were able to solve the governing equation of the YJ2015 setting analytically without any discretization error at all. This possibility was also mentioned in YJ2015, but each of the four dynamical cores used there differs significantly in aspects other than vertical discretization, and how the methods and accuracy of vertical discretization actually affect the degree of wave activity and the occurrence/non-occurrence of QBO-like oscillations has not been explored.

Based on the above background, the purpose of the present manuscript is not to explore a realistic QBO but to investigate how the vertical discretization method and accuracy affect the occurrence/non-occurrence of QBO-like oscillations in dry GCMs, by conducting numerical experiments using two dry GCMs with different vertical discretization methods, and comparing them with different vertical discretization points. Two models are used here: one is a model similar to the EUL used in YJ2015, using the spectral method with the spherical harmonic expansion in the horizontal direction and the finite difference method in the vertical direction; the other is a three-dimensional spectral model based on the formulation of Ishioka et al. (2022). The remainder of the present manuscript is organized as follows. In Section 2, descriptions of two models and experimental settings are presented. Results are shown in Section 3. In Section 4, results of additional numerical experiments are shown. Summary and discussion are given in Section 5.

2. Methods

2.1 Model description

We use two dynamical cores to study the effect of different vertical discretizations on the occurrence/non-occurrence of QBO-like oscillations. One is a three-dimensional spectral model (3DS model) constructed on the basis of the formulation presented by Ishioka et al. (2022). The model uses the primitive equations in σ-coordinate on a rotating sphere as the governing equations and the dependent variables are expanded by spherical harmonics in the horizontal direction and Legendre polynomials in the vertical direction. Time integration is performed using AM2*/AX2* method, which is an IMEX (Implicit-explicit linear multistep) method proposed by Durran and Blossey (2012), with a combination of the implicit trapezoidal scheme and a third-order three-stage Runge-Kutta method for the computation of initial two steps. In time integration, the semi-implicit method where linear gravity wave components are computed separately is adopted. For more details on the system of equations and numerical implementation, as well as the results of validation with standard test cases such as Held and Suarez (1994) and Polvani et al. (2004), see Ishioka et al. (2022). In the present manuscript, numerical experiments are carried out using the 3DS model with two settings of 85 and 170 vertical truncation wavenumbers of the Legendre polynomials (the number of vertical grid points is 128 and 256, respectively). Each setting is referred to as M85 and M170, respectively, in the following. The horizontal truncation wavenumber is set as T63, that is, the triangular truncation wavenumber of the spherical harmonic expansion is 63. The horizontal grid setting used for the spectral transform method is 256 × 128 (longitude × latitude). The other is a vertical finite difference (VFD) model, which has the same formulation as the three-dimensional spectral model above, except that it uses the finite difference method for vertical discretization. The implementation of vertical difference in this VFD model is based on the description in Chapter 8 of Durran (2010), which is similar to Hoskins and Simmons (1975) and Bourke (1974). Energy conservation in discrete form is also considered following Corby et al. (1972). The vertical grid point distribution of the VFD model is based on YJ2015. However, as YJ2015 uses a hybrid coordinate, the following procedure is used to approximate and convert them to the corresponding σ-coordinates. All YJ2015 numerical experiments were carried out with 55 vertical layers, where the pressure p at each interface of the layers was given by the following equation (Eq. A1 of YJ2015),

  

where p_s is the surface pressure, p₀ = 1000 hPa, and (a_k+1/2, b_k+1/2) are predetermined constants (Table A1 of YJ2015). In the present manuscript, assuming p_s ≈ p₀, each of the model interface σ-level of the VFD with 55 layers is set as follows:

  

The VFD model with 55 layers, where the σ-levels are defined in this way, is referred to as the L55 in the present manuscript as the standard setting. In the present manuscript, numerical experiments are also carried out for the VFD model in a setting with higher vertical resolution. In those, 110 layers are used, which will be referred to as L110. There, each layer defined by the L55 is divided into two layers using cubic spline interpolation in the log σ coordinate, so that the layer depths vary smoothly. As with the 3DS model, the VFD model has also been tested in standard test cases such as Held and Suarez (1994) and Polvani et al. (2004) (not shown). The vertical grid point distributions are shown in Fig. 1, including those of the 3DS model. Note that for the VFD models, the σ-coordinates of the midpoint of each layer are shown.

Fig. 1

Vertical grid distributions for (L55 and L110) VFD models and (M85 and M170) 3DS models. In the top panel, σ is shown on a linear scale, whereas in the bottom panel, σ is shown on a logarithmic scale.

2.2 Experimental settings

The basic setup of the numerical experiments in the present manuscript follows that of YJ2015. First, the forcing introduced in Held and Suarez (1994) is imposed. That is, a Rayleigh friction is added to the equations of motion at low levels (σ > 0.7), and a Newtonian relaxation towards an equilibrium state is imposed on the evolution equation of the temperature field. The atmosphere is a dry atmosphere and the effects of topography, seasonal variations and diabatic processes other than the Newtonian relaxation are not included. Furthermore, a sponge layer is introduced in the upper layer of the model according to YJ2015. There, Rayleigh friction is applied only to the zonal flow; YJ2015 imposed a Rayleigh friction coefficient K_r(p/p₀) determined as a function of p/p₀ in the region where the air pressure p is smaller than 1 hPa. As the models used in the present manuscript use the σ-coordinate system in the vertical direction, full compliance with this setting would incur some extra computational cost, so a form of this setting is mimicked, where the Rayleigh friction coefficient K_r is set as K_r(σ) for σ < 0.001. For the horizontal diffusion term, the models in the present manuscript use the same setting as Held and Suarez (1994), i.e., a hyperviscosity of a Laplacian raised to the fourth power (∇⁸) is imposed on both the wind and temperature fields, and the e-folding time for the horizontal truncation wavenumber is 0.1 days. This setting differs from the EUL model of YJ2015, but this difference will be mentioned again in Section 4.1. Note that no explicit vertical diffusion is used, following YJ2015.

All numerical experiments in the present manuscript are performed as follows. The initial state is an isothermal stationary atmosphere at 300 K with a small temperature perturbation, from which a time integration is performed for a spin-up period of 200 days. The results of the last day of the spin-up period (day 200) are stored and used again as the initial conditions for numerical time integration. Whereas YJ2015 performed ensemble numerical experiments and constructed some initial states using reanalysis data, we do not use such an approach. One reason for this is that the system of equations is essentially chaotic and the states after sufficient time evolution are not sensitive to the initial state, at least statistically. Another reason is that the initial state based on reanalysis data should contain waves that cause the QBO in the real atmosphere, and such waves could cause QBO-like oscillations in the numerical experiments in the dry GCMs used in the present manuscript, at least in the early stages of time integration. As the aim of the present manuscript is to investigate whether QBO-like oscillations are spontaneously induced by waves excited in the dry GCMs, reanalysis data are not used.

The time step used for the time integration is 720 s for all vertical resolutions (L55 and L110) for the VFD model, but for the 3DS model, it is 120 s for the spin-up phase for M85 and 300 s thereafter, 60s for the spin-up phase for M170 and 150 s thereafter. This is because the vertical resolution in the 3DS model is higher than in the VFD model near the lower atmospheric boundary, and also because during the spin-up period, the deviation from the balanced state is large and gravity waves with higher frequencies are strongly excited. It is certainly possible that differences in the time steps could affect the experimental results. However, we have confirmed that the results show little difference depending on the the time steps by actually performing the calculation with a time step of 150 s for all the models, so the above time steps are adopted to reduce the calculation time.

2.3 Spectral analysis methods

a. Temperature disturbances

Wavenmnber-frequency spectral analyses of the temperature field at low latitudes are performed as follows. After 3600 days of time integration, 900 days of hourly data are stored. We then calculate the temperature of specified σ-levels by linear interpolation, as the VFD and the 3DS model have different vertical grid point distributions and it is not appropriate to compare the results obtained in the original σ-levels. The symmetric part T_s and the antisymmetric part T_a of the temperature field with respect to the equator are calculated and the discrete 2D Fourier transform is performed at each latitude as follows:

  

  

  

Here, T(λ,ϕ,t) is the temperature field, λ is the longitude, ϕ is the latitude, t is the time, λ_j = 2π_j/J (j = 0,1,…, J − 1) is the grid points in the longitudinal direction, and J = 256 is the number of grid points, t_k (k = 0, 1, …,K − 1) is the time of the hourly data, K = 900 × 24 is the number of the stored hourly data, m = −N, …, 0, 1, …, N is the zonal wavenumber, N = 63 is the horizontal truncation wavenumber, v = 0, Δv, …, (K/2 − 1)Δv is the frequency, and Δv = 1/900 day⁻¹. Power spectral density P_s/a(m, v, ϕ) is defined as follows:

  

By averaging P_{s, a}(m, v, ϕ) in 15°S–15°N, we obtain the wavenumber-frequency spectra of the temperature field for the low latitude region.

b. Vertical momentum flux

We also conduct spectral analyses of the vertical momentum flux in the following steps. After 3600 days of time integration, we stored 900 days of hourly velocity data interpolated to a prescribed p-coordinate. Each level of this p-coordinate is set to p = p₀σ for each level of the original σ-coordinate. The following discrete 2D Fourier transform is then performed at each pressure level and latitude grid, analogous to the previous subsection:

  

  

Here, the primed quantities are the perturbations from the zonal mean field, u is the zonal velocity, and ω is the vertical pressure velocity. The zonal wavenumber m = −N, …, −1, 1, …, N, and the number of the hourly data points is set as either K = 900 × 24 or 120 × 24, depending on whether the period of days to be analyzed is 900 days or 120 days. The vertical momentum flux is then summed for each phase velocity as follows:

  

  

Here, the overbar denotes the zonal mean, Re{·} denotes the real part of the complex number, the dagger denotes the complex conjugate, c_p(m, v) is the zonal phase velocity of each wave, defined by c_p(m, v) = 2πav/m, where a is the radius of the earth. In (10), the bins for the phase velocities are determined by setting c = 0, ±1, ±2, … (the unit is m s⁻¹), and Δc = 0.5 m s⁻¹. Also note that in (9) and (10), Δv is set as either 1/900 day⁻¹ or 1/120 day⁻¹, depending on whether the period of days to be analyzed is 900 days or 120 days. By averaging and in an equatorial region of 2°S–2°N at each pressure level, we can examine how the wave components contribute to the vertical momentum flux in the wavenumber-frequency space and the zonal phase velocity space, respectively. Such an analysis was also carried out, for example, in Fig. 18 in Horinouchi and Yoden (1998).

3. Results

3.1 Zonal wind profile and static stability distribution

In order to investigate whether different vertical discretization methods and different resolutions affect whether QBO-like oscillations occur or not, the time evolution of the zonal mean zonal wind over the equatorial region (averaged in 2°S–2°N) is shown for the VFD (L55 and L110) and 3DS (M85 and M170) models (Fig. 2). The time evolution of the zonal mean zonal wind obtained by the VFD models is strongly dependent on the vertical resolution, with the L55 VFD model showing a QBO-like oscillation (Fig. 2a), while the L110 VFD model shows no oscillatory variation after 5 years of time integration (Fig. 2c). In the L55 VFD model, the period of the QBO-like oscillation is about 3 years, which is considerably shorter than that obtained in the EUL of YJ2015 (about 15 years). Although the periods do not match, the downward phase propagation of QBO-like oscillations in the L55 VFD model is similar to that of the EUL in YJ2015. That is, the region with eastward wind descends to around σ = 0.02, while the region with westward wind only descends to around σ = 0.01. The 3DS model also shows dependence on vertical resolution, although not as much as the VFD, and no QBO-like oscillations occur at either vertical resolution. The M85 3DS model (Fig. 2b) shows dominant eastward winds in 0.0002 < σ < 0.05, while the M170 3DS model (Fig. 2d) shows westward winds in 0.001 < σ < 0.002. Even in models that did not generate QBO-like oscillations, however, the phase propagates downwards in the early stages of time evolution in the first year (M85 3DS) or for about four years (L110 VFD and M170 3DS). This downward phase propagation may be due to the shortness of the spin-up period to reach the equilibrium state. The 200 day of spin-up period simply follows the setting of Held and Suarez (1994), who mainly focused on the troposphere where 200 days of spin-up period seems to be sufficient. In this study, however, we focus mainly on the stratospheric QBO-like oscillations, which have much longer periods than 200 days. However, the data analyses in the following sections are carried out well after the equilibrium state has been reached, so the analyses are not affected by this short spin-up period and the initial downward phase propagation. The initial downward propagation of the phase in these models is similar to the results of the FV model of YJ2015, where no QBO-like oscillations occur.

Fig. 2

Time-σ cross section of zonal mean zonal wind averaged in 2°S−2°N (unit is m s⁻¹). The monthly (30-day) mean data after the spin-up period is shown. The horizontal axis is the model year (360 days) and the vertical axis is σ. Contour interval is 4 m s⁻¹, (a) L55 VFD, (b) M85 3DS. (c) L110 VFD, and (d) M170 3DS model.

Whereas the occurrence of QBO-like oscillations at the equator depends on the resolution as well as the vertical discretization method, the meridional structure of zonal winds depends mainly on the vertical discretization method. Figure 3 shows latitude-σ cross section of the zonal and monthly mean zonal wind, where the average is taken over day 2970–3000. In the region where σ > 0.1, the location and strength of the eastward jets do not change and its structure is similar in all models. On the other hand, in the region where σ < 0.1, the latitudinal extent of the strong zonal wind over the equator depends less on the vertical resolution and mainly on the vertical discretization method. Specifically, the eastward wind region is 10°S–10°N in the VFD model (Figs. 3a, c), but 20°S–20°N in the 3DS model (Figs. 3b, d). For the correspondence with the EUL model in YJ2015, the result of the L55 VFD model is consistent in that the latitudinal extent of the eastward wind area over the equator is 10°S–10°N and the extent of the westward wind area is 20°S–20°N (Fig. 3a).

Fig. 3

Latitude-σ cross section of zonal and monthly mean zonal wind, where the average is taken over day 2970–3000 (unit is m s⁻¹). The horizontal axis is latitude and the vertical axis is σ. Contour interval is 4 m s⁻¹ (a) L55 VFD, (b) M85 3DS. (c) L110 VFD, and (d) Ml70 3DS model.

As shown above, the zonal mean zonal wind structure differs significantly depending on both the vertical discretization method and the vertical resolution, but the zonal mean static stability fields show little difference among the models. The result of the L55 VFD model is shown in Fig. 4 as a representative example. In this experimental setting, there are two distinct regions over the equator; a low static stability region in the lower atmosphere (σ > 0.2) and a high static stability region in the upper atmosphere (σ < 0.1). Accordingly, we hereafter refer to this σ-level of 0.1 as the “tropopause” in the equatorial region.

3.2 Spectral analysis

a. Wavenumber-frequency spectra of the temperature disturbances

Next, we analyze the wave activity to investigate the causes of the differences in the occurrence/non-occurrence of QBO-like oscillations in different models. Figure 5 shows the results of the wavenumberfrequency analyses of the temperature field at σ = 0.002, the central altitude of the QBO-like oscillations observed in the L55 VFD model in Fig. 2a, using the method described in Section 2.3 for four different model setups. There, the negative (positive) zonal wavenumber in each panel represents westward (eastward) propagation. Comparing the four models, the L55 VFD model has the strongest wave activity among the four models, especially for the symmetric component (Fig. 5a), which is consistent with the finding that only the L55 VFD model generates QBO-like oscillations. A closer look at the spectra shows that, regardless of the vertical resolution, in both the VFD and 3DS models there are spectral peaks at low frequencies and low zonal wavenmnbers (∣m∣ < 6, v < 0.3 cpd), especially for the symmetric component, near dispersion curves corresponding to Rossby and Kelvin waves (Figs. 5a, c, e, g). However, the extent and intensity of such spectral peaks vary with model settings, particularly for the symmetric components. Below we will focus on the regions where the value of the common logarithm shown in Fig. 5 is larger than −4. For the symmetric components of the L55 VFD model (Fig. 5a), the intensity and extent of the spectral peak of the westward and eastward components are comparable. However, for the L110 VFD model (Fig. 5e), the peak for eastward components is weaker. For the L55 VFD, a strong and broad peak is seen in the region of the dispersion curve corresponding to the Kelvin wave of h > 12 m, while for the L110 VFD it is mainly seen only near the region corresponding to the Kelvin wave of h ≈ 200 m. Here h is the equivalent depth of the waves. With regard to the 3DS models, the M85 and M170 3DS models have similar intensity and extent of the spectral peaks for the westward symmetric component, whereas the M85 3DS model has a narrower spectral peak for the eastward symmetric component (Figs. 5c, g).

Fig. 4

Latitude-σ cross section of Brunt-Väisälä frequency of zonal mean field at day 3000 in the time evolution of the L55 VFD model (unit is s⁻¹). The horizontal axis is latitude and the vertical axis is σ. Contour interval is 2.5 × 10⁻³ s⁻¹

Fig. 5

Wavenumber-frequency spectra of the temperature field P_s/a σ = 0.002 averaged over 15°S–15°S. The units are K² and drawn in their common logarithm. (a, b) L55 VFD, (c, d) M85 3DS, (e, f) L110 VFD, (g, h) M170 3DS model. The left panel of each pair is for the symmetric components and the right one is for the anti-symmetric components. The dispersion curves are drawn overlaid with the following three equivalent depths h: (solid line) h = 200 m, (dashed line) 50 m, and (dotted line) 12 m. For the symmetric component, the eastward dispersion curve through the origin is for Kelvin waves; for the antisymmetric component, the dispersion curve leading from a relatively high frequency eastward to a low frequency westward is for Rossby-gravity waves; the relatively low frequency (v < 0.15 cpd) westward component of the symmetric and antisymmetric correspond to Rossby waves, and parabolic dispersion curves at relatively high frequencies (v > 0.3 cpd) in the symmetric and antisymmetric components correspond to gravity waves.

As seen above, depending on whether QBO-like oscillations were present or not, the level of wave activity was indeed very different, but care must be taken when interpreting the results, as the upward propagating waves may be filtered by the mean zonal wind, which varies considerably among the models. Since the vertical wavelengths become short and the vertical group velocity approaches zero as the gravity waves approach their critical level, where their phase velocity is equal to the background horizontal wind velocity, the different wave activities seen above may be the result of the different zonal wind profiles obtained in the different models. To investigate this effect, we perform spectral analyses at σ = 0.1, below which the zonal wind profiles are similar in all the models used here. The results are shown in Fig. 6. All the models show similar wave activity at σ = 0.1, except that the L55VFD model has slightly weaker wave activity than the others, with spectral peaks at lower frequencies and lower zonal wavenumbers (∣m∣ < 6, v < 0.2 cpd) for the symmetric components. This result suggests that the strength of the upward propagating wave that enters from below σ = 0.1 is not significantly different among all the models. Thus, there are at least three possible reasons for the different wave activities at σ = 0.002; different wave filtering by the background zonal wind, different wave dissipation depending on the vertical discretization or resolution, and different wave generation at 0.002 < σ < 0.1. That is, we cannot deduce which one(s) is (are) occurring from the results shown so far.

Fig. 6

Same as Fig. 5, but results for σ = 0.1 are shown.

Fig. 7

Zonal phase velocity-pressure distributions of the vertical momentum flux in day 3600–4500 averaged over 2°N–2°S. The units are m Pa s⁻². (a) L55 VFD, (b) M85 3DS, (c) L110 VFD, (d) M170 3DS model. The solid curves show the zonal mean zonal velocity profiles averaged over the corresponding time and latitude. The value of 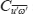shown here is multiplied by 2 × 10⁷. The color gradations are drawn on a logarithmic scale.

b. Wave contribution to the vertical momentum flux in the zonal phase velocity space

To clarify the reason why the wave activities are different at σ = 0.002 but not significantly different at σ = 0.1 as shown in the previous subsection, the wave contributions to the vertical momentum flux in the zonal phase velocity space are examined using the method described in Section 2.3. The result for day 3600–4500 is shown in Fig. 7. Note that a positive (negative) zonal phase velocity represents an eastward (westward) propagating wave and that negative values of the contributions to the momentum fluxes indicate upward fluxes of eastwardmomentum, as the fluxes are shown in the forms of . Note also that in Fig. 7, the vertical coordinate is the pressure. In Fig. 7, there is no significant difference in the dependence of the momentum fluxes on the wave phase velocity among the models in the region of p > 100 hPa, which is consistent with the fact that there was no significant difference in the spectral distribution of the temperature disturbances among the models at σ = 0.1. On the other hand, in the region of p < 100 hPa, the vertical propagation of the waves differs significantly among the models. In particular, it is clear that the differences depend on the realized zonal mean zonal wind profile (indicated by the solid curves in Fig. 7). The vertical momentum fluxes shown in Figs. 7a–d indicate that, in all the cases, the vertical propagation of the waves is significantly suppressed at the critical levels, and that the positive and negative upward flux of the eastward momentum roughly corresponds to the sign of the difference between the wave phase velocity and the zonal mean zonal wind velocity. This result suggests that the upward energy fluxes are all positive for p < 100 hPa for each phase velocity wave components. One notable difference in Fig. 7 is that in all cases except for Fig. 7a for the L55 VFD, the zonal mean zonal wind is eastward around p = 50 hPa, where the upward momentum fluxes of the eastward waves are sharply reduced, i.e., the upward propagation of the eastward waves is suppressed (Figs. 7b–d). This suppression of the vertical propagation of the eastward moving waves is also visible in Fig. 7a around p = 20 hPa, but is not as sharp as in Figs. 7b–d. These results indicate that the formation of strong eastward winds around p = 50 hPa and at higher altitudes, and the presence of sharp suppression of the vertical propagation of eastward moving waves there, determine the degree of penetration of eastward propagating waves to higher altitudes. Such suppression is not strong in Fig. 7a and the momentum fluxes of eastward propagating waves remain large up to around 2 hPa, which may be the reason why L55 VFD (Fig. 5a) shows a larger eastward component of the temperature disturbance than L110 VFD (Fig. 5e), M85 3DS (Fig. 5c) and M170 3DS (Fig. 5g).

In the L55VFD model, the mean zonal wind profile changes significantly over the 900-day period for which the spectral analysis was performed in Fig. 7. Therefore, it is necessary to consider the effect of temporal changes in the zonal wind profile, in particular to discuss the relationship between the suppression of vertical wave propagation and the zonal wind profile. For this reason, a similar analysis is performed for the L55 VFD model using 120 days of data. Figure 8 shows the results for days 3960–4080 and 4380–4500. We have chosen these periods as representative of the westward and eastward shear phases around p = 5 hPa. Here, eastward (westward) shear refers to . In Fig. 8, in both phases (Figs. 8a, b), an eastward vertical shear of the zonal mean zonal wind appears at the pressure levels around p = 20 hPa, and the vertical profile of the momentum flux shows that the upward propagation of waves is suppressed in the region of the shear, again similar to that seen in Fig. 7a. However, the suppression of upward propagation is not as sharp as that in the same altitude region in the other models, such as the L110 VFD. In addition to this, the result of the eastward phase in the L55 VFD model (Fig. 8b) shows that even in the eastward shear around p = 5 hPa, fast phase speed waves (c_p > 16 m s⁻¹) that do not reach their critical level are not sharply suppressed there and propagate higher up. This result is in contrast to that of the L110 VFD model (Fig. 7c), where eastward-moving waves are sharply reduced around p = 5 hPa even if such waves do not reach their critical levels. The above results suggest that the representation of the wave-mean-flow interaction is altered by the vertical resolution, which may be the reason why the eastward zonal wind formation around p = 50 hPa seen in the other models is not seen in the L55 VFD model.

Fig. 8

Same as Fig. 7, but analyses are conducted using 120 days data of the L55 VFD model. (a) Westward phase around p = 5 hPa for days 3960–4080, (b) Eastward phase around p = 5 hPa for days 4380–4500.

3.3 Zonal wind acceleration in the VFD models

a. Transformed Eulerian mean analyses

In order to quantitatively investigate the causes of the different zonal wind profiles obtained in the L55 VFD model and the L110 VFD model, we perform the transformed Eulerian mean analyses. The zonal wind acceleration is expressed by the following equation, the form of which follows that used in YJ2015:

  

Here, the definitions for symbols not already mentioned so far are as follows: f is the Coriolis parameter, and are the meridional velocity and the vertical pressure velocity of the residual circulation, respectively, and F_ϕ and F_p are the meridional and vertical components of the Eliassen-Palm (EP) flux vector, respectively, and X represents the residual. Each component of the meridional velocity and the EP flux vector is defined by the following equations:

  

  

  

  

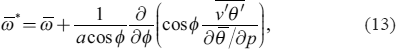where θ is the potential temperature and v is the meridional velocity. The four terms on the right-hand side of (11) are the horizontal and the vertical advection terms of the angular momentum by the residual circulation, the EP flux divergence term, which represents the acceleration due to the wave-mean-flow interaction resolved in the models, and the residual term, which represents the effect of explicitly and implicitly added diffusion, including at least the effects of the horizontal diffusion and Rayleigh friction in the experimental setting of this study. Note that when evaluating these terms from the output of the models, the derivatives are evaluated in the σ-coordinate, then transformed and interpolated to the p-coordinate and zonally averaged.

The results of the transformed Eulerian mean (TEM) analyses for day 3600 – 5000 are shown in Fig. 9, and this period captures approximately 1.3 cycles of the QBO-like oscillation in the L55 VFD model. In the remainder of this section, we focus mainly on the region above 20 hPa, where the QBO-like oscillation is seen in the L55 VFD model. Figures 9c and 9d show the acceleration due to the vertical and meridional advection, where the L55 VFD model and the L110 VFD model show similar features in the eastward shear region. That is, the eastward shear regions show strong eastward accelerations (0.2 – 0.4 m s⁻¹ day⁻¹. In the L55 VFD model, this strong eastward acceleration mainly contributes to the descent of the eastward phase of the zonal mean zonal wind. It should also be mentioned that, although not shown in the figure, the meridional advection term for both the VFD models shows westward accelerations in the eastward shear region with values of −0.1 m s⁻¹ day⁻¹ to −0.2 m s⁻¹ day⁻¹, in contrast to the YJ2015 results where the acceleration due to the meridional advection was weak (with its values in the range of ±0.03 m s⁻¹ day⁻¹). However, this acceleration by the meridional advection is overwhelmed by the strong acceleration due to the vertical advection, so that the net advection term shows the above feature.

Fig. 9

Time-pressure cross section of zonal and monthly mean zonal wind accelerations due to each TEM component, averaged over 2°N – 2°S. (a, b) total acceleration, (c, d) advection term, (e, f) EP flux divergence, (g, h) residual term, (i, j) residual term minus diffusion. The left panel of each row is for the L55 VFD model and the right panel of each row is for the L110 VFD model. The units are m s⁻¹ day⁻¹. The contours represent the zonal and monthly mean zonal wind averaged over the corresponding latitudes. The contour interval is 8 m s⁻¹.

In contrast to the advection term, the EP flux divergence term shows different features between the L55 VFD model (Fig. 9e) and the L110 VFD model (Fig. 9f). For the L55 VFD model, westward accelerations (∼ −0.1 m s⁻¹ day⁻¹) can be seen in the westward shear regions, which is a major contributor to the descent of the westward phase of the QBO-like oscillation. In the eastward shear regions for the L55 VFD model, since both westward and eastward accelerations occur, this term does not directly contribute to the descent of the eastward phase. On the other hand, in the eastward shear regions for the L110 VFD model, the acceleration due to the EP flux divergence is almost entirely westward and the westward acceleration has large absolute values (∼ −0.4 m s⁻¹ day⁻¹), almost canceling out the eastward accelerations of the advection term.

The residual term (Fig. 9g for L55 VFD model and 9h for L110 VFD model), obtained by subtracting the advection and the EP flux divergence terms seen so far from the net acceleration, has small absolute values (±0.01 m s⁻¹ day⁻¹) and it is accounted for by the diffusion tendency, both for the L55 VFD model and the L110 VFD model. This is because the residual term minus the diffusion tendency is close to zero (Fig. 9i for the L55 VFD model and Fig. 9j for the L110 VFD model), which means that the momentum budget is almost completely balanced. The diffusion term includes the hyperdiffusion, the Rayleigh friction introduced by following YJ2015 in the sponge layer (σ < 0.001), and the Rayleigh friction of Held and Suarez (1994) near the lower boundary (σ > 0.7). In the altitude region shown here, the effect of the horizontal hyperdiffusion is dominant, and the diffusion tendency has much smaller absolute values than the result of YJ2015. This is because the hyperdiffusion used in the present manuscript is the Laplacian raised to the fourth power (∇⁸), which mainly dissipates waves of small horizontal scale and has practically no effect on the large scale zonal wind.

The acceleration characteristics of the L55 and L110 VFD models differ mainly in the EP flux diver-gence in the eastward shear regions, and these differences lead to the differences in the total acceleration in the eastward shear regions. To clarify what causes this difference in the eastward shear regions, the EP flux divergence is decomposed into the meridional (Figs. 10a, b) and vertical components (Figs. 10c, d). For both the L55 and L110 VFD models, the meridional component (Figs. 10a, b) shows similar strong westward acceleration in the eastward shear regions. The vertical component (Figs. 10c, d), on the other hand, shows a much stronger eastward acceleration in the L55 VFD model, while it is not as strong in the L110 VFD model. The result that the acceleration due to the vertical component of the EP flux divergence is significantly different between the two models in the altitude range we are now considering (p < 20 hPa) is consistent with the finding in Section 3.2b that the negative associated with eastward propagating waves has larger absolute values for the L55 VFD model than for the L110 VFD model in the altitude range we are now focusing on.

Fig. 10

The EP flux divergence terms shown in Figs. 9e and 9f are shown split into the meridional component and the vertical component. (a, b) the meridional component, (c, d) the vertical component.

Before closing this subsection, we would like to mention a point that some readers may wonder about, namely, why strong shear can be maintained in the L110 VFD model, especially for the eastward shear at 10 – 6 hPa and the westward shear at 6 – 2 hPa. We believe that this is due to the weakness of the diffusion term. In this experimental setting, the diffusion term is very weak and the zonal mean zonal wind is hardly weakened directly by the diffusion. Therefore, the zonal mean winds can be maintained once they are formed in the early stages of time evolution by wave-mean-flow interactions with then abundant gravity waves.

To summarize this subsection, the downward phase propagation observed in the L55 VFD model is mainly supported by the acceleration due to the advection in the eastward wind shear region, and the wave-meanflow interaction in the westward shear region. In the L110 VFD model, the advection term causes large eastward accelerations in the eastward shear region, but these accelerations are almost canceled out by the EP flux convergence, resulting in small net accelerations. In both the L55 and L110 VFD models, the characteristics of the advection term and the meridional component of the EP flux divergence are similar. It is the vertical component of the EP flux divergence term that is mainly different between the L55 and L110 VFD models, and this difference can be attributed to the differences in the upward propagating waves.

Fig. 11

Latitude-pressure cross section of (vectors) zonal mean residual circulation, (contours) zonal mean zonal velocity, and (color map) vertical velocity of residual circulation, averaged over days 3600 – 4680. (a) L55 VFD, (b) L110 VFD model. The unit vectors represent (meridional) 0.1 m s⁻¹ and (vertical) 0.2 mm s⁻¹. The units of the color maps are m s⁻¹. The vertical component of residual circulation is converted from the pressure velocity to the geometric velocity, using the approximate relationship (see the text). The contour interval is 8 m s⁻¹.

b. Residual circulations

The TEM analysis revealed that the advection term contributes to the descent of the downward phase propagation in the L55 VFD model. However, in YJ2015, this term did not contribute significantly to the descent of the zonal wind phase. Therefore, in this subsection we will focus on the residual circulation, particularly on the vertical component, since the accelerations due to the vertical advection are larger than those due to the meridional advection. The latitudepressure cross sections of the zonal mean residual circulation averaged over days 3600 – 4680 are shown in Fig. 11. This period captures almost one cycle of the QBO-like oscillation obtained in the L55 VFD model. Note that the residual pressure velocity is converted to the residual vertical velocity using the following approximation to see the differences clearly;

  

Here, R = 287 J K⁻¹ kg⁻¹ is the gas constant for the dry atmosphere, g = 9.806 m s⁻² is the gravitational acceleration, and T₀ = 200 K is the reference temperature, which is a representative value in the altitude range shown in Fig. 11. The result for the L55 VFD model (Fig. 11a) shows a dominant downward motion (∼ −0.2 mm s⁻¹) over 5°S – 5°N in p ≲ 30 hPa. This altitude range corresponds to that in which the QBO-like oscillation occurred. This downward motion is more similar to the result of the YJ2015 SLD than the YJ2015 EUL.

On the other hand, for the L110 VFD model (Fig. 11b), while strong downward motions (∼ −0.3 mm s⁻¹) are seen in the eastward shear regions over the equator, especially for 4 hPa < p < 9 hPa and p < 1.5 hPa, weak upward motions (∼ 0.1 mm s⁻¹) are seen in the westward shear regions. This pattern of upward (downward) motion in the westward (eastward) shear zone is similar to the QBO-induced secondary circulation in the real atmosphere (Choi et al. 2002). That is, the vertical wind field is modulated by the zonal wind shear associated with the QBO through the thermal wind balance, resulting in upward (downward) motions in the westward (eastward) shear regions. Therefore, the strong eastward accelerations by the advection term in the eastward shear regions for the L110 VFD model shown in Fig. 9d appear to be due to this downward motion, induced by the secondary circulation.

To investigate the time evolution of the vertical motion in the L55 VFD model, the time series of the residual vertical pressure velocity at p = 4.9 hPa, the central pressure level of the QBO-like oscillation in the L55 VFD model, is shown in Fig. 12, where the time evolution of the zonal wind at the same level is also shown. It is clear that the time evolution of the vertical pressure velocity is followed by that of the zonal wind velocity, suggesting that the vertical motion is modulated by the zonal wind shear in a manner similar to the QBO-induced secondary circulation in the real atmosphere. In addition, the vertical velocity is predominantly downwelling, with a brief period of a weak upwelling. Taken together with the results in Fig. 11a, the downwelling, which is different from the Brewer-Dobson upwelling in the real equatorial atmosphere, is dominant in the 5°S – 5°N for the L55VFD model and this downwelling is modulated by the secondary circulation. These results show that the strong acceleration due to vertical advection in the eastward shear region for the L55 VFD model is caused by the enhancement of the downwelling by the secondary circulation.

Fig. 12

Time evolution of (dashed curve, left axis) zonal mean zonal velocity and (solid blue curve, right axis) residual vertical pressure velocity averaged over 2°N – 2°S at 4.9 hPa. The result of the L55 VFD model is shown.

4. Additional numerical experiments

4.1 Numerical experiment as close as possible to the YJ2015 EUL setting

As described in Section 2, the present manuscript uses a hyperdiffusion of the Laplacian raised to the fourth power (∇⁸) as the horizontal diffusion, following Held and Suarez (1994), while the YJ2015 EUL uses a hyperdiffusion of the Laplacian raised to the second power (∇⁴), and considering the value of the hyperdiffusion coefficient used there, for the total wavenumber of spherical harmonic functions below 50, the time constant of dissipation is smaller than the setting in the present manuscript. In addition, the Robert-Asselin time-filtered Leapfrog scheme was used as the time integration method in the YJ2015 EUL, which can also contribute to the differences in the results. To check the effects of these differences with YJ2015 EUL, a numerical experiment is carried out using the same hyperdiffusion and time integration method as for YJ2015 EUL case. The rest of the numerical setup is the same as for the standard L55 VFD model. The time evolution of the zonal mean zonal winds in this case is shown in Fig. 13. In this case, a QBO-like oscillation with a period of about 4 years is generated, which is longer than in the case of the standard L55 VFD (Fig. 2a). However, the period is still shorter than in the YJ2015 EUL case (about 15 years). This remaining difference may be due to differences in specific implementations, such as the semi-implicit method for the following reason: In order to implement the semi-implicit method, we need to specify a reference state from which the governing equations are linearized. In the present manuscript, this reference state is set to a 300 K isothermal atmosphere at rest, while such a reference state is not explicitly described in YJ2015. If the reference state is different, the behavior of the linear waves calculated with a finite time step may be different. However, pursuing this difference is beyond the scope of this paper and will not be considered further.

Fig. 13

Same as Fig. 2a, but for the L55 VFD model with setting the hyperdiffusion and time integration scheme being the same as EUL in YJ2015.

4.2 Partially higher resolution setting

As seen in Section 3.1, doubling the number of vertical layers from L55 to L110 in the VFD model eliminated QBO-like oscillations, but it was not clear at which altitude the increased resolution led to the suppression of these QBO-like oscillations. Numerical experiments were therefore conducted with a VFD model in which the vertical resolution was doubled from the L55 VFD model only at a certain altitude range. The number of the vertical grids at the altitude range shown below is doubled by cubic spline interpolation, in a similar manner to the L110 VFD model. The corresponding σ ranges and the total numbers of the vertical layers are, (a): 0.12 < σ < 0.49, L66, (b): 0.028 < σ < 0.12, L62, (c): 0.028 < σ < 0.49, L74, (d): 0.0067 < σ < 0.49, L81, and (e): 0 < σ < 0.49, L96, respectively. Figure 14 shows the time evolution of the zonal mean zonal wind for these additional numerical experiments. The experimental setup is identical to that of the L55 VFD model, except that the number of vertical grid points is increased. In Fig. 14a, a QBO-like oscillation is observed, with a period of about 3 years. In Figs. 14b and 14c, QBO-like oscillations do not occur. These two settings (Figs. 14b, c) show two altitude regions with eastward zonal wind and two altitude regions with westward zonal wind. In Fig. 14d, in the region with increased vertical resolution (0.0067 < σ < 0.49), a steady eastward wind region and a westward wind region are formed. However, in regions where the vertical resolution is not increased, QBO-like oscillations occur with a period of about 8 years. In Fig. 14e, where the vertical resolution is increased to the top of the model, three eastward and three westward wind regions are formed and no QBO-like oscillations occur. It is worth noting here that in the setting for Fig. 14b, the number of vertical grid points is only increased by seven compared to the L55 VFD, but steady and strong eastward wind region above 16 m s^-1 is formed in 0.01 < σ < 0.05 and QBO-like oscillations are no longer observed at all. In addition to this, a comparison of the results in Figs. 14e and 14d shows that in the region of 0.02 < σ < 0.05, where the vertical resolution is similarly high, an eastward wind of about 8 m s⁻¹ is commonly formed. However, the behavior in the region of σ < 0.0067, where the vertical resolution is different, is significantly different. In Fig. 14d, in which the vertical resolution in the σ < 0.0067 region is lower, QBO-like oscillations occur, whereas in Fig. 14e, in which the vertical resolution is higher, strong eastward winds of more than 16 m s^-1 are formed and no QBO-like oscillations occur. These results suggest that the vertical resolution in the σ < 0.12 region is strongly related to the formation of a steady eastward wind region, and in particular the formation of a strong eastward wind region above 16 m s⁻¹ is in turn strongly related to the non-occurrence of QBO-like oscillations.

4.3 VFD model with additional Rayleigh friction over a specific range of altitudes and latitudes

As we have seen, from comparing the results of the L55 VFD model with those of the other models, and from calculations with partially increased vertical resolution, it appears that the difference between the occurrence/non-occurrence of QBO-like oscillations is strongly related to the formation/absence of a strong steady eastward zonal wind near or above 50 hPa. To investigate the influence of this eastward wind region on the occurrence of QBO-like oscillations, an experiment is performed in which additional Rayleigh friction is applied to weaken the eastward wind in the L110 VFD model. Specifically, the friction is applied to the zonal mean zonal wind only as follows:

  

  

  

Fig. 14

Same as Fig. 2a, but for the results for partially higher vertical resolutions. The number of vertical grid points are doubled in the following σ-ranges. (a) 0.12 < σ < 0.49, (b) 0.028 < σ < 0.12, (c) 0.028 < σ < 0.49, (d) 0.0067 < σ < 0.49, and (e) 0 < σ < 0.49.

Here, k₀ is the Rayleigh friction coefficient, the value of which is set to 1/3 day⁻¹. the same as for the sponge layer, and z_* = −h₀ log σ is an approximate logarithmic pressure height, where h₀ = 7 km is the scale height. The values of the parameters are set as follows: z_b = 21.5 km, z_t = 26.5 km, H = 1 km, ϕ₀= arcsin 0.3, and L = 1/15. With such a setup, the zonal mean zonal wind is selectively weakened at −25° < ϕ < 25° and 0.02 < σ < 0.05, but the wave components (m ≠ 0) are not affected. Note that in (17), the part written as “(the other standard terms)” is the zonal mean of the terms included in the time evolution of u in the original model equations. The result of day 3600 of the standard L110 VFD model without the additional Rayleigh friction term is used as an initial state, then the time evolution is calculated thereafter with the friction term. The resulting time evolution of the equatorial zonal wind (Fig. 15) shows that, above the altitude range where the additional Rayleigh friction term is added, the zonal wind phase slowly descends for the first four years or so, after which the zonal mean zonal wind profile settles down to an almost steady state. In this case, it appears that the strong eastward zonal wind is eventually maintained above the altitude region where the additional Rayleigh friction term is added, thereby preventing the occurrence of the QBO-like oscillations in the higher altitude region. This result, together with the results of the L110 VFD model and those of Section 4.2, suggests that the occurrence/non-occurrence of the QBO-like oscillations is strongly related to the formation of a strong eastward wind region: once a strong eastward wind region is formed, the upward propagation of eastward moving waves is inhibited, suppressing the occurrence of the QBO-like oscillations.

Fig. 15

Same as Fig. 2c, but for the results for the L110 VFD model with an additional Rayleigh friction over a specific range of altitudes and latitudes (0.02 < σ < 0.05 and −25° < ϕ < 25°). The result of day 3600 of the L110 VFD model is used as the initial state, which corresponds to the leftmost year 10 in this figure.

5. Summary and discussion

5.1 Summary

In the present manuscript, with reference to YJ2015, we investigated whether QBO-like oscillations occur spontaneously in dry GCMs in a benchmark experimental setting of the Held and Suarez (1994) with an additional sponge layer, by performing several numerical experiments with different vertical discretization methods (finite difference method and spectral method) and different vertical resolutions. As a result, the model that uses the finite difference method for vertical discretization (VFD model) generated QBO-like oscillations when the number of vertical layers was set to the same number as in YJ2015 (L55), but did not generate QBO-like oscillations when it was doubled (L110). The model using the spectral method for vertical discretization (3DS model) did not generate QBO-like oscillations for either of the two vertical resolution settings used. These results suggest that the occurrence or non-occurrence of the QBO-like oscillation in the dry GCM with the YJ2015 setting is strongly influenced by the vertical discretization method and the vertical resolution of the model. This is consistent with the fact that QBO-like oscillations were observed in three of the four types of dynamical cores used in YJ2015 that used finite difference discretization in the vertical direction, but not in the FV model, which used floating vertical coordinates.

To investigate what determines the occurrence or non-occurrence of QBO-like oscillations, wavenumber frequency spectral analyses of the temperature field over the tropics were also performed. As shown in Figs. 5 and 6, the wave activity in the L55 VFD model was significantly higher than in the other models at σ = 0.002, but there was no significant difference among the models at σ = 0.1. This result suggests that the strength of the upward propagating wave entering from below σ = 0.1, where the profiles of the zonal mean zonal wind are similar for all the models, is not significantly different among the models.

The wave contribution to the vertical momentum flux in the pressure-zonal phase velocity space was also investigated in order to clarify the reason for the different wave activities at σ = 0.002 (Figs. 7, 8). For all the models except for the L55 VFD model. there was a sharp suppression of the upward penetration of eastward moving waves in the eastward zonal wind region around 50 hPa. The L55 VFD model result also showed such suppression around 20 hPa, but the eastward wind was weaker than those for the other models, resulting in weaker suppression of the upward penetration of eastward moving waves. This weaker suppression allowed the eastward moving waves to propagate to higher altitudes, and this is thought to be one reason why the L55 VFD model showed strong wave activity at σ = 0.002.

TEM analyses were performed to quantitatively investigate the causes of the different zonal wind profiles obtained in the L55 and L110 VFD models. In the L55 VFD model, eastward accelerations due to the advection term mainly contributed to the descent of the eastward phase, and westward accelerations due to the EP flux convergence contributed to the descent of the westward phase. The strong eastward acceleration in the L55 VFD model was produced by the predominant downward motion in the equatorial region, enhanced by the downward secondary circulation induced by the vertical shear of the zonal wind. In the L110 VFD model, there were strong eastward accelerations due to the advection term, but these accelerations were almost completely canceled out by the acceleration due to the EP flux convergence, resulting in an almost steady zonal wind. Note that the acceleration feature due to the advection term and the meridional EP flux divergence are similar between the L55 and the L110 VFD models. It is the vertical EP flux divergence in the eastward shear region that is mainly different: in the L55 VFD model, the eastward acceleration due to the vertical EP flux divergence is stronger than in the L110 VFD model. This is consistent with the vertical momentum flux analysis, where the L55 VFD model showed stronger upward propagation of eastward moving waves.

The results seen above suggested that in the L55 VFD model and the L110 VFD model, the difference in the formation of the eastward zonal wind around 0.01 < σ < 0.05 caused the differences in the upward penetration of eastward propagating waves, which in turn caused the differences in the occurrence of the QBO-like oscillation. To clarify the effect of this eastward zonal wind and the vertical resolution on the QBO-like oscillation, we performed two additional experiments on this point. The first additional experiment was to double the density of the vertical grids of the L55 VFD model in certain altitude ranges, rather than simply doubling the total number of layers. Doubling the density of the vertical grid in the range of 0.028 < σ < 0.12 and increasing the total number of layers to 62, i.e., increasing the total number of layers by only 7 from the default setting of L55, resulted in the formation of a steady eastward zonal wind around 0.01 < σ < 0.05 and the elimination of QBO-like oscillations (Fig. 14b). Note that when a steady and strong eastward wind region (above 16 m s⁻¹) formed, QBO-like oscillations did not occur, but when this steady eastward wind was weak (around 8 m s⁻¹). QBO-like oscillations occurred in the coarse vertical resolution region above this eastward wind region. The second additional experiment was to apply Rayleigh friction at an altitude range in the L110 VFD model to remove the eastward steady zonal wind around 0.02 < σ < 0.05. With this setting, the pattern of the zonal wind profile above the altitude where the additional Rayleigh friction was applied propagated downwards for the first four years, but then a strong eastward zonal wind was formed just above the additional Rayleigh friction layer and the zonal wind profile became almost steady (Fig. 15). These two additional experiments clarified that steady eastward zonal wind was formed at a certain altitude when the vertical resolution of the model was high (including the partially high case), and that once it was formed and strong, QBO-like oscillations above it were suppressed.

From the above, the conclusion of the present manuscript is that the QBO-like oscillations generated by the dry GCMs according to the setting of YJ2015 will occur only when the vertical resolution is coarse or the vertical discretization error is large in the altitude region higher than the altitude corresponding to the tropopause, and when the resolution is sufficiently high, strong eastward zonal winds will form somewhere in this altitude region, which will suppress the vertical propagation of eastward moving waves and thus prevent the QBO-like oscillations from occurring.

5.2 Discussion

As we have seen, it is clear that the differences in the wave activity among the models in the altitude region where QBO-like oscillations are observed in the L55 VFD model are primarily due to differences in the underlying zonal mean zonal wind, but why the formation of the zonal mean zonal wind depends on the vertical resolution of the model was not fully explored in this manuscript and is a topic for future work. However, one speculation for the reason is that the difference in vertical resolution caused a difference in the wave-mean-flow interaction: In the YJ2015 experimental setup, no explicit vertical diffusion is used, and it is only the nonlinear interaction that contributes to the damping of the waves with short vertical wavelength near the critical level. Therefore, increasing the vertical resolution can lead to a more correct representation of this nonlinear interaction, leading to a larger acceleration of the zonal wind in the L110 VFD and 3DS models. This difference in the representation of the vertical propagation of waves depending on the vertical resolution can come into play if the vertical wavelength of the wave is shortened, even if the waves do not necessarily reach the critical level. Consistent with this argument, a comparison of the wave contribution to the in the L110 VFD model (Fig. 7c) and in the eastward phase of the L55 VFD model (Fig. 8b) shows that the vertical penetration of fast phase velocity waves that do not reach the critical level is sharply suppressed in the L110 VFD model (around 5 hPa), while the suppression is less significant in the L55 VFD model (around 5 hPa). This trend of smaller vertical momentum fluxes due to waves in the higher vertical resolution setting was also observed in a realistic GCM study (Watanabe et al. 2015) and may be consistent with the results of the present manuscript. However, of course, note that the model used here is a bare dynamical core and is far from a realistic GCM. As seen above, it seems certain that the difference in vertical resolution alters the representation of the filtering effect of zonal winds, and affects the formation of the zonal winds themselves and the vertical propagation of the waves. However, comparing the results between the L55 VFD model and the L110 VFD model (Figs. 7a, c), the vertical momentum flux due to eastward propagating waves with fast phase velocities (e.g., 32 m s⁻¹) at about 20 hPa is larger in the L55 VFD model. This difference may not be fully explained by the above mechanism alone.

Another possible factor that could explain the difference in wave activity with different vertical discretization methods or different vertical resolutions could be overestimations of the waves connected to the vertical discretization methods, which is a numerical artifact as mentioned in YJ2015. We suspect that one mechanism by which waves could be excited due to vertical discretization errors is as follows: For example, when a physical quantity such as potential vorticity is adiabatically advected, if the isentropic surface is tilted east-west, the error in the vertical partial differentiation of the physical quantity may increase the error in the zonal advection calculation. This leads to a deviation from the geostrophically balanced state, which may lead to gravity wave excitation. Since the Brunt-Väisälä frequency in the tropics has larger values in σ < 0.1 than in the lower levels, gravity wave excitation is more likely to occur when the atmosphere is perturbed in this way. Related to this point, Lindzen and Fox-Rabinovitz (1989) showed that the vertical grid spacing required to resolve balanced quasi-geostrophic dynamics and gravity wave modes is inversely proportional to the Brunt-Väisälä frequency. Therefore, high Brunt-Väisälä frequencies in the σ < 0.1 region are more likely to produce large discretization errors, and this point may be important, not only for the artificial wave generation issue but for the overall accuracy in resolving flows. It should be noted, however, that no clear evidence of the wave excitation due to vertical discretization error is obtained in this study and these points, together with the speculation that the representation of the wave-mean-flow interaction may be altered by the vertical resolution, require further investigation.

In addition to the need for further investigation of the relationship among zonal wind, wave excitation, and vertical resolution, it should be noted here that there is also a need to investigate the occurrence/non-occurrence of QBO-like oscillations in different horizontal resolution settings, since all experiments in this manuscript are conducted in T63 horizontal resolution and horizontal resolution setting could also change the occurrence/non-occurrence of QBO-like oscillations. For example, Kawatani et al. (2010) showed that the westward acceleration of the QBO is mainly driven by small-scale gravity waves in the lower stratosphere. In the present manuscript, the horizontal resolution is T63 and such small-scale waves are not considered from the beginning. Therefore, if the horizontal resolution is higher, the westward acceleration may be strong. Indeed, in the L55 VFD model, the westward wind regions only descend to about σ = 0.01, which is a higher altitude than the altitude to which the eastward wind regions descend. This result should reflect the weaker westward forcing in 0.01 < σ < 0.02 (corresponding to the lower stratosphere) due to the absence of small-scale gravity waves. However, in the real atmosphere such small-scale waves are thought to be mainly excited by moist convection. Therefore, whether such waves can be strongly excited by dry GCMs is another question to be investigated in our future work.

Data Availability Statement

The datasets generated and analyzed in the present manuscript are available from the corresponding author on reasonable request.

Acknowledgments

We thank two anonymous reviewers for their helpful and insightful comments. We thank Mr. Hideaki Ishizaki for providing a numerical code for calculating eigenfrequency of equatorial waves. We also thank Dr. Takatoshi Sakazaki, Dr. Hiroki Kashimura, Dr. Shingo Watanabe, Dr. Shin-ichi Takehiro, and Dr. Haruka Okui for helpful comments. This work was supported by JSPS KAKENHI Grant Numbers 20K04061, 23H01245 and 24K07136. This work was also supported by computational resources of the K computer and supercomputer Fugaku provided by the RIKEN Center for Computational Science through the HPCI System Research Project (Project ID: hp190170, hp200124, hp210164, hp220173, hp230204).

The GFD-DENNOU Library (https://www.gfd-dennou.org/arch/dcl/) was used to draw the figures.

References

•  Anstey,  J. A.,  S. M.  Osprey,  J.  Alexander,  M. P.  Baldwin,  N.  Butchart,  L.  Gray,  Y.  Kawatani,  P. A.  Newman, and  J. H.  Richter, 2022: Impacts, processes and projections of the quasi-biennial oscillation. Nat. Rev. Earth Environ., 3, 588–603.
•  Bourke,  W., 1974: A multi-level spectral model. I. Formulation and hemispheric integrations. Mon. Wea. Rev., 102, 687–701.
•  Choi,  W.,  H.  Lee,  W. B.  Grant,  J. H.  Park,  J. R.  Holton,  K.-M.  Lee, and  B.  Naujokat, 2002: On the secondary meridional circulation associated with the quasi-biennial oscillation. Tellus B, 54, 395–406.
•  Corby,  G. A.,  A.  Gilchrist, and  R. L.  Newson, 1972: A general circulation model of the atmosphere suitable for long period integrations. Quart. J. Roy. Meteor. Soc., 98, 809–832.
•  Dunkerton,  T. J., 1997: The role of gravity waves in the quasi-biennial oscillation. J. Geophys. Res., 102, 26053–26076.
•  Durran,  D. R., 2010: Numerical Methods for Fluid Dynamics With Applications to Geophysics. 2nd Edition. Springer, 516 pp.
•  Durran,  D. R., and  P. N.  Blossey, 2012: Implicit-explicit multistep methods for fast-wave–slow-wave problems. Mon. Wea. Rev., 140, 1307–1325.
•  Ebdon,  R. A., 1960: Notes on the wind flow at 50 mb in tropical and sub-tropical regions in January 1957 and January 1958. Quart. J. Roy. Meteor. Soc., 86, 540–542.
•  Ebdon,  R. A., and  R. G.  Veryard., 1961: Fluctuations in equatorial stratospheric winds. Nature, 189, 791–793.
•  Held,  I. M., and  M. J.  Suarez, 1994: A proposal for the intercomparison of the dynamical cores of atmospheric general circulation models. Bull. Amer. Meteor. Soc., 75, 1825–1830.
•  Holton,  J. R., and  R. S.  Lindzen, 1972: An updated theory of the quasi-biennial cycle of the tropical stratosphere. J. Atmos. Sci., 29, 1076–1080.
•  Horinouchi,  T., and  S.  Yoden, 1998: Wave–mean flow interaction associated with a QBO-like oscillation simulated in a simplified GCM. J. Atmos. Sci., 55, 502–526.
•  Hoskins,  B. J., and  A. J.  Simmons, 1975: A multi-layer spectral model and the semi-implicit method. Quart. J. Roy. Meteor. Soc., 101, 637–655.
•  Ishioka,  K.,  N.  Yamamoto, and  M.  Fujita, 2022: A formulation of a three-dimensional spectral model for the primitive equations. J. Meteor. Soc. Japan, 100, 445–469.
•  Kawatani,  Y.,  S.  Watanabe,  K.  Sato,  T. J.  Dunkerton,  S.  Miyahara, and  M.  Takahashi, 2010: The roles of equatorial trapped waves and internal inertia-gravity waves in driving the quasi-biennial oscillation. Part I: Zonal mean wave forcing. J. Atmos. Sci., 67, 963–980.
•  Lindzen,  R. S., and  J. R.  Holton, 1968: A theory of the quasi-biennial oscillation. J. Atmos. Sci., 25, 1095–1107.
•  Lindzen,  R. S., and  M.  Fox-Rabinovitz, 1989: Consistent vertical and horizontal resolution. Mon. Wea. Rev., 117, 2575–2583.
•  Polvani,  L. M.,  R. K.  Scott, and  S. J.  Thomas, 2004: Numerically converged solutions of the global primitive equations for testing the dynamical core of atmospheric GCMs. Mon. Wea. Rev., 132, 2539–2552.
•  Reed,  R. J.,  W. J.  Campbell,  L. A.  Rasmussen, and  D. G.  Rogers, 1961: Evidence of a downward-propagating, annual wind reversal in the equatorial stratosphere. J. Geophys. Res., 66, 813–818.
•  Watanabe,  S.,  K.  Sato,  Y.  Kawatani, and  M.  Takahashi, 2015: Vertical resolution dependence of gravity wave momentum flux simulated by an atmospheric general circulation model. Geosci. Model Dev., 8, 1637–1644.
•  Yao,  W., and  C.  Jablonowski, 2015: Idealized quasi-biennial oscillations in an ensemble of dry GCM dynamical cores. J. Atmos. Sci., 72, 2201–2226.