An Explanation for the Diagonally Predominant Property of the Positive Symmetric Ensemble Transform Matrix

Abstract

In the ensemble transform Kalman filter (ETKF), an ensemble transform matrix (ETM) is a matrix that maps background perturbations to analysis perturbations. All valid ETMs are shown to be the square roots of the analysis error covariance in ensemble space that preserve the analysis ensemble mean. ETKF chooses the positive symmetric square root T^s as its ETM, which is justified by the fact that T^s is the closest matrix to the identity I in the sense of the Frobenius norm. Besides this minimum norm property, T^s is observed to have the diagonally predominant property (DPP), i.e., the diagonal terms are at least an order of magnitude larger than the off-diagonal terms.

To explain the DPP, first, the minimum norm property has been proved. Although ETKF relies on this property to choose its ETM, this property has never been proved in the data assimilation literature. The extension of this proof to the scalar multiple of I reveals that T^s is a sum of a diagonal matrix D and a full matrix P whose Frobenius norms are proportional, respectively, to the mean and the standard deviation of the spectrum of T^s. In general cases, these norms are not much different but the fact that the number of non-zero elements of P is the square of the ensemble size whereas that of D is the ensemble size causes the large difference in the orders of elements of P and D. However, the DPP is only an empirical fact and not an inherently mathematical property of T^s. There exist certain spectra of T^s that break the DPP but such spectra are rarely observed in practice since their occurrences require an unrealistic situation where background errors are larger than observation errors by at least two orders of magnitude in all modes in observation space.

1. Introduction

In the ensemble transform Kalman filter (ETKF) (Bishop et al. 2001; Wang et al. 2004; Ott et al. 2004), analysis perturbations are obtained by applying a linear transformation on background perturbations. Denoting analysis and background perturbations by n × k matrices X^a and X^b, respectively, this transformation is represented by a right-multiplication of X^b by a k × k matrix T   

where n is the size of the state vectors, and k is the ensemble size. Here each column of X^b represents the difference between each forecast member x^b and the ensemble mean calculated from all forecast members. A similar definition using the analysis ensemble is applied for the columns of X^a.

The matrix T is called the ensemble transform matrix (ETM), and it is formulated so that the resulting analysis error covariance P^a = X^aX^aT/(k − 1) obeys the Kalman filter equation for the second moment of the posterior distribution   

where R is the observation error covariance, H: ℝⁿ → ℝ^m is the observation operator, which is assumed to be linear, m is the number of observations, and P^b = X^bX^bT/(k − 1) is the background error covariance. Using the Sherman-Morrison-Woodbury identity, P^a can be rewritten as   

where Y^b = HX^b is the background perturbations mapped into observation space. It is easy to check that any factorization SS^T of the matrix P̃a=(I+Y^bTR⁻¹Y^b / (k − 1))⁻¹ yields an ETM S. Here, we call such matrix S a square root of P̃^a with a certain abuse of the mathematical notion of square root.

Suppose that the spectral decomposition of Y^bTR⁻¹Y^b / (k − 1) is given by CΓC^T, where the orthogonal matrix C contains the eigenvectors in its columns, and the diagonal matrix Γ contains the eigenvalues γⁱ on its diagonal. Since C is orthogonal, we have I = CC^T, and this helps to simplify P̃^a   

Note that since γ_i are nonnegative, it is legitimate to take the inverse (I + Γ)⁻¹. Based on this form, Bishop et al. (2001) proposed choosing the matrix C(I + Γ)^−1/2, which is clearly a square root of P̃^a, as the ETM to be used in practice. However, such choice introduces a bias into the analysis ensemble mean since the sum of the resulting analysis perturbations differs from zero. This means that in addition to a square root of P̃^a, an ETM has to preserve the analysis ensemble mean. Wang et al. (2004) pointed out that the positive symmetric square root T^s = C(I + Γ)^−1/2C^T possesses this mean-preserving property. Living et al. (2008), and Sakov and Oke (2008) further demonstrated that all the square roots of P̃^a with the form T^sU also have the mean-preserving property, provided that U is any orthogonal matrix that has the vector 1 = (1 1 … 1)^T as its eigenvector. Thus, any U can be constructed by combining an arbitrary set of orthonormal vectors in the orthogonal complement of the vector 1 with the normalized one to form its eigenvectors.

Hunt et al. (2007) argued that three properties of T^s justify its use as the ETM in practice: (1) T^s preserves the analysis ensemble mean; (2) T^s depends continuously on P̃^a; and (3) T^s is the closest matrix in the Frobenius norm to the identity matrix I (note that the Frobenius norm of a matrix T is defined as , where t_ij are the elements of T). However, it is clear that the first two conditions also hold for any ETM in the form T^sU. Thus, the third condition is the only condition that privileges the choice of T^s. Underlying this condition is a simpler condition saying that when the impact of observations becomes negligible, X^a should be identical to X^b, or equivalently T^sU → I when Γ → 0. Since T^s → I in this case, this implies that U = I. This means that by simply choosing U = I, we maintain balance in analysis perturbations which has already been achieved in background perturbations. Any rotation U ≠ I, which is equivalent to taking linear combinations of background perturbations as analysis perturbations, will introduce certain imbalance in analysis perturbations. When the impact of observations becomes significant, the best we can do is to minimize the distortion of physically coherent structures in analysis perturbations introduced by assimilation through minimizing which also leads to U = I. This condition is of particular importance when local analyses are performed as in the local ensemble transform Kalman filter (LETKF), since we can have both grid points that are far from any observation and grid points that abound with observations nearby. It is noteworthy that Reich and Cotter (2015) placed this condition under a broader view established by the optimal transport theory to construct ETMs in the ensemble transform particle filter.

As an example, Fig. 1 shows entries of three T^s matrices computed at three different grid points that we obtained from an experiment with the LETKF using conventional observations and 50 ensemble members (Duc et al. 2015). A noticeable feature in this figure is the dominance of diagonal elements over off-diagonal elements (Saito et al. 2017). Reich et al. (2011) have also noticed this property of T^s and utilized it in a procedure called hydrostatic balancing to reduce initial imbalance in analysis ensemble members. The entries in the j th column of an ETM can be interpreted as the weights in the construction of the j th analysis perturbation from all background perturbations by a linear combination. Therefore, the dominance of diagonal elements in T^s implies that the largest contribution to the j th analysis perturbation comes from the j th background perturbation.

Fig. 1.

Entries of 50 × 50 T^s matrices at different grid points obtained from an LETKF experiment with conventional observations. The grid point in panel (a) is in the region with dense observations, whereas the grid point in panel (c) is far from observations. The grid point in panel (b) is between those in panels (a) and (c). From left to right, the average values of the diagonal elements are 0.39, 0.69, and 0.99.

How can we explain such an interesting property of T^s, which we call the diagonally predominant property (DPP) of T^s? The first possible explanation can be traced back to Hunt et al. (2007) in their argument for choosing T^s as the ETM in LETKF. Their argument implies that the DPP of T^s is likely due to its similarity to the identity I. In Fig. 1c, the average value of the diagonal elements is approximately 0.99, which seems to verify this hypothesis. However, the corresponding values in Figs. 1a and 1b are 0.39 and 0.69, respectively, which are much smaller than 1; consequently, it is difficult to see the similarity between these T^s matrices and the identity I. This suggests that the distance between T^s and I should be quantified, which may give us a clue to understanding these large deviations from 1.

Hunt et al. (2007) did not provide any proof for this minimum norm property of T^s − I, but referred to Ott et al. (2002, 2004) for the proof. However, Ott et al. (2004) tried to seek a left-multiplication n × n matrix Z to transform X^b to X^a subjected to the constraint in Eq. (2) rather than a right-multiplication matrix T as in (1)   

The matrix Z was chosen so that the distance between X^a and X^b was minimized. They also demonstrated that a right-multiplication matrix T, which they called Y, can be derived from Z so that X^bT yields the same X^a. However, the fact that T^s is the closest ETM to the identity I has not yet been proven.

In this paper, first, we fill in this theoretical gap in the literature by providing a proof for the minimum norm property of T^s − I in Section 2. This property itself does not give much insight into the DPP. Therefore, a new mathematical view is needed to make the problem more accessible. This new mathematical treatment is presented in Section 3. Finally, Section 4 summarizes the results obtained in the paper and suggests potential applications of the DPP.

2. Minimum norm property

To prove this property, we find the ETM that minimizes the Frobenius norm of T − I among all mean-preserving ETMs T, which is expected to be T^s. In fact, this is a consequence of a more general result:

Among all square roots S of a symmetric positive-definite matrix M, the positive symmetric square root S* is the closest matrix to the identity I. Furthermore, the squared distance between S^* and I is given by   

where λ_i are the positive square roots of the eigenvalues of M. The detailed proof is given in Appendix A.

When we apply this result into our case with M = P̃^a and S = T, T^s will play the role of S^*. Since T^s also has the mean-preserving property, this verifies the minimum norm property of T^s − I. To estimate the squared distance as given in (6), we need to know the spectrum of T^s, which depends on the spectrum of P̃^a. This, in turn, is determined by the spectrum of the matrix Y^bTR⁻¹Y^b/(k − 1), which we denote by G. Therefore, (4) implies the following form of the eigenvalues of T^s   

where γ_i are the eigenvalues of G. It is easy to verify that all λ_i are bounded within [0, 1].

Plugging λ_i in (7) into (6) has the following value   

where r is the rank of G. Noting that (λ_i − 1)² ≤ 1 because 0 ≤ λ_i ≤ 1 for all i, we see that is at most r. In general, when the number of influence observations m that contribute to the analysis at a given grid point is less than the number of ensemble members k, r is equal to m. Therefore, if a point is far from all observations, r will become smaller, leading to a smaller distance . This explains why T^s in Fig. 1c is almost identical to I. However, in the region with many observations, r attains its maximum k − 1 and all γ_i are greater than 0, which makes all λ_i deviate from 1 and T^s to be more dissimilar to I, as illustrated in Fig. 1a.

3. Diagonally predominant property

The minimum norm property of T^s − I alone cannot explain why we see the DPP of T^s, especially when all λ_i are far from 1 and as a result, T^s becomes more dissimilar to I. The choice of I for comparison with T^s is reasonable when influence of observations is small and we expect that the analysis perturbations are more or less similar to the background perturbations. However, when influence of observations becomes significant, we expect that the observations will help us to reduce the uncertainty in the background perturbations considerably. In such a case, the identity I is clearly not a good choice for comparison, and we should instead use something like αI where α is the reduction factor resulting from assimilation of observations, i.e. 0 < α < 1.

Therefore, we extend the minimization problem in Section 2 by adding a parameter α, and find the ETM T and the parameter α that minimize the distance ‖T − αI‖_F. Again, we can obtain a more general result for an arbitrary symmetric positive-definite matrix: Among all square roots S of a symmetric positive-definite matrix M, the positive symmetric square root S^* is the closest matrix to a scalar multiple of the identity I. The scalar multiple of I closest to S^* in this case is the matrix α^*I = λ̅I, where λ̅ is the mean of the eigenvalues of S^*. Furthermore, the distance ‖S^* − α^*I‖_F between S^* and α^*I is given by   

where σ_λ is the standard deviation of the eigenvalues of S^*. The detailed proof is given in Appendix B.

Applied into our case where S^* becomes T^s and λ_i are given in (7), this result suggests that we can decompose T^s into the sum of a diagonal matrix D and a perturbation matrix P   

All the off-diagonal entries of T^s are also the off-diagonal entries of P. While the Frobenius norm of D is , the Frobenius norm of P can be derived from (9), which is . This enables us to estimate the typical magnitude of an element in P as . To check the validity of this estimation, for each matrix T^s given in Fig. 1, we plot in Fig. 2 the histograms of the absolute values of the elements of its corresponding matrix P. It can be seen that approximately 90 % of the elements concentrate on the 1-sigma interval around the mean. The typical magnitudes for the entries of P are also given in Fig. 2 as “Estimated” for comparison. These values reflect quite well the magnitudes of elements of P, which are also the off-diagonal elements of T^s. By contrast, the typical magnitude of an element along the diagonal of D is simply λ̅. This is exactly the average value of the diagonal elements of T^s, since λ̅ = tr(T^s)/k.

Fig. 2.

Histograms of elements of the perturbation matrices P corresponding to the ETMs T^s in Fig. 1. Statistics are derived from the absolute values of all elements. To have a fair comparison, these values are normalized using their means and standard deviations. In each case, nine bins with the same width set to the standard deviation are used to construct the histogram. The typical magnitudes of the entries of P as suggested by the theory are denoted by “Estimated”.

To roughly estimate the difference in the orders between the diagonal and off-diagonal elements of T^s, we assume that in the general case without any information about G, all λ_i are realizations of a uniform distribution over [0, 1]. Based on this assumption, , and the ratio for an ensemble size of 50 members is approximately 12. For the T^s in Fig. 1a which is a matrix T^s associated with assimilation of dense observations, this ratio is approximately 16, which is not too different from the rough estimate of 12. This means that the diagonal elements of T^s are generally an order of magnitude larger than the off-diagonal elements for an ensemble size on the order of 50. This difference in orders tends to become larger when all λ_i cluster around 1, like the case in Fig. 2c, with the ratio of approximately 315 when the impact of observations is small.

Although we call P the perturbation matrix to emphasize that T^s is mostly similar to the diagonal matrix D, its norm is generally not much smaller than the norm of D, i.e., compared to . If we again use the assumption of the uniform distribution for λ_i, the norm of D is only times larger than that of P. Recalling that the square of the Frobenius norm of a matrix is the sum of squares of all the elements of that matrix, we can explain why the typical magnitudes of elements of the two matrices are quite different. This sum in the case of D only comprises k diagonal elements, whereas that in the case of P comprises k² elements. As a result, a typical element of P is times less than a typical element of D. This ratio is equivalent to one order of magnitude for a typical ensemble size k = 100 in practice. It is this large difference in the number of non-zero elements between P and D that causes the large difference in the orders of magnitude between the diagonal and off-diagonal elements of T^s.

It is informative to discuss the condition or situation in which the DPP may cease to hold. In this paragraph, we aim to demonstrate that such a situation rarely happens in practice. The quantity , which characterizes the difference in the orders between the diagonal and off-diagonal elements of T^s, depends not only on k but also on the ratio λ̅/σ_λ. Thus, it is anticipated that the diagonal predominance will no longer be observed if this ratio is of the order or lower order. This can happen if , which is equivalent to 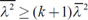. The fact that λ_i are bounded between 0 and 1 implies that . Therefore, the inequality λ̅ ≥ (k + 1)λ̅² is the necessary condition so that the DPP ceases to hold. It is easy to check that this inequality gives an upper bound 1/(k + 1) for λ̅. Therefore, for diagonal and off-diagonal elements of T^s to be of comparable order, for a typical ensemble size k = 100, λ̅ must be less than 10⁻², which is equivalent to the lower bound 10⁴ for γ_i. In other words, background errors must be 100 times greater than observation errors almost in all modes, which cannot be met in practice.

4. Summary and conclusion

In this study we have developed a mathematical framework to explain the DPP observed in the positive symmetric ETM T^s used in ETKF. This property has a close connection with the minimum norm property of this matrix, which states that T^s is the closest matrix in the Frobenius norm to the identity I among all potential ETMs. There exist many valid ETMs that can yield the same analysis error covariance without altering the analysis ensemble mean. ETKF relies on the minimum norm property of T^s to justify its choice of this matrix as the ETM in its formulation. This property has been stated but has never been proved in the data assimilation literature.

Therefore, our first step in understanding why the diagonal terms dominate over the off-diagonal terms in T^s is to prove the minimum norm property, since this proof can provide an important guide in the subsequent mathematical argument. We have found that this property follows from an important theorem on square roots S of a symmetric positive-definite matrix M: Among all square roots of M, the positive symmetric square root S^* is the closest matrix to the identity I. This theorem suggests that instead of I, we can further compare S with a scalar multiple of I. This leads to another important theorem: Among all square roots of M, S^* is the closest matrix to a scalar multiple of I, and the scalar multiple of I closest to S^* in this case is λ̅I, where λ̅ is the average of the eigenvalues of S^*.

This is the second theorem that gives an explanation for the DPP of T^s. The matrix T^s can be decomposed into a sum of a diagonal matrix D and a perturbation matrix P which is a full matrix whose off-diagonal elements are identical to those of T^s. The Frobenius norm of D is , whereas that of P is . Thus, the two norms are associated with the first two moments of the spectrum of T^s. Although the norm of P is in general not much smaller than that of D, the fact that the number of non-zero elements of P is proportional to the square of the ensemble size causes its elements to be much smaller than the elements of D whose number of non-zero elements is only the ensemble size. This explains why the diagonal elements of T^s dominate over its off-diagonal elements.

It must be emphasized that the DPP is not an inherently mathematical property of T^s. There exist certain distributions of λ_i that break the DPP such as when all λ_i cluster around zero. However, realizations of such distributions rarely occur in practice since their occurrences require very large differences in orders between background errors and observation errors at all scales. Thus, it is almost certain that we do not observe the ETMs that do not possess the DPP in practice.

A natural question is how we utilize this DPP in practice. The hydrostatic balancing procedure in Reich et al. (2011) is an example of its application. This property is a consequence of the fact that a mean-preserving ETM derived from P̃^a most resembles a scalar multiple of I when it is T^s, and the corresponding diagonal matrix is λ̅I. This suggests that we can use the best approximation λ̅I as a replacement for T^s in ETKF. In fact, the diagonal ETM λ̅I can be shown to be a special case of what we call the diagonal ETKF (Duc et al. 2019: manuscript in revision).

The diagonal approximation, when applied to ensemble forecasting, is equivalent to an ensemble generation method that combines two aspects of ETKF and the breeding method (Toth and Kalnay 1993). In this method, we rescale all forecast perturbations by the same factor λ̅ at the end of each breeding cycle. Compared to the original breeding method proposed in Toth and Kalnay (1997), where the rescaling factors are derived from climatological statistics, our proposed method is appealing in that it can adaptively incorporate EKTF-induced information on the posterior error variances that reflects both the flow-dependent forecast errors and the observation network. The advantage of the proposed method, in comparison to the ensemble generation by ETKF, is presumably better dynamical balance that should be achieved by not mixing up different perturbations. We note, however, that precisely for the same reason, it will also be more prone to converge all perturbations into a single fastest growing mode, losing the EKTF's merit of avoiding such a convergence (Wang and Bishop 2003). We postulate that this issue would be less problematic in applications such as regional ensemble prediction systems, in which lateral boundary perturbations are fed into ensemble members in different directions during the course of integration as demonstrated by Saito et al. (2012). We will test this potential application of λ̅I as an ETKF-based ensemble generation method in our next study.

Acknowledgments

This work was supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT) through the Strategic Programs for Innovative Research, the FLAGSHIP2020 project (Advancement of meteorological and global environmental predictions utilizing observational “Big Data”, hp160229), and the JSPS Grant-in-Aid for Scientific Research (Study of optimum perturbation methods for ensemble data assimilation, 16H04054).

Appendix A: The minimum point of the distance ‖S − I‖_F where S is a square root of a symmetric positive-definite matrix M

Let M be a k × k symmetric positive-definite matrix, and S be a square root of M. Suppose that S has the singular value decomposition (SVD) S = UΛV^T. Since S is a square root of M we have   

This equation indicates that all vectors ui must form an eigenbasis of M, and the squares of all scalars λ_i have to be the eigenvalues of M. Thus, any eigen-decomposition of M yields the left singular vectors and the singular values of S, and the right-singular vectors vi can be chosen arbitrarily from any orthonormal basis.

Given this general form of S, we will find S^* that minimizes the squared Frobenius norm of S − I. From the definition of the Frobenius norm of a matrix, we have   

where the symbol tr stands for the trace operator. Since UΛ²U^T = M and the trace is invariant under the transpose, this can be simplified as   

Therefore, will attain its minimum when tr(UΛV^T) attains its maximum.

Applying the cyclic property of the trace operator, we obtain the value of tr(UΛV^T)   

where the symbol 〈 〉 denotes the inner product. Then it is easy to see that   

Since all λ_i are constants that are determined by the spectrum of M, this implies that tr(UΛV^T) attains its maximum when 〈u_i, v_i〉 = 1 or equivalently u_i = v_i. In other words, attains its minimum when S = UΛU^T, which is the positive symmetric square root of M. Now the calculation of the squared distance is straightforward   

Note that we have used the fact that tr(M) = ∑_iλ² to obtain this equation.

Appendix B: The minimum point of the distance ‖S − αI‖_F where S is a square root of a symmetric positive-definite matrix M and α is a scalar variable

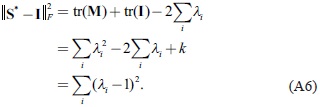The minimization problem here is an extension of the minimization problem in Appendix A. Now instead of the squared distance , we minimize the squared distance , where we augment the minimization space by introducing a new variable α in addition to the matrix S. When the same mathematical notions and operations are used as in Appendix A, this squared distance can be represented as   

By dividing this distance by k, and denoting , and β = ∑_iλ_i 〈u_i, v_i〉/k, we obtain a function of two variables   

where β is bounded within [−λ̅, λ̅]. The bounded interval of β can be verified from the following inequality   

Note that the equality occurs in two cases, when u_i = v_i and u_i = −v_i for all i. In other words, β = λ̅ if S is the positive symmetric square root of M, and β = −λ̅ if S is the negative symmetric square root of M.

The critical point of the function d (α, β) is (α, β) = (0, 0), which is a saddle point. This means that d (α, β) can only attain its minimum on the boundary of its domain. When β is fixed, d (α, β) is a quadratic function, and it attains its minimum when α is equal to this fixed value. Therefore, d (α, β) has two minimum points (λ̅, λ̅) and (−λ̅, −λ̅). It is easy to understand why we have two minimum points here, because the function d (α, β) is symmetric with respect to (α, β): d (−α, −β) = d (α, β). Thus, we only need to consider the positive minimum point in this case and this point yields the minimum point (S^*, α^*) = (UΛV^T, λ̅) of the squared distance . Again, like the minimization problem in Appendix A, we obtain the positive symmetric square root of M at the minimum point. Thus, we have found that S resembles a scalar multiple of I most when it is the positive symmetric square root, and the scalar multiple of I in this case is λ̅I. The minimum squared distance is easy to estimate now   

where σ_λ is the standard deviation of the spectrum of S^*.

References

•  Bishop,  C. H.,  B. J.  Etherton, and  S. J.  Majumdar, 2001: Adaptive sampling with the ensemble transform Kalman filter. Part 1: Theoretical aspects. Mon. Wea. Rev., 129, 420-436.
•  Duc,  L.,  T.  Kuroda,  K.  Saito, and  T.  Fujita, 2015: Ensemble Kalman Filter data assimilation and storm surge experiments of tropical cyclone Nargis. Tellus A, 67, 25941, doi:10.3402/tellusa.v67.25941.
•  Hunt,  B. R.,  E. J.  Kostelich, and  I.  Szunyogh, 2007: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Physica D, 230, 112-126.
•  Livings,  D. M.,  S. L.  Dance, and  N. K.  Nichols, 2008: Unbiased ensemble square root filters. Physica D, 237, 1021-1028.
•  Ott,  E.,  B. R.  Hunt,  I.  Szunyogh,  M.  Corazza,  E.  Kalnay,  D. J.  Patil,  J. A.  Yorke,  A. V.  Zimin, and  E. J.  Kostelich, 2002: Exploiting local low dimensionality of the atmospheric dynamics for efficient ensemble Kalman filtering. arXiv.org, e-Print Archive, 24 pp. [Available at http://arxiv.org/abs/physics/0203058v3.]
•  Ott,  E.,  B. R.  Hunt,  I.  Szunyogh,  A. V.  Zimin,  E. J.  Kostelich,  M.  Corazza,  E.  Kalnay,  D. J.  Patil, and  J. A.  Yorke, 2004: A local ensemble Kalman filter for atmospheric data assimilation. Tellus A, 56, 415-428.
•  Reich,  S., and  C.  Cotter, 2015: Probabilistic Forecasting and Bayesian Data Assimilation. Cambridge University Press, 297 pp.
•  Reich,  H.,  A.  Rhodin, and  C.  Schraff, 2011: LETKF for the nonhydrostatic regional model COSMO-DE. COSMO Newsl., 11, 27-31.
•  Saito,  K.,  H.  Seko,  M.  Kunii, and  T.  Miyoshi, 2012: Effect of lateral boundary perturbations on the breeding method and the local ensemble transform Kalman filter for mesoscale ensemble prediction. Tellus A, 64, 11594, doi:10.3402/tellusa.v64i0.11594.
•  Saito,  K.,  M.  Kunii,  L.  Duc, and  T.  Kurihana, 2017: Perturbation Methods for Ensemble Data Assimilation. RIKEN International Symposium on Data Assimilation, Kobe, Japan. [Available at http://www.dataassimilation.riken.jp/risda2017/program/abstracts/pdf/19_2_K.Saito.pdf.]
•  Sakov,  P., and  P. R.  Oke, 2008: Implications of the form of the ensemble transformation in the ensemble square root filters. Mon. Wea. Rev., 136, 1042-1053.
•  Toth,  Z., and  E.  Kalnay, 1993: Ensemble forecasting at NMC: The generation of perturbations. Bull. Amer. Meteor. Soc., 74, 2317-2330.
•  Toth,  Z., and  E.  Kalnay, 1997: Ensemble forecasting at NCEP and the breeding method. Mon. Wea. Rev., 125, 3297-3319.
•  Wang,  X., and  C. H.  Bishop, 2003: A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes. J. Atmos. Sci., 60, 1140-1158.
•  Wang,  X.,  C. H.  Bishop, and  S. J.  Julier, 2004: Which is better, an ensemble of positive-negative pairs or a centered spherical simplex ensemble? Mon. Wea. Rev., 132, 1590-1605.