2020 Volume 98 Issue 3 Pages 511-525
2020 Volume 98 Issue 3 Pages 511-525
The accurate estimation of precipitation is an important objective for the Dual-frequency Precipitation Radar (DPR), which is located on board the Global Precipitation Measurement (GPM) satellite core observatory. In this study, a Bayesian correction (BC) approach is proposed to improve the DPR's instantaneous rainfall rate product. Ground dual-polarization radar (GR) observations are used as references, and a log-transformed Gaussian distribution is assumed as the instantaneous rainfall process. Additionally, a generalized regression model is adopted in the BC algorithm. Rainfall intensities such as light, moderate, and heavy rain and their variable influences on the model's performance are considered. The BC approach quantifies the predictive uncertainties associated with the Bayesian-corrected DPR (DPR_BC) rainfall rate estimates. To demonstrate the concepts developed in this study, data from the GPM overpasses of the Weather Service Surveillance Radar (WSR-88D), KHGX, in Houston, Texas, between April 2014 and June 2018 are used. Observation errors in the DPR instantaneous rainfall rate estimates are analyzed as a function of rainfall intensity. Moreover, the best-performing BC model is implemented in three GPM-overpass cases with heavy rainfall records across the southeastern United States. The results show that the DPR_BC rainfall rate estimates have superior skill scores and are in better agreement with the GR references than with the DPR estimates. This study demonstrates the potential of the proposed BC algorithm for enhancing the instantaneous rainfall rate product from spaceborne radar equipment.
The Global Precipitation Measurement (GPM) Core Observatory satellite was launched on February 27th, 2014. It is expected to improve precipitation measurements from space across the globe, especially in regions with sparse ground-based observations (Hou et al. 2014). The GPM satellite carries the first space-borne Dual-frequency Precipitation Radar (DPR) operating at both Ku (13.6 GHz) and Ka (35.5 GHz) bands. The DPR algorithm considers the effects of attenuation, non-Rayleigh scattering, phase identification, non-uniform beam filling, etc., (Iguchi et al. 2017; Liao and Meneghini 2019). Some of the important products offered by the DPR include instantaneous rainfall rate, rainfall type classification, and vertical rainfall profiles, which are valuable in hydrological and meteorological applications. Compared with its predecessor, the Tropical Rainfall Measuring Mission precipitation radar, the DPR has a better capability for observing light rainfall and snowfall, which is critical to understanding the hydrological processes at various scales (Skofronick-Jackson et al. 2018).
More recently, ground-based dual-polarization radar (GR) offers new opportunity for examining and validating the physical and statistical interpretation of satellite-based precipitation retrievals (Chandrasekar et al. 2008). Previous literature has contributed significantly toward evaluating DPR rainfall retrievals (Biswas and Chandrasekar 2018; Le et al. 2016; Petracca et al. 2018; Toyoshima et al. 2015). However, the challenge for the DPR is to retrieve high-accuracy instantaneous rainfall rates for widely varying rainfall types and extreme events, such as hurricanes (Battaglia et al. 2015; Petracca et al. 2018; Speirs et al. 2017). For instance, the DPR underestimates rainfall rates in convective events in the southeastern United States, although the reflectivity of the Ku-/Ka-band corresponds well with the GR references (Biswas and Chandrasekar 2018).
Notable efforts have been made to improve the detection and accuracy of rainfall properties from the DPR (Liao and Meneghini 2019; Seto and Iguchi 2015; Seto et al. 2013). As most of the attenuation is from precipitation particles and mixed-phase hydrometeors, the main objective is to find the paired profiles of DSD parameters regarding rainfall rate patterns and then perform attenuation correction (Iguchi et al. 2017). Seto and Iguchi (2015) and Seto et al. (2013) developed a robust attenuation-adjusted approach for improving the DPR rain rate retrievals by merging Histchfeld-Bordan's (HB) correction method, the dual-frequency ratio (DFR), and the surface reference technique (SRT), i.e., the H-D-S method. Liao and Meneghini (2019) further modified the standard DFR approach and added a constant coefficient for the Ka-band precipitation radar (KaPR). The benefits of adjusting the DSD parameters are likely to retrieve more rewarding rainfall profiles. The DPR data might also be limited to light and heavy rainfall due to greater uncertainty in quantifying the DSD profiles from the overlapping parts of the Ku-/Ka-band (Liao et al. 2014). New efforts are encouraged to obtain more accurate DPR rainfall rate estimates.
This study proposes a Bayesian framework to improve DPR rainfall rate estimates using GR observations as references. A flowchart of the proposed Bayesian correction (BC) approach is shown in Fig. 1. The use of a Bayesian model analysis for improving rainfall estimates is not a new approach. Attempts have been made to merge precipitation estimates from various sources (e.g., satellite, radar, and gauge) at subdaily, daily, and monthly scales (Bruno et al. 2014; Kim et al. 2018; Ma et al. 2018; Verdin et al. 2015). The key points of this study are as follows:

A sketch flowchart of the Bayesian correction approach used in this study.
The proposed BC algorithm is described in Section 2. The adapted spaceborne and ground-based radar rainfall products are introduced in Section 3. Section 4 provides parameter estimation, model evaluation, comparison, and application. The study concludes with a summary and discussion in Section 5.
Let GR s, t be the real surface rainfall rate at site s and time t as observed by the GR. It is more convenient to work with the instantaneous rainfall rate after natural logarithm transformation, since it closely follows a Gaussian distribution (Fuentes et al. 2008). Therefore, the rainfall process is modeled at a natural logarithm scale, i.e., Ys, t = log (GR s, t). The log-transformed rainfall rate is parameterized as:
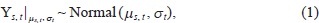 |
Let Xs, t be further defined as a covariate that is related to the DPR instantaneous rainfall rate estimate, where Xs, t = log (DPRs, t) is the natural log-transformed DPR rainfall rate at site s and time t. Given the observation errors and the spatial/temporal misalignment between the DPR estimate and the GR reference at site s and time t, the mean value of μs, t is modeled as a generalized linear function of Xs, t below:
 |
A simple model, denoted as M1, comprises the general model specified in Eq. (2). The offset and slope parameters are fixed in space and do not vary between sites at a certain time t. They are expressed as:
 |
 |
According to the rainfall intensity at site s and at time t, the rainfall is divided into four categories: light (< 2.5 mm h−1), moderate (2.5–7.6 mm h−1), heavy (7.6–50 mm h−1), and violent (> 50 mm h−1) (Glickman 2000). The effect of rainfall intensity is considered in the following BC models due to different measurement errors from the DPR under various rainfall intensities.
A complex model, denoted as M2, is designed such that the offset γ1t varies in space s at time t, but the slope parameter γ2t is fixed in space at the same time. An adjustment term β1t is added in Eq. (3) on the basis of M1. The varying offset β1t follows a Gaussian distribution with a mean of zero and variance in terms of  , which is expressed below:
, which is expressed below:
 |
 |
 |
In model M3, the slope coefficient γ2t in Eq. (2) varies between sites at time t, but the offset parameter γ1t is fixed in space at the same time. An adjustment term β2t is added in Eq. (4) on the basis of M1. The varying slope β2t is also normally distributed around zero with unknown variance in terms of  , which are repeated as:
, which are repeated as:
 |
 |
 |
Considering that both the offset and slope parameters in Eq. (2) are impacted by rainfall intensity, M4 is designed with the additional adjustment terms, β1t and β2t, in Eqs. (3) and (4), respectively. They are expressed as:
 |
 |
 |
 |
In the models M1 to M4, the parameters θ are denoted as {α1t, α2t, σt}, {α1t, α2t, σβ1, σt}, {α1t, α2t, σβ2, σt}, and {α1t, α2t, ρβ, σβ1, σβ2, σt}, respectively. According to Bayes' theorem, the joint posterior distribution p (θ | Ys, t) for each model can be written as:
 |
The physical structure of the BC algorithm is summarized in Fig. 2, which includes three blocks: Data, Parameter, and Model. The Data module is used to organize the associated datasets of the predictor and predictand. The Parameter module covers the parameters and associated hyperparameters that are applied in the BC approach. The Model module consists of prior information and proposed likelihood function, which are the key components in the Bayesian framework.

The physical structure of the Bayesian correction approach used in this study.
The traditional calculation of the posterior distribution p (θ | Ys, t) in Eq. (15) is a challenge as its dimension grows with the number of sites and parameters. Thus, a Markov Chain Monte Carlo (MCMC) technique compiled in the Stan programming language (http://mc-stan.org) is applied to address this problem (Carpenter et al. 2017; Gelman et al. 2013). Weakly informative priors with objective or diffuse meanings have minimum impacts on the posterior distribution in the Bayesian analysis (Gelman et al. 2013). They are adapted so that it is more convenient to execute posterior parameter estimation using the MCMC technique. The purpose of weakly informative priors is for regularization and to ensure Bayesian inferences in an appropriate range. The priors of the parameters are thus initialized as uniform distribution. Considering that the variance values in the above models are constrained to be positive, the parameters ρβ, σβ1, σβ2, and σt have a uniform prior with a lower-bound zero.
As the Bayesian parameters are estimated based on the training data at site s and at time t, an evaluation of the BC model's performance is required with validation data at a new site s′ for the corresponding time of observation t before the model's implementation. Let Rs′, t be the natural log-transformed rainfall rate at site s′ and time t. The conditional distribution of ƒ (Rs′, t | Ys, t) is mathematically defined as:
 |
The posterior inferences of Rs′, t | Ys, t from Eq. (16) are generated based on the posterior distributions of θ at the training site s and at time t using the MCMC samplings (Renard 2011; Verdin et al. 2015). Let N be the size of the post-convergence MCMC sample. The above process is repeated N times and produces a predictive posterior distribution at the validated site s′ and at time t. The statistical values (e.g., the mean, median, 5 %, and 95 % credible intervals) are calculated from the posterior distribution at each site s′ and at time t. In this study, the median value at site s′ is used as the Bayesian-corrected DPR (DPR_BC) rainfall-rate estimates within the validation process. It is followed by comparing it with the corresponding GR references to evaluate the performance of the BC model.
Consequently, the best-performing BC algorithm is applied to the regions of interest in GPM-overpass cases with rainfall records. In the application, the estimated parameters are implemented in the same region for the corresponding time period, i.e., the calculation of the DPR_BC rainfall-rate product on the basis of Eq. (16) is performed at sites that are also used for parameter estimation.
The DPR comprises both KaPR and KuPR (Fig. 3b). The swath widths for the KuPR and the KaPR are 245 km and 120 km, respectively. Both have 49 footprints with a horizontal resolution of 5 km. The KuPR's scan mode is known as normal scan, whereas the KaPR has two modes: matched scan (MS) and high-sensitivity scan (HS). The range resolution for the KuPR is 250 m, and it samples at 125-m intervals. The resolution and sampling intervals of the KaPR in MS mode are the same as the KuPR, although in HS mode, the resolution is 500 m and the sampling interval is 250 m (Iguchi et al. 2017). In this study, version 5 of the GPM 2ADPR algorithm is used. The “precipRate NearSurface” product from the solver module is considered.

(a) Locations of the Weather Service Surveillance Radar (WSR-88D), i.e., NEXRAD KHGX in Houston–Galveston, Texas; KLIX in New Orleans, Louisiana; and KMLB in Melbourne, Florida; (b) the GPM–DPR scan pattern, which refers to Iguchi et al. (2017); (c) to (e) a display of the spatial patterns of instantaneous DPR Ka-band MS near-surface rainfall as the GPM overpasses the KHGX radar on August 20th, 2015, in orbit 8383; the KLIX radar on July 21st, 2017, in orbit 1929; and the KMLB radar on February 22nd, 2017, in orbit 1697, respectively.
The Weather Service Surveillance Radar (WSR-88D) network is located in the southeastern plains of United States and provides ground references in consideration of the uncertainties that could be present in GR observations in mountainous regions. Three radars are used in this study: KHGX, KLIX, and KMLB. The KHGX radar (29.4719°N, 95.0792°W, 5.48 m) is located in Houston-Galveston along the Gulf of Mexico in Texas. The KLIX radar (30.3367°N, 89.8256°W, 7.31 m) is situated in New Orleans, Louisiana. The KMLB radar (28.1133°N, 80.6542°W, 10.66 m) is stationed in Melbourne, Florida (Fig. 3a). The other reason for the location of the radars is that heavy rainfall and severe flooding occur more frequently across the southeastern United States (Bedient et al. 2000; Zhang et al. 2018). This highlights the significance of acquiring a deeper knowledge of DPR rainfall rate products in the southeastern plains and is also beneficial to extending its application into other regions with frequent rainfall events.
The radars have a beam width of 1°, a range resolution of 250 m, and a frequency range of 2700–3000 MHz. It usually takes around 5 min to complete a volume scan, which consists of 14 plan position indicator scans from 0.5° to 19.5° in elevation (Crum et al. 1998). The Next Generation Weather Radar (NEXRAD) Level II data are processed by the dualpolarization radar rainfall algorithm, DROPS2.0, which is detailed by Chen et al. (2017). This algorithm is developed by a region-based hydrometeor classification mechanism and shows good performance for polarimetric radar applications (Wingo et al. 2018). Additionally, the DROPS2.0 rainfall product proves excellent performance with rain-gauge observations in the Dallas–Fort Worth area (Chen and Chandrasekar 2015). To ensure the rainfall accuracy of GR observations in this study, DROPS2.0 and NEXRAD Single-/Dual-polarization (Pol) rainfall products are intercompared with the collected Automated Surface Observing System (ASOS) gauges at the KHGX radar inside a 100-km radius of the Hurricane Harvey event between August 25th and 29th, 2017 (Fig. 4a). The normalized mean absolute error (NMAE), the correlation coefficient (CORR), and the root mean square error (RMSE) of the DROPS2.0 product reach 34.9 %, 0.92, and 3.86 mm h−1, respectively. It is evident that the DROPS2.0 product has better skill scores compared with both Single-Pol and Dual-Pol products (Figs. 4b–d). The use of the NMAE index is preferred to the mean or normalized mean bias, as it might be counterbalanced by the positive and negative signed biases in the statistics (Tang et al. 2016). Furthermore, to ensure the creditability of the GR references in the regions of interest, the KHGX, KLIX, and KMLB samples beyond a range of 100 km are not considered in this study.

(a) Spatial distribution of the Automated Surface Observing System (ASOS) gauges at the KHGX radar (inside 100-km radius) and the hourly scatter plots for ground-based radar rainfall products, including (b) DROPS2.0, (c) NEXRAD Dual-polarization (Dual-Pol), and (d) NEXRAD Single-polarization (Single-Pol), compared with ASOS gauge observations between August 25–29th, 2018, during the Hurricane Harvey event.
As the spatial resolution is 5 km, and the temporal resolution is instantaneous for the training data in the BC model, these datasets are carefully chosen to ensure that the relative time difference between the overpass of the GPM and the GR scan is less than 5 min. Next, volume matching is performed to place both the GR and DPR data in a common grid at 5 × 5 km2 before evaluating with the BC model. Details of the volume-matching algorithm can be found in the work by Bolen and Chandrasekar (2003) and Schwaller and Morris (2011).
There are two concerns regarding the BC model's performance: with less training data, the parameter estimates contain greater variance, while with less validation data, the variance of the performance statistics is greater. In general, there is no ideal tradeoff for partitioning the training and validation datasets; therefore, this study applies the 80/20 rule. Moreover, an additional experiment to test the robustness of the best-performing BC algorithm. We randomly repeat the operation of selecting training data at ten times and reexamine the model performance, respectively.
A total of 75 volume-matched DPR–GR datasets from the GPM overpasses of the KHGX radar from April 2014 to June 2018 are used. Model parameters are estimated using randomly selected data from 80 % of the volume-matched DPR–GR statistics. The remaining 20 % of the volume-matched data are used for model validation (Fig. 5a). The goodness of fit of the natural log-transformed GR rainfall rate for the proposed BC algorithm is also examined graphically using a quantile–quantile (QQ) plot based on the training data in this study. Figure 5b shows the probabilistic density function (PDF) curve of the natural log-transformed GR training data. All data are approximately close to the theoretical line with the assumption of normal distribution (Fig. 5c). To demonstrate the role of rainfall intensity in the BC algorithm, the spatial patterns and associated PDF curves of log-transformed DPR training data under various rainfall intensities are also shown in Figs. 6a and 6b.

(a) Spatial distributions of volume-matched DPR instantaneous rainfall-rate estimates for calibration (blue dots) and validation (red dots), respectively, as the GPM overpasses the KHGX radar (inside 100-km radius) between April, 2014 and June, 2018; (b) the probabilistic density function (PDF) curve of the log-transformed rainfall rate from GR measurements in the training period; (c) The quantile-quantile (QQ) plot of the log-transformed GR rainfall rate in the training period. The red line is a theoretical line with the assumption of a normal default.

(a) Spatial distributions and (b) their log-transformed PDF curves of various rainfall intensities, including light (gray), moderate (blue), heavy (yellow), and violent (red) rain for the original DPR estimates in the training period as the GPM overpasses the KHGX radar (inside 100-km radius) between April 2014 and June 2018.
In the model application, the best-performing BC algorithm is applied as the GPM overpasses the KHGX radar (on August 20th, 2015), the KLIX radar (on July 21st, 2017), and the KMLB radar (on February 22nd, 2017) with heavy rainfall records across the southeastern United States. The spatial patterns of the volume-matched DPR instantaneous rainfall rate estimates for the three GPM overpasses are presented in Figs. 3c–e. The parameters are, respectively, estimated using the volume-matched data and the bestperforming BC model for each GPM-overpass case and are then applied across the corresponding overpass region for the duration of observation.
This section demonstrates an example of parameter estimation for model M4. The posterior distributions for the M4 model's parameters shown in Fig. 7 reveal that a Bayesian analysis is able to simulate parameter uncertainty compared with a traditional statistical approach. The fixed offset α1t and slope α2t show the PDF curves with various mean and SD values (Fig. 7a), where the mean (SD) values of α1t and α2t are 0.03 (0.20) and 0.91 (0.10), respectively (Table 1). The fixed offset is close to 0.03 with a larger SD at 0.20, and the fixed slope has a lower SD in terms of 0.10 (Table 1). Figures 7b and 7c display the posterior PDF curves of the varying offset β1t and the varying slope β2t, which are influenced by various rainfall intensities. The mean (SD) values of β1t are −0.06 (0.20), −0.03 (0.21), 0.23 (0.26), and −0.08 (0.33) for light, moderate, heavy, and violent rainfalls, respectively (Table 1). The effect of varying offset on heavy rainfall is more significant than for the other rainfall categories, but the associated uncertainties increase with light to violent rainfall. The mean (SD) values of β2t are 0.02 (0.10), 0.06 (0.10), −0.04 (0.11), and −0.06 (0.10) for light, moderate, heavy, and violent rainfalls, respectively. Positive effects on the slope parameter are evident for light and moderate rainfalls, while negative effects are detected with heavy and violent rainfalls. The uncertainties for the influence of rainfall intensity on the varying slope are similar in terms of SD at around 0.10. The hyperparameters σβ1 and σβ2, which are related to varying intercept β1t and varying slope β2t parameters, show the PDF curves with mean (SD) values of 0.33 (0.23) and 0.13 (0.11), respectively. The distribution of σβ2 is narrower than that of σβ1, which implies that the residual error of varying slope is smaller than that of varying offset (Fig. 7e). The residual error σt shows a PDF curve in terms of the mean and SD values at 1.0 and 0.01, respectively (Fig. 7d).


The PDF curves of some inferred posterior parameters of model M4 based on the training data as the GPM overpasses the KHGX radar (inside 100-km radius) between April, 2014 and June, 2018. (a) Fixed offset (α1t) and slope (α2t), (b) varying offset (β1t), (c) varying slope (β2t), (d) residual error (σt), and (e) hyperparameters σβ1 and σβ2.
These posterior parameters are important for model inference and clarification. The residual errors (i.e., σβ1, σβ2, and σt) quantify the imperfect nature of regression models. This example shows that these parameters (α1t, α2t, β1t, β2t, σβ, σβ2, and σt) follow different PDF curves with a certain variance. Table 1 contains more details of the model's parameters.
4.2 Model inference, comparison, and clarificationTo demonstrate the performances of BC models M1 to M4, the independent 20 % volume-matched DPR–GR rainfall rate datasets of the GPM's overpasses with the KHGX radar between April 2014 and June 2019 are used for model validation and comparison based on the inferred posterior parameters.
Table 2 reveals that the best performance among the four BC models is demonstrated by M4. The corresponding RMSE, NMAE, and CORR indices are 8.74 mm h−1, 58.11 %, and 0.755, respectively. Compared with the original DPR rainfall-rate estimates, the RMSE and NMAE values for M4 decrease by 10.38 % and 8.21 %, respectively, while its CORR increases by 3.40 %. Additionally, M1 has higher RMSE and NMAE values at 8.82 mm h−1 and 59.63 % but lower CORR in terms of 0.737 compared with M2 and M3 during the validation period. The results of the statistical summary imply that it is very important to consider the impact of rainfall intensity in the BC algorithm for improving the DPR instantaneous rainfall-rate estimates. It is noteworthy that M1 does not consider the effect of rainfall intensity, and it also demonstrates the worst performance among the four BC models; however, M1 still shows better skill scores than the original DPR rainfall rate retrievals. Additionally, in terms of RMSE, NMAE, and CORR, both M2 and M3 show similar performances at 8.80 mm h−1/8.78 mm h−1, 58.24 %/58.19 %, and 0.752/0.753, respectively. This indicates that the influence of rainfall intensity on varying offset and varying slope parameters is more or less of equal strength in the BC algorithm.

Table 3 displays the summary of statistical error indices of DPR and DPR_BC in the validation period with ten random operational tests as the GPM overpasses the KHGX radar between April 2014 and June 2018. The DPR_BC rainfall rate estimates corrected by M4 reveal similar performances in the validation period among the ten random tests. For each experiment, the signed bias of M4 is expected to be smaller than that of the original DPR instantaneous rainfall rate estimates. The RMSE index of M4 ranges between 7.15 and 10.06 mm h−1, which is lower than the original DPR estimates between 8.57 and 11.18 mm h−1; i.e., the RMSE index of the DPR_BC decreases by 10.0–18.2 % compared with the DPR during the ten random tests. In terms of the NMAE index, the DPR_BC also shows higher performances than the original DPR, where the NMAE value of the DPR_BC decreases by 7.7–14.4 %, accordingly. Additionally, a higher correlation is also evident between the DPR_BC and GR products in terms of the CORR value at 0.664–0.758. In total, there is a considerable decrease for both RMSE and NMAE values and an increase for CORR in terms of the DPR_BC. By applying the best-performing BC algorithm, the average improvement ratios of the RMSE, NMAE, and CORR values are 13.6, 10.1, and 4.8 %, respectively, regarding the DPR_BC in the validation period for the ten random tests. This proves that the observation errors of the DPR instantaneous rainfall-rate estimates could be minimized if the impact of rainfall intensity is adequately considered in the BC algorithm.

As described in Section 4.2, M4 shows the best performance among the four BC models. In this section, M4 is used to extend the model's application in three rainfall events as the GPM overpasses three NEXRADs (i.e., KHGX, KLIX, and KMLB) across the southeastern United States, respectively. Heavy rainfall records exist for each GPM-overpass case in the model application (Figs. 3c–e).
a. Case: August 20th, 2015, KHGXAs seen from Fig. 3c, on August 20th, the GPM overpasses over Houston and captures a widespread thunderstorm moving into the coastal region with a peak rainfall rate above 50 mm h−1. The original DPR instantaneous rainfall rate product reveals an overestimation for light rainfall and an underestimation for heavy rainfall within a 100-km radius of the KHGX radar scan (Fig. 8a). The PDF curve's peak for the DPR_BC is much closer to GR than to DPR, which indicates that the DPR_BC estimate performs better compared with the DPR. As discovered from the statistical summary in Fig. 9, the DPR_BC product demonstrates higher skill scores in terms of RMSE, NMAE, and CORR at 13.98 mm h−1, 66.58 %, and 0.625, respectively. Compared with the original DPR product, the RMSE and NMAE values of the DPR_BC decrease by 11.5 % and 9.5 %, respectively, while its CORR increases by 6.9 %. The spatial maps of the DPR_BC and its associated predictive uncertainties are also shown in Figs. 10a–c. The median value and credible intervals (i.e., the 5th and 95th percentiles) of the DPR_BC reveal similar spatial patterns in the survey region.

The PDF curves of the DPR (blue) and the DPR_BC (red) instantaneous rainfall-rate estimates and the GR references (black) as the GPM overpasses the KHGX radar (August 20th, 2015), (b) the KLIX radar (July 21st, 2017), and (c) the KMLB radar (February 22nd, 2017), respectively.

Bar plots of statistical error indices (RMSE, NMAE, and CORR) with regard to the DPR and the DPR_BC instantaneous rainfall-rate estimates compared with the GR references as the GPM overpasses the KHGX radar (August 20th, 2015), (b) the KLIX radar (July 21st, 2017), and (c) the KMLB radar (February 22nd, 2017), respectively.

Spatial maps of the predictive DPR_BC rainfall-rate product and its credible intervals as the GPM over-passes the KHGX radar (August 20th, 2015), (b) the KLIX radar (July 21st, 2017), and (c) the KMLB radar (February 22nd, 2017), respectively.
Figure 3d shows a GPM-overpass rainfall event over the KLIX radar in New Orleans on July 21st, 2017. Most regions have light and moderate rainfall with instantaneous values below 8 mm h−1, except for a convective cell with a rainfall rate of about 50 mm h−1 located in the northeast. Similar to the case survey of August 20th, 2015, at the KHGX radar, there is an overall overestimation for the DPR product on July 21st, 2017. For this GPM-overpass rainfall event, a larger bias exists for light and moderate rainfalls, but a smaller bias is evident for heavy rainfall (Fig. 8b). The RMSE, NMAE, and CORR values of the DPR are 10.34 mm h−1, 78.19 %, and 0.635, respectively. Based on model M4, the accuracy of the DPR_BC estimates has increased in terms of the RMSE, NMAE, and CORR values at 6.51 mm h−1, 61.84 %, and 0.745, respectively. As shown in Fig. 9, the improvement ratios of the above three metrics are 37.1, 20.9, and 17.4 %, respectively. The PDF curves show that the DPR_BC performs better than the DPR as the rainfall rate is higher than 2.0 mm h−1. However, the density value of the peak curve for the DPR_BC is higher than that of both the DPR and the GR as the GPM overpasses the KLIX radar. This is attributed to an overestimation for DPR in terms of rainfall rate between 1.0 and 2.5 mm h−1 (Fig. 8b). After M4 adjustment, the corresponding DPR_BC accounts for a higher proportion for light rainfall and thus has a higher peak curve with a density of 0.40. The rainfall map and its DPR_BC uncertainties are presented in Figs. 10d–f, where the heaviest rainfall is detected in the center of each figure but with various peak values.
c. Case: February 22nd, 2017, KMLBA rainfall event on February 22nd, 2017, is chosen for model application. Figure 3e presents a GPM overpass of the KMLB radar in Melbourne, Florida. As summarized in Fig. 9, the DPR_BC demonstrates better skill scores in terms of RMSE, NMAE, and CORR at 3.49 mm h−1, 48.35 %, and 0.651, respectively, compared with the original DPR rainfall product. Similar to the evaluated results at both the KHGX and KLIX radars, the RMSE and NMAE values of the M4 results at the KMLB radar decline by 27.5 % and 59.4 %, respectively, while the CORR increases by 10.5 %. Furthermore, the DPR_BC product demonstrates a closer PDF curve with GR observations than the original DPR data. This again proves that M4 has the ability of improving DPR instantaneous rainfall rate estimates for GPM-overpass cases. From Fig. 8c, it seems that DPR_BC is insensitive to the presence of DPR, as the rainfall rate is more than 5.0 mm h−1. This is because the volume-matched DPR rainfall data performed well for rainfall rates above 5.0 mm h−1, as the GPM overpasses the KMLB radar on February 22nd, 2017. However, the bias correction result of M4 is not very obvious under this condition. Moreover, as revealed by Figs. 10g–i, similar spatial patterns in terms of the median and its credible intervals are found for DPR_BC for this GPM-overpass rainfall event.
In total, the statistics and their intercomparison at three different locations in the southeastern United States demonstrate that the best-performing BC algorithm, M4, can reduce the retrieval bias and some potential errors of the standard DPR instantaneous rainfall rate product using GR observations as references.
This study proposes a new approach for improving the instantaneous rainfall rate product from space-borne radar under a hierarchical Bayesian framework. The modeling experiment was performed using Dual-Pol radar rainfall products as references as the GPM overpasses the GR across the southeastern United States. The volume-matched DPR–GR instantaneous rainfall rate estimates in terms of spatial resolution at 5 × 5 km2 are used as training data for parameter calculation and model evaluation.
The four BC models, M1 to M4, are intercompared to study the impacts of various rainfall intensities on the DPR rainfall rate retrievals during the GPM overpasses of the KHGX radar between April, 2014 and June, 2018. A log-transformed Gaussian distribution is used to represent the instantaneous rainfall process. The best performance in terms of RMSE, NMAE, and CORR at 8.74 mm h−1, 58.11 %, and 0.76, respectively, is demonstrated by M4. During ten randomly cross-validated tests, the RMSE, NMAE, and CORR values of the DPR_BC improve by 13.6, 10.1, and 4.8 %, respectively, compared with the original DPR rainfall rate estimates. The inclusion of rainfall intensity categories in the BC algorithm is crucial for minimizing the measurement errors in the standard DPR rainfall rate estimates. Considering that several other factors (e.g., raindrop-size parameterizations (Liao et al. 2014) and attenuation (Seto et al. 2013)) will influence the rainfall rate retrieval accuracy of the DPR, it is suggested that more physical variables should be incorporated into the BC algorithm in the future work.
The best-performing BC model, M4, is further applied to three rainfall events as the GPM overpasses KHGX (August 20th, 2015), KLIX (July 21st, 2017), and KMLB (February 22nd, 2017) radar sites across the southeastern United States. In most cases, the PDF curve corresponding to the DPR_BC correlates better with the GR observations compared with the original DPR product. If there are larger biases regarding the presence of the DPR, the proposed BC algorithm is capable of reducing the original DPR observation errors with better performance, which is evident in both Figs. 8a and 8c in terms of light rainfall. However, as there is less difference between volume-matched DPR and GR data, the behavior of the DPR_BC does not exhibit an obvious advantage compared with the standard DPR product. In summary, the application of the best-performing BC model clarifies the reliability of improving instantaneous DPR rainfall rate estimates using GR observations as references.
At this current stage, the BC algorithm is only applied in cases when both DPR and GR have rainfall records. Yang et al. (2012) reported that a single Tweedie distribution exists between precipitation occurrence and the associated daily amounts. Bruno et al. (2014) also attempted to adapt zero-inflated distributions for simulating zero records from GR observations. Moreover, this study mainly examines the BC method on GPM-overpass cases across the southeastern United States. The challenge of complex terrain for ground-based radar rainfall estimates provides the motivation for proposing a more robust Bayesian algorithm for improving the DPR instantaneous rainfall rate estimates over the mountainous regions of the United States. The application of this BC algorithm on a global basis is promising, since this model is performed with volume-matched instantaneous DPR rainfall rate estimates in terms of spatial resolution at 5 × 5 km2 for the training data. The next stage is to perform a full application as the GPM over-passes ground radars around the globe. Additionally, one interesting concern is how to extend the best-performing BC algorithm for the DPR as the GPM overpasses regions with sparse GR observations. The exploration of spatial dependences for the Bayesian parameters would be beneficial and could be the focus for future study.
This research is supported by the NASA GPM/PMM program. Additionally, we sincerely thank the editors and anonymous reviewers for their helpful comments and suggestions.