2021 Volume 99 Issue 4 Pages 933-972
The boreal summer intraseasonal oscillation (BSISO) is among the most pronounced subseasonal variability in the tropics during boreal summer. Compared with its wintertime counterpart, the so-called Madden–Julian oscillation (MJO), the BSISO convection displays more complicated spatiotemporal evolution, characterized by northward propagation over the northern Indian Ocean and western North Pacific as well as eastward propagation along the equator. It exerts a strong effect on a broad range of tropical weather and climate phenomena, such as tropical cyclogenesis, monsoon onset, and active/break cycles, among others. Our fundamental understanding of the BSISO has steadily advanced: so far various aspects of the BSISO have been described, and several theories that aim to elucidate its northward propagation have been proposed. Yet, our skill to simulate the BSISO by general circulation models remains unsatisfactory, though it has been improved. This paper reviews some fundamental aspects of the BSISO from the viewpoint of observation, theory, and modeling.
The tropical intraseasonal oscillation (ISO), marked by a 30–60 (901)-day periodicity, is the most predominant subseasonal variability in the tropics. It was discovered in a series of studies by Madden and Julian (1971, 1972). Owing to the discoveries, the oscillation has been referred to widely as the Madden–Julian oscillation (MJO), in particular after the publication of the study by Swinbank et al. (1988) and Lau, N.-C. et al. (1988) (a comprehensive historical review can be found in the study by Madden and Julian 2012). The MJO is characterized by a coupling between the large-scale Kelvin–Rossby wave structure and convectively active region, which move together eastward at a slow-phase speed of ∼ 5 m s−1 over the warm pool. Contrarily, in the Western Hemisphere, the upper tropospheric circulations move at a much faster-phase speed (∼ 20–40 m s−1), and the accompanying lower tropospheric signals are sometimes observed (Knutson and Weickmann 1987; Kikuchi and Takayabu 2003; Straub 2013).
However, due to the seasonal cycle in the boundary conditions (e.g., Fig. 1) and associated circulations, such a typical behavior is most pronounced during boreal winter, and another mode emerges during boreal summer. The eastward propagation over the warm pool is shared by this mode, whereas the northward propagation at a speed of ∼ 1 m s−1 over the northern Indian Ocean (IO) and western North Pacific (WNP) is also pronounced. The circulation structures basically follow that of the MJO, whereas the Rossby-wave response is more pronounced in the northern hemisphere. This mode has been referred to variously as the boreal summer intraseasonal oscillation (BSISO) (e.g., Wang and Xie 1997; Kemball-Cook and Wang 2001), monsoon intraseasonal oscillation (MISO) (e.g., Sengupta et al. 2001; Hoyos and Webster 2007), boreal summer intraseasonal variability (BSISV) (e.g., Annamalai and Sperber 2005; Sperber and Annamalai 2008), or summertime MJO. Hereinafter, this mode is referred to as the BSISO according to the author's preference.
Although the distinct behavior of the ISO between boreal summer and winter had been well recognized, the validity of considering them as different modes has been confirmed by a series of recent studies based on different approaches. As discussed in detail in Section 2.2, Kikuchi et al. (2012) developed a new ISO index in which at any given time, the state of the ISO is represented in terms of either the MJO mode or the BSISO mode. Such a representation is based on the judgment of how the spatiotemporal structure of intraseasonal outgoing longwave radiation (OLR) anomalies resembles that of the typical MJO or BSISO by employing the extended EOF (EEOF). They revealed that the MJO mode predominates from December to April whereas the BSISO mode from June to October; the predominant mode tends to switch from one to the other in May and November. On the other hand, Kiladis et al. (2014) demonstrated how the canonical pattern of the ISO changes on a daily basis. They developed another all-season OLR-based ISO index (referred to as an OLR–MJO index in their paper) by calculating the EOFs centered on each day of the calendar year using a sliding window. As is defined, the patterns of the leading two EOFs vary only slightly from one day to the next, whereas they appear to exhibit a bimodal nature, as suggested by the significant drop in the eigenvalue in May and around November (see their Fig. 1). On the basis of nonlinear Laplacian spectral analysis, a dimension reduction technique used for the extraction of spatiotemporal patterns from high-dimensional data, Szekely et al. (2016) revealed that the BSISO and MJO modes naturally emerge as a distinct family of modes in the field of cloudiness. Thus far, several comprehensive review papers have been published on the MJO (e.g., Madden and Julian 1994; Zhang 2005; Jiang et al. 2020), and some aspects of the BSISO have been addressed in those papers in the context of the BSISO being regarded as a variation of the MJO. To the author's knowledge, there are only a few, if any, comprehensive review articles specifically focused on the BSISO.
The BSISO has a profound influence on various space-time scales, such as Asian monsoon onset, active-break cycles, tropical cyclone (TC) genesis, and midlatitude phenomena, such as Meiyu/Baiyu and teleconnections. Moreover, the frequency of BSISO events during boreal summer in a year determines the seasonal mean precipitation amount in the Indian summer monsoon region (Sperber et al. 2000; Goswami and Mohan 2001; Goswami et al. 2006). Thus, it is important to understand the fundamental characteristics, dynamics, and physics of the BSISO and to accurately simulate and predict its behavior.
This paper reviews several fundamental aspects of the BSISO with a heavy focus on observational aspects (Sections 3, 4), although the existing theories (Section 5) and simulating aspects (Section 6) are also briefly reviewed. To address various aspects of the BSISO in a consistent manner, we base our analysis on the BSISO index of the bimodal ISO index (Kikuchi 2020), which may be considered to be among the most reasonable BSISO indices to capture the spatiotemporal structure of the BSISO (Wang, S. et al. 2018).
We use various datasets to describe different aspects of the BSISO. Daily NOAA interpolated OLR dataset at a horizontal resolution of 2.5° latitude/longitude (Liebmann and Smith 1996) is utilized to derive the bimodal ISO index and describe convective activity. The APHRODITE precipitation product was created in an attempt to construct a reliable high-resolution daily gridded precipitation dataset over land covering the whole of Asia using rain gauge observations (Yatagai et al. 2012), is used to determine the relationship between the BSISO and precipitation variability associated with the Asian summer monsoon in Section 4.1. To describe the relationship between monsoon low-pressure systems and the BSISO in Section 4.2, the global monsoon disturbance track dataset developed by Hurley and Boos (2015) is utilized. The International Best Track Archive for Climate Stewardship (IBTrACS) version 4 dataset (Knapp et al. 2010) is used to describe TC genesis associated with the BSISO in Section 4.2. JRA-55 (Kobayashi et al. 2015) is also used in this study to examine some dynamical fields. Monthly NOAA Optimum Interpolation sea surface temperature (SST) V2 (Reynolds et al. 2002) is used to describe the SST anomalies during El Niño and the Southern Oscillation (ENSO) in Section 3.4. TRMM 3B42 version 7, which provides high spatial (0.25° × 0.25°) and temporal (3 h) precipitation data, is used in Section 4.1. The period for each data used in this study is presented in Table 1.
We briefly describe the bimodal ISO index, introduced by Kikuchi et al. (2012) and slightly revised recently by Kikuchi (2020). First, to isolate the intraseasonal component, a 25–90-day Lanczos bandpass filter (Duchon 1979) is applied to the OLR data. Then, EEOF analysis (Weare and Nasstrom 1982) with three time lags (−10, −5, and 0 days) is conducted on the intraseasonal OLR data to extract the typical spatiotemporal behavior of the ISO convection during boreal summer and winter individually. The summer and winter months are defined as June–October (JJASO) and December–April (DJFMA), respectively. The first two EEOFs for each season are used to define the BSISO and MJO modes, respectively. Finally, the corresponding principal components (PCs) for the entire period are obtained by projecting the extended intraseasonal OLR anomaly fields composed of the same three time lags onto each EEOF for each mode, giving rise to the BSISO and MJO indices, respectively. At any given time, the state of the ISO is classified into significant BSISO, significant MJO, or insignificant ISO based on the normalized amplitude (A* = (PC1*2 + PC2*2)1/2) and non-normalized amplitude A = (PC12 + PC22)1/2 of the BSISO and MJO indices, where PC* indicates the normalized PC by one standard deviation during the period the EEOF analysis is conducted (see Kikuchi et al. 2012; Kikuchi 2020 for a more detailed discussion). Figure 2 presents the leading two EEOFs for JJASO and DJFMA. The EEOFs are reasonably scaled so that the amplitudes reflect the typical magnitude of a significant event. It is clear that the BSISO and MJO modes have distinct spatiotemporal structures (their behaviors are addressed more in detail in the next section). On the basis of the classification discussed above, the occurrence frequency of significant ISO days as a function of month is presented in Fig. 3. It is evident that the occurrence frequency of significant ISO days is reasonably identified over the course of the year: the BSISO is predominant for JJASO whereas the MJO for DJFMA, and May and November are transitional months. As discussed in the introduction, this bimodality nature of the ISO was corroborated by later studies (Kiladis et al. 2014; Szekely et al. 2016).
Climatological-mean sea surface temperature (SST) (°C) for (a) JJASO and (b) DJFMA based on 34 years of Optimum Interpolation SST (OISST).
Evolution of the ISO convection patterns during boreal summer (left) and winter (right) represented in terms of the first two EEOFs of intraseasonal (25–90-day) OLR anomalies in W m−2. The EEOFs in the left and right panels are calculated using the JJASO and DJFMA data (top), respectively, for the period 1979–January 2017, which are utilized to define the MJO and BSISO modes, respectively. The contribution of each EEOF mode to the total variance is presented above each panel. Note that the EEOFs are scaled by multiplying by one standard deviation of the corresponding PCs during the period that each EEOF analysis is conducted so that the amplitudes reflect the typical magnitude of a significant event and the pair of the first two EEOFs represents half of the life cycle of each ISO mode. Adapted from Kikuchi (2020).
Occurrence frequency of significant ISO days as a function of calendar month normalized by the number of days available each month for the MJO mode (blue) and the BSISO mode (red). Adapted from Kikuchi (2020).
This section discusses some fundamental features of the BSISO: its spatiotemporal behavior and structure (Section 3.1), seasonal cycle (Section 3.2), initiation, longevity, termination (Section 3.3), and interannual variability (Section 3.4).
3.1 Historical background and fundamental behaviorIt was in the early 1970s (Madden and Julian 1971, 1972) or even earlier (see Li et al. 2018) that atmospheric scientists noticed that the ISO variability is prominent in the tropics. However, it was not until the late 1970s or early 1980s that the ISO started receiving considerable attention after the study by Yasunari (1979) (noted as “a breaking point” by Madden and Julian 1994) who discovered that the northward propagation of cloudiness over the Indian continent occurs in association with the eastward propagation of the ISO and that it has significant control over active/break cycles of the Asian summer monsoon. Yasunari's findings were confirmed by a series of following studies in the early 1980s (Yasunari 1979; Sikka and Gadgil 1980; Yasunari 1980, 1981; Krishnamurti and Subrahmanyam 1982). The advent of several years of global OLR data and objective analysis data made it possible to describe the detailed structures of the ISO on a global scale and its seasonal cycle in the late 1980s to early 1990s in a more statistically robust manner (Lau and Chan 1986; Knutson and Weickmann 1987; Wang and Rui 1990) on which much of our current knowledge is based.
Figure 4 presents the evolution of the composite BSISO convection and lower tropospheric circulation in conjunction with that of the MJO for comparison. The composites are constructed based on the BSISO and MJO indices of the bimodal ISO index discussed in Section 2.2 (see Kikuchi 2020 for detailed procedures). In phase 1, the BSISO convection starts appearing over the central IO. The convection develops with time and becomes elongated in phase 2. In phase 3, the convection seems to split into two parts: one moving eastward and the other moving northward or northwestward in the northern IO. In phase 4, the northward-propagating component covers the entire Indian subcontinent, whereas the eastward-propagating component reaches the western Pacific, making an elongated convective band that stretches from northwest to southeast as a whole, which is a major signature of the BSISO. The elongated convective band is more evident in phase 5. In phase 6, the northward-propagating component over the northern IO dissipates, whereas the convection over the western Pacific starts moving northwestward. Meanwhile, the eastward-propagating convection, albeit much weaker, along the Pacific intertropical convergence zone (ITCZ) is also observed. In phases 7 and 8, the convection over the WNP continues to move northwestward and weakens with time, whereas the eastward-propagating convection along the ITCZ continues to move eastward in the eastern North Pacific (ENP). Over the course of the life cycle, it is inferred that the northward-propagating convective element is closely tied with low-level cyclonic circulations.
Composite life cycle of the (a) BSISO and (b) MJO in terms of OLR anomalies in W m−2 (shading) and 850-hPa streamlines. The number of composite samples is denoted in the upper-right corner of each panel. Significant values at the 99 % level according to the t-test with the degree of freedom being one-sixth of the number of composite samples (taking account of persistence) are only drawn for OLR anomalies.
Contrarily, the MJO exhibits much different structure and propagation characteristics (Fig. 4b). Throughout its life cycle, the MJO convection shows a more symmetric structure about the equator and does not demonstrate a pronounced northward propagation. Moreover, the MJO convection and the associated Rossby-wave response to the west of the convection appear to be broader in the meridional direction.
It is beyond doubt that the distinct behavior between the BSISO and MJO is closely related to the underlying boundary conditions. The northward propagation of the BSISO convection in the northern IO and WNP is facilitated by the high SST there (Fig. 1a). As in the MJO convection, the SST exhibits a more symmetric structure about the equator, and an extremely high SST region (≥ 28°C) is extending further westward in the IO during boreal winter (Fig. 1b).
Next, to gain a sense of actual convective processes occurring in the BSISO convective envelope, infrared satellite imagery is presented in Fig. 5 when a recent significant BSISO event occurred. Since mesoscale convective systems (MCSs), the major building blocks of the BSISO (and MJO) convection, come in a variety of sizes and shapes (Houze 2004), this example may not be a typical one, although it offers implications and includes some essential features. This particular date corresponds to BSISO phase 6, which is characterized by a northwest–southeast convective band (Fig. 4a). The large-scale convective features as a whole bear strong resemblance to the composite structures of OLR. In reality, the northwest–southeast convective band from the Arabian Sea to the South China Sea (SCS), in this case, consists of three well-defined storm systems. In the Arabian Sea, Bay of Bengal (BOB), and SCS, TCs Maha, Bulbul, and Nakri can be seen, respectively. A close inspection indicates that the locations of these cyclones roughly correspond to the centers of the convection and large-scale low-level cyclonic circulations in the corresponding basins in the composite (Fig. 4a). This suggests that in individual BSISO events, MCSs tend to develop in these locations in this particular BSISO phase, although their types, sizes, and shapes greatly vary from event to event. It is worth noting that November offers a favorable condition for the development of TCs in the northern IO (Kikuchi and Wang 2010), and this is probably why MCSs in the northern IO took on the form of TCs in this particular case.
A snapshot of merged IR on November 5, 2019. One of the recent significant BSISO events in phase 6. Three tropical cyclones were formed in association with this event. Maha in the Arabian Sea, Bulbul in BOB, and Nakri in the SCS. At this time, Maha had weakened, whereas Bulbul and Nakri were in the TC strength. The reconstructed BSISO OLR anomalies (EEOF1 × PC1 + EEOF2 × PC2) are represented by a solid green line at the contour level of −5 W m−2.
Shown in Fig. 6 is a schematic summarizing the BSISO life cycle in terms of the convection and low-level horizontal winds superimposed on the SST anomalies. This schematic is drawn based on the composites discussed above. In phase 1, the major BSISO convection starts to develop over the central IO, whereas organized, albeit weaker, the convection is also observed in the ENP, which is the remnant of the previous BSISO cycle. Meanwhile, positive SST anomalies exist in the northern IO due to the convectively suppressed phase of the BSISO in the previous cycle. In phase 3, MCSs appear in the northern IO surrounded by low-level cyclonic circulations, whereas MCSs in the tropics are associated with low-level easterlies and move eastward along the equator. In phase 5, the eastern flank of the BSISO convection reaches the equatorial western Pacific, whereas several MCSs that occur in association with low-level cyclonic circulations develop both in the northern IO and SCS. In phase 7, the eastern flank of the convection in association with low-level easterlies continues to move eastward on its way to the ENP, whereas the convection in the northern IO has dissipated and the northwestward-propagating convection in the WNP has reached the Philippine Sea. Over the course of the life cycle, positive SST anomalies lead the BSISO convection by about a quarter cycle.
Schematic summarizing the life cycle of the BSISO. The convective activities associated with the BSISO are represented by clouds. Arrows indicate low-level, large-scale atmospheric circulation associated with the BSISO. SST anomalies associated with the BSISO are also shown.
Do the characteristics of the BSISO vary over the course of the summer? Kemball-Cook and Wang (2001) suggested that the spatiotemporal behavior of the BSISO in early summer and late summer are distinct. To determine how the propagation characteristics vary during the season, we present in Fig. 7 the propagation vector following Wallace et al. (1988) and Lau and Lau (1990) in conjunction with the standard deviation of intraseasonal OLR anomalies. Propagation vectors are calculated at each grid point by measuring the distance from the strongest positive center on the −5-day lag-correlation map to the strongest positive center on the +5-day lag-correlation map and dividing it by 10 days. We split an extended summer (May 16–November 15) into early (May 16–July 15), middle (July 16–September 15), and late (September 16–November 15) periods. Although the patterns of OLR anomaly variances vary between the periods, the differences in the fundamental propagation characteristics seem rather subtle, and common propagation characteristics are observed in each basin. Away from the equator in the northern hemisphere, northward propagation is pronounced in the northern IO, SCS, and western part of the WNP, whereas westward propagation is pronounced in the eastern part of the WNP. Contrarily, eastward propagation appears to be pronounced around the equator in the Indo-western Pacific region. These features are consistent with the composite structures of the BSISO (Fig. 4a). Hence, it may be reasonable to conclude that although the BSISO may exhibit some differences in its spatiotemporal structure over the course of the summer, its fundamental features remain the same.
Propagation vectors in m s−1 based on ±5-day lag-correlation maps and standard deviation of intraseasonal OLR anomalies in W m−2 (shading) for (a) May 16–July 15, (b) July 16–September 15, and (c) September 15–November 15.
How about the periodicity? Previous studies suggested that the periodicity of the BSISO is around 30–40 days (Hartmann et al. 1992; Wang et al. 2006), which is slightly shorter than that of the MJO (Zhang and Dong 2004). We examine the periodicity of the BSISO through the application of spectral analysis to high-pass-filtered BSISO PC time series. The high-pass-filtered PC time series is obtained in the same manner as that described in Section 2.2, except for the use of high-pass-filtered OLR anomalies, which are obtained by subtracting the climatological mean and three harmonics of the climatological annual cycle. In the interest of brevity, we focus on PC1 alone, although the same can be said for PC2. Here, we employ the conventional Fourier transform and wavelet transform. The Fourier-based spectrum is estimated by applying the fast Fourier transform to the high-pass-filtered PC time series in June to October each year. The wavelet-based spectrum is estimated following Torrence and Compo (1998). The Fourier spectrum provides an average energy distribution estimate during a particular period, whereas the wavelet spectrum provides an instantaneous energy distribution estimate at any given time. Figure 8 presents the climatological Fourier- and wavelet-based spectra during JJASO (i.e., averaged over each year) and its time series based on the wavelet transform. The Fourier- and wavelet-based spectra are in good agreement, and both indicate that the average periodicity over JJASO is around 50 days (Fig. 8a). However, the time series of the wavelet spectrum (Fig. 8b) demonstrates that the BSISO periodicity varies over the course of the summer. In early summer, the BSISO tends to have a shorter periodicity of ∼ 40 days, whereas the periodicity tends to become gradually longer with time to ∼ 50 days in late summer. Why does the periodicity vary? The EEOF result (Fig. 2) indicates that it takes about 40 days for the typical BSISO to complete its whole cycle. However, in reality, some BSISO events go through stagnation in progress during their life cycle for some reason, thus leading to a longer periodicity. For instance, during the summer of 2008, a series of significant BSISO events2 occurred quite regularly without stagnation, and their periodicities are suggested to be ∼ 40 days throughout the summer (not shown). Therefore, Fig. 8b may suggest that the BSISO events in early (late) summer are less (more) likely to be disrupted during their life cycle.
Climatological power spectra of PC1. (a) Spectra during JJASO based on the Fourier transform (black) and wavelet transform (green) as well as the (b) wavelet spectrum as a function of time. The PC1 time series used to estimate the spectra is obtained using high-pass-filtered OLR data (see the text for details). Both spectra are reasonably scaled.
Both composite life cycle and spectral analysis suggest that the BSISO tends to repeat itself on the intraseasonal timescale. To better understand the nature of individual BSISO events, this subsection investigates in detail the statistics of BSISO initiation, longevity, and termination. We classify the BSISO events into “primary” and “successive” using the method of Straub (2013). The primary events represent those with no immediately preceding BSISO event, whereas the successive events represent those that immediately follow a preceding event (Matthews 2008). For the sake of simplicity, we consider only the BSISO index of the bimodal ISO index (i.e., ignoring the transition between the MJO and BSISO modes). The detailed procedures are as follows: an event whose normalized BSISO amplitude (A*) increases from less than 1 to greater than 1 in a particular phase and retains its amplitude (A* ≥ 1) for at least five phases (i.e., more than half of a complete BSISO cycle) is defined as a primary event. Contrarily, an event whose normalized amplitude is equal to or greater than 1 both in the previous and following two phases is identified as a successive event in that phase. In addition, we define a termination event when either a primary or successive BSISO event terminates (i.e., its normalized amplitude becomes less than 1) in a particular phase.
Figure 9 presents the total numbers of primary, successive, and termination events as a function of BSISO phase. As in the study by Straub (2013), successive events (white bars) are much more common than primary events (black bars), indicating that significant BSISO events tend to last for a certain period of time once they are initiated. In fact, the average e-folding time, based on the BSISO index, is as long as about 36 days (Kikuchi et al. 2017). The relatively smaller numbers of successive events in phases 1, 2, 4, and 8 indicate that BSISO events are likely to be terminated as they reinitiate over the IO or move from the IO to the WNP (Fig. 4). The latter may be due to the presence of the MC, which sometimes prevents the MJO convection from crossing during boreal winter (Kerns and Chen 2016).
Number of primary, successive, and termination events as a function of BSISO phase. The primary, successive, and termination events are represented by bars with black, white, and gray colors inside. Dash dotted and dotted lines indicate the average number and one standard deviation from it across phases, respectively. Note that the average numbers of the primary and termination events are the same, whereas the one standard deviation is larger for the primary events.
Then, how long does each event tend to last? Figure 10 presents the longevity of the primary BSISO events. Note that each primary event has to go through at least five phases as described above. The average longevity in each BSISO phase, which slightly varies from phase to phase, is around 11, indicating that most significant BSISO events complete more than one whole cycle. Contrary to the average longevity, longer-lasting BSISO events tend to be initiated in phases 1 and 2, whereas BSISO events initiated in phase 6 tend to have shorter longevity. It should be noted that these statistics may reflect the difference in the number of primary events in each phase (Fig. 9) (i.e., a larger number of primary events in a given phase may have larger chances of having longer-lasting events) and whether any important dynamics or physics are involved in accounting for these statistics is still unclear at this point. It is of interest to note that the longest BSISO event occurred in 2008, covering an entire extended summer from middle April to middle November, which went through as many as 40 phases.
The longevity of primary BSISO events as a function of the BSISO phase. The ordinate indicates the number of phases a primary BSISO event experiences until it terminates. The average longevity is denoted by black circles, and the minimum and maximum longevities are denoted by upper and lower horizontal lines, respectively. The longevity of individual events is represented by green circles.
Finally, we discuss why most BSISO events tend to repeat themselves, focusing in particular on the reinitiation phase over the IO in phase 1. This issue does not seem to have been satisfactorily addressed, which is in contrast to the MJO counterpart (e.g., Blade and Hartmann 1993; Kikuchi and Takayabu 2003; Ray et al. 2009; Zhao et al. 2013; Takasuka et al. 2018). In the MJO, global circumnavigating signals are pronounced in various fields, and some previous studies stressed their role in the MJO reinitiation over the IO (Kikuchi and Takayabu 2003; Seo and Kim 2003; Powell and Houze 2015). As for the BSISO, in contrast, such circumnavigating signals are less pronounced, and most previous studies highlighted more localized dynamics that operate in the Asian monsoon region. Based on observational data analysis and idealized model simulations, Jiang and Li (2005) argued that it is the Gill-type solution in response to suppressed convection over the eastern equatorial IO (which may be interpreted as part of the previous BSISO event; see, e.g., phase 6 in Fig. 4) in the presence of the Asian monsoon circulation that is responsible for boundary-layer convergence. Such a convergence appears in the western IO, which eventually leads to the reinitiation of the BSISO. Seo and Song (2012) also suggested that the response to the previous suppressed convection plays an important role; moreover, they adopted potential vorticity thinking in the interpretation of how low-level convergence is generated. Other previous studies emphasized the role of the northward-propagating BSISO convection (Drbohlav and Wang 2005; Bellon and Sobel 2008). Based on a two-dimensional latitude-height model, Drbohlav and Wang (2005) and Bellon and Sobel (2008) revealed that when the BSISO convection is located further in the north (∼ 20°N), barotropic divergence appears to the south of the equator in response to the interaction between the circulation associated with the northwardpropagating BSISO convection and the seasonal mean vertical motion and vertical wind shear. The resulting barotropic divergence induces boundary-layer convergence and eventually precipitation. Recently, West et al. (2018) highlighted the oceanic processes in creating positive SST anomalies over the equatorial central IO that appear prior to the reinitiation of the BSISO convection (see, e.g., Fig. 6).
3.4 Interannual variabilityThe BSISO exhibits pronounced year-to-year variability (Salby and Hendon 1994; Lawrence and Webster 2001; Teng and Wang 2003; Goswami et al. 2006), although what controls the BSISO activity is still not perfectly understood. Most previous studies have attempted to understand the interannual variability of the BSISO in relation to SST anomalies. Recent observational studies have demonstrated that the BSISO variability, as measured by intraseasonally filtered OLR anomalies, in different regions are influenced by different SST anomaly patterns. For example, the BSISO variability over the central Pacific is enhanced during El Niño years (Liu et al. 2016; Wu and Cao 2017), whereas that over the WNP is enhanced in association with a more complex SST anomaly pattern characterized by cooling over the equatorial Pacific and northern IO as well as warming over the northern tropical central Pacific (Liu et al. 2016; Wu and Cao 2017; Li and Mao 2018), which may be perceived as the La Niña decaying summer (Wu and Cao 2017).
As opposed to the relationship between local BSISO variability and SST anomalies, it is less clear how the overall level of the BSISO activity, as measured by an index, is related to SST anomalies. Since ENSO is the most pronounced interannual SST anomaly, we focus on the relationship between the BSISO and ENSO. It has been well known that the overall activity of both MJO and BSISO has little to do with ENSO (Hendon et al. 1999; Slingo et al. 1999; Hendon et al. 2007; Kikuchi 2020). Figure 11 presents the time series of the JJASO mean BSISO amplitude, in terms of the BSISO index, and ENSO state, as measured by the Multivariate ENSO Index version 2 (MEI.V2), which is the latest version of the MEI (Wolter and Timlin 1993, 1998). It is evident that the BSISO amplitude exhibits pronounced year-to-year variations. The correlation between the BSISO amplitude and MEI is relatively low (0.21), indicating that the overall level of the BSISO activity is not significantly correlated with ENSO.
Interannual variations of the BSISO amplitude in terms of the JJASO average of the PC amplitude (line) and the state of ENSO in terms of MEI (bar). The years defined as El Niño and La Niña years are denoted by stars.
Then, is the spatiotemporal evolution of the BSISO influenced by ENSO or not? As discussed above, previous studies have demonstrated that the BSISO activity in some regions is influenced by ENSO (Liu et al. 2016; Wu and Cao 2017; Li and Mao 2019). From the time series of the MEI, we define El Niño years as having an MEI index of above 0.5 from June to October and La Niña years as having an MEI index of below −0.5. As a consequence, seven El Niño years (1982, 1986, 1987, 1993, 1994, 1997, and 2015) and eight La Niña years (1988, 1989, 1998, 1999, 2007, 2008, 2010, and 2011) are identified. In the same procedure as the derivation of the normal BSISO index described in Section 2.2, the BSISO index for El Niño and La Niña is developed using only the El Niño years and La Niña years, respectively, and composites are constructed based on them. Figure 12 presents the SST anomalies, one standard deviation of the intraseasonal OLR anomalies, and the composite life cycle of the BSISO during El Niño and La Niña years. During El Niño, the intraseasonal OLR variability (Fig. 12c) tends to be stronger over the equatorial western and central Pacific, whereas around the MC, it tends to be weaker. This contrast is consistent with that in previous studies (Teng and Wang 2003). Conversely, the intraseasonal OLR variability tends to be weaker over a large area from the northern IO to the western and central Pacific during La Niña (consistent with that in the study by Li and Mao 2019).
Composite structures of (top) SST anomalies in K, (middle) one standard deviation of the intraseasonal OLR anomalies in W m−2, and (bottom) life cycle of the BSISO in terms of OLR anomalies in W m−2 for El Niño (left) and La Niña (right) years. A nine-point smoothing is applied to the one standard deviation of the OLR anomalies for presentation purposes. The number of composite samples is denoted in the upper-right corner of each panel in e and f.
Regardless of these large differences in the intraseasonal OLR variability, the life cycles of the BSISO appear to be similar in both ENSO states in numerous fundamental respects (Figs. 12e, f). As in the normal composite (i.e., based on the entire period regardless of the ENSO state; see Fig. 4), the BSISO convection starts to appear in the equatorial central IO in phase 1 and moves northward over the northern IO in phases 2–5. Meanwhile, the BSISO convection over the western Pacific starts to appear in phase 4. As a combination of the northward propagation over the northern IO and the emergence over the equatorial western Pacific, an elongated rainband appears in phases 4–6. Finally, the convection in the western Pacific moves northwestward. Certainly, some notable differences can be observed. The BSISO convection is much stronger (weaker) and elongated eastward (confined westward) in the WNP during El Niño (La Niña) years, which is consistent with the contrast in the intraseasonal OLR variability in Figs. 12c, d.
This section focuses on the relationship of the BSISO with other significant atmospheric components, such as the Asian summer monsoon (Section 4.1); higher-frequency variability, including synoptic-scale disturbances, TCs, and quasi-biweekly oscillation (QBWO) (Section 4.2); and extratropical variability (Section 4.3).
4.1 BSISO and summer monsoonAs will be discussed below, it has long been well recognized that the BSISO has a profound influence on the onset and active/break cycles of the Asian summer monsoon. This subsection briefly addresses these issues.
a. Monsoon onsetAccording to the characteristics of the rainy season, such as the onset, retreat, and peak, the Asian summer monsoon may be perceived as being composed mainly of three different parts: Indian summer monsoon (ISM), western North Pacific summer monsoon (WNPSM), and east Asian summer monsoon (EAM) (Wang and LinHo 2002), the former two of which reside in the tropics.
Numerous previous studies have demonstrated that the BSISO strongly regulates the onset of both ISM (Sikka and Gadgil 1980; Yasunari 1980, 1981; Krishnamurti and Subrahmanyam 1982; Murakami et al. 1984; Krishnamurti and Gadgil 1985; Chen and Murakami 1988; Chen et al. 1988; Joseph and Pillai 1988; Goswami and Xavier 2005; Wang et al. 2009a; Bhatla et al. 2017; Taraphdar et al. 2018) and WNPSM (Chen and Chen 1995; Zhou and Chan 2005; Straub et al. 2006; Hung and Hsu 2008; Tong et al. 2009; Chi et al. 2015; Shao et al. 2015).
In many years, the first northward-propagating ISO (i.e., the first BSISO event in a year) can be observed from late April to middle May in the BOB (Li, K. et al. 2013). Although many of these events may be classified as MJO (see Fig. 3), they demonstrate northward propagation to a certain extent (i.e., displaying hybrid characteristics). Thus, in most cases, they are accompanied by a well-defined low-level cyclonic circulation (Li et al. 2016), which is a prominent feature of the BSISO (see Fig. 6), and sometimes produce strong storms (Li, Z. et al. 2013), such as Nargis that formed in late April 2008 and battered Myanmar in early May (e.g., Webster 2008; Kikuchi et al. 2009). It may have eventually led to the monsoon onset over the BOB (Wu et al. 2013). However, these early BSISO-like events may not lead to the ISM onset as a whole. The monsoon onset over Kerala (MOK), the southernmost state of India, has been considered as the start of the Indian principal rainy season. It normally occurs from late May to early June with the mean onset date of around June 1 (Ananthakrishnan and Soman 1988; Joseph et al. 2006). As a result, significant first northward-propagating ISO events may be perceived as bogus onset (Flatau et al. 2001, 2003) or pre-monsoon rain peak (Joseph and Pillai 1988; Joseph et al. 1994); the next northward-propagating convective event associated with the BSISO occurring in late May or early June plays an important role in the ISM onset in the majority of years (Bhatla et al. 2017; Taraphdar et al. 2018), perhaps by facilitating the formation of so-called monsoon onset vortex (Krishnamurti et al. 1981; Rao and Sivakumar 1999).
Conversely, the monsoon onsets of the WNPSM and EAM are signaled by the monsoon onset over the SCS (Tao and Chen 1987; Lau, K.-M. et al. 1988; Ding 1992; Lau and Yang 1997; Wang and LinHo 2002), which normally occurs during the fourth pentad of May (Wang et al. 2004, 2009b; Ciesielski and Johnson 2006; Shao et al. 2015). A recent study by Shao et al. (2015) revealed that the SCS monsoon onset occurs exclusively when the BSISO convection moves northwestward over the WNP.
Here, we discuss how the BSISO and monsoon onsets are linked in terms of climatological BSISO (CBSISO), which was referred to as the climatological ISO in some previous studies (Wang and Xu 1997; Kang et al. 1999). As the term implies, the CBSISO is defined as the climatological average over many years, and if there are no phase-locking features, the CBSISO amplitude should be small. Figure 13 presents the time series of the CBSISO index and time-latitude plots of the TRMM 3B42 precipitation in conjunction with reconstructed CBSISO OLR anomalies in the WNP and northern IO. In general, the monsoon onset over the SCS is characterized by an abrupt precipitation increase and wind reversals in the upper and lower troposphere, the former of which is usually caused by a merging of the near-equatorial rain belt with the South China rain belt (Lau and Yang 1997; Matsumoto 1997; Wang and LinHo 2002; Ding and Chan 2005). That feature is observed around middle May in the climatological-mean precipitation field in Fig. 13b. Although the amplitude of the CBSISO is not so large around that time (Fig. 13a), a reconstructed negative CBSISO OLR anomaly is observed to propagate northward from the equatorial region (Fig. 13b), which appears to be closely related to the northward migration of the near-equatorial rain belt. This indicates the important role of the BSISO in the SCS monsoon onset. The amplitude of the CBSISO then begins to amplify and remains high (e.g., in excess of 0.5) until the end of June. Contrary to the SCS monsoon onset, the MOK is usually indicated by a gradual northward shift of convective area from the equator (Ding 2004; Joseph et al. 2006), which is observed in Fig. 13c. The climatological-mean precipitation is enhanced just after June 1 over Kerala (∼ 10°N), the climatological date of the MOK, during which the CBSISO has a relatively large amplitude and the associated northward-propagating convection passes over Kerala, suggesting the important role of the BSISO in the MOK. It is interesting to note that the MOK does not exhibit a large year-to-year variation in the onset date (Ananthakrishnan and Soman 1988) compared to the SCS monsoon onset (Wu and Wang 2001). The phase-locking features of the BSISO discussed above are qualitatively in excellent agreement with the previous study by Nakazawa (1992). Why does the CBSISO exhibit such a phase-locking features? At this point, the reason is not well understood. One possible explanation would be that the BSISO events that trigger the monsoon onset tend to be stronger through the interaction with the monsoon onset compared with the BSISO events that do not. As a result, even if the phase of the BSISO were at random each year, the BSISO events that trigger the monsoon onset would stand out in the CBSISO. Moreover, it is notable that the periodicity of the CBSISO in early summer appears to be ∼ 40 days (Fig. 13a), which is in good agreement with the spectral analysis result (Fig. 8b).
(a) Time series of climatological BSISO index in terms of PC1 (black) and PC2 (green), (b) (c) time–latitude section of climatological-mean (1998–2018) TRMM 3B42 precipitation in mm day−1 (shading) in conjunction with reconstructed CBSISO OLR anomalies (contour at −2.5 W m−2) averaged between 110–120°E and 60–80°E, respectively. The normal onset timings for the South China Sea and Indian Ocean are represented by a thick dashed box and line, respectively. When the normalized BSISO amplitude is greater than 0.3, 0.4, and 0.5 are lightly, moderately, and darkly shaded, respectively, in the background in (a). For presentation purposes, 5-day running mean is applied to the TRMM 3B42 precipitation in (b) and (c). The reconstructed OLR anomalies are obtained using the following equation: EEOF1 × PC1 + EEOF2 × PC2.
Next, we determine the relationship between the active and break cycles of monsoon precipitation and the BSISO. This issue has been addressed by numerous studies (Krishnamurti and Blalme 1976; Yasunari 1979; Sikka and Gadgil 1980; Gadgil and Asha 1992; Goswami and Mohan 2001; Annamalai and Sperber 2005; Hoyos and Webster 2007; Pai et al. 2011). To examine the relationship between monsoon active/break cycles, we utilize the APHRODITE precipitation data to document precipitation over land. Following Rajeevan et al. (2010), we define the active and break spells of ISM rainfall events. That is, we calculate the daily precipitation over the ISM core zone, roughly from 18°N to 28°N and 65°E to 88°E [for the exact definition, see Fig. 4 of the study by Rajeevan et al. (2010)]. Then, we subtract the climatological precipitation amount during JJASO and divide by its daily standard deviation. The break and active spells are identified as the period during which the standardized rainfall anomaly is less than −1.0 or more than +1.0, respectively, for 3 days or more in a row. Note that Rajeevan et al. (2010) used only the JJA period while we use the JJASO period to examine the relationship over the course of the extended summer. We check the consistency between our results and those of Rajeevan et al. (2010) and confirm that the active and break periods are consistently defined. In addition, we examine the relationship between active/break cycles and the BSISO over the SCS in the same manner.
Figure 14 presents the relationship between the active/break cycles of ISM and SCS and the BSISO in the phase space. The pronounced control of the BSISO on ISM is evident. Both the active and break spells of the ISM rainfall are strongly affected by the BSISO phase in the presence of significant BSISO events (Figs. 14a, b). For instance, most active spells occur in BSISO convective phases over the Indian subcontinent (Fig. 4a), in particular phases 5 and 6 that together account for about 40 % of the total active events. Conversely, most break spells occur in the convectively suppressed phases of BSISO, in particular phases 8 and 1–2 that together account for about 40 %. The same can be said for the active/break cycles of the SCS summer monsoon (Figs. 14c, d). Over 50 % of active events occur in BSISO phases 4–6 that correspond to the convectively active phase of the BSISO (Fig. 4a), whereas over 40 % of break events occur in phases 8 and 1–2 that correspond to the convectively suppressed phase of the BSISO.
The relationship between the monsoon active (left)/break (right) cycles of (a) (b) the ISM and (c) (d) the SCS with the BSISO represented in the phase space. The state of the BSISO when an individual active/break spell began is represented by dots. The numbers in the parentheses indicate the fraction of events (%) that occurred in the corresponding BSISO phase.
Although we have paid particular attention to the Asian summer monsoon, it is worth northing that the Asian summer monsoon is not the only monsoon affected by the BSISO. Some previous studies (Higgins and Shi 2001; Barlow and Salstein 2006; Lorenz and Hartmann 2006) revealed that the BSISO also exerts a strong influence on the North American monsoon. The influence of the BSISO on the North American monsoon can be inferred from the composite figure presented in Fig. 4a. In phases 8 and 1–2, the BSISO convection, albeit the relatively weak amplitude, is located in the EP.
4.2 BSISO's influence on higher-frequency disturbances a. Synoptic-scale disturbancesThe convective envelope of the BSISO mainly consists of a number of MCSs that tend to occur in association with a variety of synoptic-scale systems (e.g., Fig. 5). Of them, a class of synoptic-scale systems, which are referred to as monsoon low-pressure systems (LPSs) in general, or variously called monsoon lows, TDs, and easterly waves, accounts for a large fraction of the total precipitation (e.g., Mathon et al. 2002; Yoon and Chen 2005; Berry and Thorncroft 2012; Hurley and Boos 2015). In other words, LPSs serve as the major building blocks of the BSISO convection from time to time. Thus, it is not surprising that the activity of LPSs is influenced by the BSISO. In fact, previous observational studies have demonstrated that the activity of LPSs is strongly regulated on the intraseasonal time scale in many different basins, including the northern IO (Goswami et al. 2003; Krishnamurthy and Ajayamohan 2010), WNP (Straub and Kiladis 2003), and ENP (Crosbie and Serra 2014; Rydbeck and Maloney 2014, 2015). Recently, Haertel and Boos (2017) conducted a global survey on the relationship between the ISO and LPSs during both summer and winter.
Here, we conduct an analysis similar to that by Haertel and Boos (2017), although we focus on LPS genesis rather than activity. We utilize the global monsoon disturbance track dataset developed by Hurley and Boos (2015). Figure 15 presents the number of LPSs formed in each BSISO phase. In general, LPSs are ubiquitous and could potentially form in any BSISO phase. Meanwhile, the likelihood of LPS genesis seems to strongly depend on the BSISO phase: they tend to occur in the convectively active phase of the BSISO. To elucidate this point, Fig. 15b presents the number of LPS genesis as a function of BSISO phase in different regions. Since the number of significant BSISO days is different among different phases, we normalize the number so that each represents the likelihood of LPS genesis per significant BSISO day in a particular phase. It is now evident that in each region, LPS genesis is more likely to occur in the BSISO convectively active phase than in the suppressed phase by a factor of 2–3.
(a) LPS genesis locations with respect to the BSISO phase and (b) the occurrence likelihood of LPS in three different regions defined by the colored boxes in (a). Blue and red shades in (a) represent the convectively active and suppressed regions of the BSISO, respectively, with shading starting at ±5 W m2 and ±15 W m2. The occurrence likelihood is normalized so that the numbers of LPSs are likely to occur per day in a particular phase of the BSISO.
As in LPSs, the BSISO exerts a strong effect on TC genesis in many basins, in particular in the northern hemisphere, including the northern IO (Kikuchi et al. 2009; Kikuchi and Wang 2010; Yanase et al. 2012; Bhardwaj et al. 2019), WNP (Nakazawa 1986; Liebmann et al. 1994; Kim et al. 2008; Ko and Hsu 2009; Li and Zhou 2013a, b; Yoshida et al. 2014; Zhao et al. 2015a, b), ENP (Maloney and Hartmann 2000b; Molinari and Vollaro 2000; Higgins and Shi 2001; Aiyyer and Molinari 2008; Jiang et al. 2012; Crosbie and Serra 2014), and Atlantic (Maloney and Hartmann 2000a; Barrett and Leslie 2009; Klotzbach 2010; Ventrice et al. 2011; Klotzbach and Oliver 2015).
Similar to Fig. 15, Fig. 16a presents the locations of TC genesis that occurred in a particular BSISO phase. In various basins in the northern hemisphere, it is observed that many more TC genesis takes place in the BSISO convectively active region than in the suppressed region. The relationship is clearer in Fig. 16b. The likelihood of TC genesis in the BSISO convectively active phases is a few or several times larger than that in the suppressed phases. The contrast is more obvious in the northern IO and WNP, whereas it is also observed in the ENP and Atlantic Ocean. These results are consistent, at least qualitatively, with those of previous studies.
The same as in Fig. 15, except for TC genesis.
Then, how does the BSISO affect the likelihood of TC genesis? The BSISO modifies the large-scale dynamical and thermodynamical conditions under which TC genesis occurs. Some previous studies have argued which aspects of the BSISO play important roles in affecting TC genesis in terms of the so-called genesis potential index (GPI), which is a convenient measure of evaluating the environmental forcing on TC genesis (Gray 1979; Emanuel and Nolan 2004). In the pioneering study of this kind, Camargo et al. (2009) suggested that the mid-level relative humidity and low-level absolute vorticity play primary and secondary roles, respectively, which is consistent with a recent diagnosis by Zhao et al. (2015b) who focused on the WNP. Recently, Moon et al. (2018) developed an intraseasonal GPI (ISGPI), with the aim of better quantitatively measuring the impact of the BSISO on TC genesis. Moreover, they demonstrated that 500-hPa vertical motion plays the most critical role, followed by low-level relative vorticity weighted by the Coriolis parameter and vertical shear of zonal winds.
Although these analyses may offer some clues, the detailed dynamical and physical processes by which the BSISO influences TC genesis are yet to be revealed. Take, for example, the WNP, most TC genesis (∼ 60–70 %) occurs within the monsoon trough, in particular in the monsoon shear line and then in the confluence region (Ritchie and Holland 1999; Yoshida and Ishikawa 2013). The composite results of Ritchie and Holland (1999) indicated that TC genesis in the shear line tends to occur in association with the breakdown of the monsoon trough due to the combined barotropic and baroclinic instability in response to the convection (Charney 1963; Hack et al. 1989; Guinn and Schubert 1993; Ferreira and Schubert 1997; Wang and Magnusdottir 2005). Conversely, TC genesis in the confluence region tends to occur in association with the energy accumulation and scale contraction of easterly waves (Holland 1995; Sobel and Bretherton 1999; Kuo et al. 2001; Maloney and Hartmann 2001; Tam and Li 2006; Done et al. 2011). In this view, the BSISO influences the likelihood of TC genesis by modifying the shape, strength, and location of the monsoon trough. In fact, much more TC genesis is attributable to the shear line and confluence region in the convectively active phases of the BSISO than its suppressed phases (Zhao et al. 2015a). It is worth noting that the way the BSISO influences TC genesis may vary over the course of boreal summer (Huang et al. 2011; Choi and Ha 2018).
Although the majority of previous studies have paid particular attention to TC genesis, TC tracks and landfalls are also influenced by the BSISO, and those aspects have gained considerable attention in recent years (Kim et al. 2008; Chen et al. 2009; Li and Zhou 2013a; Yang et al. 2015; Chen et al. 2019; Wang, Q. et al. 2019; Nakano et al. 2021).
c. Quasi-biweekly oscillationNext, we determine the relationship between the BSISO and QBWO. The QBWO, which is characterized by a 10–20-day periodicity, is another significant mode of intraseasonal oscillation during boreal summer. It exhibits a distinct spatiotemporal behavior from the BSISO (e.g., Chen and Chen 1993; Fukutomi and Yasunari 1999; Kikuchi and Wang 2009; Qian et al. 2019). Similar to the BSISO, the QBWO exerts a strong control on LPSs (Goswami et al. 2003) and ISM active/break cycles, in particular when the convectively active or suppressed phase of the QBWO is in phase with that of the BSISO (Krishnamurti and Gadgil 1985; Karmakar et al. 2017). It is probable that the BSISO and QBWO interact with each other, although little is known about their relationship. Some previous studies have demonstrated that the QBWO are initiated by the BSISO in the BOB at times (Chen and Chen 1993; Hatsuzuka and Fujinami 2017). Contrarily, on the interannual time scale, it was revealed that the activity of the BSISO and QBWO tends to be anti-correlated over the SCS in some summer months (Kajikawa and Yasunari 2005; Yang et al. 2008).
Here, we specifically determine whether BSISO events modulate the activity of the QBWO. Following Torrence and Compo (1998), we calculate the wavelet transform at each grid point to isolate the QBWO energy in terms of the scale-averaged wavelet power over 10–20-day band. Figure 17 presents the composite QBWO wavelet power anomalies in BSISO phases 4 and 6. In both phases, the BSISO convection is characterized by the slantwise rainband, although its major convective center is located in the northern IO and WNP in phases 4 and 6, respectively (see also Fig. 4a). It is clear in both phases that the QBWO activity tends to be enhanced within the convectively active region of the BSISO and vice versa. However, it should be noted that the QBWO activity appears to be more strongly modulated in such regions as having a larger QBWO variability (Kikuchi and Wang 2009), such as the Arabian Sea, BOB (Fig. 17a), SCS, and Philippine Sea (Fig. 17b).
Composite structures of the QBWO activity in terms of scale-averaged wavelet power anomalies over 10–20-day band in BSISO (a) phase 4 and (b) phase 6. The wavelet power is represented by shade in units of (W m−2)2, and the BSISO convection is represented by contours at the level of −5 W m−2 and 5 W m−2.
Contrary to the MJO (e.g., Seo et al. 2016; Seo and Lee 2017), there are few studies on the influence of the BSISO on the extratropics (Stan et al. 2017), although it has gained more attention in recent years, in particular with emphasis on the northern hemisphere. Some recent studies revealed that the BSISO exerts a significant influence on extreme weather phenomena in East Asia, such as the likelihood of extreme precipitation events in southern China (Hsu et al. 2016) and heatwave events over Japan and Korea (Hsu et al. 2017). Moreover, the BSISO influence can be felt in numerous parts of the world (e.g., Moon et al. 2013), including the Arctic and Antarctic areas (Seo and Lee 2017), through the propagation of Rossby waves (e.g., Hoskins and Karoly 1981; Held 1983), giving rise to so-called teleconnection patterns (Wallace and Gutzler 1981). However, the teleconnection patterns occurring in association with the BSISO strongly vary with the BSISO phase (not shown), and it may not be easy to understand them in a comprehensive manner. Perhaps, it would be worthwhile to organize our knowledge based on two pronounced teleconnection patterns that tend to occur when the major part of the BSISO convection is located in the northern IO or WNP.
Figure 18 presents the composites of 200-hPa geopotential height anomalies in such two contrasting BSISO phases. In phase 4, in which the center of the BSISO convection is located over and around the Indian subcontinent (see Fig. 4a), a significant wave train is observed from South Asia to the North Pacific across East Asia (Fig. 18a). In previous studies, similar wave patterns were observed that tend to occur in association with convection over the northern IO on the intraseasonal time scale (Yasunari 1986; Ambrizzi et al. 1995; Annamalai and Slingo 2001; Ding and Wang 2007). The wave pattern may be interpreted as a Rossby-wave response to tropical heating that propagates along the Asian Jet acting as a waveguide (Ambrizzi et al. 1995). In contrast, when the BSISO convection is located in the WNP (Fig. 18b), it gives rise to a different wave pattern, which appears to bear a resemblance to the so-called Pacific–Japan (PJ) pattern (Nitta 1987) or East Asia/Pacific (EAP) pattern (Huang 1992). The latter is marked by a wave train traveling downstream over the North Pacific with anticyclonic circulation anomalies over East China and Japan and cyclonic circulation anomalies over the Sea of Okhotsk in response to the convective activity over the WNP. Previous studies indicated that the PJ pattern can be excited by various intraseasonal phenomena, including the QBWO (Fukutomi and Yasunari 1999, 2002) and BSISO (Kawamura et al. 1996; Wang et al. 2016). As will be discussed in Section 5.1, the BSISO convection is considered to enhance both barotropic and baroclinic Rossby waves due to the presence of the mean vertical shear. Conversely, barotropic Rossby waves are considered to be primarily responsible for these teleconnection patterns because baroclinic Rossby waves tend to be more strongly trapped within the tropics (Lee et al. 2009). However, in some cases, the baroclinic component may also play an important role (Kosaka and Nakamura 2006).
Composite of 200-hPa geopotential height anomalies in BSISO (a) phase 4 and (b) phase 7. The BSISO convection is represented by thick solid and dashed lines in terms of OLR anomalies with contour levels of −5 W m−1 and 5 W m−1, respectively. The geopotential height anomalies are represented by thin contours, and significant values at the 99 % level are indicated by color shading.
As discussed, the northward propagation of convection in conjunction with large-scale, low-level cyclonic circulation over the northern IO and WNP is the signature that distinguishes the BSISO from the MJO. Much of the theoretical work with regard to the BSISO has been devoted to explaining this northward propagation feature. It is evident that the unique behavior of the BSISO is attributable to various aspects of the Asian summer monsoon, such as strong zonal and meridional vertical shear, high SST, and abundant moisture. This section reviews some of the existing theories.
5.1 Wind shearThe vertical shear in the mean flow in the troposphere is among the most pronounced aspects of the Asian summer monsoon. As discussed below, some previous studies highlighted the role of the zonal wind component (Fig. 19a), whereas others emphasized the role of the meridional wind component (Fig. 19b). In their pioneering work, Wang and Xie (1997) revealed that their intermediate model linearized about the climatological July mean basic state is able to reproduce the northward propagation of convection, which appears to capture many of the major characteristics of the observed BSISO, including the slantwise rainband. They concluded that the northward propagation of convection is caused by the emanation of Rossby waves destabilized and modified by the easterly vertical shear via the coupling between the barotropic and baroclinic components (Wang and Xie 1996). In the 2000s, several theoretical studies in the simpler latitude-height plane setting discussed the northward propagation mechanism of the BSISO in detail. Jiang et al. (2004) and Drbohlav and Wang (2005) stressed the importance of the vertical shear of the zonal wind component regardless of whether the beta effect is included (Drbohlav and Wang 2005) or not (Jiang et al. 2004). Conversely, Bellon and Sobel (2008) highlighted the importance of meridional wind component.
Climatology of JJASO mean fields based on 39 years (1979–2017) of JRA-55 for the (a) vertical shear of zonal wind between 200 hPa and 850 hPa in units of m s−1, (b) vertical shear of meridional wind between 200 hPa and 850 hPa in units of m s−1, (c) meridional wind averaged over the boundary layer (900–1000 hPa) in units of m s−1, (d) specific humidity averaged over the boundary layer (900–1000 hPa) in units of g kg−1, (e) specific humidity averaged over the lower troposphere (600–900 hPa) in units of g kg−1, and (f) horizontal winds averaged over the lower troposphere (600–900 hPa) in units of m s−1.
To understand the effect of the vertical shear of zonal and meridional wind components, like the model of Jiang et al. (2004), we consider a simple 2.5-layer model (i.e., two layers of free atmosphere plus boundary layer) in the latitude-height plane in the f plane approximation in the presence of mean background flow u̅ = [u̅ (p), v̅ (p)]. After some manipulation, the time evolution of the anomalous barotropic vorticity equation is obtained as follows:
 |
Schematic showing how barotropic vorticity is generated to the north of a convective center and elucidating the northward propagation of the BSISO in the northern hemisphere. (a) In the presence of background vertical shear (left panel), deep convection is located at a certain latitude that is accompanied by baroclinic divergence (D− > 0) and negative baroclinic vorticity (ζ− < 0) (right panel). (b) The meridional distributions of baroclinic divergence and baroclinic vorticity give rise to the negative (positive) latitudinal difference of baroclinic divergence (vorticity) to the north of the convective center. (c) In the presence of baroclinic zonal and/or meridional shear, a positive barotropic vorticity is created to the north of the convective center. In a and c, the typical height levels are indicated on the right. After Jiang et al. (2004) and Bellon and Sobel (2008).
Whether or not the β effect plays a vital role in the northward propagation of the BSISO remains ambiguous. In the vertical wind shear mechanism discussed in the previous subsection, the β effect is not essential, although Bellon and Srinivasan (2006) suggested that the β effect cannot be ignored in correctly explaining the scale selection. Contrarily, Boos and Kuang (2010) emphasized the role of the so-called beta drift (Rossby 1948; Adem 1956; Holland 1983). Apart from the 2D latitude-height model discussed above, let us consider the 2D longitude–latitude plane. Suppose a vortex with a solid body rotation is placed in a resting atmosphere with absolute vorticity increasing with latitude. To the west of the vortex center, the relative vorticity increases due to the southward flow of the vortex, whereas the relative vorticity decreases to the east. This results in the westward propagation of the vortex. Meanwhile, the positive relative vorticity to the west and the negative relative vorticity to the east create a northward flow across the vortex center. These combined effects eventually enable the vortex to move northwestward.
5.3 Moisture–convection feedbackApart from the dynamical processes discussed in the previous subsections, moisture perturbation in the boundary layer may also contribute to the northward propagation of convection (Jiang et al. 2004). The anomalous moisture tendency in the boundary layer on a latitude plane may be written as follows:
 |
) is positive up to ∼ 20°N in the BOB and WNP (Fig. 19d) and the meridional wind response to convective heating is southward (northward) to the north (south) of the heating, this term also creates positive moisture tendencies to the north of the convective center.
In addition, efforts have been recently made to examine the northward propagation of the BSISO from the viewpoint of the so-called “moisture mode” theory. The moisture mode was originally introduced to understand the slow eastward propagation of the MJO (Raymond 2001; Sobel et al. 2001), in which the MJO convection propagation is largely determined by processes that control the variability of column-integrated moisture or moist static energy (MSE). As with the eastward propagation of the MJO, it has been suggested that it is the low-level horizontal advection that plays a vital role in the column-integrated MSE variability for the northward propagation of the BSISO based on the MSE budget analysis (Adames et al. 2016; Pillai and Sahai 2016; Jiang et al. 2018; Wang and Li 2020). However, it is still controversial as to which specific processes are relatively more important. In analogy with Eq. (2), but including the zonal component, the anomalous column-integrated MSE tendency can be written as follows:
 |
The discrepancies among these previous studies are probably due to the different regions that are being focused on (and also additionally to the different approaches used). In fact, we could qualitatively understand how each term in the lower troposphere would be sensitive to the choice of region by considering a simple thought experiment as follows. Let us suppose that the BSISO-related MSE anomalies (and specific moisture) are similar to the BSISO-related OLR anomalies, which is in fact a reasonable assumption (Adames et al. 2016; Pillai and Sahai 2016; Jiang et al. 2018; Wang and Li 2020). Imagine two contrasting cases: the convection center of the BSISO is located in the northern IO (e.g., phase 3) and in the WNP (e.g., phase 5). Due to the slantwise structure of the BSISO convection (Fig. 4), ∂MSE/∂x tends to be negative to the north of the convection center in both cases. Contrarily, the background zonal winds may be different between the two cases (Fig. 19f): strong westerly winds prevail in the northern IO, whereas in the WNP, weak westerlies (easterlies) exist to the west (east) of the Philippines. Hence, to the north of the convection center, term i tends to be positive in the northern IO, whereas it can be either positive or negative depending on the location in the WNP. Based on similar considerations, it can be imagined that term ii tends to be negative in the northern IO (u > 0 and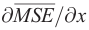 
> 0; see Figs. 4a, 19e) but positive in the WNP (u > 0 and 
< 0). As for terms iii and iv, they appear to cause opposite effects in both regions: term iii tends to be positive (v̅ > 0 and ∂MSE/∂y < 0), whereas term iv tends to be negative (v > 0 and 
> 0). The aforementioned discussion is summarized in Table 2.
Although the relative significance of each term cannot be argued from the above discussion, our argument appears to be essentially consistent with the results of the previous studies. First, it is agreed that term i plays an important role over the northern IO (Jiang et al. 2018; Wang and Li 2020). The importance of term i over the northern IO was also suggested by Pillai and Sahai (2016) and Adames et al. (2016). However, the former did not separate the horizontal advection term into terms i and ii as mentioned above, and the latter used a unique composite technique that treats the northern IO and WNP together. It is probably for this reason that they suggested that term ii is another major contributor (perhaps mainly in the WNP; see Table 2). Second, the conclusion of Wang and Li (2020) that term iii plays a key role both in the northern IO and WNP is in good agreement with our discussion (Table 2). Moreover, from Table 2, it can be inferred that the conclusion of Pillai and Sahai (2016) that the meridional advection (i.e., the sum of terms iii and vi ) is a key player over the WNP is reached because of the effect of term iii.
5.4 Air–sea interactionIt is recognized from observations that on the intraseasonal time scale, SST fluctuations occur coherently with the BSISO convection, with positive SST anomalies leading the BSISO convection by about a quarter cycle (Sengupta et al. 2001; Sengupta and Ravichandran 2001; Vecchi and Harrison 2002; Duvel and Vialard 2007; Vialard et al. 2012; Roxy et al. 2013; see also Fig. 6). Then, how could the SST perturbations alter the behavior of the BSISO? Perhaps, there are two major potential roles. First, the SST variability influences the boundary-layer convergence/divergence by changing the boundary-layer temperature (Lindzen and Nigam 1987). Second, the SST variability rectifies sensible and latent heat flux exchanges at the air–sea interface.
In the last two decades, modeling studies have been conducted in various settings to elucidate the role of air–sea interaction in the BSISO. Most previous studies have suggested that air–sea coupling improves the reproduction of the BSISO in terms of strength and reality (Kemball-Cook et al. 2002; Fu et al. 2003; Fu and Wang 2004; Seo et al. 2007; Sharmila et al. 2013), although this may not always be the case (Neena et al. 2017). Perhaps, it is widely agreed that the BSISO is essentially caused and maintained by atmospheric dynamics, whereas the air–sea interaction plays a secondary role in one way or the other. The fact that air-sea coupling does not affect only the BSISO behavior alone but also the mean state through which the behavior of the BSISO is influenced (Klingaman and Woolnough 2014) makes this issue difficult to resolve. In addition, the frequency of air–sea coupling might also be a factor: some studies suggested that high-frequency coupling significantly improves the BSISO simulation (Klingaman et al. 2011; Hu et al. 2015). Recent observational diagnosis (DeMott et al. 2013; Wang, T. et al. 2018; Gao et al. 2019) suggested that the positive SST anomalies ahead of the BSISO convection favor the northward propagation of the convection, although their importance is ambiguous. Wang, T. et al. (2018) evaluated the moisture budget in the lower troposphere over the WNP. They revealed that the positive moisture tendencies to the north of the convection center are entirely created by SST anomalies due to latent heat fluxes and moisture convergence, whereas atmospheric processes tend to exhibit negative tendencies. Contrarily, in terms of column-integrated MSE budget, Gao et al. (2019) demonstrated that surface fluxes due to the SST variability contributes a relatively small fraction (up to 20 %) of intraseasonal MSE variability both in the northern IO and WNP.
5.5 Convective momentum transportRecent studies by Kang et al. (2010) and Liu et al. (2015) highlighted the role of convective momentum transport (CMT) in the northward propagation of the BSISO, with the former highlighting its role in the baroclinic component and the latter in the barotropic component. Here, we follow the model of Kang et al. (2010) to illustrate the role of CMT. As in Section 5.1, we consider a 2D latitude-height model. Ignoring the advection terms and assuming that the CMT is proportional to precipitation (i.e., lower-level convergence) and can be parameterized in terms of precipitation and the mean vertical shear, the momentum equation may be written as follows:
 |
 |
Some modeling studies in the 1980s have emphasized the role of land processes. Webster (1983) emphasized the sensible heat input in the boundary layer, whereas Goswami and Shukla (1984) stressed the latent heat from the surface. Since the northward propagation of the BSISO is most prominent over the ocean, the degree to which such land processes are important in the northward propagation of the BSISO is elusive.
5.7 DiscussionHow do the above-discussed theories operate in the real atmosphere? As presented in Fig. 19, it should be realized that the background mean fields are different across the Asian monsoon region. For instance, the easterly vertical shear is much stronger in the northern IO than in the WNP. Contrarily, the northerly vertical shear is stronger and moderate in the BOB and in the WNP, respectively, and is virtually absent in the Arabian Sea. In fact, recent attempts by Chou and Hsueh (2010) and DeMott et al. (2013) to evaluate the roles of individual processes revealed that the relative importance of each mechanism varies in different parts of the Asian monsoon region. Nonetheless, they agreed that the barotropic vorticity effect (in which the vertical shear plays an essential role, as discussed in Section 5.1) appears to be pronounced across the IO and WNP. Chou and Hsueh (2010) noted that the barotropic vorticity effect due to the northerly vertical shear is pronounced across the entire region, whereas the barotropic vorticity effect due to the easterly vertical shear is relatively important only in the IO. They also agreed that the boundary-layer moisture advection (discussed in Section 5.3) is another important process, although it is uncertain whether it is pronounced across the entire region (DeMott et al. 2013) or only in the IO (Chou and Hsueh 2010). Further studies are required to obtain robust conclusions with regard to whether the northward propagation of the BSISO is controlled by a common mechanism in which a single or a combination of a few major processes discussed above plays a critical role all across the broad Asian monsoon region, or is accomplished by a complex combination, which might depend on the geographical location, season, or events of the various processes discussed in this section.
It is also worth arguing the commonalities and differences between the BSISO and MJO from a theoretical point of view. First, why is the northward propagation of the convection particularly pronounced for the BSISO? Figure 21 presents the several background fields discussed earlier, but for December–April. It is evident that these background fields are distinct from those during boreal summer (Fig. 19). Moreover, neither of the mechanisms, the wind shear (Section 5.1) and moisture-convection feedback (Section 5.3), appears to support the northward propagation of the convection during boreal winter. Then, is there any possibility that some other processes that have been proposed to elucidate the eastward propagation of the MJO, such as the cloud-radiative feedback and multiscale interactions, play a role in the northward propagation of the BSISO? In the framework of the moisture mode theory discussed in Section 5.3, it is possible that the cloud-radiative feedback plays a key role like it does in the MJO (e.g., Raymond 2001; Sobel and Maloney 2012; Adames and Kim 2016; Zhang et al. 2020). The cloud-radiative feedback may contribute to the destabilization of the BSISO by enhancing upward motions and moisture import that sustain the convection due to the longwave radiative heating associated with the upper-level clouds of the BSISO. Likewise, it is possible that multiscale interactions play a role in the northward propagation of the BSISO. As presented in Fig. 6 (see also, e.g., Straub and Kiladis 2003; Hoyos and Webster 2007), the BSISO exhibits a multiscale nature: the BSISO convection is composed of several MCSs occurring in close association with the synoptic-scale systems embedded in large-scale circulations. Thus, by nature, interactions among these components occur through the exchange of heat, momentum, and moisture. As discussed in Section 5.5, the effect of momentum transport has been evaluated to some extent, although our efforts so far have been much less extensive compared with those for the MJO counterpart (Biello and Majda 2005; Majda and Stechmann 2009, 2011; Wang and Liu 2011; Thual et al. 2014). After all, little is known about the degree to which multiscale interactions are important in the dynamics and physics of the BSISO northward propagation.
The same as in Fig. 19, except for DJFMA.
In this section, we review the current status of our ability to simulate the BSISO in long-term climate simulations that are run over many years (Section 6.1) and in short-term predictions that are run over tens of days (Section 6.2).
6.1 Long-term GCM simulationsThe simulation of the BSISO with fidelity in a GCM remains a formidable challenge. Rigorous efforts in the past decade or so have made it possible to reveal the common deficiencies across numerous different models (Lin et al. 2008; Sperber and Annamalai 2008; Sabeerali et al. 2013; Neena et al. 2017; Nakano and Kikuchi 2019): weak BSISO variance, lack of the northwest-southeast tilted rainband, and inaccurate representation of the seasonal cycle. In most GCMs, the BSISO variance (e.g., 30–60-day component) has only half of the observed. In the Coupled Model Intercomparison Project phase 3 (CMIP3) models, only 2 out of 17 models are able to capture the tilted rainband structure (Sperber and Annamalai 2008). Nonetheless, many of the models capture the northward propagation (Lin et al. 2008), indicating that the concerted action between the eastward and northward propagations (Lawrence and Webster 2002; Jones et al. 2004a) is not well reproduced. However, over the course of the decade, much improvement has been made. Compared with the previous generation, recent GCMs have more realistic, although not perfect, amplitude of intraseasonal OLR variance and its spatial distributions (Sperber et al. 2013): although some models are able to capture the tilted rainband, the majority of them still have difficulty probably because they have difficulty simulating the transition of the convection from the IO to the WNP. Recently, Nakano and Kikuchi (2019) revealed that a fraction (∼ 15 % on average) of significant ISO events during boreal summer erroneously display rather MJO features than BSISO features in most CMIP5 models.
In contrast, recent simulations of the BSISO by high-resolution models (e.g., horizontal resolutions being at least 50 km, Haarsma et al. 2016) may suggest that they are able to reproduce a better life cycle of the BSISO, although the amplitude is still weaker, regardless of whether cumulus parameterization is adopted (Mizuta et al. 2012) or not (DeMott et al. 2011, 2013; Goswami et al. 2013; Kikuchi et al. 2017). Hypothetically, these high-resolution models are better able to represent precipitation processes compared with conventional coarse-resolution models. However, how the better representation of the BSISO is achieved is not necessarily clear. Further studies to understand why high-resolution models tend to outperform conventional ones would be helpful in reducing the model biases and understanding the underlying propagation and maintenance mechanism of the BSISO.
Finally, it should be mentioned that, as discussed in Section 5.4, air-sea coupling may play a secondary role and not drastically improve the BSISO simulation.
6.2 Predictability and predictive skill a. Potential predictabilityIn the last two decades, efforts to estimate the potential predictability and predictive skill of the BSISO have been made. As for the predictability, the majority of previous studies have been conducted by means of GCMs on the basis of so-called perfect model assumption, although the range of the predictability significantly varies across models. It is generally accepted that dynamical fields are more predictable than the convection (e.g., Waliser et al. 2003; Liess et al. 2005). Earlier studies based on atmospheric-only GCMs suggested that the potential predictability is around 30 days (Waliser et al. 2003; Liess et al. 2005; Reichler and Roads 2005). Fu et al. (2007) and Fu et al. (2008) revealed that the inclusion of air–sea coupling extends the predictability by about a week, whereas Kim and Kang (2008) concluded that it has no significant effect. Recent studies by Lee et al. (2015) and Wang, S. et al. (2019) estimated the predictability of the BSISO, based on multiple coupled GCM (CGCM) results and ensemble-mean method, to be in the range of 23–55 days, depending on the model and strength of the BSISO events, with longer predictability for stronger events (the ECMWF model tends to have longer predictability). Conversely, using observational data, Ding et al. (2011) estimated the predictability of the BSISO to be close to 5 weeks using the nonlinear local Lyapunov exponent (NLLE) method. These predictability estimates based on both GCMs and observations are in line with the notion that the predictability is dependent on the period of the phenomenon of interest (van Den Dool and Saha 1990).
b. Predictive skillCompared with the range of the potential predictability discussed above, almost all GCMs [perhaps except for the ECMWF (Wang, S. et al. 2019)] exhibit a much shorter range of predictive skills, indicating that there is much room for improvement. As in the case of the predictability, the predictive skill significantly varies across models (Fu et al. 2013; Lee et al. 2015; Jie et al. 2017; Wang, S. et al. 2019), and dynamical fields are more predictable than convection; moreover, stronger events are more predictable than weaker events (Seo et al. 2005; Jiang et al. 2008; Lee et al. 2015). Based on a series of single-model simulations with prescribed SST, Seo et al. (2005) revealed that the predictive skill is in the range of 1–2 weeks for rainfall. Since the time scale of the BSISO is between synoptic weather and seasonal climate, it is apparently believed that the accurate prediction of the boundary conditions is critical to the accurate prediction of the BSISO. However, Seo et al. (2009) revealed that air–sea coupling only slightly improves the predicting skill. However, this issue does not seem to have been rigorously examined yet. It has been shown that ensemble-mean forecasts are more skillful than single-member forecasts (Lee et al. 2015; Jie et al. 2017). Recently, relatively comprehensive assessments based on multiple CGCMs suggest that the predictive skill of ensemble-mean forecasts is in the range of 1–5 weeks, with ECMWF tending to exhibit the highest skill whereas most models having the skill of less than 3 weeks (Lee et al. 2015; Jie et al. 2017; Wang, S. et al. 2019). It is interesting to note that models with a higher prediction skill of the MJO (i.e., the ISO during boreal winter) appear to exhibit a higher prediction skill of the BSISO (Neena et al. 2014; Lee et al. 2015; Wang, S. et al. 2019).
Does the predictive skill depend on the BSISO phase? Some studies suggested that the break phase of the BSISO is more predictable than its active phase in the ISM based on the observed rainfall (Goswami and Xavier 2003) and NCEP Climate Forecast System Version 2 (CFSv2) (Abhilash et al. 2014). However, such phase dependency may not be common. Comprehensive assessments of the predictive skill across different models do not seem to exhibit initial or target phase dependence (Lee et al. 2015; Wang, S. et al. 2019). This indicates that the so-called MC barrier is not observed in the BSISO prediction (Wang, S. et al. 2019), which may be at odds with the situation in long-term simulations discussed in Section 6.1.
Meanwhile, a variety of statistical models have been proposed to predict the BSISO on the basis of various approaches, including multiple linear regression (Goswami and Xavier 2003; Jones et al. 2004b; Jiang et al. 2008; Seo et al. 2009), singular value decomposition (Waliser et al. 1999), self-organizing map (Chattopadhyay et al. 2008; Borah et al. 2013), and low-order nonlinear stochastic modeling (Chen and Majda 2015). These statistical models exhibit a good performance that is comparable or even superior to that of dynamical models, in particular the model of Chen and Majda (2015). Also, the combination of a dynamical and a statistical model (Fu et al. 2013) could be a useful approach.
Finally, we discuss how we can improve the predictive skill of the BSISO in dynamical models. Perhaps, there are several issues. First, the model physics is not perfect. Zhang and van Den Dool (2012) demonstrated that the CFSv2 exhibits a remarkable improvement in the predictive skill over the CFSv1 (2–3 weeks vs. nearly 1 week) probably due, in large part, to model physics improvements. Second, the initial conditions that are given to the model are not accurate. Many previous studies have demonstrated that the ISO tends to be significantly underestimated (by up to a few factors) in various fields in almost all reanalysis datasets, including NCEP (Shinoda et al. 1999), ECMWF (Fu and Wang 2004; Fu et al. 2006), ERA-interim (Fu et al. 2011), ERA-5 (Jiang et al. 2019), and JRA-55 (Kikuchi 2020). Fu et al. (2009) and Fu et al. (2011) revealed that the predictive skill significantly improves when rectified initial conditions are adopted. Third, the air–sea interaction may not be accurately represented in models. As discussed above, to accurately predict the BSISO, it is hypothesized that we need to provide accurate initial conditions and boundary conditions over the course of its life cycle. However, the degree to which the air–sea interaction is instrumental is yet to be revealed.
In light of its predominance in boreal summer and its impact on other phenomena on a wide range of space-time scales, it is important to fully understand the nature of the BSISO and to simulate it accurately in numerical models. In the last four decades, we have seen a great progress in our understanding of the BSISO in numerous respects, as discussed in this paper. However, there are still areas of research that need to be advanced. This final section discusses some future challenges.
First, the interaction aspects of the BSISO with other phenomena are poorly understood. How the BSISO interacts with higher-frequency disturbances in the tropics and with mid-latitude weather and climate systems has not necessarily been examined in great detail. As discussed in Section 4, the BSISO exerts a strong control on synoptic-scale disturbances, such as LPSs and QBWO, as well as on TCs. However, the detailed processes by which the BSISO influences them are not clear. Moreover, whether these higher-frequency disturbances, in turn, feed back to the BSISO, if any, plays a key role in the dynamics of the BSISO is unclear. Similarly, the interaction between the BSISO and extratropical weather and climate systems deserves further exploration.
Second, our understanding of the dynamics and physics of the BSISO is incomplete. As discussed in Section 5, most previous studies have attempted to explain the northward propagation of the BSISO. However, the most fundamental question of whether the northward propagation is essential to the development and maintenance of the BSISO or is it just a byproduct of the eastward-propagating branch has not been well addressed. In other words, what controls the activity of the BSISO? The fact that we cannot adequately explain the interannual variations of the overall level of the BSISO activity (Section 3.4) is a manifestation of the lack of our understanding. A more holistic view would be necessary.
Third, as discussed in Section 6, there is much room for improvement in BSISO modeling. In long-term simulations, almost all current GCMs tend to significantly underrepresent the amplitude of the BSISO. Moreover, most GCMs are unable to correctly represent the northwest–southeast tilted rainband. In shortterm simulations, there is a large gap between the potential predictability and predictive skill. We need to improve numerous aspects, such as model physics, initial conditions, and air–sea (and also perhaps air–land) interaction processes, to enable GCMs to better simulate the BSISO.
This research was supported by NOAA Grant NA17OAR4310250. Additional support was provided by the JAMSTEC through its sponsorship of research activities at the IPRC (JICore). Interpolated OLR, NOAA_OI_SST_V2, and MEI.V2 data were provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at https://www.esrl.noaa.gov/psd/. The JRA55 dataset was obtained from https://jra.kishou.go.jp/JRA-55/index_en.html. The global monsoon disturbance track dataset was provided by Dr. Boos (https://worldmonsoons.org/global-monsoondisturbance-track-dataset/). The IBTrACS data was obtained from https://www.ncdc.noaa.gov/ibtracs/index.php?name=ib-v4-access. The TRMM 3B42 data were provided by the NASA/Goddard Space Flight Center's Mesoscale Atmospheric Processes Laboratory and PPS, which develop and compute the TRMM 3B42 as a contribution to TRMM, and archived at the NASA GES DISC. The APHRODITE data was obtained from http://aphrodite.st.hirosaki-u.ac.jp. The author sincerely appreciates Dr. Masaki Satoh for giving me the opportunity to write this review article. Discussion with Drs. Tomoe Nasuno, Satoru Yokoi, Masuo Nakano, and Ryosuke Shibuya helped improve this manuscript. Invaluable comments from two anonymous reviewers are also greatly appreciated to improve the manuscript.
1Perhaps, 30–60 days is most widely used to characterize the ISO periodicity (Lau and Waliser 2012), because the spectral peak of the ISO is usually observed within that range, although the spectrum actually spreads over a wider range of roughly 30–90 days; thus, 30–90 days instead of 30–60 days is sometimes used in some literature (e.g., Zhang 2005).
2The time series of the BSISO PCs can be found in the following website: http://iprc.soest.hawaii.edu/users/kazuyosh/Bimodal_ISO_hist.html.
