2021 Volume 99 Issue 5 Pages 1169-1183
2021 Volume 99 Issue 5 Pages 1169-1183
This study proposes an algorithm detecting atmospheric blocking by extracting topological features of geopotential height data at 500 hPa. The algorithm uses topological flow data analysis (TFDA) providing a unique symbolic representation, named the partially cyclically ordered rooted tree (COT) representation, and a discrete graph structure, called a Reeb graph, to each structurally stable Hamiltonian vector field based on the mathematical theory of topological classifications for streamline patterns. It recognizes blocking events more simply and effectively using fewer meteorological parameters than conventional algorithms. Furthermore, the algorithm can determine morphological types of blocking events, an Omega shape or a dipole pattern, whereas no effective algorithm has been available so far. The identified blocking events and their morphological types are consistent with synopticians' subjective judgments.
Atmospheric blocks are large anomalous anticyclones persisting for a week or longer, frequently emerging in mid and high latitudes throughout the year (Tibaldi and Molteni 1990). Because the geostrophic balance – clockwise/counter-clockwise circulation around the anticyclones/cyclones in the Northern Hemisphere – dominates in the extratropics, atmospheric blocking induces meandering flows, disrupting the westerly flow sometimes sandwiched between high pressures in the tropical side and low-pressures in the polar side. It causes to prolonged abnormal weather such as heatwaves, chilly winds, droughts and wet spells through heat and moisture advection, which are often observed in North America (Casola and Wallace 2007), Europe (Buehler et al. 2011; Pfahl and Wernli 2012), and Australia and New Zealand (Ummenhofer et al. 2013). Atmospheric blocking is not only one of the most high-impact weather patterns in the midlatitudes, but a great concern for future climate predictions (Woollings et al. 2018). However, because of a lack of comprehensive definition of blocking states, it is challenging to identify the occurrence of blocking events objectively.
Atmospheric blocking is analyzed on weather charts in the isobaric surface in the upper troposphere, in which the horizontal wind vector is almost along an isopleth of geopotential height, following the quasi-geostrophic dynamics without the effect of topography and turbulence in the planetary boundary layer. Some weather centers have archived atmospheric data such as geopotential height, horizontal wind vector, and air temperature as the format of longitude-latitude grid points at a time interval, usually 6 hours. Hence, an atmospheric block can be recognized as an anomalous and persistent high using contour graphs based on a time sequence of gridded data. An objective algorithm to identify blocking events from the data helps analyze blocking frequency estimated from a historical record of atmospheric data that can date back to the 1960s. The blocking identification algorithm is also required for studies on climate change, analyzing a massive amount of atmospheric data to consider several futures (Woollings et al. 2018).
Most atmospheric blocking states are morphologically classified into a dipole type, omega (Ω)-shaped, or open ridge. A dipole-type blocking has a pair of high- and low-pressure regions splitting the jet into two branched northern and southern flows (Rex 1950) as illustrated in Fig. 1a. An Ω-shaped blocking is characterized by an amplified ridge with noticeable meandering (Sumner 1955), and Fig. 1b shows its typical geopotential height pattern. An open ridge type block is also discriminated from them, but this type is not considered because it is weak and immature (Liu et al. 2018). Forecasters and synopticians operationally judge blocking morphology based on their empirical knowledge as experts. Despite that the flow reversal could be related to the dipole pattern formation, no effective algorithm has yet been proposed to discern morphological types directly. Hence, the objective morphological identification of blocking events from geopotential height data remains a big challenge, as discussed by Woollings et al. (2018).
Many blocking identification algorithms have been proposed to incorporate various meteorological aspects such as anomalous high pressures and westerly flow reversal, which can be classified into two groups. Tibaldi and Molteni (1990) detected the longitudes of blocks by flow reversal at absolute geopotential heights, which has been extended to detect blocking events (Pelly and Hoskins 2003). Dole and Gordon (1983) defined two-dimensional blocking events as persistent, positive anomalies in geopotential heights. Later, Barriopedro et al. (2010) proposed an algorithm by combining these two methods. It is one of the most frequently-used algorithms, because it is more consistent with synopticians' intuition. Recently, Dunn-Sigouin et al. (2013) effectively improved Barriopedro's algorithm, which has been a more popular method of objective-blocking identification.
Although sophisticated algorithms described above have been proposed, no consensus exists about a universal method for identifying atmospheric blocking. Recently, another objective approach, characterizing multiscale topological features embedded in data, has been developed. Inatsu et al. (2017) applied persistent homology to identify extratropical cyclones from the maximum of gridded relative-vorticity data. Although this approach is a trial to identify cyclones from a snapshot of atmospheric data, it indicates that the isopleth of geopotential height falls into some of typical topological categories of stream-function. Ma and Wang (2005) investigated the topological classification of streamline patterns generated by structurally stable Hamiltonian vector fields. Later, the theory was extended to the flows on two-dimensional domains with solid boundaries in a uniform flow (Yokoyama and Sakajo 2013; Sakajo and Yokoyama 2018; Uda et al. 2019). It shows that these topological structures of streamline patterns are in one-to-one correspondence with symbolic expressions, called partially cyclically ordered rooted tree (COT) representations, and their associated planar graphs having the height information, named Reeb graphs. This discrete characterization of topological streamline patterns in flow data is referred to as topological flow data analysis (TFDA). This study proposes an objective TFDA algorithm to detect blocking events using geopotential height data. Moreover, it is confirmed that the proposed algorithm successfully identifies the morphology of blocking events using COT representations and quantitative indices associated with them.
The paper is constructed as follows. In Section 2, Dunn-Sigouin et al.'s identification algorithm (2013) is briefly reviewed. In Section 3, after reviewing the topological classification theory of streamline patterns for structurally stable Hamiltonian vector fields (Yokoyama and Sakajo 2013), we explain how to assign COT representations and Reeb graphs to the geopotential height data at 500 hPa. For blocking identification using these algorithms, we use the 6-hourly geopotential height at 500 hPa of 1960 from JRA55 reanalysis data (Kobayashi et al. 2015). Section 4 describes a procedure based on TFDA to identify blocking events and their morphological types. Section 5 shows that our TFDA algorithm extracts blocking events effectively with less objective parameters. Also, a comparison with the Dunn-Sigouin algorithm is made. Finally, it is shown that the TFDA algorithm successfully identifies the morphology of atmospheric blocking, and no prior meteorological knowledge is required to identify the morphological type of atmospheric blocking. The last section is the conclusion.
In the algorithm by Dunn-Sigouin et al. (2013), the Northern Hemisphere blocking events are defined based on 500 hPa geopotential height z (λ, φ) and its anomalies, that is, the deviation from the 6-h climatology (Sausen et al. 1995), za (λ, φ), in which λ and φ are longitudinal and latitudinal coordinates respectively. The identification procedure comprises two steps. The first step is evaluating the positive anomaly condition. It extracts a two-dimensional block domain where za exceeds 1.5 standard deviations of geopotential height anomalies over 30°N to the North Pole for three months, centered around a given month. The criterion ranges from 117 m in July to 188 m in January. The domain is labeled if the following three conditions are satisfied. (1) The area is larger than 2.5 ´ 106 km2. (2) The overlap of the temporally adjacent images exceeds 84 % of the smaller images. (3) The time sequence of the two-dimensional domains has a lifetime longer than 96 hours. The second step is evaluating the flow reversal condition. The labeled domain is withdrawn if
 |
Our data analysis method is based on a topological classification theory of streamline patterns generated by Hamiltonian vector fields u = (u (x, y), v (x, y)) at (x, y) ∈ ℝ2, whose components are represented by u = ∂yH and v = −∂xH for a given scalar function H (x, y). The function is called the Hamiltonian, and particle orbits generated by the vector field agree with the isopleths of the Hamiltonian owing to ∇H · u = 0. Since one of the most important examples of Hamiltonian vector fields is flows of incompressible fluids, the Hamiltonian and its isopleths are referred to as the stream-function and streamlines respectively. Furthermore, our attention is restricted to a special class of Hamiltonian vector fields that are structurally stable. By structural stability, we mean that the topological structure of streamline patterns is unchanged under arbitrary small perturbations of vector fields in the space of continuously differentiable functions. This restriction is not critical theoretically or practically. It is shown mathematically that any structurally unstable Hamiltonian vector fields is approximated continuously by a sequence of structurally stable Hamiltonian vector fields (Yokoyama and Sakajo 2013). In other words, most Hamiltonian vector fields are practically regarded as structurally stable. Furthermore, structurally unstable Hamiltonian vector fields hardly appear in most flow data because of perturbations from noise in measurements and errors in numerical computations.
As explained in Section 1, the isopleths of the geopotential height at 500 hPa can be regarded as stream-lines representing the westerly jet stream. Hence, geostrophic atmospheric flows is regarded as structurally stable Hamiltonian vector fields in the jet flow whose Hamiltonian is equivalent to the geopotential height. The height data are provided on the annular domain 𝒟 := [0°W, 0°E] × [20°N, 89°N] in the Northern Hemisphere with a periodic boundary condition in the longitudinal direction, that is, 0°W = 0°E and 180°W = 180°. Although visualize the annular domain by cutting the longitudinal line 0°W = 0°E, the topological classification of streamline patterns is conducted for the zonal flows in the annulus. Note also that the annular domain contains no physical obstacles. It follows from the mathematical theory (Yokoyama and Sakajo 2013) that, when no solid obstacles exist in two-dimensional flow domains, the topological streamline structure of any structurally stable Hamiltonian vector field in the uniform flow consists of the following two local streamline patterns.

Blocking morphology and topological isopleth structures. (a) Dipole type: A high-pressure region is accompanied with a low-pressure region in its southern neighborhood. (b) Ω type: An isolated high-pressure region is embedded in the westerly jet.

Local topological streamline patterns appearing in structurally stable Hamiltonian flows. (a) An orbit with one self-connected saddle separatrix. (b) An orbit with two self-connected saddle separatrices.
To explain the correspondence between symbolic expressions and topological structures of streamlines, we describe the topological classification theory for structurally stable Hamiltonian flows in the plane. Although the plane is topologically different from the annulus, the symbolic representations are used in this TFDA for geopotential height data as explained later. Let us first define a basic streamline structure, called the root structure, representing a uniform flow from left to right as illustrated in Fig. 3a. Square symbols □ia i = 1, …,n in this illustration indicate that n local streamline structures symbolized as a± in Fig. 3b can be embedded as its local inner structures. Then the symbol aØ (□1a · □2a · … · □na), which is called a COT symbol, is provided to the root structure. Notice that the square symbols are arranged according to the streamline structures from the bottom to the top when the uniform flow goes from left to right. Figure 3b illustrates local streamline structures with one saddle-connected by a self-connected separatrix embedded in the uniform flow. Since the flow orientation is distinguished in the topological classification theory, two possible streamline patterns exist. When the direction of the self-connected separatrix is counter-clockwise, the pattern is symbolized by a+ (□b+). For the pattern having a clockwise self-connected saddle separatrix, the COT symbol a− (□b−) is assigned to the streamline structure. Any number of a± streamline structures can be embedded in the root structure, that is, □ia ∈ {a+, a−} for i = 1, …, n. Inside the domain enclosed by the self-connected separatrix, another square symbol □b± is observed. It indicates that either a streamline structure in Fig. 3c or an elliptic center in Fig. 3d is embedded here. Figure 3c shows streamline structures comprising two self-connected separatrices. A figure-eight orbit structure going in the counter-clockwise (resp. clockwise) direction has the COT symbol b++{□b+, □b+} (resp. b−−{□b−, □b−}). The parenthesis { } indicates that the inner structures inside the pattern are arranged in a cyclic order. On the other hand, there exists a streamline structure where one self-connected saddle separatrix is enclosed by the other self-connected saddle separatrix. The COT symbol of this streamline pattern is given by b+− (□b+, □b−) (resp. b−+ (□b−, □b+)) when the outer saddle separatrix is going in the counter-clockwise (resp. clockwise) direction. As shown in each COT symbol, further inner structures can be embedded in □b±. That is to say, □b+ ∈ {b++, b+−, σ+} and □b− ∈ {b−−, b−+, σ−}. Figure 3d shows an elliptic center surrounded by counter-clockwise (resp. clockwise) periodic orbits in its neighborhood, symbolized as σ+ (resp. σ−) as its COT symbol. This is an innermost structure having no internal orbit structures.

Streamline patterns and COT symbols that are topologically identifi ed by the proposed algorithm. (a) A uniform flow, aØ(□1a · □2a · … · □na) (b) Patterns with one self-connected saddle separatrix, a± (□b±). (c) Patterns with two self-connected saddle separatrices, b±±{□b±, □b±} and b±∓ (□b±, □b∓). (d) Elliptic centers, σ+ and σ−.
The procedure for assigning COT symbols is described as follows. Starting from the root structure, we embed local streamline structures until they reach innermost elliptic centers. Simultaneously, whenever inner streamline structures are embedded in an outer streamline structure, directed edges are created from the outer structure as a parent node to its inner structures as child nodes. Since each node represents either a saddle or an elliptic center, it can be associated with its corresponding Hamiltonian value. Hence, this provides a graph whose nodes hold the Hamiltonian values, called a Reeb graph. It has been shown that COT representations and their corresponding Reeb graphs are in one-to-one correspondence with topological streamline structures generated by structurally stable Hamiltonian vector fields (Sakajo and Yokoyama 2018).
To conduct TFDA for a long time-series of the geopotential height data, we use a computer software, named psiclone, running on the Python platform. It converts array data of Hamiltonian values on structured/unstructured grid points into a Reeb graph using the mathematical theory of persistent homology (Uda et al. 2019). Here, we use COT representations of the form aØ for structurally stable Hamiltonian flows in the plane to identify Reeb graphs and streamline patterns, although we are interested in zonal flows in the annulus. As a matter of fact, the algorithm computes Reeb graphs by regarding northernmost/southernmost streamlines of westerly jet flows with no topological structures as the northern/southern boundaries of the annular domain. And it is mathematically justified that, under this boundary condition, Reeb graphs can be converted uniquely to COT representations of the form aØ in spite of the topological difference between the flow domains. Since Reeb graphs hold the height value of the Hamiltonian function at each node, nodes and edges whose height difference is less than a prescribed threshold can be eliminated. Since they correspond to unrobust small streamline structures, the threshold functions as a low-pass filter removing small-scale orbit structures. This threshold is used to extract an appropriate scale of streamline patterns from flow data. Moreover, the software successfully identifies bounded regions enclosed by self-connected saddle separatrices in streamline structures a±, b±± and b±∓, which are referred to as regions of influence. Therefore, it yields quantities such as areas and geometric centers of regions of influence associated with COT representations, which play an important role in the identification of atmospheric blocking.
3.2 Applying TFDA to geopotential height dataLet us apply the topological classification theory stated above to a geopotential height data at 1800 UTC on February 9, 1960. Figure 4a is an output of psiclone for the geopotential height data. Its COT representation,
 |

(a) Isopleth plot of the geopotential hight data at 500 hPa at 18:00 UTC on February 9, 1960. The COT representation and its corresponding Reeb graph are shown. (b) The partition plot associated with the COT representation.
Assume that the COT representation for a given geopotential height data H on the domain 𝒟 is of th form aØ (□1a, …, □na) for a non-negative interger n. Then, Ai+(H) (resp. Ai−(H)) denotes the region of influence associated with the a+ (resp. a−) structure in the ith box □ia = a+ (□b+) (resp. □ia = a− (□b−)), which corresponds to the colored regions of the partition plot in Fig. 4b. Let I+ be the set of all indices i with □ia = a+ (□b+) and J− be the set of all indices j such that □ja = a−(□b−) with j = i ± 1 for some i ∈ I+. A subset A(H) ⊂ 𝒟 is then defined as
 |
Let Ht for t = 0, 1, …, T be a discrete time-series of geopotential height data. For a fixed discrete time window Δt ∈ ℤ, we count how long regions of influence associated with a± structures exist over each location x ∈ 𝒟 during the period [t − Δt/2, t + Δt/2). It is mathematically defined as follows.
 |

(a) The histogram Ct,Δt(x) at t = 195 with Δt = 16. (b) Connected components {Bt,n} where the value of Ct,Δt(x) at t = 195 exceeds h = Δt/2 = 8. (c) Creating chronologically backward links between the dark red connected components around [50°W, 63°N] from t = 194 to 196.
To detect a blocking event from the histogram at each time t, we extract sub-domains of 𝒟 where the value of Ct,Δt(x) is greater than or equal to a given lower bound 0 < h < Δt. Consequently, the domain of the histogram is decomposed into some connected components, say Bt, n, n = 0, 1, …, Nt, where Nt denotes the number of components at time t. Note that these domains are mathematically defined by
 |
Assume now that the domain of interest is  := [0°W, 0°E] × [40°N, 80°N] (⊂ 𝒟), where the blocking phenomena are frequently observed. Then, let ℬ be the set of connected components Bt, n for all time t ∈ [Δt/2, T − Δt/2) whose geometric center belongs to the domain of interest:
:= [0°W, 0°E] × [40°N, 80°N] (⊂ 𝒟), where the blocking phenomena are frequently observed. Then, let ℬ be the set of connected components Bt, n for all time t ∈ [Δt/2, T − Δt/2) whose geometric center belongs to the domain of interest:
 |
 are excluded, thereby avoiding the detection of blocking events in the equatorial and polar regions.
4.2 Step 2: Connecting Bt,n in the temporal direction
are excluded, thereby avoiding the detection of blocking events in the equatorial and polar regions.
4.2 Step 2: Connecting Bt,n in the temporal direction
When the geometric center of a domain Bt+1,n′ at time t + 1 is contained in a certain domain Bt,n at time t, namely γ(Bt+1,n′) ∈ Bt,n the domain Bt+1,n′ is judged to move from the domain Bt,n. We then create a link (a directed edge) between the two domains as nodes, that is, Bt,n ← Bt+1,n′, Note that it is less likely to create links between small connected components, since they hardly satisfy the inclusion condition. Figure 5c illustrates how chronologically backward links are created. Let us focus on the large connected component around [50°W, 63°N] colored with dark red in the middle panel, which is identified as Bt0,n0 with t0 = 195 and n0 = 2119. At t = t0 + 1 = 196 in the right panel, the geometric center of a dark red connected component Bt0+1,n′0 with n′0 = 2139 around [50°W, 63°N] is contained in Bt0,n0, and a backward link is created between them. Similarly, at t = t0 − 1 = 194 in the left panel, a dark red connected component Bt0−1,n″0 with n″0 = 2098 around [50°W, 63°N] is linked from Bt0,n0. This figure also indicates that no links are created between small connected components, appearing as small dots between [60°W, 80°W] in Fig. 5c. Consequently, this step creates a directed ecyclic graph (DAG) among the connected components, generically organizing the elements in ℬ as nodes into a set of paths in the chronologically backward direction. In what follows, the same notation ℬ is used to express the DAG, and each path in the DAG encapsulates connected components in a time series of a region of influence. Note that each connected component in the DAG has more than one links merging backward from connected components in general, since the domain Bt,n can possibly split into several domains at time t + 1. Figure 6 shows some paths in the DAG ℬ obtained in the period t = 190 to 224. Each node (box) contains so me information associated with the corresponding connected component, e.g., time, identification number, the geometric center and index L1 = χTFDA defined by (6).

Paths in the DAG ℬ constructed from t = 190 to 224. Each node (box) corresponds to a connected component B ∈ ℬ, which is linked to the chronologically backward direction. In each box, time t, its identification number, the geometric center γ(B), and χTFDA (B) (as L1) are shown. Sequences of nodes with χTFDA(B) < 0.3 in solid boxes at t = 191𠄱97 and t = 216𠄱219 are judged to be blocking events.
For each node Bt,n in the DAG ℬ, we first compute the index
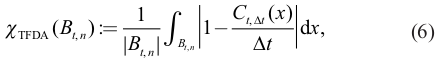 |
 |
We now consider a path of length ℓ ≥ 0 in the DAG ℬ, namely,
 |

Note that the choice of ε1 is not serious, since the topological information is robust under any small perturbation of parameters. As a matter of fact, in Fig. 6, even if we increase or decrease the value of ε1 by 10 %, a few nodes are affected, and the lifetime of the links only slightly increases or decreases. This indicates that it does not substantially affect the detection of the blocking event from the DAG.
4.4 Step 4: Identification of the morphological typesThe morphology of blocking events is identified as follows. For a given blocking event (Bt,n(t))t0≤t≤t0+ℓ, the time when the index χTFDA (Bt,n(t)) becomes the minimum is defined by
 |
The proposed TFDA algorithm is applied to a one-year time series of geopotential height data from 00:00 UTC on January 1, 1960 (t = 0) to 00:00 UTC on January 1, 1961 (t = 1464). Since the data are available every six hours and the duration of blocking events is longer than four days, Δt = 16 is used. The lower bound h is provided by h = Δt/2 = 8, and the threshold used in the definition of E1 is fixed to ε1 = 0.3. Table 2 summarizes the number of blocking events detected by the TFDA algorithm and Dunn-Sigouin's algorithm with/without the flow reversal condition. The flow reversal condition does not contribute to the Omega/dipole shape classification for the geopotential height data in this period. Hence, we consider the blocking events detected by the TFDA algorithm and Dunn-Sigouin's algorithm with the flow reversal condition in what follows. According to Table 2, the TFDA algorithm extracts 28 blocking events, whereas the Dunn-Sigouin algorithm detected 21 during the same period. For a consistent comparison between the two algorithms, some blocking events detected by TFDA are regarded as one event, when their lifetimes are close to that of a Dunn-Sigouin's one and the high-pressure region is over the same region. Note that both algorithms contain some parameters controlling the lifetime as explained in Sections 2 and 4, but they are independently chosen in the algorithms. Consequently, the total number of blocking events is reduced to 25, of which 14 are the same blocking events as those detected by Dunn-Sigouin's algorithm. The detailed information of the blocking events are listed in Table 1. Section 5.2 illustrates how the morphology of blocking events is identified by TFDA, which is a challenging task for most objective identification algorithms. In the meantime, there exist seven blocking events that the Dunn-Sigouin algorithm detects but TFDA cannot. A reason will be explained in Section 5.3. On the contrary, TFDA successfully finds 11 new blocking events that cannot be detected by the Dunn-Sigouin algorithm, but are confirmed to be in a state of blocking according to synopticians' subjective judgment. We discuss the reason for the difference in detail in Section 5.4.

As explained in Section 4, a blocking event is morphologically identified as a dipole-type, if the region of influence associated with an a+ structure (a high-pressure region) at t = tb is accompanied with a region of influence associated with an a− structure (a low-pressure region) in its southern neighborhood. On the other hand, it is identified as Ω type, if the region of influence associated with an a+ structure is isolated at t = tb. In what follows, picking up blocking events #01 and #03 detected by both the TFDA and Dunn-Sigouin's algorithms, we see how the morphological feature of the blocking events is identified. Figure 7a shows the partition plot of the geopotential height at tb = 40 for blocking event #01 from t = 36 to 44. The COT symbol a+ is highlighted in red in the COT representation at the header. Therefore, the blocked high-pressure region around [0°W, 40°W] × [40°N, 75°N], which is enclosed by its corresponding separatrix as a solid curve, is the region of influence associated with the a+ structure. The high-pressure region is isolated and no a− structure exists in its southern neighborhood. Thus the blocking event is identified as an ω type. Note that the morphological identification can be accomplished by comparing the geometric centers of the regions of influence without observing the partition plot. Figure 7b is the partition plot of the geopotential height at tb = 170 for the blocking event #03 from t = 164 to 174. The COT symbols a− · a+(b+−) corresponding to the blocking structure in [30°W, 70°W] × [40°N, 70°N] are highlighted in red in the COT representation. The low-pressure region enclosed by the self-connected separatrix of the a− structure as a dashed curve is located in the southern neighborhood of the high-pressure region represented by a+(b+−) that is enclosed by its corresponding separatrix as a solid curve. Comparing the geometric centers of the two regions, we identify the blocking event as dipole type. The morphological types of the 25 blocking events are listed in Table 1, and they agree with those judged subjectively by synopticians. Accordingly, the proposed TFDA algorithm can identify the morphological type of blocking events successfully by quantifying the regions of influence associated with COT symbols. We note that, although the morphological type may change in the lifetime of one blocking event in principle, we have confirmed that the identified morphological type remain the same in most cases in practice.

Partition plots of the geopotential height data at time tb. The blocking domains are identified by the regions of influence associated with the COT symbols colored in red. (a) Blocking event #01, tb = 40. An ω-type blocking region is enclosed by the saddle separatrix drawn as a solid curve. (b) Blocking event #03, tb = 170. A dipole blocking consisting of two regions enclosed by two saddle separatrices drawn as solid and dashed curves.
Table 2 shows that there are seven blocking events that are detected not by TFDA but by the Dunn-Sigouin algorithm. The periods of these cases are t ∈ [289, 306], [312, 339], [570, 605], [946, 981], [1077, 1099], [1100, 1166] and [1259, 1284] as listed in Table 1. Choosing the blocking event from t = 312 to 339 as an example, we observe why TFDA does not detect the blocking event. Figure 8 a is the partition plot of the geopotential height at t = 313. A high-pressure region in the domain [0°E, 20°E] × [50°N, 70°N] is judged to be a blocking region by the Dunn-Sigouin algorithm. However, it illustrates that the high-pressure region is not enclosed by a self-connected saddle separatrix. Hence, the TFDA algorithm cannot detect this high-pressure region, since it cannot be a connected component belonging to ℬ. On the other hand, 36 hours later at t = 319, there appears a region of influence associated with an a+ structure, which is enclosed by a solid separatrix, in almost the same domain in Fig. 8b. This means that the topological structure resented by a+ is fragile, which did not cause a connected componentic ℬ over this domain. Consequently, TFDA does not detect the blocking event in this period. Since the region of influence associated with the a+ structure is accompanied with no steady low-pressure region in its southern neighborhood, it is a (topologically weak) blocking event of Ω type, which agrees with synopticians' judgment. Note that a similar reason applies to the other six cases.

(a) Partition plot of the geopotential height data at time t = 313 when no blocking event is detected by the TFDA algorithm. (b) Partition plot of the geopotential height data at a later time, t = 319. An ω-type blocking region is enclosed by the saddle separatrix drawn as a solid curve.
Eleven blocking events recognized by the TFDA algorithm are undetected by the Dunn-Sigouin algorithm. These cases frequently satisfy both the flow reversal condition and the positive anomaly condition in the Dunn-Sigouin algorithm over the event period. The principal reason for rejection is violating the area and/or lifetime conditions. If the area criterion is reduced to 1.0 × 106 km2,theDunn-Sigouinalgorithm detects 13 more events, three of which are recognized by the TFDA algorithm. There are eight rejected events because of small areas and/or a short lifetime, and the remaining for other reasons.
As a typical example of a small blocking area domain, we consider an anticyclonic anomaly in the Atlantic during t ∈ [1175, 1194]. Figure 9a shows the isopleths of the 500 hPa geopotential height, in which the grid points where the anomaly exceeds the criterion are drawn as circles. Here, the flow reversal condition is satisfied in the longitudes around the blocking center. However, as we see the time-series of the area identified as this blocking event in Fig. 9b, the blocking marginally exceeds the area criterion during t ∈ [1181, 1193], which is 72 hours. Hence, the Dunn-Sigouin algorithm hence rejects this blocking event for violating the lifetime condition. Reducing the area criterion to 1.0 × 106 km2 saves this event because the lifetime gets longer. On the other hand, the TFDA algorithm successfully identifies this region around [0°W, 40°W] × [40°N, 75°N], which is blocking event #24 from t = 1181 to 1185. This is a dipole-type blocking represented by the COT symbols a− · a+ as we see the partition plot at tb = 1185 in Fig. 9c.

(a) An isopleth plot of the 500 hPa geopotential height at t = 1185. The circles represent grid points contained in a candidate blocking region detected by the Dunn-Sigouin algorithm. (b) The time-series of the area of the region from t = 1175 to 1195, indicating the lifetime condition is not satisfied. (c) Partition plot from the TFDA algorithm at tb = 1185 in event #24. It detects a distinct dipole-type blocking around [0°W, 40°W] × [40°N, 75°N] consisting of regions of influence enclosed by a solid curve and a dashed curve.
An objective algorithm of topological flow data analysis is proposed, detecting atmospheric blocking from a data set of the geopotential height at 500 hPa. It is based on the mathematical classification theory for structurally stable two-dimensional Hamiltonian vector fields. The algorithm extracts all topologically characteristic isopleth patterns, and it describes the configurations between them in terms of discrete expressions, named COT representations and Reeb graphs. The algorithm contains four objective parameters: namely, (i) the time window A t expressing the duration of one blocking event, (ii) the lifespan l measuring how long a blocking state persists, (iii) the lower bound h extracting blocking regions, and (iv) the parameter ε1 of E1 in terms of the index χTFDA judging the occurrence of blocking events. This indicates that the algorithm requires fewer parameters from meteorology than the existing algorithms that use many prior meteorological parameters.
The TFDA algorithm is applied to a one-year time-series of the geopotential height data of 1960, and the results are compared with those obtained by the Dunn-Sigouin algorithm in the same period. It is found that several blocking events are undetected by the Dunn-Sigouin algorithm but detected by the TFDA algorithm, and vice versa, indicating that it would be safe to use both of the algorithms in order to avoid overlooking blocking events. On the other hand, the TFDA algorithm can identify the morphological type of atmospheric blocking objectively by observing specific symbols in the COT representation. This is a new feature brought by the proposed algorithm, since it is a challenging task for existing algorithms. The morphological identification is made possible by extracting some geometric quantities from regions of influence associated with COT representations. It is important to note that the blocking events and their morphological types agree with subjective judgments made by forecasters and synopticians.
Let us mention the future direction of this study. By applying the proposed algorithm to geopotential height data in the last 60 years, statistical analysis of blocking events can be conducted, investigating the distributions of sizes, locations, times, and duration of blocking events with morphological types. These statistical properties reveal the geographical distribution and seasonality of atmospheric blocking, and informative for climate change predictions, which will be reported in the future.
T. Uda is supported by Japan Science and Technology, ACT-X (#JPMJAX1906). T. Sakajo is supported by Japan Science and Technology, MIRAI (#18076942) and the RIKEN iTHEMS program. M. Inatsu is supported by Japan Society for Promotion of Science, KAKENHI Grant (#18K03734) and by the Research Field of Hokkaido Weather Forecast and Technology Development (endowed by Hokkaido Weather Technology Center Co. Ltd.).