2021 Volume 99 Issue 6 Pages 1483-1499
2021 Volume 99 Issue 6 Pages 1483-1499
Understanding of the tropical atmosphere is elaborated around two elementary ideas, one being that density is homogenized on isobars, which is referred to as the weak temperature gradient (WTG), and the other being that the vertical thermal structure follows a moist-adiabatic lapse rate. This study uses simulations from global storm-resolving models to investigate the accuracy of these ideas. Our results show that horizontally, the density temperature appears to be homogeneous, but only in the mid- and lower troposphere (between 400 hPa and 800 hPa). To achieve a homogeneous density temperature, the horizontal absolute temperature structure adjusts to balance the horizontal moisture difference. Thus, water vapor plays an important role in the horizontal temperature distribution. Density temperature patterns in the mid- and lower troposphere vary by about 0.3 K on the scale of individual ocean basins but differ by 1 K among basins. We use equivalent potential temperature to explore the vertical structure of the tropical atmosphere, and we compare the results assuming the temperature following pseudo-adiabat and reversible-adiabat (isentropic) with the effect of condensate loading. Our results suggest that the tropical atmosphere in saturated convective regions tends to adopt a thermal structure that is isentropic below the zero-degree isotherm and pseudo-adiabatic above it. However, the tropical mean temperature is substantially colder and is set by the bulk of convection, which is affected by entrainment in the lower troposphere.
The two principles underpinning theoretical understanding of the tropical atmosphere are that gravity waves are effective in homogenizing the horizontal temperature in the free troposphere (Charney 1963; Bretherton and Smolarkiewicz 1989), and that in convecting regions, the thermodynamic stratification follows the moist-adiabatic lapse rate of the near surface air (Betts 1982; Xu and Emanuel 1989).
These principles are thought to work together to set the thermal structure of the free troposphere even in regions well removed from deep precipitating convection, i.e., across the broader tropics. Were it not for the gravity waves, then convection would arise everywhere to set the vertical stratification to that associated with the adiabatic ascent of the near surface air and thereby counter the destabilization of the tropical atmosphere by radiative processes. In this case, however, the free troposphere would adopt a thermal structure that mirrored the inhomogeneities of the underlying surface. The smallness of the Coriolis parameter combined with the fast speed of deep gravity waves instead adjusts, or homogenizes, the temperature in the atmosphere, an effect encoded in the Weak Temperature Gradient approximation (WTG, Sobel and Bretherton 2000). The gravity waves adjust the temperature in the nonconvective regions to that in the convecting regions, effectively inhibiting convection at a lower convective temperature. This process titrates the convection, concentrating it to the area where the convective temperature is higher than some threshold whose value allows just enough convection to balance the radiative cooling globally. Hence, these two elements (vertical homogenization by convection along the local moist adiabat, and nonlocal horizontal homogenization by gravity waves) provide the theoretical underpinnings of our broader understanding of the tropical atmosphere. However, in reality—or as nearly as we can approximate it—how accurate are these two principles?
Above, and more generally, the term “moist adiabat” is applied loosely, and thus it is often unclear which thermodynamic process it actually is meant to encapsulate. As discussed by Betts (1982) and others, when picturing a moist-adiabatic process as saturated ascent of moist air, it makes a difference whether condensate precipitates or remains suspended, for instance, by updrafts. The pseudo-adiabatic process assumes that the condensate is removed from the atmosphere immediately upon formation, which makes it an irreversible process. A reversible, and hence isentropic, process requires not only the absence of external heating but also the condensed water to remain in the updraft. In this case, the condensate loading must be accounted for when calculating the density. Ice processes compound these differences, as the available fusion enthalpy is contingent on the amount of condensate that can be frozen. More generally, the thermodynamic processes affecting the ascent of air in deep convection may also deviate from being strictly adiabatic, as mixing and radiative processes may also play a role.
Both Betts (1982) and Xu and Emanuel (1989) analyzed soundings in areas of deep convection and concluded that the tropical atmosphere is neutrally stratified with respect to the reversible-adiabatic ascent from the sub-cloud layer, suggesting that the tropical temperature follows a reversible-adiabatic (or isentropic) lapse rate. They justified their finding with two arguments. The first was that condensate loading is maintained either by virtue of being suspended in convective updrafts, or by continuity of the precipitate field—precipitation lost to the air below is balanced by what is gained from above. The second argument was that although mixing is a characteristic of clouds, in a convecting atmosphere, some favored air-parcels are shielded from their environment, thereby rising without dilution, and it is the thermodynamic properties of this air that determines the overall stratification.
The idea that the undilute ascent of air within convecting regions determines the stratification of the tropical atmosphere is disputed by a number of studies. In simulations of radiative convective equilibrium (RCE), Romps and Kuang (2010) found that undilute ascent is very rare, with only 1 % of the convective mass flux at 4 km could qualify as undilute. Romps and Kuang (2010), and later Singh and O'Gorman (2013) using similarly configured simulations, also showed that the convective available potential energy (CAPE) associated with undilute ascent is substantial, but the actual cloud buoyancy fails to realize this CAPE due to dilution through entrainment. Interpreting these studies is difficult. For one reason, because the simulations do not represent organized convection, but also because of subtleties in how parcel buoyancy is calculated. If gravity waves efficiently homogenize the density temperature, then the actual temperature—equivalently the saturation moist static energy—must increase with its saturation deficit. Hence, estimating the buoyancy of undilute ascent based on the saturated moist-static energy of unsaturated air will overstate the buoyancy in proportion to the saturation deficit.
Studies analyzing sounding data taken from non-convective regions also make the case for entrainment playing a fundamental role in setting the stratification of the tropical troposphere. Mapes (2001) computed the temperature lapse rates for both Western and Eastern Pacific mean soundings and found a region of anomalously weak stability between 2 km and 5 km. The stability of this layer is described as anomalously weak in that it is in accordance with what one would expect if the temperature were decreasing more rapidly with height than it would following either a reversible or pseudo-adiabat. This could arise through the entrainment of dry air. Later, Folkins and Martin (2005) also found similar deviations. However, both studies estimated the stability based on the temperature rather than the density temperature, which again must decrease more rapidly with altitude in progressively more sub-saturated conditions, if the density temperature is constrained to be homogeneous.
These considerations highlight how efforts to understand the processes that determine the vertical stratification of the tropical atmosphere are intertwined with assumptions as to the what determines the horizontal distribution of this stratification, i.e., the efficacy of gravity waves in annihilating horizontal gradients of buoyancy.
So far our understanding of the tropical atmosphere has been built upon radiosonde measurements, global modeling with parameterized convection, or simulations that explicitly represent convection, albeit for very idealized situations over small domains. The main limitation of radiosondes is their sparse spatial coverage, particularly in the tropics. Additionally, radiosondes can be influenced by biases, from poor moisture sensors, or the effects of solar heating or sensor wetting during the period of severe weather. In terms of modeling, simulations over a large domain in the tropics are mainly achieved by global climate or numerical weather prediction models. However, convection usually happens at kilometer scales, which are much finer than the grid size of most global models (typically at 50–200 km). Therefore, moist convection must be parameterized as a subgrid scale process. These parameterizations are problematic and often incorporate assumptions regarding those things we wish to test. In addition, moist convection is an important source of gravity waves in the tropics. Whether it is resolved or parameterized has been shown to be able to impact the characteristics of these waves (Müller and Hohenegger 2020; Stephan et al. 2019), which is something that might influence the temperature adjustment through the troposphere.
To overcome the parameterization dilemma, one can increase the model resolution to avoid the use of convective parameterization. Models that adopt this approach are often referred to as convection-permitting models or storm-resolving models (SRMs). Kilometer-scale resolution (typical grid spacings for such models are 3–5 km) is computationally expensive, something which in the past has limited the simulations to relatively small domains, either through regional “downscaling” approaches or by adopting an idealized configuration (Prein et al. 2017; Wing et al. 2018a; Bao and Sherwood 2019). In recent years, with the increasing computational capacity, it has become possible to conduct global storm-resolving model (GSRM) simulations (Stevens et al. 2019; Satoh et al. 2019). The first intercomparison project of GSRMs, DYAMOND, which stands for The DYnamics of the Atmospheric general circulation Modeled On Nonhydrostatic Domains, was initiated in 2017 (Stevens et al. 2019). These simulations discard convective parameterization while at the same time ensuring a global domain, offering an opportunity to rejoin the questions outlined above in ways that were not previously possible.
In this study, we investigate the thermodynamic structure of the tropical atmosphere using output from the DYAMOND project. Our aim is to answer two intertwined questions: how homogeneous is tropical temperature horizontally and which process sets the vertical thermodynamic structure of the troposphere. Additionally, we ask to what extent the answer depends on processes that are still unresolved or poorly resolved in models with a grid spacing of a few kilometers. We describe the data in Section 2 and theory and methodology in Section 3. In Section 4, we analyze to what extent and on what scales gravity waves can horizontally homogenize the vertical stratification in the tropics. In Section 5, we develop techniques that allow us to infer the stratification in the convecting regions from its value in the nonconvecting region, under the assumption of the weak temperature gradient. Finally, in Section 6 we present a discussion of our findings and our main conclusions.
We analyze the model output simulated by ICO-sahedral Non-hydrostatic model (ICON; Zängl et al. 2015) with a quasiuniform horizontal mesh of 2.5 km. The simulations follow the experimental protocol for DYAMOND (Stevens et al. 2019) in which models are required to run at storm-resolving scales (5 km or less) for 40 days from August 1, 2016. The model is initialized with the global meteorological analysis at a grid spacing of 9.5 km from the European Center for Medium Range Weather Forecasts, and daily observed sea surface temperatures are forced as lower boundary conditions.
The parameterizations used in this version of ICON are typical for GSRMs. Convective parameterization is switched off for both shallow and deep convection. Physical parameterizations include a microphysics scheme with five hydrometeors (cloud water, cloud ice, rain, snow, and graupel; Baldauf et al. 2011), a turbulent mixing scheme, RRTM (Rapid Radiative Transfer Model) radiation scheme (Mlawer et al. 1997), and an interactive surface flux scheme. Further details about the ICON model as configured for DYAMOND are provided by Hohenegger et al. (2020).
The data from the last 10 days of the simulations are used in the analysis. As the thermodynamic structure of the tropical atmosphere is a relatively stable characteristic (particularly when averaging spatially), having a short time span of data is not a severe limitation. Most of the analysis is focused on the tropical oceanic grids (10°N–10°S). The key conclusions from ICON are compared with other models in the DYAMOND project listed in Table 1. Radiosonde observational data at two tropical sounding stations—Ponape (6.96°N, 158.21°E) and Pago Pago (14.33°S, 170.71°W)—retrieved from the University of Wyoming archhive1 are also utilized to assist in the interpretation of the simulations.

Thermodynamic quantities are defined following Stevens and Siebesma (2020). Thus, the atmosphere is represented as two component fluid, consisting of dry air and water. Subscripts indicate component properties, e.g., subscript “d” refers to dry air, whereas subscript v, l, i, and t denote gaseous (vapor), liquid, solid (ice), and total water (sum over all phases). Subscript s denotes a saturation value. As examples, qd denotes the specific mass of dry air, and ps the saturation vapor pressure. The “equivalent” reference state is denoted by “e” and corresponds to the hypothetical situation in which qt = ql.
In this system, the density temperature Tρ is an effective temperature that measures the ratio between the air pressure p and density ρ, such that
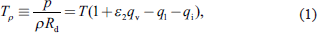 |
The equivalent potential temperature (θe) of the air is conserved for isentropic transformations of the closed system. Subject to a few common and simple assumptions (including ice processes neglected), and with cp denoting (composition dependent) the isobaric specific heat, θe can be expressed as
 |
 |
 |
 |
Physically, θe can be thought of as a condensation (potential) temperature (cf. Betts 1982). It measures the temperature the air would have after a two step process: (i) an adiabatic expansion that results (asymptotically) in all vapor condensing to liquid; (ii) an adiabatic compression to standard pressure (p0) of the air-condensate system, with the two components in thermal, but not mechanical, equilibrium. The second step retains the water in its condensate phase, and thus loses none of the enthalpy gained through condensation (first step) to re-vaporization. We subsequently refer to the process that conserves θe as isentropic. On a thermodynamic diagram θe-isopleths are called isentropes, which assumes the system is closed.
The pseudo-equivalent potential temperature is defined following Bolton (1980) as
 |
 |
If moist air undergoes an isentropic expansion without any exchange of mass, then T would change in a way that keeps θe constant as p decreases for the given qt. Choosing θe as a coordinate (with qt specified) results in this quantity remaining unchanged. Likewise, psuedo-adiabats are vertical lines in a coordinate system whose abscissa measures θ̃s.
The advantage of describing the state of the atmosphere using either θe or θ̃s as a coordinate is that these quantities are not expected to change under certain types of transformations. Hence, measuring how much θe or θ̃s does change can be indicative of the thermodynamic processes associated with a particular process, for instance deep moist convection. The trivial example, and the one many researchers apply as a mental model, is that of moist convection being pseudo-adiabatic and gravity waves efficiently acting within the free troposphere to adjust the temperature along isobars to its value in the convective region. In this example, θ̃s would adopt a single value throughout the free troposphere. This expectation motivates analyses of the thermodynamic structure of the troposphere with θ̃s as a thermodynamic coordinate. However, convection may not be pseudo-adiabatic. Consider the case that, as argued by Betts (1982) and Xu and Emanuel (1989), convection follows an isentrope. In that case, if one adopted θe as a thermodynamic coordinate, then θe profile should exhibit a constant vertical line, varying only with p. However, this will only be the case if θe is computed with the value of qt in the saturated convective region where the isentropic process occurs, which we denote as qt, c.
To avoid local variations in qt masking an isentropic temperature profile, one can fix qt in the calculation of θe to the value qt, c, which it has in the saturated convective region. To indicate when we calculate θe in this fashion, we write θe (T, p; qt, c). The semicolon notation indicates that when evaluating Eq. (2), qt is fixed as a parameter with value qt, c, which is either known or must be estimated. Fortunately, the bias from over estimating or underestimating qt, c by a small amount is also small, and estimates of qt, c are strongly constrained by the constancy of cloud base in the convective region. This relative insensitivity of θe (T, p; qt, c) to the estimate of qt, c can be inferred by inspection of Eq. (2). The main effect of the qt on θe is through the qv term. As long as qt > qs, qv = qs. Hence, qv is given by T and p. The small influence on the specific heat results in a small (0.25 K) decrease in θe in the lower troposphere for a 1 g kg−1 overestimation of qt, c. This bias increases with height, to a value about twice as large in the upper troposphere, but two times a small number is still small.
To help interpret the state of the atmosphere using θe and p as thermodynamic coordinates, Fig. 1 illustrates the fundamental lines associated with different processes when plotted in these coordinates. The profile representing an isentropic process shows a constant line in θe coordinate, whereas the pseudoadiabatic profile computed in θe coordinate decreases roughly linearly with geometric height (and hence expoentially with pressure), so that values in the upper troposphere will be reduced by as much as 10 K. The fundamental lines that incorporate additional processes, such as ice formation, show similar deviations. For instance, an isentrope that allows for freezing implies considerably larger values of θe, starting with the release of fusion enthalpy as liquid condensate freezes at the triple point temperature.

Profiles of T derived from idealized processes plotted in θe coordinate (left) and θ̃s coordinate (right).
The situation is reversed if one adopts θ̃s as a thermodynamic coordinate (Fig. 1b). In that case, should T follow an isentrope, it implies a progressive increase in θ̃s, mirroring the decrease of θe associated with pseudo-adiabatic temperature profiles. Understanding this difference also aids the interpretation of the other fundamental lines, for instance, for an entraining plume, which for this simple example is modeled as an exponential relaxation to a 5 K lower θe over a 150 hPa layer.
3.3 Estimating the effective convective temperature profile TcThe question this study poses is whether profiles of T and qt throughout the global tropics can inform us about the effective convective temperature profile, Tc. For our purposes, and unlike what is done in most other studies, Tc is not associated with any preconceived idea of convection, rather it is the temperature profile that the tropical troposphere appears to be adjusting too. As such it should be identifiable from profiles of T and qt throughout the global tropics. The reason for adopting this method to estimate the effective convective temperature profiles rather than to analyze the profiles in the actual convective regions is that we do not know exactly which convection sets the temperature horizontally. With this method, we can compare across the effective convective temperature profiles inferred from all grid points over the tropical oceans and then determine what fraction of convection sets the temperature in the tropical mean state. Irrespective of what process determine Tc, we do not expect this to determine T throughout the global tropics. If anything, the profile of the density temperature, Tρ, is what will be adjusted by gravity waves. In that case, one expects isopleths of Tρ to be parallel to isobars. This makes inferring the profile of Tc from profiles of T more delicate, as doing so must properly account for differences in qt, c and qt.
Our approach is illustrated with the help of the schematic in Fig. 2. Rather than guessing which grid columns are representative of the convecting regions, we attempt to infer Tc from local (usually nonconvective) profiles of Tρ. Assuming Tρ is constant on isobars, this implies that Tρ, c ≈ Tρ. Depending on the disposition of the condensate in the convecting regions, two possibilities bound our thinking. The first is that Tc follows an isentropic process. In this case, condensate is present in the convecting region, and
 |

Schematic of how the effective convective temperature (Tc) is calculated by accounting for the density effect on buoyancy.
A difficulty that arises when estimating Tc from Tρ, c is that the resulting profile is sensitive to what one assumes about qt, c. Two examples illustrate this point. For the first example, we take the case of pseudoadiabatic atmosphere but is assumed to be isentropic in the calculation so that qt, c is held constant. According to Eq. (7), incorrectly assuming an isentropic profile implies Tρ, c is increasingly (with height) burdened by condensate loading, which must be balanced by an overestimation of Tc for a given Tρ, c. Consequently, θe increases with height. Figure 3 shows the result, whereby θe increases to a maximum in the middle-upper troposphere (solid line). The reversal and progressive decrease of θe in the upper troposphere arises from an increasingly important and countervailing bias that arises by failing to account for the loss of condensate enthalpy associated with a psuedo-adiabatic temperature profile (e.g., as shown by the gray line in the left panel of Fig. 1). The second example shows how the situation reverses (dotted line in Fig. 3) if Tc follows an isentrope but is estimated from its remote Tρ profile by assuming it follows an pseudo-adiabat.

Effects of density adjustment on remote estimates of Tc: θe estimated from a pseudoadiabatic temperature profile but is assumed to be isentropic in the calculation so that qt is held constant (solid line); θ̃s estimated for an isentropic temperature profile but is assumed to be pseudo-adiabatic in the calculation (dashed line).
Before applying the above theory to vertical profiles of model output, or data, in this section, we first explore how well the Weak “Temperature” Gradient is satisfied in the simulations. We begin our analysis by examining the ICON-simulated spatial distribution of precipitable water (PW), which is the total vertically integrated atmospheric water vapor (Fig. 4). Figure 4 illustrates that dry and moist regions are well separated. PW is high mainly over regions near the Maritime Continent. Additionally, there is a long narrow band of high PW at around 10°N, indicating the location of the Inter Tropical Convergence Zone (ITCZ). PW is low mainly in the Southern Hemisphere including the Eastern and Central Pacific and the South Atlantic. The PW distribution reflects the location of convection as well as non-convecting environment due to the effect of convective moistening or subsidence drying.

Mean spatial distribution of precipitable water (PW) over the 10-day period.
To investigate the horizontal temperature distribution, we choose two levels: 300 hPa and 600 hPa representing the upper and mid-troposphere respectively. Figure 5 shows the spatial distribution of temperature (T) and the density temperature (Tρ) anomaly (relative to domain-mean value) at 300 hPa and 600 hPa. The difference in T and Tρ indicates mainly the impact of water vapor. At 300 hPa, T and Tρ are almost identical due to little water vapor existing there (Fig. 5). Moist regions like the Western Pacific and oceans near the Maritime Continent are generally warmer than dry regions like the Eastern Pacific. The maximum anomaly between the Western and Eastern Pacific is over 3.5 K. However, at 600 hPa, both T and Tρ are more homogeneous: over the Pacific Ocean, the maximum Tρ anomaly is less than 1 K, and over the Atlantic Ocean, the Tρ anomaly is also reduced. Despite being more homogeneous locally at 600 hPa, structure is evident on large (60° of longitude) scales, which appear to align with different ocean basins. The 1 K difference between a colder Atlantic and a warmer Eastern Pacific is particularly pronounced. This seems to suggest that the different ocean basins are adjusting to convection at different temperatures and that inter basin communication may be hindered either by the distances between the basins or by land masses, where orography and the diurnal cycle influence the atmospheric structure.

Mean spatial distribution of temperature (T) and the density temperature (Tρ) anomaly (relative to the domain-mean value) at 300 hPa and 600 hPa over the 10-day period.
Because Tρ is horizontally more homogeneous at 600 hPa than at 300 hPa, there must be a larger lapse rate in places where Tρ at 300 hPa is smaller. This is confirmed in Fig. 6a, which plots δzTρ = Tρ | 600 hPa − Tρ | 300 hPa. Over the Eastern Pacific and the Southern Atlantic δzTρ is anomalously large, whereas over the Western Pacific and the Maritime Continent it is anomalously small. The pattern of δzTρ resembles the pattern of PW. This apparent correlation is quantified in Fig. 6c, which shows that PW and δzTρ anomalies are negatively correlated with a correlation coefficient of −0.66.

(a, b) Mean spatial distribution of the horizontal anomaly of increase in the density temperature (δz Tρ: Tρ600 – Tρ300) and temperature (δzT: T600 – T300) at 600 hPa relative to 300 hPa. (c, d) Scatter plots showing the relationship between precipitable water (PW) and δzTρ or δzT.
The negative correlation between PW and δzTρ is not due to the vapor buoyancy effect as water vapor is included in the calculation of Tρ, and thus should act to reduce the horizontal heterogeneities in Tρ. Instead, it implies that gravity waves are less effective at homogenizing the buoyancy field in the upper (300 hPa) troposphere than they are in the mid-troposphere (600 hPa). If gravity waves were equally effective at homogenizing Tρ at both levels, there would be no difference in δzTρ horizontally. Without considering the vapor buoyancy effect, δzT anomaly is larger (Fig. 6b) and the negative correlation becomes more robust between PW and δzT anomaly (Fig. 6d). The vapor buoyancy effect can be interpreted by considering a simple idealized case where Tρ is homogeneous throughout the entire free troposphere. According to Eq. (1), T and Tρ differs when water vapor exists; this means that in the upper troposphere, T is almost homogeneous, whereas in the mid- to lower troposphere T varies depending on the horizontal differences in water vapor. Given the same Tρ, the difference in water vapor enhances T in dry regions and reduces T in moist regions because moist air is less dense than dry air at the same temperature. As the only deciding factor is water vapor, the vapor buoyancy effect would lead to a strong negative relationship between PW and δz T. However, the results in Fig. 6 indicate that the vapor buoyancy effect is not the dominant factor but contributes to the negative relationship between PW and δzT.
To better understand the temperature structure and the vapor buoyancy effect, we calculate the pattern correlation between PW and T, or Tρ, at different pressure levels. The variation of the correlation coefficient with pressure is plotted in Fig. 7. Differences in how T and Tρ correlate with PW is indicative the vapor buoyancy effect. If two profiles overlap, it means that either there is little water vapor (as is the case above 300 hPa) or the vapor buoyancy effect is not dominant (in the boundary layer). For comparison, we plot the same figure with data from the Radiative-Convective Equilbrium Model Intercomparison Project (RCEMIP; Wing et al. 2018b). The data that we use are from the ICON-LEM (Dipankar et al. 2015) configured over an elongated channel domain (6000 km × 400 km) and applying a horizontal grid spacing of 3 km. As there is no rotation and the domain is small compared with the global simulations (albeit orders of magnitude larger than the simulation domains used in many previous studies), Tρ is extremely homogeneous throughout the entire free troposphere. This is illustrated by near-zero correlation coefficients between PW and Tρ. Given the homogeneous Tρ, water vapor becomes the only factor impacting T, which leads to strong negative correlations between PW and T. Thus, idealized simulations of radiative-convective equilibrium provides a setting where gravity waves function effectively throughout the free troposphere. In reality, and on larger domains, we expect the vapor buoyancy effect to become more dominant in the relationship between PW and T under the condition that Tρ becomes more homogeneous.

Profiles of pattern correlation coefficients between precipitable water (PW) and T (solid lines) or Tρ (dashed lines) from ICON simulations in RCEMIP (a) and DYAMOND (b). Colors from black to light gray in (b) indicate results of different analysis regions.
For the DYAMOND simulations of a more realistic setting, first we focus on the ICON output over the region from 10°N to 10°S. Figure 7b indicates that there are two positive correlation maxima: one near the top of the boundary layer and one near 300 hPa. The high correlations in the boundary layer are expected as the boundary layer is well mixed and feels strongly the imprint of the temperature at the sea surface. The other peak at 300 hPa confirms that T is not homogeneous in the upper troposphere but varies similarly as PW. Between 400 hPa and 800 hPa, PW has weak positive correlation with Tρ, and negative correlation with T. This means that the vapor buoyancy effect becomes more important in the midtroposphere, thereby denoting a more homogeneous Tρ.
When the analysis is performed over the broader tropics, to also include the subtropics, both Tρ and T exhibit positive correlations with PW (Fig. 7). The correlation coefficients are above 0.5 throughout the entire troposphere over 30°N–30°S, implying that Tρ is not homogeneous even in the mid-troposphere and such a large area cannot be effectively influenced by the tropical convection through gravity waves. The poleward increase of the coriolis parameter increasingly allows the atmosphere to balance density gradients away from the equator. This analysis indicates that to the extent it is a valid approximation, the weak gradients of Tρ or weak buoyancy gradient (WBG) describes the thermal structure of the atmosphere equatorward of 10° or maybe 20°, and mostly between 400 hPa and 800 hPa.
We hypothesize that differences in the degree to which Tρ is homogenized with height reflects the effectiveness of gravity waves in communicating, and hence homogenizing, density anomalies there. The gravity waves that cause widespread subsidence over nonconvective regions are deep, with a half-wavelength, which spans the depth of the heating layer (Mapes 1993). However, the wave transports of buoyancy become less effective near the upper and lower boundaries, both because it is hard to get strong subsidence motion near these boundaries (Bretherton and Smolarkiewicz 1989) and because the gravity wave propagation speed is proportional to the vertical wavelength. Thus, proportionally smaller vertical modes are required to homogenize density anomalies confined to shallower layers. Shallow density anomalies arising from imbalances between diabatic (radiative) heating and subsidence warming are thus less effectively homogenized by gravity waves. We speculate that far away from the convection, the ability of convectively generated gravity waves to generate sufficient subsidence to balance the radiative cooling, thereby equilibrating the temperature to that in the convective region, is thus diminished. Thus, upper-tropospheric temperature in nonconvective regions is colder.
The above results highlight the important role that water vapor plays in the temperature lapse rate and reaffirm that horizontally Tρ is homogeneous mostly in the mid-troposphere (400–800 hPa) in the deep (10°N–10°S) tropics.
In this section, we focus on the vertical temperature structure. From the previous section, we saw that although gravity waves do more efficiently adjust Tρ than T, variations in Tρ of about 1 K emerge in the mid-troposphere across the inner tropics and that these temperatures become more pronounced and positively corelated with PW in the upper and lower troposphere. These differences should help guide our interpretation of the value and vertical structure of Tc as deduced from profiles of T and qt.
5.1 Estimating Tc from global profiles of T and qtHere we use profiles of T and qt simulated by ICON over the inner (10°N–10°S) tropics. From these, we use the methodology described in Section 3.3 to infer profiles of Tc, which we then render in θe and θ̃s coordinates to see how they vary, both in the vertical and as a function of PW. The former should be indicative of the thermodynamic processes in the saturated convective regions that to a first approximation, set the thermal structure of the tropics; the latter should be indicative of the extent to which other, non-convective processes, cause deviations from this. Recall that the manner in which Tc is estimated differs depending on which thermodynamic coordinate is adopted. For reference, we also show uncompensated temperature profiles using the θ̃s coordinate, which amounts to taking Tc = T. The three coordinates are summarized with the help of Table 2, which also sets the nomenclature.

Following the outline of Table 2, θ̃s (T), θ̃s (Tc), and θe (Tc; qt, c) are plotted in Fig. 8. Profiles are constructed for different values of PW, thereby showing how Tc varies across moisture space in the tropics. Calculation of θ̃s(Tc) and θe(Tc; qt, c) assumes that Tρ is homogenized by gravity waves. As discussed in the previous section, this is most approximately true in the free troposphere, near 600 hPa, but not in the unstratified boundary layer, where waves are not supported. This point notwithstanding Fig. 8 shows that variations in θe (Tc; qt, c) [equivalently θ̃s (Tc)] depend only weakly on PW in the free troposphere (above 800 hPa). Additionally, and most importantly, the use of Tc inferred from Tρ better collapses (groups) the data than does T. This is most evident in the elimination of the apparent local maximum in θ̃s(T) that emerges in the driest columns near 800 hPa (Fig. 8a).

Mean profiles of θ̃s (T), θ̃s(Tc), and θe(Tc; qt, c), sorted based on precipitable water (PW). Colors from red to blue indicate profiles with PW from the driest 10 % to the most humid 10 % grids.
Although θ̃s(T) is larger in moist regions and smaller in dry regions in the upper troposphere (200–400 hPa), the opposite is true in the lower and middle tropospheres (400–800 hPa). This implies large differences in temperature lapse rates, consistent with the observational analyses by Mapes (2001) and Folkins and Martin (2005), which also were based on T. To a large extent, the differences in the mid- and lower-tropospheric θ̃s (T) can be traced to the impact of water vapor as θ̃s(Tc) becomes more uniform by applying Tc assuming constant Tρ. This suggests that the apparently strong deviations from the pseudo-adiabat or the isentrope that these studies identified in the lower troposphere (600–800 hPa) may have resulted from neglecting the water vapor effect on buoyancy.
A prominent feature in all three panels of Fig. 8 is its increase with moisture in the upper troposphere. This implies that neither T nor Tρ is homogeneous (irrespective of how one estimates Tc) and the wave homogenization mechanism there may not function as well as that in the mid-troposphere. These profiles are consistent with the analysis in Section 4 and indicates that in the upper troposphere, regions close to deep convection are expected to be warmer than more distant regions. Such differences can be expected to support a large-scale circulation in the upper troposphere analagous to that discussed by Mapes (2001).
The profiles in Fig. 8 suggest that an isentrope [constant θe(Tc; qt, c)] is a good description of the lower troposphere (below roughly 600 hPa). Above 600 hPa, θe(Tc; qt, c) more closely approximates the ice-pseudo-adiabat, as inferred by comparison to the theoretical profiles in Fig. 1. In this interpretation, our eye is drawn to the increase with height above 600 hPa (to a local maximum near 400 hPa) and subsequent fall off with height above that point, reaching a local minimum value between 250 hPa and 200 hPa.
Similar profiles are also found in the atmosphere with the most extreme values of PW, which we take to be representative of regions of the deepest convection. Figure 9 presents profiles of θ̃s(T), θ̃s(Tc), and θe(Tc; qt, c) for the 99.999 percentile of PW (which comprises approximately 100 samples per time-step). Because the profile of θ̃s(Tc) in Fig. 9 do not differ from θ̃s(T), this confirms that our selection identifies saturated grid columns. As none of the profiles exhibits a constant structure throughout the full depth of the troposphere, it suggests that even in the most water-laden columns, no single process (either pseudoadiabatic or isentropic) can describe the thermal structure in these saturated regions alone. However, a combination of the pseudo-adiabatic and the isentropic processes seems like a good description; below about 600 hPa, the profile follows more closely a saturated isentrope, whereas a pseudo-adiabat appears a good representation of the thermal structure above.

Mean profiles of θ̃s(T), θ̃sTc), and θe (Tc; qt, c) from the grid points with precipitable water (PW) exceeding 99.999th percentile.
There is a temptation to conclude that because the mean profile of θe(Tc; qt, c) is similar in shape to the profile in the moistest regions, these latter regions dictate the thermal structure of the tropical troposphere. A substantially larger mid-troposphere θe(Tc; qt, c) in the extremely moist columns (345 K), as compared to the average (342 K), suggests that this is not the case, nor can it be concluded that just because a profile follows one or the other fundamental line, it is determined by the process associated with this line. For instance, a constant-like θe(Tc; qt, c) for the mean state in the lower troposphere could also arise as a result of several processes compensating each other. In the next section, by compositing on progressively moister columns, we explore both of these points in more depth.
5.2 Processes determining the mean thermal structure of the troposphereIt may seem contradictory that in Section 4 we conclude that Tρ is horizontally homogeneous especially in the mid-troposphere, yet above identify relatively large (3 K) deviations of mid-troposphere θe(Tc; qt, c) in the very moistest columns. Because regions of such extreme PW are so rare, their ability to influence the structure of the troposphere as a whole is likely limited; likewise, their ability to exist out of balance with the mean structure of the troposphere will be considerable. Thus, although not contradictory, it does raise the question as to what fraction of the convecting atmosphere, or which percentile of the PW distribution, is responsible for setting the mean properties of the tropical troposphere.
To investigate this issue more systematically, we compare the Tρ anomaly at 600 hPa as a function of percentiles of PW. Figure 10 shows that the Tρ anomaly changes relatively little (approximately 0.3 K) below the 99th percentile of PW. By contrast, Tρ anomaly increases sharply (note the log-axis) above the 99th percentile. From this we infer that the tropical temperature profile is adjusting to the average temperature profile set by convection in roughly the moistest (as measured by PW) 1 % of the tropics. Profiles of θe(Tc; qt, c) and θ̃s(Tc) for columns within the upper PW decile are plotted in Fig. 11 and support this inference. The columns with yet more extreme values of PW are considerably warmer than the mean, but that already at the 99th percentile, the temperature is very close to the tropical mean.

Tρ anomaly (relative to the domain-mean value) at 600 hPa as function of percentiles of precipitable water (PW). Red dashed lines are references corresponding to the 99th percentile of PW.

Mean profiles of θ̃s(Tc) and θe (Tc; qt, c) averaged over all grid points (black) and extremely humid grid points [colors from yellow to blue correspond to the 90th, 99th, 99.9th, 99.99th, and 99.999th percentiles of precipitable water (PW)]. Freezing levels are marked in red.
Profiles of θe(Tc; qt, c) also hint at what processes might be influencing the thermal structure of the troposphere in the mean state (Fig. 11). A feature that captures our attention is the systematic increase (with decreasing percentile of PW) of the θe(Tc; qt, c) lapse rate below 600 hPa. Although the 99.999th percentile has a slightly increasing value of θe(Tc; qt, c) with height, the profile of the 99th and 90th percentiles is slightly decreasing (larger lapse rate). Increasing θe(Tc; qt, c) is a signature of pseudo-adiabatic effects, whereas decreasing θe(Tc; qt, c) is a signature of entrainment. However, in a drier atmosphere (as expected in the lower percentiles), entrainment is more effective in reducing the updraft buoyancy (temperature), so even if the most moist convection is entraining the same as convection in drier regions, it will be less evident. This supports the idea that in the tropical mean state, the isentropic-like profiles of Tc in the lower troposphere arise from our analysis not because the convection follows a saturated isentrope, rather due to the competing effects of a pseudo-adiabatic process on the relationship between buoyancy and temperature that we use to diagnose Tc and the effect of entrainment on Tc directly. Our analysis of the ICON simulations thus supports the arguments by Singh and O'Gorman (2013) that the tropical mean condition is not determined by the warmest air parcels that are nearly undiluted but rather by the bulk of convection subject to the influence of entrainment in the lower troposphere.
The shape of the profiles above 600 hPa is more difficult to interpret. The moistest profiles (99.999th percentile) appear more pseudo-adiabatic, in which case ice processes are only a small perturbation. However, the drier profiles are more stably stratified, as they approach the moister profiles with decreasing pressure. We speculate that the convection that can reach the upper troposphere is very rare, and only those with very high boundary-layer θe in the saturated environment can survive in the upper troposphere, whereas more convection can get to the mid-troposphere. Hence, the high stability in the drier profiles in the upper troposphere indicates that with decreasing pressure, the temperature is more controlled by the convection with higher θe.
In summary, the saturated regions with deep convection in ICON appear to be well described by an isentropic profile below 600 hPa and by a pseudo-adiabat aloft. However, this does not appear to be indicative of the mean state actually being described by these processes but rather through a compensation of competing effects, with different balances in the lower versus upper troposphere.
5.3 Testing the robustness of inferences from ICON outputA sensible question to ask is whether the above conclusions hold in other DYAMOND models or in data from tropical radiosondes. Figure 12 shows profiles of θe(Tc; qt, c) from six DYAMOND models for the mean and the humid conditions. A first impression of Fig. 12 is that most models convect at a similar temperature [at 600 hPa, θe(Tc; qt, c) ≈ 342 K], GEOS being somewhat warmer and SAM being somewhat colder than the other models. The models also appear to differ with respect to the exact thermodynamic process, which sets the temperature structure in the convective regions. SAM and IFS show a tendency for θe(Tc; qt) to decrease with height, which can only be explained by a greater role for entrainment. GEOS and FV3 are similar to ICON, and NICAM has more pronounced increase in θe(Tc; qt, c) with height, indicative of a slightly more pseudo-adiabatic profile below 600 hPa. Notwithstanding these differences, some further inferences from the analysis of ICON hold across these models. First, most models show that the tropical mean θe(Tc; qt, c) overlaps with θe(Tc; qt, c) over the upper percentile of PW in the mid (600 hPa) troposphere. Second, all models have a tropical mean θe(Tc; qt, c) that decreases between 400 hPa and a local minium near 200 hPa, as one would expect if convection followed a pseudo-adiabat in the upper troposphere. Third, most models show that θe(Tc; qt, c) in the most humid regions is significantly larger than the tropical mean value, and the “cold-point” temperature locates at lower pressure.

Mean profiles of θe(Tc; qt, c) averaged over all grid points (black) and the extremely humid grid points [colors from yellow to blue correspond to the 90th, 99th, 99.9th, 99.99th, and 99.999th percentiles of precipitable water (PW)] from different DYAMOND models. Freezing levels are marked in red.
Finally, and as a sanity check, we compare the model results with measurements by tropical radiosondes. Although there is no reliable observational product covering the entire tropics, the advantage of the above analysis is that it shows that for many questions one can infer the convective profiles from anywhere in the tropics. Only the apparent dependence of θe(Tc; qt, c) on PW in the upper troposphere needs soundings that adequately sample moist and dry regions. For many places in the tropics, the seasonal migration of ITCZ allows an individual station to sample the dry and the moist tropics and hence, by adjusting for sampling biases, to address this question. Here we show results from two stations in the tropical Pacific (Fig. 13). In general, the observations corroborate the main findings from ICON. That the two soundings appear less consistent with respect to which convection sets the tropical mean lapse rate. That the mean profile at Pago Pago (14.33°S, 170.71°W), is less well adjusted to the upper decile, or percentile, may reflect its distance from the equator, which influences the adjustment process as shown in the analysis of Section 4, Fig. 7.

Mean profiles of θe(Tc; qt, c) averaged over all grid points (black) and the extremely humid grid points [colors from yellow to green correspond to the 90th–99.9th percentiles of precipitable water (PW)] from two tropical soundings. Freezing levels are marked in red.
This paper presents our analysis of simulations from a global storm-resolving model (ICON) to investigate the validity of the two important principles of the tropical atmosphere: the horizontal temperature in the free troposphere is homogeneous, which is referred to as the weak temperature gradient (WTG) approximation, and that the vertical structure follows a moist-adiabatic lapse rate—albeit often without a precise definition of the moist adiabat. Our results show that horizontally, the density temperature (Tρ) is roughly homogeneous in the mid- and lower troposphere except those regions with deep convection (∼ 1 %) being substantially warmer than the rest of the tropical domain. Vertically, the tropical atmosphere in the saturated convective regions tends to adopt a thermal structure that is isentropic below the zero-degree isotherm and pseudo-adiabatic above. However, the tropical mean temperature is substantially colder and is set by the bulk of convection, which is affected by entrainment in the lower troposphere.
The results highlight the important role that water vapor plays in the horizontal temperature (T) distribution. The vapor buoyancy effect arises from the unbearable lightness of the water molecule (H2O) is much smaller than that cocktail of N2, O2, and Ar known as “dry air”. At the same pressure and temperature, moist air is less dense than dry air. In the tropics, where the horizontal buoyancy differences are efficiently eliminated by gravity waves, the density temperature (Tρ), a compensated temperature that includes the density effect of water vapor (and condensate loading when present), is expected to be homogeneous. Hence, for Tρ to be horizontally homogeneous, T has to vary with the specific humidity. The model results show that Tρ is relatively homogeneous between 400 hPa and 800 hPa, which defines the mid and lower mid-troposphere. Because of the effect of vapor on air density, the absolute temperature is colder in moist regions and warmer in dry regions. The latter gives rise to an apparent inversion in the dry regions. Above 400 hPa, both the absolute temperature and the density temperature are also less homogeneous and vary as a function of moisture. This is indicative of a less effective homogenization by gravity waves at these levels, and we speculate the tendency of the upper troposphere to be more strongly influenced by more θe-rich convection, whose rareness makes its effects most pronounced in its local environment.
We use equivalent potential temperature to explore the vertical structure of the tropical atmosphere. Two thermodynamic coordinates are adopted. One, θ̃s, is constant for a pseudo-adiabat, other, θe, is invariant following a saturated isentrope. Deviations of the atmospheric thermal structure from an isopleth in these coordinates are used to explore thermodynamic processes that set the thermal structure in the convecting regions—albeit without the need to first identify these regions. To perform this analysis, it is necessary to estimate the convective profile, Tc ( p), consistent with the local temperature and moisture profile and an assumed buoyancy homgenization (WBG). In ICON in the most saturated regions of the tropical troposphere, this analysis identifies a thermal structure that is isentropic below the zero-degree isotherm and pseudo-adiabatic above. This structure is also evident in the mean. Nonetheless, by comparing profiles conditioned on PW, we conclude that in the mean state, the apparent isentropic profile in the lower troposphere is a result of entrainment masking the effects of pseudoadiabatic ascent and its implication for the buoyancy, if not the temperature, profile. This contradicts early observational studies that tropical atmosphere is neutral to the isentropic ascent from the subcloud layer (Betts 1986; Xu and Emanuel 1989) but supports recent work using idealized simulations in which the fundamental role of entrainment in tropical lapse rate has been recognized (Singh and O'Gorman 2013; Seeley and Romps 2015).
Using the the effective convective temperature profile, Tc, to calculate θ̃s (Tc) also greatly reduces the horizontal spread in the mid- to lower troposphere. Furthermore, we show that in the lower troposphere, the vapor buoyancy effect strongly conditions T in ways that easily bias the interpretation of θ̃s (T) profiles. Our finding recasts work by Yang and Seidel (2020) who have previously also emphasized how a large vapor buoyancy effect can lead to 1.5 K horizontal temperature differences in the lower troposphere and explored the implications of this for radiative transfer. As convective instability is often inferred from the profile of T, apparently unstable profiles may arise because of vertical gradients of water vapor (which condition the gradients of T). Raymond and Flores (2016) defined an instability index using the saturation moist entropy averaged over 1–3 km minus that over 5–7 km. By basing this calculation on T, the dry tropics, i.e., nonconvecting areas, will appear more unstable because of an apparent decrease in moist entropy, which arises from a disproportionate effect of water on the temperature at lower levels. Using the effective convective temperature, Tc, as we define it, avoids this bias. Another consequence of the atmosphere being generally dry is that estimating upper tropospheric warming as being proportional to lower-tropospheric temperatures without accounting for differences in the absolute humidity will overstate the warming because the lapse rate in a dry atmosphere is often larger than that in a moist atmosphere due partly to the density effect of water vapor. To what extent this might matter for controversies regarding the expected versus measured upper tropospheric warming remains to be evaluated.
To what extent the WTG holds in the tropical free-troposphere depends on how one defines “weak”. The idea of a weak buoyancy, or density, gradient is better founded, but even this is limited in its applicability. Already poleward of 10°, we begin to see large departures from the assumption of a weak density gradient in the mid-troposphere. Even across ocean basins the density temperatures can vary substantially, as it does above and below the lower middle and middle (400–800 hPa) troposphere. The larger deviations from the weak buoyancy gradient (WBG) approximation that we note in the upper and lower troposphere are less evident in idealized simulations, even within relatively large domain RCE studies. This suggests that despite support from idealized studies of how the troposphere adjusts to convective heating, an unqualified application of WTG (or WBG) and the moist adiabat, whereas an attractive simplification, is not something that can be taken for granted. Possible deviations from this balance need to be evaluated for quantitative work.
Most of the key results from our analysis of ICON can be generalized to other DYAMOND models and are also apparent in observed tropical soundings. Among the models, however, differences are apparent in terms of the vertical thermal structure. These may be a signature of differences in their treatment of thermodynamic or microphysical processes, a question that we are looking forward to investigating further.
We would like to thank the modeling groups participating in the DYAMOND and RCEMIP project. The DYAMOND and RCEMIP data as well as further management were provided by the German Climate Computing Center (DKRZ). DYAMOND project was supported through the projects ESiWACE and ESiWACE2. The projects ESiWACE and ESiWACE2 have received funding from the European Union's Horizon 2020 research and innovation programme under grant agreements No. 675191 and 823988. We also would like to thank the University of Wyoming for providing access to the upper atmospheric sounding data. We thank Steven Sherwood, Kerry Emanuel, Claudia Stephan, and Haile Xue for enlightening discussions and Tobias Becker for the internal review. The primary data and scripts used in the analysis that may be useful in reproducing the results of this paper are archived by the Max Planck Institute for Meteorology and can be obtained by contacting publications@ mpimet.mpg.de.
1http://weather.uwyo.edu/upperair/sounding.html