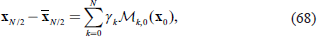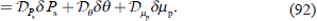2.1 Cost function
a. Formulation
In the variational DA method, the analysis value is obtained by minimizing the cost function. The cost function of ASUCA-Var is defined as follows:
where
Jb is a background term to measure the distance of the unknown model state from the background state,
Jo is an observation term to measure the distance of the unknown model state from the observations,
Jbc is a VarBC (
Dee 2004;
Cameron and Bell 2018) term to estimate observation bias, and
Jdf is a penalty term to reduce the gravity wave as noise using a digital filter (DF; e.g.,
Gustafsson 1992;
Lynch 1997;
Gauthier and Thépaut 2001;
Wee and Kuo 2004).
First, the background term Jb is given as follows:
where
x0 is the state vector at time
t0,
xb0 is the state vector of the first guess at time
t0,
B0 is the background error covariance matrix, and
t0 is the start time of assimilation window.
B0 is constructed assuming that the error distribution is Gaussian and is given as a positive definite symmetric matrix by prior statistics investigation (Subsection 2.7). In this study, we solve the problem under the assumption where
B−10 exists following the formulation of traditional variational methods and refer to
Ide et al. (1997) for notation.
Second, the observation term Jo measures the distance of the unknown model state from observations yio at observed time ti. An observation operator Hi to compute the model state corresponding to observation state at ti is described as follows:
where
Mi,0 is the nonlinear model operator based on ASUCA. The role of
Mi,0 is the time propagation from
x0 to
xi as follows:
Using those operators,
Jo is given as
where
P (
β) is observation bias,
Ri is the observation error covariance matrix, and [
t0,
tn ] is the range of the assimilation window.
Third, the VarBC term Jbc to estimate the observation bias is given as follows:
where
β is a control variable for bias correction,
βb is the first guess of
β, and
Bbc is the background error covariance matrix for VarBC. The VarBC is only applied to satellite observations in our operational system (see Subsection 2.5).
Finally, the penalty term Jdf is given as follows:
where
γk and
Bdf are weighting coefficients at the
k-th timestep (
k = 0, …,
N) and a diagonal matrix for DF, respectively; see Subsection 2.6.
b. Basic field update
Solving the problem of minimizing the linearized cost function yields the analysis value. By expanding the cost function around the basic field, the problem to be solved is transformed into a complete quadratic form, allowing for stable numerical calculations. In this study, the basic field refers to the trajectory of the model variables given by the nonlinear model in the model space. Because optimization is based on linear theory, it was not possible to incorporate the effects of nonlinear processes, but the basic field update (Trémolet 2008) alleviated this problem and allowed the effects of nonlinear processes to be included in optimization.
For the basic field update, the basic field at the first iteration is equal to the trajectory of the first guess. After minimizing the cost function to obtain the analysis value (inner loop), the basic field is recalculated from the analysis value using a nonlinear NWP model. The newly calculated basic field is used to re-linearize and minimize the cost function for the next iteration. This iterative updating and minimization of the basic field yields the final analysis value. Such cycles of the basic field computation and the inner loop are called the outer loop. The specific procedure of the basic field update in MA is explained in Section 3. Briefly, the outer loop is repeated thrice in MA. The first inner loop has 20 iterations, and the second and third inner loops have 15 iterations each. The basic field is updated twice at the connection of inner loops.
The cost function linearized around the j-th basic field based on Trémolet (2008) is defined as follows:
where
j is the number of iterations of the basic field update, and the number of iterations in inner loop is omitted to avoid complexity. For example, the basic field update with
j = 1 is conducted after the first 20 iterations. The details of the cost function will be described below. The
j-th increment
δx(j)0 is given as follows:
and the
j-th difference of the background is given as follows:
where
x(j)0 is the basic field at the
j-th update. Similarly, the increments for VarBC are defined as follows:
The basic field for the initial iteration
j = 1 is the same as the first guess
xg0 and
βg:
xg0 is given by the forecast from the previous analysis, and
βg is succeeded from the previous analysis.
The tangent-linear operators Hi(j), M(j)i,0, and P(j) are obtained by tangent linearizing the nonlinear operators Hi, Mi,0, and P around the basic field x(j-1)0 and β(j-1). The relationships of nonlinear operators and tangentlinear operators are written as follows:
where we ignore the second- and higher-order terms on the right-hand side. The matrix elements of the tangent-linear operators in
Eqs. (18)–
(20) are replaced by the basic field update. The
j-th innovation is given as follows:
using the nonlinear operators. In the incremental approach, the model operator used to calculate the cost function in the iteration is a low-resolution model
Mi,0, and
di {= y
oi −
Hi [
Mhi,0(x
g0)] −
P(
βg)} is an innovation estimated with a high-resolution model
Mhi,0, which is invariant in the optimization and independent of basic field updates. Additionally, the first guess (·)
g is used for the background state (·)
b.
The model operator in the DF term is linearized around the basic field. The weighted average of the basic field trajectory is given as follows:
and the perturbation around the basic field trajectory is given as follows:
where the tangent-linear operator for the DF is defined as follows:
Because of the limitation of computation time in operational runs, as mentioned earlier, the number of basic field updates in the MA was set to two, with the three-time inner loops (20, 15, and 15 iterations). For forecasting heavy rain events, which are greatly affected by nonlinear processes in NWP models, the accuracy can be improved if the number of basic field updates is increased.
2.2 Analysis variables
The elements selected for variational optimization are described as follows:
at assimilation window start time (
t = t0). The descriptions of these elements are given in the following list:
-
・u (m s−1), x axis wind component;
-
・v (m s−1), y axis wind component;
-
・Tg (K), soil temperature;
-
・Ps (Pa), surface pressure;
-
・θ (K), potential temperature;
-
・Wg (unitless), soil volumetric water content;
-
・µp (unitless), pseudo relative humidity.
is defined as
µp =
qv/
qbsat (
Dee and da Silva 2003), where
qv (kg kg
−1) is the mixing ratio of water vapor and
qbsat (kg kg
−1) is saturated water vapor fixed by the first guess value.
µp has a greater benefit compared with
qv, being closer to Gaussian-shaped error distributions. These elements are not the same as the prognostic variables in the forecast model. The prognostic variables of the model are derived from these analysis variables in
Eq. (25). However, both hydrometeors and vertical velocity are not included in the set of analysis variables and are initialized with the first guess values and 0 m s
−1, respectively, at the assimilation window start time.
The space to be optimized by data assimilation is discretized into cubic cells using the finite volume method, the same as ASUCA. The vector variables u and v are placed at the centers of the sides of the cell (u-point and v-point). Thus, they are staggered in the grid representation. The scalar variable is placed at the center of the cell (p-point), and its value is the cell average.
2.3 Background term
The background term measures the distance between the unknown model state and first guess as the background state. The distance is normalized by the background error covariance matrix B0, which is defined by the statistical error of the background state xb0 from the true state xt0 at t = t0. B0 is given as follows:
where ⟨·⟩ indicates the expectation value (e.g.,
Bannister 2008). The number of dimensions of the full
B0 is huge, approximately 10
9 × 10
9 as estimated based on the degrees of freedom of MSM, and it is difficult to practically calculate. By assuming that some variables are uncorrelated and making the background error covariance matrix sparse, the calculation cost can be significantly reduced. For simplicity, we omit the error correlations between some of the elements and divide
B0 into four blocks as follows:
where the background errors of
u and
v are independent of other elements, those of
Tg,
Ps, and
θ are assumed to be correlated, and those of
Wg and
µp are assumed to be correlated. In our system, the error correlation between the potential temperature and wind velocities is ignored because it is statistically smaller than the other error correlations. This assumption facilitates the modeling of error covariance and can reduce the computational cost of the optimization. The background error is estimated using the National Meteorological Center (NMC) method (
Parrish and Derber 1992). The NMC method estimates the background error using the difference between the 6-h forecast
xf (
t = 6 h) and 3-h forecast
xf (
t = 3 h) at the same valid time, as follows:
where
α is a scaling factor. The 3-h difference is due to the 3-h data assimilation window. In the actual calculation, both
xf (
t = 6 h) and
xf (
t = 3 h) are calculated using the same lateral-boundary condition. This method is called the lagged NMC method (
Široká et al. 2003) and eliminates the source of error that comes from the lateral-boundary condition. We assume that the vertical background error is independent of the horizontal background error. Horizontal background error correlations are independent between the
x and
y directions. The shape of the horizontal background error correlation is given in Gaussian form. The statistics data are taken as the 10th–19th of each month from March 2018 to February 2019. The background error was calculated separately for land and sea grid points and classified by 3-hourly local time.
The scaling factor α was adjusted to match the new background error variance with the previous operational variance at approximately 500 hPa, keeping a balance between background error and observation error. Figure 1 shows the variance profiles on land and sea grid points. Horizontal winds u and v have large variance inside the boundary layer at night on the land grid points and small variance during the daytime when vertical convection mixing is strong. Conversely, the variance of horizontal winds over the sea has negligible time dependency. The variance of ground temperature and potential temperature is large on the land grid point and small on the sea grid point. The bottom-level variances of Tg and Wg are 0 because the climate values are given as boundary conditions in the forecast model. Figure 2 shows the error correlation in the vertical direction corresponding to BTg, Ps, θ on land and sea. Because there is no Tg in the sea, the off-diagonal components of the vertical error correlation matrix associated with Tg are 0. Both on land and sea, Ps is negatively correlated with θ. Characteristically, in the lower atmosphere (e.g., the model levels from 1 to 5), the error correlation distance of θ in the vertical direction on land is larger than that on sea. The variance of pseudo relative humidity (RH) is smaller on the land grid point than that on the sea grid point (e.g., Fig. 1d). The few layers near the model top are damping layers to merge the parent model, and then, the growth of forecast error in those layers is suppressed. Consequently, the background error covariance around the model top reaches 0. Figure 3 shows the horizontal autocorrelation length of background error for each analysis element calculated using the lagged NMC method. The horizontal autocorrelation lengths are taken to be different in the x and y directions but are not classified by land, sea, or local time. One of the reasons we did not classify the horizontal autocorrelations in local time was that it did not improve the forecast accuracy.

The observation term measures the distance between the observation and model state. To compare the observation and model, the NWP model is integrated to the observation time using the model operator and observation is simulated using the observation operator. This section details the model and observation operators.
a. Model operator
The 4D-Var method iteratively runs the time integration of the NWP model during variational optimization, accounting for most of the computational cost. To reduce the calculation cost, an incremental method with the basic field updates (see Subsection 2.1b) is used, and it runs the time integration at low resolution. In the incremental method, the first guess is calculated using a high-resolution model to obtain the misfit with observation. Conversely, a low-resolution model is used in the iteration of the optimization calculation for minimizing the cost function.
ASUCA-Var uses the JMA nonhydrostatic model ASUCA as its non-linear model operator. Table 1 shows the ASUCA configuration as model operator for high and low resolution. The low-resolution model variants are classified as nonlinear (NL), tangent-linear (TL), which is a tangent form of the NL, and adjoint (AD), which is the transpose of the TL.

The high-resolution model is the same as the MSM. The grid spacing of the high-resolution model is 5 km, and the number of vertical layers is 76. The model's top height is approximately 22 km. The ground temperature is divided into eight layers, and soil volumetric water content is divided into two layers. The prognostic variables are as follows: ρ (kg m−3) is air density; ρu, ρv, and ρw (kg m−2 s−1) are the flux forms of (u, v, and w) wind components in Cartesian coordinates, respectively; ρθm (kg m−3 K) is the flux form of virtual moist potential temperature; ρqα (α = v, c, r, i, s, g) (kg m−3 kg kg−1) is the flux form of water vapor and hydrometeors; Tg is the soil temperature; and Wg is the soil volumetric water content.
The NL model is basically the same as the high-resolution model except for its low resolution and the convective parameterization. The horizontal grid spacing of the low-resolution model is 15 km, and the number of vertical layers is 38. The height of the model top is the same as that of the high-resolution model. The parameters of physics schemes (e.g., convective parameterization), which depend on the grid spacing, are modified to be suited for the 15 km grid spacing of the NL model.
The grid spacing and number of layers in the TL model are the same as in the NL. The dynamics in the TL model are linearized without simplifying the dynamics of the NL model. The physics schemes of the TL model are simplified to avoid severe linear approximation errors due to the strong nonlinearity of the NL model. Table 1 shows a summary of each scheme. The boundary layer scheme has a fixed diffusion coefficient of the background field. The surface process fixes the background bulk coefficients. Radiation has a very simple implementation based on Mahfouf (1999). The cloud microphysics process converts water vapor perturbations into precipitation perturbations through tangent-linearized saturation adjustment. Other elementary processes of cloud microphysics and convective parameterization are not linearized, and those perturbations are ignored.
Figure 4 shows the comparison between a NL perturbation, Mi,0 (xg0 + δx0) − Mi,0 (xg0), and TL perturbation, Mi,0 δx0, in the initial condition of MSM at 0000 UTC 7 July 2018. Figure 4a shows the integrated qv in the vertical direction in the background field. To compare the NL and the TL perturbations, the pseudo initial perturbation of qv is set at the 10th layer. The shape of the initial perturbation is Gaussian with the standard deviation of 7-grid/3-layer in horizontal/vertical direction, and the horizontal distribution of it is shown in Fig. 4b. There is no significant difference between the NL and TL perturbations of the water vapor field after the time integration of 3 h in the assimilation window [T − 3 h, T + 0 h] (Figs. 4c, d). However, the TL perturbations of precipitation are smaller than the NL perturbations, and particularly, the TL cannot predict well convective precipitation over the southern region of Japan (Figs. 4e, f). This difference in predicted perturbation is caused by the limitation of TL with simplified physical processes. This result also implies the necessity of the basic field update by NL.

The AD model is described by a code that is an exact transposition of the TL model code. The accuracy of the transposed code is required to satisfy the verification equation in a double-precision system as follows:
where the assimilation window
tn is 3 h.
b. Observation operator
The observation operator computes the model version of the observation, which is projected from the model state into the observation space. Table 2 shows the acronyms related to observations. Wind speed, temperature, and RH, as observed by radiosonde and SYNOP, are provided with spatial interpolation and diagnostic processes, transforming the model variables into observed variables. RH is given in the guide (World Meteorological Organization 2017, PART I Chapter 4) and is calculated as follows:
where
p (Pa) is the hydrostatic pressure,
qv is the specific humidity,
rv [=
qv (1 −
qv)
−1] is the mixing ratio,
Rd (= 287.05 J kg
−1 K
−1) is the gas constant for dry air,
Rv (= 461.5 J kg
−1 K
−1) is the gas constant for water vapor, and
esat (Pa) is the water-saturated water vapor pressure from Tetens formula (
Tetens 1930).
Surface observations (e.g., SYNOP, AMeDAS, and ASCAT) are assimilated using the observation operator based on the surface flux scheme (Beljaars and Holtslag 1991). Wind speed at 10 m altitude is given as follows:
where
z1 and
u1 are the altitude and wind speed at the bottom layer of the model's atmosphere,
z10m and
u10m are the altitude and wind speed at 10 m from the surface, and
Cm (·) is the momentum bulk coefficient (
Beljaars and Holtslag 1991).
The temperature at 1.5 m is calculated from the potential temperature at 1.5 m and the surface pressure. The potential temperature and specific humidity at 1.5 m are given as follows:
where
θ1 and
qv1 are the potential temperature and specific humidity at the bottom layer of the model's atmosphere.
θs,
Tg,skin,
πs,
qvs,
qsat,s,
β, and
Wg are the potential temperature, ground temperature, Exner function, specific humidity, saturated specific humidity, evaporation rate, and volumetric soil moisture content at the model's skin layer.
Ch (·) and
Cq (·) are the heating and latent heating bulk coefficient (
Beljaars and Holtslag 1991). The surface grid for calculating the meteorological elements of the earth's surface has land tiles and sea tiles. The surface flux
F depends on the type of those surfaces and is given by
where
Csea is the covered rate of sea and
Fland (
Fsea) is surface flux from the land (sea) in the inner model. The effects from surface observations along the coastline are weighted based on
Csea in the adjoint operator.
Doppler velocities observed using Doppler radar are simulated by only the horizontal wind component of air. As shown in Ishikawa and Koizumi (2006), only low elevation scans below 5.9° are used for assimilation, so the contributions of hydrometeors and vertical velocity of air to Doppler velocities are ignored for simplification. The Doppler velocity Vr (m s−1) at altitude z (m) is as follows:
where
uk, vk, and
zk are the
x direction wind component,
y direction wind component, and altitude at the model's
k-th layer, respectively;
nz is the number of model layers;
d (m) is the distance from the radar site; and
δφ (= 0.3°) is the beam width of the antenna pattern. Additionally, radar reflectivity is assimilated as RH derived from it using the One-dimensional Maximum Likelihood Estimation (1D-MLE)+4D-Var method (
Ikuta and Honda 2011;
Ikuta et al. 2021).
Model PWV is obtained by integrating the mass of water vapor from the surface to the top model layer ztop as follows:
where
ρ is air density. Ground-based GNSS observations widely deployed in Japan have been assimilated for PWV (
Ishikawa 2010).
The Radar/Raingauge-Analyzed Precipitation (R/A; Nagata 2011) and precipitation retrievals from satellite data are assimilated as the amount of 1 h accumulation in MA. Only precipitation observations above 0.5 mm h−1 are used, and no-precipitation information is not used. The observation error and probability density function (PDF) for precipitation observations are defined as in Koizumi et al. (2005), and the observation term for precipitation in the cost function is approximated in quadratic form as follows:
The R/A assimilation is used with the inflation factor
rinf = 1 and the asymmetricity factor
rasy = 3. The precipitation retrievals from satellite data are assimilated with
rinf = 2 and
rasy = 5.
ŷprc and
ŷoprc are variables modified from the 1 h accumulated precipitation from the forecast
yprc (mm h
−1) and observed
yoprc (mm h
−1) as described below. Originally, this formulation was applied to the original precipitation values
yprc and
yoprc, but it was very sensitive to rain intensity and PDF of the observation error remained non-Gaussian, which negatively affected the accuracy of the predictions. Therefore,
yprc was converted to the new variable
ŷprc in a manner similar to the Box–Cox transformation (
Box and Cox 1964) method:
where
λ = 1/3. This parameter was determined through trial and error to improve the forecast accuracy.
ŷoprc is calculated from
yoprc in the same way as
ŷprc.
Brightness temperatures of satellite observations are simulated using Radiative Transfer for TOVS (RTTOV; Saunders et al. 2018) and have been assimilated as clear sky radiance (Kazumori 2014; Ikuta 2017a). Refractivity is simulated from GNSS radio occultation measurements using ROPP (Radio Occultation Processing Package: Radio Occultation Meteorology Satellite Application Facility 2019) and has been assimilated in MA (Hirahara et al. 2017). These external simulators are integrated in a common interface of ASUCA-Var's observation operators. By packaging the external simulators in this way, their version dependence in the DA core is reduced and development efficiency is improved.
c. Variational quality control
Some observations are subject to variational quality control (VarQC: Andersson and Järvinen 1999). In MA, the VarQC covers radiosonde, wind profiler (WPR), and aircraft observations (Yoshimoto 2010). A VarQC PDF is defined as a mixture of normally distributed (N) and uniformly distributed (F) PDFs as follows. F derived from gross error is given by
where
σo is the standard deviation of a single observation error that is the subject of VarQC; 2
dσo is a range of possible observation values, and
d is a parameter that determines the range. The mixed PDF
pQC comprising
N and
F is defined as follows:
where
pg is the rate at which gross errors occur and
Jo is an observation term of the cost function for a single observation. The observation term of the cost function based on
pQC is written as follows:
The gradient of
JQC is given as follows:
where

is called VarQC weight.
Figure 5 shows
Jo,
JQC, ▽
Jo, and ▽
JQC. For large innovation values, ▽
JQC approaches 0, and the observation impact is lost. The observation term for wind observation is described as follows:
where
u is the
x direction wind velocity,
Juo is an observation term,
pug is the gross error occurrence rate, and
du is the coefficient that determines the observable range. Variables with the subscript
v, which is
y direction wind, are defined in the same way. The allocation of costs shared by
u and
v is given as follows:
VarQC is enabled from the first iteration in the optimization. Therefore, outliers are invalidated at the first iteration. However, as the current system assimilates a wide variety of observations, the analysis increment is calculated by assimilating observations other than outliers. Then, the cost function is minimized, and basic field is updated. The basic field update changes the VarQC weight in
Eq. (50). If the VarQC weight of an observation that was an outlier in the first iteration is increased after the basic field updates, the observation has a chance of recovering to effective observation.
2.5 Variational bias correction term
The VarBC method in our system is used to correct for the satellite brightness temperature bias. The brightness temperature bias in the clear sky region is estimated by several predictor variables. The predictors are defined as follows:
-
・p1, constant (= 1);
-
・p2, function of sea surface temperature Tsst (K) at scan position;
-
・p3, function of satellite angle θsat (rad);
-
・p4, function of orbit flag lorbit.
These predictors are determined with reference to
Sato (2007), and the form of the functions are shown below in
Eqs. (56)–
(58). To simplify the discussion, we consider the case where there is only
k-th observation to which VarBC is applied. The bias in this case is given as follows:
where
Np (= 4) is the number of predictors and the subscript
l (
k) indicates the subset to which the
k-th observation belongs. Specifically, the subset is grouped by satellite, sensor, and channel. The predictors corresponding to
k-th observation are defined as follows:
where
Tsst, k,
θsat, k, and
lorbit, k are the values corresponding to the
k-th observation. These predictors can only be derived from observation information and are independent of the forecast model because
Tsst is fixed in the JMA regional forecast model. Thus, the bias corresponding to the predictors is corrected, although TL and AD of the predictors are not required in the calculation of the cost function gradient.
The VarBC background error is defined by the method of Cameron and Bell (2018) as follows:
where
σo is the observation error,
mavg is the average number of observations assimilated during the last 3 days,
mmin is a lower limit of the number of observations, and
n is a parameter that specifies the bias halving time for the convergence of coefficient learning. The halving time parameter of the MA was set as
n = 8 and that of the LA was set as
n = 24. These halving time parameters were determined based on the number of assimilations per day for each system (
Fig. 6). By setting these halving-times, the rapid fluctuation of the coefficients calms down in approximately 10 days in an experiment that starts with the VarBC coefficients of all satellites as 0. Such insensitivity is necessary to reduce the effects of sudden outliers of observation. We can slow down the response of background error to the presence or absence of observations in the assimilation window by using the average number of observations. This is especially useful for the assimilation of polar-orbiting satellites in a regional model where the forecast domain is limited. In a regional model, a polar-orbiting satellite is only available twice a day; therefore, it is not appropriate to determine
Bbc depending only on the number of observations assimilated in a single previous analysis. However, by using
mavg, we can maintain a history of approximately 3 days to provide a stable bias correction for observations that are less frequently revisited.

The old MA that was in operation until March 25, 2020, did not use VarBC but instead used the VarBC coefficients of the Global DA System (Kazumori 2014). The commonality of bias correction coefficients between models with completely different resolution and physical processes is not necessarily validated and cannot correct for bias well. For example, Benáček and Mile (2019) demonstrated the effectiveness of VarBC in a regional model by comparing bias correction with VarBC coefficients by global DA and those by the limited-area model DA. At the JMA, the clear sky brightness temperature assimilation and VarBC for the LA were introduced simultaneously (Ikuta 2017a). In the MA, VarBC was introduced at the same time as the introduction of ASUCA-Var (Ikuta et al. 2020). It is shown in Subsection 4.2 that bias correction accuracy is greatly improved by using the MA VarBC.
2.6 Penalty term
The predictions of the NWP model from initial conditions, comprising the first guess plus an increment, will cause high-frequency oscillations due to artificial gravity waves. We implemented a DF method (Lynch 1997) with a low-pass filter as a constraint to remove these oscillations. In this DF method, the noise in the center of the assimilation window is removed by a filter using the Chebyshev window function. DF using the Chebyshev window function has been applied in several 4D-Var systems (e.g., Gustafsson 1992; Polavarapu et al. 2000; Gauthier and Thépaut 2001), including the previous MA based on JNoVA (Honda and Sawada 2010; Sawada and Honda 2008). The elements to be filtered, based on Wee and Kuo (2004), are the same as those of the background error variance. Bdf in Eq. (7) was calculated using the diagonal component of the background error B0 as follows:
where
λ is the weighting parameter. The time span for the low-pass filter is described as
Ts =
MΔ
t, with timestep Δ
t of time integration and
M related to the number of total steps as
N = 2
M + 1. The filtered state at
N/2 is given as follows:
where
αk is defined as follows:
and the Dolph–Chebyshev window function is given by
where 1/
x0 = cos (
θs/2), 1/
r = cosh (2
M cosh
−1 x0),
θm = 2
πm/N, θc is the cutoff frequency,
θs is the stopband edge, and
T2M is the Chebyshev polynomial of degree 2
M:
The high-frequency oscillations that will be filtered out are defined as follows:
where the coefficient
γk is given as follows:
In the operational system, the assimilated observations are used under strict quality control. Additionally, the density of the atmosphere at the beginning of the time integration is built based on the hydrostatic assumption. Thus, the noise caused by the large oscillation of artificial gravity waves is considerably suppressed. Particularly, in an ongoing assimilation cycle, the cost of the penalty term is kept small compared with the cost of other terms because ASUCA eliminates the generation of artificial noise as much as possible.
2.7 Preconditioning
a. Control variables
A simplification is applied to the background term by transforming the analysis variables into control variables to solve the optimization problem efficiently. The analysis increment δx0 is described by the analysis variable x0 and background variable xb0 as follows:
The control variable
χ is given as follows:
where
B1/20 is the square root of the background error covariance matrix and
χ0 is the control variable for the model state.
B1/2bc and
χbc are the square root of the covariance matrix and control variable for VarBC. The transformed
χ is a dimensionless quantity and each component is uncorrelated. This transformation into control variables is called preconditioning, which makes it unnecessary to calculate the inverse of the background error covariance matrix.
The calculation is further simplified by assuming that vertical and horizontal background errors are independent. We define B1/20, decomposed into horizontal and vertical directions, as follows:
where
B1/2v is the square root of the vertical error covariance matrix,
C1/2h is the square root of the horizontal error correlation matrix, and
V is a transformation matrix of the vertical coordinate.
C1/2h is an isotropic recursive filter (RF) (Purser et al. 2003) that acts as a self-adjoint quasi-Gaussian filter. The RF is applied in the x direction and then in the y direction. Defining the operations in the x direction as C1/2hx and the operations in the y direction as C1/2hy, C1/2h can be written as follows:
First, we focus on the operations in the
x direction. As the same operation is performed in the
y direction, we do not describe it. Assuming the correlation distance is horizontally uniform,
C−1/2hx can be Cholesky decomposed as
C−1/2hx =
UTU, and this inverse matrix can be written as follows:
where
U is an upper triangular matrix. With any input vector
p, intermediate vector
q, and output vector
s, the operations of
U−1 (
UT)
−1 can be described by two separate calculations as follows:
These equations can be rewritten as follows:
where
β = 1/
Ui,i and
αj = −
Ui,i+ j/β. In the recurrence formulas
Eqs. (78),
(79),
qi is calculated from
pi in the
x direction where
i increases and
si is calculated from
qi in the
x direction where
i decreases. The order of the RF n is set to 4. For a finite domain RF, boundary conditions must be set appropriately. The boundary condition in a finite domain
i ∈ [1,
N] is given as follows:
where
L̂ is a lower triangular
n × n matrix, of which the elements are
L̂i,i = 1 and
L̂i+j,i = −
αj;
Û is an upper triangular
n × n matrix, of which the elements are
Ûi,i+j = −
αn−j.
ŝN is a subvector of
s and defined as
ŝN = (s
N+1−n, …,
sN)
T.
q̂N is a subvector of
q in the same way as
ŝN. In the operational system,
αj and
β are precomputed assuming twice the number of grids in
x and
y direction of actual analysis area, and only components in the effective area are extracted and used. This preparation suppresses postfiltering distortion near the boundary. For example, without the preparation for boundary condition of RF, analysis increments near the boundary are excessively suppressed.
The square root of the vertical background error covariance matrix is given as follows:
where Λ
v is the diagonal matrix whose elements are the eigenvalues of
Bv and
Uv is the orthogonal matrix composed of the eigenvectors of
Bv. The model's vertical coordinate is the terrain following coordinate. Conversely, the control variables are located in a vertical coordinate system that is less dependent on terrain. In
Eq. (73),
V is the transformation matrix of the vertical coordinate for the control variable to the model's vertical coordinate, as in
Fujita (2010) and
Fukuda et al. (2011). In ASUCA-Var,
V is defined for each
u-, v-, and
p-point where the control variables are located.
Figure 7 shows the impact of the transformation of the vertical coordinate. By using the transformation, the analysis increments distorted along the terrain are better eliminated than in the case without using it.
b. Parameter transformation
The initial perturbation of the TL model is created by a parameter transformation from the analysis increment δx0 = (δu, δv, δTg, δPs, δθ, δWg, δµp)T to a perturbation of the prognostic variables of the NWP model. Conversion to perturbation for the mixing ratio is described from the analysis increment of pseudo RH as follows:
where
Qµp is Jacobean. The moist potential temperature
θm is given as follows:
where
i indicates the kind of hydrometeors: cloud water, rain, cloud ice, snow, or graupel. The perturbation of
θm is given as follows:
where the perturbation of the mixing ratio for hydrometeors is ignored because the mixing ratios are not analysis variables. The Exner function
π at altitude
z (m) is determined from the surface pressure
Ps (Pa) at the surface altitude
zs (m) and the moist potential temperature
θm (K) based on hydrostatic balance, as follows:
where
P00 = 100 000 Pa,
Rd is the gas constant,
cp (= 7/2
Rd) is the heat capacity for dry air at constant pressure, and
g (= 9.80665 m s
−2) is gravity acceleration. Air density is calculated from the Exner function and the moist potential temperature:
The perturbation of density is given as follows:
The transformation matrix from analysis variables to prognostic variables is written as follows:
δTg and
δWg are assumed to be uncorrelated with each other and are transformed by identity matrix
I. The flux of a scalar variable that ignores perturbations is written as follows:
where
α includes the mixing ratios of hydrometeors and turbulent kinetic energy. The left sides of
Eqs. (93),
(94) are the initial perturbations of prognostic elements of the TL model.
c. Perfect quadratic form of the cost function
The cost function is rewritten in a perfect quadratic form
where
The modified innovation of observation
d̃(j)i is given as follows:
The modified innovation of DF
g̃(j) is given as follows:
The gradient of the cost function is given as follows:
The optimized control variable
χa is given as follows:
This minimization problem is solved using the limited-memory Broyden–Fletcher–Goldfarba–Shanno (LBFGS) quasi-Newton minimization method algorithm (
Nocedal 1980;
Liu and Nocedal 1989).
χa is converted into the analysis variables
xa0 and
βa at the start time of the assimilation window:
In MA, the assimilation window is 3 h; thus, the model creates an initial condition of the forecast model at analysis time
tn:
2.8 Coding design
One of the issues in developing and continuing to operate 4D-Var is that the model operators used in the forecast model and assimilation will deviate as development progresses. To prevent this, NL, TL, and AD coexist in one subroutine for the purpose of sustainable development. The switching of NL, TL, and AD modes is specified by an input parameter and a conditional statement. The subroutine arguments and return values are shared by NL, TL, and AD modes. This rule will force a change in TL and AD if NL is changed, that is, the dynamics subroutines, physics library, and observation operator libraries contain NL, TL, and AD code for assimilation.
Figure 8 shows the structure of ASUCA-Var, which comprises an assimilation core to perform optimization and preconditioning, ASUCA as NWP model to perform time integration, a physics library to compute physical processes, and observation operators to simulate observations. All observation operators are archived in the observation operator library. The observation operators included in the library are used via the ASUCA-Var common interface. When implementing an observation operator library developed by other developers, the common interface facilitates new implementations and updates and minimizes changes to existing code. In the operational system, RTTOV and ROPP have been implemented.
2.9 Parallelization
The data assimilation system is envisioned to run in a hybrid environment of message passing interface (MPI) and open multiprocessing (OpenMP). The data assimilation region is decomposed into blocks in two dimensions, each of which is processed by a different MPI process. In the following, the two-dimensional decomposed region is called a block. Observations are also arranged and processed in parallel for each of those blocks. The spatial-horizontal do-loops in that block are forked via OpenMP parallelization.
The RF method used in preconditioning is also parallelized in each block. The calculation of RF in the x direction must be sequential but independent in the y direction, so it is parallelized in the y direction. The RF in the y direction is similarly parallelized in the x direction.
In the adjoint codes for advection and the pressure tendency equation, conflicts occur when applying spatial-horizontal OpenMP parallelization without any special treatment because the adjoint variables are added to the neighboring grid points of the target grid point. To avoid this conflict, the adjoint code is parallelized by the multi-color successive over-relaxation (SOR) method (Adams and Ortega 1982). The Red-Black SOR method is used when adding to one adjacent grid point. When adding to the adjacent five grid points (or nine grid points), parallelization was performed via the five-color (nine-color) SOR method. The adjoint equations, which require the use of Red-Black, five-color, and nine-color SOR methods, are given as follows:
where
qi,j represents an arbitrary variable and the subscripts
i and
j denote the grid numbers. The optimization algorithm is also parallelized. In the computation of cost function minimization, computational efficiency is improved by calculating the inner product of the general vector, which is the input of the L-BFGS, in each block.
4. Performance
4.1 Degrees of freedom for signal
Using degrees of freedom for signal (DFS: Cardinali et al. 2004) based on Chapnik et al. (2006), we show the impact of assimilated observations on MA. The DFS, divided into subsets for each observation type, is defined as follows:
where Π
ok is a projection operator onto the
k-th subset. The actual calculation method is as follows. First, the perturbation of the observation vector with vector length
p using the random vector
ζ ∼
N (0,
Ip) is given as follows:
In practice, using this observed perturbation, DFS is calculated as follows:
where subscript
k indicates the subset for each observation type.
Figure 12a shows the DFS based on observation type. The statistical period is from 0000 UTC 13 June 2018 to 2100 UTC 23 July 2018. We can see that the Doppler velocity and Rain observations have a significant impact. Among the satellite observations, Himawari's AHI, precipitation estimated from microwaves, and RH estimated from GPM/DPR have a large impact. The combined DFS of each satellite accounts for approximately 30 % of the total DFS. Although various observations are assimilated, it is clear that satellite observations contribute to create the initial conditions for the MSM.
Figure 12b shows the DFS per observation (DFS/p). It can be seen that
in situ observations, such as radiosonde and aircraft observations, have a large impact per observation. Focusing on remote sensing observations, the DFS/p of satellite observations and those of Doppler velocity observations are relatively small, and that of DPR is large. Because the brightness temperature of satellite and the Doppler velocity have huge number of observations, the impact per observation is not large. Conversely, the number of observations of DPR is not as large as those observations. Additionally, DPR is assimilated as a RH profile (
Ikuta et al. 2021), which has 3D information of water vapor in the precipitation system. Especially over the ocean, because such RH profiles are unique in our system, the DPR has a relatively large impact per observation compared with other observational data. For example, in the Météo-France regional DA system,
Brousseau et al. (2014) showed that radar DFS is large and radiosonde DFS/p is relatively large, which is similar to our DA system.
4.2 Analysis forecast cycle
a. JNoVA and ASUCA-Var
To compare the performance of JNoVA and ASUCA-Var, with a particular focus on MA, an experiment was conducted using the mesoscale NWP system. The JNoVA experiment uses JNoVA as the data assimilation system. The setup of JNoVA is described in Section 2 of the outline of NWP at JMA (Japan Meteorological Agency 2019). The ASUCA-Var experiment uses ASUCA-Var as the data assimilation system. The forecast model for both experiments was ASUCA, MSM2003 (Ikuta et al. 2020) version.
The major differences between JNoVA and ASUCA-Var are presented in Table 3. The analysis variables of ASUCA-Var are the analysis variables of JNoVA with the addition of the underground elements Tg and Wg (see Subsection 2.2). Bv of JNoVA is independent of location and time, whereas Bv of ASUCA-Var depends on the initial time and surface type (see Subsection 2.3). The same Bh is used for both; however, JNoVA uses Cholesky decomposition and ASUCA-Var uses the RF (see Subsection 2.7a). The model operators used as strong constraints are JMA-NHM in JNoVA and ASUCA in ASUCA-Var. NL is used for the forward calculation method in the inner loop of JNoVA and TL is used in ASUCA-Var. The maximum number of iterations to find the minimum of cost function in JNoVA is 35, and the total number of iterations for ASUCA-Var is 50-time. The breakdown of the number of iterations for ASUCA-Var is as described in Subsection 3.1a. For parallel computation, JNoVA divides the domain into one-dimensional strips, whereas ASUCA-Var divides the domain into two-dimensional blocks (see Subsection 2.9).

The experimental periods are 18 June to 23 July 2018; and 23 December 2018, to 27 January 2019. The JNoVA and ASUCA-Var experiments assimilate the same kind of observations. However, the treatment of observations, such as VarQC and VarBC, is different. Figure 13 shows the number of assimilated observation related to VarQC and VarBC at each initial time in JNoVA and ASUCA-Var experiments. Figure 13a shows conventional observations which have VarQC weight larger than 0.25. In Fig. 13a, the reason why there are more observations at 0300 UTC than at other initial times is that there are more radiosonde and aircraft observations, and the reason why there are fewer observations at 1800–2100 UTC is that those initial times are late at night in local time; thus, the number of aircraft observations is few. Figure 13b shows the number of observations of TB for satellite observations with VarBC in the ASUCA-Var experiment and without VarBC in the JNoVA experiment. At 0000 UTC and 1200 UTC, the number of observations is larger than other initial times because the NOAA and DMSP satellites cover the analysis region regularly. For both the conventional observation with VarQC and satellite observations related VarBC, the number of assimilated observations in the ASUCA-Var is slightly higher than the number of assimilated observations in the JNoVA, but the difference is small compared with the overall number of assimilated observations.

In the JNoVA experiment, satellite brightness temperature uses the variational bias correction coefficient of the global data assimilation system, which provides the initial condition for the global model at JMA. Conversely, in the ASUCA-Var experiment satellite observation bias is corrected based on the VarBC of MA. Figure 14 shows a boxplot of the observed brightness temperature minus the first guess of brightness temperature. The observations shown in Fig. 14 are GPM/GMI, Metop-B/MHS, Metop-B/AMSU-A, and Himawari-8/AHI. The channels 3, 5, 12 and 13 of GMI without bias correction have large bias; however, JNoVA and ASUCA-Var correct the bias successfully. In JNoVA, the channels 6 and 8 of GMI (Fig. 14a), channels 3–5 of Metop-B/MHS (Fig. 14b), channels 6–7 of Metop-B/AMSUA (Fig. 14c), and channels 2–3 of Himawari-8/AHI (Fig. 14d) have larger bias than uncorrected observation. However, all of them are very well corrected in ASUCA-Var. From the above, in the JNoVA experiment, the brightness temperature bias is not fully corrected, and the divergence of the bias correction factor from the global analysis is the cause of bias in some channels. Conversely, in the ASUCA-Var experiment, bias is corrected as expected based on the VarBC.

The impact on the forecast is shown next. Figure 15 shows the bias score and equitable threat score (ETS) of the 3-h accumulated precipitation forecast against R/A. These scores are averaged over the lead time of 3–39 h. In the summer experiment from 0000 UTC 18 Jun 2018 to 2100 UTC 23 July 2018, the bias scores under the threshold 5 mm in JNoVA experiment indicates overprediction (Fig. 15a); however, the ASUCA-Var experiment significantly improves such overprediction (Fig. 15b). In Fig. 15c, the difference of ETS shows significant improvement in ASUCA-Var at all thresholds. In the winter experiment from 0000 UTC 23 December 2017 to 2100 UTC 27 January 2018, the difference of ETS indicates that the precipitation forecast in ASUCA-Var experiment is significantly improved under the threshold of 5 mm (Fig. 15f).

Figure 16 shows the results of the verification of 3-h accumulated precipitation using Fractions Skill Score (FSS; Roberts and Lean 2008). FSS is a scale-dependent score, and verification using FSS is expected to reduce misleading influence due to double penalty (Gilleland et al. 2009). The ASUCA-Var experiment in the summer period showed that precipitation forecasts at threshold of 1 mm were significantly worse at spatial scales of approximately 300 km but were significantly better at spatial scales under approximately 100 km (Fig. 16a). At the threshold of 5 mm, the precipitation forecast of ASUCA-Var experiment improved significantly at a spatial scale under approximately 100 km (Fig. 16b). Additionally, over the threshold of 10 mm, FSS shows that ASUCA-Var experiment is improved significantly at all spatial scales (Figs. 16c–e). In the winter period, the ASUCA-Var experiment is significantly improved at all scales under the threshold of 30 mm (Figs. 16f–i).

The accuracy of the precipitation forecast was verified by using the improvement ratio of ETS, defined as follows:
where ⟨·⟩ denotes the mean and
fci (·) denotes the 95 % confidence interval.
fci was obtained by the block bootstrap method, and ETS was obtained using R/A as the reference value.
Forecast against radiosonde and SYNOP were verified by the improvement ratio using the root mean square error (RMSE). Note that most of these observations were assimilated in MA. The indices are given by
In
Eqs. (121),
(122), the coefficient 2 is a scaling factor that simply sets the significance value to ±1. If these indicators are greater (smaller) than or equal to 1, they indicate statistically significant improvement (deterioration).
Figures 17a and 17b show the indexes in summer and winter experiments. Verified elements are 3-h accumulated precipitation; specific humidity, temperature, wind speed, and geopotential height of radiosonde; and screen-level specific humidity at an altitude 1.5 m; screen-level temperature at an altitude 1.5 m; screen-level wind speed at an altitude 10 m; surface pressure; and solar radiation.

First, in summer period (Fig. 17a), precipitation prediction was improved in the ASUCA-Var experiment. Specific humidity of lower troposphere (925–850 hPa) was degraded in some parts of the initial time, but there was no significant degradation in the almost all lead times of forecast. Temperature, wind speed, and geopotential height were improved at almost all times. Surface pressure, screen-level specific humidity, screen-level temperature, screen-level wind speed, and solar radiation have improved also in almost all lead times. The reason for the difference in the sensitivity of specific humidity between the screen-level and the lower-atmosphere is that the screen level is more affected by the underground control variables that are newly added in ASUCA-Var. Next, in winter period (Fig. 17b), indices of precipitation forecasts are improved mainly under the threshold of 5 mm and after T+24h. The improvement in precipitation forecast is greater in summer than in winter. Specific humidity at upper troposphere (200 hPa) was degraded in some lead times of forecast; however, that of lower troposphere was improved. The improvement in forecast accuracy for tropospheric temperature, wind speed, and geopotential height is greater in winter than in summer. Surface pressure, screen-level specific humidity, screen-level temperature, and solar radiation have improved in winter. The screen-level wind speed was improved at the initial time and was worsened afterward. Consequently, the absolute value of wind speed RMSE became larger.
The performance of 4D-Var, with the model as a strong constraint, naturally also depends on the characteristics of the model's performance. Thus, the improvement in prediction shown here is due to not only the enhancement of data assimilation methods, such as the newly added control variables, background errors, and VarBC, but also in no small part to differences between the inner and outer models.
























































 is called VarQC weight. Figure 5 shows Jo, JQC, ▽Jo, and ▽JQC. For large innovation values, ▽JQC approaches 0, and the observation impact is lost. The observation term for wind observation is described as follows:
is called VarQC weight. Figure 5 shows Jo, JQC, ▽Jo, and ▽JQC. For large innovation values, ▽JQC approaches 0, and the observation impact is lost. The observation term for wind observation is described as follows: