A weak coherence theorem and remarks to the Oka theory

Abstract

The proofs of K. Oka's Coherence Theorems are based on Weierstrass' Preparation (division) Theorem. Here we formulate and prove a Weak Coherence Theorem without using Weierstrass' Preparation Theorem, but only with power series expansions: The proof is almost of linear algebra. Nevertheless, this simple Weak Coherence Theorem suffices to give other proofs of the Approximation, Cousin I/II, and Levi's (Hartogs' Inverse) Problems even in simpler ways than those known, as far as the domains are non-singular; they constitute the main basic part of the theory of several complex variables.

The new approach enables us to complete the proofs of those problems in quite an elementary way without Weierstrass' Preparation Theorem or the cohomology theory of Cartan-Serre, nor L²-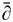 method of Hörmander.

We will also recall some new historical facts that Levi's (Hartogs' Inverse) Problem of general dimension n ≥ 2 was, in fact, solved by K. Oka in 1943 (unpublished) and by S. Hitotsumatsu in 1949 (published in Japanese), whereas it has been usually recognized as proved by K. Oka 1953, by H. J. Bremermann and by F. Norguet 1954, independently.