概要

液体に強力な超音波を照射すると，超音波キャビテーションと呼ばれる気泡の生成，成長，圧壊を伴う流動現象が生じる．気泡が圧壊する際に，局所的かつ瞬間的な高温高圧場や衝撃波が生じるが，これらの作用は洗浄や加工，化学反応の促進など，広く工業的に応用されている．超音波キャビテーションは工学的に極めて重要な研究課題であるが，強い非平衡状態であることと，キャビテーション場がミクロスケールとマクロスケールを介在することなどが，その解析を極めて困難にしている．本稿では，分子動力学シミュレーションによる超音波キャビテーションの解析を紹介する．

1　 はじめに

人間の声や楽器から聞こえてくる音など，空気中を伝わる音波は日常生活で馴染みのある物理現象である．個人差はあるが，一般的な人間の声域は100–1000 Hz，可聴域は20–20 000 Hzである．周波数が20 kHzを超える音波は超音波と呼ばれる．超音波は人間の耳では聴くことができないが，分解能が優れていることや指向性が鋭いことなどの特徴を持つため様々な分野で利用されている．例えば，魚群探知機や医療診断などの通信的な利用や，洗浄や加工などの動力的な利用が挙げられる．また，気体，液体，固体の様々な媒質を伝播するため，極めて幅広い分野で応用されている．

超音波を液体に照射すると，疎密波の伝播により気泡が生成することがある．この現象は超音波キャビテーションと呼ばれる．強力な超音波を用いた場合，気泡が圧壊することがあるが，その際，衝撃波や高温高圧場が発生し，ジェットや熱分解反応，ラジカル反応などの作用が生じることが知られている［1,2］．これらの作用は局所的かつ瞬間的なものであり，周囲の環境への影響は少ないため，安全性が高く環境負荷の低い技術として，食品，医療，バイオ，化学など，極めて幅広い分野に応用されている．しかしながら，超音波キャビテーションは非平衡下で多数の気泡が生成，成長，消滅を繰り返す極めて複雑な現象のため，そのメカニズムは十分な理解に至っていない．

超音波ホーンを用いた実験により，水中では発生した気泡のダイナミクスや，音場の特性が調べられてきた［3,4］．ホーンの形状や直径，振動数や振幅，液体の性質など様々な要因がキャビテーションの形態や音場に影響を及ぼすことが知られている．特に，気泡が超音波ホーン近傍で円錐状に分布する場合，円錐内部の化学活性が高いことは興味深い実験事実である［5,6］．工学応用上，こうしたキャビテーションの作用を高効率的に得る手法の開発が望まれている．そのためには，気泡が発生する領域を増やせばいいのであるが，気泡自身が超音波に対しては障害物となるため，単純な手法では上手くいかないというのが現状である．そのため，例えば，ホーンの近くにチャネルを配置して効率的なキャビテーション場を生成する手法などが研究されている［7］．

超音波キャビテーションを理解する上で，気泡を含む液体（気泡性液体）の音波物性を理解することは本質的である．気泡性液体は通常の液体では見られない分散性などの異常を示すことが実験的に知られている［9］．気泡性液体中の音波伝搬に関する理論研究も展開されており，超音波ホーンを用いた実験への適用なども行われている［10,11］．しかし，相転移を伴う気泡の初生過程，気液界面からの熱や物質の移動，気泡間相互作用，気泡の形状や分布の影響など未解明な部分が多くある．これらの影響の解明には，ミクロスケールの相転移ダイナミクスと，マクロスケールの音場を同時に解く数値解析手法が必須である．

著者らは分子動力学（MD）シミュレーションによる複雑流体中のカルマン渦の解析を行ってきた［8］．MDシミュレーションによる流体解析では，膨大な計算コストを代償に，分子スケールからの直接的な解析を行うことができる．本研究では，超大規模なMDシミュレーションにより超音波キャビテーションを分子スケールから解析することを目指している．本稿では，その実現に向けて著者らが取り組んできた音波解析の概要を述べる［12,13］．最後に，スーパーコンピュータ富岳を用いた超音波キャビテーションのMDシミュレーションの実現可能性に関して触れる．

2　 単純流体中の音波伝搬[12]

MDシミュレーションで超音波キャビテーションを解析するにあたり，そもそも，「MDシミュレーションで音波を扱えるのだろうか？」という疑問が生じる．意外なことに，単純流体中を伝搬する音波でさえ，その検証は行われていなかった．音波のシミュレーション自体は行われているが，衝撃波や希薄気体中の音波など［14,15］，流体力学では扱いにくい系に対する限定的なものであった．そこで，ニュートン流体中を伝播する音波の解析を，MDシミュレーションと流体力学計算でそれぞれ独立に行い，音波解析への適用性について検証を行った．

ニュートン流体は，分子シミュレーションでは標準的に用いられるLennard-Jones（LJ）流体でモデル化する．LJ流体は単原子分子で構成される流体であり，分子間のポテンシャル関数$\varphi$は次式で与えられる：

  

$$\varphi \left(r\right)=\{\begin{array}{cc}\hfill {\varphi }_0\left(r\right)-{\varphi }_0\left(r_{\mathrm{c}}\right)-{{\varphi }^{\prime }}_0\left(r_{\mathrm{c}}\right)(r-r_{\mathrm{c}})\hfill & \hfill (r\le r_{\mathrm{c}})\hfill \\ 0\hfill & \hfill (r>r_{\mathrm{c}})\hfill \end{array},$$(1)

  

$${\varphi }_0\left(r\right)=4ϵ[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6].$$(2)

ここで，$r$は分子間距離であり，$r_{\mathrm{c}}$はポテンシャル関数の切断距離である．ここでは$r_{\mathrm{c}}=2.5\sigma$とする．$ϵ$と$\sigma$はそれぞれLJ系に特徴的なエネルギーと長さのスケールを表す．プライムは$r$に関する微分を表す．以下では，全ての物理量の単位を$ϵ$，$\sigma$，及び分子質量$m$とする．時間の単位は$\sigma \sqrt{m/ϵ}$である．

図1にMDシミュレーションで用いるシミュレーションセルを示す．ここでは，$L_x=50000$，$L_y=L_z=12.5$とする．$y$と$z$方向には周期境界条件を課す．$x=0$と$x=40000$の位置に壁（LJ粒子を密度${\rho }_{\mathrm{w}}=0.79$の面心立方格子点上に固定してモデル化）を配置する．$x=0$の壁は音波を発生させるために振動させる．$x=40000$の壁は固定する．固定壁の近傍（$39000\le x\le 40000$）には音波を消去するためにランジュバン熱浴を課す．流体の熱力学状態は超臨界領域の温度$T=2$，密度$\rho =0.1$とする．分子数は$N=623338$である．振動壁は振動振幅$A$と周波数$f$で正弦的に振動させる．ここでは，$5\le A\le 20$と$0.0005\le f\le 0.002$とする．運動方程式の数値積分の際の時間刻み幅は$\mathrm{\Delta }t=0.004$である．数値積分にはLAMMPS（Large-scale Atomic/Molecular Massively Parallel simulator）［16］を用いる．

図1  シミュレーションセルの概略図．$x=0$と$x=L_x$（$L_x$は計算セルの$x$方向の長さ）の位置に，それぞれ，振動壁と固定壁を配置している．熱浴Aと熱浴Bの領域（$L_x-L_{\mathrm{th}}$）には局所ランジュバン熱浴を課している．熱浴Aではランジュバン熱浴の摩擦係数が0.0001から0.1に線形に増加し，熱浴Bでは摩擦係数は0.1としている．$y$と$z$方向には周期境界条件を課している．

流体力学計算の基礎方程式には，非線形波を良く記述するバーガース方程式［17］を用いる：

  

$$\frac{\partial p_{\mathrm{a}}}{\partial x}+\frac{1}{c_0}\frac{\partial p_{\mathrm{a}}}{\partial t}-\frac{b}{2c_0}\frac{{\partial }^2{p}_{\mathrm{a}}}{\partial t^2}-\frac{\beta p_{\mathrm{a}}}{{\rho }_0{c}_0^3}\frac{\partial p_{\mathrm{a}}}{\partial t}=0$$(3)

ここで，$p_{\mathrm{a}}$は圧力の平均値に対する変動成分であり，${\rho }_0$は静止流体の密度である．$c_0$，$b$，及び$\beta$は，それぞれ，断熱音速，減衰パラメタ，及び非線形パラメタである．これらのパラメタは比熱や体積弾性率，及び粘性係数などの輸送係数から求めることができる．LJ流体に対して平衡，及び非平衡MD計算を行って別途決定する．詳細については文献［12］を参照されたい．

図2にMDシミュレーションで得られた波形とバーガース方程式の数値解を示す．振動壁の振動数は$f=0.001$であり，赤がMDシミュレーション，黒がバーガース方程式の数値解である．波長や減衰の振る舞いなど，両者が極めてよく一致していることが見て取れる．周波数を大きくすると音響流が発生し，密度勾配が現れるためバーガース方程式を適用することができない．このような状況では，より高次の近似を用いる必要があると考えられる．少なくともバーガース方程式の成立範囲においては，MDシミュレーションの結果と流体力学計算は一致することが明らかとなった．したがって，MDシミュレーションで音波を扱うことはできると結論できる．MDシミュレーションによって，相転移を含むより非線形性の強い現象の解析も可能であると考えられる．

図2  LJ流体の超臨界状態（温度$T=2$，密度$\rho =0.1$）における波形の振幅依存性．赤はMDシミュレーションの結果であり，黒はBurgers方程式の数値解である．Burgers方程式に含まれるパラメタは別途計算を行っており，それぞれの結果は同じ流体に対して独立な方法で得られたものであることに注意されたい．

3　 音波伝搬に対する相転移の影響[13]

通常の流体の場合，音速や減衰率，非線形性などの基本的な音波物性は，流体の物理的な性質（弾性や粘性）によって決まる．しかし，気泡性液体の音波物性は，気泡の含有量やサイズ分布に強く依存する．さらに，音速に分散性が現れるなどの通常の液体では見られない異常を示すことが知られている［9］．超音波キャビテーションの理解を深める上で，その舞台となる気泡性液体の音波物性を理解することは本質的である．気泡の合体や分裂，気液界面からの熱や物質の移動を無視した理想的な状況においては，流体力学に基づく理論モデルの構築が行われており，超音波ホーンの実験への適用などが試みられている．しかし，キャビテーションの原点である気液相転移の影響に関しては十分な理解がなされていない．

本研究では，MDシミュレーションを用いて音波に対する気液相転移の影響を解析した．静止液体中の気泡の振動［18,19］や多重気泡生成［20］のMDシミュレーションは存在するが，著者らが知る限りでは音波に対する相転移の影響の解析は本研究が初めての試みである．前節で述べたように，相転移を含まない場合，MDシミュレーションによって音波物性を定量的に解析できる．また，以前の研究［21,22］でカルマン渦に対するキャビテーションの影響を解析しており，気液相転移を含む音波伝搬の解析にも有効であることが期待できる．ここでは，1次転移領域（図3の青矢印）と臨界点近傍の連続転移領域（図3の赤矢印）において相転移が音波に与える影響を調べる．

図3  Lennard-Jones系の気液相境界．シミュレーション条件（連続転移領域と一次転移領域）を赤と青の矢印でしめしている．

流体は単原子分子で構成し，分子間の相互作用は式(1)とする．$r_{\mathrm{c}}=2.5$とする．シミュレーションセルは図1に示す直方体とし，$L_x\times L_y\times L_z=50000\times 25\times 25$とする．$y$と$z$方向に周期境界条件を課す．$x=0$と$x=50000$の位置に，それぞれ，振動壁と固定壁を配置する．壁はLJ粒子を面密度0.82の正方格子点上に固定してモデル化する．$49000\le x\le 50000$の範囲にランジュバン熱浴を課す．$49000\le x\le 49500$の範囲で摩擦係数を0.0001から0.1に線形に増加させ，残りの範囲では0.1で一定とする．

初期時刻において分子はシミュレーションセル内に重ならないようにランダムに配置する．1次転移領域と連続転移領域の密度は，それぞれ，$\rho =0.6$と$\rho =0.4$とする．分子数は1次転移領域で18 749 626，連続転移領域で12 499 751である．温度$T$（1次転移領域：$0.84\le T\le 1$，連続転移領域：$0.94\le T\le 1.5$）で平衡化した後に，振動壁を振幅$A=10$，周波数$f=0.001$で正弦的に振動させて音波を発生させる．平衡化に1 000 000時間ステップ程度，振動開始後に系が落ち着くまでに5 000 000程度を費やし，その後の10 000 000時間ステップ程度を音波の測定に用いる．運動方程式の数値積分における時間刻み幅は$\mathrm{\Delta }t=0.004$である．数値積分にはLAMMPSを用いる．

図4に1次転移領域における波形の温度依存性を示す．各位置における$x$方向の流速から波形を求めた．流速は振動壁の最大速度$2\pi fA$で規格化している．温度を$T=1$から$T=0.85$（相転移温度）にすると，波長が短くなり，減衰率が増加することがわかる．$T=0.84$（相分離域）にすると，音波は振動壁近傍で急激に減衰することがわかる．減衰した後は細かい波の伝播が生じていることもわかる．密度場の時間変化を調べると，$T=0.85$では微小な気泡が生成と消滅を繰り返しており，$T=0.84$では振動壁の近傍に気相領域が生じていることが分かった．1次転移領域では相分離によって密度場が不連続に変化するため，波形が不連続に変化することが明らかとなった．一方で，波長に関しては粘性の変化程度の影響のみである．$T=1$と$T=0.85$に関しては密度勾配がほとんど無いため，バーガース方程式を用いて記述することが可能であった．$T=0.85$では気泡核の生成と消滅が生じていたが，バーガース方程式で良く記述できていることがわかる．

図4  LJ流体の一次転移領域における波形．(a)温度$T=1$，(b)$T=0.85$（相転移温度），及び(c)$T=0.84$（相分離域）．振幅$A=10$と周波数$f=0.001$の結果である．

図5に連続転移領域における波形の温度依存性を示す．温度を下げていくと，減衰率が連続的に増加していくことがわかる．1次転移領域の場合と異なり波形に不連続な変化は現れなかった．連続転移領域では密度揺らぎが連続的に増加することより，減衰率が著しく増加していると考えられる．波長に関しては1次転移領域と同様に影響は現れなかった．また，密度揺らぎが顕著な場合でも，バーガース方程式で良く記述できていることもわかった．

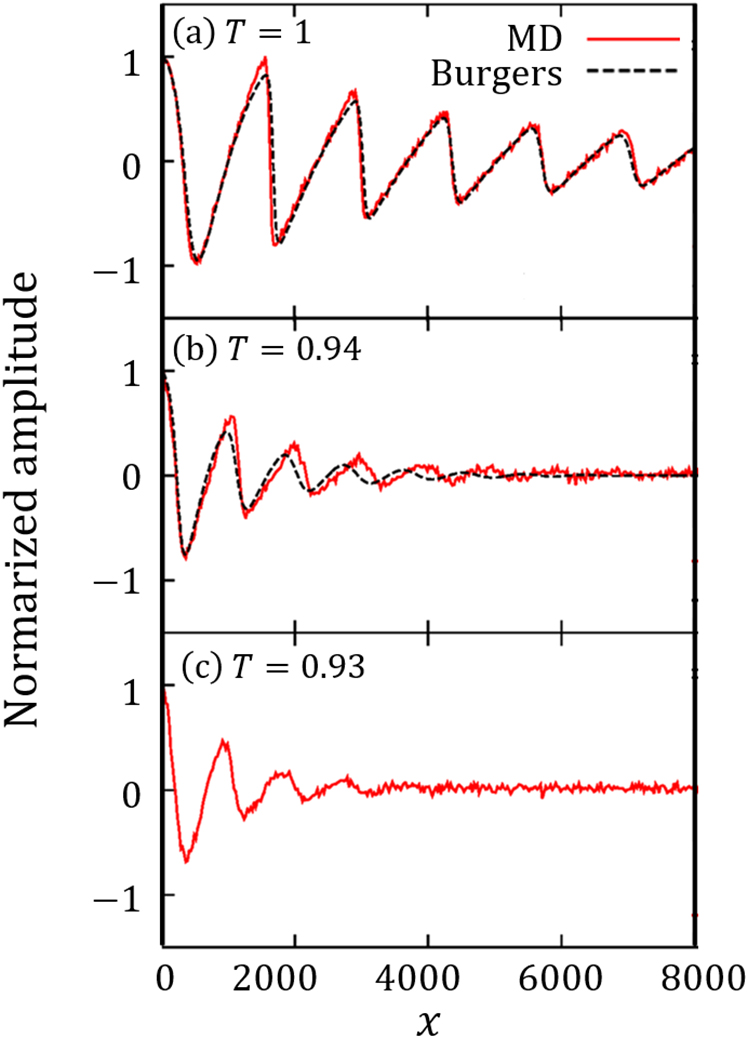
図5  LJ流体の連続転移領域における波形．(a)温度$T=1$，(b)$T=0.94$（相転移温度），及び(c)$T=0.93$（相分離域）．振幅$A=10$と周波数$f=0.001$の結果である．

1次転移領域と連続転移領域では，相転移による密度場の変化の仕方が大きく異なるため，音波への影響もそれを大きく反映したものとなることが明らかとなった．1次転移領域では気相領域の形成により波形が不連続に変化し，連続転移領域では密度揺らぎの増加により減衰率が連続的に増加する．一方で，波長に関しては，どちらの領域においても相転移が生じているにも関わらず，粘性の変化以上の影響が現れないことも明らかとなった．したがって，気泡性液体における音速の異常は，気泡と音波の相互作用に由来するものと考えられる．

系内に気泡を発生させるために，シミュレーションセルを$y$と$z$方向に大きくする．周期境界をまたいで気相領域が結合することを防ぐためである．以下では，シミュレーションセルの大きさは$L_x\times L_y\times L_z=10000\times 100\times 100$とする．1次転移領域の相転移点（$\rho =0.6$，$T=0.85$）におけるシミュレーションを行った．分子数は$N=59994000$である．周波数は$f=0.001$とし，振幅$A$を変化させる．

図6(a)は$A=10$における密度場のスナップショットである．小さな気泡（黄色と赤色部）が生成と消滅を繰り返すことがわかった．$A=5$では相転移は起こらなかったため，これらの間の振幅でキャビテーションが発生する．$A=15$では，振動壁の近傍で細かな気泡が多数生成し，それらが成長して一つの大きな気泡が生成することがわかった（図6(b)）．さらに，生成した気泡は音波との相互作用によって移動することも明らかとなった．後者はビヤークネス力［23,24］によるものであり，分子スケールからの直接的な検出は著者らが知る限り初めてである．気泡はある距離を移動した後に収縮し消滅する．それと同時に振動壁の近傍で新たな気泡が生成する．振幅をさらに増加させると，周期境界をまたいで気相領域が結合することもわかった．

図6  LJ流体の一次転移点（温度$T=0.85$，密度$\rho =0.6$）における気泡の運動．(a)振幅$A=10$，(b)$A=15$の気泡生成，及び(c)$A=15$の気泡移動と気泡初生．

気泡は音波の減衰には影響を及ぼすが，波長には影響を及ぼさないことも明らかとなった．ミナルトの式を用いると，気泡の固有振動数は$f_0\simeq 1/R_0=0.05$（$R_0\simeq 20$：気泡の平均半径）であり，振動壁の振動数（$f=0.001$）はそれより小さいため，気泡の存在により音速は低下するはずである［25,26］．したがって，多数の気泡が存在することが音速の異常において本質的であると結論できる．一方で，図6(b, c)のような場合でも，バーガース方程式が適用できることは興味深い．バーガース方程式には分散項が含まれないため，バーガース方程式の適用が可能か否かで音速の異常を検出できそうである．

MDシミュレーションにより，現象論的なモデルを用いることなく，相転移の音波への影響，音場での気泡成長や気泡と音波の相互作用を解析した．こうした分子論に基づく気泡と音波の相互作用の解析は，流体力学モデルを正当化するための強力なツールであると考えられる．したがって，MDシミュレーションによるアプローチは，気液相転移や他の相転移（固液相転移やシアバンディングなど）を伴う流れや音波をより深く理解するための大きな可能性を秘めていると結論できる．

4　 超大規模分子動力学シミュレーションに向けて

超音波キャビテーションのメカニズム解明を目指してMDシミュレーションによる解析を行ってきた．そのために必須の気泡性液体の解析には，これまでの計算規模をはるかに超える大規模なMDシミュレーションが必要になる．2023年度から，その実現可能性を検討してきた．多数の気泡が液体中で統計的な性質を現すためには，少なくとも数百個程度の気泡が系内に必要であると考えられる．前節の最後の単一気泡の解析は6千万原子規模であるから，単純計算で100億原子規模の系が必要である．果たしてこのような規模のMDシミュレーションを，ベンチマークとしてではなく，実際のプロダクションランとして実行することは可能なのだろうか？スーパーコンピュータ富岳（以下，富岳と呼ぶ）を利用することにより，この問題を克服するための準備を行ってきた．本節ではその概要を述べる．

到達可能な計算規模を推定するために，LAMMPSにおけるウィークスケーリング測定を富岳で実施した［27］．シミュレーションセルは大きさが$L_x\times L_y\times L_z=5000\times 250\times 250$の直方体とし，密度$\rho =0.6$のLJ流体を詰める．この系に192ノードを割り当てる．ノードあたりのプロセス数は4とし，プロセスあたりのスレッド数は12とする．ウィークスケーリングのために，$y$と$z$方向に$n_y$倍と$n_z$倍にした系のシミュレーションを$192\times n_y\times n_z$ノードで実施する．測定の際，プロダクションランで用いる予定の機能（熱浴，流速や密度場の測定など）を有効にした状態で5000時間ステップのシミュレーションを行う．

図7にウィークスケーリング測定の結果を示す．図中のLoopとPairは，それぞれ，運動方程式の数値積分に費やした総時間と相互作用計算に費やした総時間である．相互作用計算についてはスケーリングが取れているが，それ以外の部分でスケーリングの破れが生じていることがわかる．特に，高並列時に著しく性能が悪化することが明らかとなった．100億原子における並列化効率は20%程度と推定される．

図7  スーパーコンピュータ富岳におけるLAMMPSのウィークスケーリング測定の結果．

100億原子を超える規模では，プログラムの実行中の消費メモリが富岳の許容量を超えてしまい，OOM Killerによってプログラムが停止することがわかった．プログラムの実行中のメモリ使用量の変化を測定すると，数値積分の開始後に著しく増加することがわかった．詳細な調査は現在進めているところである．少なくとも，80億原子程度まではプロダクションランの実行が可能である．100億原子超のMDシミュレーションには，メモリ削減と演算部以外のチューニングが必要であると考えられる．したがって，本研究で想定している計算規模は決して無謀なものではないと言える．

5　 おわりに

超音波キャビテーションのメカニズム解明に向けて，分子動力学（MD）シミュレーションによる音波解析を行ってきた．MDシミュレーションによる音波解析の正当性，音波に対する相転移の影響を明らかにした．その結果，気泡性液体の性質を明らかにするためには100億原子規模のMDシミュレーションが必要であることが明らかとなった．スーパーコンピュータ富岳の利用により，それが実現できそうである．本研究は令和6年度の「富岳」若手課題（課題番号hp240112）として採択されており，解析を進めている．

 謝辞

本研究の共同研究者である東京大学物性研究所の野口博司准教授，慶應義塾大学の渡辺宙志教授に心から謝意を申し上げます．様々な助言を頂いた東北大学の川勝年洋教授に厚く御礼申し上げます．本研究は，JSPJ科研費JP23K03242の助成を受けたものです．本研究の計算には，スーパーコンピュータ「富岳」（課題番号：hp230333，hhp240112），東京大学物性研究所のスーパーコンピュータの計算資源の提供を受け，実施しました．

参考文献

• [1]   R. W.  Wood and  A. L.  Loomis, Phils. Mag., 4, 417 (1927).
• [2]   W. T.  Richards and  A. L.  Loomis, J. Am. Chem. Soc., 49, 3086 (1927).
• [3]   L.  Yusuf,  M. D.  Symes and  P.  Prentice, Ultrason. Sonochem., 70, 105273 (2021).
• [4]   Y.  Fang,  T.  Yamamoto and  S.  Komarov, Ultrason. Sonochem., 48, 79 (2018).
• [5]   A.  Moussatov,  C.  Granger and  B.  Dubus, Ultrason. Sonochem., 10, 191 (2003).
• [6]   B.  Dubus,  C.  Vanhille,  C.  Campos-Pozuelo and  C.  Granger, Ultrason. Sonochem., 17, 810 (2010).
• [7]   K.  Tan and  S.  Yeo, Ultrason. Sonochem., 58, 104666 (2019).
• [8]   浅野  優太， 渡辺  宙志， 野口  博司，分子シミュレーション学会誌アンサンブル，22, 157 (2020).
• [9]   L. V.  Wijngaarden, Ann. Rev. Fluid Mech., 4, 369 (1972).
• [10]   F. J.  Trujillo, Ultrason. Sonochem., 65, 105056 (2020).
• [11]   T.  Kanagawa,  T.  Yano,  M.  Watanabe and  S.  Fujikawa, J. Fluid Sci. Technol., 5, 351 (2010).
• [12]   Y.  Asano,  H.  Watanabe and  H.  Noguchi, J. Chem. Phys., 153, 124504 (2020).
• [13]   Y.  Asano,  H.  Noguchiand and  H.  Watanabe, Phys. Rev. Fluids., 7, 064302 (2022).
• [14]   H. A.  Bennett,  B. S.  Cazzolato,  D. M.  Huang and  A. C.  Zander, Ultrasonics, 96, 149 (2019).
• [15]   B. L.  Holian,  W. G.  Hoover,  B.  Moran and  G. K.  Straub, Phys. Rev. A, 22, 2798 (1980).
• [16]   S.  Plimpton, J. Comput. Phys., 117, 1, (1995).
• [17]   J. M.  Burgers, Adv. Appl. Mech., 1, 171 (1948).
• [18]   H.  Okumura and  N.  Ito, Phys. Rev. E, 67, 045301(R) (2003).
• [19]   R.  Hołyst,  M.  Litniewski and  P.  Garstecki, Phys. Rev. E, 85, 056303 (2012).
• [20]   H.  Watanabe,  N.  Ito and  C.-K.  Hu, J. Chem. Phys., 136, 204102 (2012).
• [21]   Y.  Asano,  H.  Watanabe and  H.  Noguchi, J. Chem. Phys., 152, 034501 (2020).
• [22]   Y.  Asano,  H.  Watanabe and  H.  Noguchi, J. Chem. Phys., 155, 014905 (2021).
• [23]   L. A.  Crum, J. Acoust. Soc. Am., 57, 1363 (1975).
• [24]   O.  Louisnard, Phys. Rev. E, 78, 036322 (2008).
• [25]   E.  Silberman, J. Acoust. Soc. Am., 29, 925 (1957).
• [26]   P. S.  Wilson,  R. A.  Roy and  W. M.  Carey, J. Acoust. Soc. Am., 117, 1895 (2005).
• [27]   浅野  優太，HPCIシステム利用研究課題　利用報告書, hp230333 (2023).

著者紹介

浅野 優太（博士（理学））

〔経歴〕2014年愛媛大学大学院理工学研究科博士課程修了，理化学研究所計算科学研究機構，名古屋大学工学研究科，東京大学物性研究所，東北大学金属材料研究所を経て，2024年から現所属．〔専門〕分子動力学シミュレーション，統計物理学．〔趣味〕音楽鑑賞，カラオケ，（誤解を恐れずに言えば）大規模計算．