2014 Volume 100 Issue 9 Pages 1076-1088
2014 Volume 100 Issue 9 Pages 1076-1088
A short historical review is given for the dislocation theory in the special reference to the mechanism of metal strengthening. Until the mid of 1950’s, the basic formalism of the dislocation theory has been completed. However, the further development has been confronted by various difficulties in the application of the theory to elucidate the strengthening mechanism, although some progress in problems, such as the visualization of individual dislocations and the measurement of the dislocation velocity, has been made. The present status of this research field, inclusive of recent developments, is described. The solution hardening, the work hardening, the low temperature strength and others are discussed in some details. Recent experimental treatises to examine the strengthening mechanisms are also overviewed.
表題として二つの項目「転位論」と「強化機構論」を掲げたが,以下の内容としては,「転位論に基づいた金属強度論」を扱うつもりである。この分野は残念ながら,まだ未解決な部分を多く含むのが現状であるが,本項では強化機構の理解の進展を歴史的に辿ることに力点を置きつつ,その上で現段階での問題点を指摘したい。
ただし,扱う問題は広範囲に亘っており,また,筆者らの力量不足の制約もあるので,取り上げる問題の偏りは避けられないし,最近の発展の詳細にまで立ち入ることが出来ない部分もある。引用文献などで補って頂けると幸いである。
本稿は最後に,新しい研究手法の項目を設けた。今後,強度の研究は,より微視的,より局所的な機構解明に向かうとともに,複合組織ほかのより複雑な問題に向かうと思われるので,そこに役立ちそうな研究手法を探ってみた。今後の研究の進展に,いささかなりとも寄与出来ればと念願している。
まずは転位論の歴史的スケッチから始めたい。転位論の開始はかなりはっきりしており,それは1934年のことであった。つまり,転位論はかなり若い学問分野であると言える。さて,この年にTaylor1),Orowan2),Polanyi3)の三人がそれぞれ独立した論文によって転位,あるいはそれに相当する概念を導入した。その後,転位論は潜伏期とも云うべき期間を経て,第二次世界大戦後(1945年以後)10年間ほどの間に,爆発的とも云える発展を遂げる。この間に,刃状転位,らせん転位,バーガースベクトル,積層欠陥,拡張転位,パイエルス力,転位源(フランク・リード源)などの言葉のほか,転位の作る応力場の計算や転位の弾性的エネルギー,転位と溶質原子との弾性的相互作用の計算,などが出そろった。さらに,結晶粒界の転位モデル,転位の運動速度における音速限界,結晶成長におけるらせん転位の役割,X線散漫散乱に与える転位の効果などについても盛んに議論された。Read4)とCottrell5)の著書にはこの期の発展の成果が手際よくまとめられている。ただし,金属強度論への転位論の応用に関しては,この期になされたものは,未だ不十分なものであったと云わざるを得ない。以下,我が国における状況にも触れつつ,転位論発展の歴史をもうすこし辿ってみたい。
ちょっと唐突に聞こえるかも知れないが,我国における転位論の発展には1953年京都で開かれた国際理論物理学会議が関係している。これは国際物理学連合からの要請をうけて日本学術会議ほかが実施したものであるが,我が国で開催された国際学会としては最初のものと言えるだろう。勿論,これの開催には湯川博士のノーベル賞受賞(1949年)が大きく影響を及ぼしたと考えられる。さて国際物理学連合の会長としてこれの開催を推進したMott博士は日本側に対して,会議の中に「Crystal Dislocation」のセッションを作ることを要求してきた。日本の物理学者達は戸惑ったらしいが,結局,要求通りにこのセッションは作られた。そのセッションでの発表者は1. N.F.Mott,2. 鈴木平・鈴木秀次,3. 橋口隆吉,4. F.Seitzであった。このあたりの事情,およびその頃の我が国の転位論の研究状況についてはHasiguti6,7)およびT.Suzuki8),H.Suzuki9,10)による回想がある。話は少しずれるが,転位論の黎明期には,とくに欧米では物理学者が多数関与していた。転位論を開始した三人の論文を見ても分かる事だが,元々,転位の概念は物性物理学的な興味から生まれたものであった。Mottにはよく知られた固溶硬化に関するMott-Nabarroの論文や,加工硬化に関する研究などがあるが,もともとは固体電子論が専門の研究者で,その方面の研究でノーベル物理学賞を受賞(1977年度)している。そのほか,例えば拡張転位を最初に唱えたShockley(トランジスタ作用の発見で1956年度ノーベル物理学賞受賞)や上昇運動を伴う場合の転位源を考えたBardeen(トランジスタ作用の発見および超伝導の理論で1956年度および1972年度ノーベル物理学賞受賞)などがいる。パイエルス力を始めて計算したPeierlsも専門は固体電子論である。これらの人達の参入によって,転位論は短期間の間に形が整えられたのであるが,この黎明期を過ぎた頃から,物理学者達の多くが他の分野へと去って行ったのも事実である。なお,この時期に活躍した人々による回想が論文集11)となっている。さて話を本題に戻すと,この国際会議の転位論セッションに関連して,研究会が国内各所で開かれるなどのことがあり,この時期に我が国での転位論への関心は一気に高まった。
さて,転位論はその弾性論的性質や結晶学的構造などの扱いやすい問題が解決した後,新しい問題へと展開していった。その新しい展開として,1956年にアメリカのLake Placidで開かれた国際会議に注目したい。この会議では転位論の金属強度論への応用が強く意識され,加工硬化や固溶硬化などに関する論文がいくつも発表されたが,その他に,転位の直接観察に関する発表が注目を集めた。それまでにも,エッチピット法などによる転位観察は報告されていたが,透過電子顕微鏡法による観察が発表されたのはこの会議が最初である。発表したのはHirschら12,13)であったが,この方法はその後,多くの研究者達によって使われ,転位論や金属強度論の研究における強力な武器へと育っていった。またこの会議で,Gilman and Johnston14)はエッチピット法による転位の運動や増殖についての観察結果を報告したが,この研究は,その後,転位の運動速度測定へと発展することになる。これらについては次節以下で改めて論じたい。
転位が最初に提案されたときには,それが観察可能とは思われていなかったようである。しかし,それが架空の存在ではないことを実験的に示す必要があったので,種々観察法が工夫された。その代表的方法として,デコレーション法,エッチピット法,X線トポグラフ法,透過電子顕微鏡法などがある。なおデコレーション法というのは透明なイオン結晶などで用いられた方法で,転位線に沿って溶質原子を析出させ,それを光学顕微鏡で透過観察するものである。これらのうち,X線トポグラフ法はやや出遅れたが,その他のものはLake Placid会議において既に登場している。その中で現在に至るまで直接観察の中心を担っているのが透過電子顕微鏡法による観察である。
Hirschらはアルミニウム試料を強酸による溶解で数百ナノメーター程度にまで薄くすることによって,電子顕微鏡による透過観察に成功したのであったが,同じ頃,Bollmann15)は電解研磨法を用いてステンレス鋼試料を薄膜化し,これによって転位の電子顕微鏡観察に成功していた。その後はこの電解研磨法が主流となる。Hirschらのグループは転位が電子顕微鏡によって何故見えるのかという問題,つまり,転位の歪み場による電子線の回折効果に関する考察,さらには電子線回折の動力学理論を使っての像計算16,17)などにおいても世界の研究をリードした。透過電子顕微鏡法は,その高い分解能という利点に加え,その場観察や局所的元素分析などのさまざまな機能を加えることによって一層の発展を遂げている。
3・2 動的相互作用上に述べたように,Lake Placidの会議においてGilman and Johnstonはエッチピット法による転位の運動や増殖の観察を報告したが,彼らはそれを発展させて,転位の運動速度を測定した18)。試料としてイオン結晶(LiF結晶)の単結晶を用いたが,短時間(1 μs程度まで)の応力印加装置なども工夫することによって12桁におよぶ転位速度の測定に成功している。その後,多くの研究者達によって,金属,半導体,イオン結晶など,多くの物質で転位速度が測定された19,20)。その大半はエッチピット法によっているが,この測定のためにはそれぞれの物質に適したエッチング液を見付ける必要があるほか,良質の(転位密度の低い)単結晶試料が必要となる21)。このような測定が可能になったことによって,転位の運動速度と金属強度との関係が議論されるようになった。
定常的な転位運動が観察される場合,その運動速度を決める相互作用は動的相互作用と呼ばれることがある。本稿でもこれを使用する。なおJohnston and Gilman18)はdynamic resistanceの用語を使っている。また,このような相互作用を与える力は摩擦力(friction)と呼ばれることも多い。しかし,転位の運動はミクロに見れば完全な定速度と見なすことは出来ず,多かれ少なかれジャキーな運動,つまり運動と静止の頻繁な繰り返しになっているので,この用語は多少不適切かも知れない。動的相互作用に対して,静的相互作用というのは,静止している転位が動き始めることを想定して,その場合の障害物との相互作用をいう。さらに,これらの用語は降伏応力に関して用いられる事が多い。すなわち,静的相互作用においては,転位が障害物から離脱して動き出すことが降伏であるが,動的相互作用においては,転位はすでに運動状態にあると仮定して,その速度がある臨界値に達したときをもって降伏と考えるのである。歴史的な意味もあるので,このあたりのことをやや詳しく説明する。
まず,転位の運動速度(v)を印加剪断応力(τ)の関数として,次式で表されるものとする。
| (1) |
ここにτ0,v0とmは定数である。このような関係は転位速度の測定結果として広く使われている。ただし,これは応力区間を限定して,その区間内だけで成立する近似式である。定数mは試料の物質や応力区間に依るのだが,実測の例ではm=2~50の程度である。Fig.1にこの関係を両対数グラフに示した。このグラフでは曲線の傾きがmとなる。なお,図には転位の動き始める応力(τS)と降伏応力(τY)および音速(vS)を記入した。よく知られているように音速(ただし,すべり面に沿う横波)は転位速度の上限となる。

Dislocation velocity (v) as a function of the shear stress (τ). The sound velocity (vS), the yield stress (τY) and the stress (τS) at which dislocations start moving are denoted.
いま,一定歪み速度の下で単結晶試料の引っ張り変形試験を行っているとする。試料に適当なすべり系を想定して,そのすべり系へ分解した剪断歪み速度を
| (2) |
で与えられる。変形試験の初期にはこの塑性的歪み速度は小さいので,試験機で与えられる歪み速度(
| (3) |
が降伏の条件となる。この時の応力(τY)は勿論転位の動き出す応力(τS)とは異なる。なお,この条件を満たすとき応力−歪み曲線はその勾配がゼロになるはずである。ただし,実際の試験では降伏と見なせる点において勾配がゼロにはならないことが多いので,これは近似的な条件式と考えるべきである。Johnstonらの扱いはこれより少し複雑で,歪みにともなう転位密度の増加や,さらに加工硬化も考慮した形で,応力−歪み曲線のシミュレーションを行っている18,22)。しかし,動的相互作用の考え方の本質は(3)式の降伏条件にある。なお,以上の説明からも明らかなように,このような動的相互作用で決められた降伏応力は必ず歪み速度(
このような計算でとくに注目すべき点は,降伏点降下(yield
drop)の出現である。動的相互作用の考え方によれば,これは転位の増殖によって,歪み速度のバランスが崩れ(すなわち,
このような動的相互作用の考え方は,現在,標準的な考え方といってよいが,強度論では動的相互作用を考えなくても良い場合も多い。これは上の枠組みで云えば,(1)式の指数mの極めて大きな場合に相当する。すなわち,このような場合は応力−転位速度の図でカーブが垂直近くに立っている場合であって,図のτSとτYとが接近しており,実質的に同じと見なせる場合である。このような場合の転位の動きは,障害物に止められて完全に静止しているか,障害物を乗り越えて音速に近い高速で動いているかのどちらかである。動的相互作用を考えなくて良い場合を具体的に挙げれば,加工硬化,析出硬化,細粒硬化,などであるが,この様な分け方は,次に述べる熱活性化過程に基づく分類でも殆ど同じになる。
本節では転位速度として(1)式の表現を与えたが,それを決める物理的機構については何も述べなかった。転位速度の上限は音速で制限されており,その近くの高速ではフォノン散乱やフォノン輻射によって速度が決まると考えられている。一方,通常の強度論で扱うような低速の領域では,後章で述べるパイエルス力か,あるいは不純物原子のような障害物との相互作用によって速度が決まると考えられる。いずれにしても,その基本には熱活性化過程を含んだ転位運動がある。次節でそれを述べる。
3・3 熱活性化過程と硬化機構の分類金属強度の関係する温度依存性は,弾性定数の温度変化は別として,殆どすべて熱活性化過程が関与している。従って,熱活性化過程と温度依存性とは殆ど同義語と言って良い。この熱活性化過程の考え方が塑性の問題に適用されたのはずいぶん古く,転位論の開始の時期にまでさかのぼる。すなわち,Orowanは転位の概念を導入した論文2)においてすでに,転位の核発生における熱活性化過程の関与を考えている。この過程はもともと化学反応論で考えられたものであるが,これを塑性変形に適用した場合には,活性化エネルギーが印加応力の関数となる点が特徴となる。
さて熱活性化過程に支配される場合について,塑性的剪断歪み速度(
| (4) |
となる。だたし,転位が障害物によって止められている場面を想定している。転位が印加応力(τ)の下で熱エネルギーの助けをかりてそれを乗り越えることによって,塑性変形が進行する。また,その場合の障害物に関する活性化エネルギーをU(τ)としている。この式でkはボルツマン定数,Tは絶対温度である。もともと転位の運動は極端な高速でない限り熱活性化過程に支配されるものであるから,この式は前節の(1)式と(2)式をまとめたものに相当すると考えてよい。指数関数の部分は確率的な意味があり,障害物に止められた転位が,与えられた時間内に,障害物を乗り越えて前進できるための確率を表している。前置因子Aには転位の振動数と転位が止められている障害物の体積密度(これには転位密度が関係する)のほか,障害物を通過した後に転位が掃く面積などが含まれる。
なお,式(4)が扱っているのは単純な場合であって,そこでは転位が一つの活性化過程において,単一の障害物とだけ相互作用を持つとしている。しかし後節(4・3)で示す様に,実際にはもっと複雑な状況,つまり複数の障害物との同時的相互作用を考えねばならないような場合もある。
以下,近似的であれ(4)式が成立すると考えて考察を進める。一般的に言って,転位は応力の助けによって動き易くなるものであるから,応力の存在によって活性化エネルギーは小さくなるべきである。このことを考慮して,(4)式の活性化エネルギーを次式で近似する。
| (5) |
これはテイラー展開の一次項までの表現とも考えられるので,ある程度普遍的に成立するものと見てよい。この場合の係数Vは体積の次元を持っているので,活性化体積と呼ばれている。以上の式,(4),(5)を前節の降伏条件,(3)式に代入すれば,結局,変形応力(τT)の温度依存性を表す式として,
| (6) |
が得られる。定数αは試験時の歪み速度(
| (7) |
とする。この関係をFig.2に示した。ここでτT=0となる温度T0=U0 /(αk)は相互作用の大きさ(U0)の目安として便利に使われる。また,図中の破線は歪み速度を高くした場合の変形応力である。この図で温度依存性が直線的となったのは,勿論,活性化エネルギーを1次関数で近似したからである。なお,この(6),(7)式はSeeger24)がfcc金属の降伏応力の温度依存性を論じるために用いた式と全く同じ形である。ただし,その論文では活性化エネルギーを与える過程として転位−転位相互作用を考えているが,それは正しくないであろう。この場合はまず転位と溶質原子との相互作用を考えるべきである。

Flow stress (τ) of a crystal as a function of the temperature (T). The stress is composed of the temperature-dependent term (τT) and the temperature- independent term (τG). The flow stress in the case of a higher strain-rate is denoted by the broken line.
なお,熱活性化過程に関する詳しい解説論文がKocksら23)によって書かれている。そこではいろんな障害物と転位との相互作用を解析しているが,比較的簡単な場合について,その活性化エネルギー(U)を次式で近似することを提案している。
| (8) |
ここにp,q,U0,τ0は定数である。例えばbcc金属のパイエルス力の場合として,p=3/4,q=4/3を推奨している。
熱活性化過程としては高温クリープなどのように原子拡散が関与してくる場合もある。このような場合は話がもう少し複雑になる20)。また,降伏応力の温度依存性が通常とは逆になる場合,つまり温度上昇に伴って降伏応力が上昇する場合25,26,27)も興味深いが,本稿では扱わない。
さて,ここで硬化機構の分類を試みる。それは温度依存性の大きなものと小さなものとの分類である。上式あるいはFig.2でも明らかなように,活性化体積の大小がこれに関係している。これはまた,相互作用エネルギー(U0)の大小とも関係が深く,大雑把に言って,関与するエネルギーが大きなものほど温度依存が小さい。通常の分類では,温度依存の小さなものとして,加工硬化(転位間相互作用力),析出硬化,細粒硬化,などを考え,大きなものとしては,固溶硬化,パイエルス機構に依る強度,などを考える。後者では熱活性化過程の考察が欠かせない。ただし,この分類はあくまでも大まかな分類であって,加工硬化などでも,精密な議論においては温度依存性を吟味することがある。
固溶硬化についての転位論的考察は,転位論のごく初期の頃からあった。しかし,その硬化メカニズムの本質についての理解はなかなか得られなかった。いくつかの論争が続いたし,現在でも研究者達の間で共通の理解に達しているとは言い難い。以下では,いくつかの論点について現在までの道筋を辿るが,まず関係するパラメータについて見ておきたい。
固溶硬化に関連したパラメータとしては,温度,合金濃度,溶質原子の種類,などがある。まず溶質原子の種類についてであるが,これは通常次のサイズ因子εで整理される。すなわち,合金の溶媒金属の原子半径をr0とし,溶質金属の原子半径をrとするとき,サイズ因子は
| (9) |
である。Fleischer28)は10種類以上のCu合金について合金による硬化を調べたが,その結果をまとめて,室温における降伏応力の増加がε3/2に比例することを報告した。ただし,パラメータとしてはεそのものではなく溶媒と溶質との剛性率の違いを加味したものを用いている。同様な測定はTakeuchi29)によってFe合金についてもなされている。この場合,サイズと剛性率を組み合わせたパラメータに対して2乗の依存性を報告している。次に溶質濃度(c)への依存性については,fcc合金の場合,降伏応力がc1/2またはc2/3に依存することが報告されている。
このようなパラメータへの依存性は,固溶硬化の機構を考える上で重要な手掛かりとなるはずであるが,事態はそれほど単純なものではない。後で述べる最近の理論(複数障害物モデル)によれば,これらへの依存性は測定する温度により異なると云う結果が得られている。
4・2 固着力モデルか摩擦力モデルか過去に降伏応力を決めている力が何かについて,上の表題のような論争があった。固着力モデルというのは,歴史的に古く,Cottrell and Bilbyの論文30)にまで遡る。彼らが扱ったのはFe-C系合金である。試料が焼鈍された状態から出発するとして,この初期状態においては,転位は固溶原子(つまりC原子)の集積により固着されていて動けないとする。そして,この固着点から動き出すのに要する応力が降伏応力である,と考えるのがこのモデルである。やや遅れて,Suzuki31,32)はこのモデルを拡張し,fcc合金に適用した。このために新しく導入した考えがfcc結晶中の拡張転位(その積層欠陥の部分)と溶質原子との相互作用(Suzuki効果)であり,この相互作用による転位の固着である。
このような溶質原子の集積による転位の固着については確かな証拠もあり,問題はない。しかし問題はこの固着力が降伏応力なり,変形応力なりを支配しているかどうか,と云う点である。とくに固着点から離脱した後での転位の運動が問題である。このモデルでは固着力の担い手としてしか溶質原子の働きを考えてないので,動き出した転位は何も抵抗力を受けない事になる。すなわち,このモデルでは降伏以後の変形応力はゼロになるはずである。現実にはゼロになることはないが,そこに溶質原子からの別の形の相互作用を期待するのであれば,もはや固着力モデルとは言えない。例えばFe-C系合金で見られる降伏点降下で言えば,確かに固着点からの離脱を思わせるものであるが,その場合には下降伏点がどのような機構によって決まるのかが合理的に説明されねばならないだろう。
次に摩擦力モデルであるが,この用語がやや不適切かも知れない。内容的には分散分布障害物モデルとでも言い換えた方が良いかもしれない。このモデルで想定している状況をFig.3に示したが,転位は各所で溶質原子に引っかかっており,時々,この障害を乗り越えて前進すると考えている。転位の各セグメントの動きは独立であるとするが,その集合として平均的には定常運動を保っていると見ている。このモデルでは,ひとつの転位セグメントが障害物を乗り越え得るかどうかは,障害物の強さ,セグメントの長さなどが関係する。

Dislocation motion in a solid solution in the case of the single-obstacle model. Dots represent solute atoms located in a slip plane. The dislocation moves segment-wise over a solute atom, as shown by a broken curve.
このFig.3のような状況において,Fleischer33,34)およびFriedel35)が変形応力の表式を導いた。またこのモデルを少し変形して,計算機シミュレーション的に変形応力を推定した論文36)もある。それらの詳細は省略するが,その結果で注目すべき点は前節で述べたパラメータ依存性を一応説明出来ることであった。すなわち,原子サイズ依存性ε3/2と溶質濃度依存性c1/2が説明できた。しかし,致命的な欠点は温度依存性を十分説明出来ない点であった。Suzuki and Kuramoto37)は熱活性化過程を考えた場合,転位と溶質原子一個との相互作用では関係するエネルギー((5)式のU0)が小さすぎること,そのため室温程度の高温になるとこのモデルの与える抵抗力はゼロになることを指摘した。Fig.2で言えばT0が室温以下になると云うことである。
1980年代になって,上記のFleischerらのモデルに熱活性化過程を取り入れたモデルがWilleら38)によって提出された。この論文はCu合金について固溶硬化を調べたものであるが,そこでは溶質原子1個ではなく,2個(Cu-Mn合金)または3個(Cu-Ge合金)のクラスターを考え,これと転位との相互作用を考えている。このようにすれば確かに相互作用エネルギーは大きくなり,室温近辺での強度も説明出来るようになるが,クラスターを考えるのはあまりにも便宜的と言わざるを得ない。
4・3 複数障害物モデル以上の話の筋を辿れば,固溶硬化理論のあるべき姿がはっきりと見えてくる。すなわち,分散分布障害物モデル(摩擦力モデル)であって,且つ,複数個の障害物が同時的に関与する様なモデルが正解であろうと思われる。このようなモデルを最初に考えたのはLabusch39)であり,Nabarro40)であった。彼らは単数障害物モデル(つまり,Fleischer-Friedelモデル)の欠点を明確に意識して,それに対抗するモデルを構築しようとした。とくに,注目すべき点は障害物の大きさを考えた点である。単数障害物モデルでは障害物を幾何学的な点として扱っている。障害物の大きさを考慮にいれた場合には,転位が一個の障害物を通過し終わらないうちに,他の障害物との相互作用が始まるので,複数個を扱う必要が生じるのである。しかし,これら初期のモデルは不完全なものであった。その大きな欠点は温度の効果つまり,熱活性化過程を十分考慮しなかった点である。
最近,熱活性化過程を考慮した複数障害物理論が筆者の一人によって提出された41)。Fig.4はその考え方を説明するためのものである。転位は障害物としての溶質原子を乗り越えて進む時に,熱活性化過程において張り出しを作ってジャンプすると考える。ただし,その時の一回のジャンプで複数個の障害物を乗り越えるものとする。図ではその転位の張り出しを三角形で近似している。この時の三角形の形と大きさは活性化エネルギーをなるべく小さくするという条件によって決定する。三角形に含まれる障害物には相互作用が正のものと負のものとが混じっているので,これを統計的に処理する必要があるが,これには揺らぎの理論を使って,一つの符号のものの過剰数を求める。このモデルはまだ改良の余地があると思われるが,とにかく重要な点は,複数個の障害物をひとつの熱活性化過程に組み入れたことである。

Dislocation motion in a solid solution in the case of the plural-obstacle model. A dislocation bulge is represented by a triangle. Plural obstacles are involved in a thermal activation event of the dislocation motion.
このモデルの詳細は省略するが,計算で得られた降伏応力の温度依存性をFig.5に示した。なお,図には固溶硬化のほかに温度に依存しない硬化成分(τG)もあるとして,これを加えてある。このモデルで得られた結果の大きな特徴は低温域に極大が現れることである。極大より高温側だけを見れば,fcc合金の実測値とかなりよく合致する。さらに,このような極大が実際に現れることも,Cu希薄合金での実験で報告されている42,43)。また説明は省略するが,このモデルはstress equivalenceと呼ばれる現象43)をうまく説明できるという特徴もある。
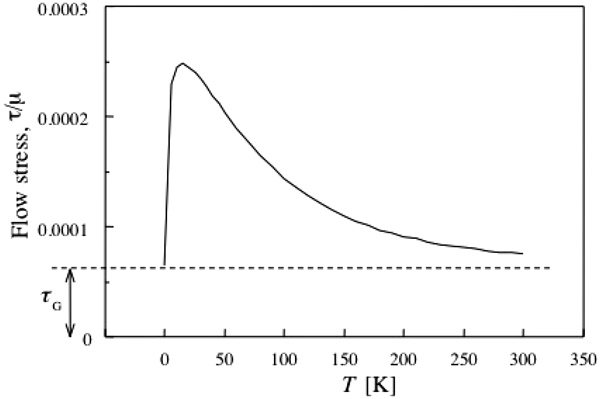
Temperature dependence of the yield stress (τ) in Cu-1.0 mol%Al crystal, calculated by the plural-obstacle model, where μ is the shear modulus. The athermal component of the yield stress (τG) is added41).
Fig.5に見られるように,このモデルでは極大より低温側に逆温度依存性が現れ,遂には絶対零度で変形応力がゼロになる。計算過程を詳細に検討すると,低温側での変形応力低下は転位の形がより直線的になることに起因していることが分かる。しかし,実際には変形応力がゼロに到達するとは考え難いので,ゼロになる前に,計算の前提となっている統計的処理に関する仮定がくずれるのでないかと思われる。これについては今後更なる検討が必要であろう。なお,このモデルは元々fcc合金の置換型溶質原子の場合を想定して作られたものであるが,最近,bcc合金の侵入型溶質原子の場合への拡張が試みられた44)。
加工硬化の転位論的研究は歴史が古く,転位論の始まりにおけるTaylorの論文1)で既にこれが考察されている。そして,そこで考えられた硬化過程の筋書きも現在と同じで,(i)変形に伴って転位密度の増加があり,(ii)その増加した転位同士が相互作用を及ぼし合って動き難くなる,つまり,変形応力が増加する,と云うことである。ここではこれら(i)と(ii)を転位蓄積の問題,変形応力の問題と呼ぶことにする。最初多くの研究者が関心を持ったのは変形応力の問題であった。つまり,どのような転位間相互作用が変形応力を支配するかと云う問題である。そこで二つの対立するモデルが現れる。しかし,その説明の前に,後での説明の便宜を考えて,単結晶の加工硬化曲線を示しておく。
Fig.6はfcc金属の単結晶に見られる応力歪み曲線を模式的に示したものである。このように変形の進行はいくつかのステージに分けることができるが,歪みの小さい方から順にステージ1,ステージ2,ステージ3と呼ばれている。ステージ1と2はまた,容易すべり域,直線硬化域,と呼ばれることもある。なお,直線硬化域が長いのがfcc結晶の特徴で,他の結晶系の場合にはもっと短く,ステージ2と3の合成のような形となることが多い。多結晶ではステージ1も現れず,概して放物線的になる。各種物質での硬化曲線やすべり系の詳細については他の文献45,46)を参照して頂きたい。次節以下ではfcc結晶のステージ2が議論の中心となるが,まずはこれらのステージ全般についての概括的理解を示しておきたい。

Stress (τ)-strain (γ) curve of a single crystal of fcc metal (a schematic sketch of a typical case).
ステージ1では主すべり系がもっぱら活動して,塑性変形を担っていることが分かっている。変形進行と共に2次すべり系も活動を始めるが,ステージ2で加工硬化率が高くなるのは,主すべり系転位と2次すべり系転位との相互作用のためと理解されている。ステージ3では加工硬化率が低下したと見えるが,これには硬化の過程に何らかの回復(動的回復)過程が重なってくると考えられている。この回復にはらせん転位の交差すべりの関与を仮定するのが一般的である。例えばAlではステージ2が短く硬化率が低いが,これはこの物質では積層欠陥エネルギーが高く,このためらせん転位の拡張幅が狭く,交差すべりが起こりやすいのが原因と考えられている。
5・2 長範囲応力モデルと林立転位モデルさて,加工硬化の機構についての議論であるが,変形応力に関する二つの対立するモデルとは,平行な転位同士の相互作用を重視するモデル(長範囲応力モデル47,48))と交差する転位同士の相互作用が支配的と考えるモデル(林立転位モデル49,50,51))である。
前者における平行転位としては当然ながら主すべり系の転位を考えている。主すべり系の転位が障害物(2次すべり系転位との反応によって生じたLomer-Cottrell転位)に止められて堆積し(20~30本の程度),その堆積した転位がまとまって大きな内部応力(長範囲応力)を生み出し,その内部応力が後続の転位の運動を妨げる,というのがこのモデルの筋書きである。これに対して林立転位モデルでは,主すべり系の転位はすべり面に交差する転位(2次すべり系転位)に引っかかりながら運動すると考える。この交差を突き破るのに要する応力が変形応力である。その様子は,Fig.3で想像出来るかも知れない。この図で,各黒点の位置に林の木立のごとく2次すべり系転位が立っていると考えればよい。
これらのモデルに対して,実験的に,また理論的に多くの検討が加えられ,モデルの支持者の間で何年にも亘る論争があった。長範囲理論モデルに対するもっとも大きな批判点は,堆積転位群の作る内部応力の性質,とくにその方向性にあった。すなわち,Mitchell52)の計算によれば,この内部応力は主すべり系転位の運動を助ける方向には大きいが,その運動を妨げる方向には大きくないのである。このため,加工硬化の原因としてはこの内部応力は考え難い。他にもこのモデルに関しては,Lomer-Cottrell転位の障害物としての有効性や逆応力を加えたときの転位配列の安定性53),潜在硬化の解釈54),などについての疑問点がある。
林立転位モデルに対してもいくつか批判が加えられた。それには,林立転位との交差は相互作用エネルギーが小さいのでないか,そのためこの障害物では変形応力の温度依存性が大きくなってしまうのでないか,との疑問,また,林立転位となる2次すべり系の転位の密度は低く,十分の抵抗力は与えないのでないか,との疑問などがあった。しかし,現在ではこれらは計算見積もりや,電子顕微鏡による実測などによって,すべて問題なしとされている。結局,現在では,加工硬化における変形応力を与えるのは林立転位との交差による抵抗力である,との見方が研究者の間で広く受け入れられているようである55)。
5・3 モデルの定式化既に述べたように,加工硬化の問題は変形応力の問題と転位蓄積の問題に分けて考えることが出来る。そして変形応力の問題は結局,変形応力(τ)と転位密度(ρ)との関係に帰着する。これについては電子顕微鏡透過観察が始められてから実験的に求められるようになったが,その結果は次式の形56)にまとめられている。
| (10) |
ここにα1は0.5の程度の定数であり,bはバーガースベクトルの大きさ,Gは剛性率である。ただし,この場合の転位密度にはバーガースベクトルに依らず,全ての転位が含まれている。なお,同様な関係がCu単結晶についてエッチピット法によっても得られている57)。
次にこのような関係を林立転位モデルに従って求めてみる。いま,主すべり系の転位が林立転位に止められているとして,これを通過するときの仕事を考える。関係する転位セグメントの長さ(l)は林立転位の平均間隔の程度と考えられるので,林立転位の密度ρfとの間にρf=1/l2の関係がある。林立転位との交差部では短い反応転位(長さy)が作られており,この反応を解消して通過するためにはセグメントが距離xだけ移動する必要があるとする。その時のエネルギーのバランスは
| (11) |
となる。ただし,転位の単位長さあたりのエネルギーはGb2,印加応力(τ)により転位セグメント加えられる力はτblであることに注意する。この式から(10)式の形が得られることは容易に見て取れよう。しかし,得られた式では転位密度としてρではなくρfが入っていることに注意が必要である。
さて次のステップは転位蓄積の問題を解くことである。これは転位密度を塑性歪みの関数として導出することが目標となる。しかし,この問題に対しては,現在のところ,よい回答は得られていない。主すべり系転位の密度と塑性的剪断歪みとの間には,一応論理的なつながりを付けることができる45)。しかし,林立転位モデルで必要なのは二次すべり系転位の密度なのである。理論をさらに進めるためには,たとえばρとρfとの間に比例関係を仮定するといったことが必要となる。Kocks and Meckingの理論55)ではさらに進んで,ステージ3の定式化も行っているが,いくつかの調節可能なパラメータを含んだ形を使っているため,本質論は未解決のまま残されている。
(1)実験的研究
室温程度以下の低温において,fcc金属とbcc金属とで塑性的振る舞いに大きな違いがあることはよく知られている。fcc金属が低温まで延性的であるのに対して,bcc金属は低温で著しく硬くなり,また場合によっては脆性的になる。また,この事実が両者のパイエルス力の違いに起因することも,今や広く認められているところである。さらにbcc金属では結晶構造の特徴から,らせん転位に対するパイエルス力が大きいと考えられている58)。このような見方は電子顕微鏡観察の結果とも合致する。例えば,低温変形されたα-Feでの観察59)に依れば,刃状転位が少なく,らせん転位が圧倒的に多い。これはらせん転位が大きなパイエルス力のために動き難いのが原因である,と解釈できる。
パイエルス力はこのように低温強度を支配する因子として重要である。また,パイエルス力は結晶の凝集機構そのものに起因する抵抗力であるので,結晶構造の違いがその大きさに反映する。パイエルス力の大きい物質としてはbcc構造の金属のほかに,ダイアモンド構造のシリコン,ゲルマニウムなどもよく知られている。また,金属間化合物も概してパイエルス力が大きい。なお,パイエルス力が降伏を支配している場合,降伏応力の低温域での温度依存性が極めて大きくなるのが普通である。
実験的にはこれは,他の硬化要素(固溶硬化,加工硬化など)をすべて排除した状態で,単結晶の降伏応力として測定される。ただし,低温では脆性破壊とも競合するので注意が必要である。Kuramotoら60,61)はFeの単結晶で4.2 Kまでの降伏応力を測定しているが,破壊を避けるために細い試料を使っている。その測定では300 K以下の低温における降伏応力の急激な上昇が注目される。すなわち,この温度域がパイエルス力の支配域と言えるだろう。なお,この様にして測定された降伏応力を絶対零度まで外挿して得られるのがパイエルス応力であって,これは基本的な量として重要視される。
(2)理論的研究
パイエルス力は転位の運動抵抗力としてもっとも基本的なものであるので,転位研究の初期から関心が持たれてきた。これに関する転位論は一応二つに分ける事が出来る。その一つは言わば絶対値の問題であって,絶対零度における降伏応力(パイエルス応力)を求める問題であり,他の一つは降伏応力の温度依存性を求める問題である。前者に関する研究としてはPeierls62)とNabarro63)の先駆的研究がある。これは弾性論と原子論との巧みな組み合わせと言えるものであったが,その後も計算機を使った原子論的理論計算が数多くなされている。しかし,この絶対値の問題には結晶凝集力の定量という本質的に困難な問題が関係しているので,見通しは良くない。これに対して後者の温度依存性の問題に関しては成果がみられる。Dorn and Rajnak64)以来,転位論的モデルが種々検討されてきたが,それらの結果は互いにそれ程異なるものではない。概括的に言って,理論の結果はbcc金属の降伏応力の低温における温度依存性をかなり良く表現していると言えそうである。なお,これらの詳細に関しては,他の解説記事65,66)などを参照して頂きたい。
6・2 細粒硬化ほか一般に多結晶試料において,その結晶粒が小さくなれば試料強度は増加する。この硬化は次に示すHall-Petchの式67,68)で表すことができる。
| (12) |
ここにσyは降伏強度,σ0は摩擦力,kは定数,dは結晶粒の平均直径である。これは実験結果をまとめた表現であるが,式が発表されて以来長年に亘って研究や実用のための指針として使われてきた。しかし,最近,より微細な結晶粒の試料が製作されるようになって,少し事情が変化してきた。すなわち,強度は粒径低下と共にどこまでも増加するものではなく,上限があることが認められるようになった。つまり,1μm程度以下の微細粒の試料では上式の関係からの離脱が顕著になり,さらには逆に強度低下にまで至るのである。この問題は,微細粒試料の製作方法も含めて,現在盛んに研究がなされているところである。
上式の転位論的解釈については,いわゆる転位pile-upモデルが議論の中心となってきた。これは,一つの結晶粒の中の堆積転位列(pile-up)による応力集中が隣の結晶粒のすべりを誘発すると考え,その誘発条件が降伏応力を支配すると考えるモデルである。この場合,そこに必然的に結晶サイズが含まれ,上式が導かれる。これに対し,いくつか他のモデルも唱えられてきたが,最近では,言わば転位密度モデルとでも言うべきモデルが有力になっているようである。これは,結晶粒が小さいほど転位の密度増加が速く進み,この転位密度が降伏応力を支配するとする見方である。これは加工硬化と似た問題になる。これらの詳細は省略するが,最近,微細結晶粒材料に関する国際シンポジウム(Intern. Symp. of Strength of Fine Grained Materials,(2013年7月東京))が開かれたので,そのプロシーディングなどを参照して頂きたい。
材料強度の問題としては,以上の他にも議論すべきことが多い。例えば析出硬化や高温強度の問題などがあり,その他,疲労や破壊との関連,また,複合組織の強度など,重要な問題が残っている。しかし,本稿では紙数の制約もあるのでこれらには立ち入らない。
前章までは金属強度に関係する要素的過程を概観してきた。しかし,実用材料まで視野を広げるとき,これら基本的過程の理解だけでは処理できない問題も多いことが分かる。基本的過程を扱う場合には暗々裏に材料の均質性を仮定することが多いが,実用材料では概して組織が複雑で,強度の異なる相の複合となっている場合も多い。さらに高温低温と云った過酷な条件でのみ現れる特性が重要になる場合もある。本章では転位論の使われる範囲が,このような問題に拡大される場合を想定して,材料の局所的性質,特殊条件での性質,組織における個々の構成要素の性質などを明らかにするような研究手法を取り上げる。また,将来への夢を含んだ新しい手法の提案もいくつか行いたい。
7・1 ナノインデンテーション(1)微細組織の硬度測定
微細な組織の局所的力学挙動を調べる手法としてナノインデンテーションと呼ばれる手法がある。圧子型硬度計から発展した手法であるが,硬度だけでなく,荷重と押し込み深さとの関係を精度良く計測することが出来るので,局所的変形抵抗を測定する手法として極めて有用である69)。Fig.7にその圧痕の写真例を示した。圧痕はこのように1 μm以下と小さいので,この装置は普通走査プローブ顕微鏡(SPM)を組み込んだ形で使われる。まず,微細組織の硬度測定に使われた例から見ていく。

SPM image of a surface of Fe alloy after nanoindentation tests. Triangles are pits formed by the indenter.
硬度計としては,応力を加える領域が格段に小さいという特徴を活かした使い方が中心となる。筆者らはこれをFe-Cマルテンサイト鋼の強化機構解析70,71,72,73)に応用した。マルテンサイト組織中のブロックマトリクスの硬さ測定によって,ブロック境界が転位のすべり運動への障害として強化因子となることや,焼戻し軟化の過程においてセメンタイトの形態変化に起因して400 °Cに軟化曲線の遷移点があることなどを示した。また,SUS316鋼に応用した例74,75)では,長時間時効した材料の析出物とマトリクスの強度を分離評価し,M23C6やσ相などの単独強度を定量的に測定することに成功している。時効処理後の材料は,析出強化によってマクロ強度が上昇することは従来より知られていたが,マトリクス単独の強度は時効前よりも低下していることが示された。これは,析出過程を経てマトリクス中の固溶合金元素の濃度が低下したためと考察される。
(2)荷重−変位曲線
上に述べたように,ナノインデンテーションは従来の硬度計とは違って,荷重−変位の関係を精密に記録できる点が大きな特徴となっている。Fig.8にFe-Si合金において得られた荷重−変位曲線の例を示した。この図の中には破線矢印で示すように不連続点がみられるが,これはpop-inと呼ばれる現象である。Pop-inは,荷重制御モードで圧入変形を行う場合,負荷過程で変形抵抗が急激に低下してひずみバーストを起こす現象である。その機構についてはいくつか他のモデル76,77,78)も提案されているが,一般的に受け入れられているモデルは,これを転位の生成・増殖に起因する塑性変形の開始とみるモデル79)である。この見方の根拠の一つは,pop-in以前の荷重−変位関係が,Hertz接触の式80)に一致することである。このことはpop-in前の挙動において弾性変形が支配的であることを意味している。もう一つの重要な知見は,圧子下の最大せん断応力が,理想強度に近い極めて高い値を示すことである。圧入変形下における最大せん断応力τmaxは,同じくHertzの接触理論を用いて次式,
| (13) |

A typical load-displacement curve of Fe-Si alloy obtained by a nanoindentation test.
で与えられるが,荷重値Pとして,Fig.8より見積もられるpop-inの臨界荷重Pc=350 μNを代入すると,τmaxは約12 GPaと算出される。これは剛性率83 GPaの約1/7の極めて高い値である。なお,上式でRは圧子先端の曲率半径,E*は有効ヤング率である。
(3)Pop-in現象の利用
上に述べたように,pop-in現象が塑性変形開始に対応するとすれば,これを利用して,各種の材料で塑性変形開始応力を評価することが出来るだろう。一方,理論的には結晶の理想強度は剪断応力で表して,G/2πと求められている32)ので,これとの比較を試みる。ここにGは剛性率である。Fig.9は種々の純金属単結晶での測定結果をまとめたもので,pop-in荷重から求められる最大せん断応力τmaxを,除荷曲線から求められるヤング率から変換した剛性率Gに対してプロットしたものである81)。このようにτmaxはGと比例関係にあり,さらに,その値はG/2πに近い。この結果は,これらの材料での塑性変形が理想剪断強度に近い応力で開始することを示している。

Relation between the maximum shear stress τmax calculated from the Pc of the pop-in phenomena and the shear modulus G for various metals81).
Pop-in現象は材料強化機構の研究にもいろいろ利用されている。例えば,鉄中の固溶炭素の影響については,IF(interstitial-free)鋼と0.004 mass%の固溶炭素を含むULC(Ultra Low Carbon)鋼を比較した例がある82,83)。ULC鋼は初期転位密度が低い場合には高いpop-in荷重を示すのであるが,初期転位密度が高い場合にはpop-in荷重が著しく低下し,負荷曲線上に観察されなくなる。すなわち,高転位密度では,炭素による転位固着作用が抑制されるとも見える。更なる検討を要する問題である。鉄合金中の炭素の挙動については,室温時効の影響を調べた興味深い結果がある。すなわち,Ahnら84)はFe-C-Si-Mn合金において,引張変形6%の予ひずみを加えた試料で室温時効の効果を調べた。加工直後はpop-inが発生しない(pop-in荷重が低くて確認できない)のに対し,30時間の室温時効後にはpop-inが現れるようになり,さらに3週間後にはpop-in荷重が顕著に上昇することを示した。この結果は,塑性変形開始に対して,炭素による固着と考えられる静的ひずみ時効の効果が大きく影響することを示している。
(4)硬度計の改良(実験の提案)
ナノインデンテーションにおいては,圧子変位の精密制御という機能を付加することによって,得られる情報量が飛躍的に増えている。同様なことが従来型の硬度計でも行えないだろうか。ナノとの違いは荷重を加える領域のサイズだけであるが,大きくすることによって大域的な情報が得られるだろう。つまり,これにより通常の強度試験の荷重−伸び曲線に見合うものが得られるのではないだろうか。この方法は材料の(準)非破壊検査という大きな利点があるので,検討に値するかも知れない。
7・2 電子顕微鏡の関連技術(1)透過電子顕微鏡
電子顕微鏡の透過観察が開始された最初から,格子欠陥の同定に関心が持たれた。たとえば転位のバーガースベクトルを転位像の消滅条件から決定することや,積層欠陥の型をその像コントラストから決めること,などである。このようなことが可能なのは欠陥の像が回折効果に依存しているためである。この様な点についてはHirschらの著書17)に詳しい記述がある。その後の新しい観察法としてはweak beam法や多波構造像などがある。前者は結像に預かるブラッグ反射の回折条件をぎりぎりまで外すことによって,転位の像幅を小さくする方法である。また,多波構造像では対物絞りを広くして多数の反射を結像に関与させ,これによって格子像を得ている。このような観察法の工夫のほか,電子顕微鏡に別の装置を組み込むことも行われている。いわゆるその場(in situ)観察では,観察中の試料に力を加えたり,試料温度を変化させたりして,その応答を調べている。
観察による成果は枚挙に暇がないところであるが,とくにweak beam法について言えば,これは格子欠陥の微細構造の観察への寄与が大きい。例えば,拡張転位の幅の測定あるいは転位ノードの形状計測からの積層欠陥エネルギー決定85)がある。積層欠陥エネルギーの測定は現在でもこれが唯一の方法と言って良い。
また,最近のweak beamの応用として電子線トモグラフィーがある。これは関与する反射ベクトル(g)を変化させずに,gベクトルを軸として試料を回転させ,これにより転位配列などの3次元構造を観察する方法である。Barnardら86)はこの方法によって,GaN試料で転位配列の3次元的再構築に成功した。この方法ではgベクトルと垂直なバーガースベクトルを持つ転位は観察できない可能性があるが,さらに2軸傾斜トモグラフィーが提案されており,視野中の転位を網羅的に観察できることが示されている87)。
その場観察についでは最近の試みが少ないが,インデンテーション法と組み合わせた手法が注目される。Minorら88)はこの方法で,純Al中の転位生成を調べている。筆者ら89)は,微小なFe-Si単結晶をTEM内で圧縮変形させた実験を行い,動的像観察と同時に応力ひずみ関係を取得することに成功した。
電子顕微鏡はいまなお進歩しつつあり,分解能の向上も続いている。多波構造像を使えば,転位芯での原子配列の決定が可能となるかも知れない。このような方向の観察例としては,例えばシリコンでの拡張転位の観察90)があるが,原子配列が可成りの程度まで捉えられている。今後の発展を見守りたい。
(2)その場観察の可能性(実験の提案)
その場観察は今後さらに発展して欲しい技術であるが,高温あるいは低温と応力印加とを組み合わせた観察などは不可能だろうか。もしこれが出来れば,ある種の合金で見られる,高温での降伏強度の逆温度依存性の機構解明や,低温でのらせん転位と刃状転位の動き方の違いの把握など,いろいろ活躍の場がありそうに思われる。
(3)走査電子顕微鏡
走査電子顕微鏡は観察が試料表面に限られるという制約はあるが,非破壊的に観察出来るという利点がある。さらに,最近では電子線背面散乱(EBSD)装置を組み込むことによって,用途が大きく広がった91)。しかし現在のところ,この顕微鏡は組織観察には力を発揮しているものの,強化機構の問題への直接的寄与は少ないように思う。単結晶でこれを使えばすべり線や局所的格子回転のデータなどがたやすく得られるはずであるので,もっと活用の場があるのでないかと思われる。
7・3 X線回折と中性子線回折(1)X線トポグラフ法(実験の提案)
本稿の第1章に述べたように,転位観察の初期の頃にはX線トポグラフ法も活躍した。しかし,その後これが使われなくなってから久しい。その原因は分解能が低いと云う点の他に,従来のX線源からのX線では金属に対しては透過力が弱すぎるという点にもあったかも知れない。このためか合金での観察は殆どなされていない。筆者らは希薄Cu-Al合金単結晶の転位の応力下挙動を調べるために,AgKα線(波長0.056 nm)を使ったトポグラフ観察を試みたことがあるが92),ボルマン法(異常透過法)による観察だったため,十分なものとは言えなかった。しかし,今や大型放射光施設(SPring-8)ほかの放射光X線源が利用可能となっているので状況は異なる。もし,0.02 nm程度の短波長のX線を使うことができれば,1 mm程度の厚さの試料をラング法(通常の方法)で透過観察できるはずである。これは試みる価値があろう。
(2)X線回折による内部応力測定
X線回折の利用はいろいろあるが,ここでは話を内部応力の測定に限りたい。内部応力は材料強度を考える場合しばしば存在が仮定されるが,その実在を示すのはそれほど容易ではない。Mughrabiら93)はX線回折法の巧みな利用によって,引っ張り変形したCu単結晶における内部応力の測定に成功した。その様子をFig.10で説明する。この場合の内部応力は転位のセル構造に起因する。加工硬化した試料のなかにセル構造が生じていることは電子顕微鏡観察で示されているところであるが,これの加工硬化への寄与の仕方については明らかでない。セル構造ではセル壁とセル内部とでは転位密度が10倍程度異なるので,引っ張り変形したときに応答がかなり異なるはずである。すなわちセル壁が伸び難いのに対し,セル内部は変形しやすいと考えられる。従って,試料変形後,荷重を除去した状況では,セル壁は周囲からの拘束により引っ張り方向の内部応力を持つことになり,セル内部は逆に圧縮方向の内部応力を持つことになる。実験ではこのような応力による弾性歪みを格子面間隔の変化として捉えている。その結果から推定した内部応力は印加応力の3割(セル内部)にも及ぶ大きなものであった。彼らはさらに,この内部応力の加工硬化への寄与を議論しているが,その部分はまだ今後の検討が必要であろうと筆者には思える94)。詳細については当該論文を参照して頂きたい。

Schematic illustration of internal stresses in cell walls (shaded areas) and in cell interiors in the unloaded state after an elongation test. The large arrow represents the direction of the tensile axis. A tensile stress remains in a wall and a compressive one in an interior.
(3)中性子線回折による内部応力測定
中性子線は透過力が強いのでバルクの試料をそのまま調べ得ると云う利点がある。また,飛行時間法計測によれば,試料固定のまま波長分散(エネルギー分散)型の回折データを得ることが出来る。ただし,線源の利用はJ-PARCセンター(茨城県東海村)の中性子源(スパレーション・パルス型)などに限られる。
さて,本稿では前節に合わせて,話を内部応力測定に限ることにする。この場合の測定原理はX線回折と同じで,弾性歪みを格子面間隔の変化として捉えることである。これに関してはTomotaら95,96)により活発な研究が行われており,多結晶構造に起因する内部応力と複合組織に起因する内部応力の両方が調べられている。後者の場合の状況はFig.10に似ている。すなわち,硬い組織と軟らかい組織とが混在していて,それらの変形量に違いがあるときに内部応力が発生するのである。各種の複合組織が調べられたが,例えばパーライト鋼を引っ張り変形した場合97,98)では,フェライト相の塑性変形の開始後,塑性変形しないセメンタイト相との間で内部応力に応じた応力分配が発生する。測定結果には,試料変形の進行に伴って,これら二つの相で応力分配が発達する様子が明確に捉えられている。なお,このような観察に基づく組織強度の議論については原論文を参照して頂きたい。
以上,転位論と金属強度論について研究の歴史を辿りつつ,現時点での到達点を示そうと努めてきた。転位論は格子欠陥の理論としてはそれなりの発展を遂げ,一応の完成を見たと言えるかもしれないが,金属強度論としての部分はまだまだ力不足である。また,この方面の研究がここ数十年に亘って停滞しているように見えることも,研究者の一人として残念に思うところである。
停滞と見るかどうかは別にして,現時点での問題点を挙げれば,その一つは転位論の基礎部分における定量的評価の困難さであろう。例えば,転位の線エネルギー(線張力)の問題である。これは弾性論的に見積られているが,よく知られているように転位芯の打ち切り半径の曖昧さは避けようがない。弾性論の限界を克服するため,原子論的に二体ポテンシャルを使った計算もなされてきた。これは計算機の発達に呼応して,古く1960年代から行われているのであるが,これも正しい見積りを得るには至っていない。今後の第一原理計算の進展などを見守りたい。同様な定量性の問題は,パイエルス力の見積りや,転位と溶質原子との相互作用の見積りにもあるが,言わば同根の問題である。
他の問題点として,実際的な強度の問題で未解決の部分が多いことが挙げられよう。これは,反論のあることを承知で云えば,いままでの研究者の努力不足と言えるかも知れない。残念ながら,本稿でも記述が基礎的問題に偏った傾きがあったが,第7章などの記事が,多少なりとも今後の研究への刺激となればと願っている。