Effect of Flux Addition Method on Hot Metal Desulfurization by Mechanical Stirring Process

Synopsis:

Effect of a flux addition method on hot metal desulfurization by a mechanical stirring was investigated in a 1/12-water model and a 70 kg hot metal desulfurization tests. Following flux addition method was employed; top addition on bath surface at the first period of desulfurization, continuous addition from the top and powder blasting with nitrogen gas. Desulfurization rate of powder blasting is larger than continuous addition and top addition. The obtained aggregated slag (desulfurization flux) particle diameters after desulfurization were 0.76 mm (top addition) and 0.38~0.44 mm (powder blasting), respectively. Desulfurization behavior was analyzed assuming the interfacial area between the flux and the hot metal is proportional to the estimated aggregated slag particle size. Based on the analysis, the effect of powder blasting with nitrogen gas on improvement of desulfurization efficiency was interpreted to be the combined results of a) promotion of flux dispersion, avoiding aggregation at the time of flux addition and b) prevention of slag particle aggregation in hot metal during stirring.

1. 緒言

近年，鋼の高品質化への要求が高まるにつれ，鉄鋼材料の高特性化が進み，高純度化が要求されている。量産高級鋼での要求特性の高まりは，特に厚板，ラインパイプ材で顕著であり，特に，石油や天然ガスの開発，輸送に関連して使用される鋼材は，延性，低温靭性，溶接性，耐水素誘起割れ性などの特性において，厳しい仕様が要求されている。介在物として生成する硫化物は，鋼材の機械的性質に影響を及ぼす。例えば，MnSは熱間圧延の際に伸長されて鋼材の異方性を高めたり，腐食環境下では錆の起点として働くなどの悪影響を及ぼすため，硫黄濃度が0.001 mass%以下の極低硫化が必須である。このような溶接用材，ラインパイプ材などからの低硫化の要求に応える形で，いくつかの溶銑予備処理における溶銑脱硫方法が試行されてきたが，中でも機械撹拌による溶銑脱硫法は，撹拌羽根(インペラー)の回転という比較的簡便な方法で脱硫剤を効率良く溶銑中に巻込ませ，高効率な溶銑脱硫を行える方法として，工業化され，現在では各社で多く使用されている。

機械撹拌式の溶銑脱硫法としては，1966年に考案されたDemag-Ostberg(DORA)法¹⁾，1968年に考案されたRheinstahl法²⁾が挙げられる。国内では，Kanbaraら³⁾がKR法の開発によって短時間で0.003 mass%以下までの脱硫処理を行うことに成功している。この機械撹拌式脱硫法においても，脱硫反応効率向上を目的として従来から種々の研究開発が行われており^4,5,6,7)，脱硫剤に関する報告も多い。一方で，脱硫剤，および，発生スラグ原単位削減の観点から，さらなる脱硫反応の高効率化が望まれる。

筆者らはこれまでに，インペラー攪拌による粒子の基本的分散挙動について検討し，フラックスの分散促進とともに凝集抑制が重要であることを述べてきた^8,9)。本報では，脱硫剤，および，発生スラグ量削減のため，機械撹拌式脱硫法における更なる反応効率向上を目標に脱硫剤の添加方法が脱硫反応へ及ぼす影響について調査した。

溶銑脱硫の反応効率向上のためには，反応界面積確保が重要であり，そのため1 mm以下の脱硫剤を用いて処理を行っている。しかし，反応界面積を増大させるために，脱硫剤の更なる小径化を行った場合，上添加する際に脱硫剤添加時の飛散が増大する。飛散を防止しつつ，小径な脱硫剤を溶銑浴中へ添加させるための方法としては，溶銑中へのランスからのインジェクション添加，底吹き羽口からのインジェクション添加，上吹きランスからの投射添加などが考えられるが，インジェクション添加に関しては，設備的な負荷が高い。そこで，設備的に簡易な投射添加に着目し，その効果について検証を行うことにした。

本研究では，まず，水モデル実験によりフラックス添加時の凝集・分散挙動の観察を行った。さらに，高周波誘導溶解炉を用いた溶銑脱硫実験を行い，脱硫処理中におけるフラックス添加方法と溶銑脱硫反応との関係を調査した。また得られた脱硫剤の凝集現象を比較するために，造粒理論に基づく解析を行い，添加方法の違いによる脱硫促進のメカニズムを考察した。

2. 水モデル実験

2・1　実験方法

フラックス粒子の凝集・分散挙動を観察，検討するために濡れ性の悪い粉体(テフロン粒子)を用いた水モデル実験による観察を行った。

実験装置の概略図，および実験条件をそれぞれFig.1，Table 1に示す。相似条件は浮力と表面張力の比，およびWe(ウェーバー数:慣性力と表面張力の比)がホットモデルの条件と最も近い条件(We=4.3×10⁴/水モデル，We=5.6×10⁴/ホットモデル)でプラスチック粒子を選定した。また，投射時のガス流量は動圧近似とした。粒子添加量はフラックス容積近似とした。

Fig. 1.

 Schematic diagram of apparatus for water model experiment.

Table 1. Experimental conditions for water model experiment.

Vessel	Height	610 mm
	Diameter	350 mm
Water	Depth	280 mm
Impeller	Height	50 mm
	Diameter	160 mm
	Width	25 mm
	Rotation speed	275 rpm
	Immersion depth	120 mm
Flux addition method		①Batch addition ②Continuous addition ③Powder blasting
Continuous addition conditions	Addition rate	0.06 kg/min.
Powder blasting conditions	Addition rate	0.06 kg/min.
	Gas flow rate	75 Nl/min.
	Lance height	50 mm
Particle conditions	Diameter	φ0.12 mm
	Density	30 kg/m3
	Amount of particle	0.36 kg/ch

粉体の添加方法を，上添加での①一括添加と②連続添加，および，③ランスからの投射とした。一括添加の場合，添加時間は5秒，連続添加，および，投射添加による粉体添加速度は，0.06 kg/min.一定とした。それぞれの添加方法を用いた場合の粉体添加時の浴内への分散，および，粉体凝集挙動をビデオ撮影により確認した。

2・2　実験結果

水モデル実験にて，フラックス添加時の分散，凝集挙動の観察を行った。フラックス添加後の浴表面，および，正面方向からの観察結果をそれぞれFig.2 a)，b)に示す。Fig.2 a)より，フラックス添加後の浴表面の挙動を観察すると，一括添加では浴表面にて既に凝集がおこり，インペラー中心に向かって巻き込まれる挙動が観察された。連投の場合では一括添加の時ほど顕著ではないものの，浴表面で粒子が巻き込まれる際に一部凝集が起こる現象が観察された。

Fig. 2.

 Particle dispersion behaviors after flux addition in water model experiment: a) Surface of water, b) side view.

これに対し，投射では巻き込まれる際の凝集がほとんど観察されず，浴中に粒子が直接巻込まれていた。

また，Fig.2 b)より，一括添加では，粒子の凝集径が大きく，凝集肥大化した粒子が浴中を回転している現象が観察された。連続添加では，一括添加と比較すると，径の小さい粒子が，浴内に分散している様子が観察された。投射でも分散している粒子の径は小さく，回転攪拌中の浴内は白濁していた。

水モデル実験での観察結果から，フラックスの凝集は浴表面からインペラー中心に向かって巻き込まれる際に起こると考えられる。また，本水モデルの投射条件では浴中に粒子が直接添加されるため，巻き込まれる際の凝集がほとんどなく，浴中での分散径が小径化されることがわかった。

3. 溶銑脱硫実験

3・1　実験方法

高周波誘導溶解炉を用いた溶銑脱硫実験を行い，脱硫処理中におけるフラックス挙動と溶銑脱硫反応との関係を調査した。機械撹拌式溶銑脱硫処理の模式図をFig.3に，共通の実験条件をTable 2に示す。

Fig. 3.

 Schematic diagram of apparatus for 70 kg-scale hot metal experiments.

Table 2. Experimental conditions for 70 kg-scale hot metal experiments.

Furnace		150 kg IF φ250 mm
Metal	Chemical composition	Fe-4~5 mass%[C] -0.04 mass%[S]
	Weight	70 kg
	Depth	204 mm
Rotation speed		700 rpm
Impeller dimensions	Height	50 mm
	Diameter	100 mm
	Width	25 mm
Impeller immersion depth		150 mm
Temperature		1573 K
Flux		CaO, ≦250 μm 5 kg/t Al (0.3 kg/t)

150 kg高周波誘導炉(φ260×500 mmH)で溶銑70 kg(溶銑組成:4~5 mass%C-0.04 mass%S)を溶解し，所定の成分・温度に調整した後，黒鉛製インペラー(4枚羽根，幅100，高さ50 mm)を浸漬しモーターにより回転させる。インペラー浸漬深さは，溶銑の静止湯面からインペラー上面までの距離で定義し，100 mm一定とした。回転数は電圧により制御し，光学式回転数測定計で回転数を制御した。所定の回転数になったところで，フラックスを添加し，所定時間毎にメタルサンプリングを行うことにより脱硫挙動を調査した。

実験用フラックスは，石灰を用いた。いずれの実験条件においても石灰の粒径は，250 μm以下(平均粒径100 μm)とした。脱酸用に，アルミペレットを用い，フラックス添加前に上添加により溶銑中へ0.3 kg/t添加した。フラックス原単位は5 kg/t，実験(撹拌)時間は20分とし，脱硫実験後のスラグを回収した。

採取したスラグは0.5 mm以下，0.5~1.0 mm，1.0~2.8 mm，2.8~4.0 mm，4.0~4.75 mm，4.75~5.6 mm，5.6~6.3 mm，6.3~8.0 mm，8.0~9.5 mm，9.5~11.2 mm，11.2 mm以上，の11段階に篩い分けし，粒度分布を測定した。平均粒径は，(1)式¹⁰⁾により求めた。   

$$D_a=\frac{\sum _i\left(w_i\right)}{\sum _i\left(w_i/d_i\right)}$$(1)

ここで，D_a:平均粒径(mm)，d_i:それぞれの粒径範囲における平均粒子径(中央値)(mm)，w_i:それぞれの篩上のスラグ重量(kg)である。

フラックスの添加方法を，上添加での①一括添加と②連続添加，および，③ランスからの投射とした。実験水準をTable 3に示す。一括添加の場合，添加時間は5秒，連続添加によるフラックスの添加時間は，10分とした。

Table 3. Conditions of flux addition in 70 kg-scale hot metal experiments.

No.	Flux addition	Addition time	Powder blasting gas flow rate
A	Batch	5 s.	–
B	Continuous	10 min.	–
C	Powder blasting		200 Nl/min.
D			100 Nl/min.
E		3 min.	200 Nl/min.

投射添加時は，SUS管(φ4 mm)から窒素ガスをキャリアガスとして，フラックスを浴面に供給した。フラックスの供給時間は，フラックス添加開始から3分および10分とした。フラックス供給量は5 kg/tで一定であるので，フラックス供給速度がそれぞれ0.5，1.67，kg/min.tとなる。窒素ガス流量は，100 Nl/min.および200 Nl/min.の2条件で行った。投射ランス先端から静止状態での溶銑浴面までの距離は10 mmとした。

3・2　実験結果

3・2・1　脱硫挙動

フラックス添加条件を変化させた場合の実験A~Cにおける実験中[S]の経時変化をFig.4に示す。また，各時間における[S]を処理前S濃度([S]i)で除した値 [S]/[S]_iの経時変化をFig.5に示す。脱硫速度は，C:投射，B:連続添加，A:一括添加の順に大きい結果であった。Fig.5から，実験A~Cでの脱硫速度を比較すると，処理時間12分程度までの違いが顕著であった。

Fig. 4.

 Desulfurization behaviors in hot metal experiments (condition A, B and C).

Fig. 5.

 Changes of [S]/[S]_i in hot metal experiments (condition A, B and C).

さらに，投射添加において，投射の条件を変えた実験C~Eにおける実験中の[S]，[S]/[S]_iの経時変化をFig.6，7に示す。Fig.7から，添加時の脱硫速度は，3分間で投射した場合が一番大きかったが，添加後の脱硫速度は停滞していた。投射時間を10分間と同じとした場合でも，ガス流量の少ない実験Dでは，脱硫速度の増加は少なく，投射ガス流量の影響があることがわかった。

Fig. 6.

 Desulfurization behaviors in hot metal experiments (condition C, D and E).

Fig. 7.

 Changes of [S]/[S]_i in hot metal experiments (condition C, D and E).

3・2・2　スラグ粒径変化

脱硫処理後(20分)のスラグを回収し，粒度分布測定を行った。ラボ実験において採取されたスラグ外観の一例として，実験A(原単位:5 kg/t，一括添加)の条件において，20分処理後に採取したスラグの外観をFig.8に示す。添加したフラックスの初期粒径は250 μm以下であるが，処理後は，粒径が数mmのスラグが多く存在していることがわかる。実験A~Cにおいて，スラグを篩い分けして得られたスラグ粒度分布をFig.9に示す。A:一括添加と比較して，B:連続添加，C:投射の場合は，1 mm以下のスラグの比率が高いことがわかる。

Fig. 8.

 Photograph of appearance of desulfurization slag after treatment (condition A).

Fig. 9.

 Changes of particle size distribution in hot metal experiments (condition A, B and C).

算出された平均スラグ粒径をFig.10にまとめて示す。A:一括添加の場合の脱硫処理後の平均スラグ粒径が0.76 mmであったのに対し，B:連続添加，C~E:投射添加の場合の処理後スラグは，いずれもそれより小さい。Fig.10から，B:連続添加，C:投射添加の場合のスラグ粒径は同等であるが，脱硫挙動，特に実験初期10分までの脱硫速度，到達[S]が異なる。従って，B，Cによる脱硫挙動の違いは処理後の脱硫スラグ粒径だけでは説明出来ない。そこで，フラックス添加後の凝集挙動を推定し，脱硫反応界面積を評価することにより，フラックス添加条件による脱硫挙動の違いを以下に考察する。

Fig. 10.

 Average particle diameters of slag after treatment.

4. 考察

4・1　凝集粒径の推定

実験後のスラグ粒径は同じであっても，処理中の凝集挙動が異なり，それが脱硫挙動に影響を与えている可能性がある。そこで，前報⁹⁾にて導出したフラックスの凝集モデルを用いて，このフラックス添加方法を変化させた場合の凝集挙動を評価することとした。

液体中の粉体分散と凝集現象に関しては，粉体粒子間のポテンシャルエネルギーと距離の関数で表され，凝集による単分散粒子の変化は，2分子反応の式で表されるとされている¹¹⁾。すなわち，時間t後の単位体積中の粒子数をγとし，凝集速度定数をk_aとすると，凝集による単分散粒子の変化は，(1)式で示すような2分子反応の式で表される。   

$$\frac{d\gamma }{dt}=k_a\cdot {\left(\gamma -{\gamma }_e\right)}^2$$(2)

ここで，γ:溶液の単位体積中の粒子個数(population density)(−)，γ_e:平衡状態における粒子個数(−)，k_a:凝集速度定数(m³/s)，t:時間(s)である。

初期条件として，t=0の時，γ=γ_fとして，(2)式を積分すると(3)式になる。ここで，γ_f:初期の粒子個数(−)である。   

$$\gamma ={\gamma }_e+\frac{1}{k_a\cdot t+\frac{1}{\left({\gamma }_f-{\gamma }_e\right)}}$$(3)

また，Takenakaら¹²⁾は，湿式球形造粒における造粒速度式から(4)式を求めている。   

$$\gamma =\frac{W_f}{\frac{\sum \left(\pi /6\right)\cdot D^3{\rho }_f{\left(1-\epsilon \right)}^n}{\sum n}}\times \frac{1}{V_m}$$(4)

ここで，n:粒径Dの粒子個数(−)，W_f:造粒体の総重量(kg)，V_m:懸濁液の体積(m³)，ε:造粒粒子の空隙率(−)，ρ_f:粒子密度(kg/m³)である。

(4)式において，粒子形状を一定と仮定すると，粒子個数は(5)式で示され，平衡状態における粒子個数γ_e，初期の粒子個数γ_fは，それぞれ(6)，(7)式となる。   

$$\gamma =\frac{W_f}{\left(\pi /6\right)\cdot D^3{\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}$$(5)

  

$${\gamma }_e=\frac{W_f}{\left(\pi /6\right)\cdot D_e{}^3{\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}$$(6)

  

$${\gamma }_f=\frac{W_f}{\left(\pi /6\right)\cdot D_f{}^3{\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}$$(7)

ここで，D_f:添加粒子の初期粒子径(m)，D_e:添加粒子の平衡粒子径(m)である。

さらに，フラックスを連続添加した場合では，先に添加したフラックス凝集体と，新たに添加したフラックスが反応に寄与することとなる。時間tにおいて新たに添加された粒子個数γ_fnew(t)は，(8)式で示され，時間tにおける初期粒子個数γ_f(t)は，時間tまでに添加されたフラックスの凝集後の個数γ_(t–1)と新たに添加された粒子個数γ_fnew(t)との和であると定義することにより(9)式で示される。   

$${\gamma }_{fnew\left(t\right)}=\frac{W_{fnew\left(t\right)}}{\left(\pi /6\right)\cdot D_f{}^3{\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}$$(8)

  

$${\gamma }_{f\left(t\right)}={\gamma }_{\left(t-1\right)}+{\gamma }_{fnew\left(t\right)}$$(9)

よって，(3)式から時間tにおける粒子個数γ_(t)は，(10)式で表される。   

$$\begin{array}{c}{\gamma }_{\left(t\right)}={\gamma }_{f\left(t-1\right)}+{\gamma }_{fnew\left(t\right)}\\ ={\gamma }_e+\frac{1}{k_a\cdot t+\frac{1}{\left({\gamma }_{f\left(t-1\right)}-{\gamma }_e\right)}}+{\gamma }_{fnew\left(t\right)}\end{array}$$(10)

ここで，γ_fnew(t):時間tにおいて新たに添加されたフラックス粒子の個数(−)，W_fnew(t):時間tにおいて新たに添加されたフラックス量(kg)，γ_f(t):時間tにおける初期粒子個数(−)，γ_(t):時間tにおける粒子個数(−)である。

さらに，平衡粒子径D_eは，造粒体を構成する粒子間の凝集力，すなわち保形力と外部から造粒体に加わる破壊力とのつりあいによって決まる。Capes and Sutherland¹³⁾は，湿式造粒の系においては，保形力ならびに破壊力は，それぞれ，造粒体の圧漬強度ならびに，攪拌による遠心力に比例すると考えた。Newitt and Conway-Jones¹⁴⁾は造粒体の圧漬強度を示す式を表しており，この圧漬強度と遠心力がつりあう状態が平衡状態であるとすると(11)式が成り立つ。(11)式を展開して，(6)式における造粒体の平衡粒子径D_eは，(12)式で表される。   

$$K\left(\frac{1-\epsilon }{\epsilon }\right)\frac{\tau }{D_f}{D}_e{}^2=\frac{4}{3}{\rho }_f\left(1-\epsilon \right)\pi \cdot {\left(\frac{D_e}{2}\right)}^3\cdot r{\omega }^2$$(11)

  

$$D_e=\frac{6K}{\pi {\rho }_f\left(1-\epsilon \right)r{\omega }^2}\left(\frac{1-\epsilon }{\epsilon }\right)\frac{\tau }{D_f}$$(12)

ここで，K:造粒条件によって決まる定数，τ:表面張力(N/m)，r:回転半径(m)，ω:角速度(rad/s)である。

回転数700 rpmで30分間撹拌を行った後のスラグ平均粒径は，1.75 mmであった。これを平衡粒子径と仮定して，(11)式の定数Kを求めると，K=0.0598が得られた。この値を本実験における定数Kとして用いることとした。

(5)式から，時間tにおける凝集体の粒径D_(t)は，(13)式で示される。   

$$D_{\left(t\right)}={\left\{\frac{W_{f\left(t\right)}}{\left(\pi /6\right)\cdot {\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}\cdot \frac{1}{{\gamma }_{\left(t\right)}}\right\}}^{\frac{1}{3}}$$(13)

(13)式のγ_(t)に(10)式を代入すると，(14)式が得られる。   

$$D_{\left(t\right)}={\left\{\frac{W_{f\left(t\right)}}{\left(\pi /6\right)\cdot {\rho }_f\left(1-\epsilon \right)}\times \frac{1}{V_m}\cdot \frac{1}{{\gamma }_e+\frac{1}{k_a\cdot t+\frac{1}{\left(\gamma {f\left(t-1\right)}_{}-\gamma e_{}\right)}}+{\gamma }_{fnew\left(t\right)}}\right\}}^{\frac{1}{3}}$$(14)

ここで，W_f(t):時間tまでに添加されたフラックス量(kg)である。

(14)式のγ_fnew(t)，γ_f(t–1)は(8)，(9)式から求め，γ_eに(6)式を代入し，実験条件から，W_f=0.35 kg，V_m=0.01 m³，D_f=1.0×10⁻⁴ mとした。さらに，Iwaseらの結果¹⁵⁾から，粉体の真密度を3000 kg/m³，かさ密度を1300 kg/m³として，空隙率ε=0.567とした。

各実験後に得られたスラグ凝集粒子径に(14)式をフィッティングすることにより凝集速度定数k_aを求めた。各条件にて求められた凝集速度定数k_aをTable 4に，本凝集モデルにて得られたスラグ粒径の計算値を実績値とあわせてFig.11に示す。

Table 4. Obtained aggregation rate constant, k_a, and average particle diameter of slag after treatments.

No.	Flux addition	Addition time	Powder blasting gas flow rate	Average particle diameter of slag after treatment	Aggregation rate constant, ka
			Nl/min.	mm	m3/s
A	Batch	5 s.	–	0.76	7.13×10–12
B	Continuous	10 min.	–	0.39	1.76×10–12
C	Powder blasting		200	0.38	1.62×10–12
D			100	0.38	1.62×10–12
E		3 min.	200	0.44	1.57×10–12

Fig. 11.

 Changes of average particle diameter of slag (condition A, B, C and E).

Table 4から，一括添加の場合と比較して，連続添加，投射の場合には凝集速度定数が減少しており，凝集しにくい状態であったといえる。また，投射添加C~Eにおける凝集速度定数はほぼ同じであり，凝集の度合いは，添加方法により依存していると推定される。

Fig.11から，平均粒子径の経時変化をみると，実験A:一括添加の場合には，時間経過に伴い粒径が増加していくのに対して，実験B:連続添加や実験C，D:投射の場合には，フラックス添加中とフラックス添加後での粒径の増加度合いが異なり，屈曲点が生じている。実験B~Dでは，フラックス添加中の粒径増加は少なく，添加終了後に凝集が進行していると考えられる。

フラックス添加時間を実験E:3分，実験C:10分と変化させた場合，フラックス添加後の処理時間が異なり，3分で添加した実験Eでは，10分で添加した実験B，Cよりもフラックス添加後の攪拌時間が長いため，処理後の粒径が大きくなったものと考えられる。つまり，連続添加による単位時間あたりの添加量とフラックス添加後の攪拌時間の長さの違いが，スラグ粒径の経時変化とスラグの最終粒径の違いとなっていると推定された。このスラグ粒径の経時変化の違いにより，脱硫挙動の違いを説明できるかを次章にて検証する。

4・2　凝集粒子径を考慮した脱硫挙動

上記で求めたスラグ粒径の経時変化を用いて反応界面積を求めることにより，脱硫挙動を推定することとした。脱硫反応が溶鉄側境膜内物質移動律速であると仮定して，(15)式の脱硫反応速度式⁴⁾で評価を行った。   

$$-\frac{d\left[S\right]}{dt}=K_S\cdot \left[S\right]$$(15)

ここで，K_s:見かけの脱硫反応速度定数(1/min.)，[S]:溶銑中S濃度(mass %)，t:時間(min.)である。

この脱硫反応式に，フラックスの凝集による反応界面積変化を考慮することとする。(15)式において，見かけの脱硫速度定数は，反応界面積と，物質移動係数，および，溶銑体積で示すことができ，(16)式となる。(16)式において，反応界面積A(m²)が，凝集した粒子径D_(t)の粒子がn個存在する時の総表面積であると仮定する。   

$$\begin{array}{c}-\frac{d\left[S\right]}{dt}=K_S\cdot \left[S\right]\\ =\frac{A{k}_m}{V_m}\cdot \left[S\right]\\ =\frac{A{k}_m\cdot {\rho }_m}{W_m}\cdot \left[S\right]\end{array}$$(16)

フラックスの体積V_f(m³)，表面積A(m²)は，それぞれ(17)，(18)式で示される。ここでV_m:溶銑体積(m³)，W_m:溶銑重量(70 kg)，W_f:フラックス重量(kg)，ρ_m:溶銑密度(7000 kg/m³)，ρ_f:フラックス密度(3000 kg/m³)である。   

$$V_f=\frac{4}{3}\pi \cdot {\left(\frac{D_{\left(t\right)}}{2}\right)}^3\times n=\frac{W_f}{{\rho }_f}$$(17)

  

$$A=4\pi \cdot {\left(\frac{D\left(t\right)}{2}\right)}^2\times n$$(18)

(17)(18)式をnについて解くと，反応界面積Aは，(19)式で表される。   

$$A=3\times W_f\cdot \frac{1}{{\rho }_f\cdot \left(D_{\left(t\right)}/2\right)}$$(19)

(16)式から，時間tにおける[S]推定式は，(20)式で表される。(20)式中の反応界面積Aに(19)式を代入し，(19)式中の粒子径D_(t)に，(14)式で算出した粒子径D_(t)を代入することにより，[S]挙動を推定した。   

$${\left[S\right]}_{\left(t\right)}={\left[S\right]}_{\left(t-1\right)}\cdot \exp \left(-\frac{A\cdot k_m}{V_m}\cdot \Delta t\right)$$(20)

ここで，物質移動係数k_mは，実験A(一括添加，フラックス原単位:5 kg/t，700 rpm)で得られた脱硫挙動にフィッティングして求めた。得られた物質移動係数k_mは3.3×10⁻⁴ m/min.であり，従来の研究^16,17,18)の値よりもやや小さいものであった。この物質移動係数k_m=3.3×10⁻⁴ m/min.を(20)式に用いて，脱硫挙動を推定した。

(20)式から求めた脱硫挙動を実験結果とあわせて，Fig.12，Fig.13に示す。Fig.12より，添加方法の違いによる脱硫挙動を比較すると，A:一括添加とB:連続添加の場合には，モデルによる推定挙動と実績挙動がよく一致している。A:一括添加の場合には，Fig.11にて示したように添加したスラグ粒径が時間と共に凝集し，スラグ粒径が大きくなっていくため，時間と共に反応界面積が減少し，[S]の減少速度が時間と共に低下している。B:連続添加の場合には，フラックス添加初期(3分程度まで)は，添加されたフラックス量が少ないため，一括添加と比較して脱硫速度が遅いが，スラグ粒径は小さく，この凝集抑制による界面積増加の効果により，一括添加よりも到達[S]が低下したと考えられる。Fig.11にて示されたフラックス添加後(10分以降)のスラグ粒径の増加により，10分以降に実績値の脱硫速度が低下した挙動をうまく再現できている。一方，C:投射添加の場合は，推定挙動よりも実績の[S]が低く推移しており，特に，フラックス添加区間における乖離が大きい。このことから，投射添加においては，連続添加による凝集抑制，界面積増加効果だけでなく，添加中の脱硫反応が促進されている可能性がある。

Fig. 12.

 Comparison between observed and calculated desulfurization behaviors (condition A, B and C).

Fig. 13.

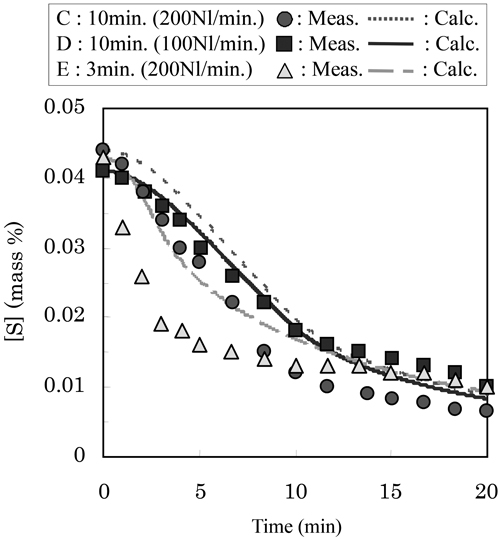
 Comparison between observed and calculated desulfurization behaviors in conditions of powder blasting (condition C, D and E).

Fig.13に実験C，D，Eにおける実験値，計算値の比較を示す。投射用の窒素ガス流量を100 Nl/min.と低下させた実験Dにおいては，実験値と計算値がよく一致している。これは，窒素ガス流量が小さいため，投射の効果が小さく，B:連続添加と同じ挙動となるため，フラックス連続供給による凝集抑制効果のみが発現していると考えられる。一方で，投射の窒素ガス流量を200 Nl/min.とした実験C，Dでは，いずれの場合もフラックス添加区間における推定挙動と実績の乖離が大きい。窒素ガス流量200 Nl/min.で投射添加を行った場合では，添加フラックスが，直接，粒径の小さい状態で溶銑浴内に進入し，フラックス添加時の脱硫促進に影響を及ぼしたものと考えられる。

そこでフラックス初期粒径を変化させ，実験C，Dにおける実験値と計算値の一致を確認した。その結果をFig.14に示す。フラックス初期粒径を30 μmとした場合に実験結果に近い脱硫挙動が得られた。フラックス初期粒径100，30 μmのケースにおける処理中のスラグ凝集径の変化をFig.15に示す。フラックス添加中の凝集径減少が顕著である。投射用の窒素ガス流量を200 Nl/minとした場合では，初期粒径30 μm以下の小径フラックスが反応に有効に寄与し，フラックス添加中のみかけの反応界面積が増加した効果によりフラックス添加中の脱硫速度が増加したと考えられるが，厳密にいえば，平均粒径100 μmのフラックスの初期粒径を平均30 μmと考えるのは不適当である。総合的に考えると，反応界面積増加以外の寄与もあった可能性があり，その要因解明については今後の検討課題としたい。

Fig. 14.

 Comparison between observed and calculated desulfurization behaviors (condition C and E).

Fig. 15.

 Changes of average particle diameter of slag in conditions of powder blasting (condition C and E).

4・3　投射添加による脱硫促進のメカニズム

以上の実験結果から，投射添加により脱硫が促進したメカニズムについて考察する。

水モデル実験，および，溶銑脱硫実験の結果と，凝集モデルから求めた脱硫挙動との比較から考えられる，一括添加/連続添加/投射添加によるフラックス分散・凝集挙動，および，実験後スラグの模式図を，実験後のスラグのEPMA観察を行って得られたSマッピング像とともにFig.16に示す。

Fig. 16.

 (a) Schematic diagrams of flux dispersion and aggregation mechanisms and (b) Sulfur mappings in desulfurization slag after treatment.

実験後のスラグのEPMA観察を行って得られたSマッピングから，いずれの場合もスラグ粒子の周辺部には，Sが分布していることがわかる。また，Fig.11に示したスラグ粒径分布測定からも明らかなようにa)一括添加と比較して，b)連続添加，c)投射添加のスラグ粒径は小径化している。b)連投添加，c)投射添加の場合には，凝集したスラグ粒子の内部に，粒子の周辺部にSが分布している小径のスラグ粒子が存在しており，処理初期の凝集粒子径が小さかった可能性を示唆している。c)投射添加のスラグ中には，S濃度の高い部分が比較的多く存在しており，フラックス添加時に小径のまま脱硫反応に寄与したフラックスが，凝集したスラグ粒子中に存在していると思われる。

以上の考察から，一括添加では，添加されたフラックスは，浴内へ巻き込まれる際に凝集していると考えられる。一方，フラックスを連続添加することにより，添加速度が減少し，添加されたフラックスの凝集が抑制される。この効果により，連続添加，投射添加においては，凝集速度が低下，脱硫処理後のスラグ粒径が小径化したものと考えられる。さらに，投射添加においては，投射時に溶銑浴中へ直接進入するフラックスがあり，添加直後の反応界面積が増加しており，これがフラックス添加中の脱硫促進に寄与していると考えられる。よって，機械撹拌式溶銑脱硫での投射添加の場合に脱硫効率が向上したメカニズムは，フラックス添加時の分散促進と連続添加による単位時間あたりの添加量の減少に伴う凝集抑制効果によるものと推定された。

5. 結言

機械撹拌式溶銑脱硫法における脱硫反応に及ぼすフラックス添加方法の影響について，水モデル実験によりフラックス添加時の凝集・分散挙動の観察を行った。また，高周波誘導溶解炉を用いた溶銑脱硫実験を実施し，脱硫処理中におけるフラックス添加方法と溶銑脱硫反応との関係を調査し，得られた脱硫剤の凝集現象を比較するために，造粒理論に基づく解析を行い，添加方法の違いによる脱硫促進のメカニズムについて考察した。

1)水モデル実験にて，フラックス添加時の凝集・分散挙動を観察した結果，一括添加では浴表面にて凝集がおこり，凝集径の大きな粒子が浴中に存在していた。一方で，投射添加では浴中に粒子が直接添加されるため，巻き込まれる際の凝集がほとんどなく，浴中での分散径が小径化された。

2)脱硫速度は，投射添加，連続添加，一括添加の順に大きい。連続添加，および，投射添加において得られたスラグ粒径は，一括添加の場合よりも小径であり，凝集したスラグ粒子の内部に，粒子の周辺部にSが分布している小径のスラグ粒子が存在しており，処理初期の凝集粒子径が小さい可能性を示唆していた。

3)フラックス凝集現象を造粒理論に基づき，凝集速度定数を用いて評価した。一括添加の場合と比較して，連続添加，投射の場合には凝集速度定数が減少していた。投射条件を変えた場合でも凝集速度定数はほぼ同じであり，凝集の度合いは，添加方法に依存していると推定された。

4)この凝集による反応界面積変化を考慮し，推定した脱硫挙動は，実績とよく一致しており連続添加の優位性を確認できた。投射ガス流量が多く，投射時間が長い条件の投射添加では，高い脱硫効率が得られており，フラックス初期粒径を30 μmとした場合に実験結果に近い脱硫挙動が得られた。

5)機械撹拌式溶銑脱硫において，投射添加を行うことにより，脱硫効率が向上した。これは，フラックス添加時の分散促進と連続添加による単位時間あたりの添加量の減少に伴う凝集抑制効果によるものであると推定される。

記 号

A:Interfacial area (m²)

D:Aggregated particle diameter (m)

D_a:Average size (mm)

D_e:Aggregated particle diameter in equilibrium state (m)

D_f:Initial added particle diameter (flux diameter) (m)

d_i:Particle size of slag (mm)

K:Constant depend on condition of granulation (–)

K_s:Apparent desulfurization rate constant (1/min)

k_a:Aggregation rate constant (m³/s)

k_m:Mass transfer rate (m/s)

n:Number of particles whose diameter is D (–)

r:Radius of impeller (m)

[S]:Sulfur content in hot metal (mass %)

t:Time (second)

V_f:Flux volume (m³)

V_m:Volume of particle dispersed liquid (hot metal) (m³)

W_f:Total weight of granulates (flux) (kg)

W_m:Hot metal weight (kg)

w_i:Weight of each size distribution (kg)

γ:Number of particles in unit volume of liquid (–)

γ_e:Number of particles in equilibrium state (–)

γ_f:Initial number of particles (–)

ε:Void ratio in aggregated particles (–)

ρ_f:Particle (flux) density (kg/m³)

ρ_m:Liquid (hot metal) density (kg/m³)

τ:surface tension (N/m)

ω:Angular velocity of impeller rotation (rad/s)

文献

• 1)   J.E.  Ostberg: Giesserei, 53(1966), 816.
• 2)   F.  Kraemer,  J.  Mots and  K.  Rohrig: Giesserei, 55(1968), 145
• 3)   K.  Kanbara,  T.  Nisugi,  O.  Shiraishi, and  T.  Hatakeyama: Tetsu-to-Hagané, 58(1972), 34.
• 4)   K.  Nakanishi,  N.  Bessho,  S.  Takada,  A.  Ejima,  M.  Kuga,  J.  Katsuki and  M.  Kawana: Tetsu-to-Hagané, 64(1978), 1528.
• 5)   N.  Kurokawa,  S.  Matsuo,  H.  Jouguchi,  K.  Yamada and  Y.  Watanabe: Sumitomo Met., 45(1993), 52.
• 6)   N.  Kikuchi,  S.  Nabeshima,  S.  Takeuchi,  T.  Yamauchi,  Y.  Kitano and  S.  Ogura: Tetsu-to-Hagané, 90(2004), 322.
• 7)   N.  Kikuchi,  S.  Nabeshima and  Y.  Kishimoto: ISIJ Int., 52(2012), 1809.
• 8)   Y.  Nakai,  I.  Sumi,  H.  Matsuno,  N.  Kikuchi and  Y.  Kishimoto: ISIJ Int., 50(2010), 403.
• 9)   Y.  Nakai,  I.  Sumi,  N.  Kikuchi,  Y.  Kishimoto and  Y.  Miki: ISIJ Int., 53(2013), 1411.
• 10)  溝口勲夫:粉体工学便覧第2版，粉体工学会編，日刊工業新聞社，東京，(1998), 8.
• 11)  小石真純，角田光雄:粉体の表面化学第3版，日刊工業新聞社，東京，(1978), 188.
• 12)   H.  Takenaka,  Y.  Kawashima and  M.  Nakashima: J. Soc. Mater. Sci. Jpn., 28(1979), 836.
• 13)   C.E.  Capes and  J.P.  Sutherland: Ind. Eng. Chem., 6(1967), 146
• 14)   D.M.  Newwitt and  J.M.  Conway-Jones: Trans. Inst. Chem. Eng., 36(1958), 422
• 15)   M.  Iwasa,  Y.  Hino,  Y.  Nakai,  I.  Sumi,  N.  Kikuchi,  S.  Nabeshima and  Y.  Kishimoto: The 4th Int. Cong. on the Science and Technology of Steelmaking (ICS 2008), ISIJ, Tokyo, (2008), 288.
• 16)   K.  Nakanishi,  A.  Ejima,  T.  Suzuki and  A.  Sudo: Tetsu-to-Hagané, 64(1978), 1323.
• 17)   K.  Narita,  Y.  Satoh,  T.  Mori,  T.  Ito and  A.  Kujime: Tetsu-to-Hagané, 62 (1976), 962.
• 18)   H.  Ooi,  Y.  Oguti and  H.  Minami: Tetsu-to-Hagané, 56 (1970), 991.